Study of the Performance of Deep Learning-Based Channel Equalization for Indoor Visible Light Communication Systems
Abstract
:1. Introduction
- (1)
- The overall network architecture is constructed by imitating the existing communication signal processing algorithm rather than treated as a black box without any expert knowledge. In addition, the initialization input of the network also contains the traditional solution instead of random numbers.
- (2)
- The refining layer with the simple Signum function is applied to the network output, which can refine the coarse bit stream and can improve the detection accuracy of the network.
- (3)
- The proposed scheme can still provide an excellent equalization performance even under cyclic prefix (CP) removal, which outperforms the traditional equalizers and demonstrates its powerful self-study and robustness ability of the DL approach.
2. System Model
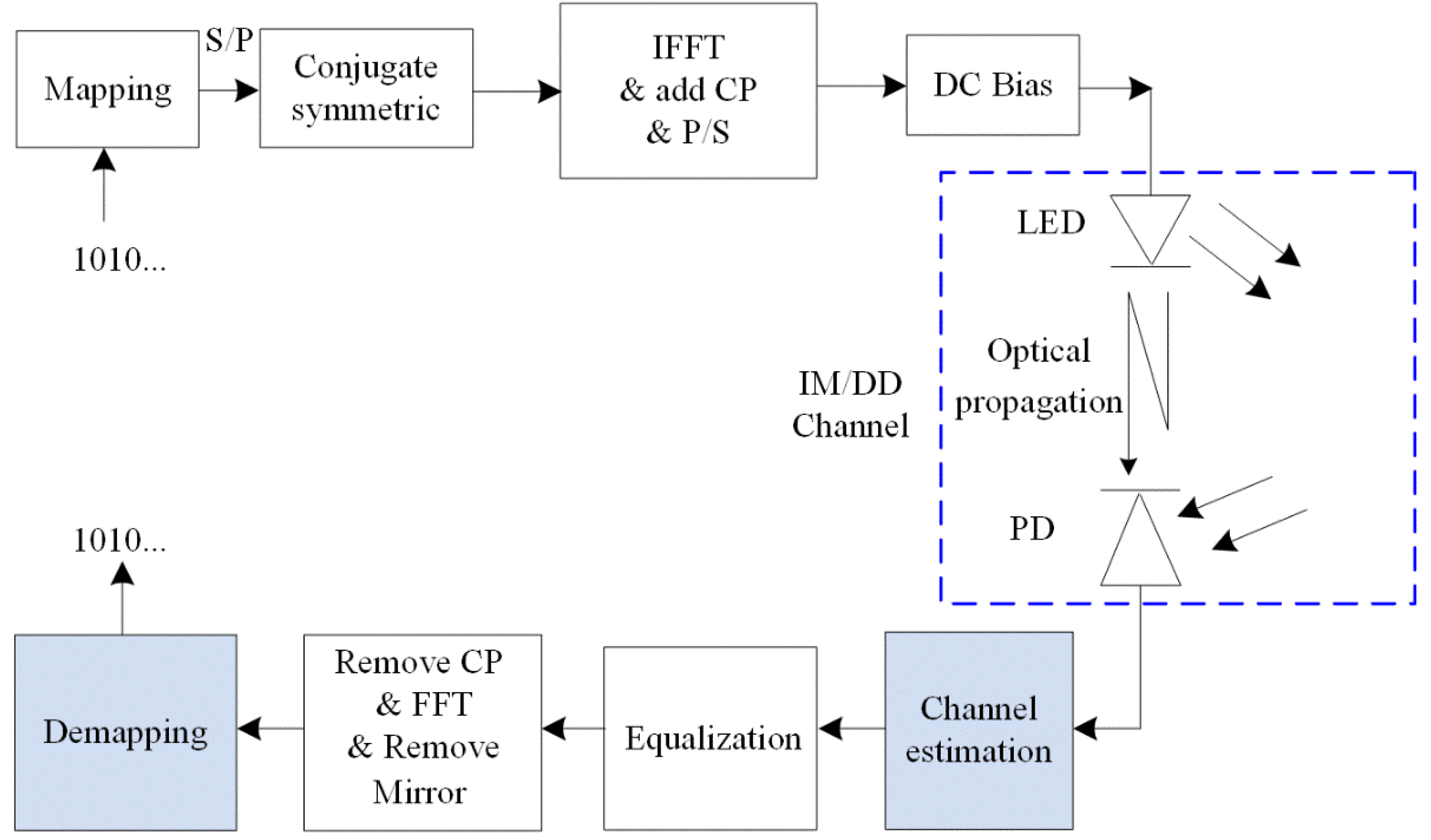
2.1. OFDM-Based VLC System
2.2. Inherent Impairment of an IM/DD Channel
3. The Proposed Scheme
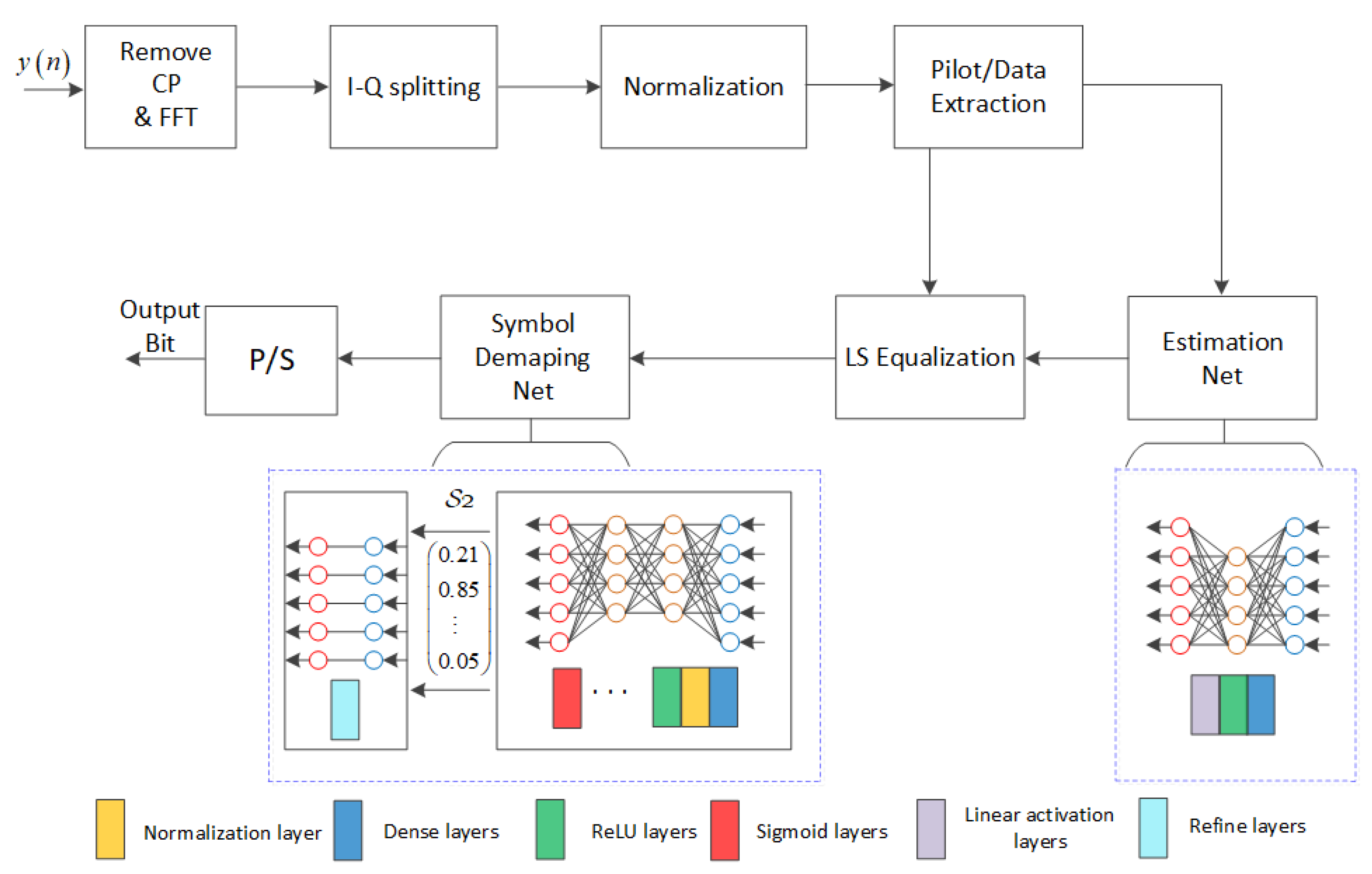
3.1. System Architecture
3.2. Training Specification
3.3. Complexity Analysis
4. Simulation Results
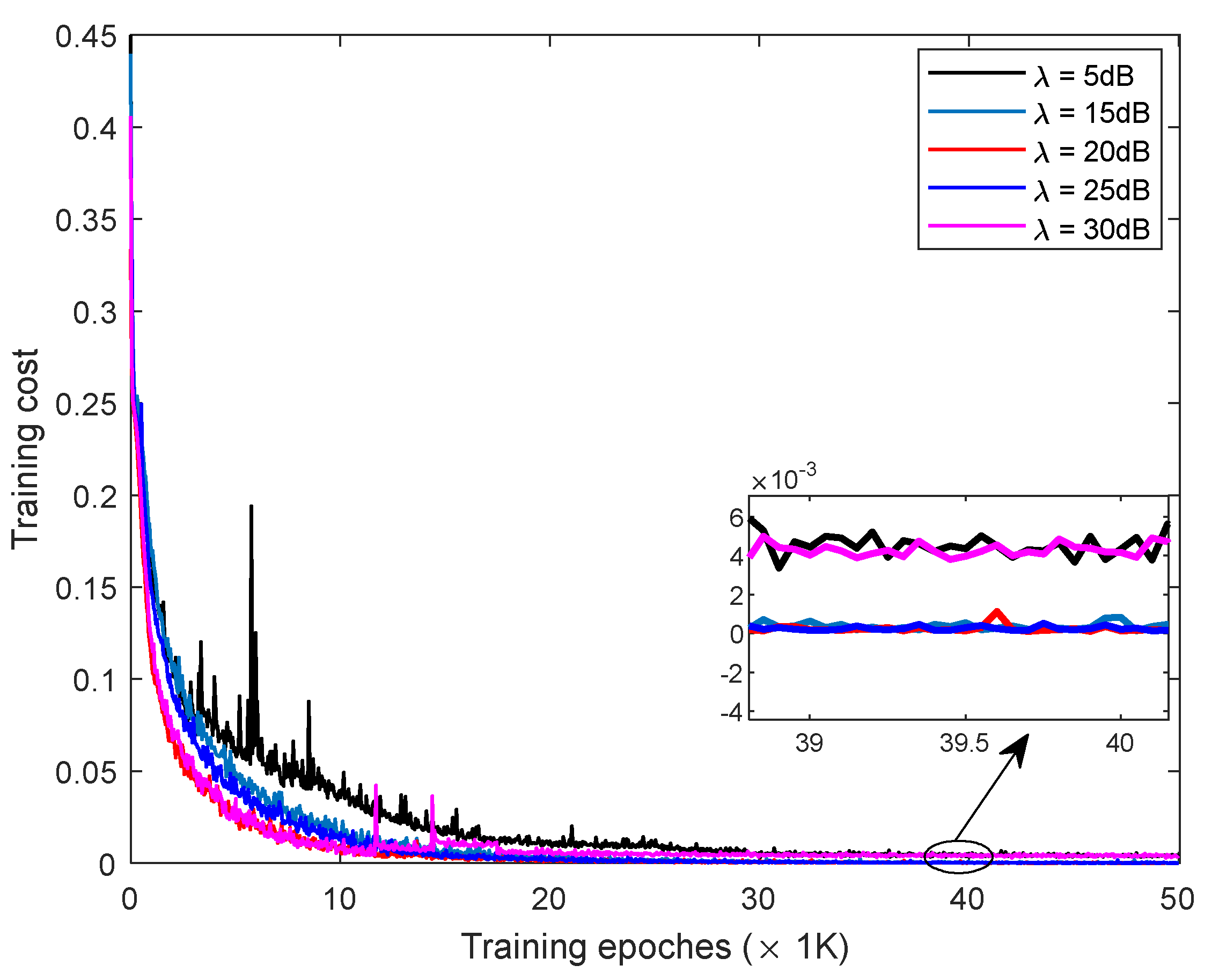
4.1. The Convergence Performance
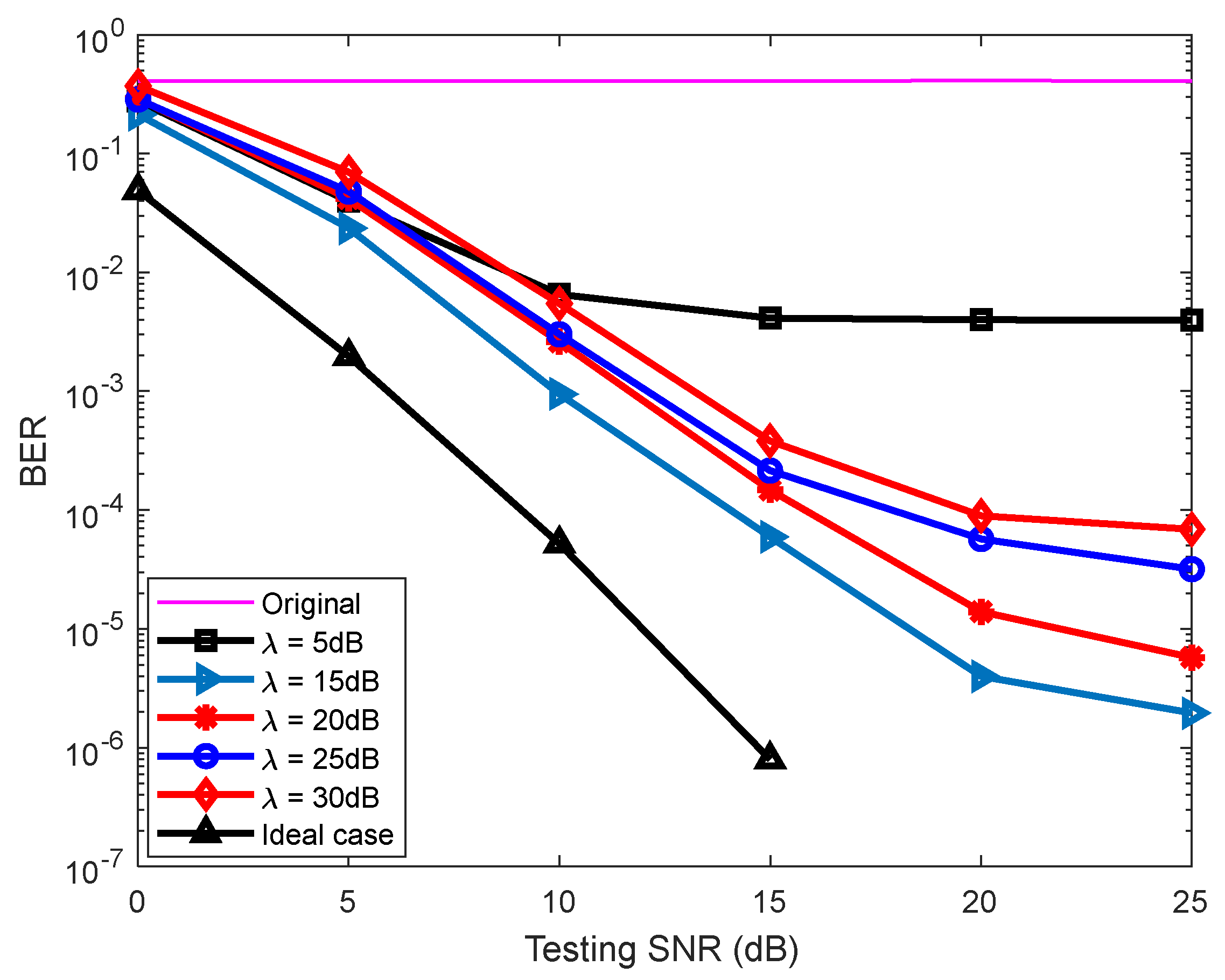
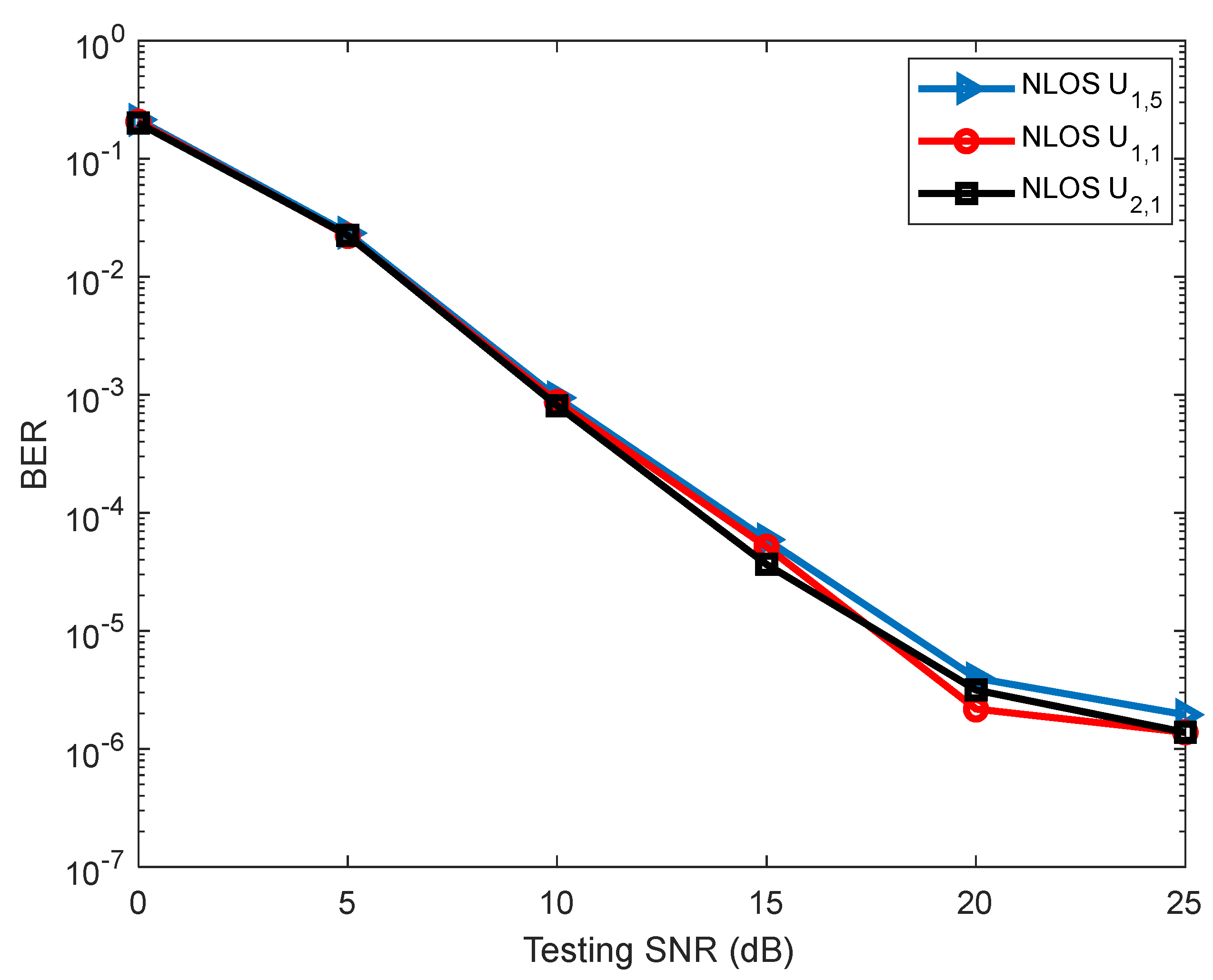
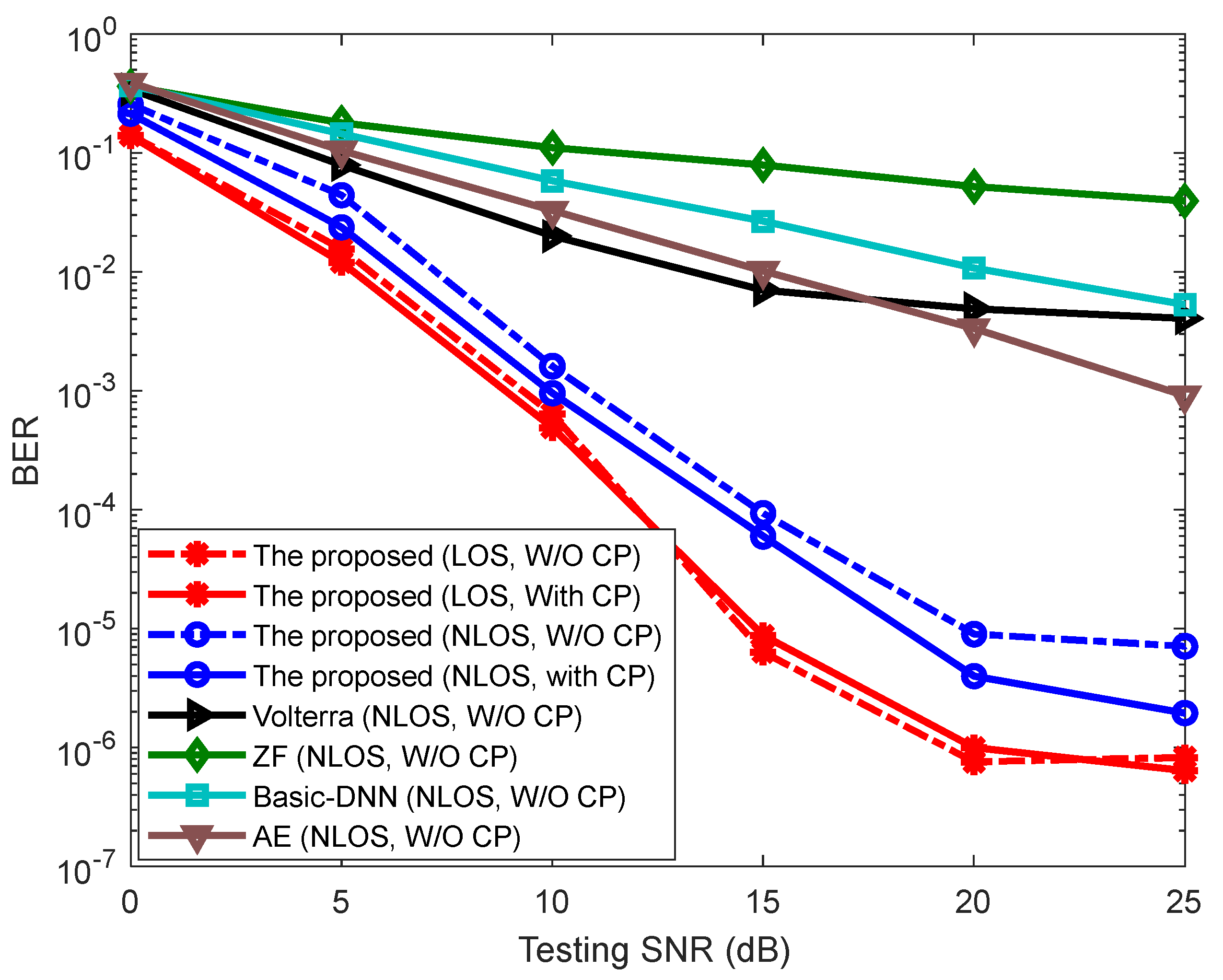
4.2. The BER Performance
4.3. Impact of CP
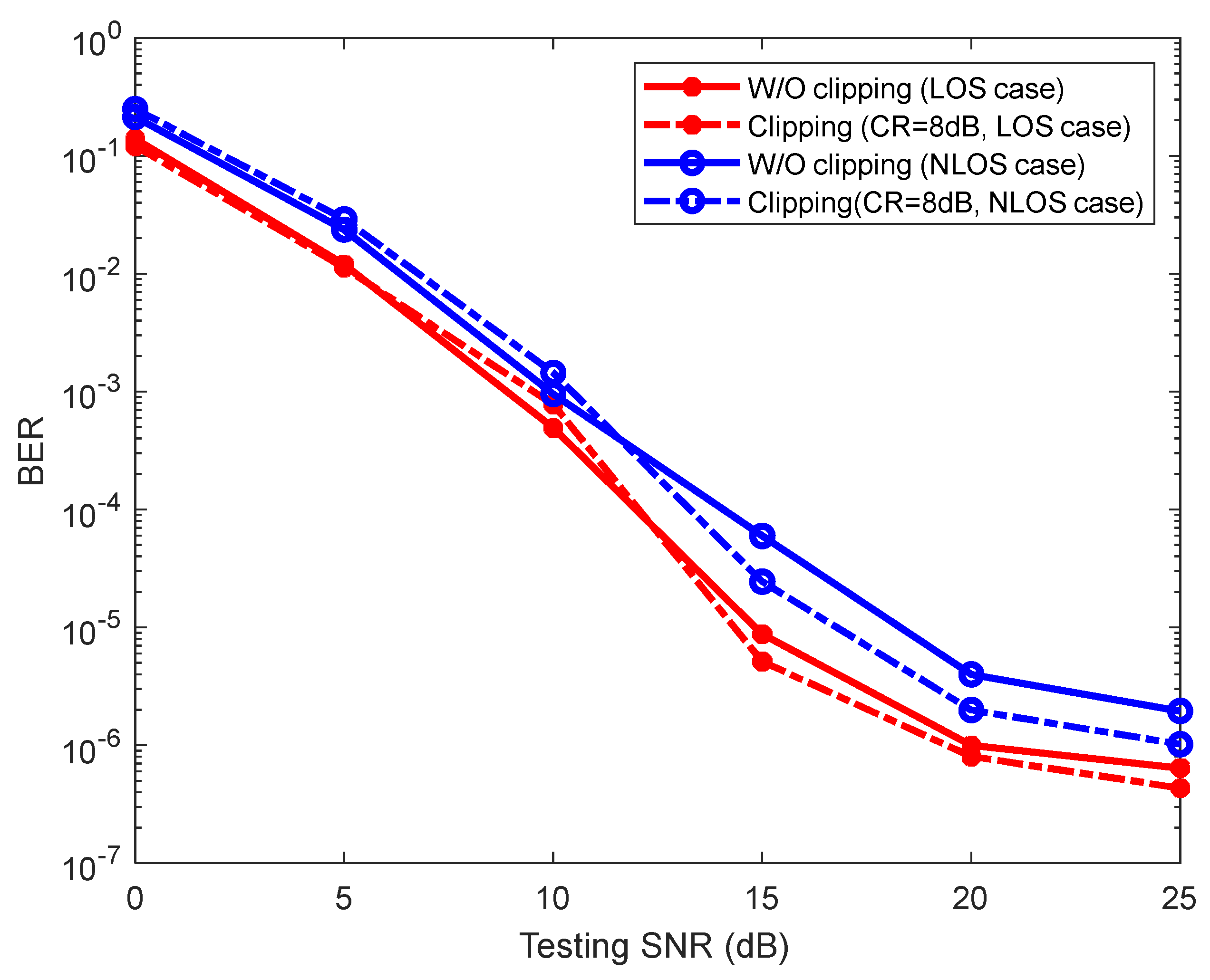
4.4. Impact of Clipping
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, L.; Shu, F.; Chen, M.; Zhang, J.; Wang, J. Joint constellation-labeling optimization for VLC-CSK systems. IEEE Wireless Commun. Lett. 2019, 8, 1280–1284. [Google Scholar] [CrossRef] [Green Version]
- Jia, L.; Shu, F.; Huang, N.; Chen, M.; Wang, J. Capacity and Optimum Signal Constellations for VLC Systems. J. Lightwave Technol. 2020, 38, 2180–2189. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Fang, Y.; Yang, Z.; Chen, P.; Li, Y. Protograph LDPC-Coded BICM-ID with Irregular CSK Mapping in Visible Light Communication Systems. IEEE Trans. Veh. Technol. 2021, 70, 11033–11038. [Google Scholar] [CrossRef]
- Chen, C.; Nie, Y.; Liu, M.; Du, Y.; Liu, R.; Wei, Z.; Fu, H.Y.; Zhu, B. Digital Pre-Equalization for OFDM-Based VLC Systems: Centralized or Distributed? IEEE Photonics Technol. Lett. 2021, 33, 1081–1084. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Y.; Sun, S.; Kang, S.; Cheng, W.; Peng, M. Vision, requirements, and technology trend of 6G: How to tackle the challenges of system coverage, capacity, user data-rate and movement speed. IEEE Wireless Commun. 2020, 27, 218–228. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, C.; Wang, J.; Wu, Y.; Lin, M.; Cheng, J. Physical layer security for indoor visible light communications: Secrecy capacity analysis. IEEE Trans. Commun. 2018, 66, 6423–6436. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.; Wang, X.; Chen, M. Transceiver design for MIMO VLC systems with integer-forcing receivers. IEEE J. Sel. Areas Commun. 2018, 36, 66–77. [Google Scholar] [CrossRef]
- Miao, P.; Qi, C.; Fang, L.; Song, K.; Bu, Q. Deep clipping noise mitigation using ISTA with the specified observations for LED-based DCO-OFDM system. IET Commun. 2018, 12, 2582–2591. [Google Scholar] [CrossRef]
- Deng, L.; Fan, Y.; Zhao, Q. A novel PAPR reduction scheme for VLC DCO-OFDM systems. Opt. Commun. 2018, 426, 164–169. [Google Scholar] [CrossRef]
- Jawhar, Y.A.; Audah, L.; Taher, M.A.; Ramli, K.N.; Mohd, N.S.S.; Musa, M.; Ahmed, M.S. A review of partial transmit sequence for PAPR reduction in the OFDM systems. IEEE Access 2019, 7, 18021–18041. [Google Scholar] [CrossRef]
- Chen, H.; Chung, K.-C. A PTS technique with non-disjoint sub-block partitions in M-QAM OFDM systems. IEEE Trans. Broadcast. 2018, 64, 146–152. [Google Scholar] [CrossRef]
- Hou, J.; Zhao, X.; Gong, F.; Hui, F.; Ge, J. PAPR and PICR reduction of OFDM signals with clipping noise-based tone injection scheme. IEEE Trans. Veh. Technol. 2017, 66, 222–232. [Google Scholar] [CrossRef]
- Lu, H.; Jin, J.; Wang, J. Alleviation of LED nonlinearity impact in visible light communication using companding and predistortion. IET Commun. 2019, 13, 818–821. [Google Scholar] [CrossRef]
- Elgala, H.; Mesleh, R.; Haas, H. Non-linearity effects and predistortion in optical OFDM wireless transmission using LEDs. Int. J. Ultra Wideband Commun. Syst. 2009, 1, 143–150. [Google Scholar] [CrossRef]
- Mitra, R.; Bhatia, V. Low complexity post-distorter for visible light communications. IEEE Commun. Lett. 2017, 21, 1977–1980. [Google Scholar] [CrossRef]
- Miao, P.; Chen, G.; Wang, X.; Yao, Y.; Chambers, J.A. Adaptive Nonlinear Equalization Combining Sparse Bayesian Learning and Kalman Filtering for Visible Light Communications. J. Lightwave Technol. 2020, 38, 6732–6745. [Google Scholar] [CrossRef]
- Mitra, R.; Bhatia, V. Unsupervised multistage-clustering-based hammerstein postdistortion for VLC. IEEE Photon. J. 2016, 9, 1–10. [Google Scholar] [CrossRef]
- Jain, S.; Mitra, R.; Bhatia, V. KLMS-DFE based adaptive post-distorter for visible light communication. Opt. Commun. 2019, 451, 353–360. [Google Scholar] [CrossRef]
- Tan, J.; Wang, Z.; Wang, Q.; Dai, L. BICM-ID scheme for clipped DCO-OFDM in visible light communications. Opt. Express 2016, 24, 4573–4581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chi, N.; Jia, J.; Hu, F.; Zhao, Y.; Zou, P. Challenges and Prospects of Machine Learning in Visible Light Communication. J. Commun. Inform. Netw. 2020, 5, 302–309. [Google Scholar]
- Mitra, R.; Bhatia, V.; Jain, S. Performance Analysis of Random Fourier Features Based Unsupervised Multistage-Clustering for VLC. IEEE Wireless Commun. Lett. 2021, 25, 2659–2663. [Google Scholar] [CrossRef]
- Khan, F.N.; Lu, C.; Lau, A.P.T. Machine learning methods for optical communication systems. In Proceedings of the Signal Processing in Photonic Communications, Washington, DC, USA, 15 July 2017. [Google Scholar]
- Lu, X.; Wang, K.; Qiao, L.; Zhou, W.; Wang, Y.; Chi, N. Nonlinear compensation of multi-CAP VLC system employing clustering algorithm based perception decision. IEEE Photon. J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Pham, T.L.; Shahjalal, M.; Bui, V.; Jang, Y. Deep Learning for Optical Vehicular Communication. IEEE Access 2020, 8, 102691–102708. [Google Scholar] [CrossRef]
- He, Y.; Jiang, M.; Ling, X.; Zhao, C. Robust BICM design for the LDPC coded DCO-OFDM: A deep learning approach. IEEE Trans Commun. 2019, 68, 713–727. [Google Scholar] [CrossRef]
- He, H.; Jin, S.; Wen, C.K.; Gao, F.; Li, G.Y.; Xu, Z. Model-driven deep learning for physical layer communications. IEEE Wireless Commun. 2019, 26, 77–83. [Google Scholar] [CrossRef] [Green Version]
- Wen, C.K.; Shih, W.T.; Jin, S. Deep Learning for Massive MIMO CSI Feedback. IEEE Wireless Commun. Lett. 2018, 7, 748–751. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhao, C.; Jiang, M. Neural network for demodulating the output signals of nonlinear systems with memory. In Proceedings of the 2017 9th IEEE International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 23 October 2017; pp. 1–5. [Google Scholar]
- Ye, H.; Li, G.Y.; Juang, B.H. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wireless Commun. 2018, 7, 114–117. [Google Scholar] [CrossRef]
- Gao, X.; Jin, S.; Wen, C.K.; Li, G.Y. ComNet: Combination of deep learning and expert knowledge in OFDM receivers. IEEE Wireless Commun. 2018, 22, 2627–2630. [Google Scholar] [CrossRef] [Green Version]
- Miao, P.; Yin, W.; Peng, H.; Yao, Y. Deep Learning based Nonlinear Equalization for DCO-OFDM Systems. In Proceedings of the IEEE International Conference on Electrical Engineering and Mechatronics Technology, Qingdao, China, 2 July 2021; pp. 699–703. [Google Scholar]
- Ye, H.; Liang, L.; Li, G.Y.; Juang, B. Deep Learning-Based End-to-End Wireless Communication Systems with Conditional GANs as Unknown Channels. IEEE Trans. Wireless Commun. 2020, 19, 3133–3143. [Google Scholar] [CrossRef] [Green Version]
- Bai, Q.; Wang, J.; Zhang, Y.; Song, J. Deep Learning-Based Channel Estimation Algorithm Over Time Selective Fading Channels. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Lee, I.; Lee, H.S. Deep learning based transceiver design for multi-colored VLC systems. Opt. Express 2018, 26, 6222–6238. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Lee, I.; Quek, T.Q.S.; Lee, H.S. Binary signaling design for visible light communication: A deep learning framework Visible Light Communication Using Deep Learning Techniques. Opt. Express 2018, 26, 18131–18142. [Google Scholar] [CrossRef] [PubMed]
- Miao, P.; Zhu, B.; Qi, C.; Jin, Y.; Lin, C. A model-driven deep learning method for LED nonlinearity mitigation in OFDM-based optical communications. IEEE Access 2019, 7, 71436–71446. [Google Scholar] [CrossRef]
- Hao, L.; Wang, D.; Cheng, W.; Li, J.; Ma, A. Performance enhancement of ACO-OFDM-based VLC systems using a hybrid autoencoder scheme. Opt. Commun. 2019, 442, 110–116. [Google Scholar] [CrossRef]
- Ulkar, M.G.; Baykas, T.; Pusane, A.E. VLCnet: Deep learning based end-to-end visible light communication system. J. Lightwave Technol. 2020, 38, 5937–5948. [Google Scholar] [CrossRef]
- Uysal, M.; Miramirkhani, F.; Narmanlioglu, O.; Baykas, T.; Panayirci, E. IEEE 802.15. 7r1 reference channel models for visible light communications. IEEE Commun. Mag. 2017, 55, 212–217. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Dimensions for | |
| Input | |
| Dense (ReLU) | 256 |
| Dense (Linear) | |
| Dimensions for | |
| Input | |
| Dense (ReLU) | 256 |
| Dense (ReLU) | 256 |
| Dense (Sigmod) | |
| Refine | signum function |
| Training and Testing | |
| Optimizer | Adam |
| Learning Rate | 0.0001~0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, P.; Yin, W.; Peng, H.; Yao, Y. Study of the Performance of Deep Learning-Based Channel Equalization for Indoor Visible Light Communication Systems. Photonics 2021, 8, 453. https://doi.org/10.3390/photonics8100453
Miao P, Yin W, Peng H, Yao Y. Study of the Performance of Deep Learning-Based Channel Equalization for Indoor Visible Light Communication Systems. Photonics. 2021; 8(10):453. https://doi.org/10.3390/photonics8100453
Chicago/Turabian StyleMiao, Pu, Weibang Yin, Hui Peng, and Yu Yao. 2021. "Study of the Performance of Deep Learning-Based Channel Equalization for Indoor Visible Light Communication Systems" Photonics 8, no. 10: 453. https://doi.org/10.3390/photonics8100453
APA StyleMiao, P., Yin, W., Peng, H., & Yao, Y. (2021). Study of the Performance of Deep Learning-Based Channel Equalization for Indoor Visible Light Communication Systems. Photonics, 8(10), 453. https://doi.org/10.3390/photonics8100453






