On-Chip Guiding of Higher-Order Orbital Angular Momentum Modes
Abstract
1. Introduction
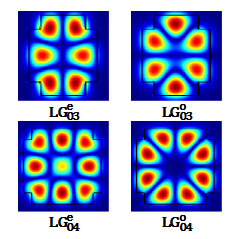
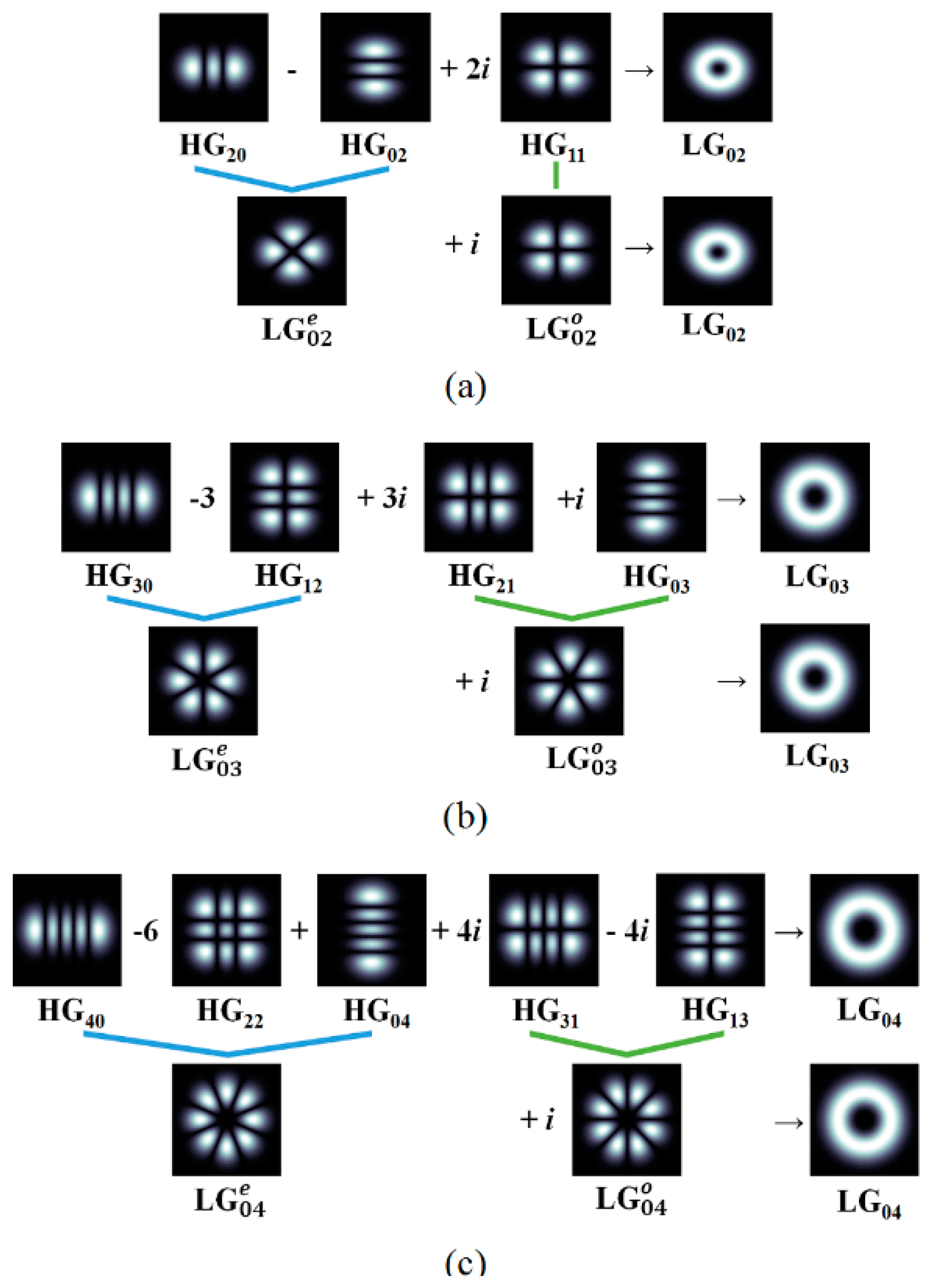
2. Decomposition of Higher-Order OAM Modes
3. Waveguide Design and Mode Analysis
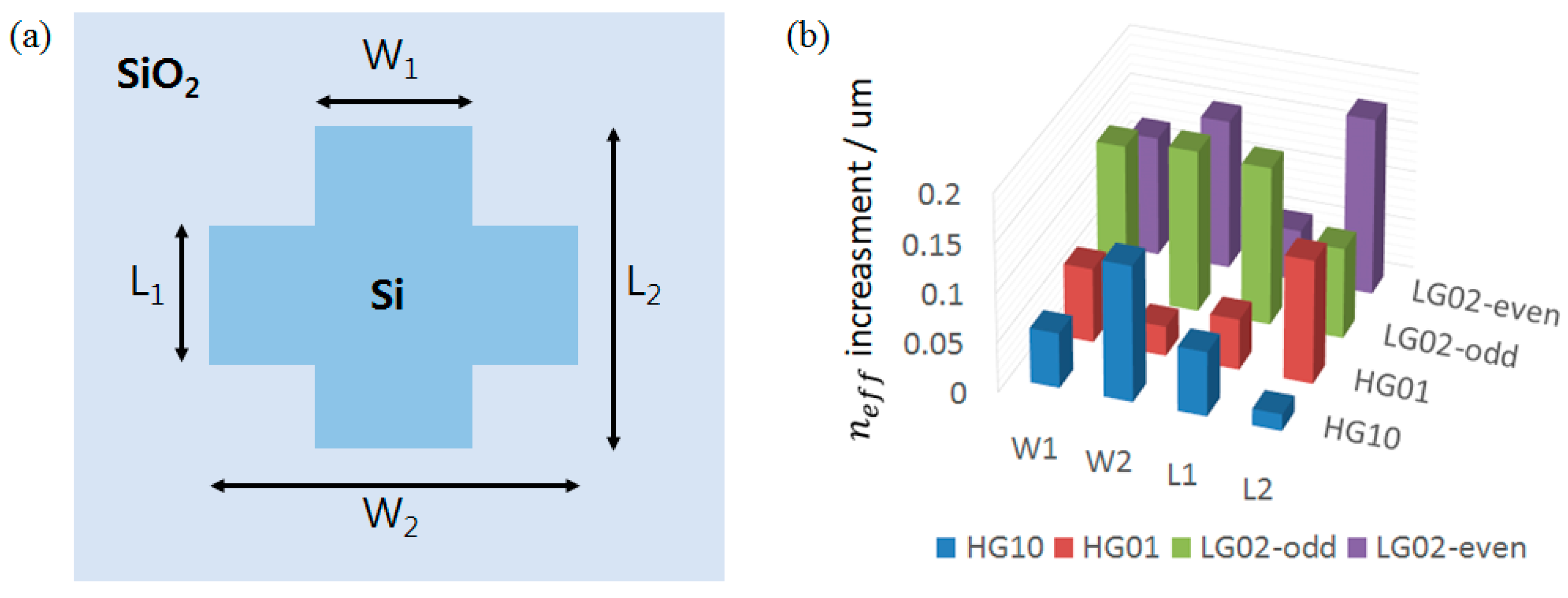
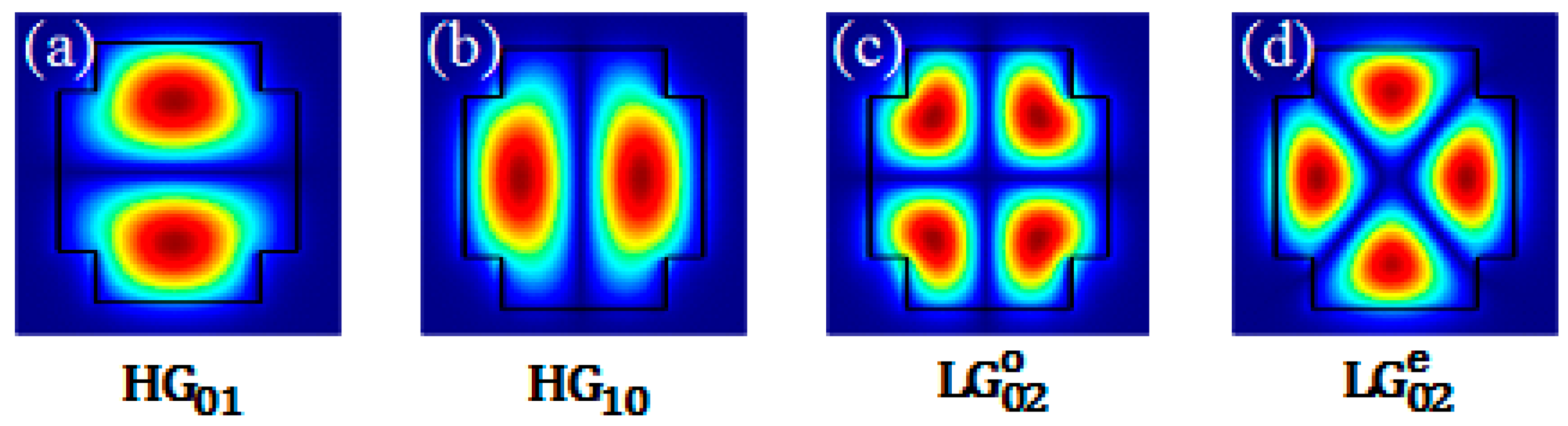
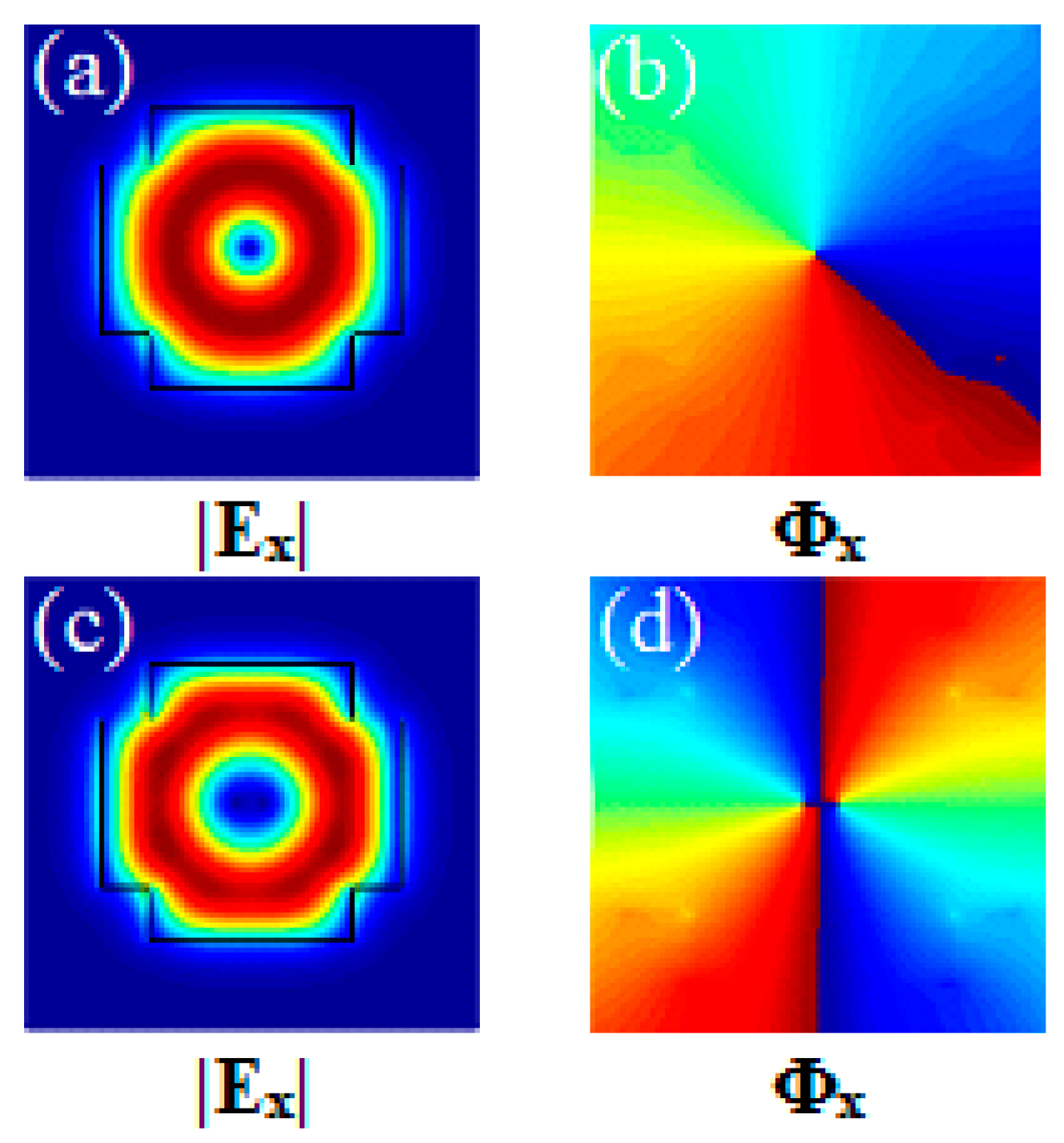
3.1. Waveguide Structure Simultaneously Supporting the l = ±1 and ±2 OAM Modes
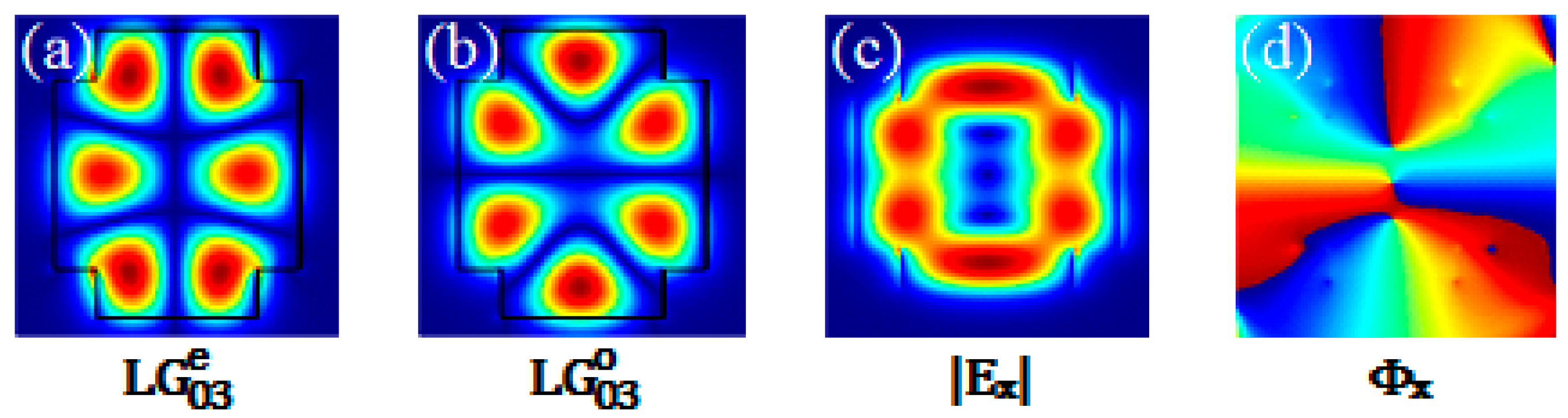
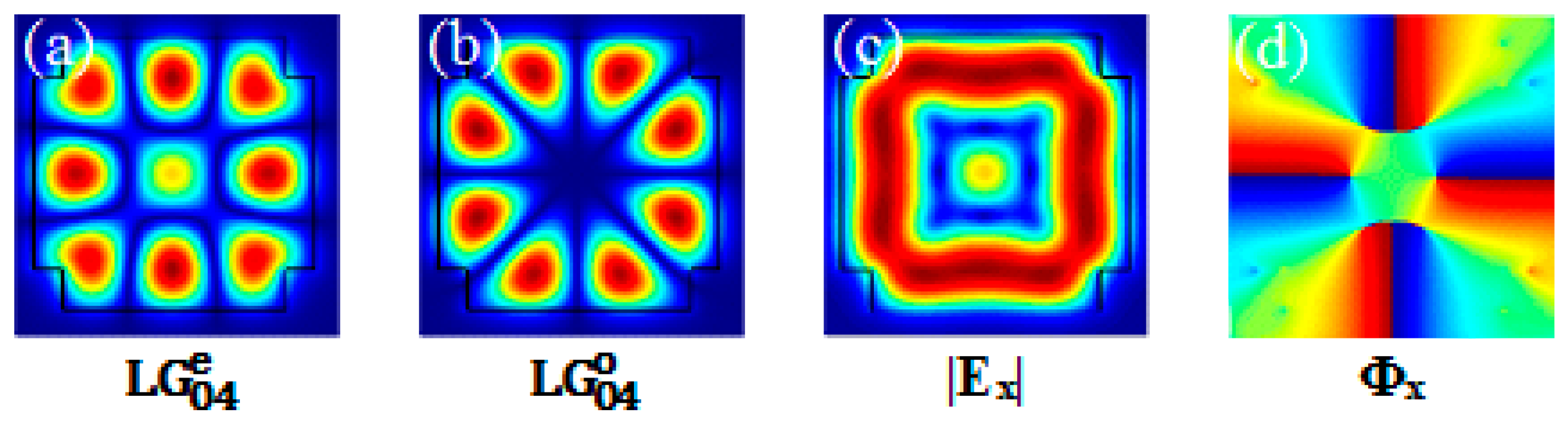
3.2. Waveguide Supporting l = ±3 or ±4 OAM Modes
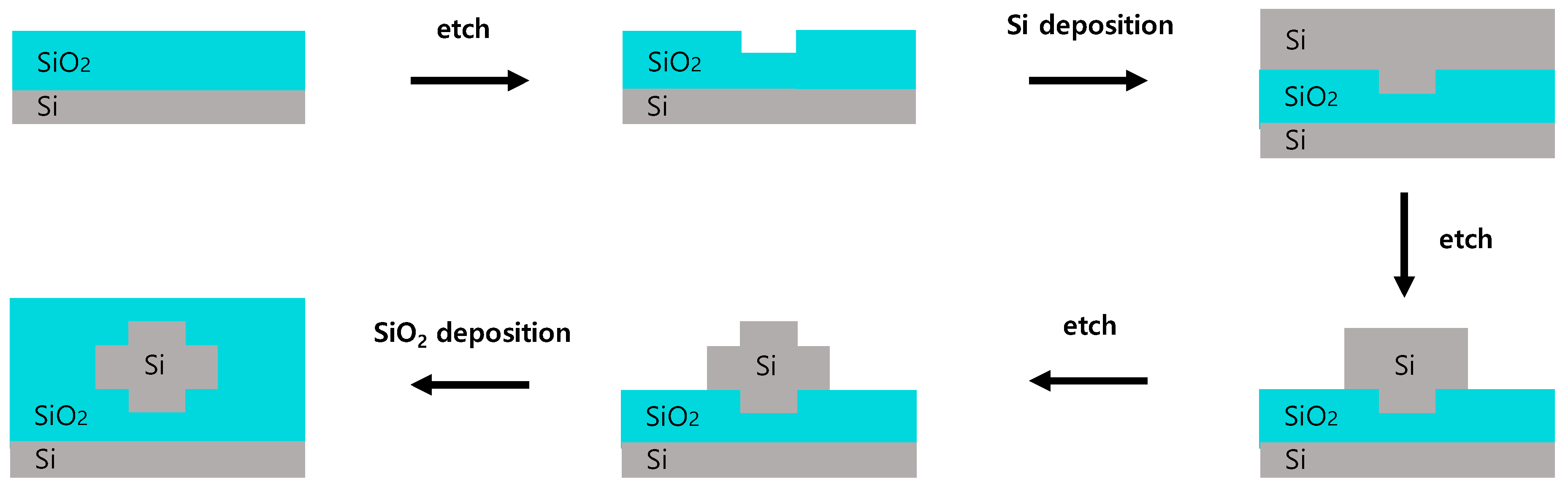
3.3. Fabrication Process of the Proposed Waveguide
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, X.; Li, Y.; Feng, L.; Wu, S.; Yang, C.; Li, W.; Tong, W.; Wu, J. All-fiber orbital angular momentum mode multiplexer based on a mode-selective photonic lantern and a mode polarization controller. Opt. Lett. 2018, 43, 4779–4782. [Google Scholar] [CrossRef] [PubMed]
- Fickler, R.; Lapkiewicz, R.; Huber, M.; Lavery, M.P.; Padgett, M.J.; Zeilinger, A. Interface between path and orbital angular momentum entanglement for high-dimensional photonic quantum information. Nat. Commun. 2014, 5, 4502. [Google Scholar] [CrossRef] [PubMed]
- Fickler, R.; Campbell, G.; Buchler, B.; Lam, P.K.; Zeilinger, A. Quantum entanglement of angular momentum states with quantum numbers up to 10,010. Proc. Natl. Acad. Sci. USA 2016, 113, 13642–13647. [Google Scholar] [CrossRef] [PubMed]
- Gecevičius, M.; Drevinskas, R.; Beresna, M.; Kazansky, P.G. Single beam optical vortex tweezers with tunable orbital angular momentum. Appl. Phys. Lett. 2014, 104, 231110. [Google Scholar] [CrossRef]
- Lee, J.; Arita, Y.; Toyoshima, S.; Miyamoto, K.; Panagiotopoulos, P.; Wright, E.M.; Dholakia, K.; Omatsu, T. Photopolymerization with light fields possessing orbital angular momentum: Generation of helical microfibers. ACS Photonics 2018, 5, 4156–4163. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J. Theoretical analyses on orbital angular momentum modes in conventional graded-index multimode fibre. Sci. Rep. 2017, 7, 3990. [Google Scholar] [CrossRef]
- Padgett, M.; Courtial, J.; Allen, L. Light’s orbital angular momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Niederriter, R.D.; Siemens, M.E.; Gopinath, J.T. Continuously tunable orbital angular momentum generation using a polarization-maintaining fiber. Opt. Lett. 2016, 41, 3213–3216. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, G.; Liu, J.; Wu, X.; Zhu, J.; Du, C.; Luo, W.; Chen, Y.; Yu, S. Orbital-angular-momentum mode-group multiplexed transmission over a graded-index ring-core fiber based on receive diversity and maximal ratio combining. Opt. Express 2018, 26, 4243–4257. [Google Scholar] [CrossRef]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; Jennewein, T.; Ralph, T.C.; Resch, K.J.; Pryde, G.J.; O’brien, J.L.; Gilchrist, A.; White, A.G. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 2009, 5, 134. [Google Scholar] [CrossRef]
- Shadbolt, P.J.; Verde, M.R.; Peruzzo, A.; Politi, A.; Laing, A.; Lobino, M.; Matthews, J.C.; Thompson, M.G.; O’Brien, J.L. Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nat. Photonics 2012, 6, 45. [Google Scholar] [CrossRef]
- Bonneau, D.; Engin, E.; Ohira, K.; Suzuki, N.; Yoshida, H.; Iizuka, N.; Ezaki, M.; Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H. Quantum interference and manipulation of entanglement in silicon wire waveguide quantum circuits. New J. Phys. 2012, 14, 045003. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J. On-chip orbital angular momentum modes generator and (de) multiplexer based on trench silicon waveguides. Opt. Express 2017, 25, 18492–18501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Feng, X.; Cui, K.; Liu, F.; Huang, Y. Generating in-plane optical orbital angular momentum beams with silicon waveguides. IEEE Photonics J. 2013, 5, 2201206. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, H.W.; Huang, B.J.; Huang, X.G. Light beams with selective angular momentum generated by hybrid plasmonic waveguides. Nanoscale 2014, 6, 12360–12365. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Hu, X.; Jin, L.; Fu, X.; Chen, Q. Generation of in-plane light beam with orbital angular momentum with an asymmetrical plasmonic waveguide. Plasmonics 2016, 11, 1323–1329. [Google Scholar] [CrossRef]
- Barnett, S.M. Optical angular-momentum flux. J. Opt. B Quantum Semiclassical Opt. 2001, 4, S7. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A Mol. Opt. Phys. 1992, 45, 8185. [Google Scholar] [CrossRef]
- Abramochkin, E.; Volostnikov, V. Beam transformations and nontransformed beams. Opt. Commun. 1991, 83, 123–135. [Google Scholar] [CrossRef]
- Kimel, I.; Elias, L.R. Relations between hermite and laguerre gaussian modes. IEEE J. Quant. Electron. 1993, 29, 2562–2567. [Google Scholar] [CrossRef]
- Longman, A.; Fedosejevs, R. Mode conversion efficiency to Laguerre–Gaussian OAM modes using spiral phase optics. Opt. Express 2017, 25, 17382–17392. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Cheng, Y.; Ni, R.; Zhang, Y.; Hu, X.; Zhu, S.; Xiao, M. Generating controllable Laguerre–Gaussian laser modes through intracavity spin-orbital angular momentum conversion of light. Phys. Rev. Appl. 2019, 11, 014038. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Citeseer: Princeton, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Liu, A.; Zou, C.; Ren, X.; Wang, Q.; Guo, G. On-chip generation and control of the vortex beam. Appl. Phys. Lett. 2016, 108, 181103. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Kwong, D.; Covey, J.; Hosseini, A.; Zhang, Y.; Xu, X.; Chen, R.T. Ultralow-loss polycrystalline silicon waveguides and high uniformity 1 × 12 MMI fanout for 3D photonic integration. Opt. Express 2012, 20, 21722. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, I.J.; Kim, S. On-Chip Guiding of Higher-Order Orbital Angular Momentum Modes. Photonics 2019, 6, 72. https://doi.org/10.3390/photonics6020072
Lee IJ, Kim S. On-Chip Guiding of Higher-Order Orbital Angular Momentum Modes. Photonics. 2019; 6(2):72. https://doi.org/10.3390/photonics6020072
Chicago/Turabian StyleLee, In Joon, and Sangin Kim. 2019. "On-Chip Guiding of Higher-Order Orbital Angular Momentum Modes" Photonics 6, no. 2: 72. https://doi.org/10.3390/photonics6020072
APA StyleLee, I. J., & Kim, S. (2019). On-Chip Guiding of Higher-Order Orbital Angular Momentum Modes. Photonics, 6(2), 72. https://doi.org/10.3390/photonics6020072