Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon
Abstract
:1. Introduction
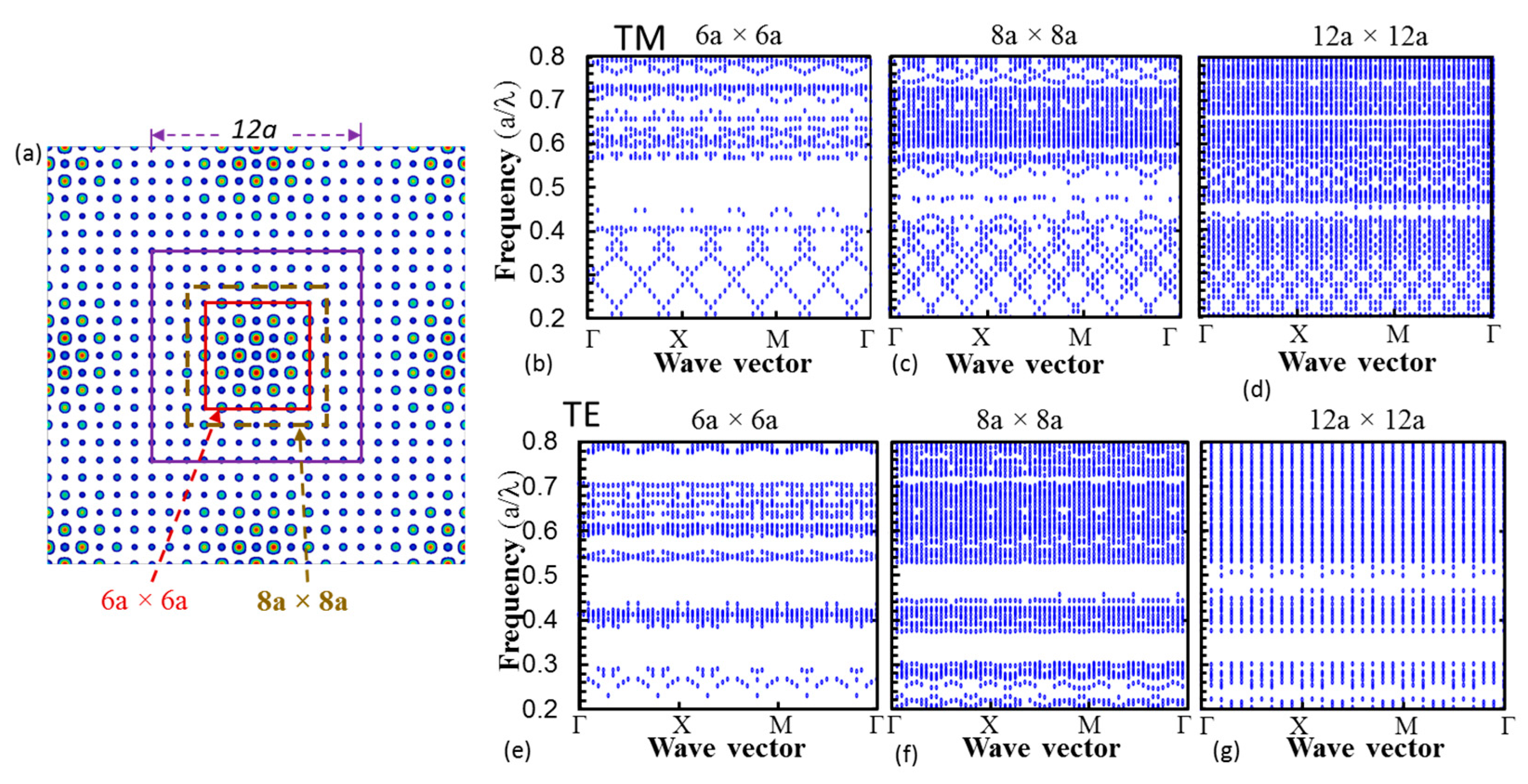
2. Photonic Band Structures in Graded Photonic Super-Crystal (GPSC) with Different Unit Cell Sizes
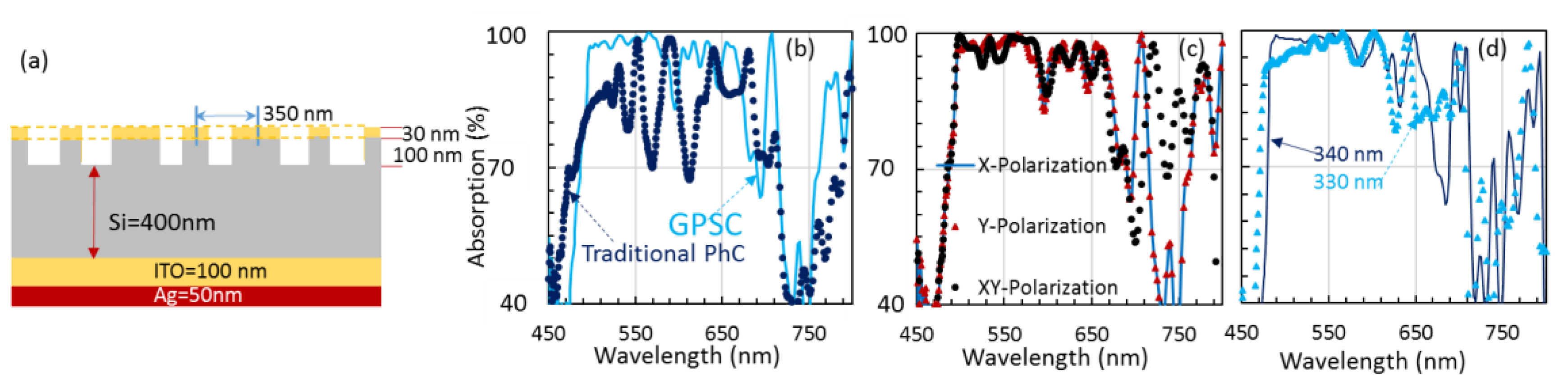
3. Broadband High Light Absorption in Si Device Patterned in GPSC
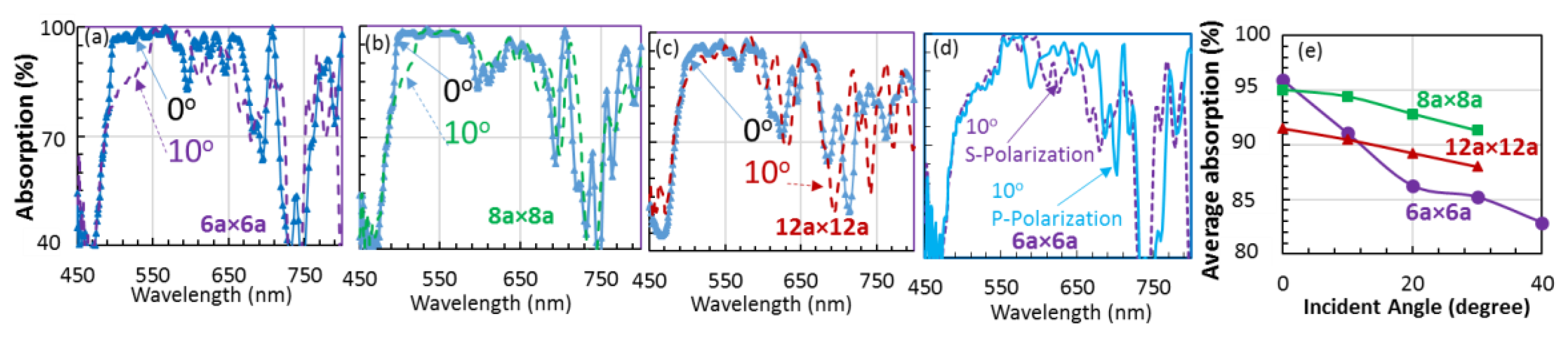
4. Unit Cell Size Effect on the Light Absorption in Si Device Patterned in GPSC
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, Y.; Herman, P.R.; Darmawikarta, K. Design and holographic fabrication of tetragonal and cubic photonic crystals with phase mask: toward the mass-production of three-dimensional photonic crystals. Appl. Phys. Lett. 2005, 86, 071117. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Bermel, P.; Luo, C.; Zeng, L.; Kimerling, L.C.; Joannopoulos, J.D. Improving thin-film crystalline silicon solar cell efficiencies with photonic crystals. Opt. Express 2007, 15, 16986–17000. [Google Scholar] [CrossRef] [PubMed]
- Mallick, S.B.; Agrawal, M.; Peumans, P. Optimal light trapping in ultra-thin photonic crystal crystalline silicon solar cells. Opt. Express 2010, 18, 5691. [Google Scholar] [CrossRef] [PubMed]
- Bozzola, A.; Liscidini, M.; Andreani, L.C. Photonic light-trapping versus Lambertian limits in thin film silicon solar cells with 1D and 2D periodic patterns. Opt. Express 2012, 20, A224. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Drouard, E.; El Daif, O.; Letartre, X.; Viktorovitch, P.; Fave, A.; Kaminski, A.; Lemiti, M.; Seassal, C. Absorption enhancement using photonic crystals for silicon thin film solar cells. Opt. Express 2009, 17, 14312. [Google Scholar] [CrossRef] [PubMed]
- Callahan, D.M.; Horowitz, K.A.W.; Atwater, H.A. Light trapping in ultrathin silicon photonic crystal superlattices with randomly-textured dielectric incouplers. Opt. Express 2013, 21, 30315. [Google Scholar] [CrossRef] [PubMed]
- Rinnerbauer, V.; Shen, Y.; Joannopoulos, J.D.; Soljačić, M.; Schäffler, F.; Celanovic, I. Superlattice photonic crystal as broadband solar absorber for high temperature operation. Opt. Express 2014, 22, A1895–A1906. [Google Scholar] [CrossRef]
- Rinnerbauer, V.; Lausecker, E.; Schäffler, F.; Reininger, P.; Strasser, G.; Geil, R.D.; Joannopoulos, J.D.; Soljačić, M.; Celanovic, I. Nanoimprinted superlattice metallic photonic crystal as ultraselective solar absorber. Optica 2015, 2, 743. [Google Scholar] [CrossRef]
- Zhang, B.; Hendrickson, J.; Guo, J. Multispectral near-perfect metamaterial absorbers using spatially multiplexed plasmon resonance metal square structures. J. Opt. Soc. Am. B 2013, 30, 656. [Google Scholar] [CrossRef]
- Hendrickson, J.; Guo, J.; Zhang, B.; Buchwald, W.; Soref, R. Wideband perfect light absorber at midwave infrared using multiplexed metal structures. Opt. Lett. 2012, 37, 371. [Google Scholar] [CrossRef] [PubMed]
- Lowell, D.; Lutkenhaus, J.; George, D.; Philipose, U.; Chen, B.; Lin, Y. Simultaneous direct holographic fabrication of photonic cavity and graded photonic lattice with dual periodicity, dual basis, and dual symmetry. Opt. Express 2017, 25, 14444–14452. [Google Scholar] [CrossRef] [PubMed]
- Lowell, D.; Hassan, S.; Sale, O.; Adewole, M.; Hurley, N.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-quasi-crystals with multiple-level gradients. Appl. Opt. 2018, 57, 6598–6604. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Adewole, M.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Lin, Y. High light extraction efficiency in organic light-emitting diodes by patterning the cathode in graded superlattice with dual periodicity and dual basis. J. Appl. Phys. 2017, 121, 233104. [Google Scholar] [CrossRef]
- Hassan, S.; Sale, O.; Lowell, D.; Hurley, N.; Lin, Y. Holographic fabrication and optical property of graded photonic super-crystals with a rectangular unit super-cell. Photonics 2018, 5, 34. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Adewole, M.; George, D.; Zhang, H.; Lin, Y. Extraordinary light-trapping enhancement in silicon solar cell patterned with graded photonic super-crystals. Photonics 2017, 4, 50. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef]
- Garnett, E.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 2010, 10, 1082–1087. [Google Scholar] [CrossRef]
- Kelzenberg, M.D.; Boettcher, S.W.; Petykiewicz, J.A.; Turner-Evans, D.B.; Putnam, M.C.; Warren, E.L.; Spurgeon, J.M.; Briggs, R.M.; Lewis, N.S.; Atwater, H.A. Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mater. 2010, 9, 239–244. [Google Scholar] [CrossRef]
- Han, S.E.; Chen, G. Toward the lambertian limit of light trapping in thin nanostructured silicon solar cells. Nano Lett. 2010, 10, 4692–4696. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Yu, Z.; Burkhard, G.F.; Hsu, C.-M.; Connor, S.T.; Xu, Y.; Wang, Q.; McGehee, M.; Fan, S.; Cui, Y. Optical Absorption Enhancement in Amorphous Silicon Nanowire and Nanocone Arrays. Nano Lett. 2009, 9, 279–282. [Google Scholar] [CrossRef] [PubMed]
- Martins, E.R.; Li, J.; Liu, Y.; Zhou, J.; Krauss, T.F. Engineering gratings for light trapping in photovoltaics: The supercell concept. Phys. Rev. B 2012, 86, 041404. [Google Scholar] [CrossRef]
- Wang, D.; Su, G. New strategy to promote conversion efficiency using high-index nanostructures in thin-film solar cells. Sci. Rep. 2014, 4, 7165. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, A.; Favuzzi, P.A.; Tanaka, Y.; Shigeta, H.; Kawakami, Y.; Noda, S. Partially-disordered photonic-crystal thin films for enhanced and robust photovoltaics. Appl. Phys. Lett. 2012, 100, 181110. [Google Scholar] [CrossRef]
- Oskooi, A.; De Zoysa, M.; Ishizaki, K.; Noda, S. Experimental Demonstration of Quasi-Resonant Absorption in Silicon Thin Films for Enhanced Solar Light Trapping. ACS Photonics 2014, 1, 304–309. [Google Scholar] [CrossRef]
- Yoon, H.P.; Yuwen, Y.A.; Kendrick, C.E.; Barber, G.D.; Podraza, N.J.; Redwing, J.M.; Mallouk, T.E.; Wronski, C.R.; Mayer, T.S. Enhanced conversion efficiencies for pillar array solar cells fabricated from crystalline silicon with short minority carrier diffusion lengths. Appl. Phys. Lett. 2010, 96, 213503. [Google Scholar] [CrossRef]
- Martins, E.R.; Li, J.; Liu, Y.; Depauw, V.; Chen, Z.; Zhou, J.; Krauss, T.F. Deterministic quasi-random nanostructures for photon control. Nat. Commun. 2013, 4, 2665. [Google Scholar] [CrossRef]
- Vynck, K.; Burresi, M.; Riboli, F.; Wiersma, D.S. Photon management in two-dimensional disordered media. Nat. Mater. 2012, 11, 1017–1022. [Google Scholar] [CrossRef]
- Rockstuhl, C.; Fahr, S.; Bittkau, K.; Beckers, T.; Carius, R.; Haug, F.-J.; Soderstrom, T.; Ballif, C.; Lederer, F. Comparison and optimization of randomly textured surfaces in thin-film solar cells. Opt. Express 2010, 18, A335. [Google Scholar] [CrossRef]
- Ferry, V.E.; Verschuuren, M.A.; Van Lare, M.C.; Schropp, R.E.I.; Atwater, H.A.; Polman, A. Optimized Spatial Correlations for Broadband Light Trapping Nanopatterns in High Efficiency Ultrathin Film a-Si:H Solar Cells. Nano Lett. 2011, 11, 4239–4245. [Google Scholar] [CrossRef] [PubMed]
- Siddique, R.H.; Donie, Y.J.; Gomard, G.; Yalamanchili, S.; Merdzhanova, T.; Lemmer, U.; Hölscher, H. Bioinspired phase-separated disordered nanostructures for thin photovoltaic absorbers. Sci. Adv. 2017, 3, e1700232. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Green, M.A. Self-consistent optical parameters of intrinsic silicon at 300 K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Syu, H.-J.; Shiu, S.-C.; Lin, C. Silicon nanowire/organic hybrid solar cell with efficiency of 8.40%. Sol. Energy Mater. Sol. Cells 2012, 98, 267–272. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, S.; Alnasser, K.; Lowell, D.; Lin, Y. Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon. Photonics 2019, 6, 50. https://doi.org/10.3390/photonics6020050
Hassan S, Alnasser K, Lowell D, Lin Y. Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon. Photonics. 2019; 6(2):50. https://doi.org/10.3390/photonics6020050
Chicago/Turabian StyleHassan, Safaa, Khadijah Alnasser, David Lowell, and Yuankun Lin. 2019. "Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon" Photonics 6, no. 2: 50. https://doi.org/10.3390/photonics6020050
APA StyleHassan, S., Alnasser, K., Lowell, D., & Lin, Y. (2019). Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon. Photonics, 6(2), 50. https://doi.org/10.3390/photonics6020050





