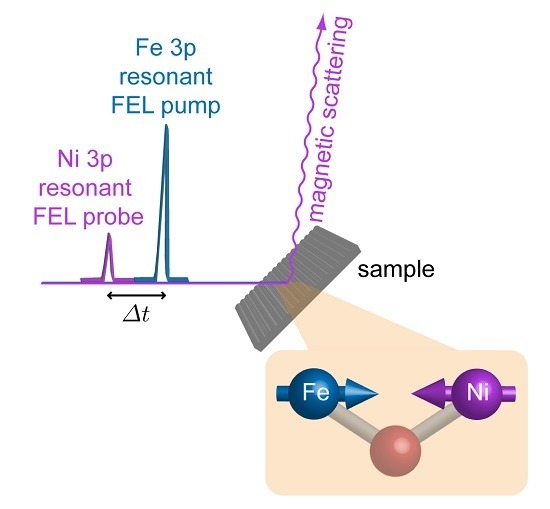
Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source
Abstract
:1. Introduction
2. Materials and Methods
2.1. Source Design
2.2. Experimental Details
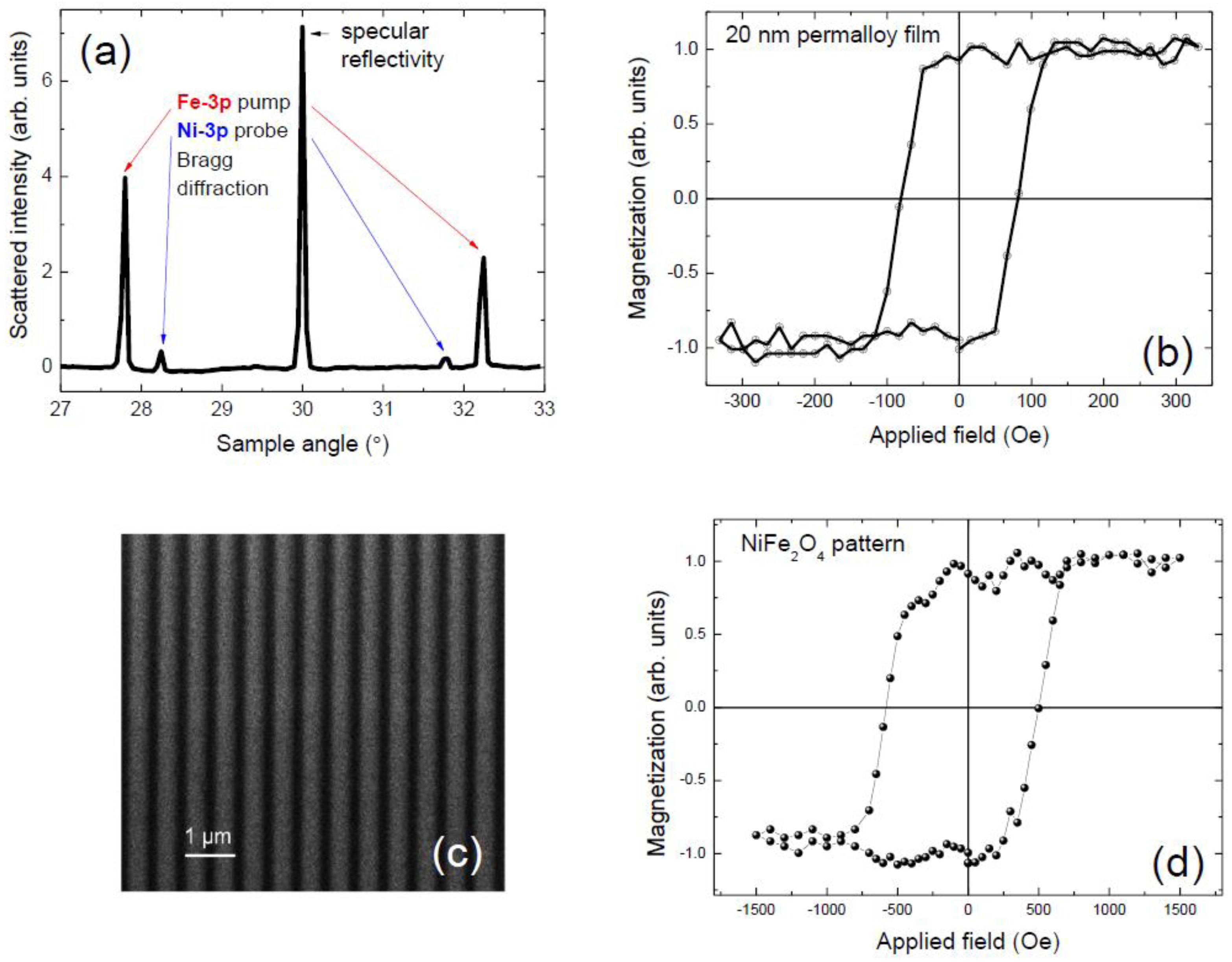
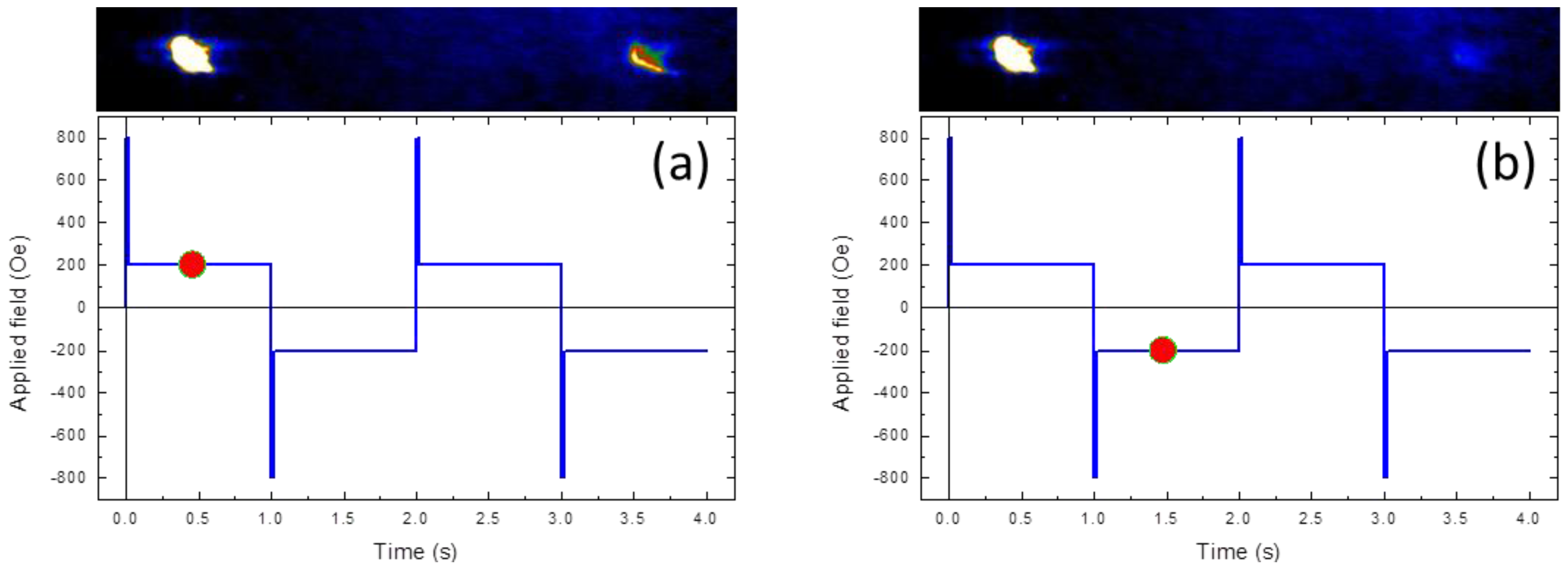
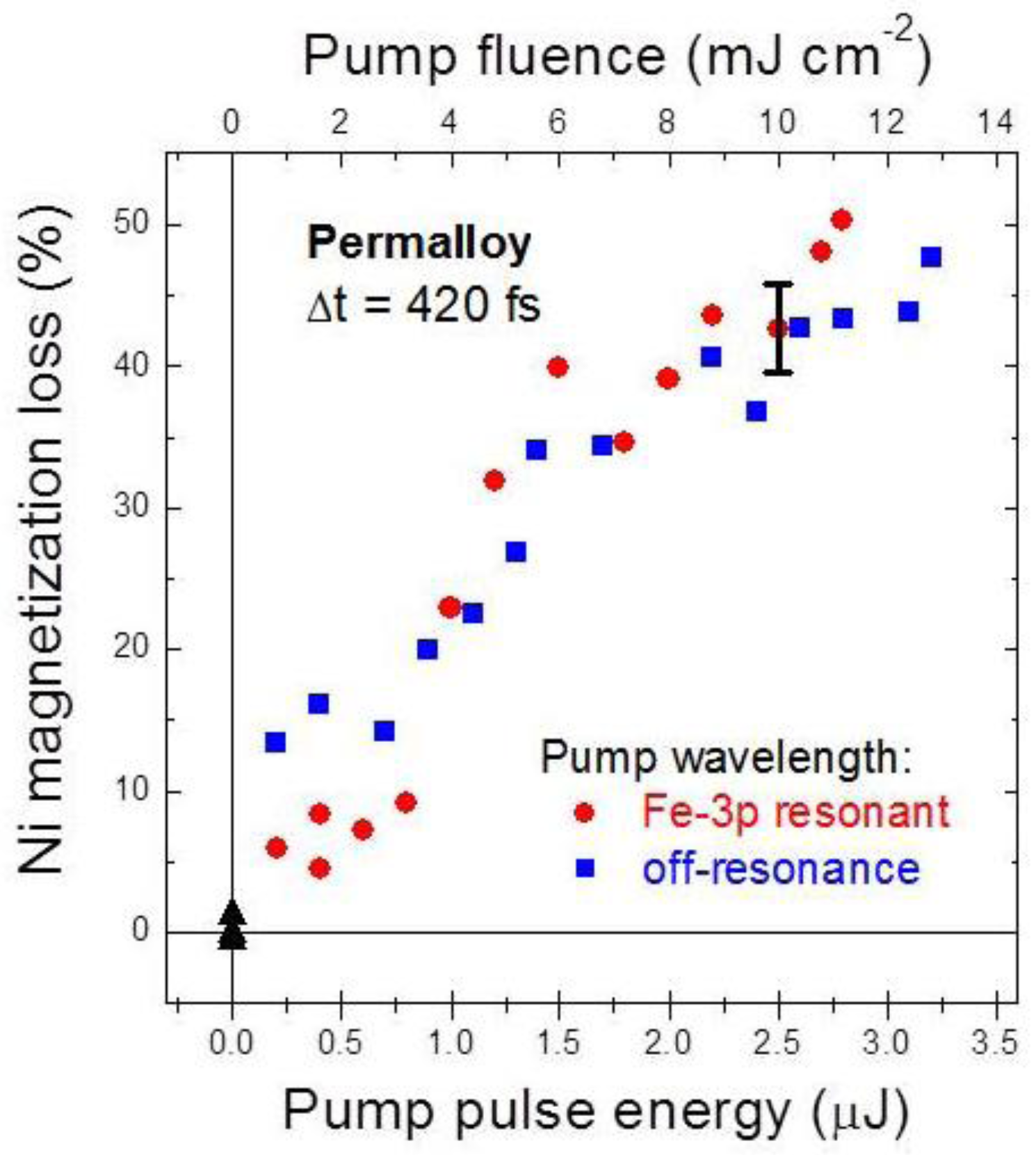
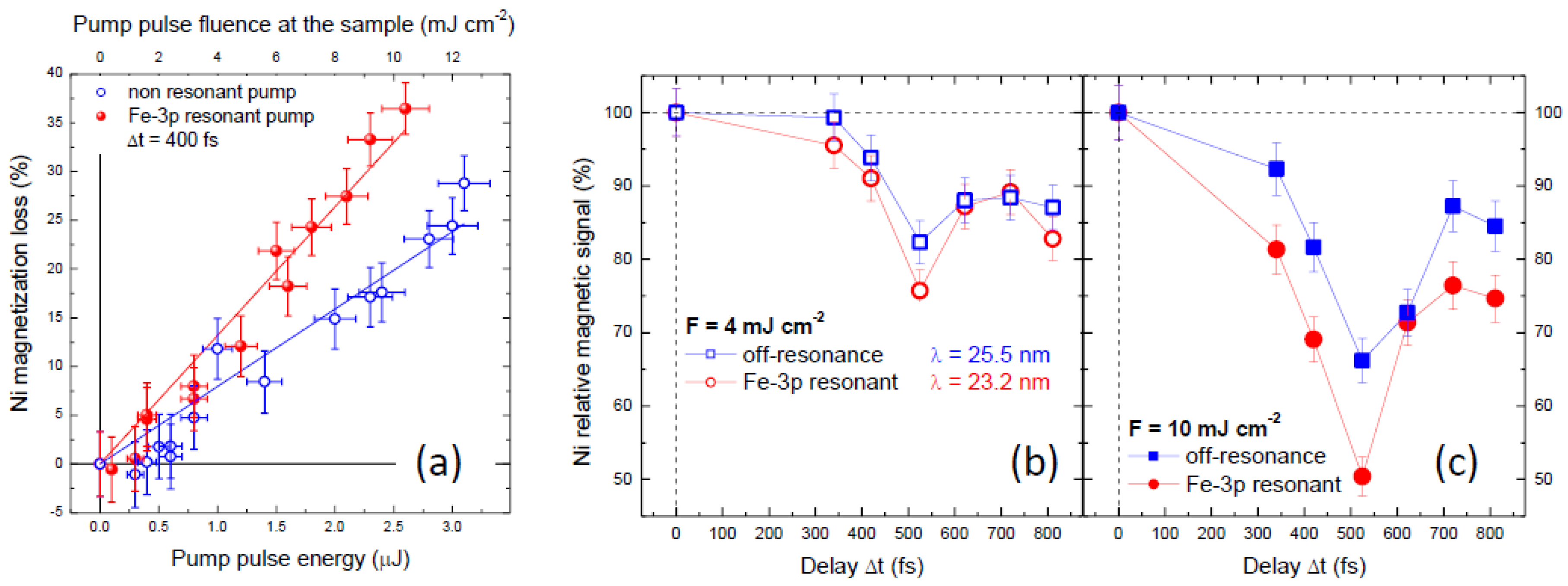
3. Results
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beaurepaire, E.; Merle, J.-C.; Daunois, A.; Bigot, J.-Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250. [Google Scholar] [CrossRef] [PubMed]
- Koopmans, B.; Malinowski, G.; Dalla Longa, F.; Steiauf, D.; Fahnle, M.; Roth, T.; Cinchetti, M.; Aeschlimann, M. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 2010, 9, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Stamm, C.; Kachel, T.; Pontius, N.; Mitzner, R.; Quast, T.; Holldack, K.; Khan, S.; Lupulescu, C.; Aziz, E.F.; Wietstruk, M.; et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 2007, 6, 740–743. [Google Scholar] [CrossRef] [PubMed]
- Boeglin, C.; Beaurepaire, E.; Halte, V.; Lopez-Flores, V.; Stamm, C.; Pontius, N.; Durr, H.A.; Bigot, J.-Y. Distinguishing the ultrafast dynamics of spin and orbital moments in solids. Nature 2010, 465, 458–461. [Google Scholar] [CrossRef] [PubMed]
- Pontius, N.; Kachel, T.; Schüßler-Langeheine, C.; Schlotter, W.F.; Beye, M.; Sorgenfrei, F.; Chang, C.F.; Föhlisch, A.; Wurth, W.; Metcalf, P.; et al. Time-resolved resonant soft X-ray diffraction with free-electron lasers: Femtosecond dynamics across the Verwey transition in magnetite. Appl. Phys. Lett. 2011, 98, 182504. [Google Scholar] [CrossRef]
- Eschenlohr, A.; Battiato, M.; Maldonado, P.; Pontius, N.; Kachel, T.; Holldack, K.; Mitzner, R.; Föhlisch, A.; Oppeneer, P.M.; Stamm, C. Ultrafast spin transport as key to femtosecond demagnetization. Nat. Mater. 2013, 12, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, E.; Spezzani, C.; Fortuna, F.; Delaunay, R.; Vidal, F.; Nikolov, I.; Cinquegrana, P.; Diviacco, B.; Gauthier, D.; Penco, G.; et al. Widely tunable two-colour seeded free-electron laser source for resonant-pump resonant-probe magnetic scattering. Nat. Commun. 2016, 7, 10343. [Google Scholar] [CrossRef] [PubMed]
- Muller, G.M.; Walowski, J.; Djordjevic, M.; Miao, G.X.; Gupta, A.; Ramos, A.V.; Gehrke, K.; Moshnyaga, V.; Samwer, K.; Schmalhorst, J.; et al. Spin polarization in half-metals probed by femtosecond spin excitation. Nat. Mater. 2009, 8, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Först, M.; Caviglia, A.D.; Scherwitzl, R.; Mankowsky, R.; Zubko, P.; Khanna, V.; Bromberger, H.; Wilkins, S.B.; Chuang, Y.-D.; Lee, W.S.; et al. Spatially resolved ultrafast magnetic dynamics initiated at a complex oxide heterointerface. Nat. Mater. 2015, 14, 883–888. [Google Scholar] [CrossRef] [PubMed]
- Wietstruk, M.; Melnikov, A.; Stamm, C.; Kachel, T.; Pontius, N.; Sultan, M.; Gahl, C.; Weinelt, M.; Dürr, H.A.; Bovensiepen, U. Hot-electron-driven enhancement of spin-lattice coupling in Gd and Tb 4f ferromagnets observed by femtosecond X-ray magnetic circular dichroism. Phys. Rev. Lett. 2011, 106, 127401. [Google Scholar] [CrossRef] [PubMed]
- Radu, I.; Vahaplar, K.; Stamm, C.; Kachel, T.; Pontius, N.; Durr, H.A.; Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 2011, 472, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Graves, C.E.; Reid, A.H.; Wang, T.; Wu, B.; de Jong, S.; Vahaplar, K.; Radu, I.; Bernstein, D.P.; Messerschmidt, M.; Müller, L.; et al. Nanoscale spin reversal by non-local angular momentum transfer following ultrafast laser excitation in ferrimagnetic GdFeCo. Nat. Mater. 2013, 12, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Le Guyader, L.; Savoini, M.; El Moussaoui, S.; Buzzi, M.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T.; Kimel, A.V.; Nolting, F. Nanoscale sub-100 picosecond all-optical magnetization switching in GdFeCo microstructures. Nat. Commun. 2015, 6, 5839. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Bencivenga, F.; Borghes, R.; Capotondi, F.; Castronovo, D.; Charalambous, P.; Cinquegrana, P.; Danailov, M.B.; de Ninno, G.; Demidovich, A.; et al. Two-colour pump–probe experiments with a twin-pulse-seed extreme ultraviolet free-electron laser. Nat. Commun. 2013, 4, 2476. [Google Scholar] [CrossRef] [PubMed]
- Hara, T.; Inubushi, Y.; Katayama, T.; Sato, T.; Tanaka, H.; Tanaka, T.; Togashi, T.; Togawa, K.; Tono, K.; Yabashi, M.; et al. Two-colour hard X-ray free-electron laser with wide tunability. Nat. Commun. 2013, 4, 2919. [Google Scholar] [CrossRef] [PubMed]
- Lutman, A.A.; Decker, F.-J.; Arthur, J.; Chollet, M.; Feng, Y.; Hastings, J.; Huang, Z.; Lemke, H.; Nuhn, H.-D.; Marinelli, A.; et al. Demonstration of single-crystal self-seeded two-color X-ray free-electron lasers. Phys. Rev. Lett. 2014, 113, 254801. [Google Scholar] [CrossRef] [PubMed]
- Marinelli, A.; Ratner, D.; Lutman, A.A.; Turner, J.; Welch, J.; Decker, F.J.; Loos, H.; Behrens, C.; Gilevich, S.; Miahnahri, A.A.; et al. High-intensity double-pulse X-ray free-electron laser. Nat. Commun. 2015, 6, 6369. [Google Scholar] [CrossRef] [PubMed]
- Lutman, A.A.; Maxwell, T.J.; MacArthur, J.P.; Guetg, M.W.; Berrah, N.; Coffee, R.N.; Ding, Y.; Huang, Z.; Marinelli, A.; Moeller, S.; et al. Fresh-slice multicolour X-ray free-electron lasers. Nat. Photonics 2016, 10, 745–750. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photon. 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Danailov, M.B.; Bencivenga, F.; Capotondi, F.; Casolari, F.; Cinquegrana, P.; Demidovich, A.; Giangrisostomi, E.; Kiskinova, M.P.; Kurdi, G.; Manfredda, M.; et al. Towards jitter-free pump-probe measurements at seeded free electron laser facilities. Opt. Express 2014, 22, 12869–12879. [Google Scholar] [CrossRef] [PubMed]
- Cinquegrana, P.; Cleva, S.; Demidovich, A.; Gaio, G.; Ivanov, R.; Kurdi, G.; Nikolov, I.; Sigalotti, P.; Danailov, M.B. Optical beam transport to a remote location for low jitter pump-probe experiments with a free electron laser. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 040702. [Google Scholar] [CrossRef]
- Pedersoli, E.; Capotondi, F.; Cocco, D.; Zangrando, M.; Kaulich, B.; Menk, R.H.; Locatelli, A.; Mentes, T.O.; Spezzani, C.; Sandrin, G.; et al. Multipurpose modular experimental station for the DiProI beamline of Fermi@Elettra free electron laser. Rev. Sci. Instrum. 2011, 82, 043711. [Google Scholar] [CrossRef] [PubMed]
- Capotondi, F.; Pedersoli, E.; Mahne, N.; Menk, R.H.; Passos, G.; Raimondi, L.; Svetina, C.; Sandrin, G.; Zangrando, M.; Kiskinova, M.; et al. Invited Article: Coherent imaging using seeded free-electron laser pulses with variable polarization: First results and research opportunities. Rev. Sci. Instrum. 2013, 84, 051301. [Google Scholar] [CrossRef] [PubMed]
- Sacchi, M.; Spezzani, C.; Torelli, P.; Avila, A.; Delaunay, R.; Hagie, C.F. Ultra-high vacuum soft X-ray reflectometer. Rev. Sci. Instrum. 2003, 74, 2791–2795. [Google Scholar] [CrossRef]
- Spezzani, C.; Ferrari, E.; Allaria, E.; Vidal, F.; Ciavardini, A.; Delaunay, R.; Capotondi, F.; Pedersoli, E.; Coreno, M.; Svetina, C.; et al. Magnetization and microstructure dynamics in Fe/MnAs/GaAs(001): Fe magnetization reversal by a femtosecond laser pulse. Phys. Rev. Lett. 2014, 113, 247202. [Google Scholar] [CrossRef] [PubMed]
- Sacchi, M.; Panaccione, G.; Vogel, J.; Mirone, A.; van der Laan, G. Magnetic dichroism in reflectivity and photoemission using linearly polarized light: 3p core level of Ni(110). Phys. Rev. B 1998, 58, 3750. [Google Scholar] [CrossRef]
- Allaria, E.; Diviacco, B.; Callegari, C.; Finetti, P.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; de Ninno, G.; Lambert, G.; Ferrari, E.; et al. Control of the polarization of a vacuum-ultraviolet, high-gain, free-electron laser. Phys. Rev. X 2014, 4, 041040. [Google Scholar] [CrossRef]
- Matzen, S.; Moussy, J.-B.; Wei, P.; Gatel, C.; Cezar, J.C.; Arrio, M.A.; Sainctavit, P.; Moodera, J.S. Structure, magnetic ordering, and spin filtering efficiency of NiFe2O4(111) ultrathin films. Appl. Phys. Lett. 2014, 104, 182404. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari, E.; Spezzani, C.; Fortuna, F.; Delaunay, R.; Vidal, F.; Nikolov, I.; Cinquegrana, P.; Diviacco, B.; Gauthier, D.; Penco, G.; et al. Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source. Photonics 2017, 4, 6. https://doi.org/10.3390/photonics4010006
Ferrari E, Spezzani C, Fortuna F, Delaunay R, Vidal F, Nikolov I, Cinquegrana P, Diviacco B, Gauthier D, Penco G, et al. Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source. Photonics. 2017; 4(1):6. https://doi.org/10.3390/photonics4010006
Chicago/Turabian StyleFerrari, Eugenio, Carlo Spezzani, Franck Fortuna, Renaud Delaunay, Franck Vidal, Ivaylo Nikolov, Paolo Cinquegrana, Bruno Diviacco, David Gauthier, Giuseppe Penco, and et al. 2017. "Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source" Photonics 4, no. 1: 6. https://doi.org/10.3390/photonics4010006
APA StyleFerrari, E., Spezzani, C., Fortuna, F., Delaunay, R., Vidal, F., Nikolov, I., Cinquegrana, P., Diviacco, B., Gauthier, D., Penco, G., Ribič, P. R., Roussel, E., Trovò, M., Moussy, J.-B., Pincelli, T., Lounis, L., Svetina, C., Zangrando, M., Mahne, N., ... Sacchi, M. (2017). Element Selective Probe of the Ultra-Fast Magnetic Response to an Element Selective Excitation in Fe-Ni Compounds Using a Two-Color FEL Source. Photonics, 4(1), 6. https://doi.org/10.3390/photonics4010006