Statistical Model and Performance Analysis of a Novel Multilevel Polarization Modulation in Local “Twisted” Fibers
Abstract
:1. Introduction
2. Theoretical Background
2.1. Birefringence Models
2.2. M-PolSK Modulations
3. Statistics of the Proposed Model
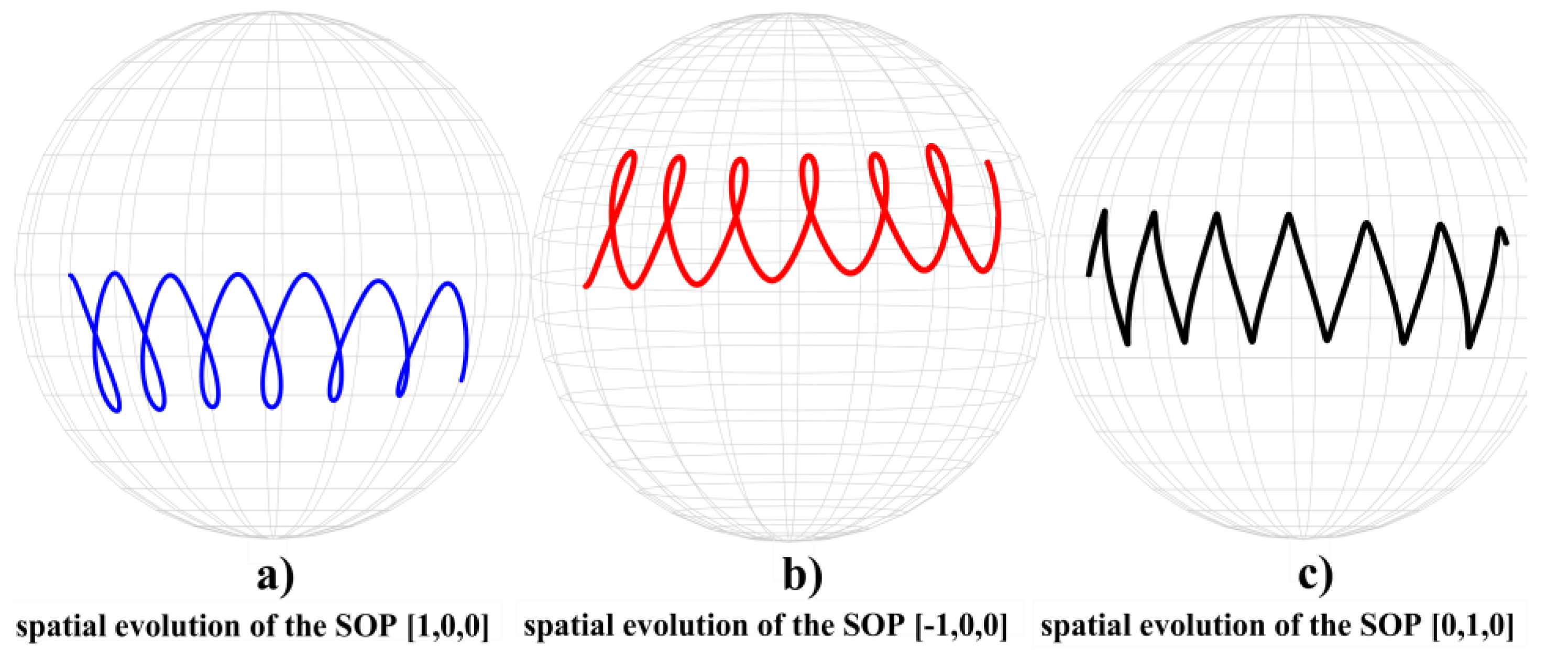
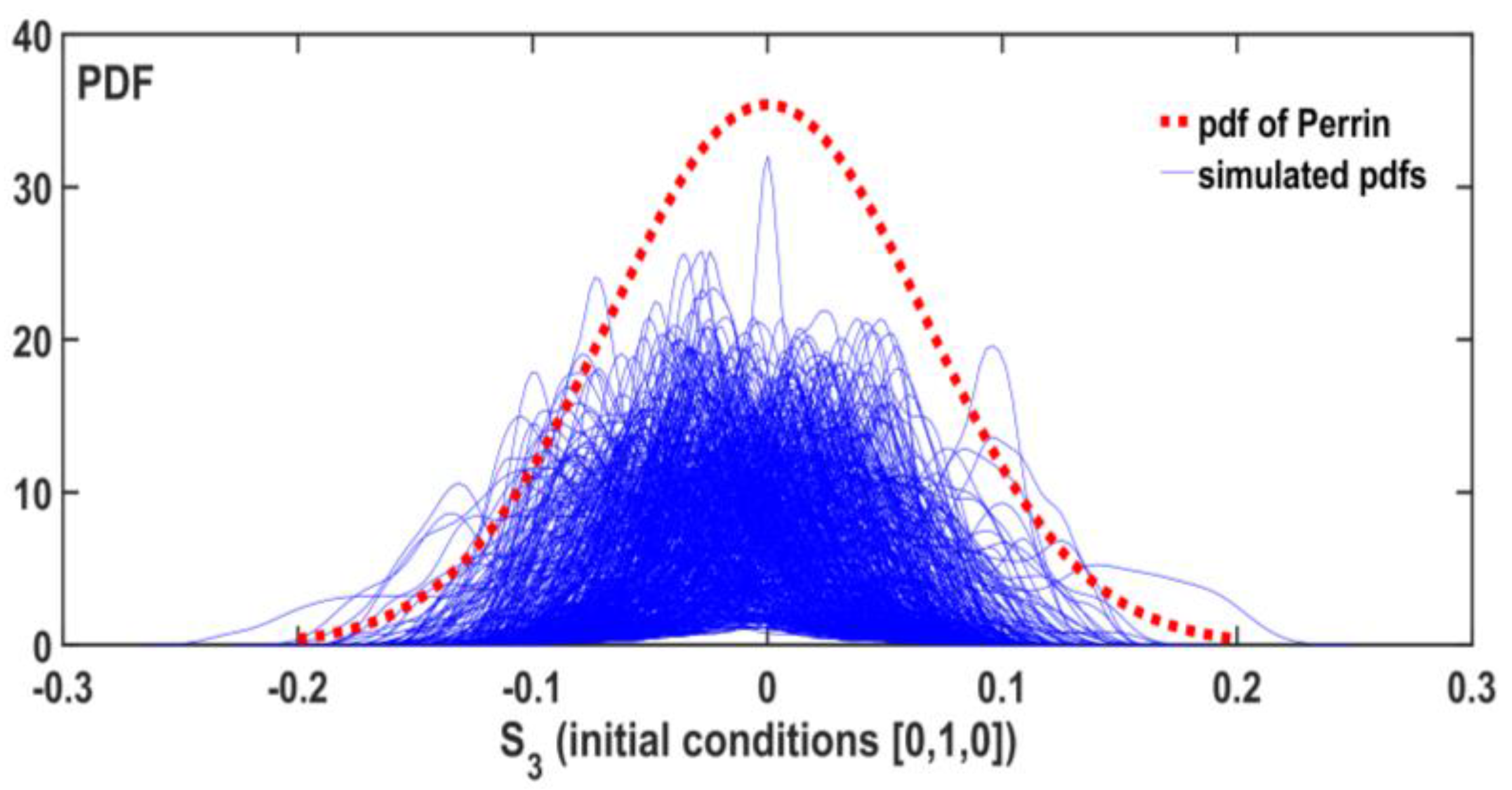
3.1. Simulation Model
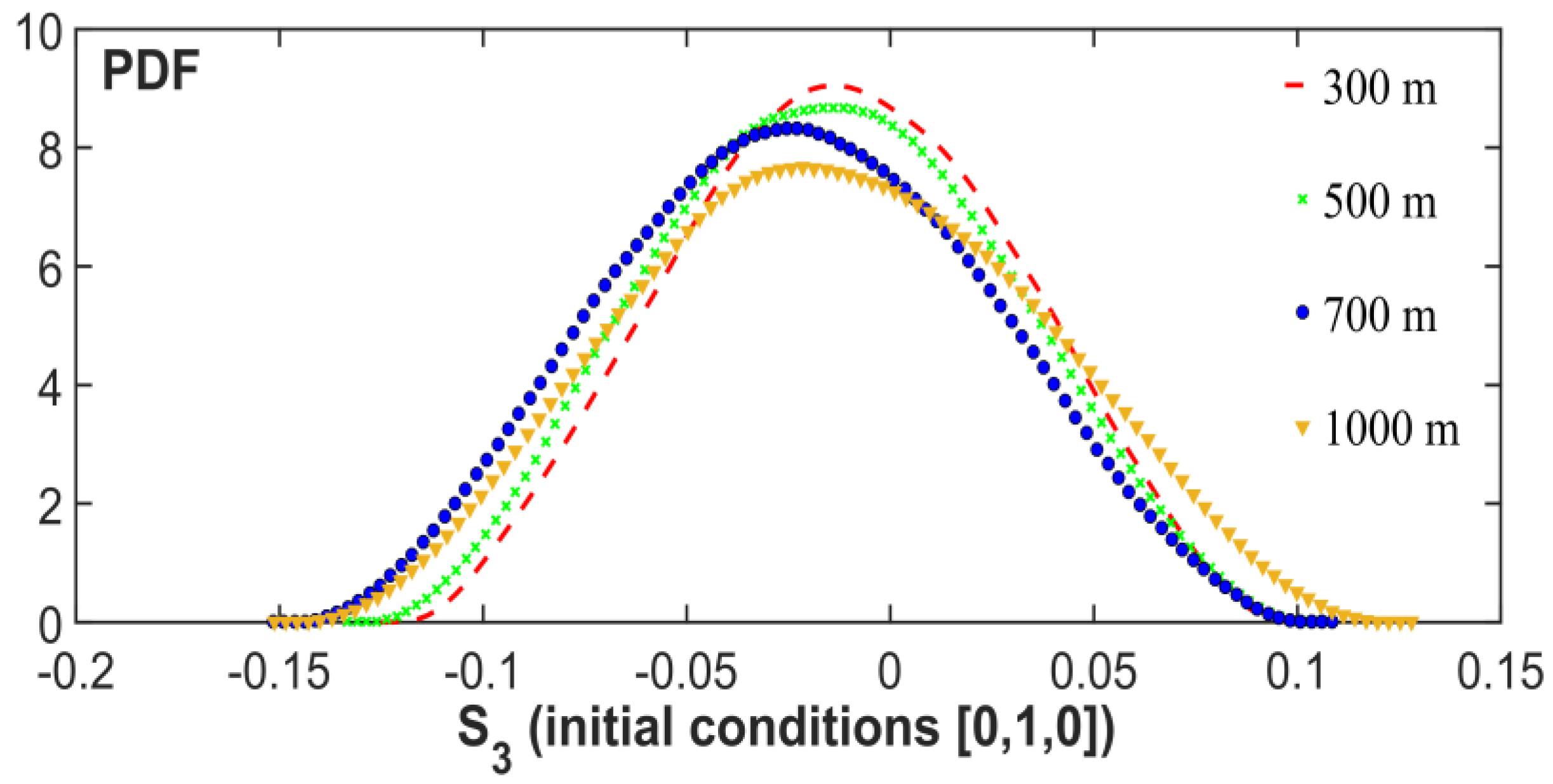
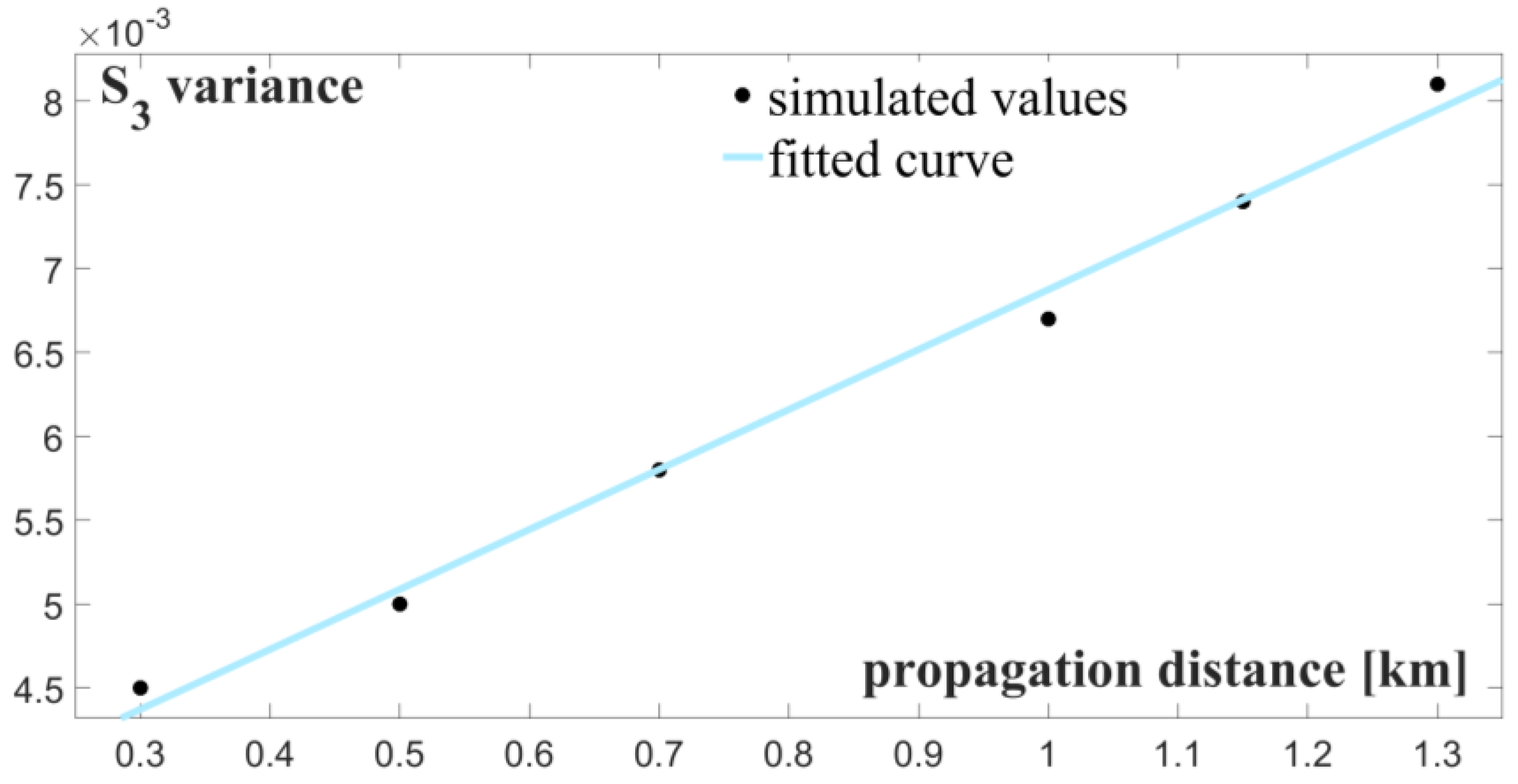
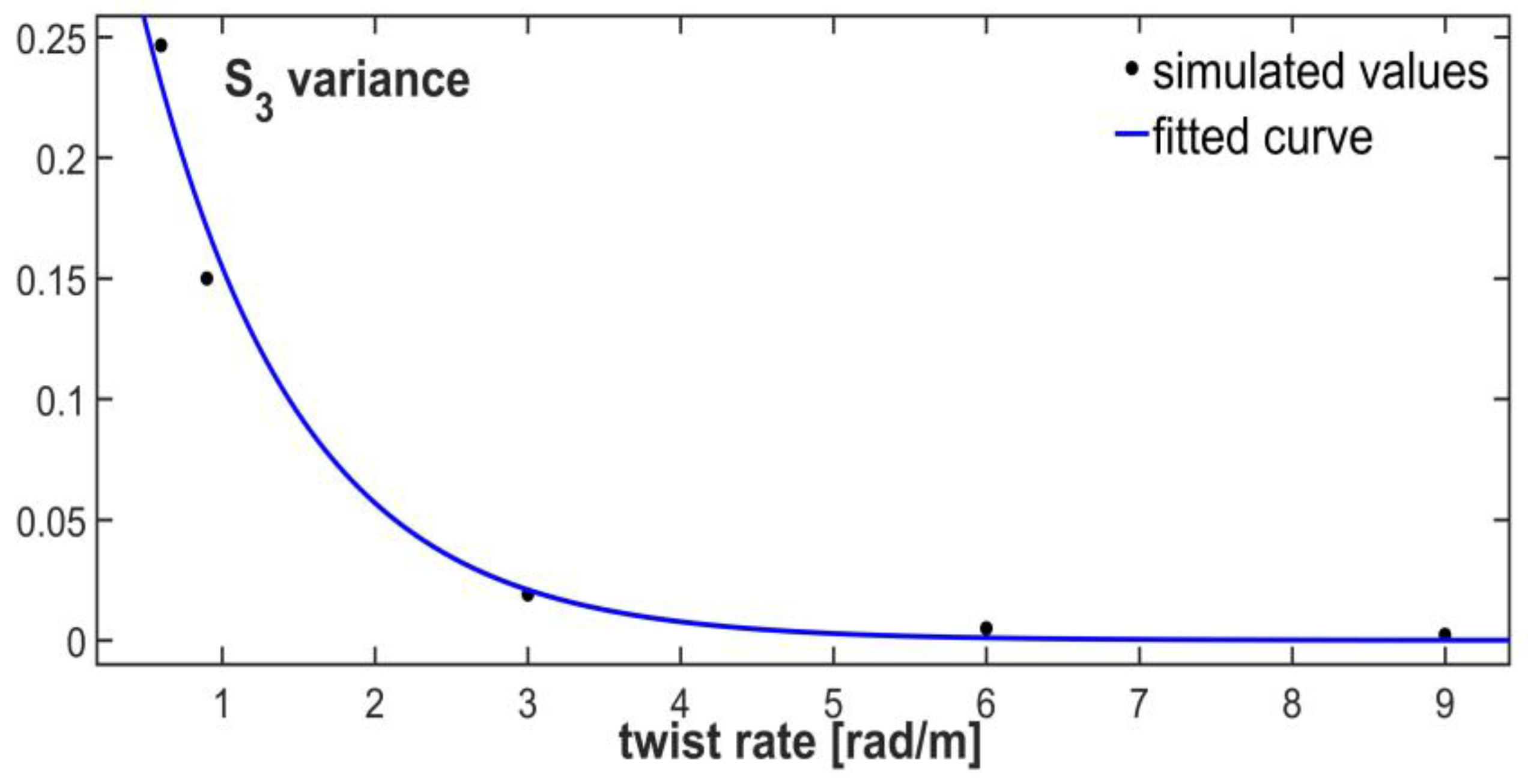
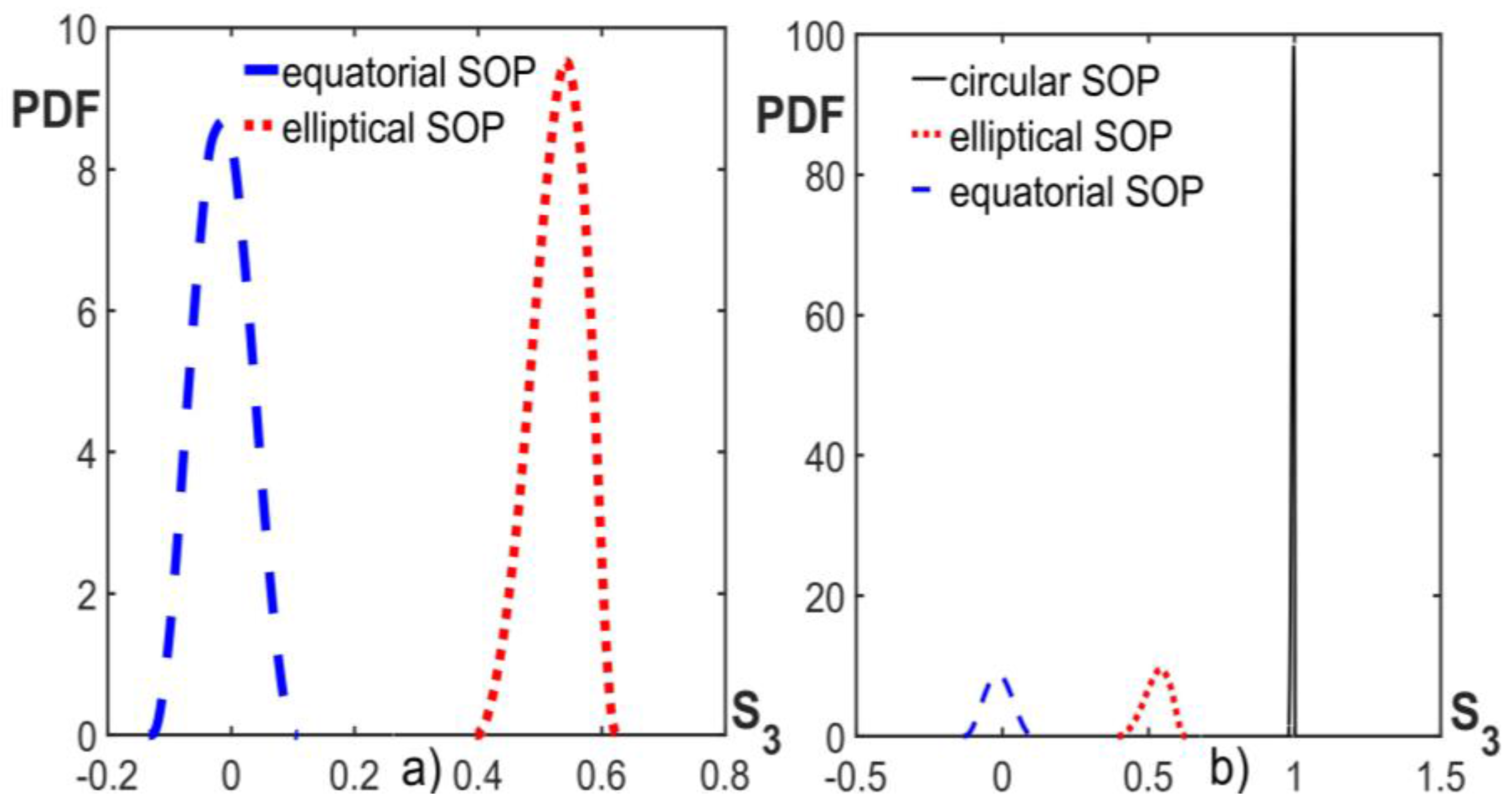
3.2. Statistical Analysis
4. Mathematical Model
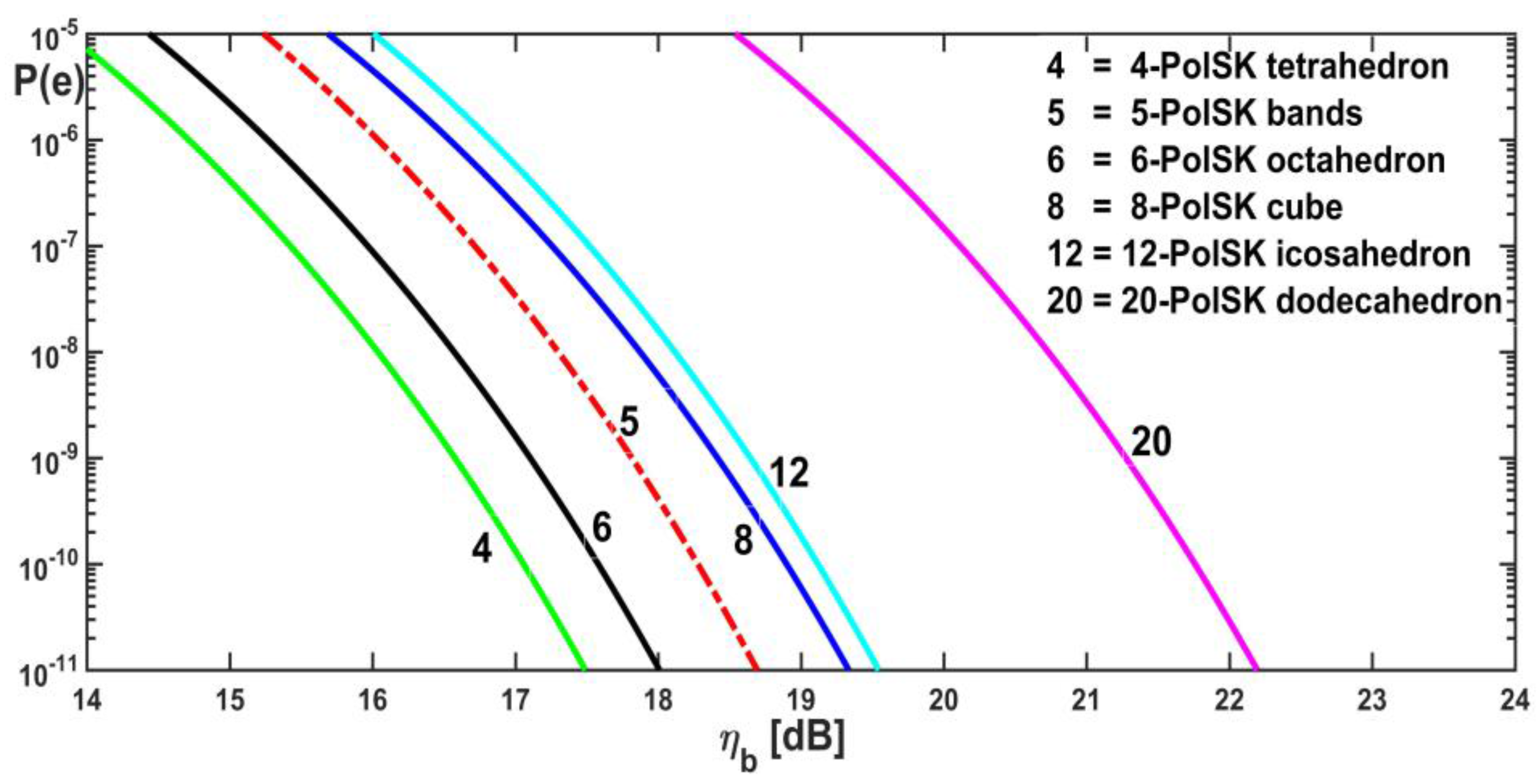
5. Performance Evaluation
5.1. Coherent Detection Performance
5.2. Direct Detection Performance
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Ulrich, R.; Simon, A. Polarization Optics of twisted single-mode fibers. Appl. Opt. 1979, 18, 2241–2251. [Google Scholar] [CrossRef] [PubMed]
- Tentori, D.; Garcia-Weidner, A. Jones birefringence in twisted single-mode optical fibers. Opt. Express 2013, 21, 31725–31739. [Google Scholar] [CrossRef] [PubMed]
- Wai, P.K.A.; Menyuk, C.R. Polarization mode dispersion, decorrelation, and diffusion in optical fibers with randomly varying birefringence. IEEE J. Lightwave Technol. 1996, 14, 148–157. [Google Scholar] [CrossRef]
- Foschini, G.J.; Poole, C.D. Statistical theory of polarization dispersion in single mode fibers. IEEE J. Lightwave Technol. 1991, 9, 1439–1456. [Google Scholar] [CrossRef]
- Galtarossa, A.; Palmieri, L. Measure of twist-induced circular birefringence in long single-mode fibers: Theory and experiments. IEEE J. Lightwave Technol. 2002, 20, 1149–1159. [Google Scholar] [CrossRef]
- Tanemura, T.; Kikuchi, K. Circular-birefringence fiber for nonlinear optical signal processing. IEEE J. Lightwave Technol. 2006, 24, 4108–4119. [Google Scholar] [CrossRef]
- Benedetto, S.; Poggiolini, P.T. Multilevel Polarization Shift Keying: Optimum Receiver Structure and Performance Evaluation. IEEE Trans. Commun. 1994, 42, 1174–1186. [Google Scholar] [CrossRef]
- Betti, S.; Curti, F.; De Marchis, G.; Iannone, E. A Novel Multilevel Coherent Optical System: 4-Quadrature Signaling. IEEE J. Lightwave Technol. 1991, 9, 514–523. [Google Scholar] [CrossRef]
- Betti, S.; Curti, F.; De Marchis, G.; Iannone, E. Multilevel coherent optical system based on Stokes parameters modulation. IEEE J. Lightwave Technol. 1990, 8, 1127–1136. [Google Scholar] [CrossRef]
- Perrone, P.; Betti, S.; Rutigliano, G.G. Optical communication system for high-capacity LAN. Microw. Opt. Technol. Lett. 2016, 58, 389–393. [Google Scholar] [CrossRef]
- Bayvel, P.; Maher, R.; Xu, T.; Liga, G.; Shevchenko, N.A.; Lavery, D.; Alvarado, A.; Killey, R.I. Maximizing the optical network capacity. Philos. Trans. R. Soc. A 2016, 374, 20140440. [Google Scholar] [CrossRef] [PubMed]
- Semrau, D.; Xu, T.; Shevchenko, N.A.; Paskov, M.; Alvarado, A.; Killey, R.I.; Bayvel, P. Achievable information rates estimates in optically amplified transmission systems using nonlinearity compensation and probabilistic shaping. Opt. Lett. 2017, 42, 121–124. [Google Scholar] [CrossRef] [PubMed]
- Perrin, F. Etude mathématique du mouvement Brownien de rotation. In Annales Scientifiques de L’école Normale Supérieure; Gauthier-Villars et Cle, Editeurs: Paris, France, 1928; Volume 45, pp. 1–51. [Google Scholar]
- Betti, S.; De Marchis, G.; Iannone, E. Polarization modulated direct detection optical transmission systems. IEEE J. Lightwave Technol. 1992, 10, 1985–1997. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Wai, P.K.A.; Menyuk, C.R. Polarization decorrelation in optical fibers with randomly varying birefringence. Opt. Lett. 1994, 19, 1517–1519. [Google Scholar] [CrossRef] [PubMed]
- Agrell, E.; Karlsson, M. Power efficient modulation formats in coherent transmission systems. IEEE J. Lightwave Technol. 2009, 27, 5115–5126. [Google Scholar] [CrossRef]
- Winzer, P.J.; Essiambre, R.J. Advanced optical modulation formats. Proc. IEEE 2006, 94, 952–985. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Simon, A.; Ulrich, R. Evolution of polarization along a single mode fiber. Appl. Phys. Lett. 1977, 31, 517–520. [Google Scholar] [CrossRef]





| N | |||
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 2 | 0 | ||
| 3 | 0 | 1 | 0 |
| 4 | 0 | − | |
| 5 | 0 | 0 | −1 |
| N | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0 | 0.765 | 1.847 | 2 | |
| 2 | 0.765 | 0 | 0.765 | 1.847 | |
| 3 | 0.765 | 0 | 0.765 | ||
| 4 | 1.847 | 0.765 | 0 | 0.765 | |
| 5 | 2 | 1.847 | 0.765 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrone, P.; Betti, S.; Rutigliano, G.G. Statistical Model and Performance Analysis of a Novel Multilevel Polarization Modulation in Local “Twisted” Fibers. Photonics 2017, 4, 5. https://doi.org/10.3390/photonics4010005
Perrone P, Betti S, Rutigliano GG. Statistical Model and Performance Analysis of a Novel Multilevel Polarization Modulation in Local “Twisted” Fibers. Photonics. 2017; 4(1):5. https://doi.org/10.3390/photonics4010005
Chicago/Turabian StylePerrone, Pierluigi, Silvello Betti, and Giuseppe Giulio Rutigliano. 2017. "Statistical Model and Performance Analysis of a Novel Multilevel Polarization Modulation in Local “Twisted” Fibers" Photonics 4, no. 1: 5. https://doi.org/10.3390/photonics4010005
APA StylePerrone, P., Betti, S., & Rutigliano, G. G. (2017). Statistical Model and Performance Analysis of a Novel Multilevel Polarization Modulation in Local “Twisted” Fibers. Photonics, 4(1), 5. https://doi.org/10.3390/photonics4010005




