Analytical Solution for the Stopping Power of the Cherenkov Radiation in a Uniaxial Nanowire Material
Abstract
:1. Introduction

2. Wave Dynamics in Uniaxial Wire Media
3. Stopping Power of Uniaxial Wire Media
3.1. Array of Charges Moving inside the Wire Medium
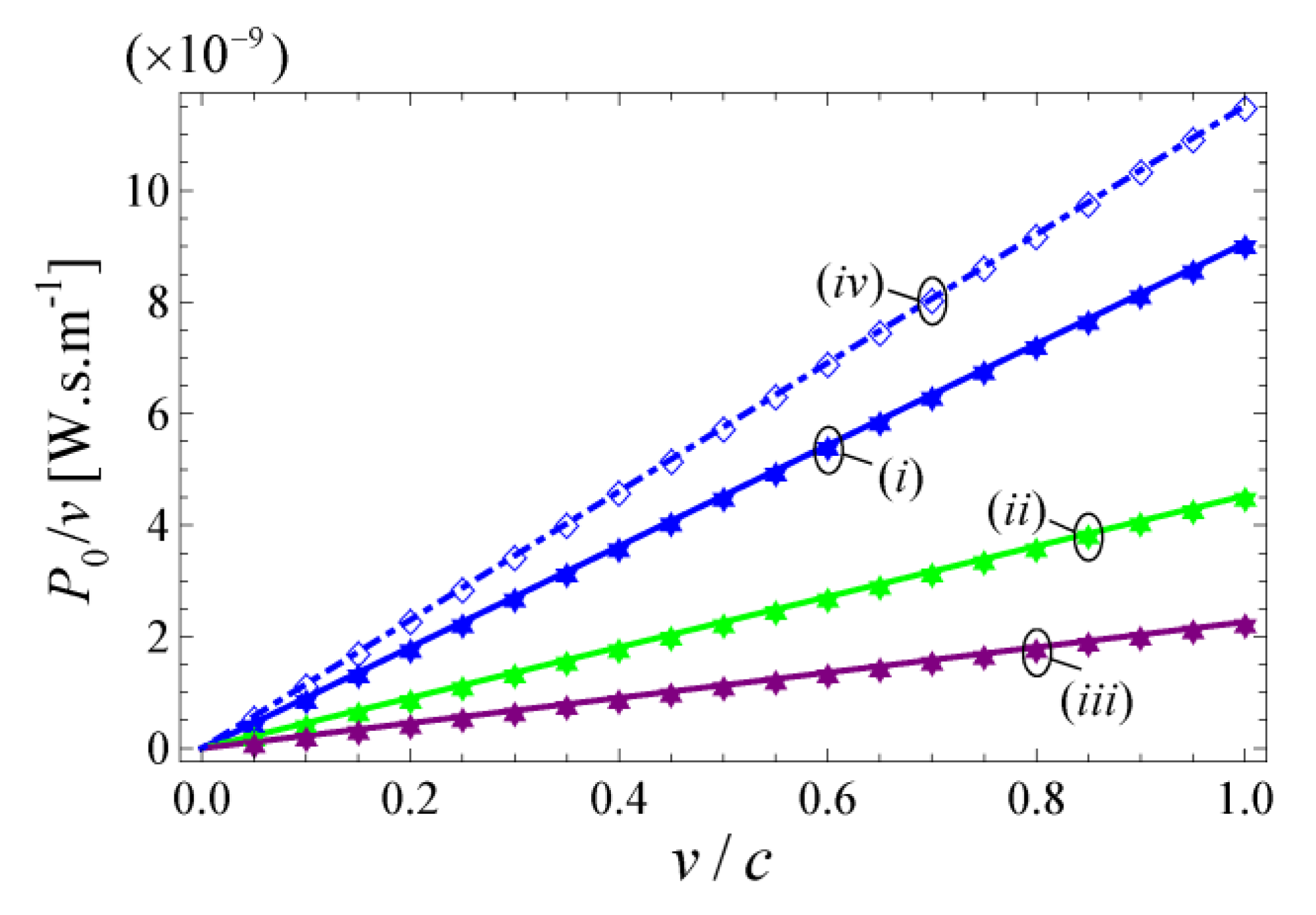
3.2. Single Charge Moving inside the Wire Medium
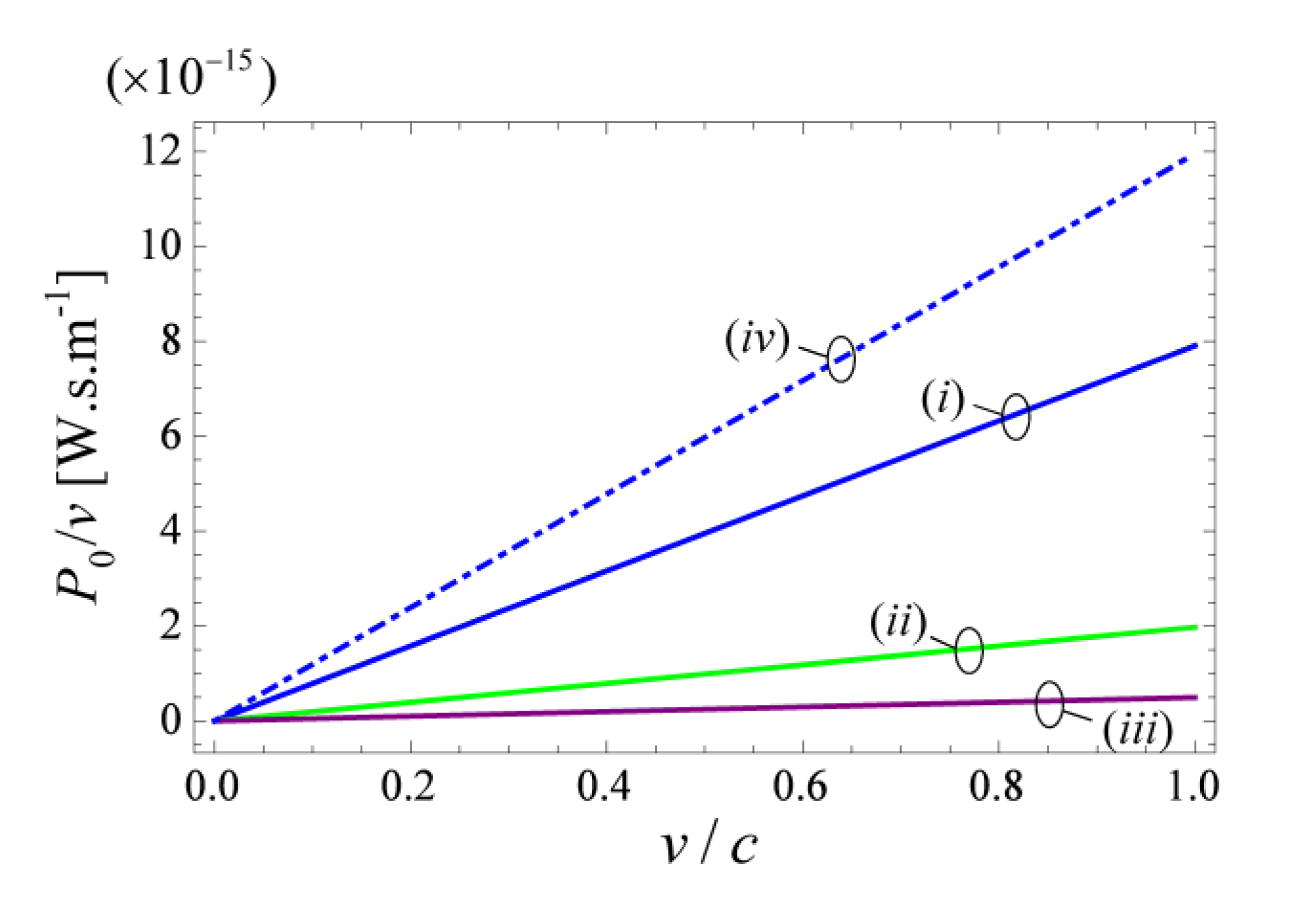
4. Generalization to Dispersive Media
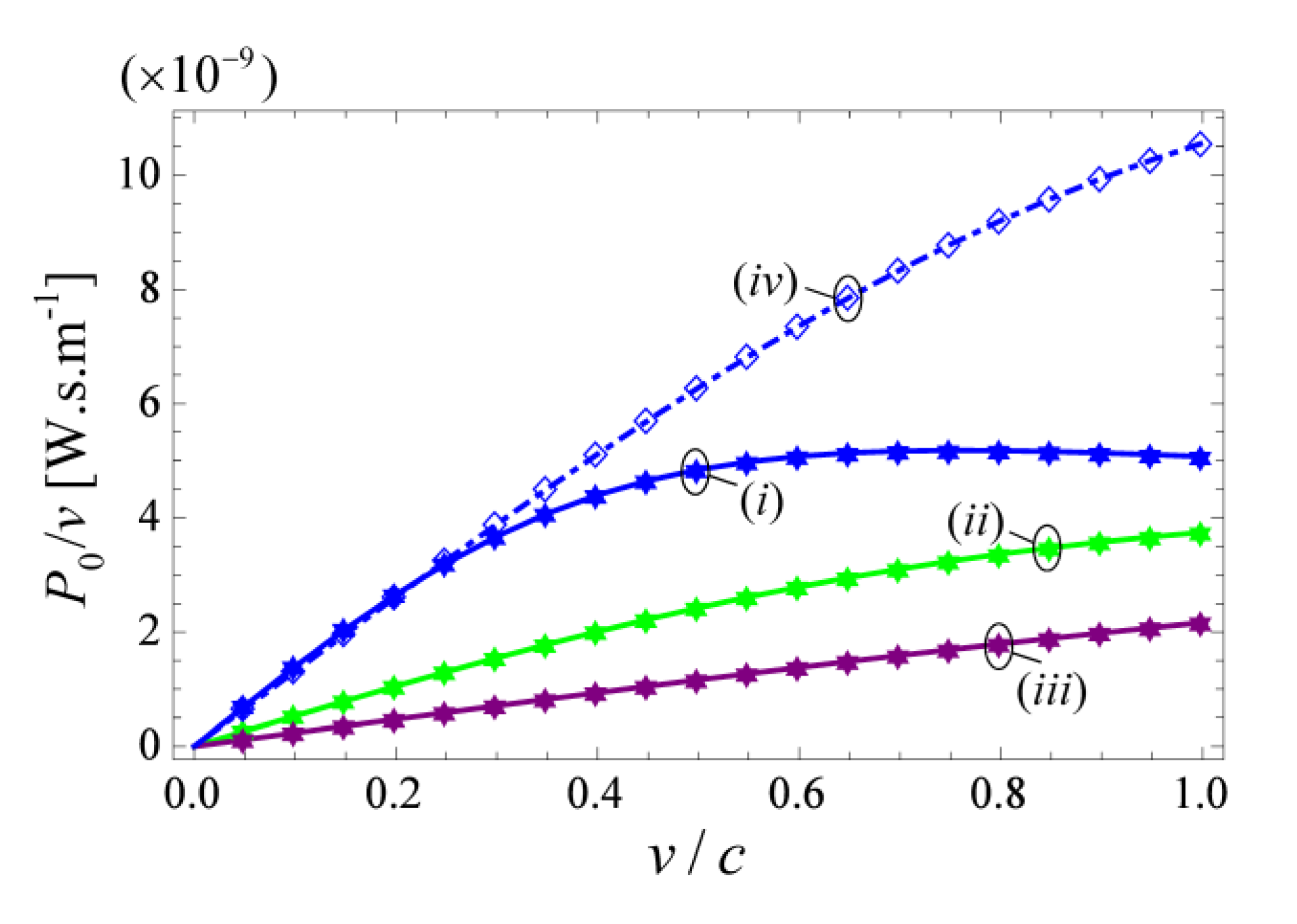
5. Conclusion
Acknowledgement
Author Contributions
Conflict of Interest
Appendix A
References
- Cherenkov, P.A. Visible Emission of Clean Liquids by Action of γ Radiation. Dokl. Akad. Nauk SSSR 1934, 2, 451–454. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1984. [Google Scholar]
- Jelley, J.V. Čerenkov Radiation and its Applications; Pergamon Press: London, UK, 1985. [Google Scholar]
- Akimov, Y.K. Cherenkov detectors in particle physics. Phys. At. Nucl. 2011, 67, 1385–1389. [Google Scholar] [CrossRef]
- Adamo, G.; MacDonald, K.F.; Fu, Y.H.; Wang, C.M.; Tsai, D.P.; de García Abajo, F.J.; Zheludev, N.I. Light well: A tunable free-electron light source on a chip. Phys. Rev. Lett. 2009, 103, 113901. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, P.; Liu, W.; Gong, S.; Zhong, R.; Zhang, Y.; Hu, M. Surface polariton Cherenkov light radiation source. Phys. Rev. Lett. 2012, 109, 153902. [Google Scholar] [CrossRef] [PubMed]
- Vijayraghavan, K.; Jiang, Y.; Jang, M.; Jiang, A.; Choutagunta, K.; Vizbaras, A.; Demmerle, F.; Boehm, G.; Amann, M.C.; Belkin, M.A. Broadly tunable terahertz generation in mid-infrared quantum cascade lasers. Nat. Commun. 2013. [Google Scholar] [CrossRef] [PubMed]
- De García Abajo, F.J.; Zabala, N.; Rivacoba, A.; Pattantyus-Abraham, A.G.; Wolf, M.O.; Echenique, P.M. Cherenkov effect as a probe of photonic nanostructures. Phys. Rev. Lett. 2003, 91, 143902. [Google Scholar] [CrossRef]
- Frank, I.M.; Tamm, I.E. Coherent visible radiation of fast electrons passing through matter. Dokl. Akad. Nauk SSSR 1937, 14, 109–114. [Google Scholar]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Lu, J.; Grzegorczyk, T.; Zhang, Y.; Pacheco, J., Jr.; Wu, B.-I.; Kong, J.; Chen, M. Čerenkov radiation in materials with negative permittivity and permeability. Opt. Express 2003, 11, 723–734. [Google Scholar] [CrossRef] [PubMed]
- Galyamin, S.N.; Tyukhtin, A.V.; Kanareykin, A.; Schoessow, P. Reversed Cherenkov-transition radiation by a charge crossing a left-handed medium boundary. Phys. Rev. Lett. 2009, 103, 194802. [Google Scholar] [CrossRef] [PubMed]
- Averkov, Y.O.; Yakovenko, V.M. Cherenkov radiation by an electron bunch that moves in a vacuum above a left-handed material. Phys. Rev. B 2005, 72, 205110. [Google Scholar] [CrossRef]
- Duan, Z.; Wu, B.-I.; Lu, J.; Kong, J.A.; Chen, M. Cherenkov radiation in anisotropic double-negative metamaterials. Opt. Express 2008, 16, 18479. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Wu, B.-I.; Lu, J.; Kong, J.A.; Chen, M. Reversed Cherenkov radiation in a waveguide filled with anisotropic double-negative metamaterials. J. Appl. Phys. 2008, 104, 063303. [Google Scholar] [CrossRef]
- Xi, S.; Chen, H.; Jiang, T.; Ran, L.; Huangfu, J.; Wu, B.-I.; Kong, J.A.; Chen, M. Experimental verification of reversed Cherenkov radiation in left-handed metamaterial. Phys. Rev. Lett. 2009, 103, 194801. [Google Scholar] [CrossRef] [PubMed]
- So, J.-K.; Won, J.-H.; Sattorov, M.A.; Bak, S.-H.; Jang, K.H.; Park, G.-S.; Kim, D.S.; Garcia-Vidal, F.J. Cerenkov radiation in metallic metamaterials. Appl. Phys. Lett. 2010, 97, 151107. [Google Scholar] [CrossRef]
- Fernandes, D.E.; Maslovski, S.I.; Silveirinha, M.G. Cherenkov emission in a nanowire material. Phys. Rev. B 2012, 85, 155107. [Google Scholar] [CrossRef]
- Vorobev, V.V.; Tyukhtin, A.V. Nondivergent Cherenkov radiation in a wire metamaterial. Phys. Rev. Lett. 2012, 108, 184801. [Google Scholar] [CrossRef] [PubMed]
- Tyukhtin, A.V.; Vorobev, V.V. Radiation of charges moving along the boundary of a wire metamaterial. Phys. Rev. E 2014, 89, 013202. [Google Scholar] [CrossRef]
- Tyukhtin, A.V.; Vorobev, V.V. Cherenkov radiation in a metamaterial comprised of coated wires. J. Opt. Soc. Am. B 2013, 30, 1524–1531. [Google Scholar] [CrossRef]
- Tyukhtin, A.V.; Vorobev, V.V.; Galyamin, S.N. Radiation excited by a charged-particle bunch on a planar periodic wire structure. Phys. Rev. ST Accel. Beams 2014, 17, 122802. [Google Scholar] [CrossRef]
- Ginis, V.; Danckaert, J.; Veretennicoff, I.; Tassin, P. Controlling Cherenkov radiation with transformation-optical metamaterials. Phys. Rev. Lett. 2014, 113, 167402. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Ibanescu, M.; Johnson, S.G.; and Joannopoulos, J.D. Cherenkov radiation in photonic crystals. Science 2003, 299, 368–371. [Google Scholar] [CrossRef] [PubMed]
- Maslovski, S.I.; Silveirinha, M.G. Nonlocal permittivity from a quasistatic model for a class of wire media. Phys. Rev. B 2009, 80, 245101. [Google Scholar] [CrossRef]
- Silveirinha, M.G.; Maslovski, S.I. Radiation from elementary sources in a uniaxial wire medium. Phys. Rev. B 2012, 85, 155125. [Google Scholar] [CrossRef]
- Belov, P.A.; Marqués, R.; Maslovski, S.I.; Nefedov, I.S.; Silveirinha, M.G.; Simovski, C.R.; Tretyakov, S.A. Strong spatial dispersion in wire media in the very large wavelength limit. Phys. Rev. B 2003, 67, 113103. [Google Scholar] [CrossRef]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer-Verlag: Berlin, Germany, 2001. [Google Scholar]
- Tyukhtin, A.V.; Doilnitsina, E.G. Effective permittivity of a metamaterial from coated wires. J. Phys. D 2011, 44, 265401. [Google Scholar] [CrossRef]
- Maslovski, S.I.; Silveirinha, M.G. Ultralong-range Casimir Lifshitz forces mediated by nanowire materials. Phys. Rev. A 2010, 82, 022511. [Google Scholar] [CrossRef]
- Maslovski, S.I.; Silveirinha, M.G. Mimicking Boyer's Casimir repulsion with a nanowire material. Phys. Rev. A 2011, 83, 022508. [Google Scholar] [CrossRef]
- Raman, A.; Fan, S. Photonic band structure of dispersive metamaterials formulated as a Hermitian eigenvalue problem. Phys. Rev. Lett. 2010, 104, 087401. [Google Scholar] [CrossRef] [PubMed]
- Silveirinha, M.G. Nonlocal homogenization model for a periodic array of ϵ-negative rods. Phys. Rev. E 2006, 73, 046612. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Artificial plasma formed by connected metallic wires at infrared frequencies. Phys. Rev. B 2009, 79, 035118. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Poynting vector, heating rate, and stored energy in structured materials: A first-principles derivation. Phys. Rev. B 2009, 80, 235120. [Google Scholar] [CrossRef]
- Costa, J.T.; Silveirinha, M.G.; Alù, A. Poynting vector in negative-index metamaterials. Phys. Rev. B 2011, 83, 165120. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W., Jr.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared - Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt 1985, 24, 4493. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morgado, T.A.; Fernandes, D.E.; Silveirinha, M.G. Analytical Solution for the Stopping Power of the Cherenkov Radiation in a Uniaxial Nanowire Material. Photonics 2015, 2, 702-718. https://doi.org/10.3390/photonics2020702
Morgado TA, Fernandes DE, Silveirinha MG. Analytical Solution for the Stopping Power of the Cherenkov Radiation in a Uniaxial Nanowire Material. Photonics. 2015; 2(2):702-718. https://doi.org/10.3390/photonics2020702
Chicago/Turabian StyleMorgado, Tiago A., David E. Fernandes, and Mário G. Silveirinha. 2015. "Analytical Solution for the Stopping Power of the Cherenkov Radiation in a Uniaxial Nanowire Material" Photonics 2, no. 2: 702-718. https://doi.org/10.3390/photonics2020702
APA StyleMorgado, T. A., Fernandes, D. E., & Silveirinha, M. G. (2015). Analytical Solution for the Stopping Power of the Cherenkov Radiation in a Uniaxial Nanowire Material. Photonics, 2(2), 702-718. https://doi.org/10.3390/photonics2020702





