Optical Scattering Cancellation through Arrays of Plasmonic Nanoparticles: A Review
Abstract
:1. Introduction
2. Analytical Models
2.1. Volumetric Homogenization
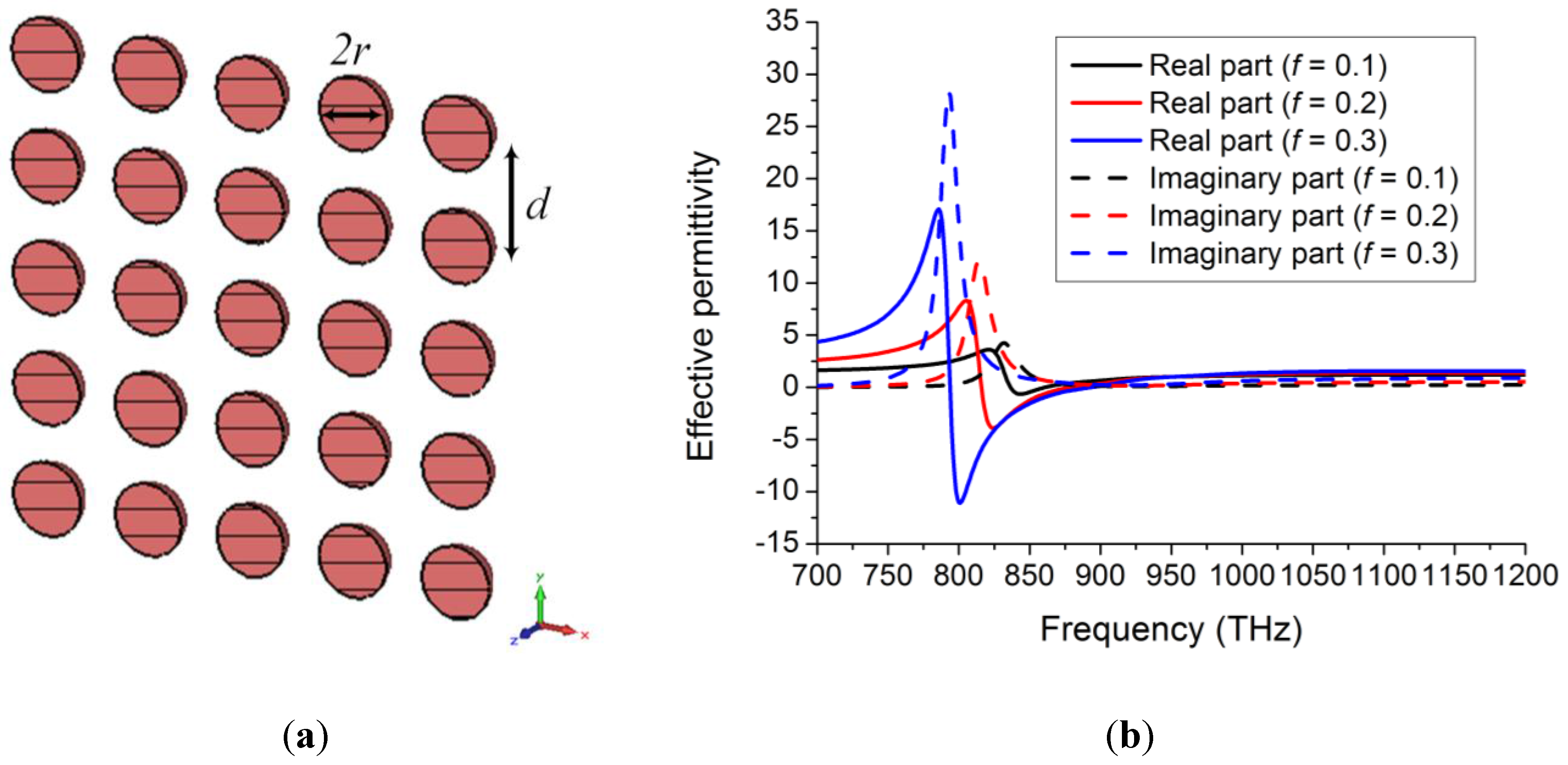
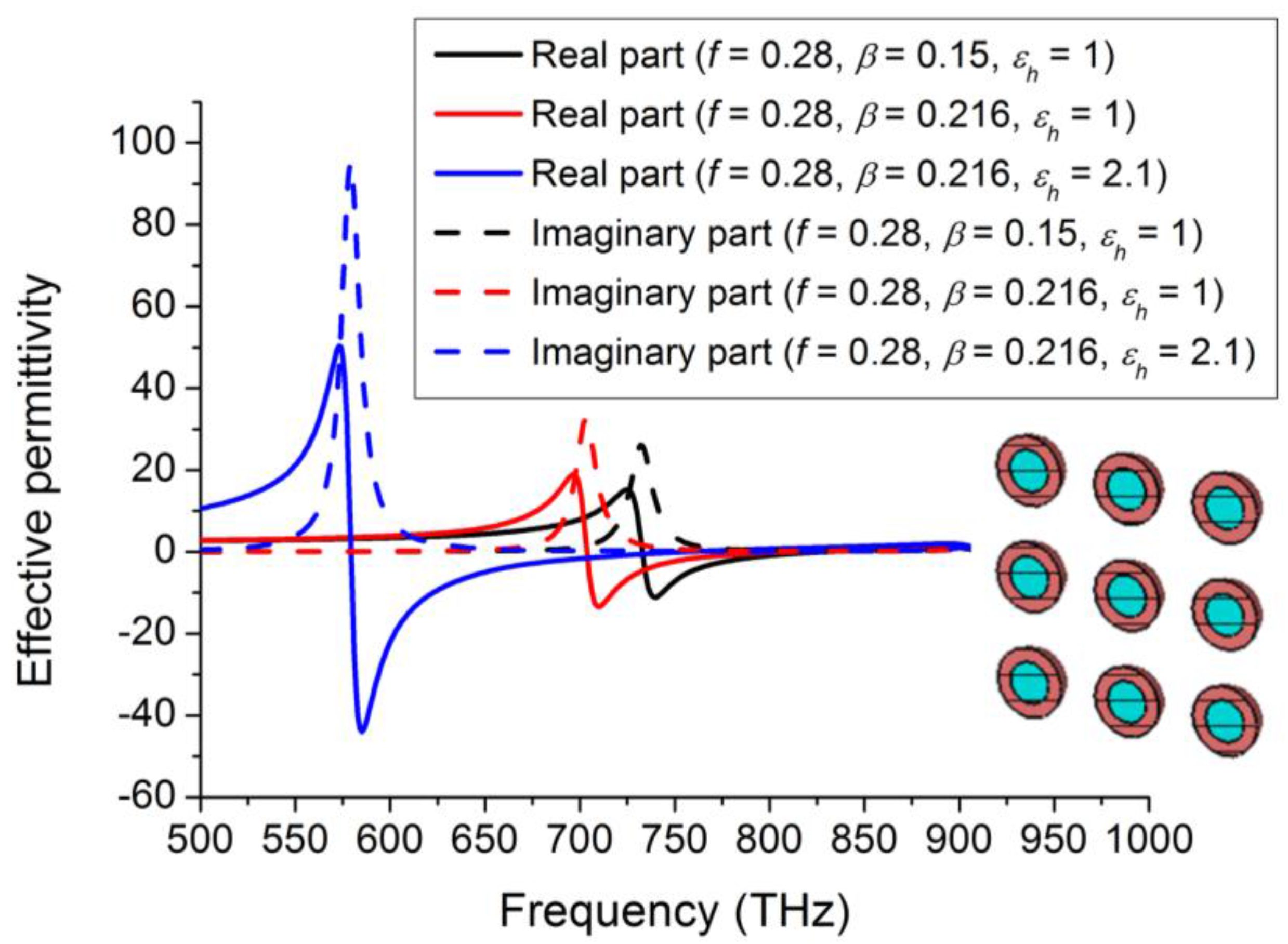
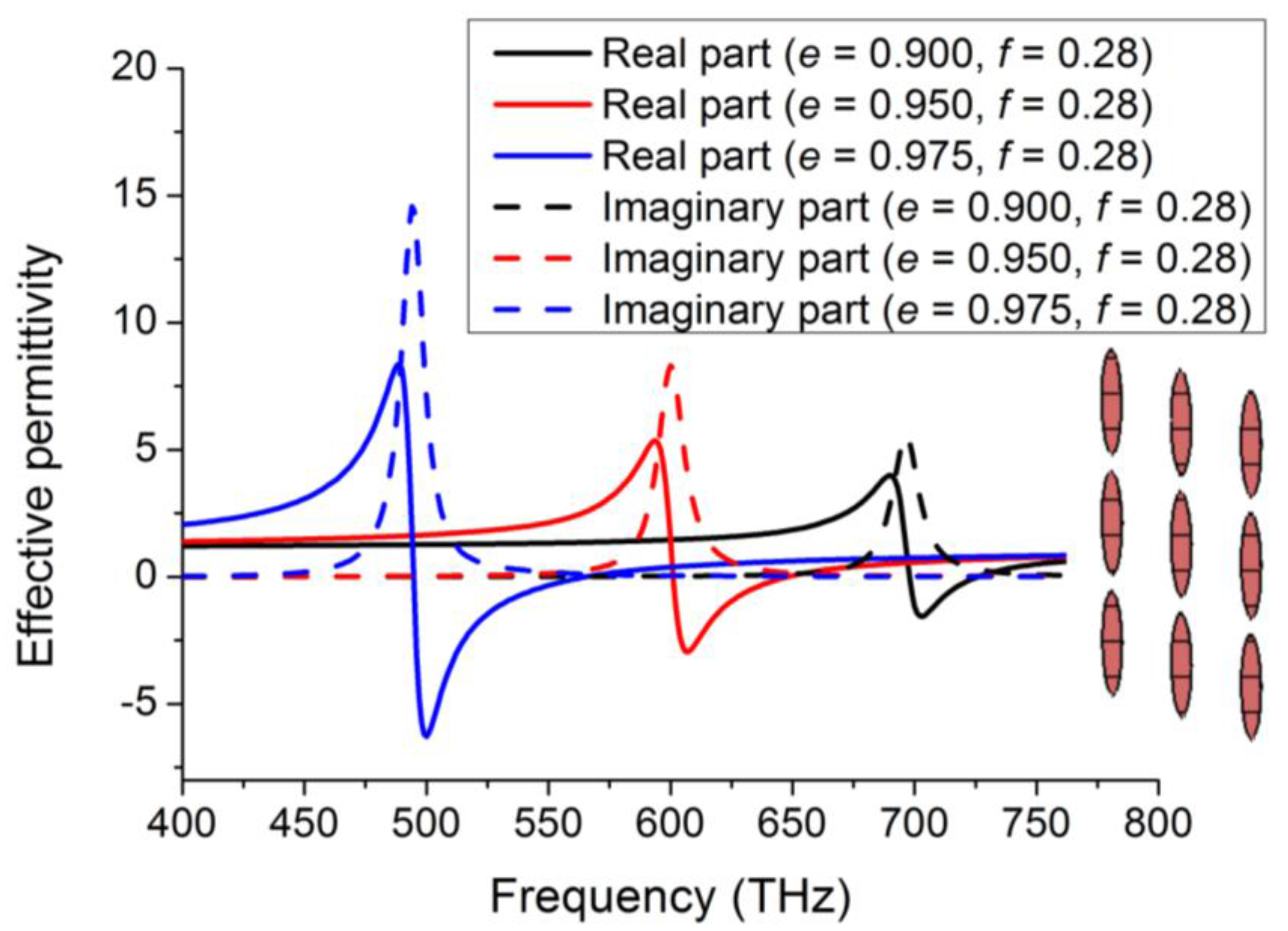
2.2. Metasurface Homogenization
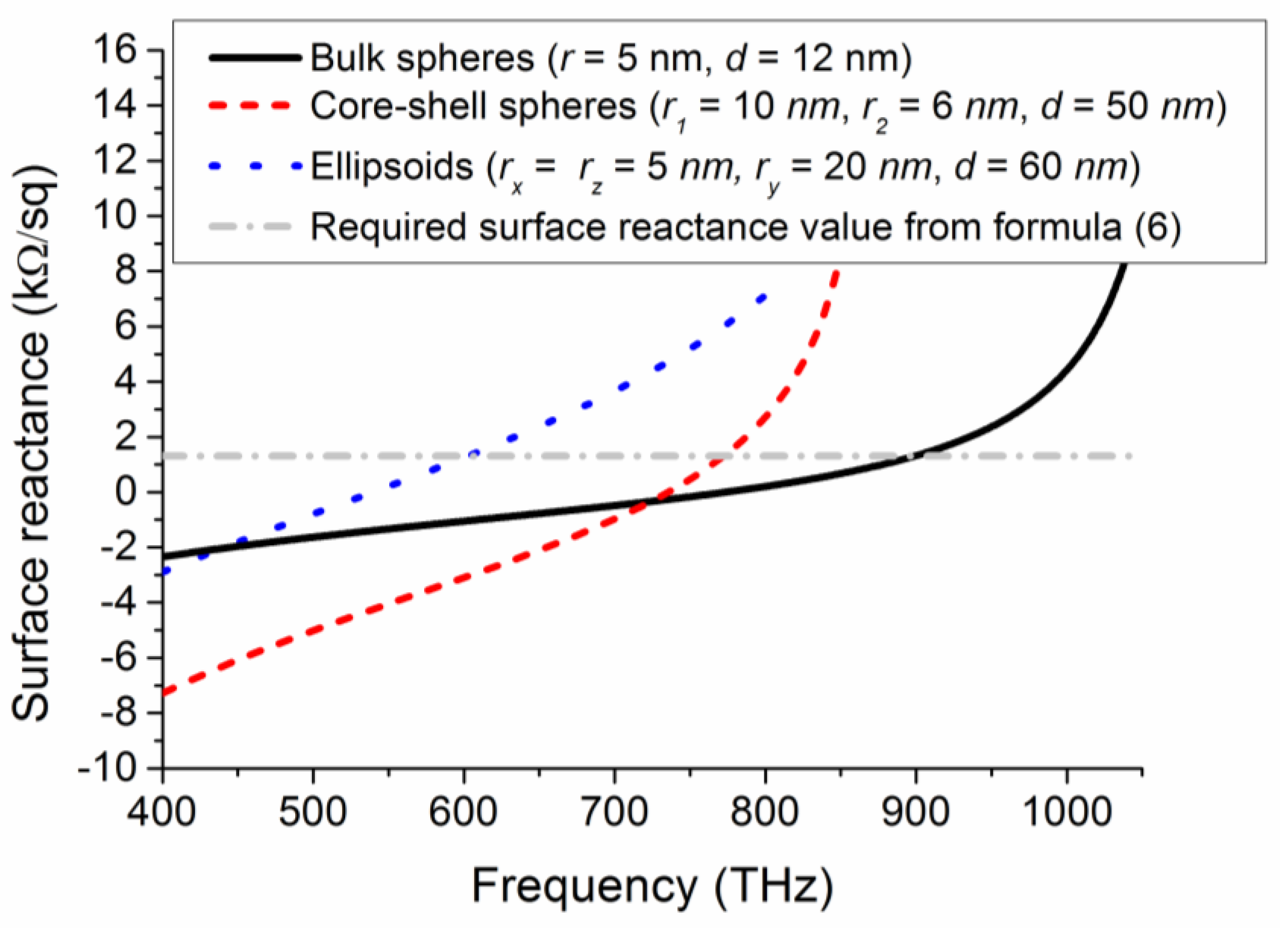
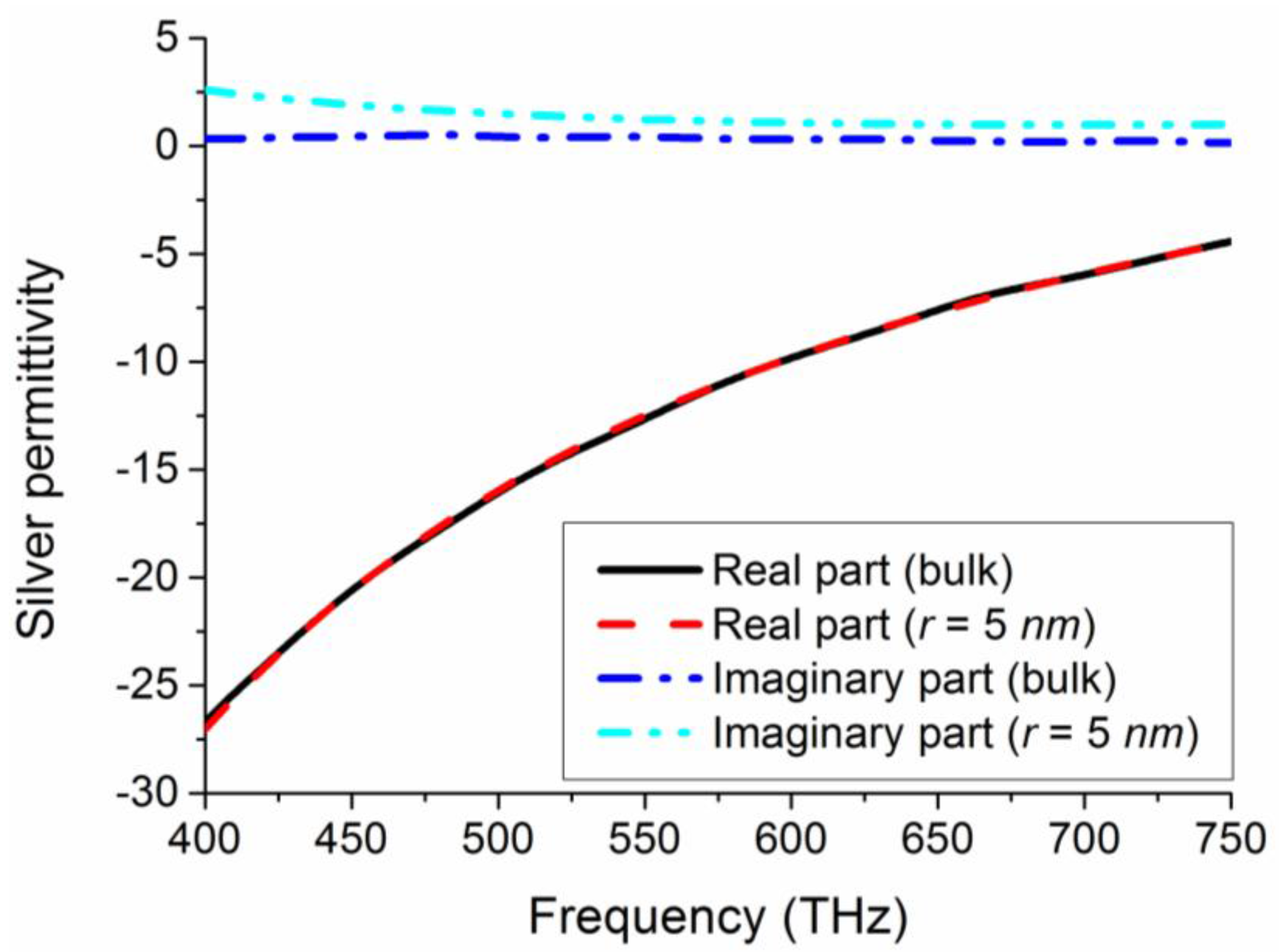
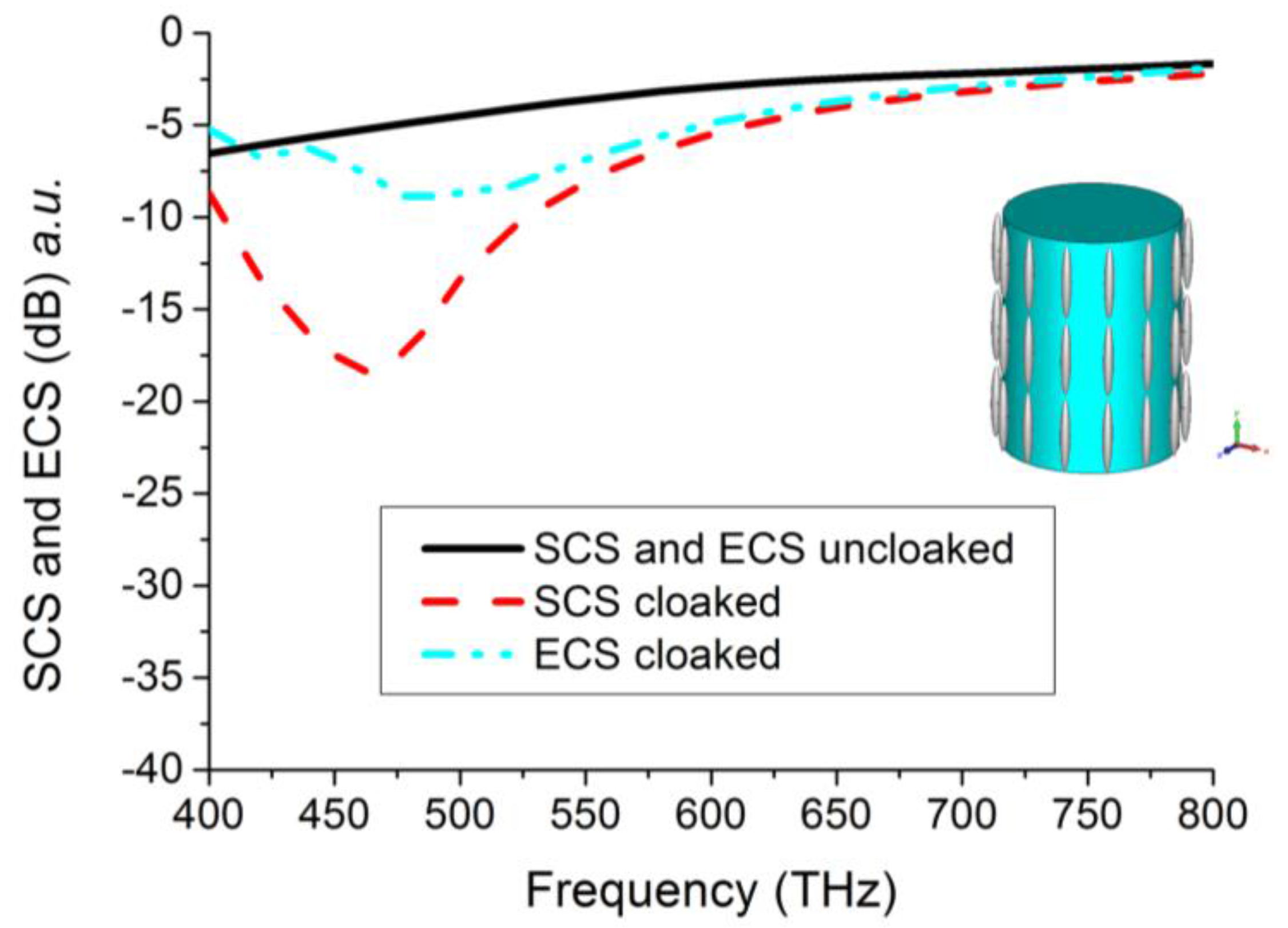
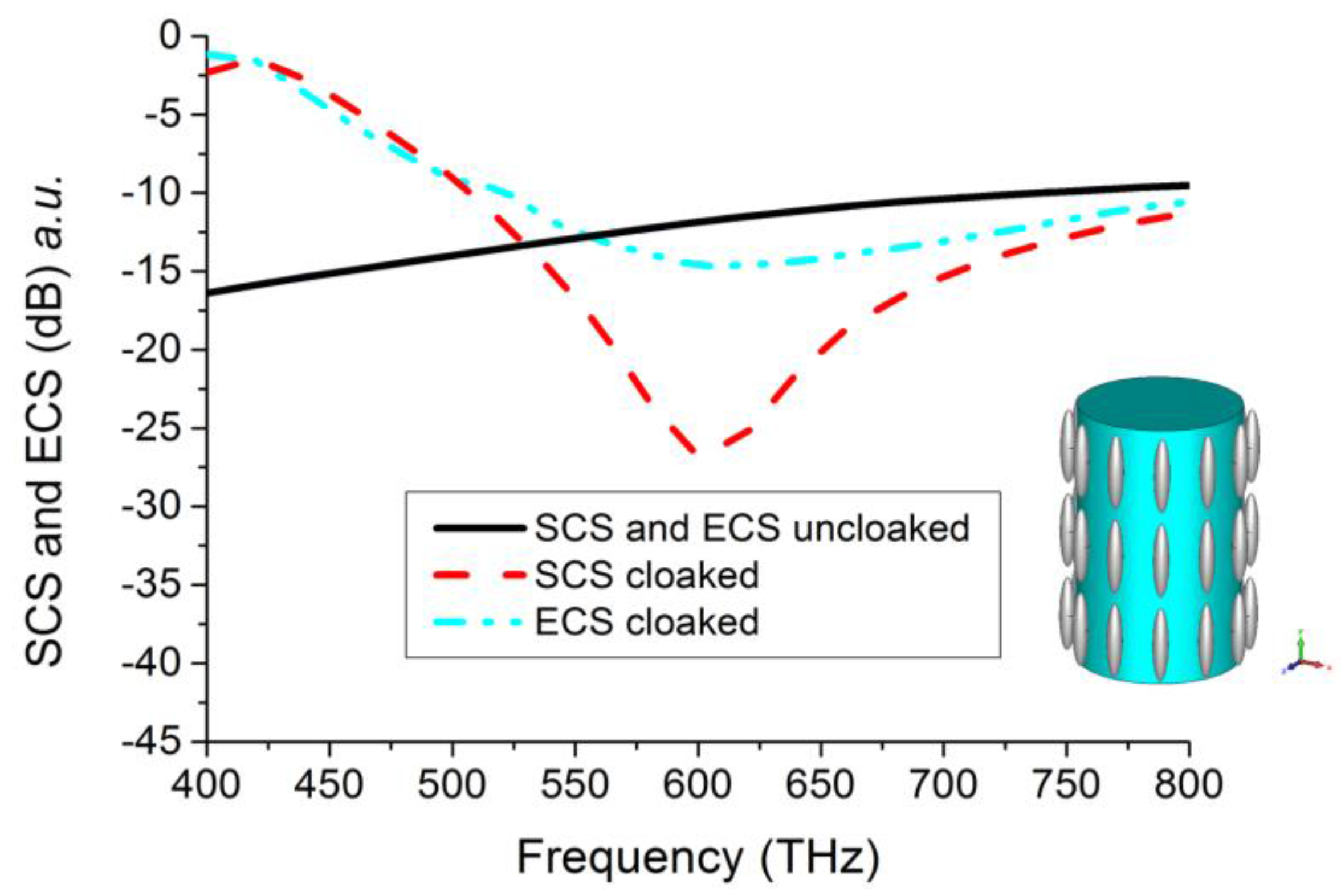
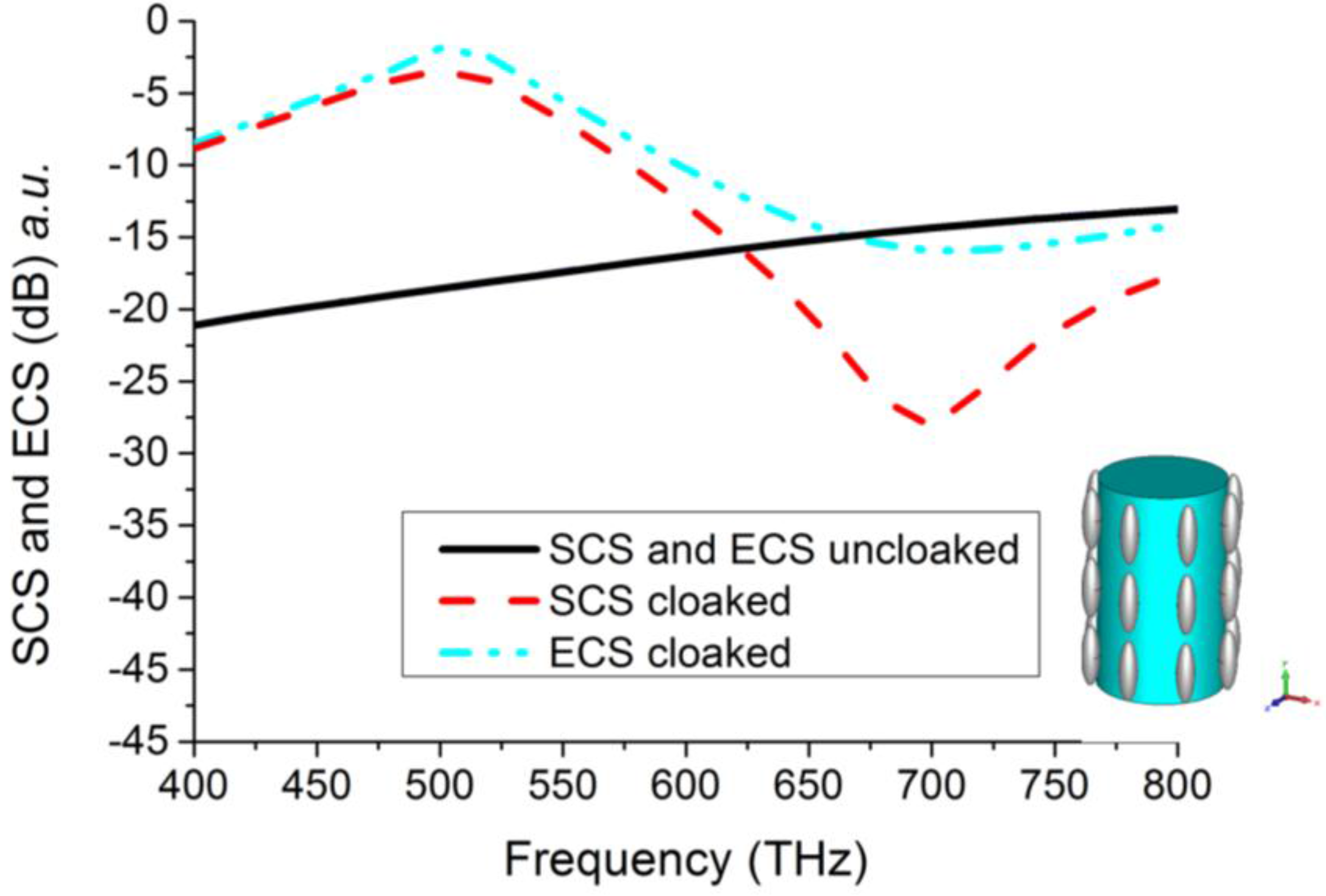
3. Full-Wave Simulations
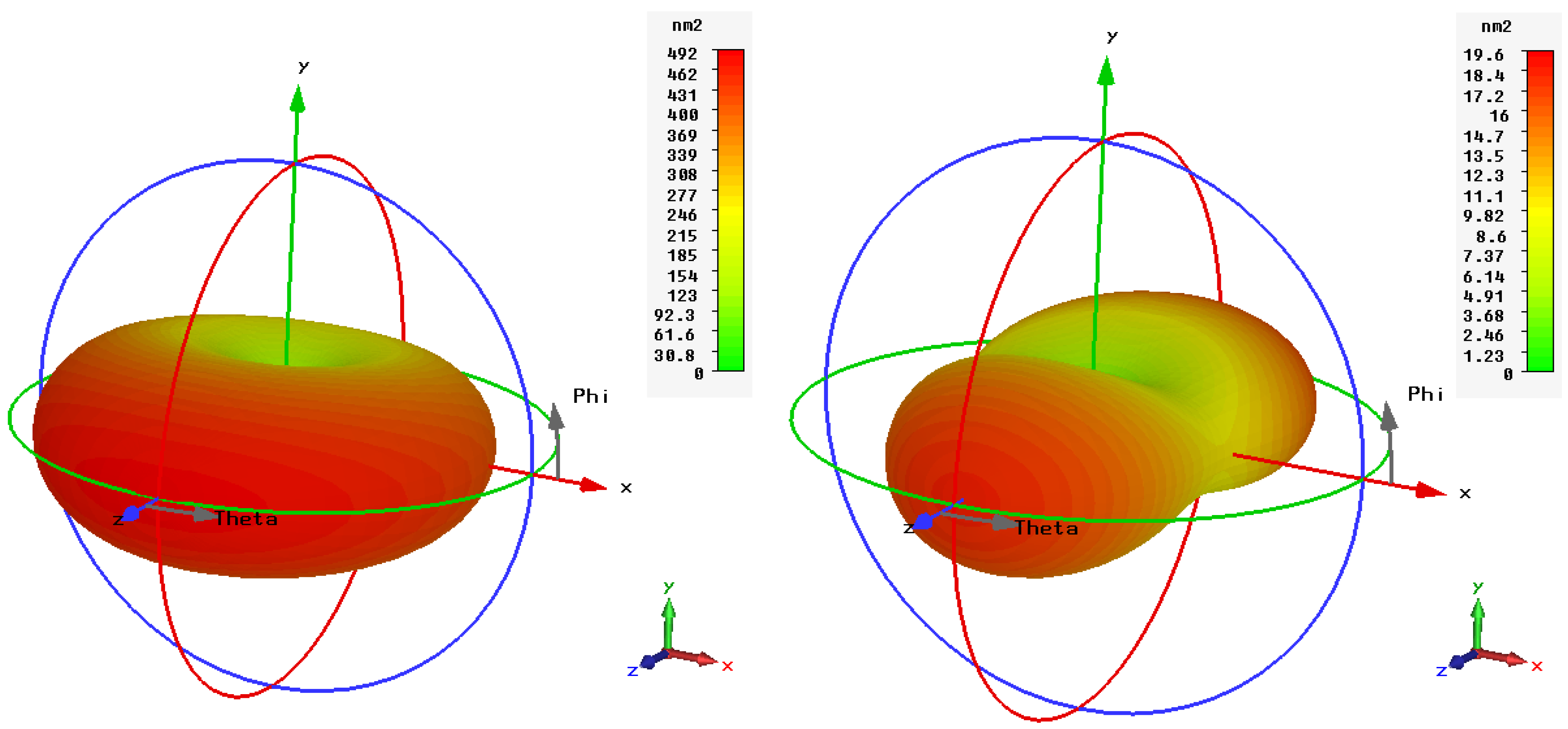
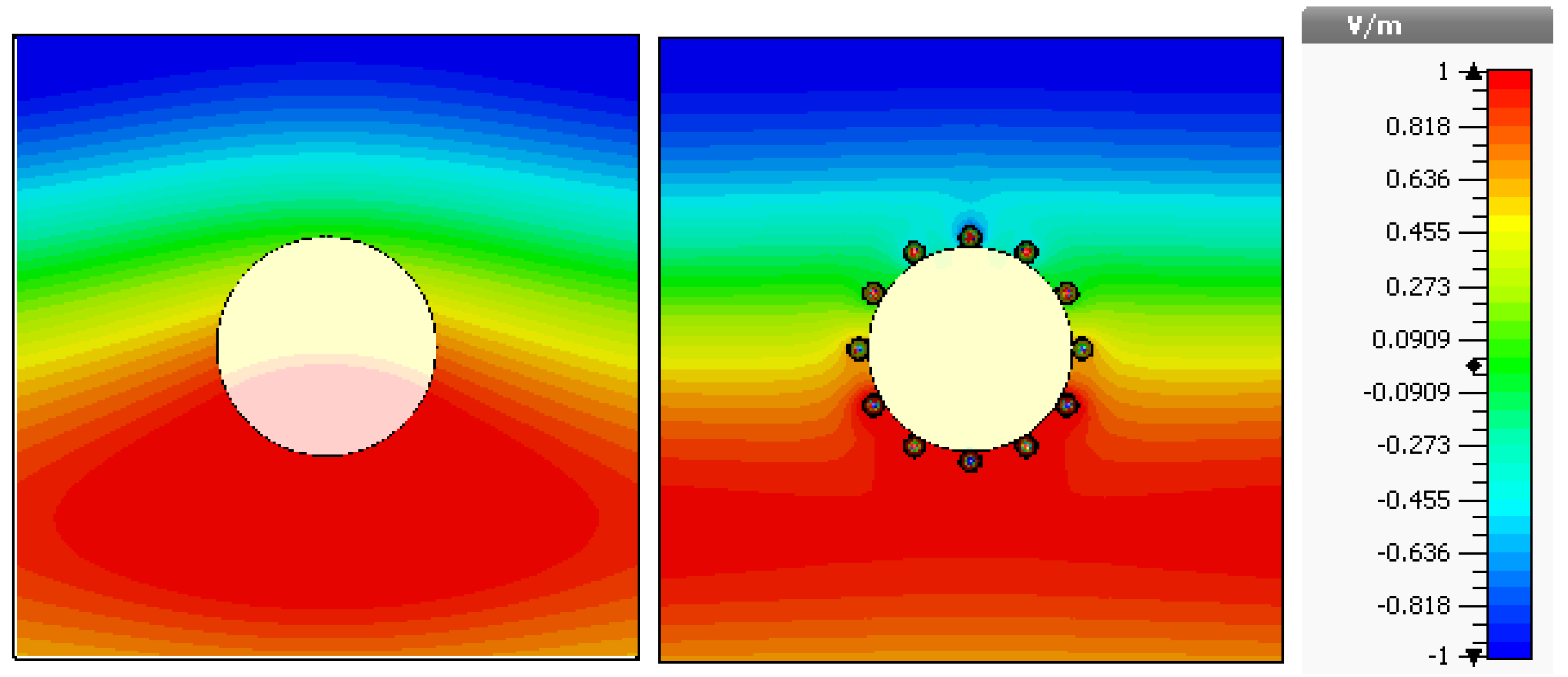
4. Conclusions
Conflict of Interest
References
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Leonhard, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Alitalo, P.; Luukkonen, O.; Jylha, L.; Venermo, J.; Tretyakov, S.A. Transmission-line networks cloaking objects from electromagnetic fields. IEEE Trans. Antenn. Prop. 2008, 56, 416–424. [Google Scholar] [CrossRef]
- Kildal, P.-S.; Kishk, A.A.; Tengs, A. Reduction of forward scattering from cylindrical objects using hard surfaces. IEEE Trans. Antenn. Prop. 1996, 44, 1509–1520. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and Metamaterial Coatings. Phys. Rev. E 2005, 72, 016623. [Google Scholar] [CrossRef]
- Alù, A. Mantle cloak: Invisibility induced by a surface. Phys. Rev. B 2009, 80, 24115. [Google Scholar] [CrossRef]
- Selvanayagam, M.; Eleftheriades, G.V. An active electromagnetic cloak using the equivalence principle. IEEE Antenn. Wirel. Prop. Lett. 2012, 11, 1226–1229. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Cloaking a receiving antenna or a sensor with plasmonic metamaterials. Metamaterials 2010, 4, 153–159. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Cloaked near-field scanning optical microscope tip for noninvasive near-field imaging. Phys. Rev. Lett. 2010, 105, 263906. [Google Scholar] [CrossRef] [PubMed]
- Bilotti, F.; Tricarico, S.; Pierini, F.; Vegni, L. Cloaking apertureless near-field scanning optical microscopy tips. Opt. Lett. 2011, 36, 211–213. [Google Scholar] [CrossRef] [PubMed]
- Monti, A.; Soric, J.; Alù, A.; Bilotti, F.; Toscano, A.; Vegni, L. IEEE Antenn. Wirel. Prop. Lett. 2012, 11, 1414. [CrossRef]
- Fan, P.; Chettiar, U.K.; Cao, L.; Afshinmanesh, F.; Engheta, N.; Brongersma, M.L. Nat. Photonics 2012, 6, 380. [CrossRef]
- Soric, J.C.; Fluery, R.; Monti, A.; Toscano, A.; Bilotti, F.; Alù, A. IEEE Trans. Antenn. Prop 2014, 62, 4220. [CrossRef]
- Padooru, Y.R.; Yakovlev, A.B.; Chen, P.Y.; Alù, A. Analytical modeling of conformal mantle cloaks for cylindrical objects using sub-wavelength printed and slotted arrays. J. Appl. Phys. 2012, 11, 034907. [Google Scholar] [CrossRef]
- Monti, A.; Soric, J.C.; Alù, A.; Toscano, A.; Bilotti, F. IEEE Trans. Antenn. Prop. 2015, 63, 1775–1788. [CrossRef]
- Schofield, R.S.; Soric, J.C.; Rainwater, D.; Kerkhoff, A.; Alù, A. Scattering suppression and wideband tunability of a flexible mantle cloak for finite-length conducting rods. New. J. Phys. 2014, 16, 063063. [Google Scholar] [CrossRef]
- Tricarico, S.; Bilotti, F.; Vegni, L. Scattering cancellation by metamaterial cylindrical multilayers. JEOS:RP 2009, 4, 09021. [Google Scholar] [CrossRef]
- Mühlig, S.; Farhat, M.; Rockstuhl, C.; Lederer, F. Cloaking dielectric spherical objects by a shell of metallic nanoparticles. Phys. Rev. B 2011, 83, 195116. [Google Scholar] [CrossRef]
- Mühlig, S.; Cunningham, A.; Dintinger, J.; Farhat, M.; Hasan, S.B.; Scharf, T.; Bürgi, T.; Lederer, F.; Rockstuhl, C. A self-assembled three-dimensional cloak in the visible. Sci. Rep. 2013, 3, 2328. [Google Scholar] [PubMed]
- Farhat, M.; Mühlig, S.; Rockstuhl, C.; Lederer, F. Scattering cancellation of the magnetic dipole field from macroscopic spheres. Opt. Express 2012, 20, 13896. [Google Scholar] [CrossRef] [PubMed]
- Monti, A.; Bilotti, F.; Toscano, A. Optical cloaking of cylindrical objects by using covers made of core-shell nano-particles. Opt.Lett. 2011, 36, 4479. [Google Scholar]
- Monti, A.; Bilotti, F.; Toscano, A.; Vegni, L. Possible implementation of epsilon-near-zero metamaterials working at optical frequencies. Opt. Commun. 2012, 285, 3412. [Google Scholar] [CrossRef]
- Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. Optical Invisibility through Metasurfaces Made of Plasmonic Nanoparticles. J. Appl. Phys. 2015, 117, 123103. [Google Scholar] [CrossRef]
- Sihvola, A. Mixing Rules with Complex Dielectric Coefficients. SSTA 2000, 1, 393. [Google Scholar]
- Saeidi, C.; van der Weide, D. Nanoparticle array based optical frequency selective surfaces: Theory and design. Opt. Express 2013, 21, 16170. [Google Scholar] [CrossRef] [PubMed]
- Saeidi, C.; van der Weide, D. Bandwidth-tunable optical spatial filters with nanoparticle arrays. Opt. Express 2014, 22, 12499. [Google Scholar] [CrossRef] [PubMed]
- Mackay, T.G. Lewin’s homogenization formula revisited for nanocomposite materials. J. Nanophoto. 2008, 2, 029503. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Noguez, C. Surface Plasmons on Metal Nanoparticles: The Influence of Shape and Physical Environment. J. Phys. Chem. C 2007, 111, 3806. [Google Scholar] [CrossRef]
- Tretyakov, S. Analytical Modeling in Applied Electromagnetic; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Drachev, V.P.; Chettiar, U.K.; Kildishev, A.V.; Yuan, H.-K.; Cai, W.; Shalaev, V.M. The Ag dielectric function in plasmonic metamaterials. Opt. Express 2008, 16, 1186. [Google Scholar] [CrossRef] [PubMed]
- Noguez, C. Optical properties of isolated and supported metal nanoparticles. Opt. Mat. 2005, 27, 1204. [Google Scholar] [CrossRef]
- Grigorchuk, N.I.; Tomchuk, P.M. Optical and transport properties of spheroidal metal nanoparticles with account for the surface effect. Phys. Rev. B 2001, 84, 085448. [Google Scholar] [CrossRef]
- Hilger, A.; Tenfelde, M.; Kreibig, U. Silver nanoparticles deposited on dielectric surfaces. Appl. Phys. B 2001, 73, 361. [Google Scholar] [CrossRef]
- Knott, E.; Tuley, M.T.; Shaeffer, J.F. Radar Cross Section; Artech House: Railegh, NC, USA, 1993. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. Optical Scattering Cancellation through Arrays of Plasmonic Nanoparticles: A Review. Photonics 2015, 2, 540-552. https://doi.org/10.3390/photonics2020540
Monti A, Alù A, Toscano A, Bilotti F. Optical Scattering Cancellation through Arrays of Plasmonic Nanoparticles: A Review. Photonics. 2015; 2(2):540-552. https://doi.org/10.3390/photonics2020540
Chicago/Turabian StyleMonti, Alessio, Andrea Alù, Alessandro Toscano, and Filiberto Bilotti. 2015. "Optical Scattering Cancellation through Arrays of Plasmonic Nanoparticles: A Review" Photonics 2, no. 2: 540-552. https://doi.org/10.3390/photonics2020540





