Dispersive Response of a Disordered Superconducting Quantum Metamaterial
Abstract
:1. Introduction
2. Model
2.1. Hamiltonian of Disordered Metamaterial
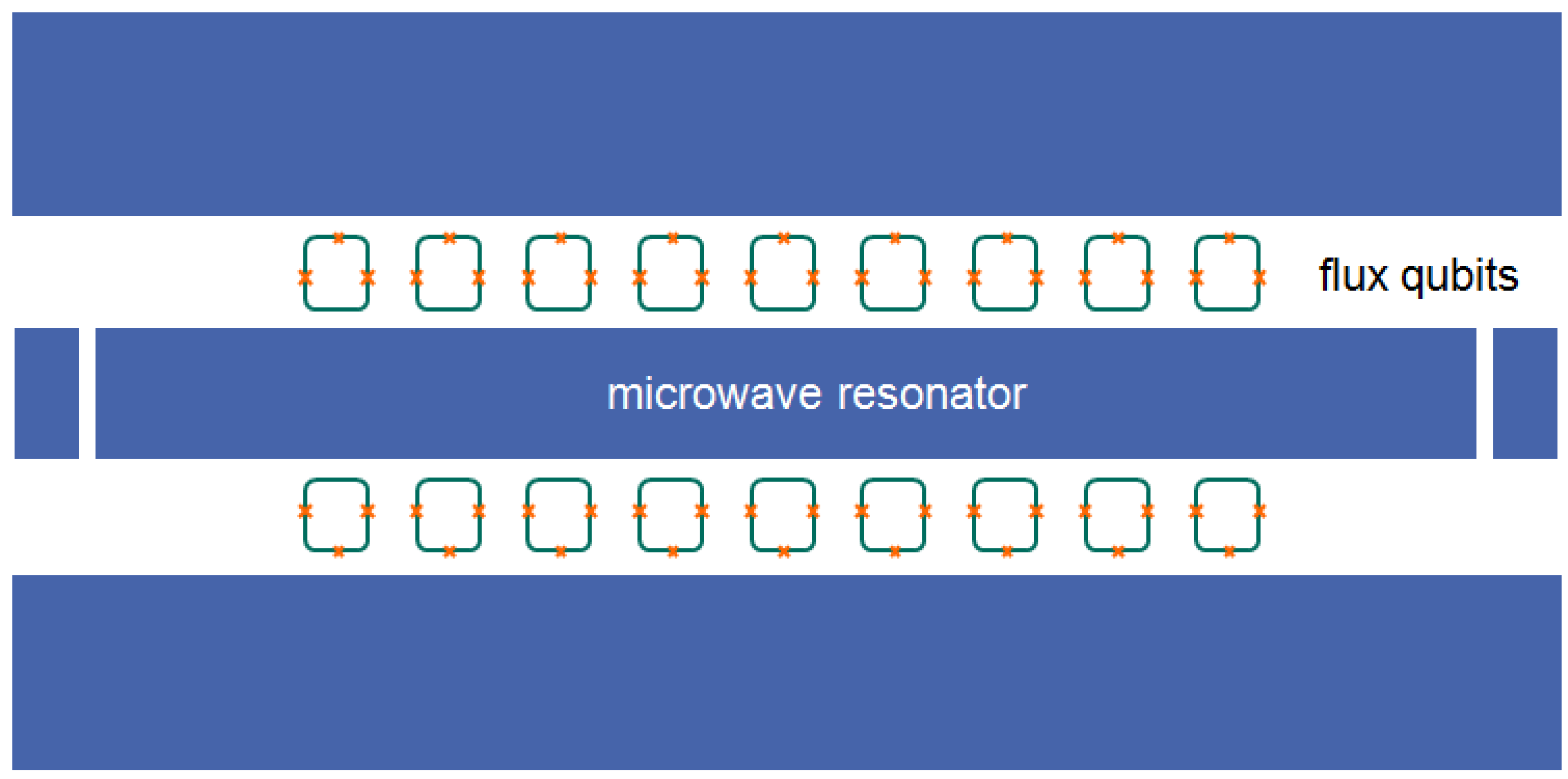
2.2. Exact Diagonalization Approach
3. Results
3.1. Strong Disorder and Large N
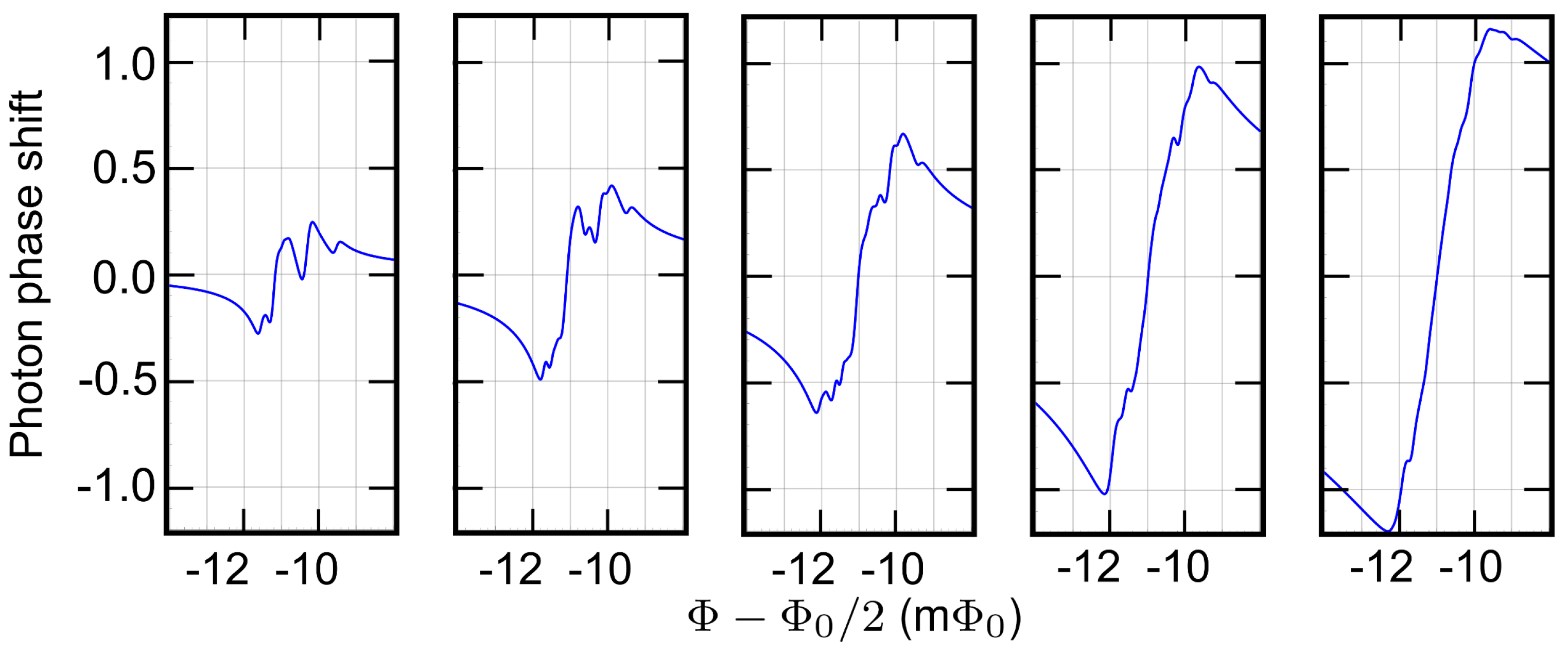
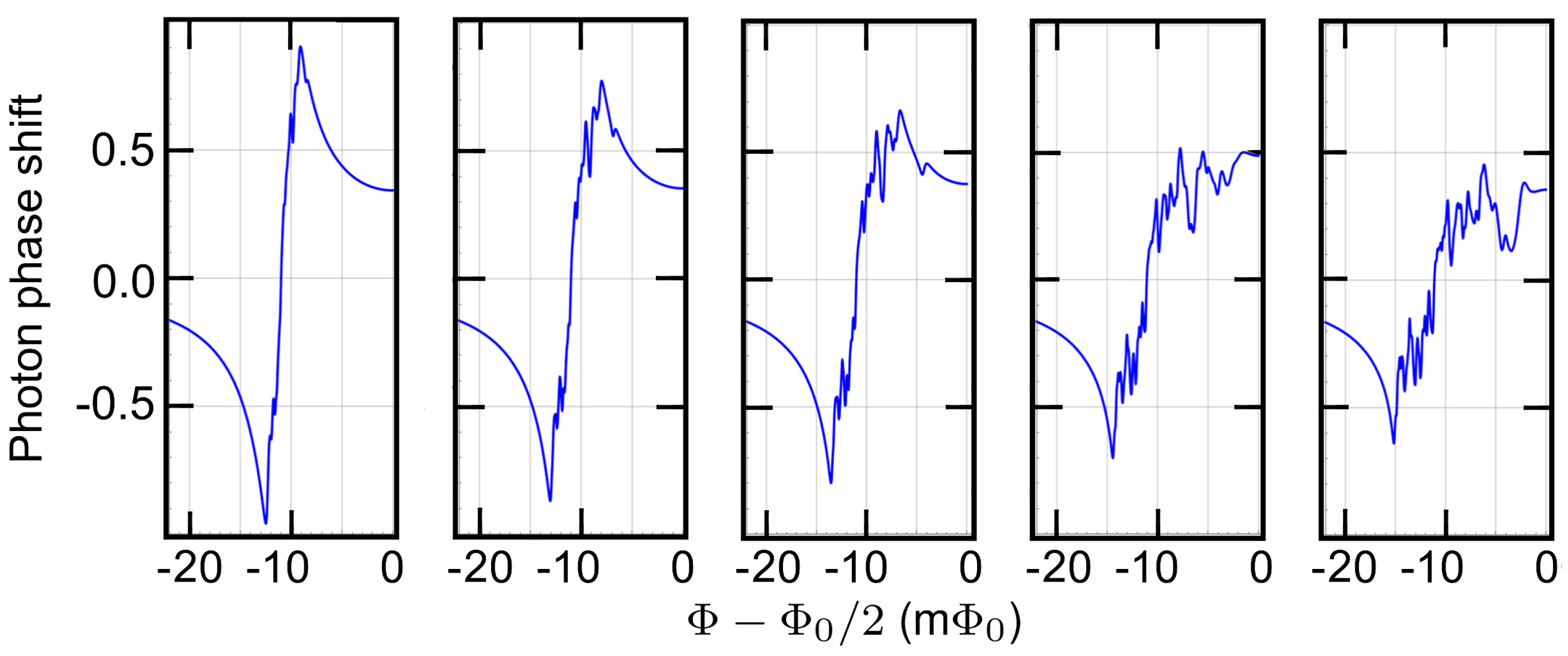
3.2. Experimental Regime, Small N
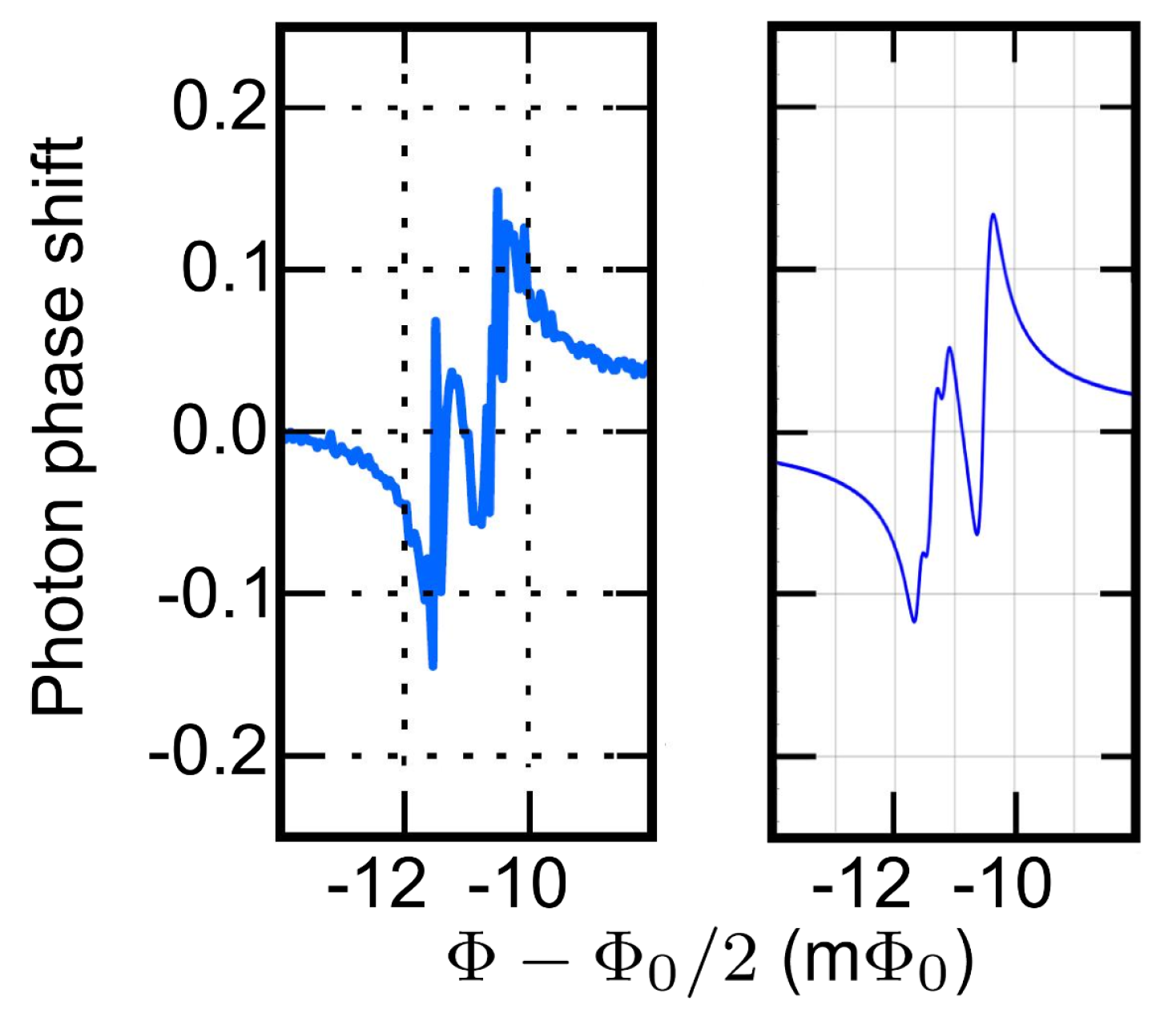
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Macha, P.; Oelsner, G.; Reiner, J.-M.; Marthaler, M.; André, S.; Schön, G.; Hübner, U.; Meyer, H.-G.; Il’ichev, E.; Ustinov, A.V. Implementation of a quantum metamaterial using superconducting qubits. Nat. Commun. 2014, 5, 5146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rakhmanov, A.L.; Zagoskin, A.M.; Savel’ev, S.; Nori, F. Quantum metamaterials: Electromagnetic waves in a Josephson qubit line. Phys. Rev. B 2008, 77, 144507. [Google Scholar] [CrossRef]
- Volkov, P.; Fistul, M.V. Collective quantum coherent oscillations in a globally coupled array of qubits. Phys. Rev. B 2014, 89, 054507. [Google Scholar] [CrossRef]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.I.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.M.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240. [Google Scholar] [CrossRef] [PubMed]
- Nation, P. D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1. [Google Scholar] [CrossRef]
- Blais, A.; Huang, R.-S.; Wallraff, A.; Girvin, S.M.; Schoelkopf, R.J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 2004, 69, 062320. [Google Scholar] [CrossRef]
- You, J.Q.; Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 2011, 474, 589. [Google Scholar] [CrossRef] [PubMed]
- Orlando, T.P.; Mooij, J.E.; Tian, L.; van der Wal, C.H.; Levitov, L.S.; Lloyd, S.; Mazo, J.J. Superconducting persistent-current qubit. Phys. Rev. B 1999, 60, 15398. [Google Scholar] [CrossRef]
- Mooij, J.E.; Orlando, T.P.; Levitov, L.; Tian, L.; van der Wal, C.H.; Lloyd, S. Josephson persistent-current qubit. Science 1999, 285, 1036. [Google Scholar] [CrossRef] [PubMed]
- Astafiev, O.; Zagoskin, A.M.; Abdumalikov, A.A., Jr.; Pashkin, Y.A.; Yamamoto, T.; Inomata, K.; Nakamura, Y.; Tsai, J.S. Resonance fluorescence of a single artificial atom. Science 2010, 327, 840. [Google Scholar] [CrossRef] [PubMed]
- Vijay, R.; Macklin, C.; Slichter, D.H.; Weber, S.J.; Murch, K.W.; Naik, R.; Korotkov, A.N.; Siddiqi, I. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback. Nature 2012, 490, 77. [Google Scholar] [CrossRef] [PubMed]
- Fink, J.M.; Bianchetti, R.; Baur, M.; Göppl, M.; Steffen, L.; Filipp, S.; Leek, P.J.; Blais, A.; Wallraff, A. Dressed Collective Qubit States and the Tavis-Cummings Model in Circuit QED. Phys. Rev. Lett. 2009, 103, 083601. [Google Scholar] [CrossRef] [PubMed]
- Bertet, P.; Chiorescu, I.; Burkard, G.; Semba, K.; Harmans, C.J.P.M.; DiVincenzo, D.P.; Mooij, J.E. Dephasing of a Superconducting Qubit Induced by Photon Noise. Phys. Rev. Lett. 2005, 95, 257002. [Google Scholar] [CrossRef] [PubMed]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Majer, J.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Approaching Unit Visibility of a Superconducting Qubit with Dispersive Readout. Phys. Rev. Lett. 2005, 95, 060501. [Google Scholar] [CrossRef] [PubMed]
- Romero, G.; García-Ripoll, J.J.; Solano, E. Microwave photon detector in circuit QED. Phys. Rev. Lett. 2009, 102, 173602. [Google Scholar] [CrossRef] [PubMed]
- Fragner, A.; Göppl, M.; Fink, J.M.; Baur, M.; Bianchetti, R.; Leek, P.J.; Blais, A.; Wallraff, A. Resolving Vacuum Fluctuations in an Electrical Circuit by Measuring the Lamb Shift. Science 2008, 322, 1357. [Google Scholar] [CrossRef] [PubMed]
- Lähteenmäki, P.; Paraoanua, G.S.; Hasselb, J.; Hakonena, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. 2011, 111, 10485. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the Dynamical Casimir Effect in a Superconducting Circuit. Nature 2011, 479, 376. [Google Scholar] [CrossRef] [PubMed]
- Tavis, M.; Cummings, F.W. Exact solution for an n-molecule-radiation-field hamiltonian. Phys. Rev. 1968, 170, 379. [Google Scholar] [CrossRef]
- Julsgaard, B.; Mølmer, K. Fundamental limitations in spin-ensemble quantum memories for cavity fields. Phys. Rev. A 2013, 88, 062324. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shapiro, D.S.; Macha, P.; Rubtsov, A.N.; Ustinov, A.V. Dispersive Response of a Disordered Superconducting Quantum Metamaterial. Photonics 2015, 2, 449-458. https://doi.org/10.3390/photonics2020449
Shapiro DS, Macha P, Rubtsov AN, Ustinov AV. Dispersive Response of a Disordered Superconducting Quantum Metamaterial. Photonics. 2015; 2(2):449-458. https://doi.org/10.3390/photonics2020449
Chicago/Turabian StyleShapiro, Dmitriy S., Pascal Macha, Alexey N. Rubtsov, and Alexey V. Ustinov. 2015. "Dispersive Response of a Disordered Superconducting Quantum Metamaterial" Photonics 2, no. 2: 449-458. https://doi.org/10.3390/photonics2020449
APA StyleShapiro, D. S., Macha, P., Rubtsov, A. N., & Ustinov, A. V. (2015). Dispersive Response of a Disordered Superconducting Quantum Metamaterial. Photonics, 2(2), 449-458. https://doi.org/10.3390/photonics2020449



