Optimum Pump Pulse Duration for X-Ray Ar-Plasma Lasing

Abstract

In plasma-driven X-ray lasers, it is critical to optimize the duration and time delay between pump pulses. In this study, we have done parametric simulations in order to systematically investigate the optimum time configuration of pump pulses. Here, we are mainly interested in soft X-ray lasers created using a Ar target irradiated with laser pulses, which operate at a wavelength $\lambda =46.9$ nm in the $2p^{5}3p^1(J=0)\to 2p^{5}3s^1(J=1)$ laser transition. It is shown that the optimum time scale required to achieve Ne-like ions, as well as the time required to generate a population inversion depend on the combined effect of the electron temperature and electron density. The electron density and temperature are respectively a factor of ≈$2.1$- and ≈5-times higher in the case of a short pulse of $0.1$ ps in comparison to a long pulse of 1,000 ps (at a constant fluence). The most effective lasing happens with short pulses with a pulse duration comparable to the total relaxation time from the upper level, namely $\Delta {\tau }_p\le 35$ ps. Power laws to predict the optimum laser intensity to achieve Ne-like $A{r}^{+8}$ are obtained.

1. Introduction

A number of ways have been proposed to increase the efficiency of laser-irradiated solid targets for plasma-driven X-ray lasing [1]. The main drawback of solid targets, however, is the presence of strong density gradients, which cause the refraction of the pump pulse, limiting the gain [2,3]. A solution to the strong density gradients we have studied is using hohlraum targets [2].

Alternatively, gas targets have several advantages over solid targets, such as the soft density gradients, lack of debris, high repetition rate and long unbroken operation [4,5,6,7,8,9,10]. For the first time, the generation of laser radiation with $A{r}^0$ gas at a wavelength of $46.9$ nm producing a gain of $0.6$ cm⁻¹ was observed in a capillary discharge by Rocca et al. [11].

In the laser-produced gas targets, the possibility of having a high repetition rate will lead to high average power for soft X-ray lasers. Besides, the advantage of the compact size and the low cost in comparison to the large-scale X-ray sources, such as free electron lasers [12] and synchrotron facilities [13], is important.

Table 1 summarizes the operating conditions used experimentally in the lasing of the Ne-like $A{r}^{+8}$ plasma at $\lambda =46.9$ nm in the $2p^{5}3p^1(J=0)\to 2p^{5}3s^1(J=1)$ laser transition [5,6,7,8,9,10]. In references [5,6,7,8,9,10], the plasma is produced with a long pulse ($\Delta {\tau }_{MP}=450$ ps), a combination of a long ($\Delta {\tau }_{PP}=600$ ps) and a short pulse ($\Delta {\tau }_{MP}=6$ ps) and double-short pulses ($\Delta {\tau }_{PP}=\Delta {\tau }_{MP}=1.5$ ps). Here, the “short pulse” means a pulse with a pulse-duration shorter or in the order of the lifetime of the upper level (lasing level). On the other hand, the “long pulse” has a pulse duration longer than the lifetime of the upper level. The lifetime of the upper level, taking into account the radiative decay (without considering collisional processes) in Ne-like $A{r}^{+8}$, is ≈100 ps (see Figure 1). Table 1 shows the gain due to the collisional excitation calculated by fitting the Linford formula [14] to the experimental data. It shows that the highest gain coefficient is $18.7$ cm⁻¹, achieved in the case of plasma driven with double-short pulses [10]. As the population inversion only persists as long as the plasma parameters are close to optimum [15], then for long pumping, the plasma will destroy the gain, and most of the possible inversions would be lost by spontaneous emission.

Table 1. A summary of the experimental-operating conditions in the lasing of the Ne-like $A{r}^{+8}$ plasma at $\lambda =46.9$ nm. Legend: $\Delta {\tau }_{PP}$, $\Delta {\tau }_{MP}$ and $\Delta t$ stand for the pulse duration of the pre-pulse, the pulse duration of the main pulse and the time delay between two pulses (pulse to pulse separation), respectively. ${\lambda }_P$, $I_{PP}$ and $I_{MP}$ stand for the pump laser’s wavelength, the pre-pulse-laser intensity and the main-pulse-laser intensity at the focusing point on the target, respectively. ${\rho }_0$ and g stand for the initial gas density of $A{r}^0$ and the gain coefficient, respectively.

$\Delta {\tau }_{\mathit{PP}}$ (ps)	$\Delta {\tau }_{\mathit{MP}}$ (ps)	$\Delta t$ (ps)	${\lambda }_P$ (nm)	$I_{\mathit{PP}}$ (W/cm2)	$I_{\mathit{MP}}$ (W/cm2)	${\rho }_0$ (mg/cm3)	g (cm−1)	Ref
-	450	-	1,315	-	$5·{10}^{12}$–$3·{10}^{13}$	0.15	1.65	[5,6]
600	6	500–2,100	1,054	$2·{10}^{11}$	$5·{10}^{13}$	4	11	[7,8,9]
$1.5$	$1.5$	1,200	1,054	$7·{10}^{14}$	$4.7·{10}^{15}$	$0.166$	18.7	[10]

Table 1. A summary of the experimental-operating conditions in the lasing of the Ne-like $A{r}^{+8}$ plasma at $\lambda =46.9$ nm. Legend: $\Delta {\tau }_{PP}$, $\Delta {\tau }_{MP}$ and $\Delta t$ stand for the pulse duration of the pre-pulse, the pulse duration of the main pulse and the time delay between two pulses (pulse to pulse separation), respectively. ${\lambda }_P$, $I_{PP}$ and $I_{MP}$ stand for the pump laser’s wavelength, the pre-pulse-laser intensity and the main-pulse-laser intensity at the focusing point on the target, respectively. ${\rho }_0$ and g stand for the initial gas density of $A{r}^0$ and the gain coefficient, respectively.

$\Delta {\tau }_{\mathit{PP}}$ (ps)	$\Delta {\tau }_{\mathit{MP}}$ (ps)	$\Delta t$ (ps)	${\lambda }_P$ (nm)	$I_{\mathit{PP}}$ (W/cm2)	$I_{\mathit{MP}}$ (W/cm2)	${\rho }_0$ (mg/cm3)	g (cm−1)	Ref
-	450	-	1,315	-	$5·{10}^{12}$–$3·{10}^{13}$	0.15	1.65	[5,6]
600	6	500–2,100	1,054	$2·{10}^{11}$	$5·{10}^{13}$	4	11	[7,8,9]
$1.5$	$1.5$	1,200	1,054	$7·{10}^{14}$	$4.7·{10}^{15}$	$0.166$	18.7	[10]

Table 1 shows that the time delays between pulses are in the range of 500–2,100 ps, which is to achieve the optimum ionization level. The wavelength of pump lasers are either 1,054 nm or 1,315 nm, and the initial $A{r}^0$ mass densities are in the range of $0.15$–4 mg/cm³. In [5,6], a pulse with intensity in the range of $5·{10}^{12}$–$3·{10}^{13}$ W/cm² is used to ionize the plasma up to the required ionization stage to produce a lasing plasma. In [7,8,9], a pulse with lower intensity $2·{10}^{11}$ W/cm² produces a pre-plasma, and then, a pulse with higher intensity $5·{10}^{13}$ W/cm² produces the lasing plasma. In [10], double pico-second pulses with intensity $7·{10}^{14}$ W/cm² and $4.7·{10}^{15}$ W/cm² rapidly produce the pre-plasma and heat it. In the plasma-driven X-ray laser, it is critical to optimize the duration and time delay (timing) between pump pulses.

All of the so far reported optimization in Ar comes from experimental studies [5,6,7,8,9,10], which had a lack of theoretical analysis. The aim of this work is to present parametric simulations in order to systematically investigate the optimum timing configuration of pump pulses.

This work is organized as follows: In Section 2, a description of modeling codes and boundary conditions is given. In Section 3, the approach used in the theoretical calculation is explained. In Section 4.1.1, the collisional ionization time of a neutral $A{r}^0$ is calculated. In Section 4.1.2, the time required to produce Ne-like ions is discussed. In Section 4.1.3, the transition times among excited levels are calculated. In Section 4.1.4, the required time to achieve a population inversion and the relaxation time from excited levels are obtained. In Section 4.2, we show how the pulse duration can affect the evolution of the electron density and temperature, which affect the time required for the production of the Ne-like $A{r}^{+8}$, the time scale of the pumping and the relaxation time. In Section 4.3, the optimum pump laser intensity with dependency on the pulse duration and initial gas density in order to have Ne-like $A{r}^{+8}$ is obtained.

2. Modeling Codes

2.1. Atomic Physics Code

The flexible atomic code (FAC) [16] was used to calculate the required atomic data, such as collisional excitation coefficients and spontaneous emission coefficients. FAC employs a fully relativistic approach based on the Dirac equation. It is a configuration interaction program for calculating atomic collisional and radiative processes, including (i) energy levels, (ii) radiative transitions and the inverse process of (iii) photo-excitation, (iv) collisional excitation and (v) ionization by electron impact and its inverse process (vi) collisional de-excitation and (vii) three-body recombination, (viii) radiative recombination and its inverse process (ix) photo-ionization, (x) auto-ionization and its inverse process and (xi) dielectronic capture. These are indeed the required coefficients we need to solve the non local thermodynamic equilibrium (NLTE) system of rate equations. Furthermore, FAC has been extensively used before for calculating atomic data by several publications [17,18,19,20].

Due to some limitations of FAC in handling the calculation of ionic distributions, the FLYCHK code from the NIST was used, too. The FLYCHK code was used to calculate ionic level populations by a solving multi-level rate equation in zero dimension, as explained extensively elsewhere [21,22].

2.2. Hydro-Code

“Hyades” [23] is a one-dimensional, three-geometry (planar, cylindrical or spherical), three-fluid (electrons, ions and radiation) hydrodynamics simulation code. The conservation equations for mass, momentum and energy are solved in a Lagrangian coordinate system. The three fluids are treated individually in a fluid approximation, each having its own temperature. Each fluid is assumed to be in LTE, which is to say that the electrons and the ions are described well in the classical limit by Maxwell–Boltzmann statistics, and the radiation field is Planckian. Electron degeneracy effects, important in low-temperature, high-density plasmas, are taken into account. The equation of state (EOS) and related thermodynamic coefficients are obtained from external tables that have been compiled using experimental data and theoretical models. The energy transport by free-electrons and ions is modeled in the flux-limited diffusion approximation (the default value for both electrons and ions is 0.4). Radiation is transported according to the photon energy, i.e., ultra-violet and soft X-rays have very short mean free paths, while the more energetic photons’ harder X-rays will penetrate deeply into the material. The absorption and emission coefficients are determined self-consistently from the atomic physics model of choice or may be supplied by the user in tabular form. The absorption of laser light by a hot plasma is dominated by inverse Bremsstrahlung at the intensity of interest to this work.

2.3. Boundary Conditions

In Section 4.2 and Section 4.3, a gas target, such as $A{r}^0$, considering an electronic flux-limit multiplier of 0.05 and a multi-group radiation transport of 50 groups (in Hyades), is studied. The plasma is created using $\lambda =$ 1054-nm Nd:glass laser (IR pulse) with a Gaussian pulse shape. The pump pulse is irradiated at an angle of ${90}^{\circ }$ (normal incidence) to the target. The arrival time of the peak of Gaussian pulse on the target is considered two-times the pulse duration. Here, the considered geometry is planar (1D Cartesian) geometry. In Section 4.2, the initial gas density of neutral $A{r}^0$ at all zones (irradiated area) is considered the same, which is 4 mg/cm³ ($6·{10}^{19}$ cm⁻³).

3. Theoretical Background

The main computational steps of the approach used in our study are (i) calculation of the ionization time and (ii) transition time and (iii) calculation of the pumping and relaxation time. These are needed to quantify the optimum timing for the pump pulses.

3.1. Ionization Time

The ionization time as given by McWhirter’s condition [24] is: $t\left[s\right]={10}^{12}/n_e$ (cm⁻³). For this calculation, McWhirter [24] considered two processes: (i) collisional ionization; and (ii) radiative recombination. However, Pert [25] pointed out that McWhirter’s criterion is overestimated by up to a factor of 10. Here, our analysis for estimating the ionization time includes the following processes: (i) collisional ionization; (ii) three-body; (iii) radiative; and (iv) dielectronic recombination. The quantity of the ionization time can be obtained considering a two-level system, in which transitions take place from one level to the other, and the solution characterized by an initial transient phase, during which the one charge level ($A{r}^{+Z}$) will be ionized to the higher charge level ($A{r}^{+(Z+1)}$) [24]. Solving rate equations [24] at the steady state, where $A{r}^{+(Z+1)}\propto A{r}^{+Z}(1-e^{-t{n}_e(S_Z+{\alpha }_{Z+1}+n_e{\beta }_{Z+1}+D_{Z+1})})$, gives the ionization time between two adjacent states as follows:

$$t_{A{r}^{+Z}\to A{r}^{+(Z+1)}}\left[s\right]=\frac{1}{n_e(S_Z+{\alpha }_{Z+1}+n_e{\beta }_{Z+1}+D_{Z+1})}$$

(1)

where $n_e$ is expressed in cm⁻³ and the collisional ionization rate $S_Z$ from charge state Z to $Z+1$ [24] in cm³s⁻¹. The terms ${\alpha }_{Z+1}$, ${\beta }_{Z+1}$ and $D_{Z+1}$ are, respectively, the radiative, collisional three-body and dielectronic recombination rates [28,29] applied to the ionic charge level Z + 1 in cm³s⁻¹, cm³s⁻¹/cm⁻³ and cm³s⁻¹, respectively. It is mentionable that Equation (1) gives the ionization time (characteristic time) when $A{r}^{+(Z+1)}$ has ≈63% of the $A{r}^{+Z}$ population.

3.2. Cooling Time

The characteristic timescale for radiative cooling is of the same order as the time it takes for the plasma to reach thermal equilibrium [26]. The equilibrium time $t_{eq}$ of the plasma is predicted as follows [27]:

$$\begin{array}{c}\hfill t_{eq}\left[s\right]\approx 3.16·{10}^{-10}\frac{A}{Z^2}{(\frac{k{T}_e}{100})}^{3/2}(\frac{{10}^{21}}{n_{i}log[(\frac{3}{2{\overline{z}}^2})·{(\frac{{(k{T}_e)}^3}{\pi e^6{n}_e})}^{1/2}]})\end{array}$$

(2)

where A is the atomic weight of the ions, Z is the atomic number, $\overline{z}$ is the average charge state, $k{T}_e$ is the electron temperature in eV, $n_e$ is the electron density in cm⁻³ and $n_i$ is the ion density.

3.3. Transition Times

Due to the selection rules, the transition from ground level (J $=0$) to the upper level (J $=0$) is only achieved by the monopole collisional excitation (Figure 1).

Figure 1. Grotrian scheme and the transitions for the lasing of the Ne-like $A{r}^{+8}$. The energy levels schematically are composed of the upper (2) and lower (1) lasing levels and the ground (0) level.

Figure 1. Grotrian scheme and the transitions for the lasing of the Ne-like $A{r}^{+8}$. The energy levels schematically are composed of the upper (2) and lower (1) lasing levels and the ground (0) level.

The X-ray produced across a plasma follows transition times as follows:

$$\begin{array}{c}\hfill {\tau }_{02}\left[s\right]=\frac{1}{n_e{C}_{02}}\\ \hfill {\tau }_{01}\left[s\right]=\frac{1}{n_e{C}_{01}}\\ \hfill {\tau }_{12}\left[s\right]=\frac{1}{n_e{C}_{12}}\\ \hfill {\tau }_{20}\left[s\right]=\frac{1}{n_e{C}_{20}}\\ \hfill {\tau }_{10}\left[s\right]=\frac{1}{A_{10}+n_e{C}_{10}}\\ \mathrm{(3)}& \hfill {\tau }_{21}\left[s\right]=\frac{1}{A_{21}+n_e{C}_{21}}\end{array}$$

where $n_e$ is in cm⁻³, $A_{ij}$ in s⁻¹ and $C_{ij}$ in cm³s⁻¹. Here, ${\tau }_{02}$ is the transition time from the ground level (0) to the upper level (2), ${\tau }_{01}$ is the transition time from the ground level (0) to the lower level (1), etc. In the transition time from the upper level (2) to the lower level (1) and from the lower level (1) to the ground level (0), the radiative decays ($A_{21}$ and $A_{10}$) are also allowed. In fact, the ${\tau }_{10}$ and ${\tau }_{21}$ depend on both radiative decay and collisional de-excitation if both are of the same order of magnitude. Otherwise, the ${\tau }_{10}$ and ${\tau }_{21}$ depend only on the largest one, which means a shorter time.

The electron collisional excitation rates ($C_{ij}^e$) between levels depend on the electron temperature [30]:

$$C_{ij}^e\left[c{m}^3{s}^{-1}\right]=1.6·{10}^{-5}\frac{<g_{ij}>}{{(k{T}_e)}^{1/2}}\frac{f_{ij}}{\Delta E_{ij}}{e}^{(-\Delta E_{ij}/k{T}_e)}$$

(4)

where $f_{ij}$ is the oscillator strength, $\Delta E_{ij}$ is the excitation energy and $<g_{ij}>$ is the Gaunt factor. For calculating the collisional de-excitation rate ($C_{ji}^d$), considering detailed balancing [31,32], one has that:

$$C_{ji}^d\left[c{m}^3{s}^{-1}\right]=\frac{{\gamma }_i}{{\gamma }_j}{C_{ij}}^e{e}^{(\Delta E_{ij}/k{T}_e)}$$

(5)

3.4. Pumping and Relaxation Time

The populations of the Ne-like levels are computed in a three-level model [33,34]; Figure 1. Oliva et al. have shown [33] that a three-level model has good agreement with their experimental data. In their model, they took into account only Doppler broadening, while collisional broadening should also be treated. Here, in our calculation, we take into account both Doppler broadening and collisional broadening. If $n_2$ and $n_1$ are the upper and lower laser level populations (Figure 1) and ${\sigma }_{stim}$ is the cross-section for the stimulated emission, the small signal gain at $\lambda ={\lambda }_0$ (${\lambda }_0$ is 46.9 nm for a Ne-like $A{r}^{+8}$ laser) is found as follows [35]:

$$g_0(\lambda ={\lambda }_0)=n_{2}F{\sigma }_{stim}(\lambda ={\lambda }_0)$$

(6)

where F is the population inversion factor, defined as follows:

$$F=1-(\frac{{\gamma }_2}{{\gamma }_1})\frac{n_1}{n_2}$$

(7)

where ${\gamma }_i$, ${\gamma }_j$ are the degeneracies of the i-th, j-th levels, and the degeneracy of each level is 2J + 1. Here, we compute the value of the gain at the center of line profile $\lambda ={\lambda }_0$.

The cross-section ${\sigma }_{stim}$ is given by [30]:

$${\sigma }_{stim}=\frac{\pi r_0{f}_{lu}\lambda }{\Delta {\lambda }_x}\frac{{\gamma }_l}{{\gamma }_u}{\phi }_x(\lambda )$$

(8)

where $\Delta {\lambda }_x$ is the spectral line width and ${\phi }_x(\lambda )$ is the normalized line shape profile. Line shape ${\phi }_x(\lambda )$ is given by the convolution integral,

$${\phi }_x(\lambda )={\int }_{-\infty }^{+\infty }{\phi }_G(\lambda ){\phi }_L({\lambda }_0-\lambda )d\lambda$$

(9)

Assume that Doppler broadening (${\phi }_G$) and collisional broadening (${\phi }_L$) act on a line profile simultaneously; then, the resulting measured line shape is a Voigt profile. In a plasma, Doppler broadening due to the thermal motion of ions produces a Gaussian-shaped line function, where $\Delta {\lambda }_D=\frac{\sqrt{2k{T}_i/M}}{c}\lambda$ is the Doppler width; where $k{T}_i$ is the ion temperature and M is the ion mass. The value of the spectral bandwidth for the full width at half maximum of this Gaussian intensity is given by [36]:

$${\Delta \lambda }_G=2\sqrt{2ln2}\Delta {\lambda }_D$$

(10)

The formula for the electron impact broadening is used to estimate [37]:

$${\Delta \lambda }_L=2·{10}^{-16}w{n}_e[1+1.75·{10}^{-4}\alpha n_e^{1/4}(1-0.00062n_e^{1/6}{T}_e^{-1/2})]$$

(11)

Here, $T_e$ in eV and $n_e$ are in cm⁻³; where α is the ion broadening parameter and w is an electron impact width.

The FWHM of the Voigt profile (the convolution of the Lorentzian and Gaussian profile) can be estimated with an accuracy of 0.02% as [38]:

$${\Delta \lambda }_x={\Delta \lambda }_V\approx 0.5346{\Delta \lambda }_L+\sqrt{0.2166{\Delta \lambda }_L^2+{\Delta \lambda }_G^2}$$

(12)

The populations of the lower ($n_1$) and upper ($n_2$) laser level populations can be obtained by solving the stationary rate equations of a three-level model [2,15]:

$$\begin{array}{c}\hfill \frac{d{n}_1}{dt}=-R_1+P_1\\ \mathrm{(13)}& \hfill \frac{d{n}_2}{dt}=-R_2+P_2\end{array}$$

where:

$$\begin{array}{cc}\hfill R_1& =n_1\left(n_e(C_{12}+C_{10})+A_{10}\right)\hfill \\ \hfill P_1& =n_e\left(n_0{C}_{01}+n_2{C}_{21}\right)+n_2{A}_{21}\hfill \\ \hfill R_2& =n_2\left(n_e(C_{21}+C_{20})+A_{21}\right)\hfill \\ \hfill P_2& =n_e\left(n_0{C}_{02}+n_1{C}_{12}\right)\hfill \end{array}$$

Here, $R_1$ and $R_2$ stand for the relaxation rate from the lower level and upper level, respectively. $P_1$ and $P_2$ stand for the pumping rate to the lower level and upper level, respectively. The pumping rate to the lower level $P_1$ includes both collisional excitation from the ground level and collisional de-excitation and radiative decay from the upper level to the lower level. Meanwhile, the pumping rate to the upper level $P_2$ includes collisional excitation from the ground level and the lower level to the upper level. Here, $n_0$ is the population in the ground level, i.e., $2p^6$ in the Ne-like system. The quasi-neutral approximation implies that $n_0=n_e/Z$, where Z is the ion charge. In other words, the population of Ne-like $A{r}^{+8}$ at $n_e={10}^{18}$ cm⁻³ is considered $n_0=1.25·{10}^{17}$ cm⁻³.

At a specific electron temperature and density, the pumping time from the Ne-like ground level and the relaxation time to the Ne-like level can be calculated as follows:

$$\begin{array}{cc}\hfill t_{pum\mathit{i}}& =\frac{n_{\mathit{i}}}{\frac{d{n}_{\mathit{i}}}{dt}{|}_{pum\mathit{i}}}\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill t_{rel\mathit{i}}& =\frac{n_{\mathit{i}}}{\frac{d{n}_{\mathit{i}}}{dt}{|}_{rel\mathit{i}}}\hfill \end{array}$$

(14b)

where $\mathit{i}$ can be considered either as one or two, corresponding to the lower level and upper level, respectively (Figure 1). Additionally, the $\frac{d{n}_{\mathit{i}}}{dt}{|}_{pum\mathit{i}}$ and $\frac{d{n}_{\mathit{i}}}{dt}{|}_{rel\mathit{i}}$ can be considered as follows: $\frac{d{n}_{\mathit{i}}}{dt}{|}_{pum\mathit{i}}=P_i$ and $\frac{d{n}_{\mathit{i}}}{dt}{|}_{rel\mathit{i}}=R_i$, where $R_i$ and $P_i$ are tabulated in Equation (13).

Taking into account Equation (14), the pumping time to the upper ($t_{pum2}$) and lower level ($t_{pum1}$) and the relaxation time from the upper level ($t_{rel2}$) and lower level ($t_{rel1}$) can be calculated.

Equation (14a) shows that the pumping time to the upper level ($t_{pum2}$) and lower level ($t_{pum1}$) depends on the population of the upper and lower levels ($n_2$ and $n_1$). Besides, Equation (14b) shows that the relaxation time from the upper level ($t_{rel2}$) and lower level ($t_{rel1}$) does not depend on the population of the upper and lower levels ($n_2$ and $n_1$).

4. Results and Discussion

For X-ray Ar-plasma lasing, parametric simulations are done, in order to systematically investigate the optimum time configuration of pump pulses. The approach is: (i) calculate the time scales for lasing, including the ionization time, pumping time and relaxation time; (ii) obtain the effect of pulse duration on the electron density and temperature of the laser-produced plasma, which have a combined effect on the time scales for plasma lasing; and (iii) study the effect of pulse shape on the X-ray lasing in Ne-like $A{r}^{+8}$.

4.1. Time Scales for the Plasma Lasing

The characterizing times are: (i) the ionization time of a neutral $A{r}^0$; (ii) the ionization time up to Ne-like $A{r}^{+8}$; (iii) the transition time among excited levels; and (iv) the pumping time and relaxation time among excited levels of Ne-like $A{r}^{+8}$.

4.1.1. Ionization Time of Neutral $A{r}^0$

In this section, we calculate the electron impact ionization time of neutral $A{r}^0$ using the collisional ionization rate recommended by Voronov [39].

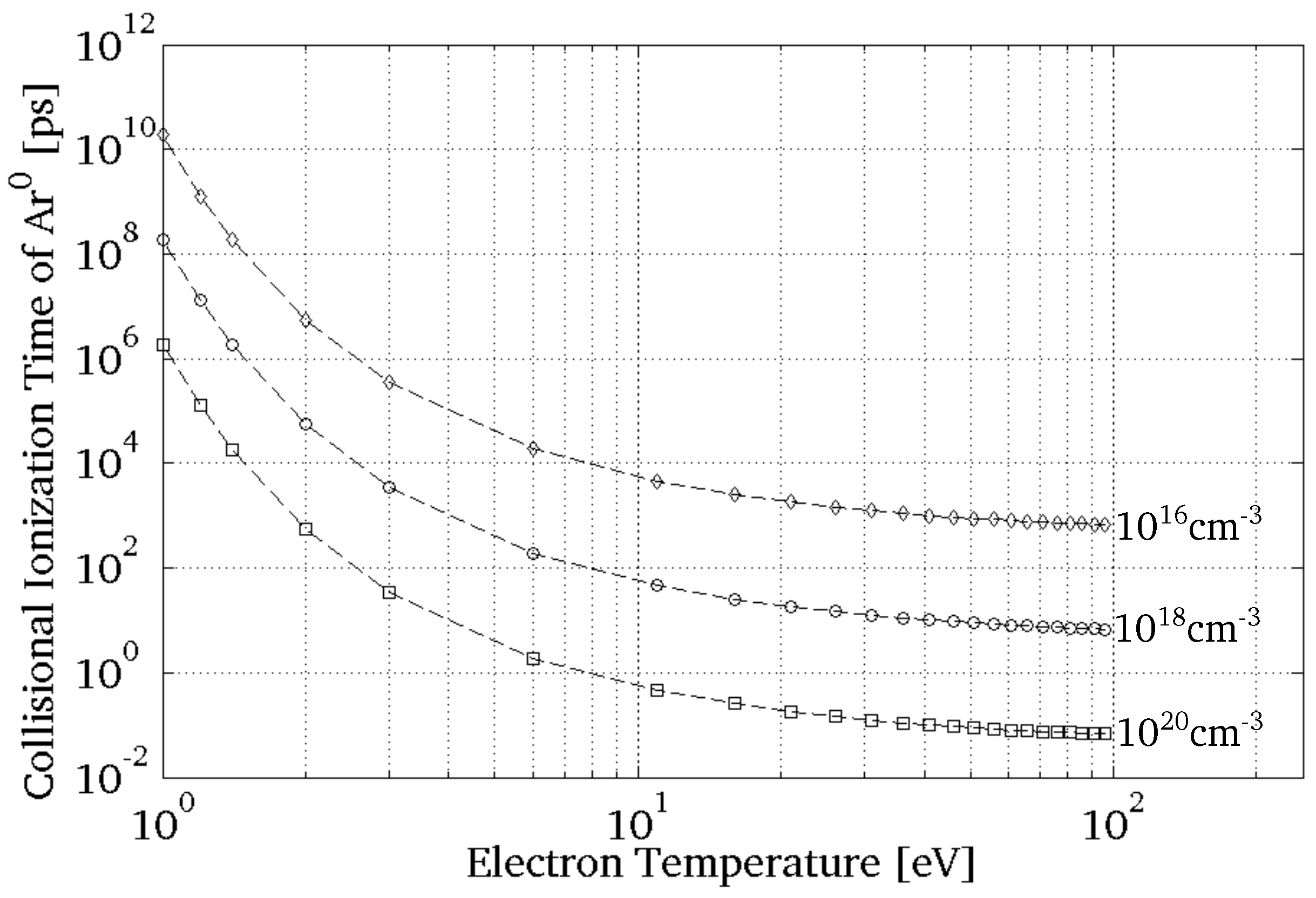
Figure 2 shows that the collisional ionization time of a neutral $A{r}^0$ is dependent on the initial electron temperature and density of the pre-plasma. It shows that the ionization time of a neutral $A{r}^0$ by electron impact scales down linearly with electron density. Besides, it shows that for $T_e⩾10$ eV, the electron impact ionization time of the neutral $A{r}^0$ will decrease by a factor as high as 6.8 with increasing electron temperature by a factor of 10. For $T_e<10$ eV, the electron impact ionization time of the neutral $A{r}^0$ will decrease as high as 3.5 orders of magnitude with increasing electron temperature by a factor of two. Namely, at $T_e<10$ eV, the collisional ionization time decreases faster by increasing the electron temperature.

Figure 2. Collisional ionization time of the neutral $A{r}^0$ as a function of the initial electron temperature for a selection of electron densities.

Figure 2. Collisional ionization time of the neutral $A{r}^0$ as a function of the initial electron temperature for a selection of electron densities.

In the next step, we estimate the time required to produce Ne-like $A{r}^{+8}$.

4.1.2. Ionization Time Up to Ne-Like Stage $A{r}^{+8}$

In this section, the ionization time for achieving $A{r}^{+8}$ is calculated by using Equation (1), which includes the following important processes: (i) collisional ionization; (ii) three-body; and (iii) radiative, and (iv) dielectronic recombination.

Figure 3 shows the time required for the ionization from $A{r}^{+6}$ to $A{r}^{+7}$, $A{r}^{+7}$ to $A{r}^{+8}$ and $A{r}^{+8}$ to $A{r}^{+9}$ for different electron temperatures without (a) and with (b) considering the dielectronic recombination effect at optimum electron density [30]. Elton [30] has reported an optimum electron density and temperature for the lasing of Ne-like $A{r}^{+8}$, which are $n_e=1.5·{10}^{19}$ cm⁻³ and $T_e=154$ eV, respectively. Dielectronic recombination has a stronger effect on the ionization time of $A{r}^{+Z}$ to have $A{r}^{+8}$ at electron temperatures less than 50 eV. At these temperature, the ionization time to achieve $A{r}^{+8}$ without (a) considering dielectronic recombination is higher than with (b) considering the effect of dielectronic recombination as high as a factor of 30. At electron temperatures $T_e>50$, the effect of dielectronic recombination to have $A{r}^{+8}$ is negligible, and the difference is as low as 14%. However, it has an effect in order to achieve $A{r}^{+9}$.

Figure 3. Time required to achieve the $A{r}^{+Z}$ ion for the following steps: (i) $A{r}^{+6}\to A{r}^{+7}$ (Na-like); (ii) $A{r}^{+7}\to A{r}^{+8}$ (Ne-like); and (iii) $A{r}^{+8}\to A{r}^{+9}$ (F-like); as a function of temperature at a constant electron density $n_e=1.5·{10}^{19}$ cm⁻³. The ionization time without (a) and with (b) taking the dielectronic recombination (DR) into consideration is shown. The ionic fractions of $A{r}^{+8}$ at each specific electron temperature are given on the curve $A{r}^{+8}\to A{r}^{+9}$ (F-like).

Figure 3. Time required to achieve the $A{r}^{+Z}$ ion for the following steps: (i) $A{r}^{+6}\to A{r}^{+7}$ (Na-like); (ii) $A{r}^{+7}\to A{r}^{+8}$ (Ne-like); and (iii) $A{r}^{+8}\to A{r}^{+9}$ (F-like); as a function of temperature at a constant electron density $n_e=1.5·{10}^{19}$ cm⁻³. The ionization time without (a) and with (b) taking the dielectronic recombination (DR) into consideration is shown. The ionic fractions of $A{r}^{+8}$ at each specific electron temperature are given on the curve $A{r}^{+8}\to A{r}^{+9}$ (F-like).

The vertical line cross of the optimum electron temperature is shown in Figure 3b. It shows that the times required for the ionization from $A{r}^{+6}$ to $A{r}^{+7}$, $A{r}^{+7}$ to $A{r}^{+8}$ and $A{r}^{+8}$ to $A{r}^{+9}$ are, respectively, 41 ps, 121 ps, and 691 ps.

Inside the circles of Figure 3b, the ionic abundance of $A{r}^{+8}$ when the equilibrium state is reached at specific electron temperatures is given (curve: $A{r}^{+8}$ to $A{r}^{+9}$). It shows that by increasing the electron temperature, the ionic abundance decreases. Besides, it shows that the plasma requires time to produce Ne-like ions. With increasing electron temperatures, the time required for ionization time between levels to be achieved is getting shorter, and the abundance of Ne-like ions is getting smaller, which can result in a low conversion efficiency in X-ray laser-produced plasmas [40]. For example, at an electron density $n_e=1.5·{10}^{19}$ cm⁻³ and electron temperatures $T_e=32$ eV, the abundance of $A{r}^{+8}$ is 92% and at $T_e=110$ eV the abundance of $A{r}^{+8}$ is 0.05%. At these conditions, the ionization time of $A{r}^{+7}$ to achieve Ne-like $A{r}^{+8}$ are $3ns$ ($T_e=32$ eV) and $0.9ns$ ($T_e=110$ eV), respectively.

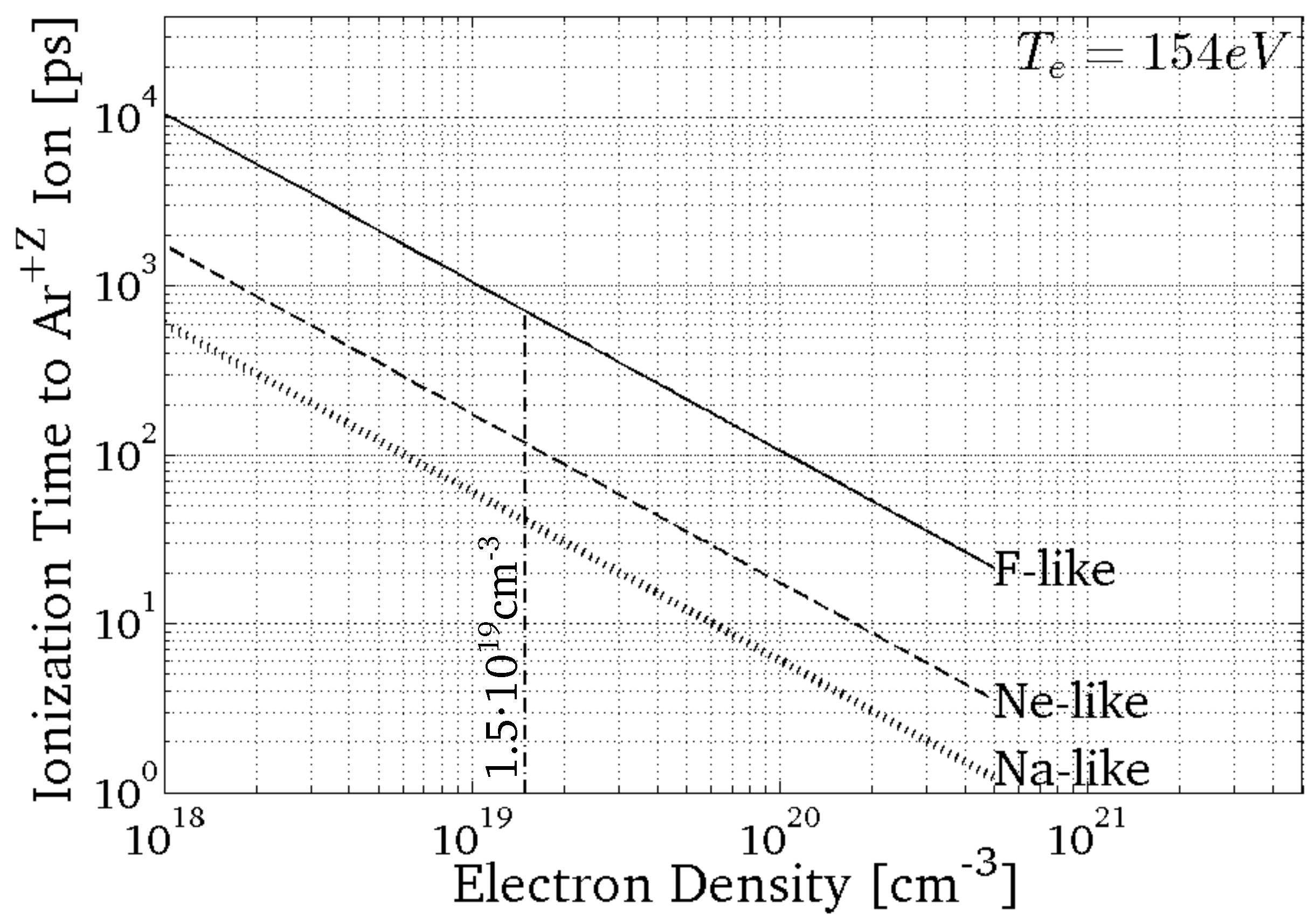
Figure 4 shows the time required for the ionization from $A{r}^{+6}$ to $A{r}^{+7}$, $A{r}^{+7}$ to $A{r}^{+8}$ and $A{r}^{+8}$ to $A{r}^{+9}$ versus electron densities at the optimum electron temperature. It shows that by increasing the electron density by a factor of 10, the ionization time between levels decreases by a factor of 10, as well (the ionization time scales down linearly with electron density).

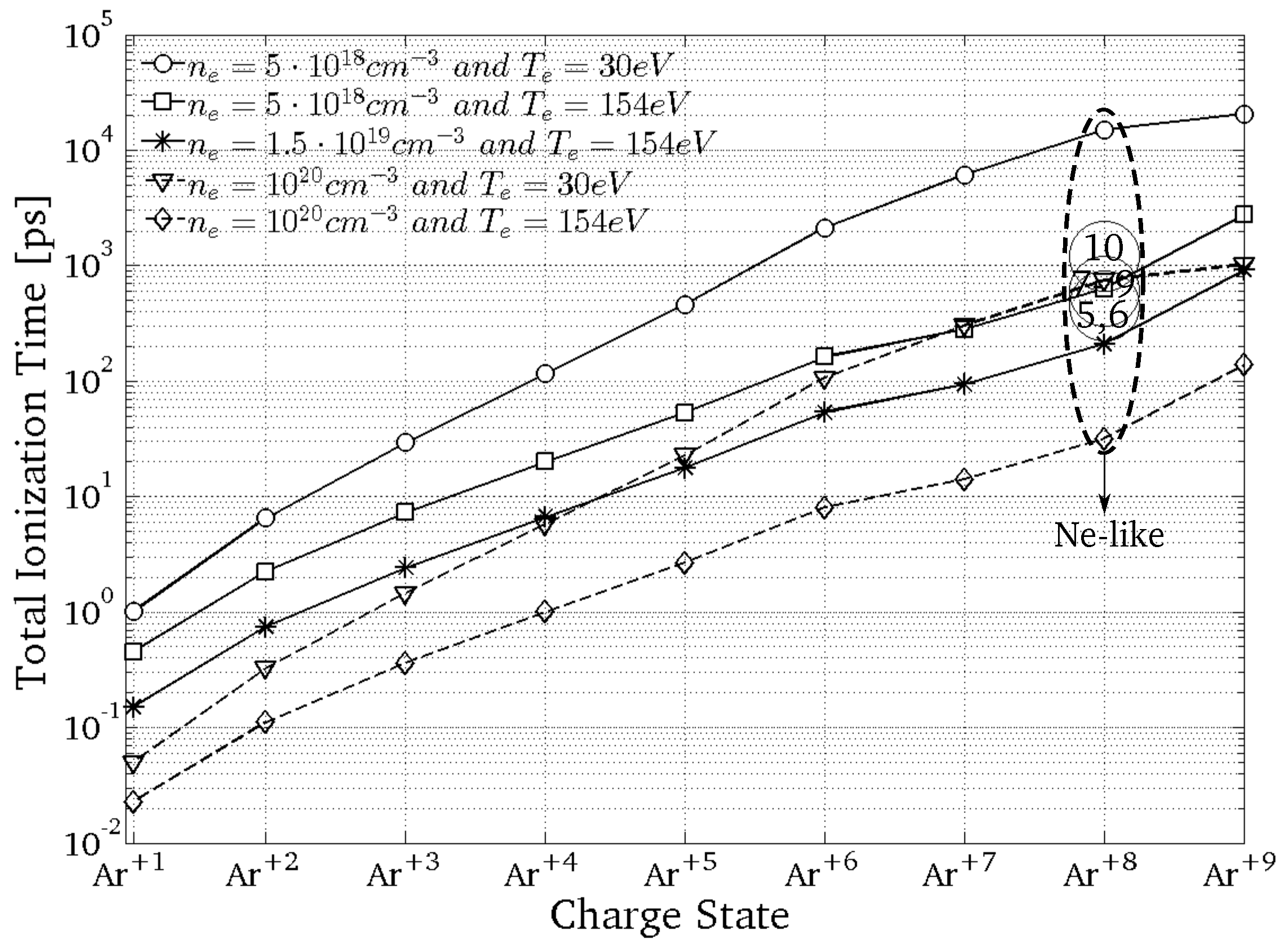
Figure 5 shows the total ionization time required to achieve each ionic charge level ($A{r}^0\to A{r}^{+Z}$) at constant values of the electron density and temperature of Ne-like $A{r}^{+8}$ (Equation (1)). “Total” means the required time to achieve each ionic charge state ($A{r}^{+Z}$). “Total” ionization time, ${\sum }_{n=1}^Z{t}_{A{r}^{+n}\to A{r}^{+(n+1)}}$, comes from the assumption that $A{r}^0$ cannot ionize directly to $A{r}^{+8}$; it should first ionize to $A{r}^{+1}$, then $A{r}^{+1}$ ionize to $A{r}^{+2}$, and so forth. In Figure 5, the dashed ellipse shows the range for the pulse duration or the time delay required to achieve Ne-like $A{r}^{+8}$. The $t_{ion}$ to reach $A{r}^{+8}$ is 210 ps and to reach $A{r}^{+9}$ is 920 ps at the optimal values [30]. This big difference in the ionization time to reach $A{r}^{+8}$ and $A{r}^{+9}$ is due to the closed shell configuration at Ne-like. The pre-pulse durations [5,6,7,8,9] and the time delay [10] from the literature are indicated with circles. Figure 5 shows that the pulse durations or the time delay between pulses [5,6,7,8,9,10] are compatible with the total ionization time for having Ne-like $A{r}^{+8}$.

Figure 4. Ionization time to achieve the $A{r}^{+Z}$ ion as a function of the electron density at the optimum electron temperature for the following: (i) $A{r}^{+6}\to A{r}^{+7}$ (Na-like); (ii) $A{r}^{+7}\to A{r}^{+8}$ (Ne-like); and (iii) $A{r}^{+8}\to A{r}^{+9}$ (F-like).

Figure 4. Ionization time to achieve the $A{r}^{+Z}$ ion as a function of the electron density at the optimum electron temperature for the following: (i) $A{r}^{+6}\to A{r}^{+7}$ (Na-like); (ii) $A{r}^{+7}\to A{r}^{+8}$ (Ne-like); and (iii) $A{r}^{+8}\to A{r}^{+9}$ (F-like).

Figure 5. Total ionization time to reach different ionization stages ($A{r}^0\to A{r}^{+Z}$) at different electron densities and temperatures. Namely, the dashed ellipse shows a range for the required total ionization time to achieve Ne-like $A{r}^{+8}$ at different electron densities and temperatures. Inside the ellipse, the pre-pulse durations or the time delay between pulses from the literature [5,6,7,8,9,10] are indicated.

Figure 5. Total ionization time to reach different ionization stages ($A{r}^0\to A{r}^{+Z}$) at different electron densities and temperatures. Namely, the dashed ellipse shows a range for the required total ionization time to achieve Ne-like $A{r}^{+8}$ at different electron densities and temperatures. Inside the ellipse, the pre-pulse durations or the time delay between pulses from the literature [5,6,7,8,9,10] are indicated.

The lasing can be efficient if the pulse duration or the time delay between pre-pulses is comparable with the time required to reach the desired ionic charge level ($A{r}^{+8}$), as shown in Figure 5.

The total ionization time is faster than the cooling characteristic time of the plasma at the optimum electron density and temperature. The cooling characteristic time is ≈823 ps (Equation (2)), which is ≈4-times longer than the total ionization time to achieve Ne-like $A{r}^{+8}$ at the optimum electron density and temperature (see Table 2).

By fitting a set of data (see Figure 5), we can predict the required total ionization time for having Ne-like $A{r}^{+8}$, with the electron temperature and electron density dependency as follows:

$$t_{ion}\left[s\right]\simeq \frac{(1.4\pm 0.4)·{10}^{13}}{n_e{T_e}^{1.61}}$$

(15)

where $n_e$ is in cm⁻³ and $T_e$ is in eV. Equation (15) is obtained for a variety of ranges of electron temperatures and electron densities. In Equation (15), $+0.4$ stands for $T_e<45$ eV and $-0.4$ stands for $T_e\gtrsim 45$ eV. The former work [41] had scaled the ionization time of Ne-like $A{r}^{+8}$, which does not have electron temperature dependency.

In the next step, we obtained the transition time between excited levels of Ne-like $A{r}^{+8}$ as a ground level.

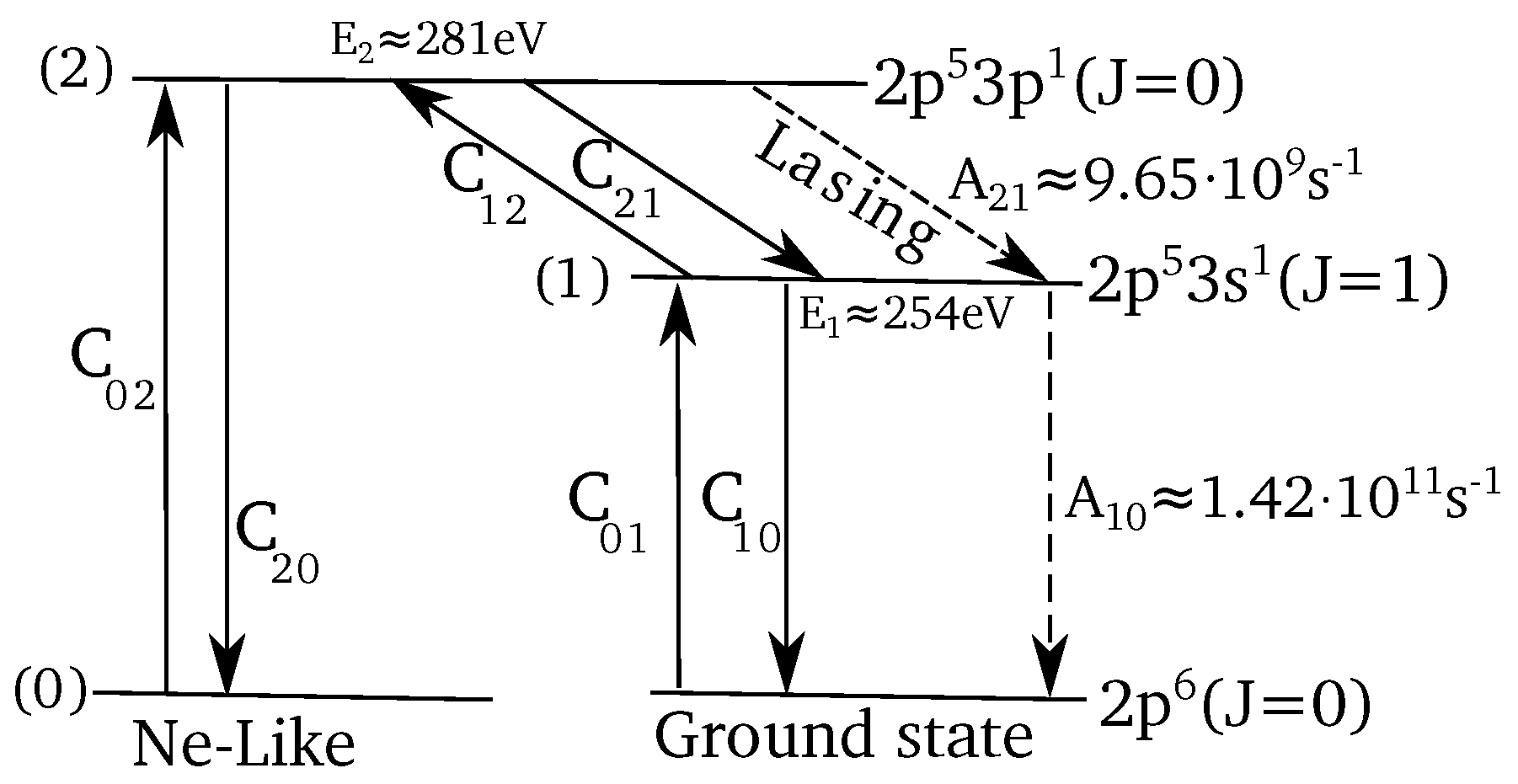
4.1.3. Transition Times among Ne-Like Levels

Transitions times between Ne-like levels were calculated by considering transient collisional excitations and radiative decays.

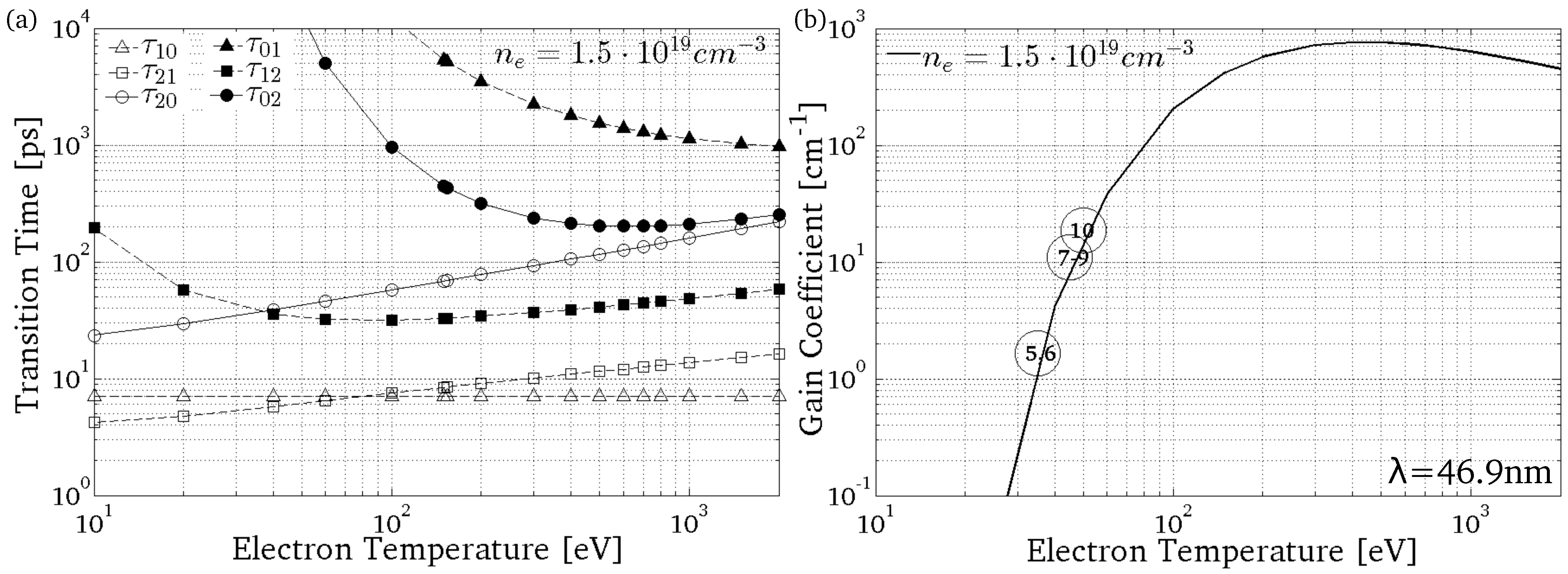
Figure 6a shows the transition time between levels composed of an upper (2) and a lower (1) laser level and the ground (0) level at the optimum electron density [30] in the electron temperature range of $T_e=10$ eV to 2,000 eV. It shows that with increasing the temperature by a factor of five, the transition time from the upper to the lower laser level (${\tau }_{21}$) and the transition time from the upper level to the ground state (${\tau }_{20}$) are increasing by a factor of 1.8 and 2.4, respectively.

Figure 6. (a) Transition time (Equation (3)) between Ne-like $A{r}^{+8}$ levels (Figure 1) at the optimum electron density of $1.5·{10}^{19}$ cm⁻³ [30] as a function of temperature. (b) Gain coefficient of the Ne-like $A{r}^{+8}$ laser at a wavelength $\lambda =46.9$ nm. Benchmarking data [5,6,7,8,9,10] from the literature (numbered circles) from experiments for gain coefficients of Ne-like $A{r}^{+8}$ laser-produced plasma are given.

Figure 6. (a) Transition time (Equation (3)) between Ne-like $A{r}^{+8}$ levels (Figure 1) at the optimum electron density of $1.5·{10}^{19}$ cm⁻³ [30] as a function of temperature. (b) Gain coefficient of the Ne-like $A{r}^{+8}$ laser at a wavelength $\lambda =46.9$ nm. Benchmarking data [5,6,7,8,9,10] from the literature (numbered circles) from experiments for gain coefficients of Ne-like $A{r}^{+8}$ laser-produced plasma are given.

It is shown that the transition time from the ground level to the upper level (${\tau }_{02}$) and the transition time from the lower to upper level (${\tau }_{12}$) are decreasing with increasing the temperatures up to 600 eV and 100 eV, respectively. However, ${\tau }_{02}$ and ${\tau }_{12}$ start to increase for $T_e>600$ eV and $T_e>100$ eV, respectively.

Figure 6b shows the calculated gain coefficient of a Ne-like $A{r}^{+8}$ at a wavelength $\lambda =46.9$ nm in the $2p^{5}3p^1(J=0)\to 2p^{5}3s^1(J=1)$ laser transition ($2\to 1$) at the optimum electron density [30] versus electron temperature. At $T_e=50$ eV, the gain coefficient is 15 cm⁻¹, while ${\tau }_{21}$ is faster than ${\tau }_{10}$ by a factor of $1.1$. Then, a comparison of Figure 6a,b shows that in the transient electron collisional excitation scheme, inversion (gain formation) happens because the collisional excitation and de-excitation processes of the upper and lower levels occur at different rates. The previous claim [42,43] of the faster radiative decay of the lower level than the upper level ($A_{10}>A_{21}$) is thus one aspect of the lasing.

It is shown that at the optimum electron density with increasing the temperatures up to 400 eV, the gain is increasing. If the temperature increases from 35 eV to 400 eV, the gain increases by $2.88$-orders of magnitude. At $T_e\approx 35$ eV, the gain coefficient is ≈1 cm⁻¹. From $T_e>400$ eV, the gain starts to decrease.

In Figure 6b, the benchmarking data [5,6,7,8,9,10] from the experiments for gain coefficients of Ne-like $A{r}^{+8}$ produced by the laser-plasma interaction are shown (see Table 1). They are shown just to demonstrate that the experimentally measured gain is always lower than the gain calculated by the theory (atomic calculation). In the experiments, the gain along its propagation path through the plasma suffers from a finite gain lifetime, traveling-wave velocity mismatch or inhomogeneous plasma conditions. All of these effects decrease the measured gain coefficient in the experiment.

Next, we estimate the pumping time versus the relaxation time among excited levels of Ne-like $A{r}^{+8}$.

4.1.4. Pumping Time versus Relaxation Time among Ne-Like Levels

Since the time it takes to maintain the inversion is equal to the upper level lifetime (the relaxation time of the upper level), the optimum value of the pulse duration of the main pulse must be equivalent to the relaxation time of the upper level ($t_{rel2}$). However, if the pulse duration of the main pulse is much longer than the lifetime of the upper level, most of the possible inversions would be lost by spontaneous emission without amplification.

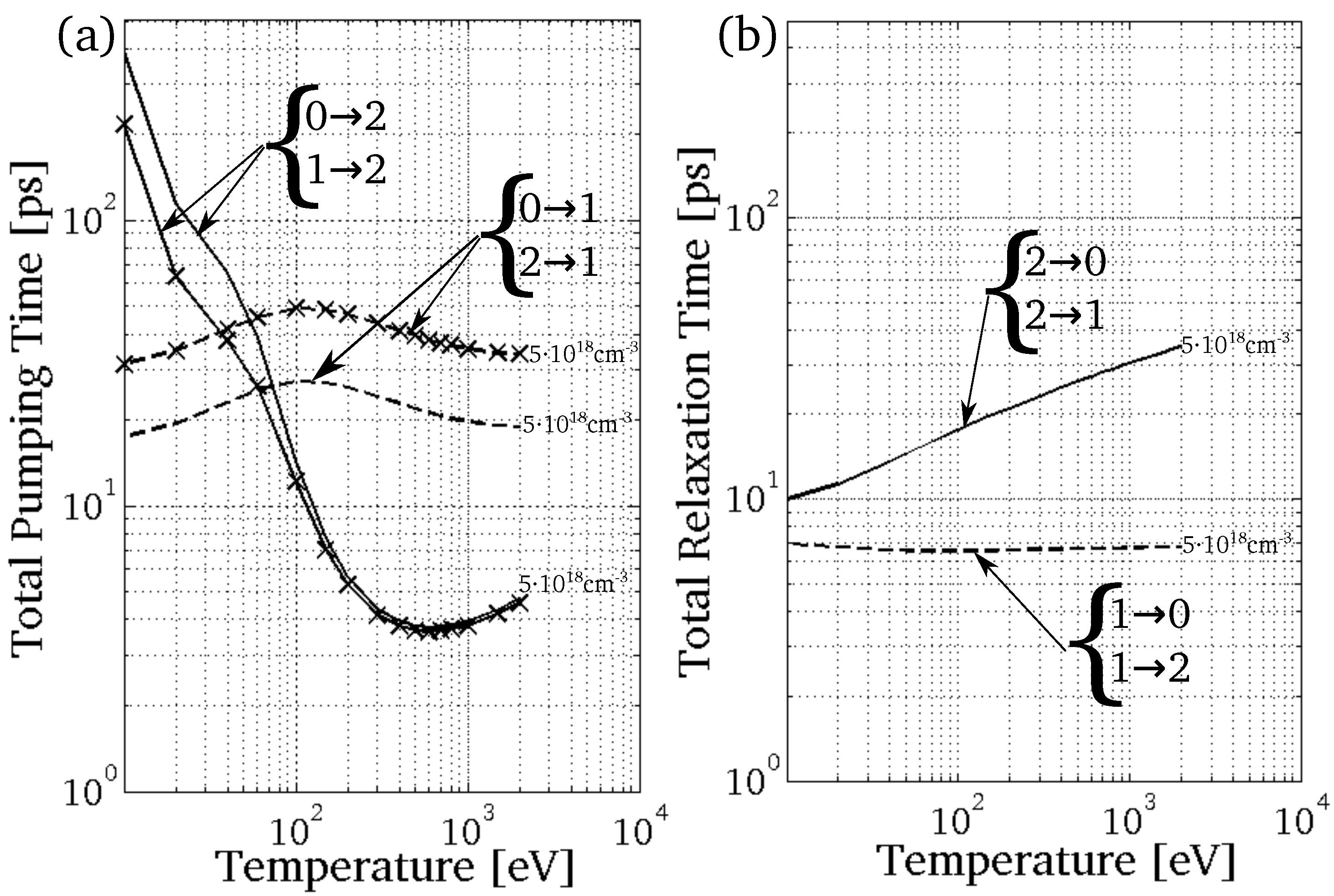
Figure 7 shows that the pumping to the upper and lower laser level, as well as the relaxation from the upper and lower level occur at different time scales. In Figure 7a, for plotting the pumping time to the lower and upper level, the optimum value of the upper level population was considered $n_2=3·{10}^{-4}{n}_0{({\lambda }_{21})}^{0.5}$[30], where ${\lambda }_{21}$ is an X-ray wavelength in angstroms. The population of the upper and lower level is calculated with considering $F=$ 50% and $F=$ 10% (Equation (7)). These values of $F=$ 50% and $F=$ 10% are conservative values.

It is shown that the relaxation time does not depend on the upper and lower level population, i.e., the relaxation time for both $F=$ 10% and $F=$ 50% are the same.

Figure 7a shows that at temperatures higher than 36 eV, corresponding to $F=$ 10%, the pumping time to the upper level is faster than the pumping to the lower level as high as a factor of ≈10.

Besides, it is shown that at temperatures higher than 72 eV, corresponding to $F=$ 50%, the pumping time to the upper level is faster than the pumping time to the lower level as high as a factor of ≈7.

Figure 7. (a) Total pumping time (Equation (14a)) to the upper level (2) and lower level (1) at an electron density of $5·{10}^{18}$ cm⁻³, considering an inversion factor of 10% (curve with marker) and 50% (curve without marker). (b) Total relaxation time (Equation (14b)) of the upper (solid line) and lower (dashed line) levels of Ne-like $A{r}^{+8}$.

Figure 7. (a) Total pumping time (Equation (14a)) to the upper level (2) and lower level (1) at an electron density of $5·{10}^{18}$ cm⁻³, considering an inversion factor of 10% (curve with marker) and 50% (curve without marker). (b) Total relaxation time (Equation (14b)) of the upper (solid line) and lower (dashed line) levels of Ne-like $A{r}^{+8}$.

Figure 7b shows that at an electron density of $5·{10}^{18}$ cm⁻³, the relaxation time from the lower level is faster than the upper level by a factor of as high as $5.2$. It is shown that the relaxation time from the upper level with increasing of the electron temperature at a constant electron density is getting slower. For an electron density of $5·{10}^{18}$ cm⁻³ and electron temperatures in the range of $10\to$2000 eV, the relaxation time from the upper level is in the range of $10\to 35$ ps.

Figure 5 and Figure 7 show that at a low electron temperature, $T_e=30$ eV and the electron density $n_e=5·{10}^{18}$ cm⁻³, the time scale in which the relaxation time from the upper level ($t_{rel2}\approx 12$ ps) and the lower level ($t_{rel1}\approx 7$ ps) occurs is much lower than the time required to achieve Ne-like ions ($t_{ion}\approx$15,000 ps) and the time required to generate a population inversion ($t_{pum2}\approx 60$ ps).

Table 2 shows that at an optimum electron density of $1.5·{10}^{19}$ cm⁻³ and increasing the electron temperature by a factor of five, the relaxation time from the upper level is getting slower by a factor of ≈$1.7$ ($T_e=154$ eV is an optimum electron temperature [30]). Meanwhile, at a constant electron temperature of $T_e=30$ eV, increasing the electron density, the relaxation time from the upper level is getting faster. With increasing the electron density by a factor of ≈3, the relaxation time from the upper level is faster by a factor of ≈3.

Table 2. Summary of the effects of the electron temperature and density on $t_{ion}$ (total ionization time to achieve Ne-like ions), $t_{pum2}$ (total pumping time to the upper level) and $t_{rel2}$ (total relaxation time from the upper level) at a wavelength $\lambda =46.9$ nm in the $2p^{5}3p^1(J=0)\to 2p^{5}3s^1(J=1)$ laser transition at $F>0$.

$n_e$ (cm−3)	$T_e$(eV)	$t_{\mathit{ion}}$(ps)	$t_{\mathit{pum}2}$(ps)	$t_{\mathit{rel}2}$ (ps)	$t_{\mathit{pum}2}/t_{\mathit{rel}2}$
$1.5·{10}^{19}$	30	5,000	15	$4.5$	$3.3$
$1.5·{10}^{19}$	154	211	$2.3$	$7.5$	$0.3$
$5·{10}^{19}$	30	1,500	8	$1.4$	$5.7$

Table 2. Summary of the effects of the electron temperature and density on $t_{ion}$ (total ionization time to achieve Ne-like ions), $t_{pum2}$ (total pumping time to the upper level) and $t_{rel2}$ (total relaxation time from the upper level) at a wavelength $\lambda =46.9$ nm in the $2p^{5}3p^1(J=0)\to 2p^{5}3s^1(J=1)$ laser transition at $F>0$.

$n_e$ (cm−3)	$T_e$(eV)	$t_{\mathit{ion}}$(ps)	$t_{\mathit{pum}2}$(ps)	$t_{\mathit{rel}2}$ (ps)	$t_{\mathit{pum}2}/t_{\mathit{rel}2}$
$1.5·{10}^{19}$	30	5,000	15	$4.5$	$3.3$
$1.5·{10}^{19}$	154	211	$2.3$	$7.5$	$0.3$
$5·{10}^{19}$	30	1,500	8	$1.4$	$5.7$

Table 2 summarizes the effect of the electron temperature and density on $t_{ion}$, $t_{pum2}$ and $t_{rel2}$ time scales. It shows that the ratio of $t_{pum2}$ to $t_{rel2}$ is smaller for larger electron temperatures. Implementation data in Table 2 show that, with increasing electron density, both values of $t_{rel2}$ and $t_{pum2}$ are decreasing. Meanwhile, with increasing electron temperature, the value of $t_{rel2}$ and $t_{pum2}$, respectively, increases and decreases.

Based on our calculation (using Equation (14)), we can estimate the total relaxation time from the upper level ($t_{rel2}$) and the total pumping time to the upper level ($t_{pum2}$) for $T_e\lesssim 300$ eV:

$$\begin{array}{c}\hfill t_{rel2}\left[s\right]\simeq \frac{(2.8\pm 0.2)·{10}^7}{n_e{T_e}^{-0.27}}\\ \mathrm{(16)}& \hfill t_{pum2}\left[s\right]\simeq \frac{(2.2\pm 0.3)·{10}^{10}}{n_e{T_e}^{1.23}}\end{array}$$

where $n_e$ is in cm⁻³ and $T_e$ is in eV. Equation (16) is retrieved by fitting the data points by considering a specific electron density and temperature and taking into account Ne-like $A{r}^{+8}$ as a ground level (see Figure 1).

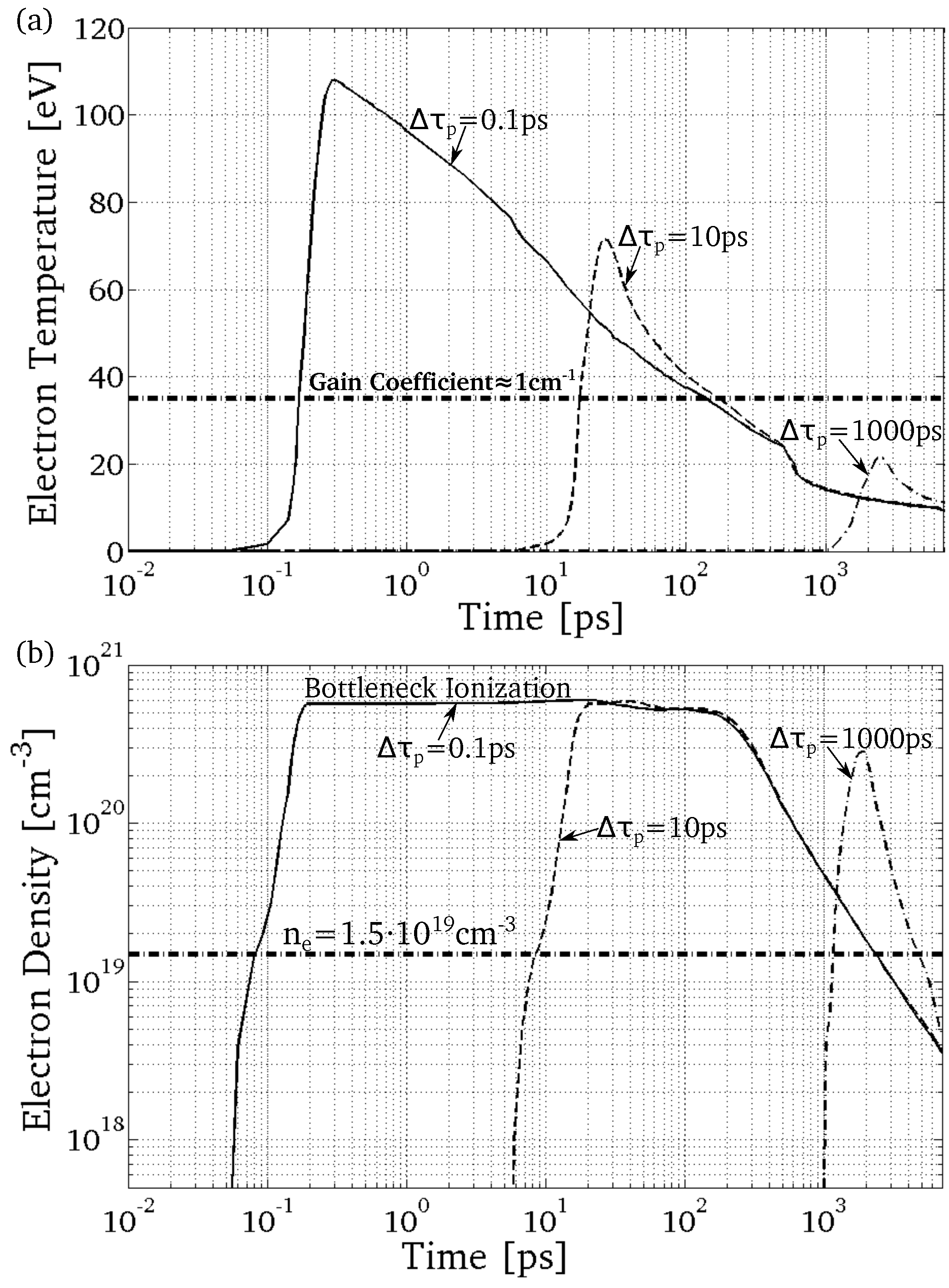
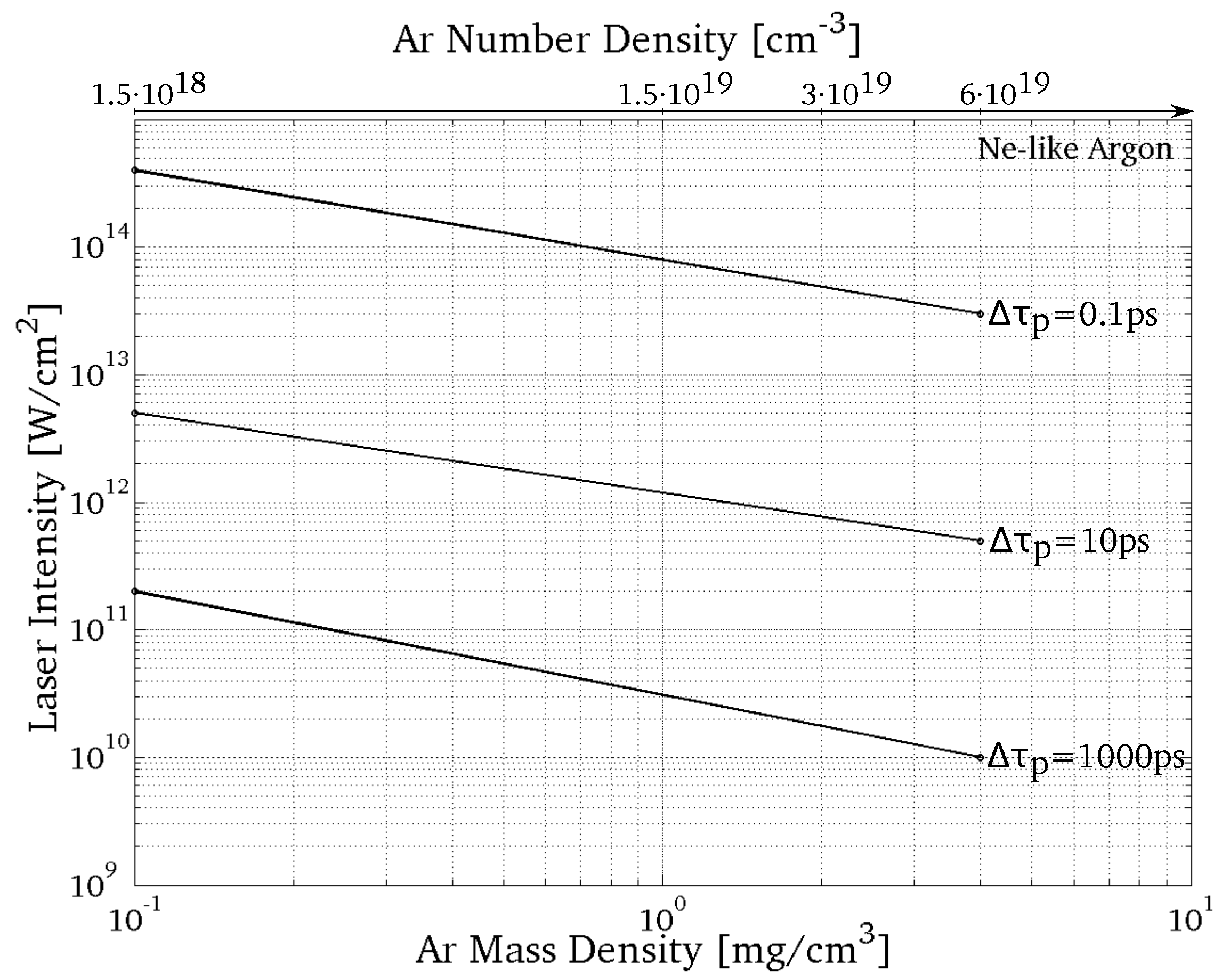
So far, the electron density and temperature influence the total ionization time required to obtain Ne-like $A{r}^{+8}$ and also affect the time scales of $t_{pum}$ and $t_{rel}$. In the next section, we show how the pulse duration can influence the quantity of the electron density and temperature in the X-ray-produced plasma.

4.2. Effect of Pulse Duration on Hydrodynamic Parameters

In order to determine the dependency of the pulse duration on the electron density and temperature of the laser-produced plasma, we studied the evolution of the electron density and temperature produced by different pulse durations.

Figure 8 shows the maximum electron temperature and maximum electron density versus time in the direction of plasma expansion. The data in Figure 8 are obtained from our calculation using a hydro-code (Hyades).

During the short laser pulse, little expansion occurs ($L_{exp}=v_{exp}·\Delta {\tau }_p$). This allows the direct deposition of a remarkable amount of the laser energy on the plasma, which means a higher electron temperature.

It is found that the electron density and temperature are respectively a factor of ≈$2.1$- and ≈5-times higher in the case of a shorter pulse of $\Delta {\tau }_p=0.1$ ps in comparison to the long pulse of $\Delta {\tau }_p=$ 1,000 ps. Implementation Figure 8 and data in Table 2 show that in the case of a shorter pulse, the time required for producing Ne-like $A{r}^{+8}$ and the $t_{pum2}$ and $t_{rel2}$ time scales will be shorter and closer together.

Figure 8. (a) Time-dependent electron temperature and (b) electron density produced with pulses with durations of 0.1 ps, 10 ps and 1,000 ps and energy fluence $j_L\approx$ 10 J/cm².

Figure 8. (a) Time-dependent electron temperature and (b) electron density produced with pulses with durations of 0.1 ps, 10 ps and 1,000 ps and energy fluence $j_L\approx$ 10 J/cm².

Figure 8b shows that in the case of the plasma produced with the pulse duration of $0.1$ ps, there is a bottleneck in the ionization level at $0.2ps\lesssim t\lesssim 4$ ps, which means that plasma for recombination and expansion needs more time. Figure 8a shows that electrons can lose energy emitting radiation and by conduction, so the temperature diminishes. Ne-like $A{r}^{+8}$ is the closed shell, making removal of an additional electron more difficult. This significantly increases the threshold for further electron ionization, which can also be considered an ionization bottleneck for a plasma at a specific temperature.

Figure 8b shows that the electron density is always less than $n_{ec}\approx {10}^{21}$ cm⁻³, where $n_{ec}$ is the critical electron density and also a turning point in the normal incidence for the pump laser with a wavelength $\lambda =$ 1,054 nm. Figure 8b shows that the plasma produced by a gas target can limit the refraction of the pump-pulse, which means the time delay between pulses cannot be an issue in order to smear-out the electron density gradient.

The line cross of optimum electron density is shown in Figure 8a, and the gain coefficient of ≈1 cm⁻¹ at this optimum electron density and electron temperature 35 eV is shown in Figure 8b. Figure 8b shows that the plasma produced by the long pulse $\Delta {\tau }_p=$ 1,000 ps is below the area with the gain coefficient of 1 cm⁻¹.

4.3. Optimum Pump-Laser Intensity for Achieving Ne-Like $A{r}^{+8}$

In this section, the optimum pump-laser intensity at the focus point of the laser on the target in order to have Ne-like $A{r}^{+8}$ is estimated.

Figure 9 shows the optimum laser intensity required to have Ne-like $A{r}^{+8}$ at different pulse durations and $A{r}^0$ mass densities, obtained from the hydro-code (Hyades). It shows that with increasing the initial gas density by a factor of 10, the required laser intensity is decreased by a factor as high as ≈7. When charged particles are accelerated in the electric field of the laser, they can ionize neutral gas molecules by collisions. Then, the process is dependent on the initial gas density (pressure).

Figure 9. Optimum laser intensity for having Ne-like $A{r}^{+8}$ as a function of $A{r}^0$ density at different pulse durations. The top axis is the number density (cm⁻³).

Figure 9. Optimum laser intensity for having Ne-like $A{r}^{+8}$ as a function of $A{r}^0$ density at different pulse durations. The top axis is the number density (cm⁻³).

Based on the results in Figure 9 and by the method of curve fitting from MATLAB code, the following power-law formula can be obtained:

$$\begin{array}{c}\hfill I_{opt}(W/c{m}^2)\approx \Delta {\tau }_p^{-1.13}(\frac{5.81·{10}^{12}}{{\rho }_0^{0.72}}),\Delta {\tau }_p<1ps\\ \hfill I_{opt}(W/c{m}^2)\approx \Delta {\tau }_p^{-1.01}(\frac{1.24·{10}^{13}}{{\rho }_0^{0.59}}),1⩽\Delta {\tau }_p⩽100ps\\ \mathrm{(17)}& \hfill I_{opt}(W/c{m}^2)\approx \Delta {\tau }_p^{-0.31}(\frac{2.78·{10}^{11}}{{\rho }_0^{0.79}}),\Delta {\tau }_p>100ps\end{array}$$

where the optimum pump-laser intensity ($I_{opt}$) for having Ne-like $A{r}^{+8}$ has dependency on the pulse duration and initial $A{r}^0$ density. In Equation (17), $\Delta {\tau }_p$ is the pulse duration in ps and ${\rho }_0$ is the initial $A{r}^0$ mass density in mg/cm³.

5. Conclusions

In this study, we systematically investigated the optimum time configuration of pump pulses.

In Section 4.1.2, we studied a neutral $A{r}^0$ ionization time scale for achieving Ne-like $A{r}^{+8}$. We found that the dielectronic recombination has an important effect at temperatures less than 50 eV. For $T_e\lesssim 50$ eV, without considering dielectronic recombination, the ionization time is overestimated as high as a factor of 30. For $T_e>50$, this difference reduces to 14%.

The total ionization time in order to achieve Ne-like ions is obtained by Equation (15).

In Section 4.1.3, we showed that in the transient electron collisional pumping scheme, lasing happens because the collisional excitation processes of the upper and lower levels occur at different rates, and not simply because of the faster rate of the radiative decay of the lower level. Thus, even if the transition time of the upper level (2) to the lower level (1) is faster than the transition time from the lower level (1) to the ground state (0), the gain coefficient can appear.

In Section 4.1.4, we demonstrated that at low temperatures ($T_e=30$ eV) and at certain an electron density ($n_e=1.5·{10}^{19}$ cm⁻³), both the total relaxation time from the upper level ($4.5$ ps) and total pumping time to the upper level (15 ps) are much shorter than the time required to achieve Ne-like ions (5000 ps).

In Section 4.1.4, we showed that the ratio of the pumping time for the population inversion to the relaxation time from the upper level can be as high as a factor of 10 for $T_e\gtrsim 20$ eV, depending on the electron density.

We found that at temperatures higher than 36 eV ($F=$ 10%) and 72 eV ($F=$ 50%), the upper level will be pumped faster than the lower level by a factor as high as 10.

It is shown that at a constant electron density ($1.5·{10}^{19}$ cm⁻³), increasing the temperature by a factor of five ($30\to 154$ eV), the ionization time to achieve Ne-like ions and the pumping time to the upper level are decreasing, by a factor of 24 and $6.5$, respectively. Meanwhile the relaxation time from the upper level is increasing by a factor of $1.7$ (Table 2).

It is found that at a constant electron temperature (30 eV), increasing the electron density by a factor of $3.3$ ($1.5·{10}^{19}\to 5·{10}^{19}$ cm⁻³), all time scales including ionization time, pumping time and relaxation time to the upper level are decreasing, by a factor of $3.3$, $1.9$ and $3.2$, respectively (Equation (16)).

Besides, the pumping time to the upper level (2) and relaxation time from the lower level (1) are estimated; Equation (16). It was found that for an electron density higher than $5·{10}^{18}$ cm⁻³, at electron temperatures in the range $10\to$ 2000 eV, the relaxation time from the upper level is as high as ${\tau }_{rel2}\le 35$ ps. The most effective lasing happens with short pulses with a pulse duration comparable to the total relaxation time from the upper level, namely $\Delta {\tau }_p\le 35$ ps.

In Section 4.2, we studied the effect of the pulse duration on the electron temperature or density for plasma lasing. The optimum time scale required to achieve Ne-like ions, as well as the time required to generate a population inversion depends on the combined effect of the temperature and density (Table 2).

In Section 4.3, a formula for calculating optimum laser intensity for producing the Ne-like $A{r}^{+8}$ is obtained; Equation (17). This equation can be used for different pulse durations and considering different initial gas densities of $A{r}^0$.