Deep-Subwavelength Negative Refraction of Hyperbolic Plasmon Polariton at Visible Frequencies
Abstract
1. Introduction
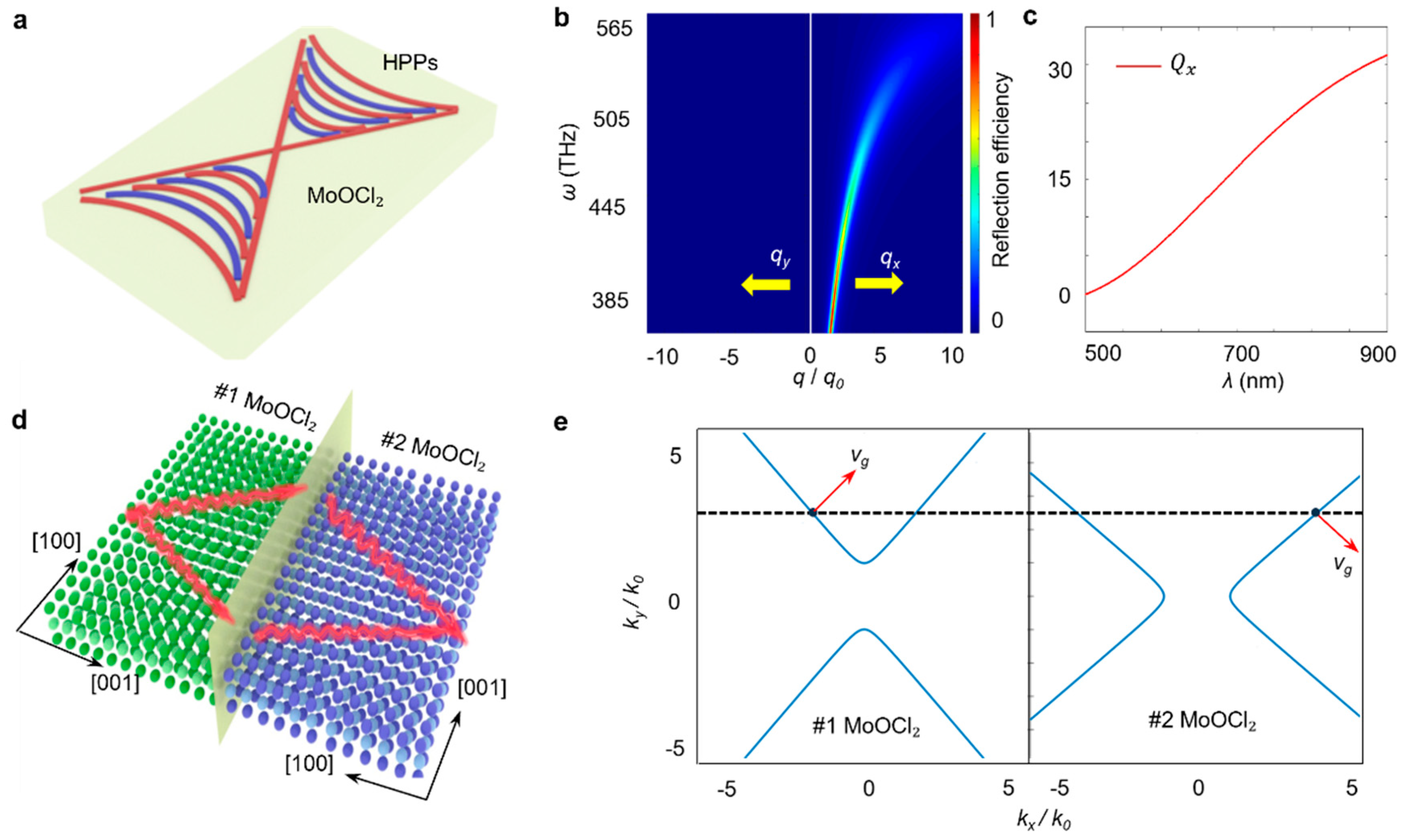
2. The Principle and Design of Heterojunctions
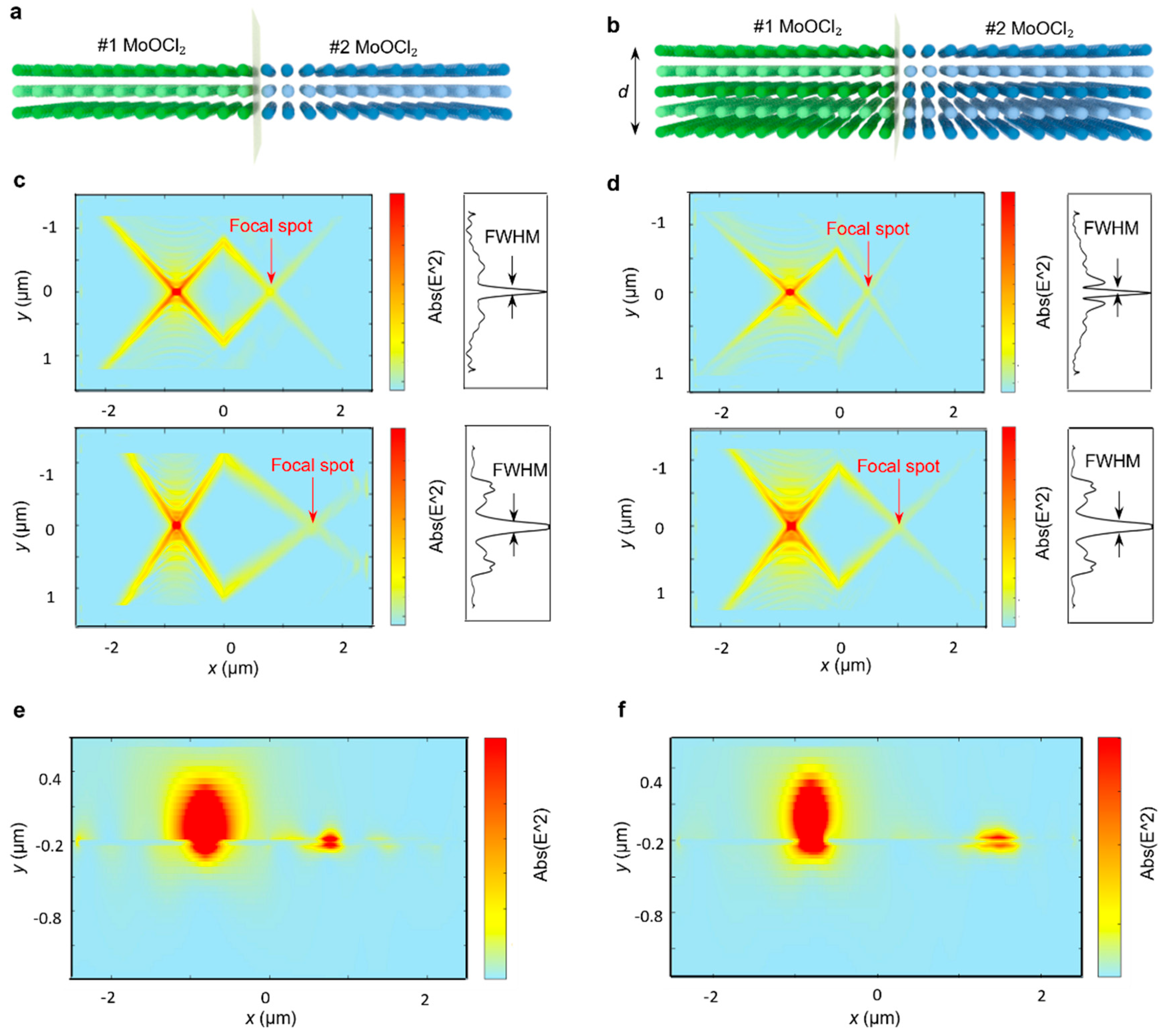
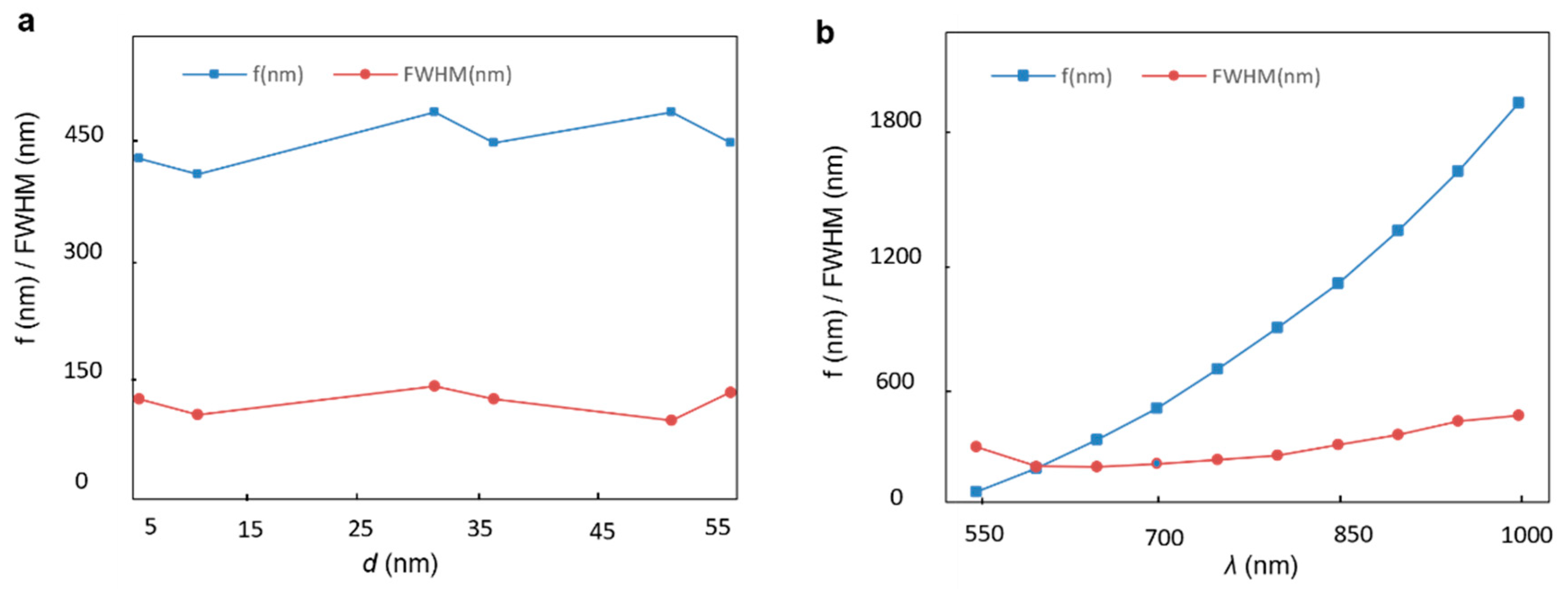
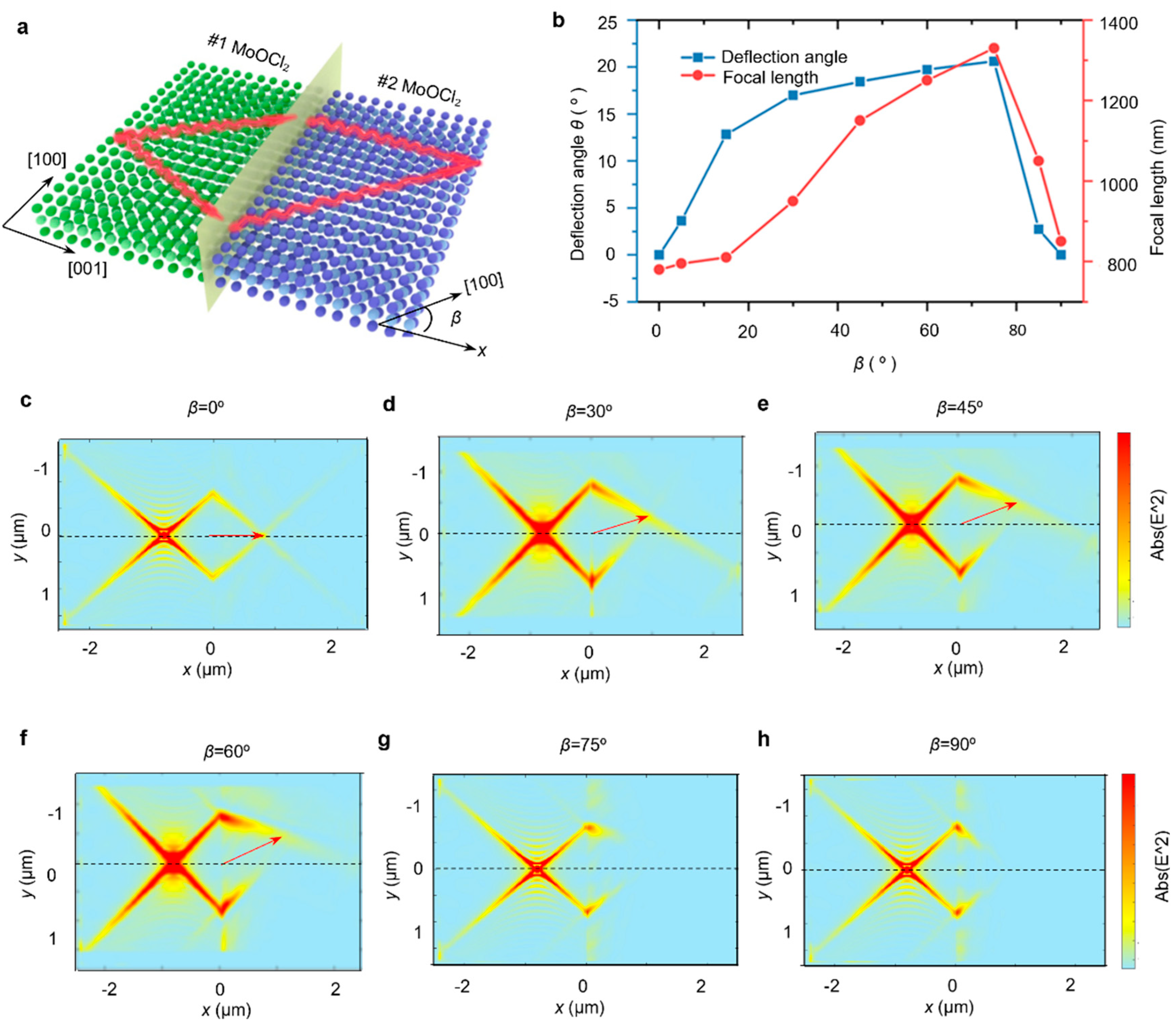
3. The Results and Analysis of the Numerical Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Álvarez-Pérez, G.; Duan, J.; Taboada-Gutiérrez, J.; Ou, Q.; Nikulina, E.; Liu, S.; Edgar, J.H.; Bao, Q.; Giannini, V.; Hillenbrand, R.; et al. Negative reflection of nanoscale-confined polaritons in a low-loss natural medium. Sci. Adv. 2022, 8, eabp8486. [Google Scholar] [CrossRef]
- Hu, H.; Chen, N.; Teng, H.; Yu, R.; Xue, M.; Chen, K.; Xiao, Y.; Qu, Y.; Hu, D.; Chen, J.; et al. Gate-tunable negative refraction of mid-infrared polaritons. Science 2023, 379, 558–561. [Google Scholar] [CrossRef]
- Jiang, J.; Lin, X.; Zhang, B. Broadband Negative Refraction of Highly Squeezed Hyperbolic Polaritons in 2D Materials. Research 2018, 2018, 2532819. [Google Scholar] [CrossRef]
- Sternbach, A.J.; Moore, S.L.; Rikhter, A.; Zhang, S.; Jing, R.; Shao, Y.; Kim, B.S.Y.; Xu, S.; Liu, S.; Edgar, J.H.; et al. Negative refraction in hyperbolic hetero-bicrystals. Science 2023, 379, 555–557. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhen, Z.; Yang, Y.; Gan, G.; Jariwala, D.; Cui, X. Negative refraction inspired polariton lens in van der Waals lateral heterojunctions. Appl. Phys. Lett. 2019, 114, 221101. [Google Scholar] [CrossRef]
- Zhang, T.; Zheng, C.; Chen, Z.N.; Qiu, C.-W. Negative Reflection and Negative Refraction in Biaxial van der Waals Materials. Nano Lett. 2022, 22, 5607–5614. [Google Scholar] [CrossRef] [PubMed]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Staude, I.; Schilling, J. Metamaterial-inspired silicon nanophotonics. Nat. Photonics 2017, 11, 274–284. [Google Scholar] [CrossRef]
- Goban, A.; Hung, C.-L.; Yu, S.-P.; Hood, J.; Muniz, J.; Lee, J.; Martin, M.; McClung, A.; Choi, K.; Chang, D.; et al. Atom–light interactions in photonic crystals. Nat. Commun. 2014, 5, 3808. [Google Scholar] [CrossRef]
- Sekoguchi, H.; Takahashi, Y.; Asano, T.; Noda, S. Photonic crystal nanocavity with a Q-factor of ~9 million. Opt. Express 2014, 22, 916–924. [Google Scholar] [CrossRef]
- Lundeberg Mark, B.; Gao, Y.; Woessner, A.; Tan, C.; Alonso-González, P.; Watanabe, K.; Taniguchi, T.; Hone, J.; Hillenbrand, R.; Koppens, F.H. Thermoelectric detection and imaging of propagating graphene plasmons. Nat. Mater. 2017, 16, 204–207. [Google Scholar] [CrossRef]
- Thongrattanasiri, S.; Manjavacas, A.; de Abajo, F.J.G. Quantum Finite-Size Effects in Graphene Plasmons. ACS Nano 2012, 6, 1766–1775. [Google Scholar] [CrossRef]
- Jacob, Z. Hyperbolic phonon–polaritons. Nat. Mater. 2014, 13, 1081–1083. [Google Scholar] [CrossRef]
- Zhang, Q.; Ou, Q.; Hu, G.; Liu, J.; Dai, Z.; Fuhrer, M.S.; Bao, Q.; Qiu, C.-W. Hybridized Hyperbolic Surface Phonon Polaritons at α-MoO3 and Polar Dielectric Interfaces. Nano Lett. 2021, 21, 3112–3119. [Google Scholar] [CrossRef]
- Chakraborty, S.; Marshall, O.P.; Folland, T.G.; Kim, Y.-J.; Grigorenko, A.N.; Novoselov, K.S. Gain modulation by graphene plasmons in aperiodic lattice lasers. Science 2016, 351, 246–248. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Fei, Z.; Ma, Q.; Rodin, A.S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Gannett, W.; Regan, W.; Watanabe, K.; et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 2014, 343, 1125–1129. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Ma, Q.; Andersen, T.; Mcleod, A.S.; Fei, Z.; Liu, M.K.; Wagner, M.; Watanabe, K.; Taniguchi, T.; Thiemens, M.; et al. Subdiffractional focusing and guiding of polaritonic rays in a natural hyperbolic material. Nat. Commun. 2015, 6, 6963. [Google Scholar] [CrossRef] [PubMed]
- Ni, G.X.; Wang, L.; Goldflam, M.D.; Wagner, M.; Fei, Z.; McLeod, A.S.; Liu, M.K.; Keilmann, F.; Ozyilmaz, B.; Neto, A.H.C.; et al. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photonics 2016, 10, 244–247. [Google Scholar] [CrossRef]
- Qian, C.; Lin, X.; Yang, Y.; Gao, F.; Shen, Y.; Lopez, J.; Kaminer, I.; Zhang, B.; Li, E.; Soljačić, M.; et al. Multifrequency Superscattering from Subwavelength Hyperbolic Structures. ACS Photonics 2018, 5, 1506–1511. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Yoxall, E.; Schnell, M.; Nikitin, A.Y.; Txoperena, O.; Woessner, A.; Lundeberg, M.B.; Casanova, F.; Hueso, L.E.; Koppens, F.H.L.; Hillenbrand, R. Direct observation of ultraslow hyperbolic polariton propagation with negative phase velocity. Nat. Photonics 2015, 9, 674–678. [Google Scholar] [CrossRef]
- Cohen, K.; Dolev, S.; Bartal, G. Deep-Subwavelength Focusing and Reflectionless Negative Refraction in Visible-Light Hyperbolic Metasurface. Adv. Opt. Mater. 2025, 13, 2402591. [Google Scholar] [CrossRef]
- Shin, H.; Fan, S. All-Angle Negative Refraction for Surface Plasmon Waves Using a Metal-Dielectric-Metal Structure. Phys. Rev. Lett. 2006, 96, 073907. [Google Scholar] [CrossRef]
- Lezec, H.J.; Dionne, J.A.; Atwater, H.A. Negative Refraction at Visible Frequencies. Science 2007, 316, 430–432. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, W.; Zhu, J.; Lu, Y.; Xiang, B.; Yang, S.A. Highly anisotropic two-dimensional metal in monolayer MoOCl2. Phys. Rev. B 2020, 102, 245419. [Google Scholar] [CrossRef]
- Ruta, F.L.; Shao, Y.; Acharya, S.; Mu, A.; Jo, N.H.; Ryu, S.H.; Balatsky, D.; Su, Y.; Pashov, D.; Kim, B.S.Y.; et al. Good plasmons in a bad metal. Science 2025, 387, 786–791. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, L.-F.; Moreo, A.; Dagotto, E. Orbital-selective Peierls phase in the metallic dimerized chain MoOCl2. Phys. Rev. B 2021, 104, L060102. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, M.; Zhao, J.; Chen, C.; Huang, H.; Wang, X.; Liu, P.; Wang, J.; Xiang, J.; Feng, C.; et al. Fermi liquid behavior and colossal magnetoresistance in layered MoOCl2. Phys. Rev. Mater. 2020, 4, 041001. [Google Scholar] [CrossRef]
- Venturi, G.; Mancini, A.; Melchioni, N.; Chiodini, S.; Ambrosio, A. Visible-frequency hyperbolic plasmon polaritons in a natural van der Waals crystal. Nat. Commun. 2024, 15, 9727. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhang, W.; Li, X.; Tang, J.; Xiao, J.; Zhang, G.; Liao, X.; Jiang, P.; Liu, Q.; et al. Broadband near-infrared hyperbolic polaritons in MoOCl2. Nat. Commun. 2025, 16, 6172. [Google Scholar] [CrossRef]
- Gao, H.; Ding, C.; Sun, L.; Ma, X.; Zhao, M. Robust broadband directional plasmons in a MoOCl2 monolayer. Phys. Rev. B 2021, 104, 205424. [Google Scholar] [CrossRef]
- Barreda, Á.; Vitale, F.; Minovich, A.E.; Ronning, C.; Staude, I. Applications of Hybrid Metal-Dielectric Nanostructures: State of the Art. Adv. Photonics Res. 2022, 3, 2100286. [Google Scholar] [CrossRef]
- Louis, B.; Huang, C.-H.; Melendez, M.; Sánchez-Iglesias, A.; Olmos-Trigo, J.; Seth, S.; Rocha, S.; Delgado-Buscalioni, R.; Liz-Marzán, L.M.; Marqués, M.I.; et al. Unconventional Optical Matter of Hybrid Metal–Dielectric Nanoparticles at Interfaces. ACS Nano 2024, 18, 32746–32758. [Google Scholar] [CrossRef]
- Dou, L.; Xu, J.; Zhou, Z.; Li, S.; Wei, Z.; Jiang, T.; Wang, Z.; Cheng, X. Two-dimensional negative refraction steering of hybrid polaritons in graphene/twisted bilayer α-MoO3 heterostructures. Opt. Express 2025, 33, 3881–3889. [Google Scholar] [CrossRef]
- Teng, H.; Chen, N.; Hu, H.; de Abajo, F.J.G.; Dai, Q. Steering and cloaking of hyperbolic polaritons at deep-subwavelength scales. Nat. Commun. 2024, 15, 4463. [Google Scholar] [CrossRef]
- Chen, N.; Teng, H.; Hu, H.; Liu, M.; Jiang, C.; Xue, Z.; Zhu, H.; Gui, J.; Li, P.; Alù, A.; et al. Flatland wakes based on leaky hyperbolic polaritons. Nat. Mater. 2025, 24, 1569–1575. [Google Scholar] [CrossRef]
- Duan, J.; Álvarez-Pérez, G.; Lanza, C.; Voronin, K.; Tresguerres-Mata, A.I.F.; Capote-Robayna, N.; Álvarez-Cuervo, J.; Martín-Luengo, A.T.; Martín-Sánchez, J.; Volkov, V.S.; et al. Multiple and spectrally robust photonic magic angles in reconfigurable α-MoO3 trilayers. Nat. Mater. 2023, 22, 867–872. [Google Scholar] [CrossRef]
- Passler, N.C.; Paarmann, A. Generalized 4 × 4 matrix formalism for light propagation in anisotropic stratified media: Study of surface phonon polaritons in polar dielectric heterostructures. J. Opt. Soc. Am. B 2017, 34, 2128–2139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Qi, S.; Chen, X.; Lv, H.; Wang, Y.; Zhu, J.; Yan, J.; Zhang, Q. Deep-Subwavelength Negative Refraction of Hyperbolic Plasmon Polariton at Visible Frequencies. Photonics 2026, 13, 146. https://doi.org/10.3390/photonics13020146
Qi S, Chen X, Lv H, Wang Y, Zhu J, Yan J, Zhang Q. Deep-Subwavelength Negative Refraction of Hyperbolic Plasmon Polariton at Visible Frequencies. Photonics. 2026; 13(2):146. https://doi.org/10.3390/photonics13020146
Chicago/Turabian StyleQi, Shuxin, Xuanbin Chen, Haoran Lv, Yuqi Wang, Jihong Zhu, Jiadian Yan, and Qing Zhang. 2026. "Deep-Subwavelength Negative Refraction of Hyperbolic Plasmon Polariton at Visible Frequencies" Photonics 13, no. 2: 146. https://doi.org/10.3390/photonics13020146
APA StyleQi, S., Chen, X., Lv, H., Wang, Y., Zhu, J., Yan, J., & Zhang, Q. (2026). Deep-Subwavelength Negative Refraction of Hyperbolic Plasmon Polariton at Visible Frequencies. Photonics, 13(2), 146. https://doi.org/10.3390/photonics13020146



