Abstract
Single-pixel imaging has the characteristics of a simple structure and low cost, which means it has potential applications in many fields. This paper proposes an image reconstruction method for single-pixel imaging (SPI) based on deep learning. This method takes the Generative Adversarial Network (GAN) as the basic architecture, combines the dense residual structure and the deep separable attention mechanism, and reduces the parameters while ensuring the diversity of feature extraction. It also reduces the amount of computation and improves the computational efficiency. In addition, dual-skip connections between the encoder and decoder parts are used to combine the original detailed information with the overall information processed by the network structure. This approach enables a more comprehensive and efficient reconstruction of the target image. Both simulations and experiments have confirmed that the proposed method can effectively reconstruct images at low sampling rates and also achieve good reconstruction results on natural images not seen during training, demonstrating a strong generalization capability.
1. Introduction
Single-pixel imaging (SPI) is a technique that acquires target image information through a single-pixel detector devoid of spatial resolution [1,2], thereby reducing the reliance on traditional array detectors and complex focusing systems and significantly lowering the barriers to optical imaging. Initial SPI approaches primarily utilized compressive sensing (CS) theory for image reconstruction through random sampling and iterative optimization algorithms. Duarte et al. proposed the SPI method based on compressive sensing, which can reconstruct the target image accurately, but its computational complexity is high and the reconstruction speed is slow [3]. Zhang et al. proposed a single-pixel imaging technique based on Fourier spectrum acquisition, which maintains the imaging quality under ambient light interference, albeit requiring direct line-of-sight illumination [4]. Then, a convolutional sparse coding (CSC)-based single-pixel imaging method was proposed by Deng, which improves the quality of image reconstruction by combining global and local prior information but has high computational complexity and limited processing ability for high-resolution images [1].
Recent developments in deep learning have significantly advanced SPI research, markedly improving reconstruction quality and computational efficiency [5,6,7,8]. Bu et al. employed mode-selective image upconversion technology from nonlinear optics for feature extraction [9], achieving high-precision classification through deep learning integration, though their experimental system showed sensitivity to environmental noise and required enhanced hardware capabilities. A single-pixel deep convolutional neural network imaging method was developed by Mizutani et al., which accomplished precise defect localization under minimal illumination conditions [10]. However, the sample size constraints and limited environmental validation scope restricted the method’s broader applicability. Computational ghost imaging for atmospheric turbulence conditions was addressed by Xia et al. [11], while Dai et al. introduced the MAID-GAN and MAID-GAN+ networks [12]. These networks demonstrated quality image reconstruction capabilities at reduced sampling rates. Fourier single-pixel imaging reconstruction incorporating U-Net and attention mechanisms was developed by Jiang et al., resulting in enhanced image quality at lower sampling rates [13]. For high-turbidity underwater environments, Feng et al. presented an active single-pixel imaging method utilizing a dual Attention U-Net architecture [14]. This approach enabled underwater target reconstruction while maintaining reduced sampling rate requirements. Quero et al. proposed novel untrained deep learning models combining physical models and convolutional neural networks for high-quality reconstruction of 2D and 3D images from X-ray images [15]. Qu et al. introduced a hybrid attention Transformer network for the Kronecker SPI model, enhancing the single-pixel imaging performance through tensor gradient descent and dual-scale attention mechanisms, though the robustness under varying illumination conditions remains unverified [16].
Based on the above, we present a novel methodology utilizing low-dimensional compressed data features inherent in single-pixel imaging processes. Our approach implements a hybrid attention mechanism for dynamic feature weight adjustment, addressing detail degradation from interpolation and deconvolution during sampling. The integration of depthwise separable convolution into the hybrid attention mechanism enhances the computational efficiency. To address imaging noise challenges, we incorporate cascaded dense connections and residual learning, achieving refined reconstruction through multi-level feature fusion while minimizing noise interference. The implementation of dual-skip connections between the hybrid attention mechanism and dense residual blocks provides global constraints while preserving local detail information, resulting in enhanced image reconstruction quality. The methodology demonstrates robust generalization capabilities on previously unseen datasets, addressing fundamental limitations of traditional reconstruction methods and expanding single-pixel imaging applications. The comprehensive experimental validation confirms the method’s effectiveness and stability across diverse scenarios, indicating significant potential for practical implementation.
2. Methods
2.1. Imaging Scheme of L2-Norm
In single-pixel imaging methodologies based on compressive sensing [17], the sparsity of signals is utilized to reconstruct images from a limited number of measurements, which is of significant value in the field of imaging.
The mathematical model for the imaging process in a single-pixel imaging system typically involves a modulator (such as a digital micromirror device, DMD) to modulate the illumination and a single-pixel detector to capture the compressed measurements [18,19], as shown in Figure 1. This process can be mathematically described as follows:
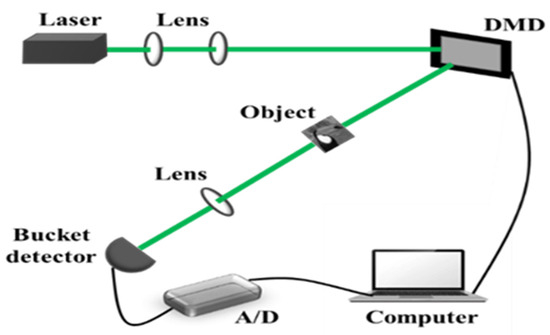
Figure 1.
Schematic diagram of the single-pixel imaging system.
Here, represents the vector of measurements or the observed data, represents the measurement matrix (also known as the modulation matrix), denotes the sparsifying basis, is the vector of coefficients of the image in the sparsifying basis, is a composite matrix that represents the combined linear transformation of and , and is a vector representing Gaussian noise, which is added to the measurements and typically has a mean of zero and some variance.
To reconstruct the image, an optimization problem must be solved. This paper employs the L2-norm for regularization to ensure the stability and smoothness of the image reconstruction process [19]. The optimization problem with L2-norm regularization can be formulated as follows:
In the above equation, is the least squares solution and signifies the reconstructed signal. In practical applications, the L2-norm helps control the complexity of the solution and prevents overfitting. It also provides a robust reconstruction in the presence of noise. Thus, clear and stable image reconstruction results can be achieved even when noise is present.
2.2. Network Structure
The DUAtt-GAN framework we propose is depicted in Figure 2. First, we select training samples from the STL-10 dataset and obtain the original input through single-pixel imaging (SPI) simulation. Next, we use the L2-norm solution from reference [20] for initial reconstruction with the CS algorithm to obtain the initial reconstructed image (Reconstructed X). This image is input into the generator together with the target image (Target X) to generate the optimized image. The discriminator evaluates the differences between the generated and target images, guiding the optimization process and driving the generator to produce an image closer to the target features. After iterative optimization through learning processes, the reconstructed image (Final Reconstructed) is produced.
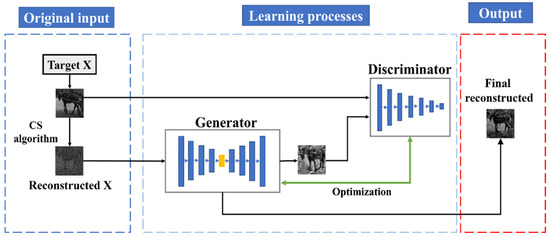
Figure 2.
Architecture of proposed network.
The generator’s network structure, detailed in Figure 3a, is composed of an encoder and a decoder, which work in tandem to transform and reconstruct input data efficiently [21]. The encoder plays a crucial role: it sequentially employs multiple downsampling layers that are designed to gradually decrease the resolution of feature maps while simultaneously capturing high-level features that are essential for generating accurate images. Each downsampling layer combines a convolutional layer with a LeakyReLU activation function, ensuring nonlinearity and efficient computation. After the downsampling layers come the Dense Upsampling Blocks. As illustrated in Figure 3b, these blocks consist of interconnected features spanning various layers, fostering a rich diversity of extracted features. Their architecture includes multiple convolutional layers paired with normalization layers, and they employ residual connections. These connections are vital as they facilitate the smooth propagation of gradients, which effectively mitigates the vanishing gradient problem commonly encountered in deep network training. The decoder also plays a significant role. It consists of three upsampling layers that aim to restore the resolution of the feature maps. These layers contain transposed convolutional layers, Depthwise Attention Blocks, two additional convolutional layers, and ReLU activation functions. The Depthwise Attention Block, shown in Figure 3c, significantly enhances the depth of the feature representation. It achieves this by integrating downsampled feature maps from the encoder with upsampled features from the decoder, utilizing skip connections to ensure continuity and coherence in data flow. Additionally, a depthwise separable convolution integrates within the attention block, an advanced operation that meticulously processes spatial and channel information separately. This addition reduces the computational load and parameter complexity, boosting the model’s computational efficiency and enabling it to swiftly process data-intensive tasks.
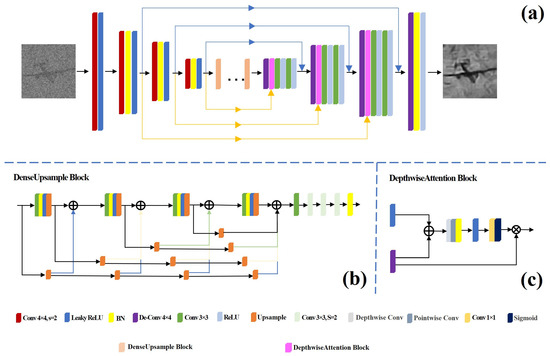
Figure 3.
(a) The overall structure of the generator. (b) DenseUpsample Block structure. (c) Depthwise Attention Block.
In the decoder, after each upsampling layer, the feature maps from the decoder are concatenated with the corresponding downsampling feature maps from the encoder through skip connections. The skip connection here helps to retain more detailed information in the generated image because it directly combines the low-level features captured in the encoder with the high-level features recovered in the decoder. Therefore, our proposed structure not only improves the quality of the feature map, but also enhances the network’s ability to retain details, which is crucial for generating high-quality images.
The discriminator is designed as a classic convolutional neural network (CNN), as shown in Figure 4. It consists of multiple convolutional layers that progressively reduce the resolution of the feature map while capturing features across different levels of abstraction. To improve the training efficiency and enhance the nonlinear capabilities, the architecture incorporates batch normalization and the LeakyReLU activation function. These components stabilize and accelerate the learning process. Then, a pooling layer simplifies the model’s structure and enhances its ability to distinguish between real and generated images. This layer condenses the extracted features, making the model more efficient and effective at identifying key patterns. Finally, a sigmoid activation function is applied to output the discrimination results. This architecture is highly effective at feature extraction and discrimination. It plays a crucial role in maintaining the quality of generated images by ensuring that they are realistic and high-quality.
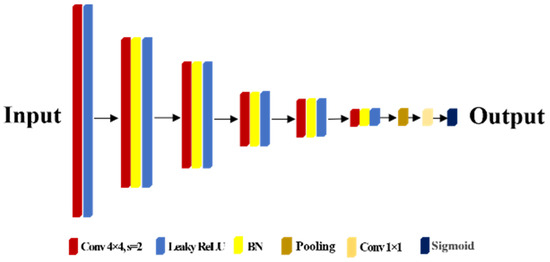
Figure 4.
Discriminator structure.
2.3. Loss Function
To improve the quality and realism of the generated image, a loss function is incorporated into the training process to optimize the parameters. Conventional loss functions, such as mean squared error, may result in the omission of high-frequency details [22]. Therefore, the original loss function for the general generator is modified.
Content loss is used to ensure content similarity between the generated image and the original image [23]. In this context, , , and represent the channel count, width, and height of an image, respectively. represents the feature map associated with the content image at a specific layer within a neural network architecture, while corresponds to the feature map of the generated image at the same layer.
Adversarial losses are used to train the discriminator to distinguish between real and generated data [24]:
Here, represents the discriminator, denotes a real data sample drawn from the data distribution , signifies a noise sample drawn from the noise distribution , and represents the generated data produced by the generator from the noise . The objective is to minimize the , so that can produce realistic samples, and to maximize the , which allows to better distinguish between real and generated samples.
The total variation (TV) loss is designed to reduce high-frequency information in an image while enhancing spatial consistency. It is formulated as follows:
In this context, represents the weight factor associated with the TV loss. This weight factor is crucial for managing the balance between the TV loss and other components in the network’s objective function. The term refers to the number of samples processed together in one iteration. The value signifies the pixel intensity at position in the image, where is the row index of the image and is the column index. The variables and are used to calculate the weighted factors for pixel differences in the horizontal and vertical directions, respectively. By minimizing this loss, the model can effectively reduce noise and eliminate discontinuous edges, resulting in smoother and more consistent imagery.
The total loss for the modified generator is a weighted sum of content loss, adversarial loss, and TV loss. The loss incurred by the discriminator is the sum of the adversarial losses associated with both the genuine and the generated images [25].
3. Results and Discussion
3.1. Training Data Preparation
After designing the architecture of the DUAtt-GAN, the next step involves a substantial image training process. To enhance the model’s generalization capability, it is imperative that the training images encompass a diverse array of categories. With this concept in mind, we randomly selected 50,000 out of the 100,000 unlabeled images from the STL-10 dataset for our experiment. These images originally had a resolution of 96 × 96 pixels. In this experiment, we converted the images to grayscale, using 8-bit depth, and resized them to 64 × 64 pixels. Next, we randomly divided these images into three separate subsets. The first subset is the training set, consisting of 35,000 images, used to build and optimize our model. The second is the validation set, containing 10,000 images, specifically used to evaluate the model’s performance during training and make necessary adjustments. Finally, the remaining images form the test set, used to assess the model’s final performance after training and validation are complete. This way of dividing the subsets ensures a structured approach to training, validating, and testing our model.
In the network architecture proposed in this paper, images processed through L2-norm are fed into the generator. After the termination of the training phase, a comprehensive evaluation of the network architecture was conducted, employing the validation set and the test set. In the present study, the entire process was systematically repeated to evaluate the impact of different sampling rates on model performance. The sampling rate (SR) is defined as the ratio of the number of measurements (K) to the total number of pixels in the image [26]. For the 64 × 64 image, the calculation formula for the sampling rate is SR = K/4096. As illustrated in Figure 5, the original image, the compressed sensing (CS) image reconstructed at a 20% sampling rate through L2-norm, and the restored image obtained by the method proposed in this paper are presented. A comparison of these images clearly demonstrates the significant advantages of the proposed method in terms of image reconstruction quality.

Figure 5.
A comparison of images and their reconstruction.
To validate the benefits of the proposed DUAtt-GAN structure, a series of simulation experiments were conducted. The original DUAtt-GAN model served as the baseline for the subsequent comparison models. These comparison models were developed by selectively removing components to accommodate the particularities of data in single-pixel imaging. These models encompassed variations such as DUAtt-GAN, which is devoid of the DU module, the DA module, or both the DU and DA modules. Additionally, there were versions that excluded content loss and TV loss. For these experiments, 2000 images were randomly chosen from the training set to ensure a robust evaluation. Throughout the study, variables were meticulously controlled, with consistency maintained in all parameters except for modifications in network structure and loss function. To assess the performance of these models, two renowned image quality metrics were employed: Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity (SSIM) [27]. These metrics provided objective measures of the image quality and structural fidelity achieved by each model configuration, offering insights into the efficacy of various architectural adjustments.
As illustrated in Table 1 and Figure 6, the impact of various components in the DUAtt-GAN architecture is demonstrated. The DU module employs dense upsampling to effectively restore high-frequency details, thereby enhancing resolution. Despite an increase in the number of parameters and some issues with image smoothness, the DU module’s ability to reuse features is notably improved. When the DU module is removed, the PSNR decreases significantly. The utilization of an attention mechanism by the DA module enhances feature correlation, thereby facilitating enhanced structural consistency and detail recovery. The absence of the DA module in the model leads to inadequate capture of the global context, manifesting as blurred textures and a substantial decline in the SSIM. Eliminating both the DU and DA modules simultaneously causes a more pronounced performance drop than removing each individually, with a PSNR decrease of 2.685 dB. This demonstrates the combined effectiveness in addressing low signal-to-noise ratios and preserving high-frequency details in single-pixel imaging tasks. In addition, after removing the TV loss, the evaluation indicators are significantly decreased compared to the baseline model; of note, the SSIM is significantly decreased, which directly affects the visual smoothness and makes the quality of the whole reconstructed image low. Removing the content loss also causes a significant decrease in the PSNR; specifically, the edge of the reconstructed image is blurred and the background texture is wrong, which affects the overall reconstruction accuracy. Therefore, all of the above are essential for high-quality reconstruction. In addition, it is necessary to adjust the weights of different loss functions to balance noise suppression and detail preservation.

Table 1.
The PSNR and SSIM values of the different models.

Figure 6.
Reconstruction results of different models.
Before the full training, an experiment was conducted to ascertain the optimal weights for the model’s loss components. The weights α, β, and γ correspond to content loss (), adversarial loss (), and total variation loss (), respectively. The initial weight for content loss was set at 0.006, derived from the pre-training feature scale calibration. Based on empirical values from classical GAN training, β was set to 10−3 and γ to 2 × 10−8. These served as benchmarks to explore how different weights impact model performance, identifying the best configuration for our network. Some experimental results are shown in Table 2, indicating that a median α achieved a superior PSNR (21.325 dB) and SSIM (0.6822), balancing pixel accuracy and structural consistency. Conversely, an α of 0.003 yielded a lower PSNR (21.315 dB) due to inadequate content loss, resulting in image blurriness. An α of 0.009 resulted in oversmoothing and a loss of detail, reflected in a PSNR of 21.304 db. For β, the median value increased the SSIM without significantly sacrificing PSNR. A lower β (SSIM = 0.6801) proved inadequate for adversarial training, and a higher β resulted in a notable PSNR drop to 21.231 dB due to overfitting. The high value of γ effectively suppresses the noise, leading to a better PSNR and SSIM compared to lower values like 2 × 10−8 and 10−8. By systematically exploring the weight space, the combination achieves the best balance between performance and stability.

Table 2.
Weight combinations and performance metrics.
3.2. Numerical Simulations
In this study, the training was conducted on a GeForce RTX 3090. We compared our reconstruction results against various traditional methods, including DGI [28,29], CGD [30], Sparse [3], deep learning methods SPIGAN [25], U-Net [31], CGAN [32], and Trans-SPI [33]. At a sampling rate of 20%, the images produced by DGI and CGD were highly blurred, displaying substantial noise and minimal visible details. The sparse images demonstrated a marginal reduction in noise; however, they retained a noticeable degree of blurriness. U-Net, leveraging deep learning, offered clearer images than traditional methods but retained notable noise with pronounced stripe-like textures. While SPIGAN and CGAN demonstrated enhancements in detail preservation, noise remained a prevalent issue. Trans-SPI provided clearer images with preserved details and reduced noise, although issues like small holes in uniformly colored areas were observed. The proposed method, at the same low sampling rate, excelled in maintaining detail in high-texture regions and suppressing background noise compared to all previously mentioned methods. Figure 7 provides a visual representation of the reconstructed images, showcasing the efficacy of the proposed method in enhancing visual details and contrast. Moreover, our approach required only 3.1 M parameters and processed each 64×64 image in 23.8 ms, surpassing SPIGAN (3.9 M, 29.6 ms) and Trans-SPI (5.1 M, 36.3 ms) both in efficiency and accuracy. This highlights the advantage in computational efficiency while delivering high-quality reconstructions.

Figure 7.
Reconstructed samples from the test dataset.
To evaluate the effectiveness of our proposed method, we tested it on a variety of datasets, including those containing natural images and urban building scenes. Figure 8 presents some of the reconstruction results. The SPI method has been demonstrated to be effective in preserving image details; however, it has been observed to encounter challenges in high-frequency areas, leading to the occurrence of distortion. While CGAN produces images with an adequate overall fidelity, it exhibits deficiencies in preserving texture and edge clarity when compared to alternative methods. Trans-SPI demonstrates an effective capacity for contour capture; however, it is prone to the formation of holes in areas characterized by uniform coloration. Conversely, DUAtt-GAN excels at retaining detailed image recovery and maintaining the overall contour integrity, with significantly fewer artifacts than the other approaches.

Figure 8.
Comparison of reconstructed images of different datasets.
Subsequent tests involved calculating the PSNR and SSIM metrics across various datasets, with the specific results detailed in Table 3. At a sampling rate of 20%, the highest PSNR values highlight the robust reconstruction capability of the method introduced in this paper, even on datasets that were not part of the training process, thereby showcasing its impressive ability to generalize. This performance indicates that the method can be effectively applied and trusted in a variety of situations beyond its initial training scope. When the sampling rate reaches 30%, the PSNR for some datasets decreases, whereas the SSIM shows varying degrees of improvement across all datasets. This indicates that the method proposed in this paper, although it experiences a decrease in the precision at the pixel level with the increase in the sampling rate in unknown datasets, still manages to improve the overall structural characteristics of the images.

Table 3.
The max PSNR and SSIM for different datasets.
As shown in Figure 9, this is the reconstruction result with the real doll as the target. In all of the methods, the recovery of image details is enhanced by an increase in the sampling rate, particularly in regions where the target and the background exhibit significant disparities. This is evidenced by the fact that the leg contour of the reconstructed image is more clearly defined than the head contour. However, the method outlined in this paper has been demonstrated to be significantly more effective than alternative methods in the recovery of detailed components, such as limbs and bow ties. These experiments demonstrate that the proposed method consistently achieves superior reconstruction in both new datasets and real images under low sampling rates and showcases strong adaptability to varied data.

Figure 9.
Reconstruction result of the doll.
3.3. Real Experiments
Three sets of experiments were performed using the setup in Figure 10. A laser with a wavelength of 532 nm was used in the experiments. The beam of this laser was first expanded by a beam expansion system consisting of two lenses and then projected onto a digital micromirror device (DMD). A variety of illumination patterns were preloaded onto the DMD for modulating the laser. The laser is modulated by the DMD to illuminate the target image and is focused by a lens onto a single-pixel detector. The detector was integrated with a data acquisition card, which facilitated the transmission of collected data to a computer for preliminary processing. The computer first employed the conventional CS method to reconstruct the image and then applied a previously trained network model to refine the reconstruction, delivering the final image.

Figure 10.
Setup diagram of the single-pixel imaging system.
The experimental results are shown in Figure 11. The figure presents the comparison results of the images reconstructed by different methods. The images include the number “5”, a bird, and the structural details of a building roof. Each object is reconstructed at a sampling rate (SR) of 20% and 30% by using traditional technologies such as compressed sensing (CS), SPIGAN, CGAN, Trans-SPI, and DUAtt-GAN. In the case of the digit “5”, the CS method performed poorly, producing heavily blurred images devoid of discernible details at both sampling rates. SPIGAN was able to ascertain the fundamental structure of the digit in both conditions; however, it exhibited a deficiency in the refinement of fine details. CGAN demonstrated enhanced performance at 30% SR; however, the outline exhibited distortion. Trans-SPI exhibited moderate clarity with partial outline recovery, though it still exhibited deficiencies in its details. Conversely, DUAtt-GAN demonstrated exceptional capability, accurately reconstructing the digit’s contours and details even at the lower sampling rate. For the bird image, the use of CS resulted in substantial blurring and loss of structural detail. SPIGAN’s approach involved the preservation of the bird’s fundamental form, albeit with a paucity of intricate details. CGAN demonstrated efficacy in enhancing structural retention; however, its capabilities were found to be constrained in terms of texture and detail accuracy. Trans-SPI captured the bird’s outline effectively, though details remained blurred. DUAtt-GAN demonstrated superiority over competing methods in terms of clarity and detail retrieval, ensuring the most accurate reconstruction. Regarding the structural detail image, CS yielded indistinct, blurred results, obscuring any recognizable structures. SPIGAN offered a slight improvement over the others but continued to miss crucial details. CGAN exhibited negligible progress in terms of sharpness at an elevated sampling rate, yet residual distortions persisted. Trans-SPI demonstrated an enhancement in the representation of the overall structure; however, the resolution of details was found to be deficient. It is noteworthy that DUAtt-GAN demonstrated a superior performance in depicting structural contours and intricate details, resulting in enhanced reconstruction quality when compared to other techniques.
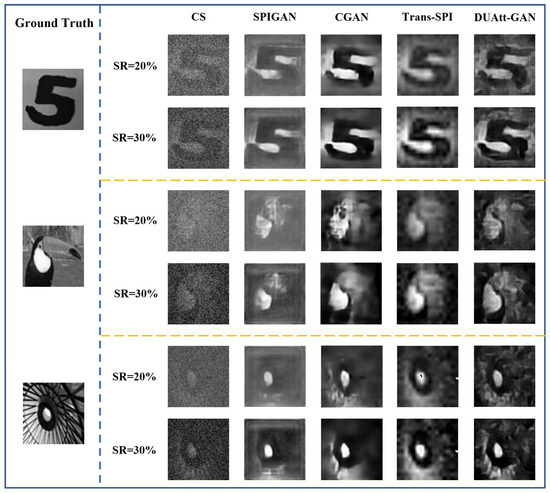
Figure 11.
Reconstruction results of CS, SPIGAN, CGAN, Trans-SPI, and DUAtt-GAN.
Overall, the evaluation across different sampling rates underscored DUAtt-GAN’s significant advantage in recovering fine details and outlines, affirming its robust adaptability and precision in low-sampling-rate scenarios.
4. Conclusions
In this paper, we propose a DUAtt-GAN approach designed to facilitate single-pixel imaging at reduced sampling rates. The innovative network structure under consideration combines dense structural components with a multifaceted attention mechanism that employs depth-separable convolutions. This design effectively broadens the range of extracted features while simultaneously minimizing computational demands and the number of required parameters. To enhance the preservation of intricate details within the generated images, a double-hop connection framework is incorporated in the generator. A comprehensive simulation and empirical investigation have been conducted to demonstrate the superior reconstruction quality achieved by this method at low sampling rates.
Extensive experimentation involving the reconstruction of various target images has consistently yielded favorable results, thereby affirming the method’s robust generalization capability across different scenarios. However, a clear discrepancy emerges between the observed experimental outcomes and the simulated results, with the experimental results failing to fully align with the simulations. This issue is primarily attributable to the impact of ambient lighting on collected real-world data. Fluctuations in ambient light can result in variations in brightness detection by the sensor, thereby compromising the quality of the reconstructed image.
Therefore, future research will focus on reducing the impact of ambient light in practical applications, improving the resolution and clarity of the reconstructed image, and enhancing the adaptability of the network to more complex and dynamic imaging environments to further improve the reconstruction performance.
Author Contributions
Conceptualization, B.X.; methodology, B.X.; software, B.X.; validation, B.X.; formal analysis, B.X.; investigation, B.X.; resources, B.X., H.W. and Y.B.; data curation, B.X.; writing—original draft preparation, B.X.; writing—review and editing, B.X., H.W., and Y.B.; visualization, B.X.; supervision, H.W. and Y.B.; project administration, Y.B.; funding acquisition, Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (61991452).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Deng, C.; Hu, X.; Li, X.; Li, X.; Suo, J.; Zhang, Z.; Dai, Q. High fidelity single-pixel imaging. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Zhai, X.; Wu, Y.; Sun, Y.; Shi, J.; Zeng, G. Theory and approach of single-pixel imaging. ILE 2021, 50, 20211061. [Google Scholar]
- Duarte, M.; Davenport, M.; Takhar, D.; Laska, J.; Sun, T.; Kelly, K. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef]
- Wu, H.; Wang, R.; Zhao, G.; Xiao, H.; Zhang, X. Deep-learning denoising computational ghost imaging. Opt. Lasers Eng. 2020, 134, 106183. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Chen, M.; Cheng, L.; Xiao, H.; Xu, L.; Wang, D.; Liang, J.; Xu, Y. Hybrid neural network-based adaptive computational ghost imaging. Opt. Lasers Eng. 2021, 140, 106529. [Google Scholar] [CrossRef]
- Ye, Z.; Zheng, P.; Hou, W.; Dian, S.; Wei, Q.; Hong, C.; Jun, X. Computationally convolutional ghost imaging. Opt. Lasers Eng. 2022, 159, 107191. [Google Scholar] [CrossRef]
- Yu, W.; Wei, N.; Li, Y.; Yang, Y.; Wang, S. Multi-party interactive cryptographic key distribution protocol over a public network based on computational ghost imaging. Opt. Lasers Eng. 2022, 155, 107067. [Google Scholar] [CrossRef]
- Bu, T.; Kumar, S.; Zhang, H.; Huang, Y. Single-pixel pattern recognition with coherent nonlinear optics. Opt. Lett. 2020, 45, 6771–6774. [Google Scholar] [CrossRef]
- Mizutani, Y.; Kataoka, S.; Uenohara, T.; Takaya, Y.; Matoba, O. Fast and accurate single pixel imaging using estimation uncertainty in explainable CNNs. AI Opt. Data Sci. V 2024, 12903, 96–98. [Google Scholar]
- Xia, J.; Zhang, L.; Zhai, Y.; Zhang, Y. Reconstruction method of computational ghost imaging under atmospheric turbulence based on deep learning. Laser Phys. 2024, 34, 015202. [Google Scholar]
- Dai, Q.; Yan, Q.; Zou, Q.; Li, Y.; Yan, J. Generative adversarial network with the discriminator using measurements as an auxiliary input for single-pixel imaging. Opt. Commun. 2024, 560, 130485. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, J.; Wu, L.; Xu, L.; Hu, J.; Zhang, J.; Zhang, Y.; Yang, X. Fourier single pixel imaging reconstruction method based on the U-net and attention mechanism at a low sampling rate. Opt. Express 2022, 30, 18638–18654. [Google Scholar] [CrossRef]
- Feng, W.; Zhou, S.; Li, S.; Yi, Y.; Zhai, Z. High-turbidity underwater active single-pixel imaging based on generative adversarial networks with double Attention U-Net under low sampling rate. Opt. Commun. 2023, 538, 129470. [Google Scholar] [CrossRef]
- Quero, C.; Leykam, D.; Ojeda, I. Res-U2Net: Untrained deep learning for phase retrieval and image reconstruction. J. Opt. Soc. Am. A 2024, 41, 766–773. [Google Scholar] [CrossRef] [PubMed]
- Qu, G.; Wang, P.; Yuan, X. Dual-Scale Transformer for Large-Scale Single-Pixel Imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 25327–25337. [Google Scholar]
- Zhu, Z.; Chi, H.; Jin, T.; Zheng, S.; Jin, X.; Zhang, X. Single-pixel imaging based on compressive sensing with spectral-domain optical mixing. Opt. Commun. 2017, 402, 119–122. [Google Scholar] [CrossRef]
- Pastuszczak, A.; Czajkowski, K.M.; Kotyński, R. Single-pixel video imaging with DCT sampling. In Proceedings of the Imaging and Applied Optics 2019 (COSI, IS, MATH, pcAOP), Munich, Germany, 24–27 June 2019; OSA: Washington, DC, USA, 2019. [Google Scholar]
- Zhang, Z.; Wang, X.; Zheng, G.; Zhong, J. Fast Fourier single-pixel imaging via binary illumination. Sci. Rep. 2017, 7, 12029. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17 October 2016; Springer: Berlin, Germany, 2016; pp. 424–432. [Google Scholar]
- Ouidadi, H.; Guo, S. MPS-GAN: A multi-conditional generative adversarial network for simulating input parameters’ impact on manufacturing processes. J. Manuf. Process. 2024, 131, 1030–1045. [Google Scholar] [CrossRef]
- Liu, Y.; Pu, H.; Sun, D. Efficient extraction of deep image features using convolutional neural network (CNN) for applications in detecting and analysing complex food matrices. Trends Food Sci. Technol. 2021, 113, 193–204. [Google Scholar] [CrossRef]
- Ghayoumi, M. Generative Adversarial Networks in Practice, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2023. [Google Scholar]
- Tan, R.; Patade, O.; Wang, H.; Yang, C.; Lee, D. Optimizing Spatial Sensing Performance with Kriging and SRGAN—A Feasibility Study. In Proceedings of the 2023 IEEE SENSORS, Vienna, Austria, 29 October–1 November 2023. [Google Scholar]
- Karim, N.; Rahnavard, N. SPI-GAN: Towards single-pixel imaging through generative adversarial network. arXiv 2021, arXiv:2107.01330. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Han, S. A method to improve the visibility of ghost images obtained by thermal light. Phys. Lett. A 2010, 374, 1005–1008. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]
- Bian, L.; Suo, J.; Dai, Q.; Feng, C. Experimental comparison of single-pixel imaging algorithms. J. Opt. Soc. Am. A 2017, 35, 78–84. [Google Scholar] [CrossRef]
- Wu, H.; Wang, R.; Zhao, G.; Xiao, H.; Zhang, X. Sub-Nyquist computational ghost imaging with deep learning. Opt. Express 2020, 28, 3846–3853. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, X.; Zhang, R. High-Quality Computational Ghost Imaging with a Conditional GAN. Photonics 2023, 10, 353. [Google Scholar] [CrossRef]
- Tian, Y.; Fu, Y.; Zhang, J. Transformer-Based Under-Sampled Single-Pixel Imaging. CJE 2023, 32, 1151–1159. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).