Characterization of a Supersonic Plasma Jet by Means of Optical Emission Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
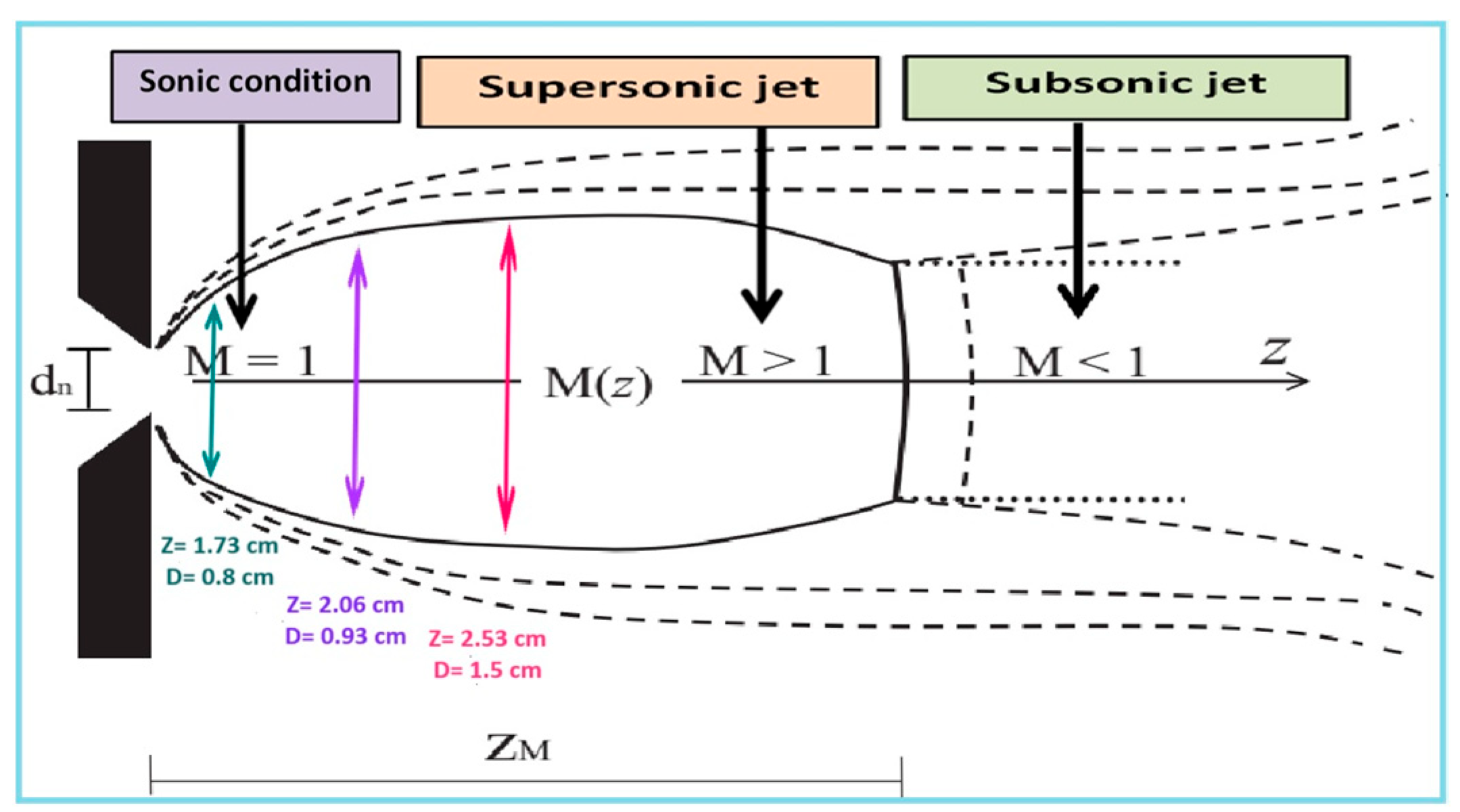
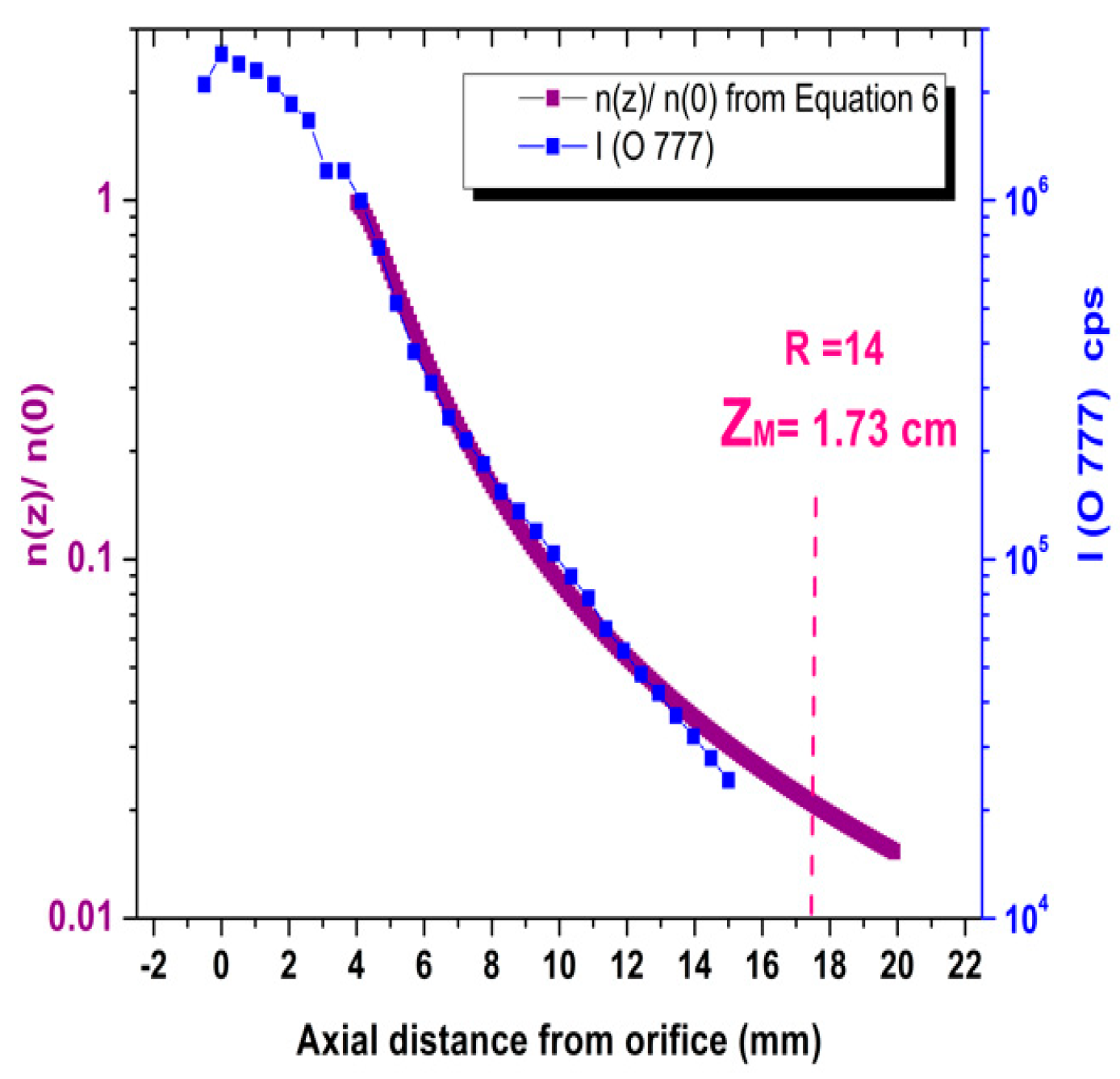
3.1. The Supersonic Plasma Jet
3.2. The Copra Plasma Source
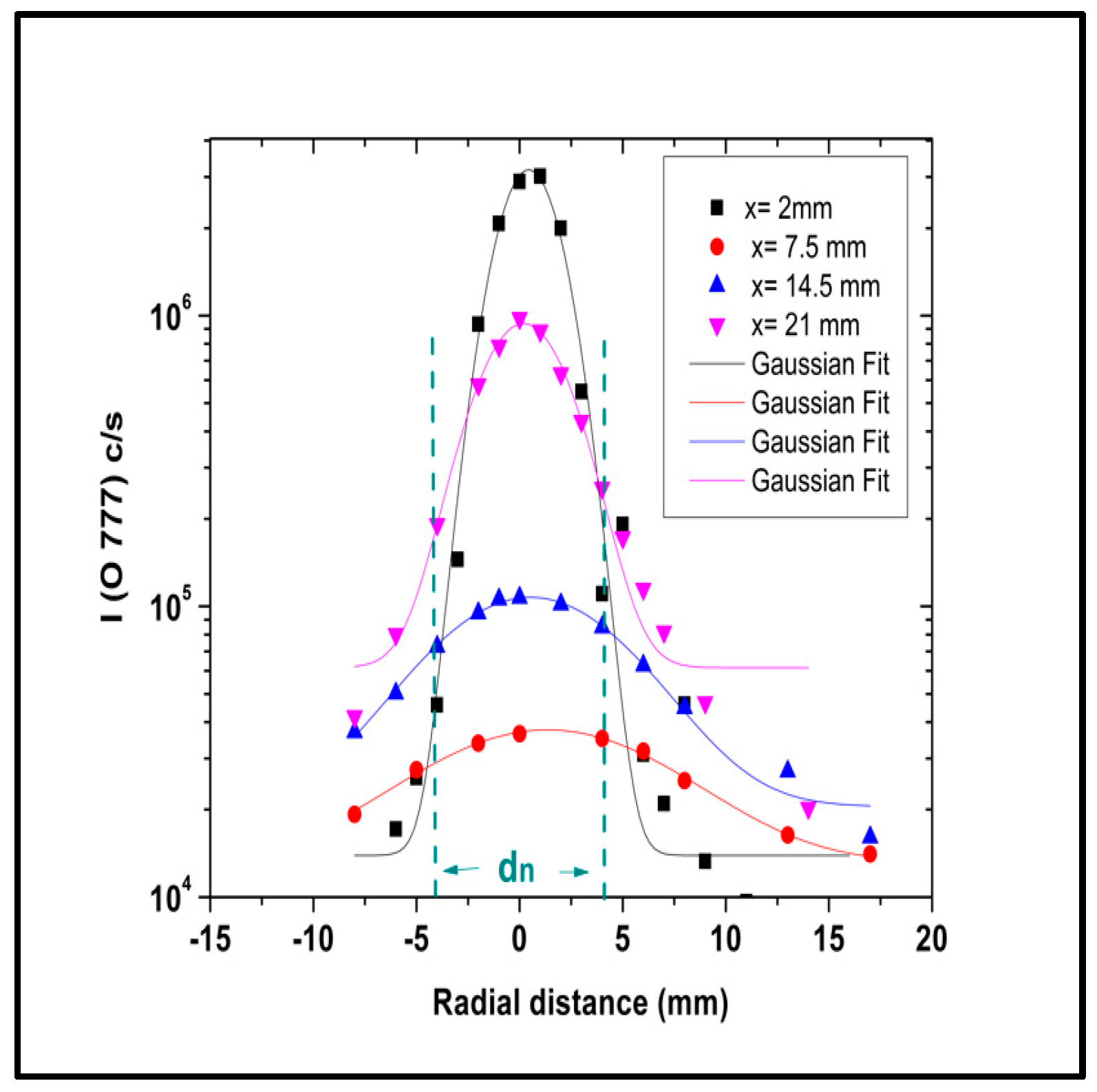
3.3. The Plume
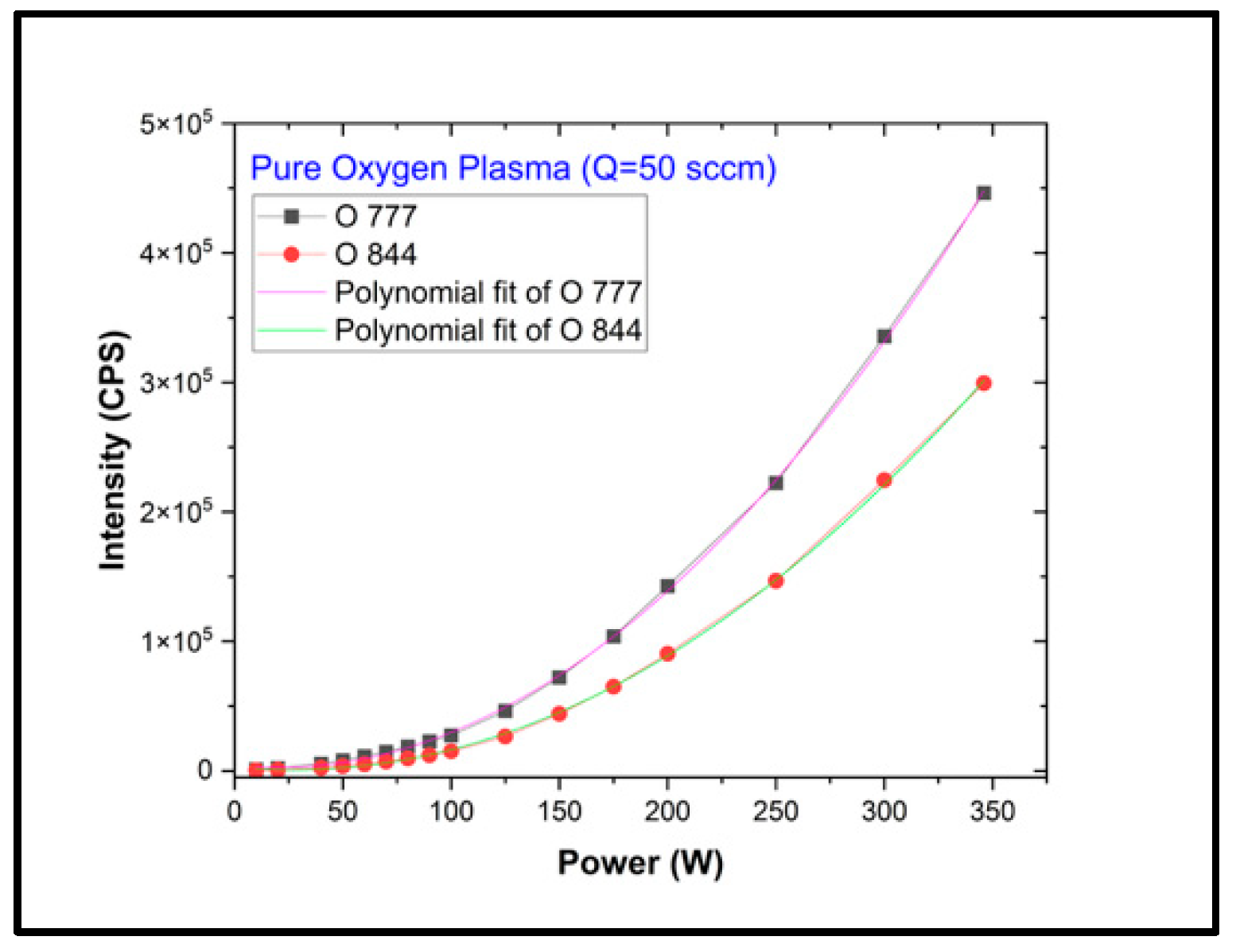
3.4. Optical Emission Spectroscopy of Oxygen Plasma Jet
3.5. Plasma Assisted Supersonic Jet Deposition of HMDSO
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PASJD | Plasma Assisted Supersonic Jet Deposition |
| OES | Optical Emission Spectroscopy |
| HMDSO | Hexamethyldisiloxane |
| PIV | Particle Image Velocimetry |
| MS | Mass Spectroscopy |
| EEDF | Electron Energy Distribution Function |
References
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge UK, 1997. [Google Scholar]
- Fantz, U. Basics of plasma spectroscopy. Plasma Sources Sci. Technol. 2006, 15, S137–S147. [Google Scholar] [CrossRef]
- Zaplotnik, R.; Primc, G.; Vasel, A. OES as a diagnostic tool for characterization of atmospheric plasma jets. Appl. Sci. 2021, 11, 2275. [Google Scholar] [CrossRef]
- Ohring, M. Materials Science of Thin Films; Academic Press: London UK, 2001. [Google Scholar]
- Mwema, F.M. Thin Film Coatings, 1st ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Biederman, H. Plasma Polymer Films; Imperial College Press: London, UK, 2004. [Google Scholar]
- Sonnenfeld, A.; Bieder, A.; Rudolf von Rohr, P. Influence of the Gas Phase on the Water Vapor Barrier Properties of SiOxFilms Deposited from RF and Dual-Mode Plasmas. Plasma Process. Polym. 2006, 3, 606–617. [Google Scholar] [CrossRef]
- Ratsch, C.; Venables, J.A. Nucleation Theory and the Early Stages of Thin Film Growth. J. Vac. Sci. Technol. A 2003, 21, S96–S109. [Google Scholar] [CrossRef]
- Budida, J.; Srinavasan, K. Review of thin film deposition and techniques. Mater. Today 2023, 92, 1030–1033. [Google Scholar] [CrossRef]
- Von Keudell, A. Surface Processes during Thin-Film Growth. Plasma Sources Sci. Technol. 2000, 9, 455–467. [Google Scholar] [CrossRef]
- Kortshagen, U.R.; Bhandarkar, U.V.; Swihart, M.T.; Girshick, S.L. Generation and Growth of Nanoparticles in Low-Pressure Plasmas. Pure Appl. Chem. 1999, 71, 1871–1877. [Google Scholar] [CrossRef]
- Caldirola, S.; Barni, R.; Roman, H.E.; Riccardi, C. Mass Spectrometry Measurements of a Low Pressure Expanding Plasma Jet. J. Vac. Sci. Technol. A 2015, 33, 061306. [Google Scholar] [CrossRef]
- Huang, C.; Nichols, W.T.; O’Brien, D.T.; Becker, M.F.; Kovar, D.; Keto, J.W. Supersonic Jet Deposition of Silver Nanoparticle Aerosols: Correlations of Impact Conditions and Film Morphologies. J. Appl. Phys. 2007, 101, 064902. [Google Scholar] [CrossRef]
- Winter, J.; Brandenburg, R.; Weltmann, K.-D. Atmospheric Pressure Plasma Jets: An Overview of Devices and New Directions. Plasma Sources Sci. Technol. 2015, 24, 064001. [Google Scholar] [CrossRef]
- Mitsugi, F.; Kusumegi, S.; Nishida, K.; Kawasaki, T. Visualization of Plasma-Induced Liquid Flow Using KI–Starch and PIV. IEEE Trans. Plasma Sci. 2021, 49, 9–14. [Google Scholar] [CrossRef]
- Traldi, E.; Boselli, M.; Simoncelli, E.; Stancampiano, A.; Gherardi, M.; Colombo, V.; Settles, G.S. Schlieren imaging: A powerful tool for atmospheric plasma diagnostic. EPJ Tech. Instrum. 2018, 5, 4. [Google Scholar] [CrossRef]
- Willems, G.; Hecimovic, A.; Sgonina, K.; Carbone, E.; Benedikt, J. Mass spectrometry of neutrals and positive ions in He/CO2 non-equilibrium atmospheric plasma jet. Plasma Phys. Control. Fusion 2020, 62, 034005. [Google Scholar] [CrossRef]
- Barni, R.; Daghetta, M.; Piferi, C.; Riccardi, C. Mass Spectroscopy of Oxygen Plasmas with Energetic Ions. AIP Adv. 2023, 13. [Google Scholar] [CrossRef]
- Berden, G.; Engeln, R. Cavity Ring-Down Spectroscopy: Techniques and Apllications; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Zhang, S.; Liu, W.; Zhang, X.; Duan, Y. Plasma-cavity ringdown spectroscopy for analytical measurement: Progress and prospectives. Spectrochim. Acta B 2013, 85, 1–12. [Google Scholar] [CrossRef]
- Weiler, M.; Lang, K.; Li, E.; Robertson, J. Deposition of Tetrahedral Hydrogenated Amorphous Carbon Using a Novel Electron Cyclotron Wave Resonance Reactor. Appl. Phys. Lett. 1998, 72, 1314–1316. [Google Scholar] [CrossRef]
- Barni, R.; Zanini, S.; Riccardi, C. Diagnostics of Reactive RF Plasmas. Vacuum 2007, 82, 217–219. [Google Scholar] [CrossRef]
- Zanini, S.; Riccardi, C.; Orlandi, M.; Grimoldi, E. Characterisation of SiOxCyHz thin films deposited by low-temperature PECVD. Vacuum 2007, 82, 290–293. [Google Scholar] [CrossRef]
- Siliprandi, R.A.; Zanini, S.; Grimoldi, E.; Fumagalli, F.S.; Barni, R.; Riccardi, C. Atmospheric Pressure Plasma Discharge for Polysiloxane Thin Films Deposition and Comparison with Low Pressure Process. Plasma Chem. Plasma Process. 2011, 31, 353–372. [Google Scholar] [CrossRef]
- Roussel, M.; Talbot, E.; Pratibha Nalini, R.; Gourbilleau, F.; Pareige, P. Phase Transformation in SiOx/SiO2 Multilayers for Optoelectronics and Microelectronics Applications. Ultramicroscopy 2013, 132, 290–294. [Google Scholar] [CrossRef]
- Plog, S.; Schneider, J.; Walker, M.; Schulz, A.; Stroth, U. Investigations of Plasma Polymerized SiOx Barrier Films for Polymer Food Packaging. Surf. Coat. Technol. 2011, 205, S165–S170. [Google Scholar] [CrossRef]
- Howells, D.G.; Henry, B.M.; Leterrier, Y.; Månson, J.-A.E.; Madocks, J.; Assender, H.E. Mechanical properties of SiOx gas barrier coatings on polyester films. Surf. Coat. Technol. 2008, 202, 3529–3537. [Google Scholar] [CrossRef]
- Li, N.; Wu, Y.L.; Hong, J.; Shchelkanov, I.A.; Ruzic, D.N. SiOx Deposition on Polypropylene-Coated Paper With a Dielectric Barrier Discharge at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2015, 43, 3205–3210. [Google Scholar] [CrossRef]
- Creatore, M.; Palumbo, F.; D’Agostino, R. Deposition of SiOx Films from Hexamethyldisiloxane/Oxygen Radiofrequency Glow Discharges: Process Optimization by Plasma Diagnostics. Plasmas. Polym. 2002, 7, 291–310. [Google Scholar] [CrossRef]
- Shirtcliffe, N.; Thiemann, P.; Stratmann, M.; Grundmeier, G. Chemical Structure and Morphology of Thin, Organo-Silicon Plasma-Polymer Films as a Function of Process Parameters. Surf. Coat. Technol. 2001, 142–144, 1121–1128. [Google Scholar] [CrossRef]
- Blanchard, N.E.; Naik, V.V.; Geue, T.; Kahle, O.; Hegemann, D. Response of Plasma-Polymerized Hexamethyldisiloxane Films to Aqueous Environments. Langmuir 2015, 31, 12944–12953. [Google Scholar] [CrossRef]
- Barni, R.; Caldirola, S.; Fattorini, L.; Riccardi, C. Tomography of a Simply Magnetized Toroidal Plasma. Plasma Sci. Technol. 2018, 20, 025102. [Google Scholar] [CrossRef]
- Ashkenas, H.; Sherman, F.S. Structure and Utilization of Supersonic Free Jets in Low Density Wind Tunnels; Academic Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Murphy, H.R.; Miller, D.R. Effects of Nozzle Geometry on Kinetics in Free-Jet Expansions. J. Phys. Chem. 1984, 88, 4474–4478. [Google Scholar] [CrossRef]
- Sanna, G.; Tomassetti, G. Introduction to Molecular Beams Gas Dynamics; Imperial College Press: London, UK, 2005. [Google Scholar]
- Otobe, Y.; Kashimura, H.; Matsuo, S.; Setoguchi, T.; Kim, H.-D. Influence of Nozzle Geometry on the Near-Field Structure of a Highly Underexpanded Sonic Jet. J. Fluids Struct. 2008, 24, 281–293. [Google Scholar] [CrossRef]
- Abouali, O.; Saadabadi, S.; Emdad, H. Numerical Investigation of the Flow Field and Cut-off Characteristics of Supersonic/Hypersonic Impactors. J. Aerosol Sci. 2011, 42, 65–77. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST Atomic Spectra Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024. Available online: http://physics.nist.gov/asd3 (accessed on 13 March 2025).
- Pearse, R.W.B.; Gaydon, A.G. The Identification of Molecular Spectra; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Krupenie, P.H. The Spectrum of Molecular Oxygen. J. Phys. Chem. Ref. Data 1972, 1, 423–534. [Google Scholar] [CrossRef]
- Bronold, F.X.; Matyash, K.; Tskhakaya, D.; Schneider, R.; Fehske, H. Radio-frequency discharges in Oxygen. J. Phys. D 2007, 40, 6583–6593. [Google Scholar] [CrossRef]
- Pattison, J.; Celotto, S.; Khan, A.; O’Neill, W. Standoff Distance and Bow Shock Phenomena in the Cold Spray Process. Surf. Coat. Technol. 2008, 202, 1443–1454. [Google Scholar] [CrossRef]
- Raizer, Y.P. Gas Discharge Physics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Lee, H.C.; Chung, C.W. Effect of Electron Energy Distribution on the Hysteresis of Plasma Discharge: Theory, Experiment and Modeling. Sci. Rep. 2015, 5, 15254. [Google Scholar] [CrossRef]
- Gornushkin, I.B.; Shabanov, S.V.; Panne, U. Abel inversion applied to a transient laser induced plasma: Implications from plasma modeling, J. Anal. At. Spectrom. 2011, 26, 1457–1565. [Google Scholar] [CrossRef]
- Barni, R.; Alex, P.; Ghorbanpour, E.; Riccardi, C. A Spectroscopical study of H2 emission in a simply magnetized toroidal plasma. Eur. Phys. J. D 2021, 75, 101. [Google Scholar] [CrossRef]
- Barni, R.; Alex, P.; Salanti, A.; Canevali, C.; Zoia, L.; Orlandi, M.; Riccardi, C. Characterization of the Electrical and Optical Properties of a Gliding Arc Tornado Device. Eur. Phys. J. D 2021, 75, 147. [Google Scholar] [CrossRef]
- Britun, N.; Gaillard, M.; Ricard, A.; Kim, Y.M.; Kim, K.S.; Han, J.G. Determination of the vibrational, rotational and electron temperatures in N2 and Ar–N2 rf discharge. J. Phys. D 2007, 40, 1022–1029. [Google Scholar] [CrossRef]
- Wünderlich, D.; Dietrich, S.; Fantz, U. Application of a Collisional Radiative Model to Atomic Hydrogen for Diagnostic Purposes. J Quant. Spectrosc. Radiat. Transf. 2009, 110, 62–71. [Google Scholar] [CrossRef]
- Phelps, A.V. Collisional kinetics of non-uniform electric field, low-pressure, direct-current discharges in H2. Plasma Sources Sci. Technol. 2011, 20, 043001. [Google Scholar] [CrossRef][Green Version]
- Gosar, Ž.; Kovač, J.; Mozetič, M.; Primc, G.; Vesel, A.; Zaplotnik, R. Characterization of Gaseous Plasma Sustained in Mixtures of HMDSO and O2 in an Industrial-Scale Reactor. Plasma Chem. Plasma Process. 2020, 40, 25–42. [Google Scholar] [CrossRef]



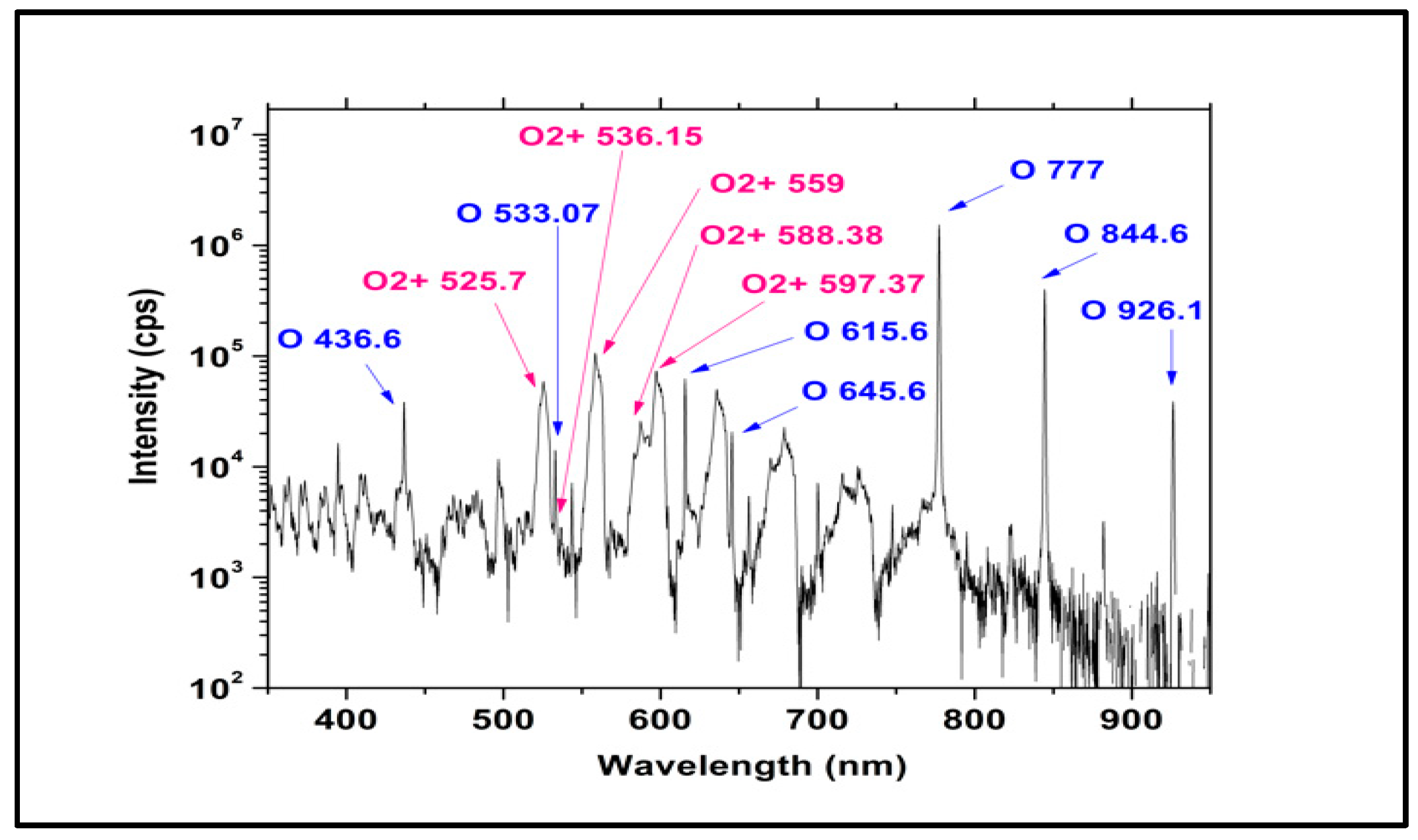
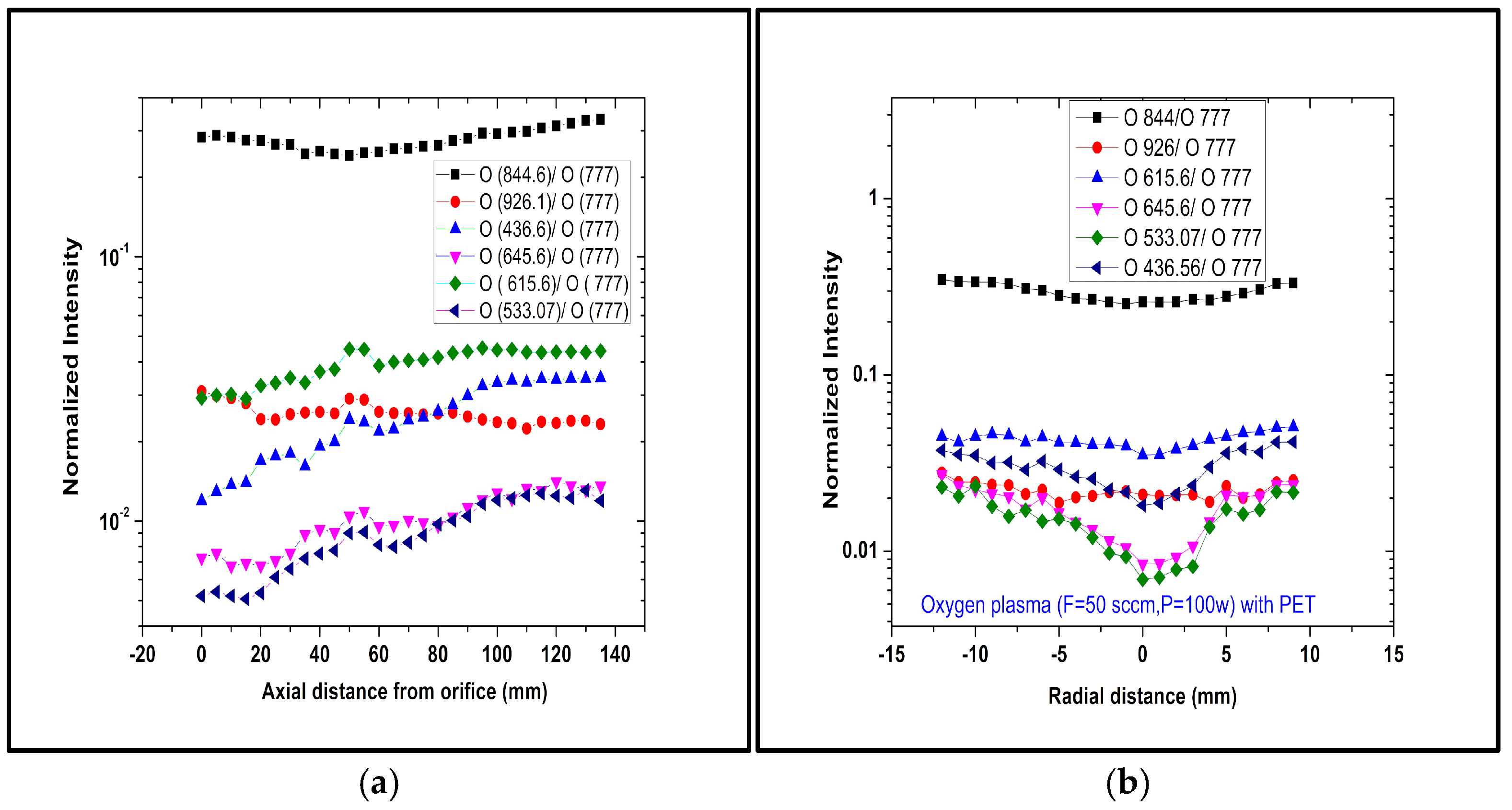
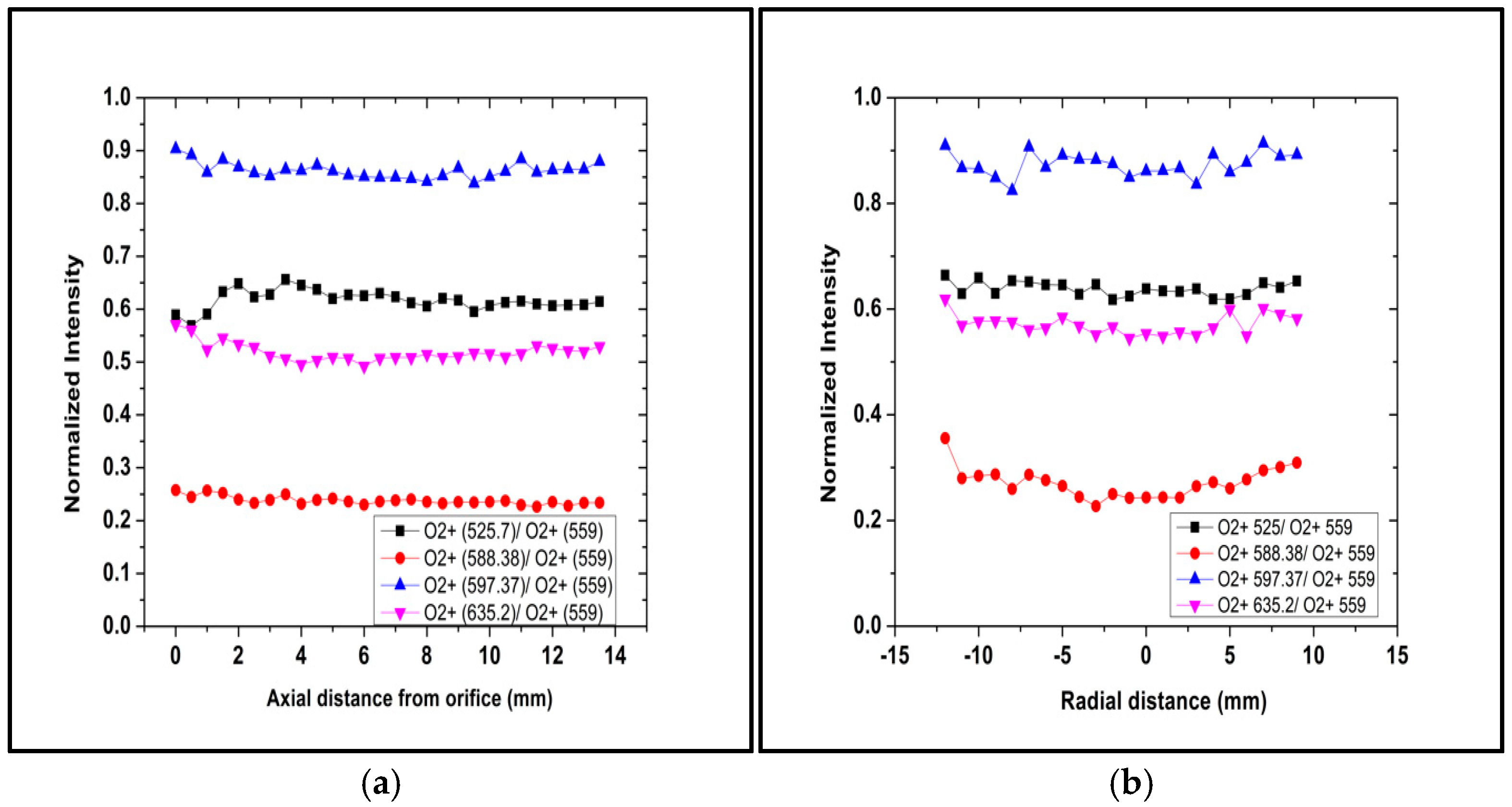



| Wavelength (nm) | Transition Rate (s−1) | Excited Level | Excited Level Energy (eV) |
|---|---|---|---|
| 777.37 | 3.69 × 107 | 5P (3p) | 10.741 eV |
| 844.64 | 3.22 × 107 | 3P (3p) | 10.989 eV |
| 926.28 | 2.97 × 107 | 5D° (3d) | 12.079 eV |
| 436.83 | 7.58 × 105 | 3P (4p) | 12.359 eV |
| 645.60 | 3.85 × 106 | 5S° (5s) | 12.661 eV |
| 615.71 | 7.62 × 106 | 5D° (4d) | 12.754 eV |
| 533.07 | 2.71 × 106 | 5D° (5d) | 13.066 eV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barni, R.; Zaka, H.; Pal, D.; Amjad, I.; Riccardi, C. Characterization of a Supersonic Plasma Jet by Means of Optical Emission Spectroscopy. Photonics 2025, 12, 595. https://doi.org/10.3390/photonics12060595
Barni R, Zaka H, Pal D, Amjad I, Riccardi C. Characterization of a Supersonic Plasma Jet by Means of Optical Emission Spectroscopy. Photonics. 2025; 12(6):595. https://doi.org/10.3390/photonics12060595
Chicago/Turabian StyleBarni, Ruggero, Hanaa Zaka, Dipak Pal, Irsa Amjad, and Claudia Riccardi. 2025. "Characterization of a Supersonic Plasma Jet by Means of Optical Emission Spectroscopy" Photonics 12, no. 6: 595. https://doi.org/10.3390/photonics12060595
APA StyleBarni, R., Zaka, H., Pal, D., Amjad, I., & Riccardi, C. (2025). Characterization of a Supersonic Plasma Jet by Means of Optical Emission Spectroscopy. Photonics, 12(6), 595. https://doi.org/10.3390/photonics12060595





