Numerical Optimization of Metamaterial-Enhanced Infrared Emitters for Ultra-Low Power Consumption
Abstract
1. Introduction
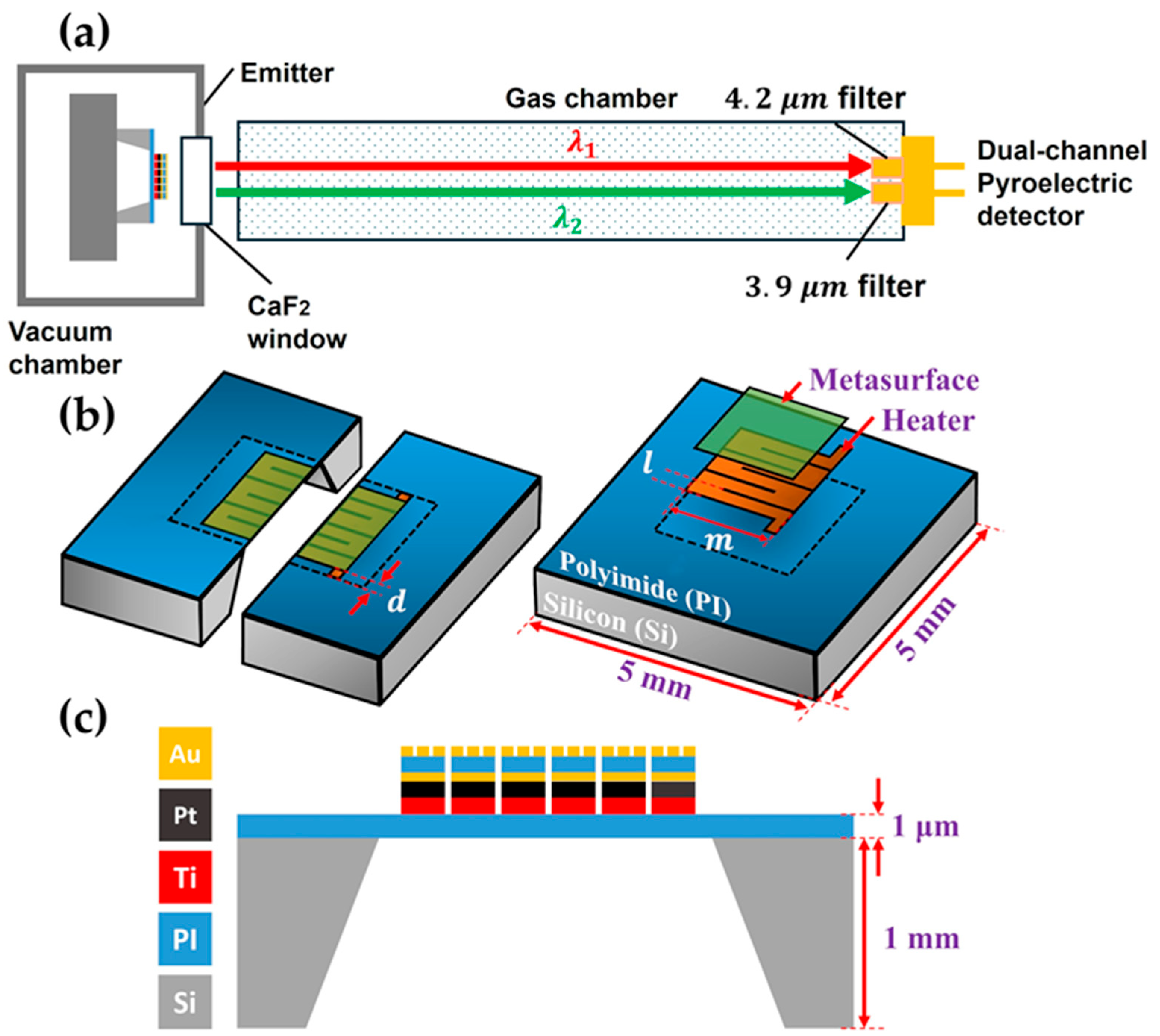
2. Design and Simulation
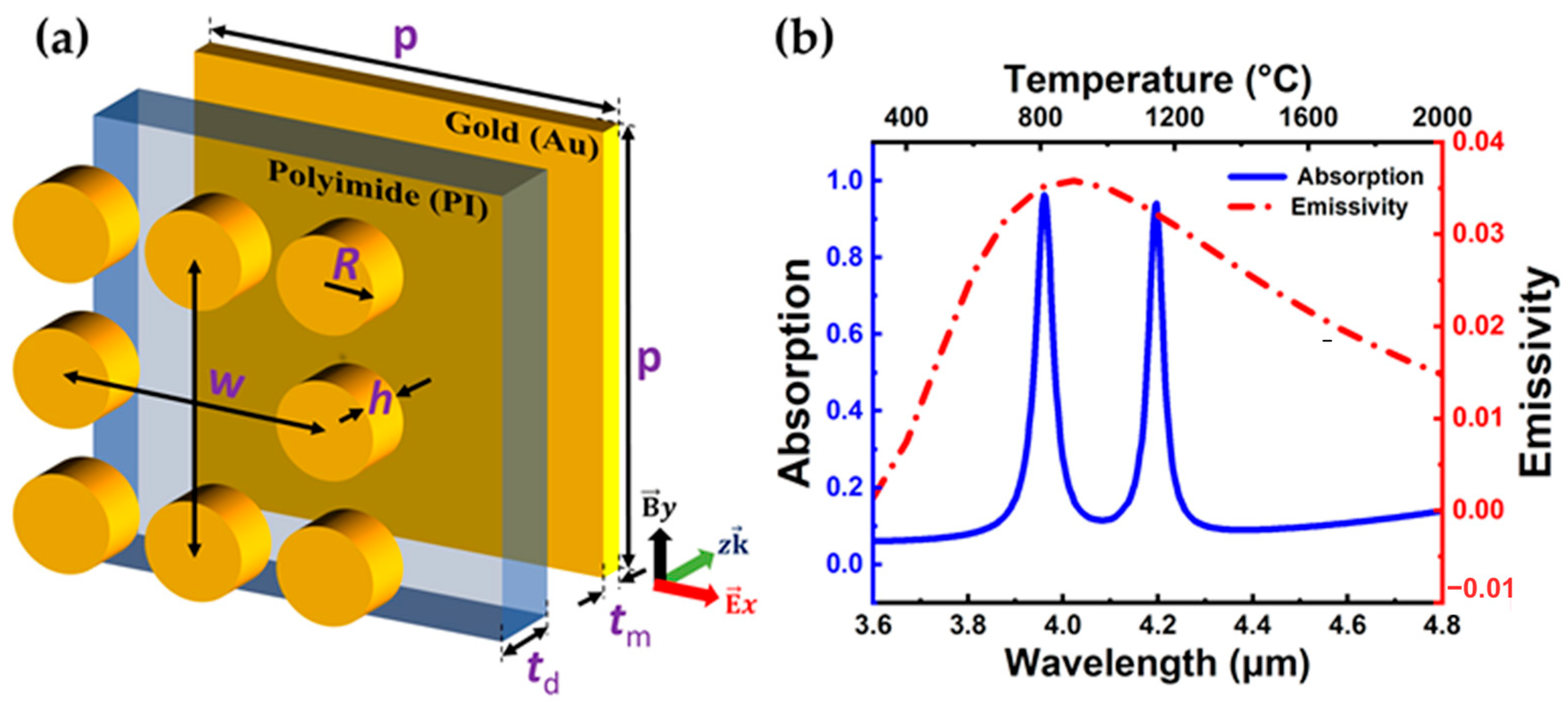
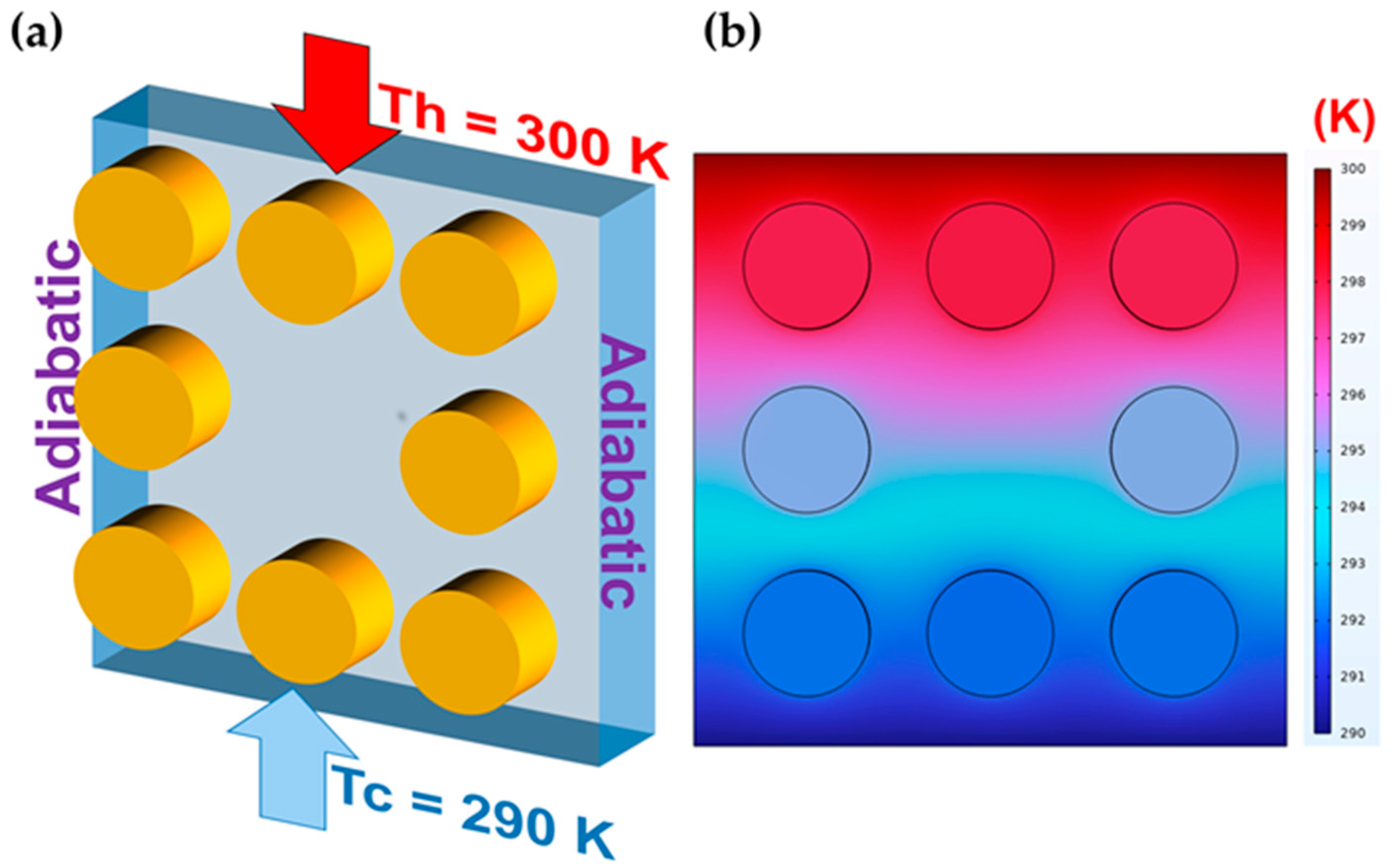
2.1. Metamaterial Design and Its Equivalent Parameters
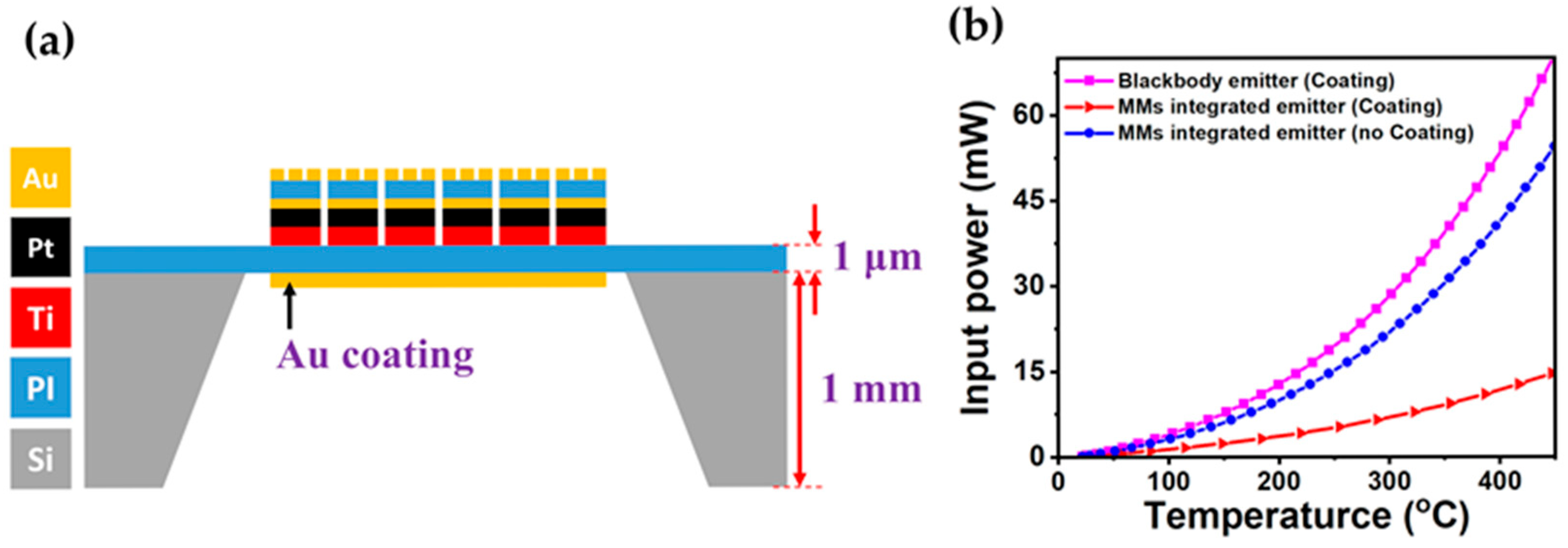
2.2. Metamaterial-Integrated Microheater Design
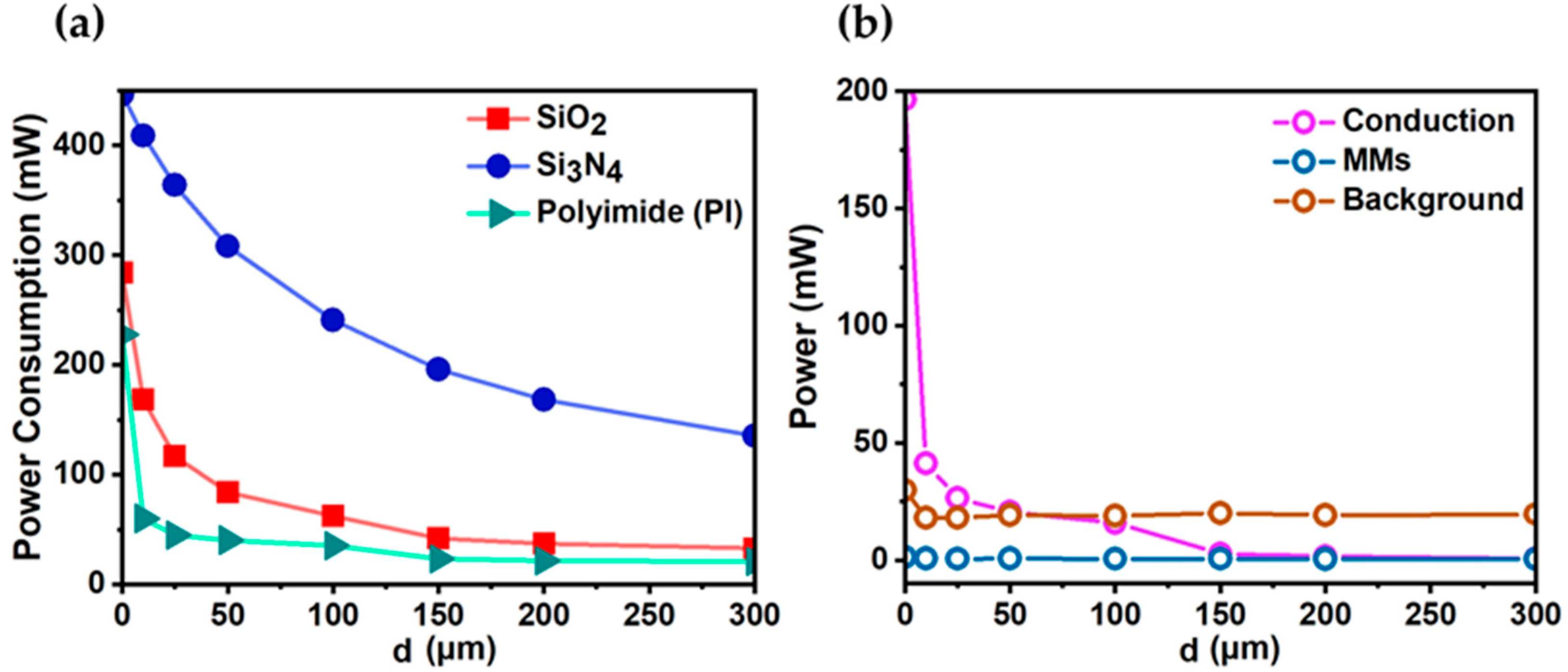
3. Results and Discussion
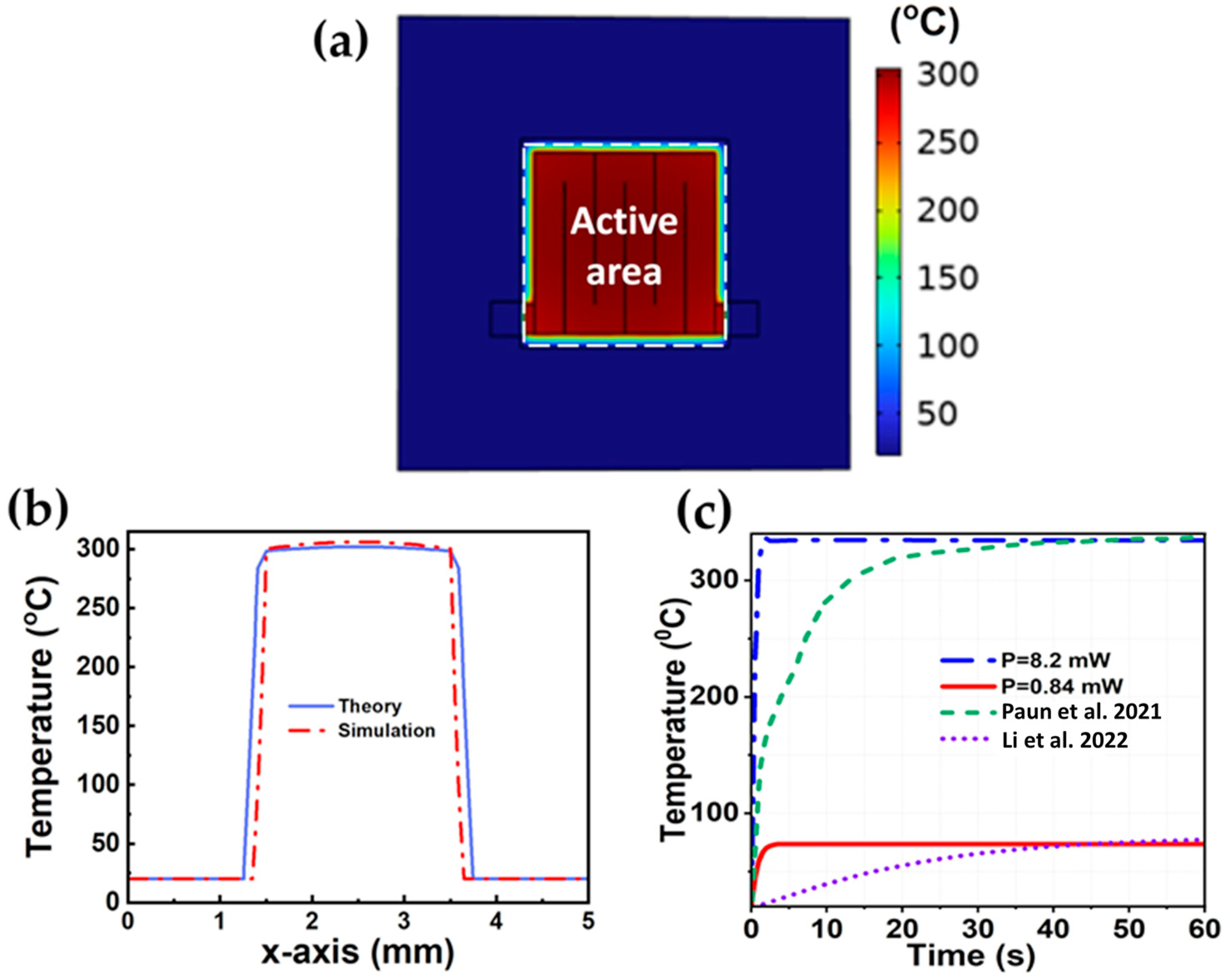
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stanley, R. Plasmonics in the mid-infrared. Nat. Photonics 2012, 6, 409–411. [Google Scholar] [CrossRef]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2013, 24, 012004. [Google Scholar] [CrossRef]
- Nguyen, H.A.; Pham, T.S.; Tung, B.S.; Khuyen, B.X.; Le, D.T.; Vu, H.Y.; Vu, D.L.; Hien, N.T. Metamaterials based on hyperbolic-graphene composite: A pathway from positive to negative refractive index at terahertz. Comput. Mater. Sci. 2025, 248, 113574. [Google Scholar] [CrossRef]
- Fan, K.; Averitt, R.D.; Padilla, W.J. Active and tunable nanophotonic metamaterials. Nanophotonics 2022, 11, 3769–3803. [Google Scholar] [CrossRef]
- Li, M.; Xu, H.; Yang, X.; Xu, H.; Liu, P.; He, L.; Nie, G.; Dong, Y.; Chen, Z. Tunable plasma-induced transparency of a novel graphene-based metamaterial. Results Phys. 2023, 52, 106798. [Google Scholar] [CrossRef]
- Ou, H.; Lu, F.; Xu, Z.; Lin, Y.-S. Terahertz metamaterial with multiple resonances for biosensing application. Nanomaterials 2020, 10, 1038. [Google Scholar] [CrossRef]
- Do, T.C.; Khuyen, B.X.; Tung, B.S.; Viet, N.N.; Ha, D.T.; Hanh, V.T.H.; Do, X.P.; Tung, D.K.; Nguyen, H.A.; Lam, V.D. Wide-angle electromagnetic wave absorption via multilayer metamaterial structures. Phys. Scr. 2025, 100, 025538. [Google Scholar] [CrossRef]
- Qu, Y.; Chen, Y.; Chen, S.; Wu, Q.; Liu, J.; Yi, Z.; Fu, L. Research on Multi-Resonance Mechanism to Achieve Ultra-Wideband High Absorption of a Metamaterial Absorber in the UV to MIR Range. Chin. J. Phys. 2024, 91, 632–643. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, J.; Chen, S.; Yi, Z.; Fu, L.; Yang, W. Bi-Directional High-Performance Metamaterial Perfect Absorber for Solar Harvesting and Refractive Index Sensing. Mater. Today Nano 2024, 26, 100487. [Google Scholar] [CrossRef]
- Bhati, R.; Malik, A.K. Multiband terahertz metamaterial perfect absorber for microorganisms detection. Sci. Rep. 2023, 13, 19685. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Chen, F.; Yang, W. Temperature and refractive index sensor based on perfect absorber in InSb double rectangular ring resonator metamaterials. Mater. Today Commun. 2024, 40, 109461. [Google Scholar] [CrossRef]
- Miyazaki, H.T.; Kasaya, T.; Iwanaga, M.; Choi, B.; Sugimoto, Y.; Sakoda, K. Dual- band infrared metasurface thermal emitter for CO2 sensing. Appl. Phys. Lett. 2014, 105, 121107. [Google Scholar] [CrossRef]
- Khuyen, B.X.; Ngoc, N.V.; Dung, D.N.; Hai, N.P.; Tung, N.T.; Tung, B.S.; Lam, V.D.; Giang, H.T.; Tan, P.D.; Chen, L.; et al. Dual-band infrared metamaterial perfect absorber for narrow-band thermal emitters. J. Phys. D Appl. Phys. 2024, 57, 285501. [Google Scholar] [CrossRef]
- Mihai, L.; Mihalcea, R.; Tomescu, R.; Paun, C.; Cristea, D. Selective mid-IR metamaterial-based gas sensor system: Proof of concept and performances tests. Nanomaterials 2022, 12, 1009. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Lin, Y.-S. Tunable infrared metamaterial emitter for gas sensing application. Nanomaterials 2020, 10, 1442. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Han, T.; Zheng, X.; Li, J.; Li, B.; Fan, S.; Qiu, C.W. Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 2021, 6, 488–507. [Google Scholar] [CrossRef]
- Pitts, D.; Sissom, L.E. Schaum’s Outline of Heat Transfer, 2nd ed.; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Wang, J.; Carson, J.K.; North, M.F.; Cleland, D.J. A new structural model of effective thermal conductivity for heterogeneous materials with co-continuous phases. Int. J. Heat Mass Transf. 2008, 51, 2389–2397. [Google Scholar] [CrossRef]
- Xue, Q. Model for effective thermal conductivity of nanofluids. Phys. Lett. A 2003, 307, 313–317. [Google Scholar] [CrossRef]
- Jia, X.; Roels, J.; Baets, R.; Roelkens, G. On-chip non-dispersive infrared CO2 sensor based on an integrating cylinder. Sensors 2019, 19, 426. [Google Scholar] [CrossRef]
- Yu, S.; Wang, S.; Lu, M.; Zuo, L. A novel polyimide based micro heater with high temperature uniformity. Sens. Actuators A Phys. 2017, 257, 58–64. [Google Scholar] [CrossRef]
- Sanowitz, S. Radiative Properties of Silicon Related Materials. Master’s Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 31 May 2016. [Google Scholar]
- Okada, T.; Ishige, R.; Ando, S. Analysis of thermal radiation properties of polyimide and polymeric materials based on ATR-IR spectroscopy. J. Photopolym. Sci. Technol. 2016, 29, 251–254. [Google Scholar] [CrossRef]
- Raghu, O.; Philip, J. Thermal properties of paint coatings on different backings using a scanning photo acoustic technique. Meas. Sci. Technol. 2006, 17, 2945. [Google Scholar] [CrossRef]
- Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley: New York, NY, USA, 2006. [Google Scholar]
- Aslam, M.; Gregory, C.; Hatfield, J.V. Polyimide membrane for micro-heated gas sensor array. Sens. Actuators B 2004, 103, 153–157. [Google Scholar] [CrossRef]
- Dibbern, U. A substrate for thin-film gas sensors in microelectronic technology. Sens. Actuators B Chem. 1990, 2, 63–70. [Google Scholar] [CrossRef]
- Simon, I.; Bârsan, N.; Bauer, M.; Weimar, U. Micromachined metal oxide gas sensors: Opportunities to improve sensor performance. Sens. Actuators B Chem. 2001, 73, 1–2. [Google Scholar] [CrossRef]
- Bhattacharyya, P.; Sen, S.; Chatterjee, A.; Saha, H. Design of the optimum microheater for smart MEMS gas sensor. In Proceedings of the ISSS 2005 International Conference on Smart Materials Structures and Systems, Bangalore, India, 28–30 July 2005. [Google Scholar]
- Kozlov, A.G. Analytical modelling of steady-state temperature distribution in thermal microsensors using Fourier method: Part 1. Theory. Sens. Actuators A Phys. 2002, 101, 283–298. [Google Scholar] [CrossRef]
- Paun, C.; Tomescu, R.; Parvulescu, C.; Ionescu, O.; Gavrila, D.E.; Cristea, D. Microheater optimized for the integration with metasurface-based IR sources for gas sensing application. Rom. J. Inf. Sci. Technol. 2021, 24, 201–212. [Google Scholar]
- Li, D.; Ruan, Y.; Chen, C.; He, W.; Chi, C.; Lin, Q. Design and thermal analysis of flexible microheaters. Micromachines 2022, 13, 1037. [Google Scholar] [CrossRef]
| Material | Thermal Conductivity (W/mK) | Electrical Conductivity (S/m) | Density (kg/m3) | Heat Capacity at Constant Pressure (J/kg/K) | Emissivity |
| SiO2 | 1.38 | 10−14 | 2200 | 730 | 0.7 [23] |
| Si3N4 | 20 | 0 | 3100 | 700 | 0.7 [23] |
| Polyimide | 0.15 | 0 | 1300 | 1100 | 0.7 [24] |
| Paint | 1.45 | 0 | 1331 | 5184 | 0.94 [25] |
| Au | 317 | 45.6 × 106 | 19,300 | 129 | 0.05 [26] |
| Ag | 429 | 61.6 × 106 | 10,500 | 235 | 0.05 [26] |
| Device | Input Power(mW) | Emission Power (mW) | Background Radiation (mW) | Conduction Loss (mW) |
| MM-integrated emitter with coating | 6.8 | 0.5 | 4.0 | 2.3 |
| MM-integrated emitter without coating | 21.8 | 0.5 | 18.7 | 2.6 |
| Blackbody emitter with coating | 28.6 | 21.6 | 4.2 | 2.8 |
| Device in Ref. [13] | 58 | 3 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khuyen, B.X.; Tan, P.D.; Tung, B.S.; Hai, N.P.; Tuan, P.D.; Phong, D.X.; Tung, D.K.; Anh, N.H.; Giang, H.T.; Vinh, N.P.; et al. Numerical Optimization of Metamaterial-Enhanced Infrared Emitters for Ultra-Low Power Consumption. Photonics 2025, 12, 583. https://doi.org/10.3390/photonics12060583
Khuyen BX, Tan PD, Tung BS, Hai NP, Tuan PD, Phong DX, Tung DK, Anh NH, Giang HT, Vinh NP, et al. Numerical Optimization of Metamaterial-Enhanced Infrared Emitters for Ultra-Low Power Consumption. Photonics. 2025; 12(6):583. https://doi.org/10.3390/photonics12060583
Chicago/Turabian StyleKhuyen, Bui Xuan, Pham Duy Tan, Bui Son Tung, Nguyen Phon Hai, Pham Dinh Tuan, Do Xuan Phong, Do Khanh Tung, Nguyen Hai Anh, Ho Truong Giang, Nguyen Phuc Vinh, and et al. 2025. "Numerical Optimization of Metamaterial-Enhanced Infrared Emitters for Ultra-Low Power Consumption" Photonics 12, no. 6: 583. https://doi.org/10.3390/photonics12060583
APA StyleKhuyen, B. X., Tan, P. D., Tung, B. S., Hai, N. P., Tuan, P. D., Phong, D. X., Tung, D. K., Anh, N. H., Giang, H. T., Vinh, N. P., Tung, N. T., Lam, V. D., Chen, L., & Lee, Y. (2025). Numerical Optimization of Metamaterial-Enhanced Infrared Emitters for Ultra-Low Power Consumption. Photonics, 12(6), 583. https://doi.org/10.3390/photonics12060583







