Dynamic Spatial Small-Target Simulation System with Long-Exit Pupil Distance
Abstract
1. Introduction
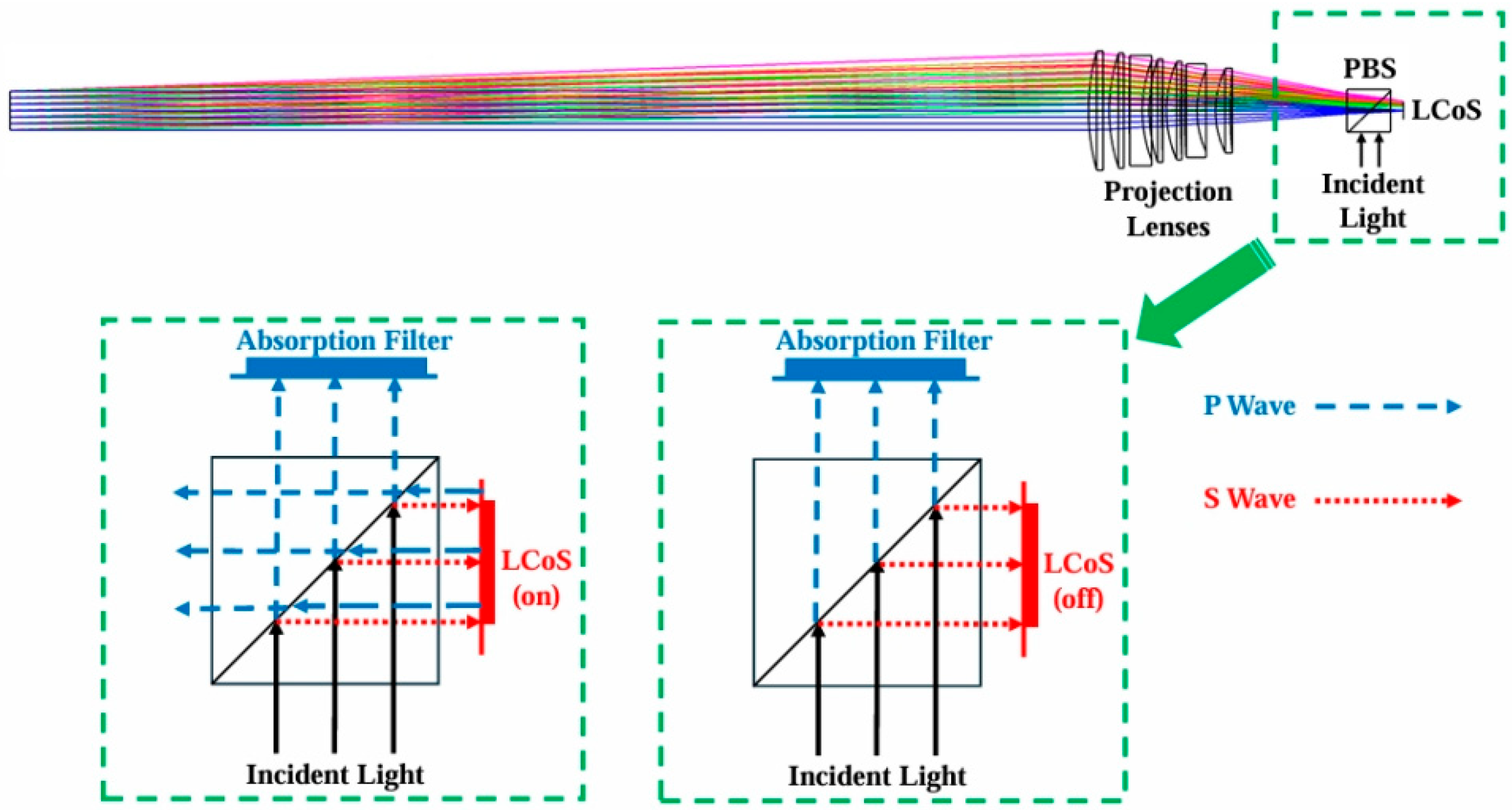
2. The Overall Architecture of a Dynamic Space Small-Target Simulation System with Long-Exit Pupil Distance
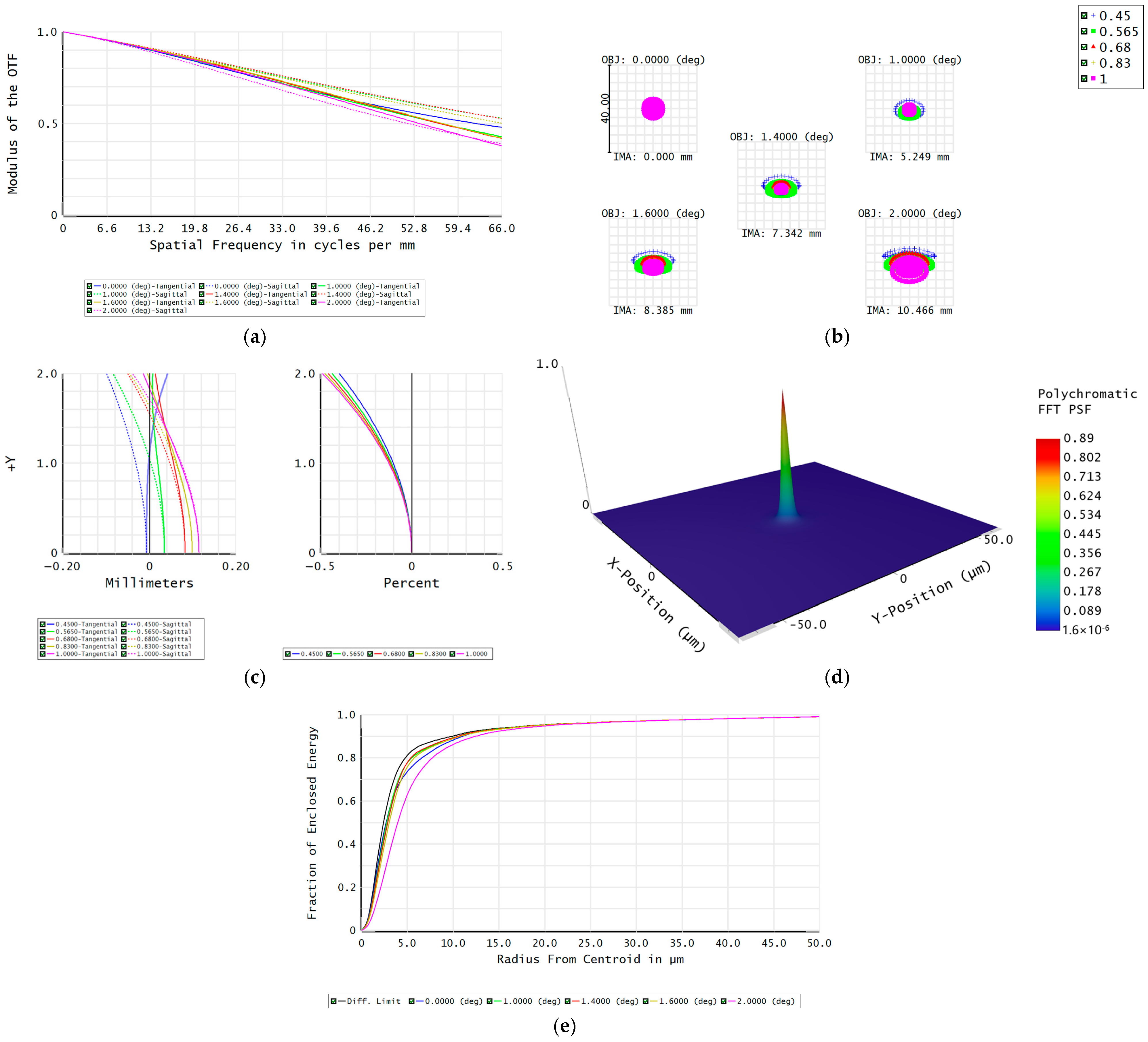
3. Design of the Long-Exit-Pupil-Distance Projection Optical System
4. Design of the Double Free-Form Surface-Illumination Optical System
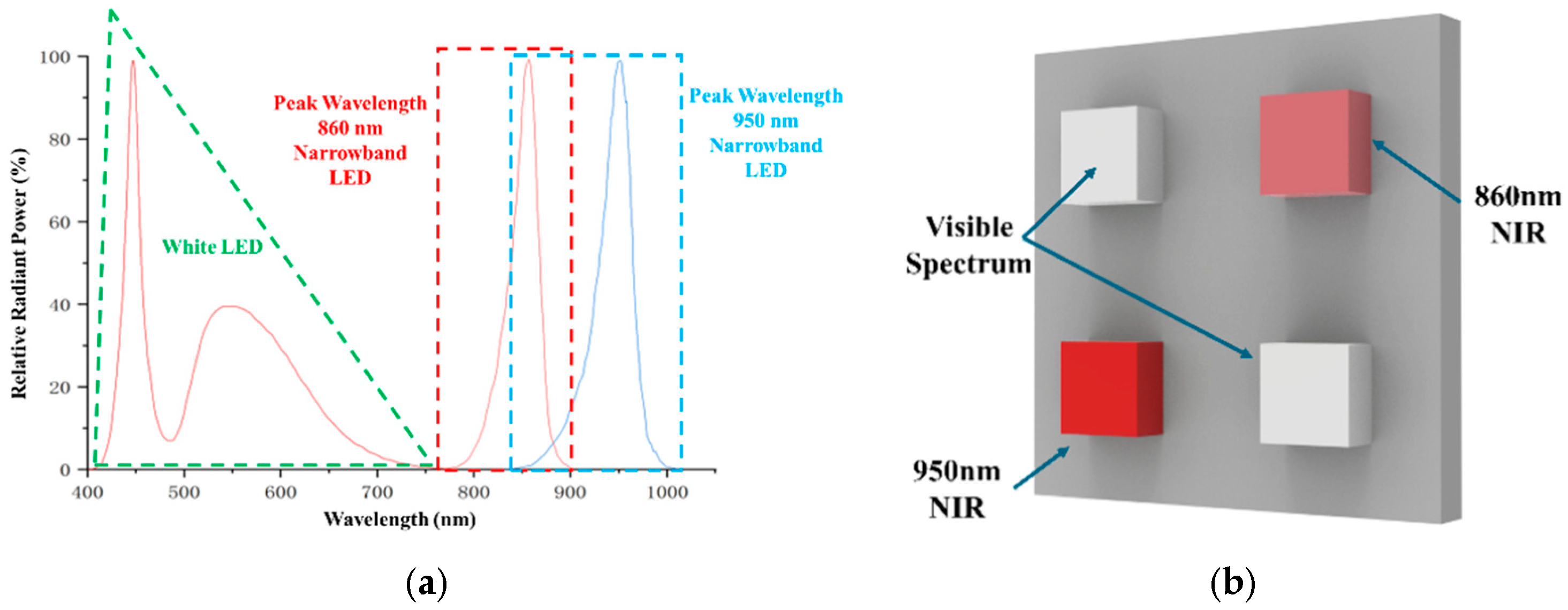
4.1. LED Selection and Arrangement
4.2. Principles of the Initial Structural Design of the Double Free-Form Surface-Illumination Optical System
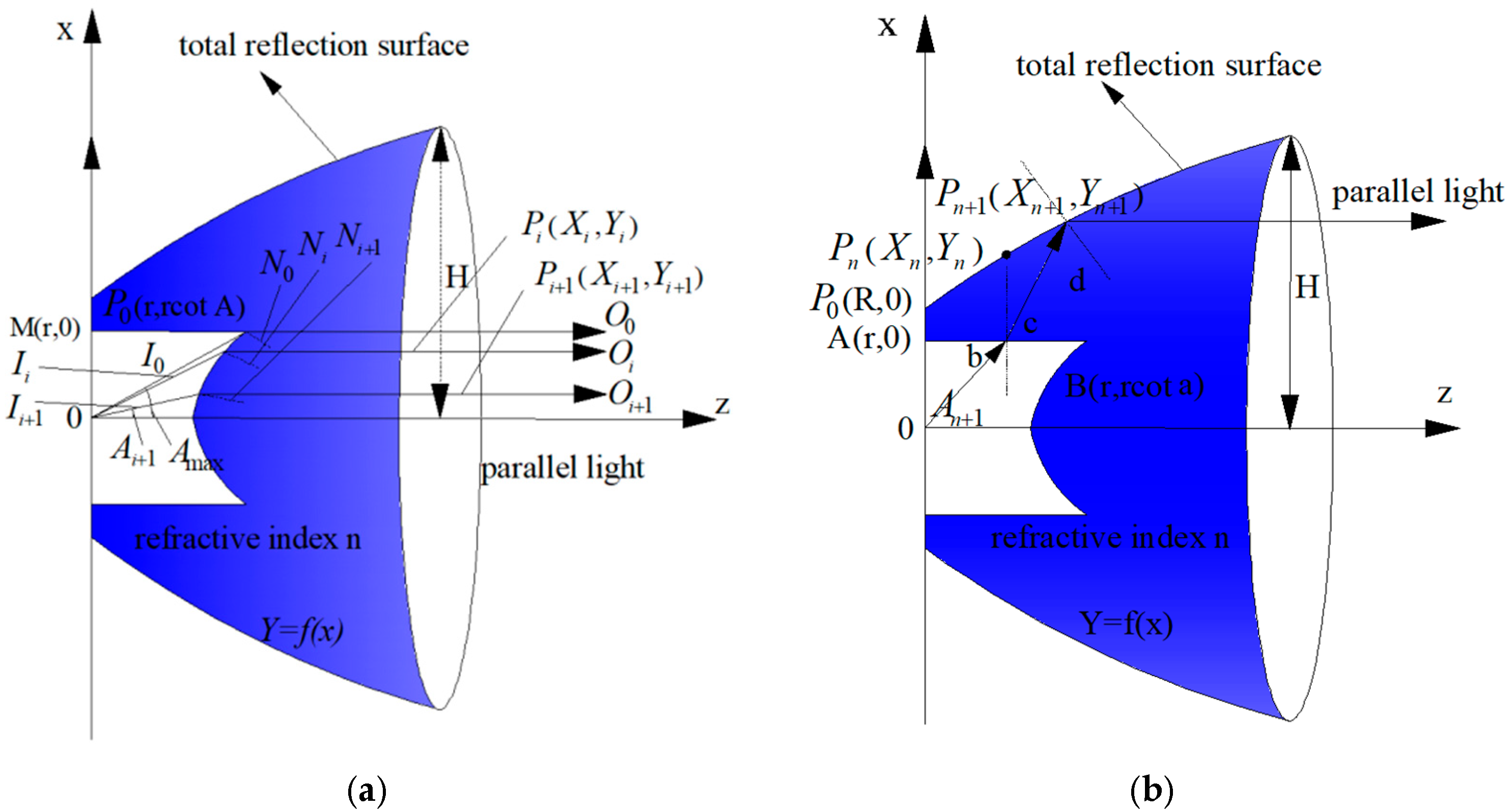
4.2.1. Design of the Incident Rotating Refracting Surfaces
4.2.2. Design of the Incident Rotating Total Reflection Surface
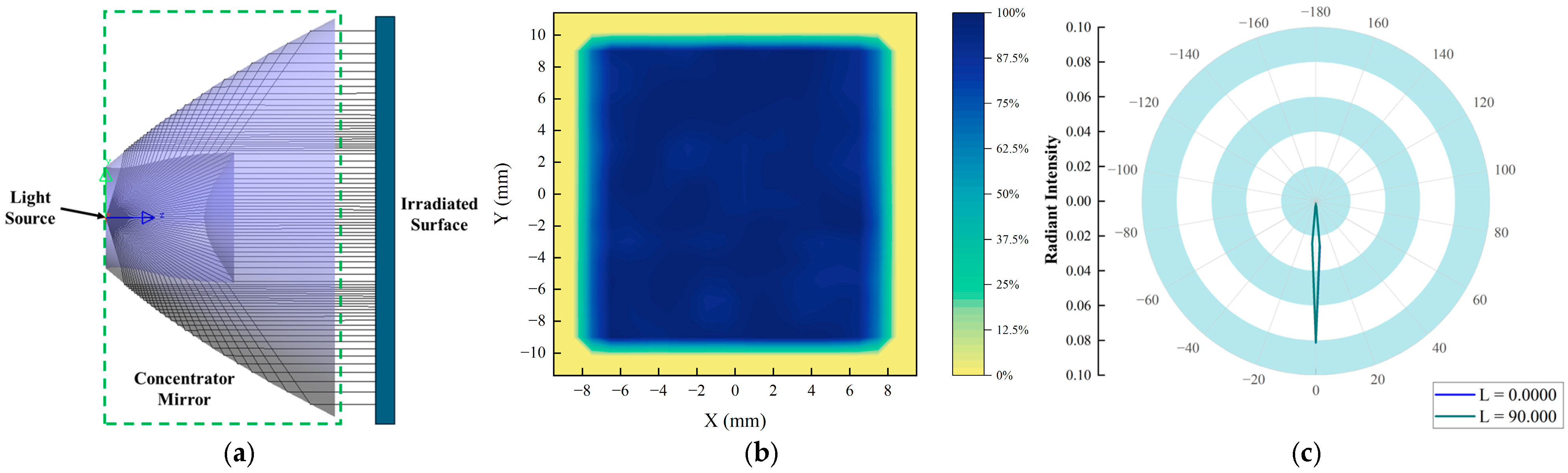
4.3. Simulation of the Double Free-Form Surface-Illumination Optical System
5. Experiments and Tests
5.1. Experimental Platform and Experimental Design
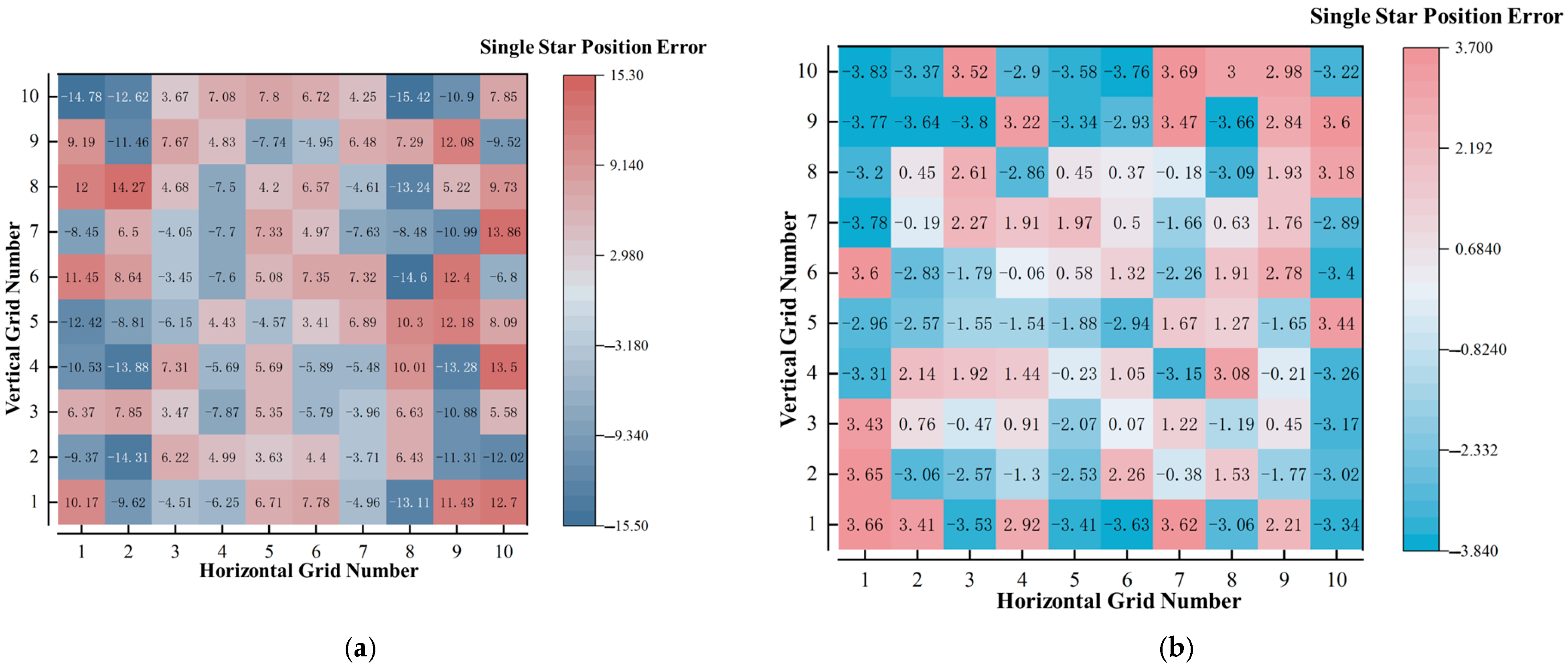
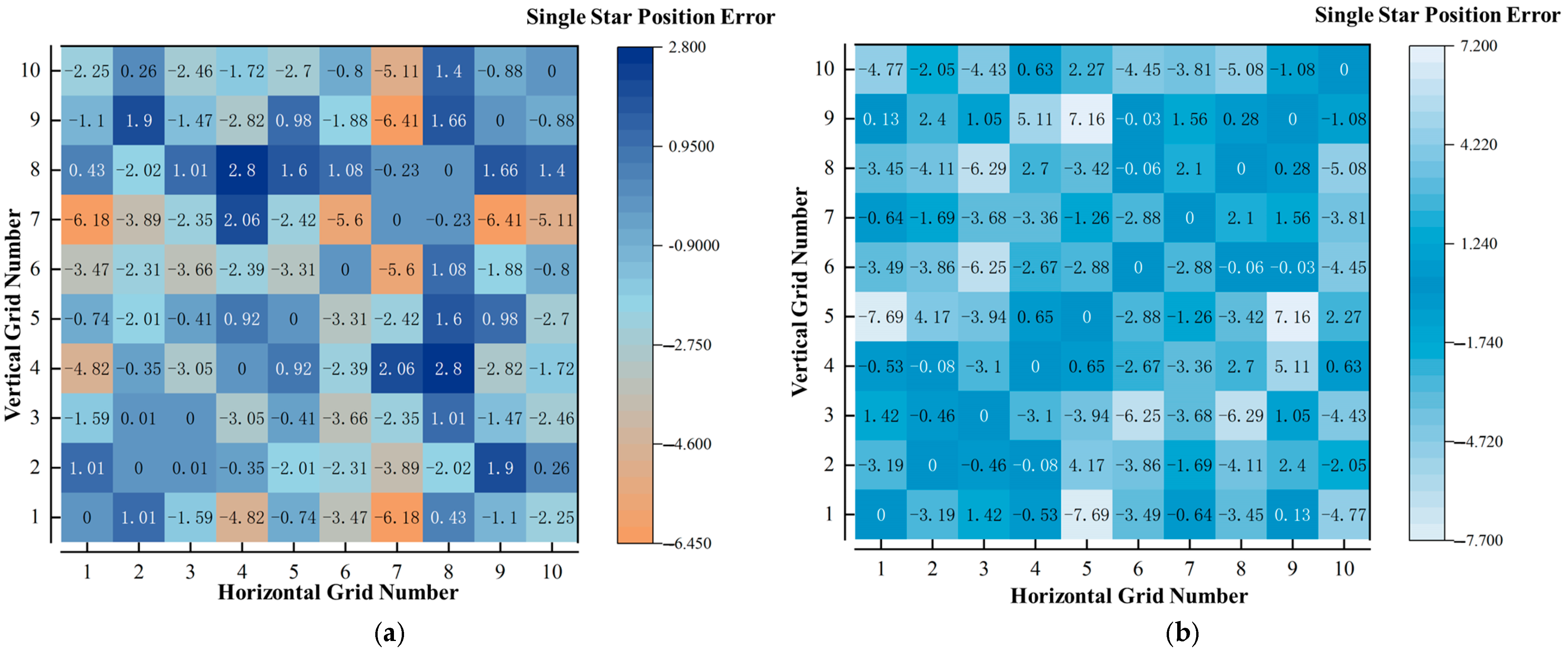
5.2. Accuracy Correction Experiment
5.3. Performance Verification Experiment
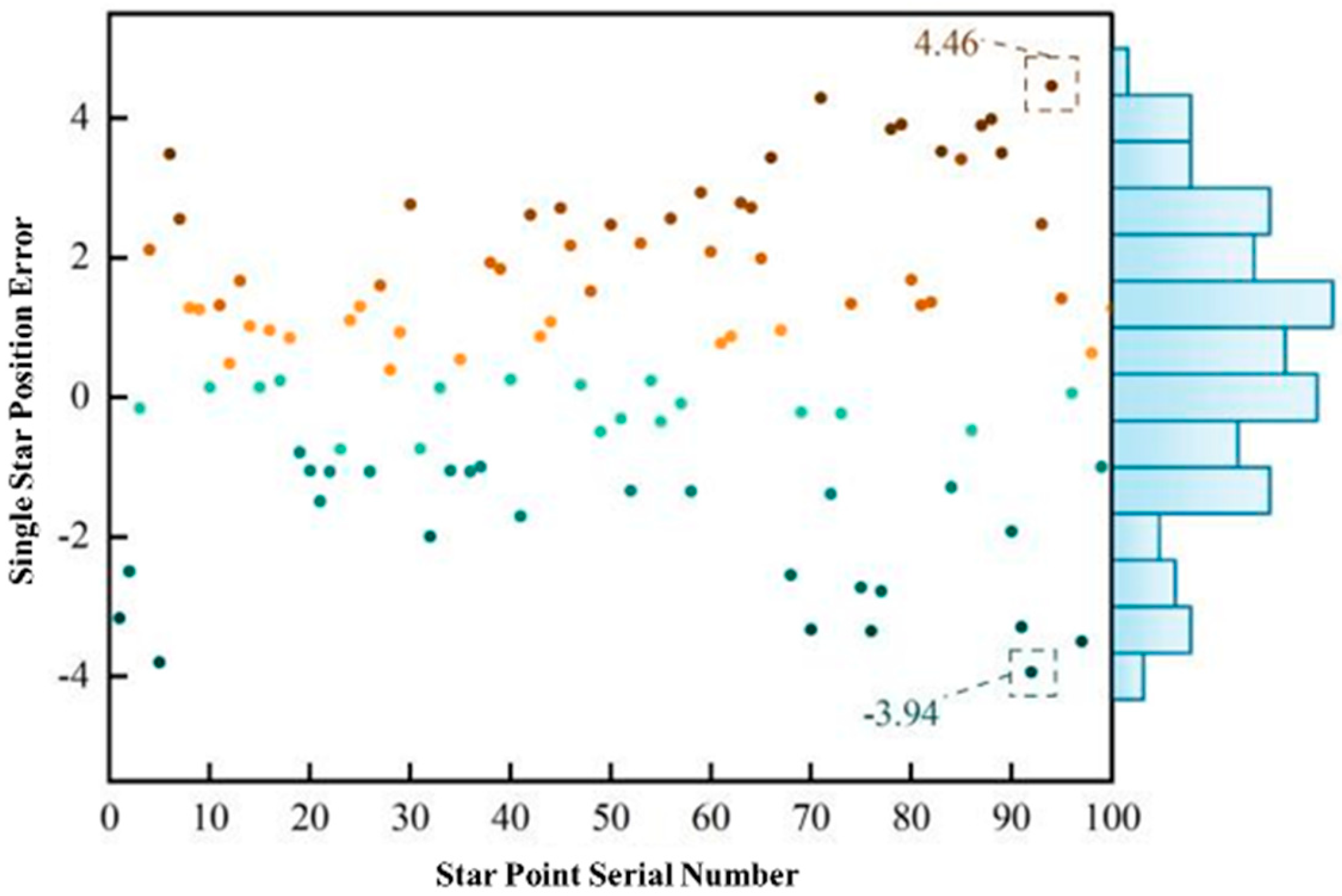
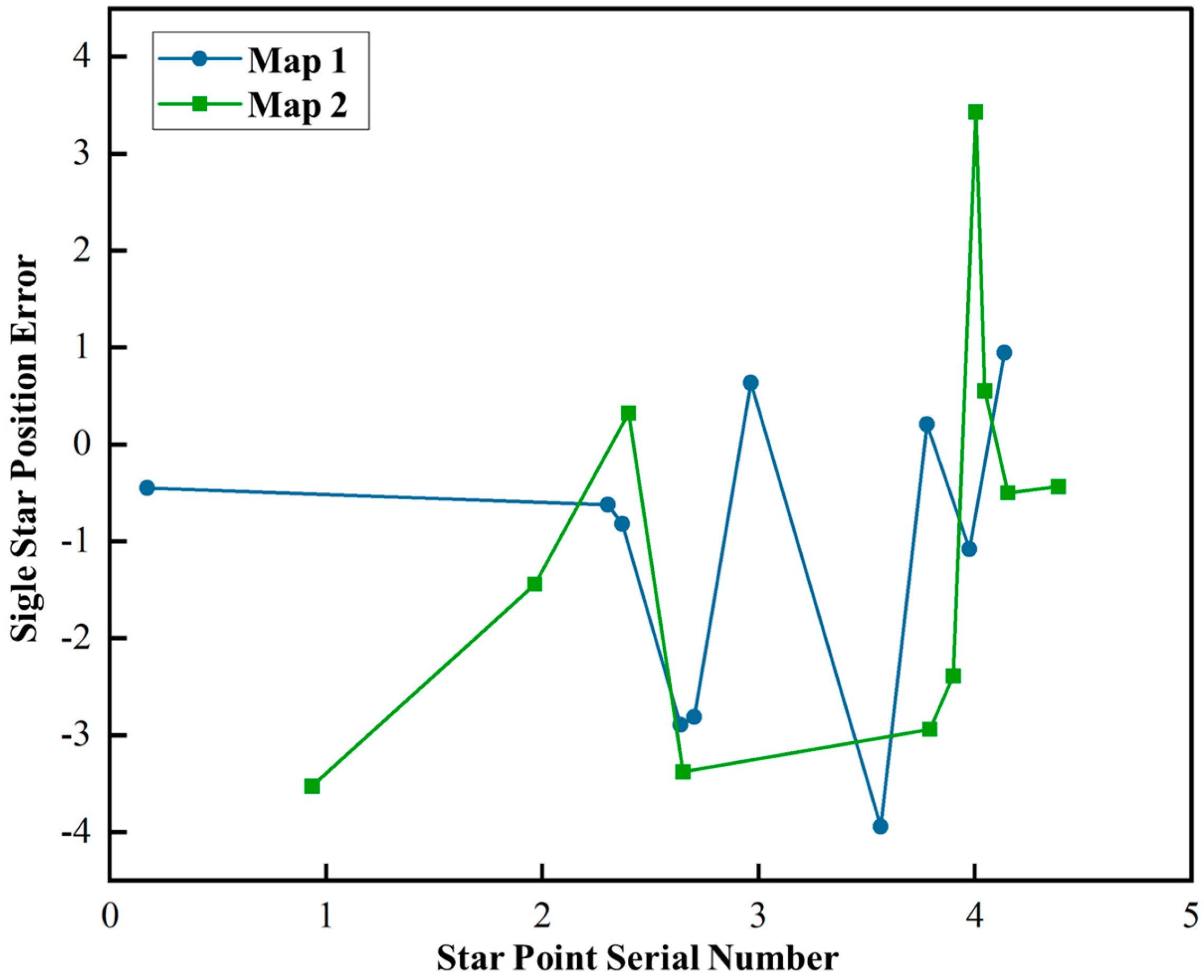
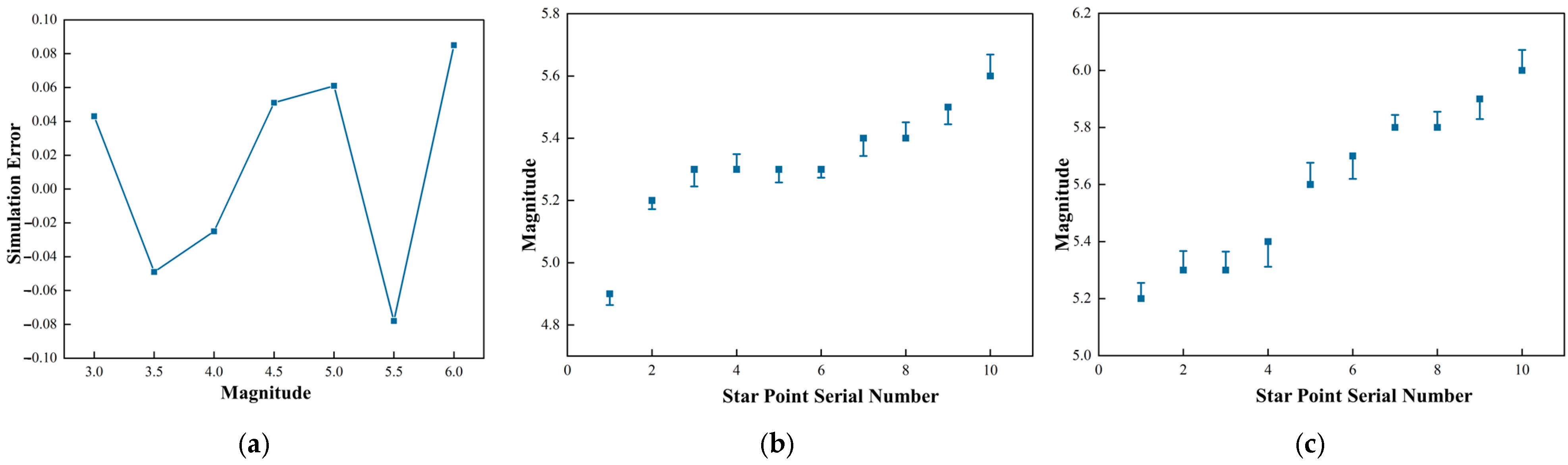
5.3.1. Accuracy of the Geometric Feature Simulation
5.3.2. Accuracy of Radiation Signature Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Dong, M.; Sun, P.; Yan, B.; Wang, J.; Zhu, L. All-parameter calibration method of the on-orbit multi-view dynamic photogrammetry system. Opt. Express 2023, 31, 11471–11489. [Google Scholar] [CrossRef] [PubMed]
- Mahi, Z.; Karoui, M.S.; Keche, M. A new star detection approach for a satellite-onboard star tracker. Adv. Space Res. 2023, 72, 2336–2350. [Google Scholar] [CrossRef]
- Cao, X.; Wang, L.; Li, G.; Zheng, R. Design of projection optical system for target imaging simulator with long exit pupil distance. Curr. Opt. Photonics 2023, 7, 745–754. [Google Scholar] [CrossRef]
- Shao, H.; Wang, L.; Zhang, H.; Li, G.; Chen, Y. Design Method for Laser Target Simulator Illumination System with High Energy Utilization and High Uniformity. IEEE Photon. J. 2024, 16, 1–7. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, X.; Pan, Y.; Hu, M. Design of projection optical system for dynamic star simulator with long exit pupil distance. J. Chang. Univ. Sci. Technol. Nat. Sci. Ed. 2021, 44, 13–18. [Google Scholar]
- Li, G.; Wang, L.; Zheng, R.; Yu, X.; Ma, Y.; Liu, X.; Liu, B. Research on Partitioning Algorithm Based on Dynamic Star Simulator Guide Star Catalog. IEEE Access 2021, 9, 54663–54670. [Google Scholar] [CrossRef]
- Yu, D.; Xin, C.; Wenming, Z.; Jie, L.; Shenglin, L. Design of optical system based on DMD for simulator with large field of view and long exit pupil distance. J. Appl. Opt. 2020, 41, 891–897. [Google Scholar] [CrossRef]
- Liu, X.R.; Xu, X.P. Structural design of a small target simulator optic based on LCOS splicing. J. Chang. Univ. Sci. Technol. (Nat. Sci. Ed.) 2019, 10, 55–60. [Google Scholar]
- Cao, T.; Wang, L.Y. Design of a dynamic target simulator optical system with a large FOV and long exit pupil distance. Appl. Opt. 2024, 63, A115–A123. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, G.; Sun, G. Design of star simulator with spatial background light. Chin. J. Space Sci. 2018, 38, 575–582. [Google Scholar] [CrossRef]
- Sun, G.; Ming, S.; Zhang, G.; Liu, S.; Xu, D. Correction Method of Star Position Error for Splicing Star Simulator. Acta Photon. Sin. 2021, 50, 0912006. [Google Scholar] [CrossRef]
- Yun, Z.; Zhang, J.; Zhang, Y.; Ren, T.; Chen, S.; Zhao, B.; Zhang, J.; Lin, G.; Zhang, G. Research on compensation method for starlight emission accuracy based on star point focal length traversal. Opt. Commun. 2024, 567, 130664. [Google Scholar] [CrossRef]
- Yang, S.Z.; Zhang, G.Y.; Sun, G.F.; Liu, S.; Xu, D. Design of star sensitizer performance test system with tunable background. Laser Optoelectron. Prog. 2022, 59, 2322001. [Google Scholar] [CrossRef]
- Zheng, R.; Li, C.Y.; Gao, Y.; Li, G.X.; Liu, B.; Sun, G. Design of an infrared star simulator optical system for uniform radiation at specific irradiance. J. Photonics Acta Photonica Sin. 2022, 51, 0428002. [Google Scholar] [CrossRef]
- Wang, H.; Wang, B.; Gao, Y.; Wu, S. Near-earth space star map simulation method of short-wave infrared star sensor. Infrared Phys. Technol. 2022, 127, 104436. [Google Scholar] [CrossRef]
- Sun, G.; Ming, S.; Zhang, G.; Liu, S.; Zhang, J.; Su, S.; Yang, S.; Zhang, R. Design of multi-magnitude star simulation system based on adjustable background. Optik 2020, 207, 164486. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, G.; Sun, G.; Liu, S.; Yang, S.; Yang, J.; Yun, Z.; Zhao, D.; Sun, J.; Zhao, D. Optical engine optimisation for faint starlight simulation systems. Opt. Commun. 2020, 471, 125833. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Y.; Zhao, B.; Meng, Y.; Ren, D.; Zhang, J.; Sun, G.; Du, Z.; Zhang, G. Simulation method for multi-source information fusion space target. Opt. Express 2024, 32, 21820–21836. [Google Scholar] [CrossRef]
- Li, S.-H.; He, H.; Ji, Q.; Zhang, X.-H.; Li, N. Design of a dynamic star simulator with high temporal and spatial resolution. Opt. Precis. Eng. 2020, 3, 515–525. [Google Scholar]
- Kang, J.; Zheng, R.; Wang, L.; Pang, C.; Li, G. Research on the Detection Method of Projection Stellar Target Simulator. Photonics 2023, 10, 1101. [Google Scholar] [CrossRef]
- Yun, Z.; Zhang, Y.; Liu, Q.; Ren, T.; Zhao, B.; Xu, D.; Yang, S.; Ren, D.; Yang, J.; Mo, X.; et al. Research on the simulation method of a BP neural network PID control for stellar spectrum. Opt. Express 2024, 32, 38879–38895. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.W.; Xu, X.P.; Pan, Y.; Zhang, L.Q.; Wang, Z.Y. Research on optical system design of star simulator. J. Changchun Univ. Sci. Technol. (Nat. Sci. Ed.) 2024, 4, 31–40. [Google Scholar]
- Zhao, D.; Zhang, G.; Xu, D.; Wang, L.; Sun, G.; Zhong, J.; Wu, L. A Diffraction Correction Method Based on Digital Mirror Device Star Simulator. Acta Photon. Sin. 2021, 50, 0912005. [Google Scholar] [CrossRef]
- Chen, N.; Yue, W.; Xu, Y.; Guo, W.; Xiao, Y.; Ren, Z.; Ding, X.; Li, M.; Xu, Y.; Wu, T.; et al. Design and simulation of a compact polarization beam splitter based on dual-core photonic crystal fiber with elliptical gold layer. Sci. Rep. 2024, 14, 18017. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Xia, Y.; Li, Y.; Sheng, L. Optimization of polarization balance in beam splitter films for weak star simulator. Opt. Express 2024, 32, 25304–25316. [Google Scholar] [CrossRef]
- Jing-Yi, F.F.; Tian-Xiang, Q.Q.; Yun-Han, H.H.; Zhi-Ying, L.L. A field-of-view splicing method for the optical system of a star simulator. Chin. Opt. 2021, 14, 1468–1475. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S.; Zheng, J.; Wang, Y.; Li, H.; Wen, Z. Research on Optical System of Dim Target Simulator Based on Polarization Stray Light Suppression. Appl. Sci. 2024, 14, 2826. [Google Scholar] [CrossRef]
- Gao, T.; Sun, G.; Zhang, G.; Du, Z.; Liu, Q.; Deng, Q.; Chen, S.; Zhang, J. Design of Parabolic Off-Axis Reflector Optical System for Large Aperture Single Star Simulators. Appl. Sci. 2024, 14, 1926. [Google Scholar] [CrossRef]
- Lan, D.C.; Wei, W. Design of a dynamic star simulator illumination optical system based on TIR lenses. J. Light. Eng. 2023, 1, 22–28. [Google Scholar]
- Nguyen, Q.-K.; Lin, Y.-J.; Lee, X.-H.; Lin, S.-K.; Wu, C.-S.; Yang, T.-H.; Wu, T.-L.; Lee, T.-X.; Chien, C.-H.; Yu, Y.-W.; et al. GaN-based mini-LED matrix applied to multi-functional forward lighting. Sci. Rep. 2022, 12, 6444. [Google Scholar] [CrossRef]
- Tabibifar, N.; Eskandari, M.; Boroumand, F.A.; Fathi, D.; Rahimi, S. Enhanced light extraction by optimizing near-infrared perovskite-based light emitting diode (PeLED). Sci. Rep. 2024, 14, 29165. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, J.; Zhang, Y.; Zhang, S.; Yang, S.; Zou, G.; Liu, L. Overall study of solar simulation optical system with large irradiated surface using free-form concentrator to improve uniformity. iScience 2023, 26, 107781. [Google Scholar] [CrossRef] [PubMed]
- Zheng, R.; Liu, B.; Gao, Y.; Wang, L.Y.; Chen, Q.M. Analysis and simulation of star point positions of infrared star simulators. J. Instrum. 2022, 9, 115–121. [Google Scholar]
- Li, G.; Wang, L.; Zheng, R.; Ma, Y.; Liu, X. Research on correction method of star point position error of dynamic star simulator. Optik 2021, 241, 167017. [Google Scholar] [CrossRef]
- Zhang, K.S.; Su, X.Q.; Liu, K. Interstellar angular distance correction method based on the effect of aberration. J. Photonics 2023, 7, 189–202. [Google Scholar] [CrossRef]
- Yang, Y.H.; Wang, X.R.; Zhu, Y.Z.; Lai, X.H.; Li, Q.T.; Chen, B.N.; Yang, J.H.; Wang, Y.H.; Rui, X.; Zhu, Y.Z.; et al. Star simulation technique based on high-precision jitter compensation system. J. Opt. 2022, 18, 111–118. [Google Scholar] [CrossRef]



| Indicator | Parameters |
|---|---|
| operating bands | 450 nm–900 nm |
| angle of view | 4° |
| exit-pupil distance | 1250 mm |
| exit-pupil diameter | 45 mm |
| Star Point Serial Number | Star Map 1 | Star Map 2 | ||||
|---|---|---|---|---|---|---|
| Star Position (°) | Magnitude | Star Position (°) | Magnitude | |||
| Azimuth | Pitch | Azimuth | Pitch | |||
| 1 | 1.776 | 1.567 | 4.9 | 2.505 | −3.601 | 5.2 |
| 2 | −3.860 | 0.944 | 5.2 | 3.355 | −2.446 | 5.3 |
| 3 | 3.596 | 1.157 | 5.3 | 2.355 | −2.973 | 5.3 |
| 4 | 2.687 | −1.251 | 5.3 | −1.882 | 1.485 | 5.4 |
| 5 | −2.220 | −0.614 | 5.3 | 3.042 | −2.670 | 5.6 |
| 6 | −3.537 | −0.441 | 5.3 | −2.040 | 1.693 | 5.7 |
| 7 | 2.049 | −1.663 | 5.4 | −1.897 | 0.509 | 5.8 |
| 8 | −3.455 | −2.276 | 5.4 | −0.904 | 0.239 | 5.8 |
| 9 | 0.102 | 0.139 | 5.5 | 3.937 | 0.728 | 5.9 |
| 10 | −2.656 | −0.495 | 5.6 | 3.720 | 1.173 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Xu, X.; Zhang, N.; Lv, Y.; Geng, H. Dynamic Spatial Small-Target Simulation System with Long-Exit Pupil Distance. Photonics 2025, 12, 578. https://doi.org/10.3390/photonics12060578
Lu Y, Xu X, Zhang N, Lv Y, Geng H. Dynamic Spatial Small-Target Simulation System with Long-Exit Pupil Distance. Photonics. 2025; 12(6):578. https://doi.org/10.3390/photonics12060578
Chicago/Turabian StyleLu, Yi, Xiping Xu, Ning Zhang, Yaowen Lv, and Hua Geng. 2025. "Dynamic Spatial Small-Target Simulation System with Long-Exit Pupil Distance" Photonics 12, no. 6: 578. https://doi.org/10.3390/photonics12060578
APA StyleLu, Y., Xu, X., Zhang, N., Lv, Y., & Geng, H. (2025). Dynamic Spatial Small-Target Simulation System with Long-Exit Pupil Distance. Photonics, 12(6), 578. https://doi.org/10.3390/photonics12060578




