Abstract
Linear thermal expansion in the 70–350 K range and nanohardness and Young’s modulus at room temperature are measured for the newly developed quaternary nonlinear optical crystal PbGa2GeSe6 applicable in the mid-IR part of the spectrum (3–25 µm).
1. Introduction
The quaternary chalcogenide PbGa2GeSe6 (PGGSe) belongs to a family of orthorhombic (space group #43, Fdd2, point group mm2) crystals with a general formula AGa2GeS(e)6 (A = Pb, Sn) possessing non-centrosymmetric structure [1,2,3,4,5]. Most interesting from an applications perspective, they exhibit second-order nonlinear polarizability, a property of materials that allows them to convert intense light from one wavelength to another. This class of non-oxide crystals is of particular interest for frequency conversion in the mid-IR part of the spectrum due to their lower phonon energies [6]. Two kinds of nonlinear structural units are present in AGa2GeS(e)6 crystals: (i) tetrahedral (Ga/Ge)–S(e)2 units and (ii) polyhedral units centered by cations with a lone electron pair (Sn2+ or Pb2+). The selenide PGGSe (i.e., A = Pb) was the first compound from this family that was discovered in 2015 [3] and it remains so far the only one that has been thoroughly optically characterized using single crystals. According to [3], its structure contains three non-centrosymmetric chromophores, [PbSe4], [GaSe4], and [Ga/GeSe4], with covalent interactions between the X and Se atoms (X = Pb, Ga, Ga/Ge). Since crystals of only ~1 mm size were obtained in [3], the band-gap of PGGSe was determined from diffuse reflectance vis/near-IR spectra while the mid-IR transmission was measured with samples diluted with dry KBr and pressed into transparent sheets. The average nonlinear response of PGGSe was evaluated in [3] from relative measurements on powders using a 2.05 μm Q-switched Ho-laser. Raman spectra in back-scattering geometry and IR reflection spectra of PbGa2GeS(e)6 revealed that the high-frequency part is dominated by the GeS(e)4 structural units [7], which determines the mid-IR transmission cut-off wavelength normally associated with two-phonon absorption. Fitting of the near band-gap absorption in [7] indicated an indirect nature of the band-gap in these compounds.
The melting temperature of PGGSe is 720 °C [8]. The growth of large size high optical quality single crystals by the vertical Bridgman-Stockbarger method [8] enabled the measurement of the transmission properties of PGGSe using thin plates and the dispersion and birefringence using oriented prisms, thus, in turn, leading to the fitting of the first Sellmeier equations for PGGSe, and the realization of the first phase-matched second-harmonic generation (SHG) in this material using a picosecond Ho-laser amplifier to derive the non-diagonal nonlinear coefficients: d31(PGGSe) = 16.8 pm/V and d32(PGGSe) = 3.6 pm/V at 2.05 µm. The band-gap energy of PGGSe was derived from transmission measurements in the visible as 2.25 eV (550 nm), larger than in [3,7], and its mid-IR transmission extends at least up to 25 µm [8]. PGGSe is an optically negative biaxial crystal with nx < ny < nz and the correspondence between the principal dielectric and the crystallographic axes is xyz = cba. The angle between the two optical axes and the principal z-axis is Vz = 64°. The birefringence of PGGSe is as large as ~0.25 at 5 µm [8]. Optical damage in the SHG experiments with PGGSe was observed at 250 MW/cm2 (1.25 mJ/cm2) at ~2 µm (~5 ps pulses at 1 kHz) in terms of peak on-axis values [8].
Here, we study the thermo-mechanical properties of PGGSe, including its linear anisotropic thermal expansion and the nanohardness and Young’s modulus using oriented test plates.
2. Thermal Expansion
The thermal expansion was studied using powdered single crystals with a Bruker D8 Discover Davinci X-ray diffractometer (Bruker Corporation, Madison, WI, USA) with Co Kα radiation at Kα1 = 1.78897 and Kα2 = 1.79285 Å, paired with an Oxford Chimera temperature control system (Oxford Cryosystems Ltd., Long Hanborough, UK).
We used FullProf (May 2021 64b) software to analyze the data in terms of a Le Bail fit. The XRD peak profiles were defined using a Thompson–Cox–Hastings formulation of the pseudo-Voigt function with axial divergence asymmetry. The background was adjusted manually and the displacement was refined only for the lowest temperature analyzed and kept fixed as temperature was increased. Figure 1 shows the PGGSe lattice parameter temperature dependence for the a, b, and c crystallographic axes. The goodness of the fits was in the χ2 = 3–4 range.
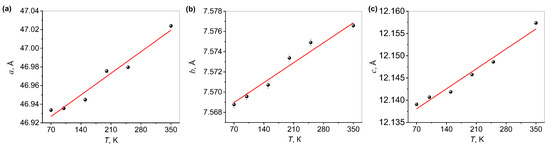
Figure 1.
Temperature (T)-dependent lattice constants of PGGSe (a–c): experimental data (symbols) and linear fits (lines).
The room temperature (RT = 293 K) values in Table 1 were calculated from the linear fits to the data. The values reported in [3] at the same temperature, 47.135(16) Å for a, 7.578(3) Å for b, and 12.161(4) Å for c are slightly larger, but such deviations can be attributed to different growth conditions or to different diffractometer calibrations.

Table 1.
Room temperature (RT) lattice constants, relative linear thermal expansion coefficients α, and coefficient of determination R2.
The relative linear thermal expansion coefficients in Table 1 were derived from the slopes of the fits. They are lower compared to the widely used, commercially available AgGaSe2 chalcopyrite (αa = 14.1 and αc = −11.2 ppm/K), the benchmark among the nonlinear selenides, which, in addition, shows anomalous behavior (i.e., opposite signs) [9].
Determination coefficients R2 exceeding 0.95 in Table 1 are indicative of strong agreement between the experimental data and the model.
3. Nanohardness and Young’s Modulus
The nanohardness and Young’s modulus were derived from RT nanoindentation tests (Nanoindenter G200, Keysight Technologies, Santa Rosa, CA, USA). The three plates used were cut normal to the principal axes directions and had a thickness of the order of 100 µm. Thermal drift correction was applied both for the tip and the sample. Optically polished fused silica served as a calibration standard. The measured reference values were Young’s modulus of 71.3 ± 0.6 GPa and hardness of 9.5 ± 0.1 Gpa, which fit into the device acceptance criteria (70–75 GPa and 8.5–10.5 GPa, respectively). Continuous stiffness mode was chosen, with oscillatory indentation load (frequency: 45 Hz, amplitude: 2 nm) and a Berkovich tip was used. The maximum penetration depth was 2 µm. Ten consecutive indents, separated by 50 µm, were performed (see Figure 2a). The surface approach velocity and distance were 10 nm/s and 1 µm, respectively.
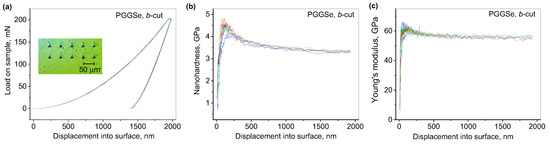
Figure 2.
Loading/unloading curves (a), depth dependence of nanohardness (b), and Young’s modulus (c) of the b-cut PGGSe sample. The inset in (a) is a micrograph of the indents. Different colors represent the individual tests.
The elastic modulus of the sample E was estimated by the Oliver–Pharr equation [10] implemented in NanoSuite 6 Software:
where ν is the material Poisson’s ratio (estimated to be 0.2), νi is the nanoindenter tip Poisson’s ratio, Ei is the elastic modulus of the indenter, and , with S—the contact stiffness (measured at each oscillatory step), A—the surface contact area projected onto a plane normal to the indendation direction, and β—a geometrical factor of the indenter (for a Berkovich tip, β = 1.034).
The nanohardness was calculated as the ratio of the contact force to the contact area A. Figure 2b shows a representative plot of the nanohardness dependences on the indentation depth for the b-cut PGGSe plate. All tests, for the three directions (a, b, and c), exhibit the typical (for nanoindentation) increased values at small depths associated with surface hardening (an effect typical for relatively soft crystals as the one studied here). Beyond ~300 nm, the nanohardness of the undisturbed material monotonically decreases with the depth. Figure 2c shows the Young’s modulus depth dependence of the b-cut PGGSe plate.
The nanohardness and Young’s modulus values obtained by averaging over the interval of 300–1900 nm are summarized in Table 2. The results reveal some anisotropy for both Young’s modulus and nanohardness. Young’s modulus and nanohardness are highest for the b-cut specimen; we note that this direction exhibits the lowest relative linear expansion coefficient. For AgGaSe2, only microhardness measurements on polycrystalline material can be found in the literature, e.g., 4.40 GPa [11].

Table 2.
Young’s modulus, nanohardness, and the temperature and thermal drift correction in the nanoindentation tests of PGGSe.
4. Conclusions
In conclusion, we present data on the anisotropic thermal expansion of the novel nonlinear chalcogenide crystal PGGSe and its nanohardness and Young’s modulus along different directions. Such information will be useful for the crystal growth and the practical application of PGGSe in nonlinear optics, i.e., for evaluation of stresses introduced, e.g., in cutting along phase-matching directions and polishing procedures, as well as for subsequent cleaning and anti-reflection coating of the optical surfaces or evaluation of thermal stress effects in high average power laser applications.
Author Contributions
Conceptualization, V.P.; methodology, M.A.S. and G.K.E.; software, A.V.G. and K.M.; validation, M.A.S., J.T.G., and G.K.E.; formal analysis, J.T.G. and K.M.; investigation, M.A.S., J.T.G., A.V.G., and G.K.E.; resources, V.P. and R.S.; data curation, A.V.G., R.S., and K.M.; writing—original draft preparation, V.P. and G.K.E.; writing—review and editing, V.P. and G.K.E.; visualization, G.K.E. and K.M.; supervision, V.P.; project administration, V.P.; funding acquisition, M.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
The diffraction component of this work was supported by the Air Force Office of Scientific Research (AFOSR) Grant No. LRIR 23RXCOR003 and FA8655-20-1-7053 and the Asian Office of Aerospace Research and Development (AOARD)—Ministry of Science and Technology of Taiwan (MOST) Grant No. F4GGA21207H002. We acknowledge also general support from the Air Force Materials and Manufacturing (RX) and Aerospace Systems (RQ) Directorates.
Data Availability Statement
Data sets generated during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest. The authors have no relevant financial or non-financial interests to disclose. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PGGSe | PbGa2GeSe6 |
| SHG | Second-harmonic generation |
| RT | Room temperature |
References
- Huang, Y.-Z.; Zhang, H.; Lin, C.-S.; Cheng, W.-D.; Guo, Z.; Chai, G.-L. PbGa2GeS6: An infrared nonlinear optical material synthesized by an intermediate-temperature self-fluxing method. Cryst. Growth Des. 2018, 18, 1162–1167. [Google Scholar] [CrossRef]
- Fedorchuk, A.O.; Parasyuk, O.V.; Cherniushok, O.; Andriyevsky, B.; Myronchuk, G.L.; Khyzhun, O.Y.; Lakshminarayana, G.; Jedryka, J.; Kityk, I.V.; ElNaggar, A.M.; et al. PbGa2GeS6 crystal as a novel nonlinear optical material: Band structure aspects. J. Alloys Compd. 2018, 740, 294–304. [Google Scholar] [CrossRef]
- Luo, Z.-Z.; Lin, C.-S.; Cui, H.-H.; Zhang, W.-L.; Zhang, H.; Chen, H.; He, Z.-Z.; Cheng, W.-D. PbGa2MSe6 (M = Si, Ge): Two exceptional infrared nonlinear optical crystals. Chem. Mater. 2015, 27 (Suppl. S1–S13), 914–922. [Google Scholar] [CrossRef]
- Lin, Z.; Li, C.; Kang, L.; Lin, Z.; Yao, J.; Wu, Y. SnGa2GeS6: Synthesis, structure, linear and nonlinear optical properties. Dalton Trans. 2015, 44, 7404–7410. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, S.; Guo, Y.; Lin, Z.; Yao, J.; Wu, Y. SnGa2GeSe6, a benign addition to the AM2IIIMIVQ6 family: Synthesis, crystal structure and nonlinear optical performance. Dalton Trans. 2019, 48, 6638–6644. [Google Scholar] [CrossRef] [PubMed]
- Petrov, V. Frequency down-conversion of solid-state laser sources to the mid-infrared spectral range using non-oxide nonlinear crystals. Prog. Quantum Electron. 2015, 42, 1–106. [Google Scholar] [CrossRef]
- Valakh, M.Y.; Dzhagan, V.M.; Mazur, N.V.; Havryliuk, Y.O.; Yukhymchuk, V.O.; Piskach, L.V.; Kogut, Y.M.; Zahn, D.R.T.; Litvinchuk, A.P. Raman and infrared phonon spectra of novel nonlinear optical materials PbGa2GeS6 and PbGa2GeSe6: Experiment and theory. Phys. Stat. Sol. (b) 2020, 527, 1900700. [Google Scholar] [CrossRef]
- Badikov, V.V.; Badikov, D.V.; Wang, L.; Shevyrdyaeva, G.S.; Panyutin, V.L.; Fintisova, A.A.; Sheina, S.G.; Petrov, V. Crystal growth and characterization of a new quaternary chalcogenide nonlinear crystal for the mid-infrared: PbGa2GeSe6. Cryst. Growth Des. 2019, 19, 4224–4228. [Google Scholar] [CrossRef]
- Aggarwal, R.L.; Fan, T.Y. Thermal diffusivity, specific heat, thermal conductivity, coefficient of thermal expansion, and refractive-index change with temperature in AgGaSe2. Appl. Opt. 2005, 44, 2673–2677. [Google Scholar] [CrossRef] [PubMed]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Ivashchenko, I.; Danylyuk, I.; Olekseyuk, I. Phase diagrams of the AgIn5Se8–AgGaSe2 and AgIn5Se8–Ga2Se3 systems of the quasi-ternary system Ag2Se–Ga2Se3–In2Se3. Chem. Met. Alloys 2012, 5, 33–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).