Dual-Channel Chaos Synchronization in Two Mutually Injected Semiconductor Ring Lasers
Abstract
1. Introduction
2. Theoretical Model and Synchronization Analysis
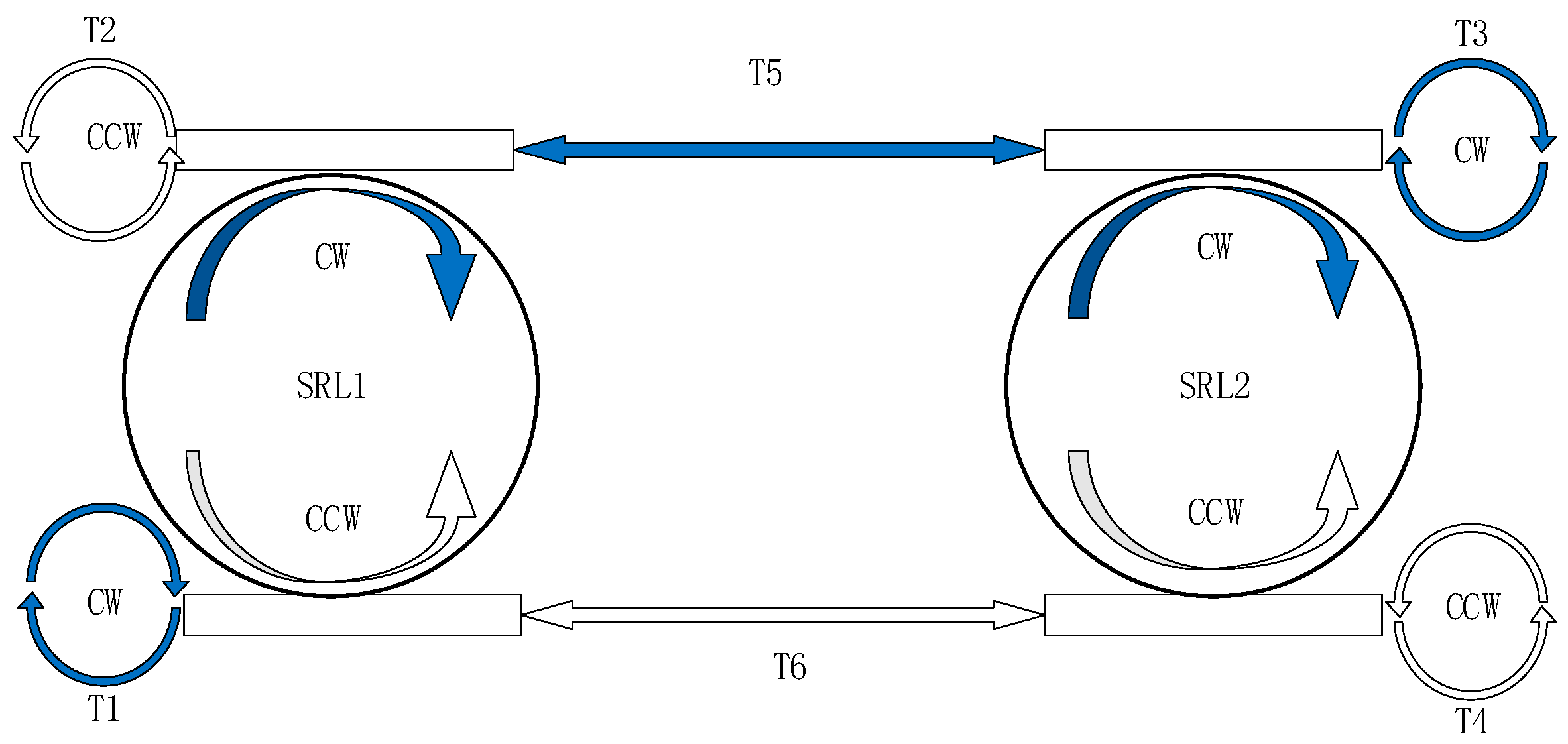
2.1. Theoretical Model
2.2. Synchronization Analysis
2.2.1. Chaos Synchronization Between the Same Modes
2.2.2. Synchronization Between the Different Modes
3. Results and Discussion
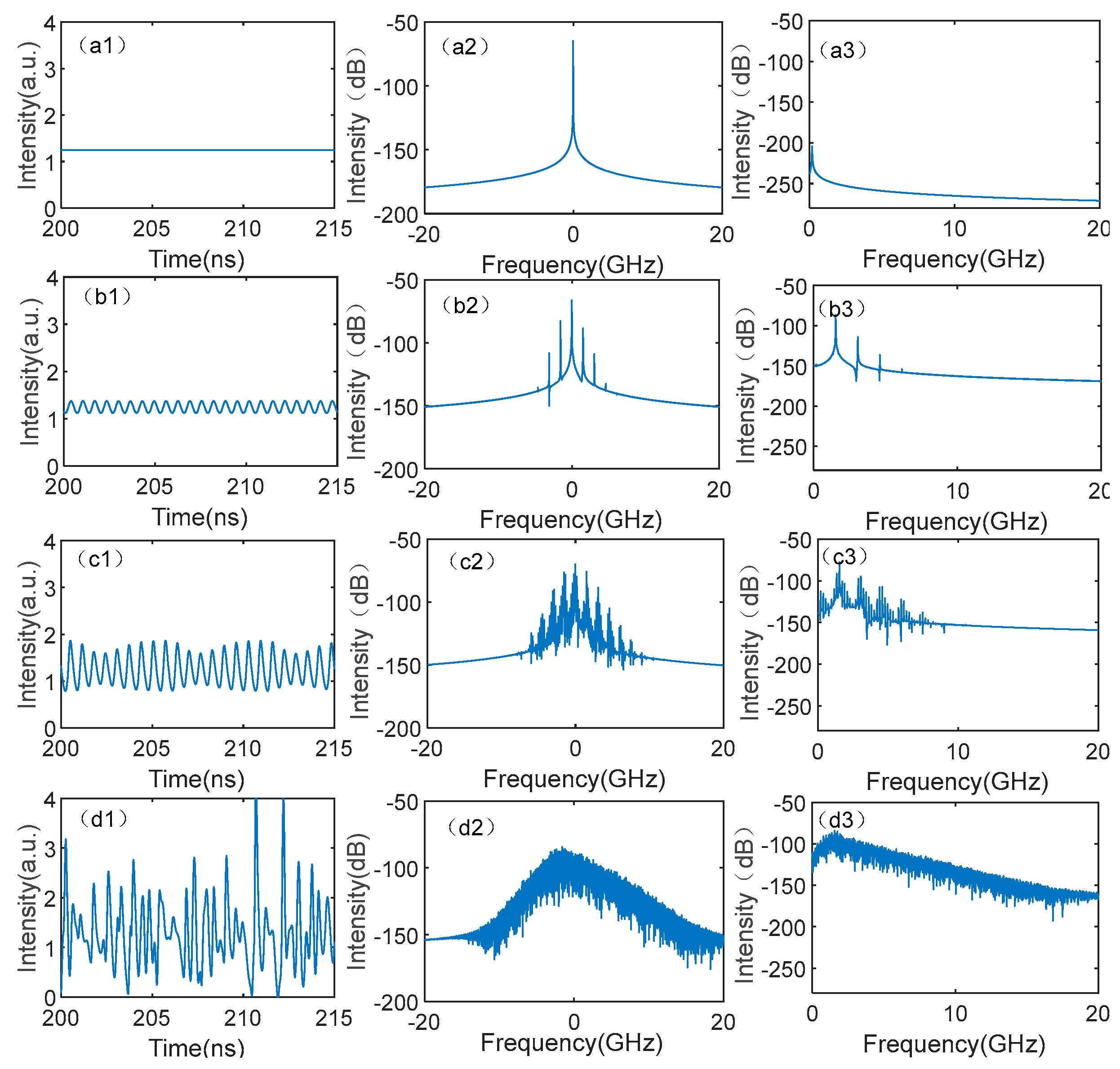
3.1. Dynamics Evolution of SRL
3.2. Synchronization Performance Analysis of Three Synchronization Modes
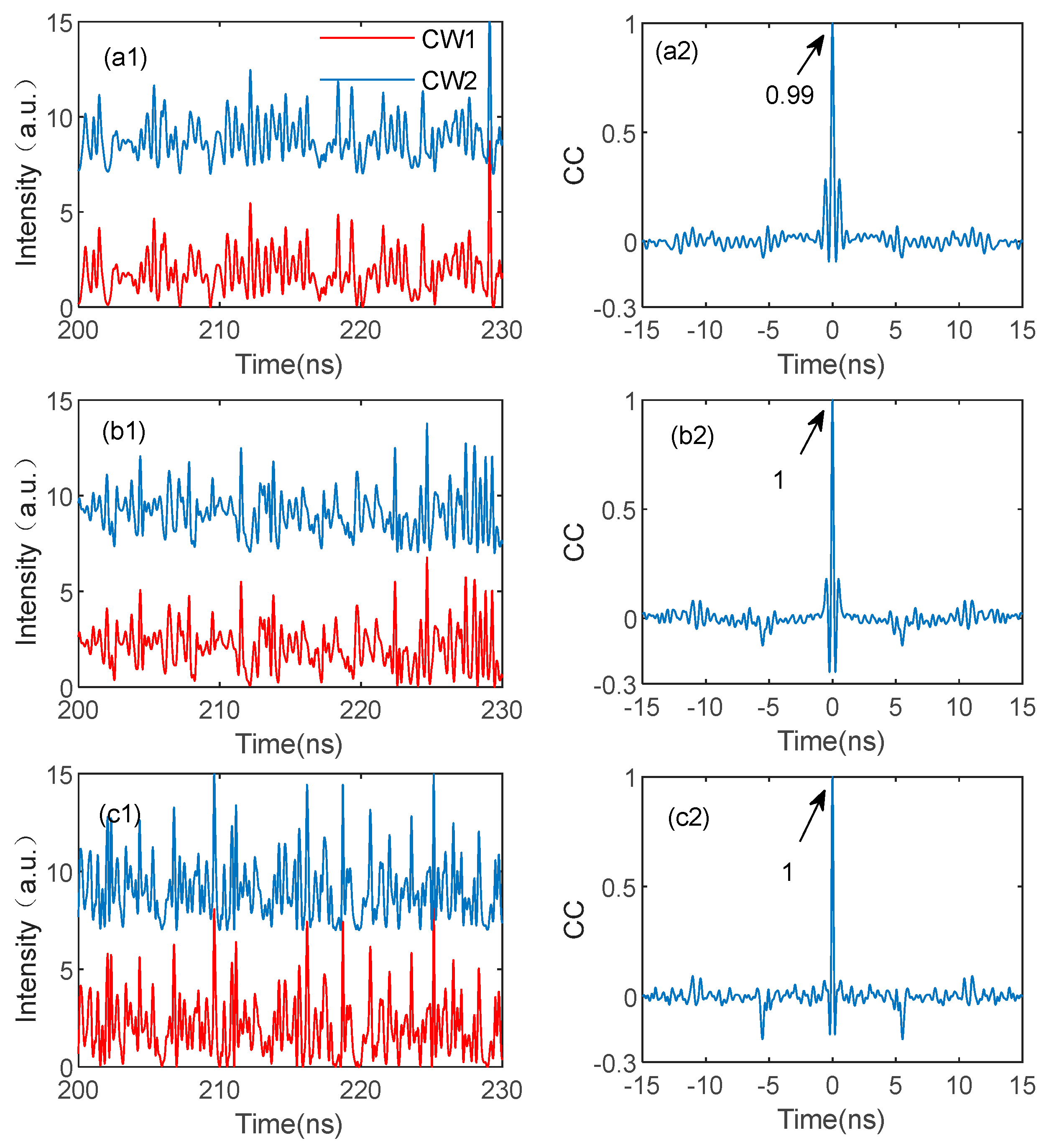
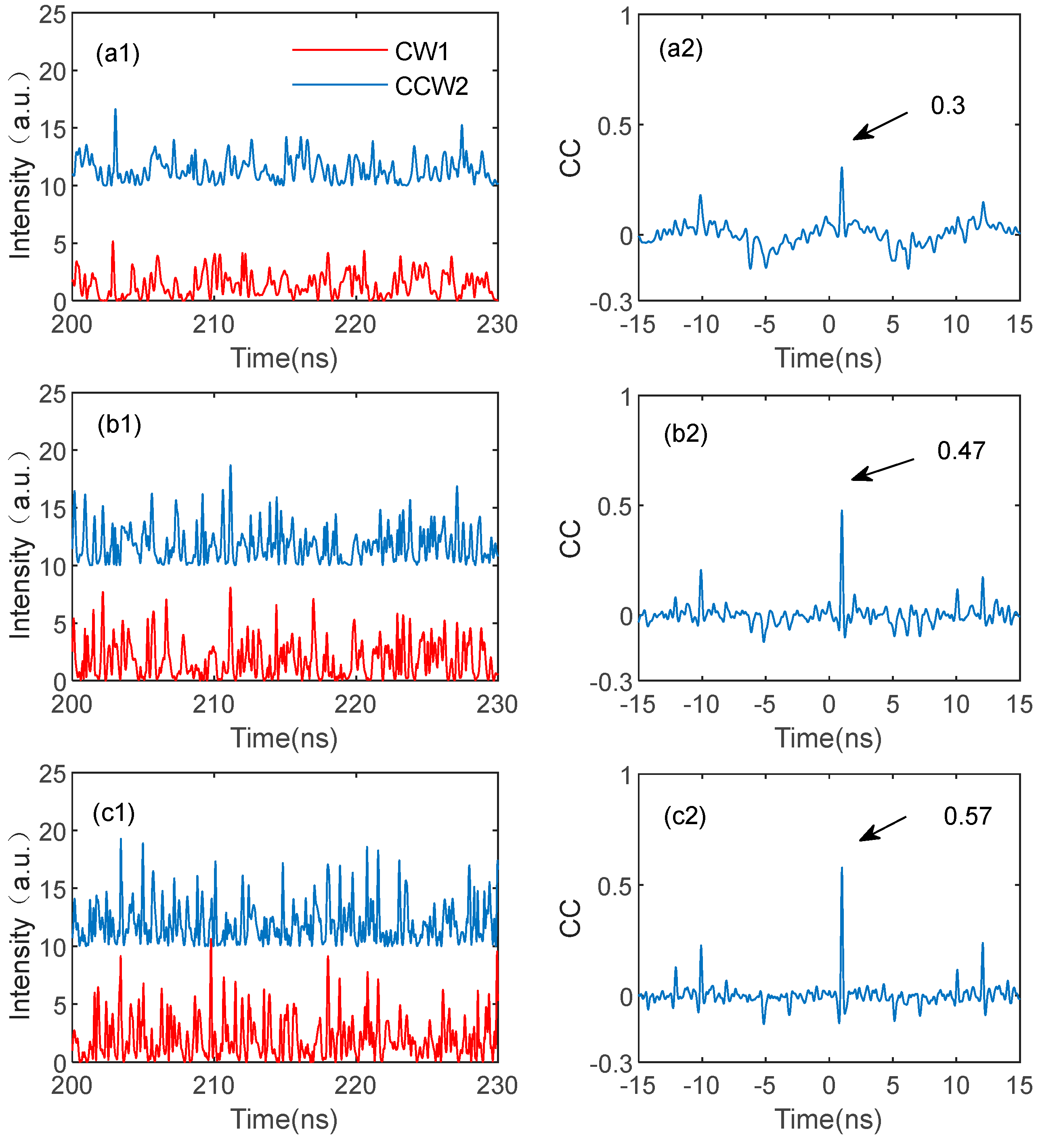
3.2.1. Isochronal Chaos Synchronization Between the Same Modes (ICSS)
3.2.2. Isochronal Chaos Synchronization Between Different Modes (ICSD)
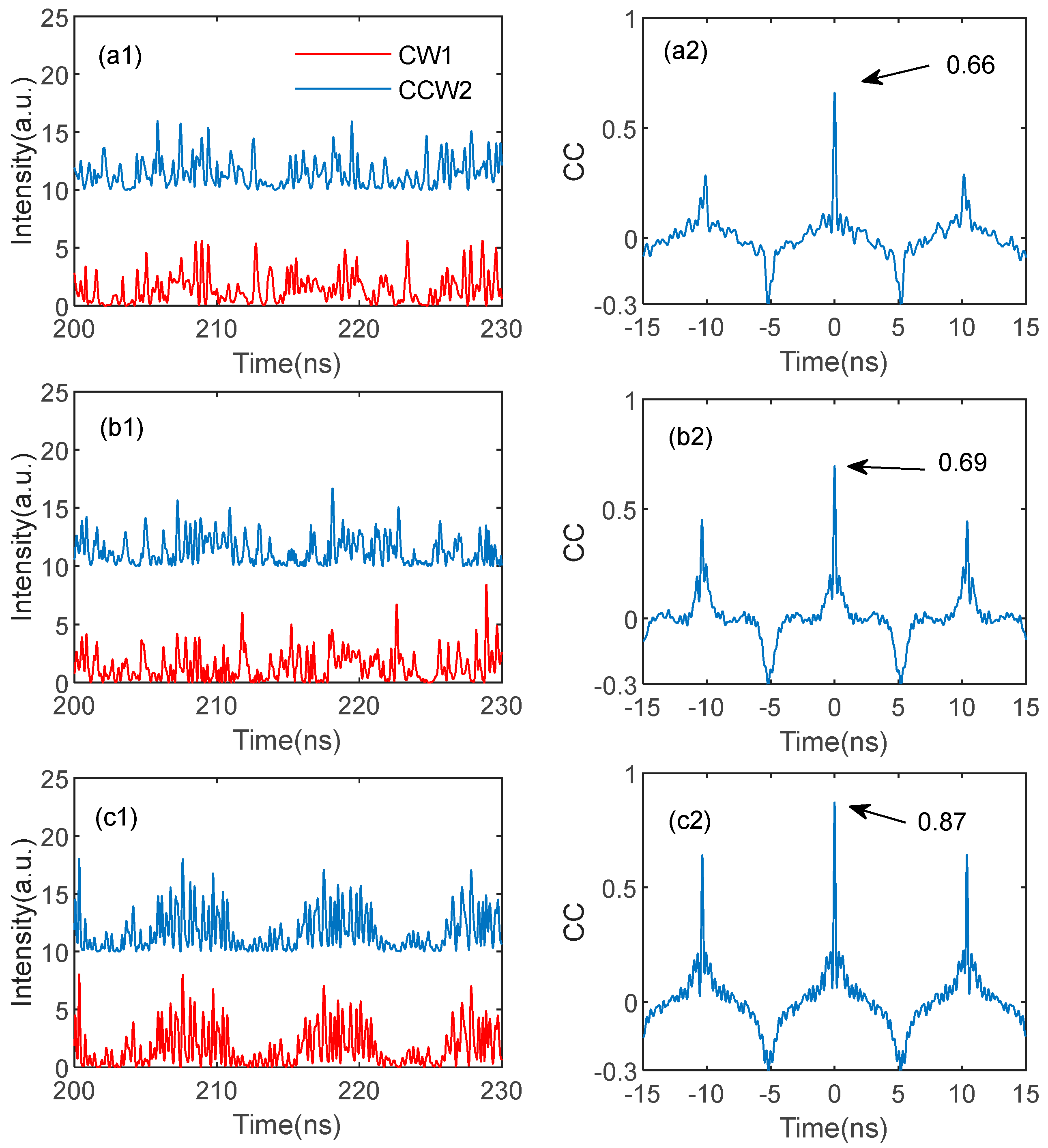
3.2.3. Leader-Laggard Chaos Synchronization Between Different Modes (LLCSD)
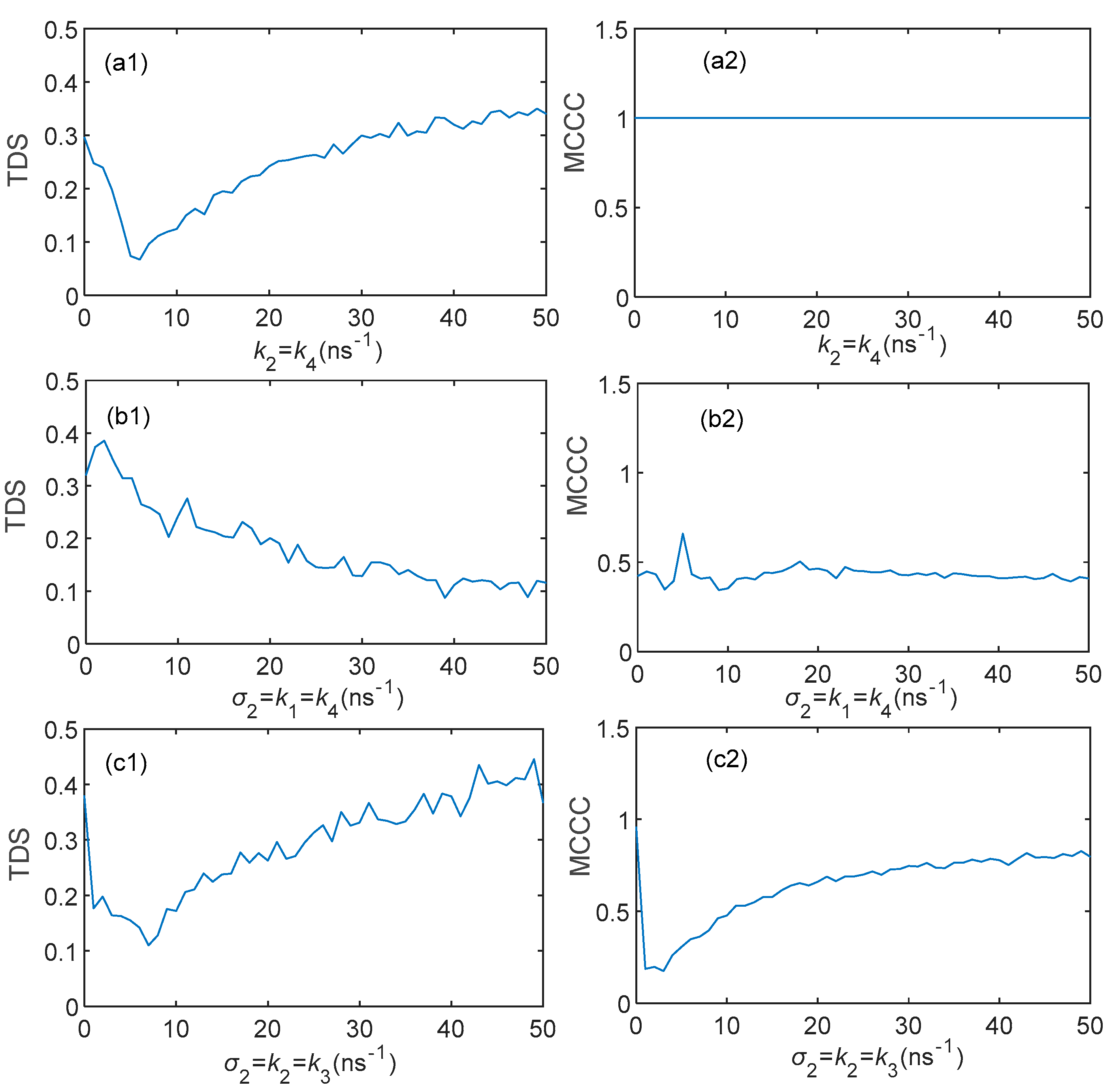
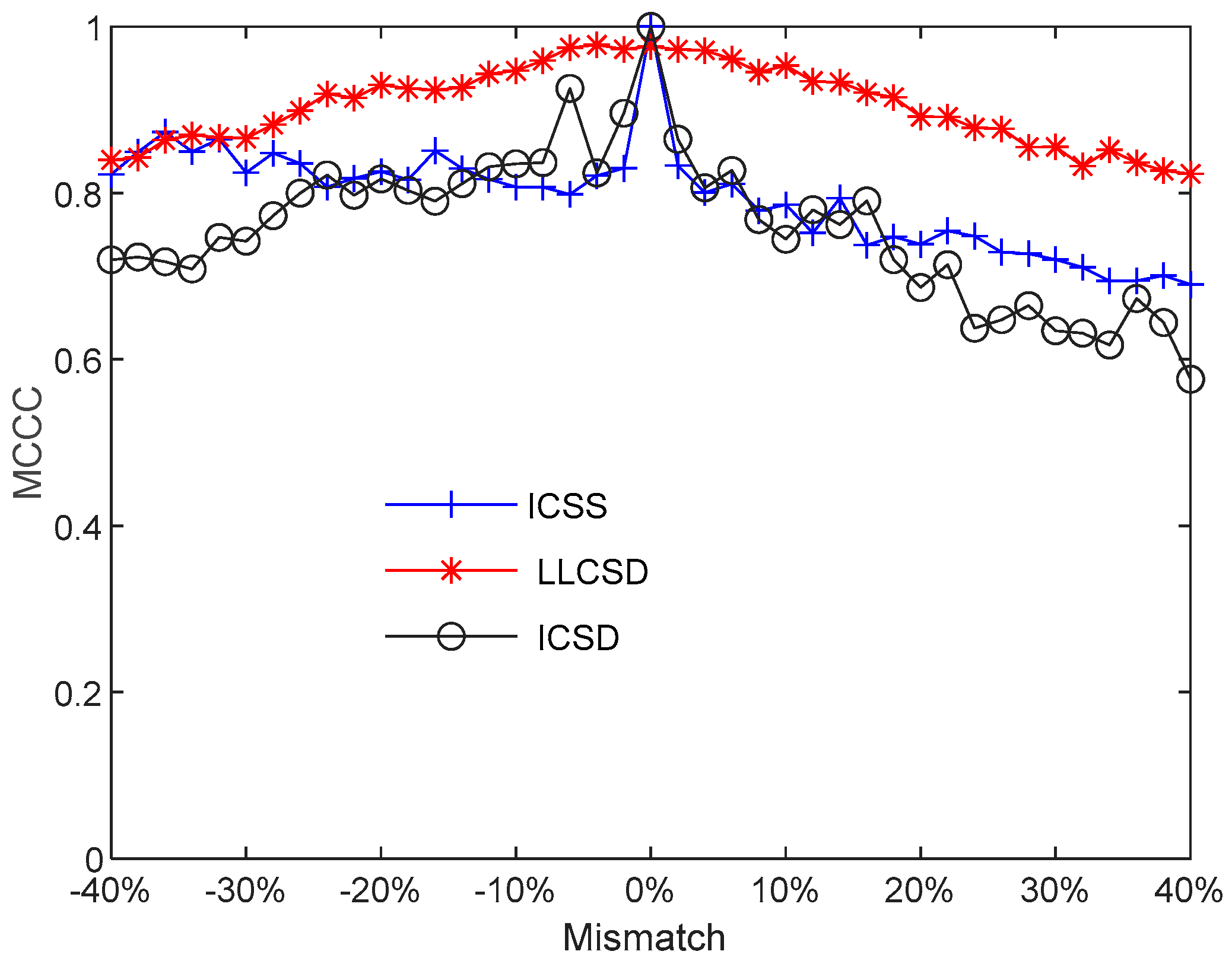
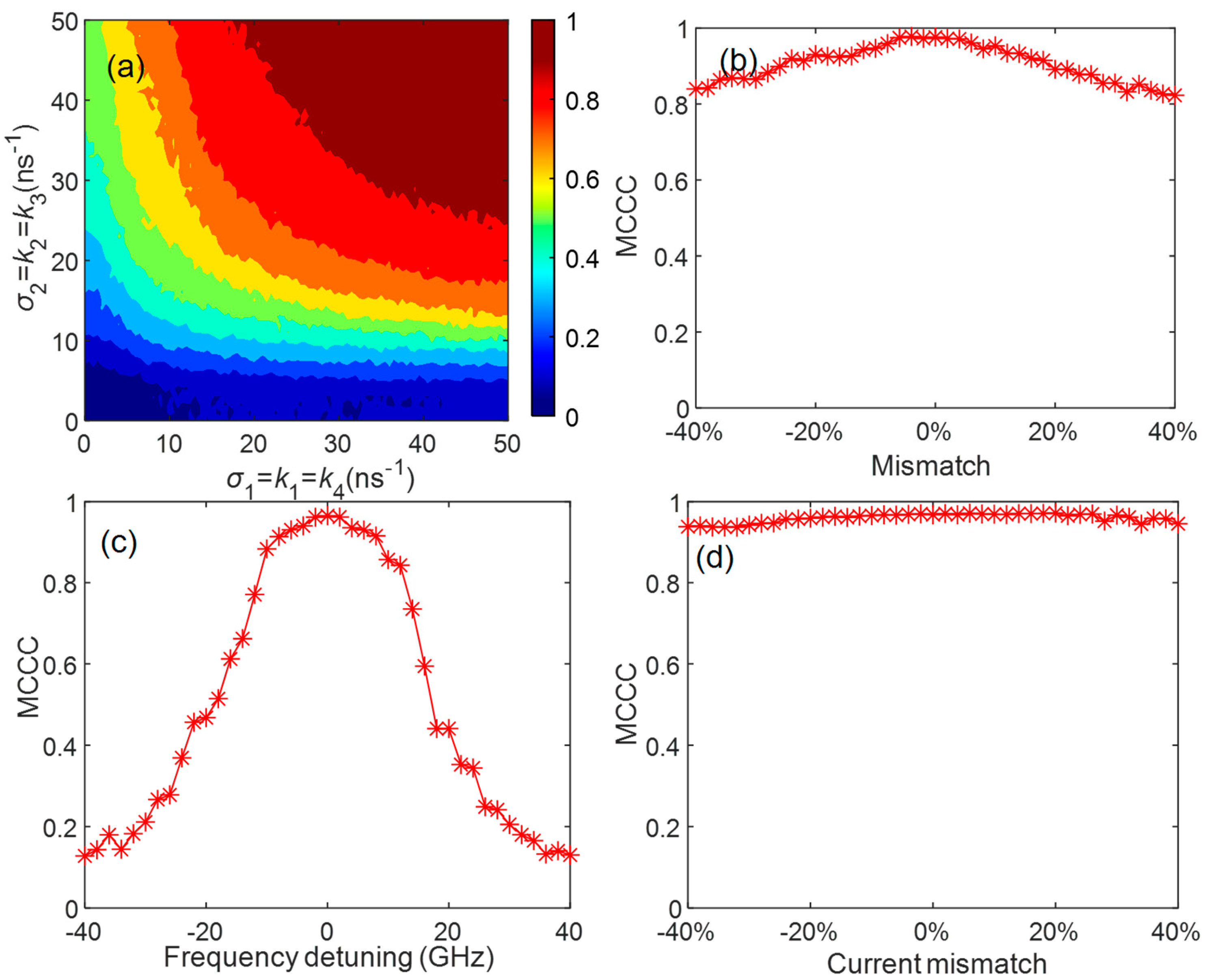
3.3. Effect of Parameter Mismatch on Three Chaos Synchronization Modes
3.4. The Impact of Noise on the Synchronization Performance of LLCSD
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MISRLs | Mutually injected semiconductor ring lasers |
| SRLs | Semiconductor ring lasers |
| SLs | Semiconductor lasers |
| CCW | Counter-clockwise |
| CW | Clockwise |
| ICSS | Isochronal chaos synchronization between the same modes |
| ICSD | Isochronal chaos synchronization between different modes |
| LLCSD | Leader-laggard chaos synchronization between different modes |
| CC | Cross-correlation |
| MCCC | Maximum cross-correlation coefficient |
References
- Pecora, L.M.; Carroll, T.L. Synchronization in Chaotic Systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex Photonics: Dynamics and Applications of Delay-Coupled Semiconductors Lasers. Rev. Mod. Phys. 2013, 85, 421–470. [Google Scholar] [CrossRef]
- Ke, J.; Yi, L.; Xia, G.; Hu, W. Chaotic Optical Communications over 100-Km Fiber Transmission at 30-Gb/s Bit Rate. Opt. Lett. 2018, 43, 1323. [Google Scholar] [CrossRef] [PubMed]
- Sciamanna, M.; Shore, K.A. Physics and Applications of Laser Diode Chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Donati, S.; Horng, R.-H. The Diagram of Feedback Regimes Revisited. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1500309. [Google Scholar] [CrossRef]
- Kelleher, B.; Wishon, M.J.; Locquet, A.; Goulding, D.; Tykalewicz, B.; Huyet, G.; Viktorov, E.A. Delay Induced High Order Locking Effects in Semiconductor Lasers. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 114325. [Google Scholar] [CrossRef]
- Fischer, A.P.A.; Andersen, O.K.; Yousefi, M.; Stolte, S.; Lenstra, D. Experimental and Theoretical Study of Filtered Optical Feedback in a Semiconductor Laser. IEEE J. Quantum Electron. 2000, 36, 375–384. [Google Scholar] [CrossRef]
- Fischer, A.P.A.; Yousefi, M.; Lenstra, D.; Carter, M.W.; Vemuri, G. Experimental and Theoretical Study of Semiconductor Laser Dynamics Due to Filtered Optical Feedback. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 944–954. [Google Scholar] [CrossRef]
- Naumenko, A.; Besnard, P.; Loiko, N.; Ughetto, G.; Bertreux, J.C. Characteristics of a Semiconductor Laser Coupled with a Fiber Bragg Grating with Arbitrary Amount of Feedback. IEEE J. Quantum Electron. 2003, 39, 1216–1228. [Google Scholar] [CrossRef]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; García-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-Based Communications at High Bit Rates Using Commercial Fibre-Optic Links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Ke, J.; Yi, L.; Yang, Z.; Yang, Y.; Zhuge, Q.; Chen, Y.; Hu, W. 32 Gb/s Chaotic Optical Communications by Deep-Learning-Based Chaos Synchronization. Opt. Lett. 2019, 44, 5776–5779. [Google Scholar] [CrossRef] [PubMed]
- Zhao, A.; Jiang, N.; Liu, S.; Zhang, Y.; Qiu, K. Generation of Synchronized Wideband Complex Signals and Its Application in Secure Optical Communication. Opt. Express 2020, 28, 23363–23373. [Google Scholar] [CrossRef] [PubMed]
- Zhong, D.; Yang, H.; Xi, J.; Zeng, N.; Xu, Z. Exploring New Chaotic Synchronization Properties in the Master-Slave Configuration Based on Three Laterally Coupled Semiconductor Lasers with Self-Feedback. Opt. Express 2020, 28, 25778–25794. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, P.; Jia, Z.; Wang, W.; Xu, B.; Shore, K.A.; Wang, Y. Synchronization of Polarization Chaos in Mutually Coupled Free-Running VCSELs. Opt. Express 2021, 29, 17940–17950. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, N.; Zhang, Y.; Wang, C.; Zhao, A.; Qiu, K.; Zhang, Q. Secure Key Distribution Based on Hybrid Chaos Synchronization between Semiconductor Lasers Subject to Dual Injections. Opt. Express 2022, 30, 32366–32380. [Google Scholar] [CrossRef]
- Chlouverakis, K.E.; Mikroulis, S.; Stamataki, I.; Syvridis, D. Chaotic Dynamics of Semiconductor Microring Lasers. Opt. Lett. 2007, 32, 2912–2914. [Google Scholar] [CrossRef]
- Ermakov, I.V.; Van Der Sande, G.; Danckaert, J. Semiconductor Ring Laser Subject to Delayed Optical Feedback: Bifurcations and Stability. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4767–4779. [Google Scholar] [CrossRef]
- Takougang Kingni, S.; Van Der Sande, G.; Gelens, L.; Erneux, T.; Danckaert, J. Direct Modulation of Semiconductor Ring Lasers: Numerical and Asymptotic Analysis. J. Opt. Soc. Am. B 2012, 29, 1983–1992. [Google Scholar] [CrossRef]
- Meng, B.; Singleton, M.; Hillbrand, J.; Franckié, M.; Beck, M.; Faist, J. Dissipative Kerr Solitons in Semiconductor Ring Lasers. Nat. Photonics 2022, 16, 142–147. [Google Scholar] [CrossRef]
- Mu, P.; Wang, K.; Liu, G.; Wang, Y.; Liu, X.; Guo, G.; Hu, G. Spike Dynamics Analysis in Semiconductor Ring Laser. Electronics 2024, 13, 260. [Google Scholar] [CrossRef]
- Mashal, L.; Nguimdo, R.M.; Van Der Sande, G.; Soriano, M.C.; Danckaert, J.; Verschaffelt, G. Low-Frequency Fluctuations in Semiconductor Ring Lasers with Optical Feedback. IEEE J. Quantum Electron. 2013, 49, 790–797. [Google Scholar] [CrossRef]
- Kacmoli, S.; Sivco, D.L.; Gmachl, C.F. Unidirectional Mode Selection in Bistable Quantum Cascade Ring Lasers. Opt. Express 2022, 30, 47475–47484. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Pan, W.; Xiang, S.; Luo, B.; Yan, L.; Zou, X. Hybrid Chaos-Based Communication System Consisting of Three Chaotic Semiconductor Ring Lasers. Appl. Opt. 2013, 52, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Pan, W.; Yan, L.; Luo, B.; Zou, X. Enhanced Chaos Synchronization and Communication in Cascade-Coupled Semiconductor Ring Lasers. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1874–1883. [Google Scholar] [CrossRef]
- Li, J.; Xiang, S.; Wang, H.; Gong, J.; Wen, A. A Novel Image Encryption Algorithm Based on Synchronized Random Bit Generated in Cascade-Coupled Chaotic Semiconductor Ring Lasers. Opt. Lasers Eng. 2018, 102, 170–180. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, X.; Wang, Z. Generation and Synchronization of Feedback-Induced Chaos in Semiconductor Ring Lasers by Injection-Locking. Optik 2014, 125, 1950–1953. [Google Scholar] [CrossRef]
- Sorel, M.; Giuliani, G.; Scire, A.; Miglierina, R.; Donati, S.; Laybourn, P.J.R. Operating Regimes of Gaas-Algaas Semiconductor Ring Lasers: Experiment and Model. IEEE J. Quantum Electron. 2003, 39, 1187–1195. [Google Scholar] [CrossRef]
- Ermakov, I.V.; Kingni, S.T.; Tronciu, V.Z.; Danckaert, J. Chaotic Semiconductor Ring Lasers Subject to Optical Feedback: Applications to Chaos-Based Communications. Opt. Commun. 2013, 286, 265–272. [Google Scholar] [CrossRef]
- Scire, A.; Perez, A.; Perez, T.; Van Der Sande, G.; Colet, P.; Mirasso, C.R.; Balle, S. Bistability and All-Optical Switching in Semiconductor Ring Lasers. In Proceedings of the 2007 9th International Conference on Transparent Optical Networks, Rome, Italy, 1–5 July 2007; IEEE: Rome, Italy, 2007; pp. 21–24. [Google Scholar]
- Chiang, M.C.; Chen, H.-F.; Liu, J.-M. Synchronization of Mutually Coupled Systems. Opt. Commun. 2006, 261, 86–90. [Google Scholar] [CrossRef]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van Der Sande, G. Loss of Time-Delay Signature in Chaotic Semiconductor Ring Lasers. Opt. Lett. 2012, 37, 2541–2543. [Google Scholar] [CrossRef]
- Ortín, S.; Gutiérrez, J.M.; Pesquera, L.; Vasquez, H. Nonlinear Dynamics Extraction for Time-Delay Systems Using Modular Neural Networks Synchronization and Prediction. Phys. Stat. Mech. Its Appl. 2005, 351, 133–141. [Google Scholar] [CrossRef]
- Wang, D.; Wang, L.; Zhao, T.; Gao, H.; Wang, Y.; Chen, X.; Wang, A. Time Delay Signature Elimination of Chaos in a Semiconductor Laser by Dispersive Feedback from a Chirped FBG. Opt. Express 2017, 25, 10911–10924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Pan, W.; Yan, L.; Luo, B.; Zou, X.; Xiang, S.; Li, N. Conceal Time-Delay Signature of Mutually Coupled Vertical-Cavity Surface-Emitting Lasers by Variable Polarization Optical Injection. IEEE Photonics Technol. Lett. 2012, 24, 1693–1695. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M.; Wang, A.; Zhang, M.; Ji, Y.; Wang, Y. Time-Delay-Signature-Suppressed Broadband Chaos Generated by Scattering Feedback and Optical Injection. Appl. Opt. 2018, 57, 6314–6317. [Google Scholar] [CrossRef]
- Wang, A.; Yang, Y.; Wang, B.; Zhang, B.; Li, L.; Wang, Y. Generation of Wideband Chaos with Suppressed Time-Delay Signature by Delayed Self-Interference. Opt. Express 2013, 21, 8701–8710. [Google Scholar] [CrossRef]
- Xiang, S.; Wen, A.; Shang, L.; Zhang, H.; Lin, L. Time-Delay Signatures in Chaotic Semiconductor Ring Lasers with Cross Mutual Injection. In Proceedings of the 2013 12th International Conference on Optical Communications and Networks (ICOCN), Chengdu, China, 26–28 July 2013; IEEE: Rome, Italy, 2013; pp. 1–4. [Google Scholar]
- Wang, Y.; Wang, X.; Mu, P.; Guo, G.; Liu, X.; Wang, K.; He, P.; Hu, G.; Jin, G. Influence of Linewidth Enhancement Factor on the Nonlinear Dynamics and TDS Concealment of Semiconductor Ring Lasers. Electronics 2022, 11, 2007. [Google Scholar] [CrossRef]
- Klein, E.; Gross, N.; Rosenbluh, M.; Kinzel, W.; Khaykovich, L.; Kanter, I. Stable Isochronal Synchronization of Mutually Coupled Chaotic Lasers. Phys. Rev. E 2005, 73, 066214. [Google Scholar] [CrossRef]
- Klein, E.; Gross, N.; Kopelowitz, E.; Rosenbluh, M.; Khaykovich, L.; Kinzel, W.; Kanter, I. Public-Channel Cryptography Based on Mutual Chaos Pass Filters. Phys. Rev. E 2006, 74, 046201. [Google Scholar] [CrossRef]
- Bogris, A.; Rizomiliotis, P.; Chlouverakis, K.E.; Argyris, A.; Syvridis, D. Feedback Phase in Optically Generated Chaos: A Secret Key for Cryptographic Applications. IEEE J. Quantum Electron. 2008, 44, 119–124. [Google Scholar] [CrossRef]


| Symbol | Description | Value |
|---|---|---|
| κ | Field decay rate | 100 ns−1 |
| s | Self-saturation coefficient | 0.005 |
| c | Cross-saturation coefficient | 0.01 |
| α | Linewidth enhancement factor | 3.5 |
| γ | Carrier inversion decay rate | 0.2 ns−1 |
| kd | Dissipative coupling rate | 0.033 ns−1 |
| kc | Conservative coupling rate | 0.44 ns−1 |
| ω | Free-running angular frequency | 1.216 × 1015 rad/s |
| µ | Renormalized bias current | 3.5 |
| τp | Photon lifetime | 10 ps |
| β | Spontaneous emission coefficient | 5 × 10−3 ns−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Jiang, Z.; Zhang, D.; Wang, J. Dual-Channel Chaos Synchronization in Two Mutually Injected Semiconductor Ring Lasers. Photonics 2025, 12, 348. https://doi.org/10.3390/photonics12040348
Tang R, Jiang Z, Zhang D, Wang J. Dual-Channel Chaos Synchronization in Two Mutually Injected Semiconductor Ring Lasers. Photonics. 2025; 12(4):348. https://doi.org/10.3390/photonics12040348
Chicago/Turabian StyleTang, Ruiyi, Zaifu Jiang, Dingmei Zhang, and Jinhui Wang. 2025. "Dual-Channel Chaos Synchronization in Two Mutually Injected Semiconductor Ring Lasers" Photonics 12, no. 4: 348. https://doi.org/10.3390/photonics12040348
APA StyleTang, R., Jiang, Z., Zhang, D., & Wang, J. (2025). Dual-Channel Chaos Synchronization in Two Mutually Injected Semiconductor Ring Lasers. Photonics, 12(4), 348. https://doi.org/10.3390/photonics12040348




