Tunable Slow Light in Valley-Locked Topological Photonic Crystal Waveguide
Abstract
1. Introduction
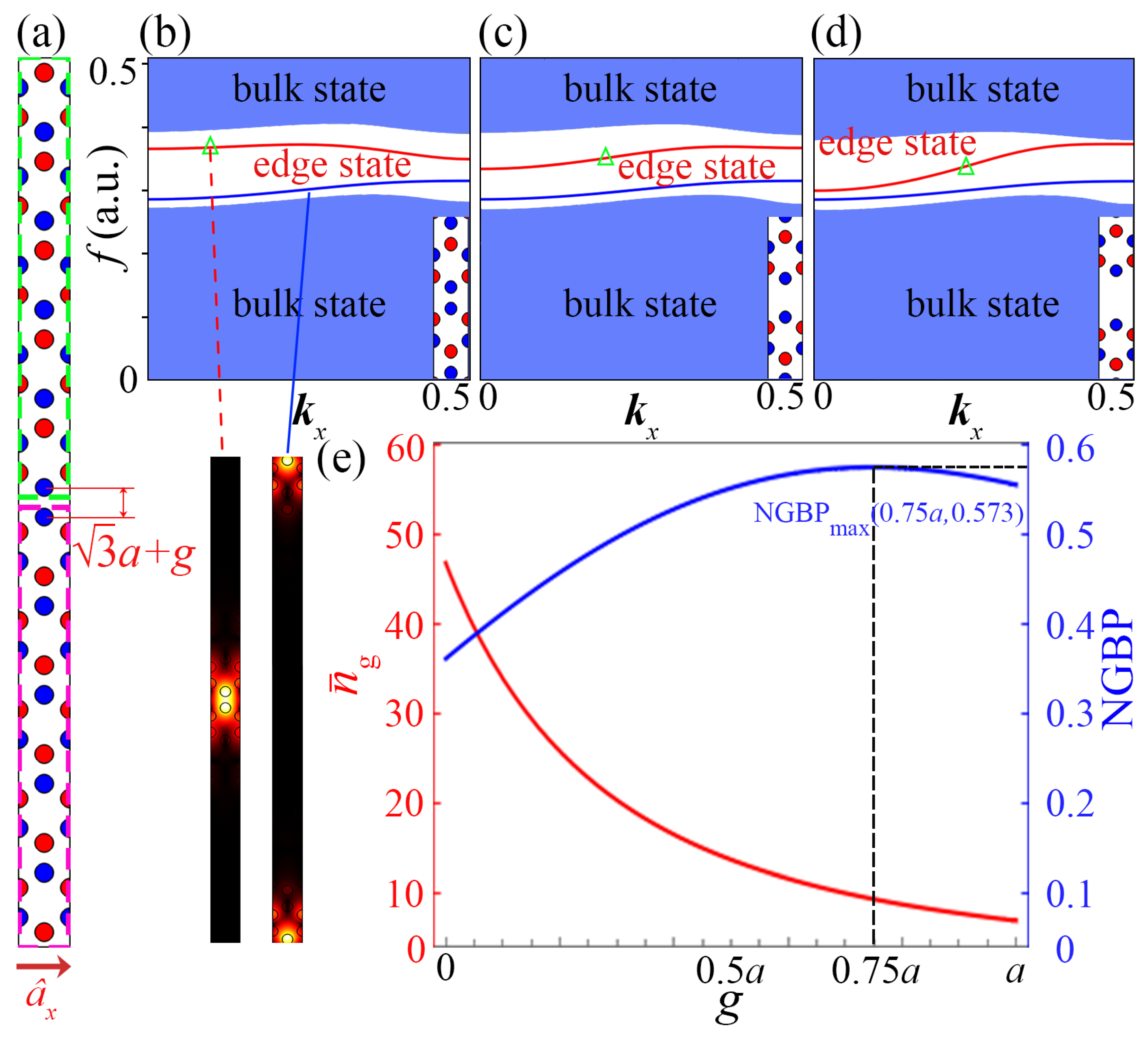
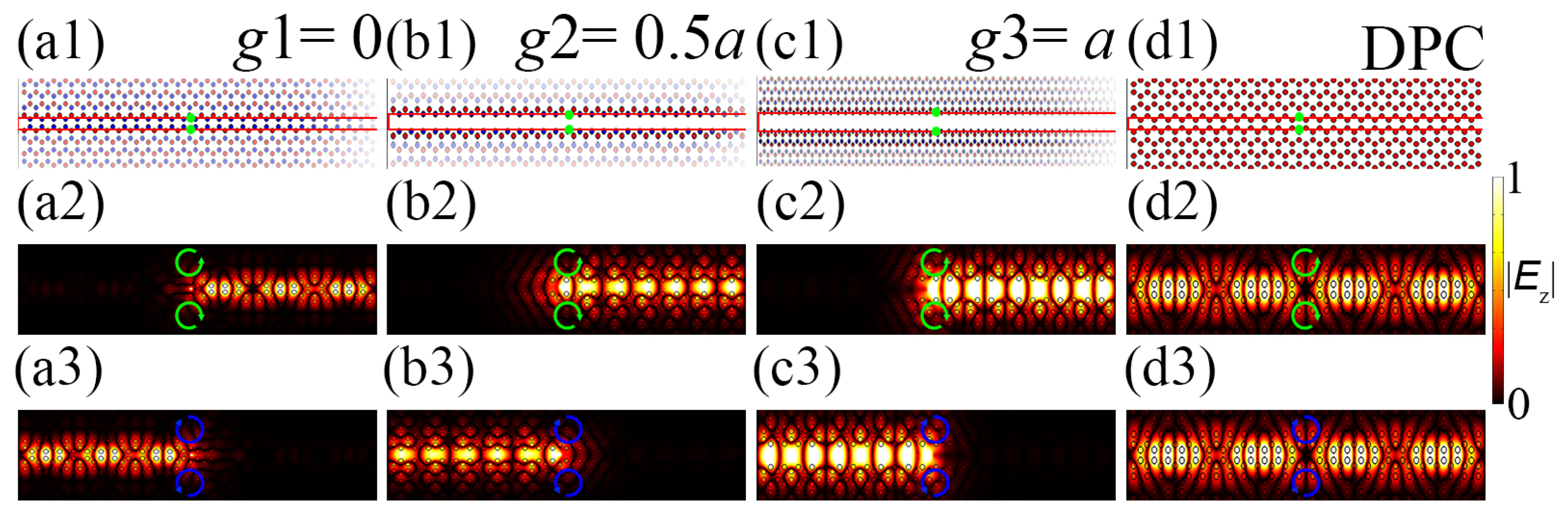
2. Design of the Topologically Protected PhC Waveguides
3. Tunable Slow Light in Valley-Locked PhC Waveguides
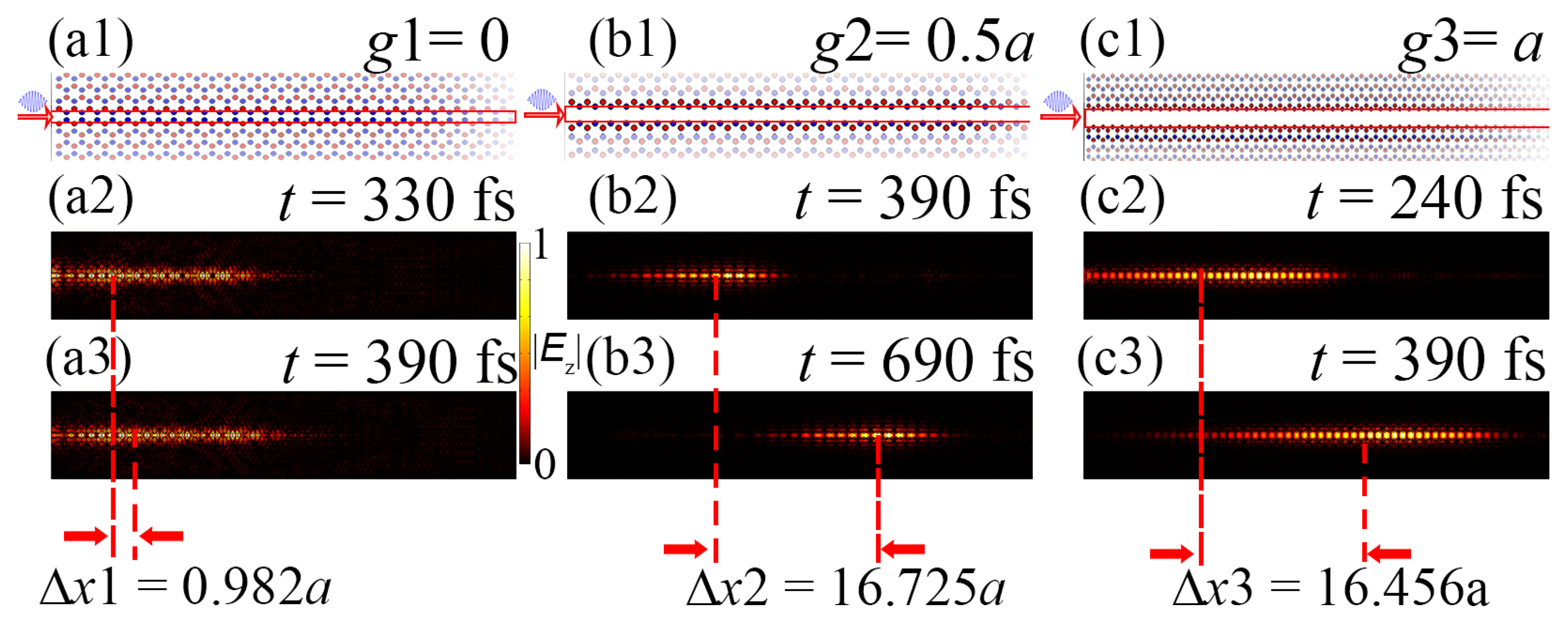
4. Topological Transmission Characteristics of Valley-Locked PhC Slow-Light Waveguides
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PhC | photonic crystal |
| VTPC | Valley Topological Photonic Crystal |
| NGBP | normalized group index–bandwidth product |
Appendix A. Group Index and Bandwidth Variation with g
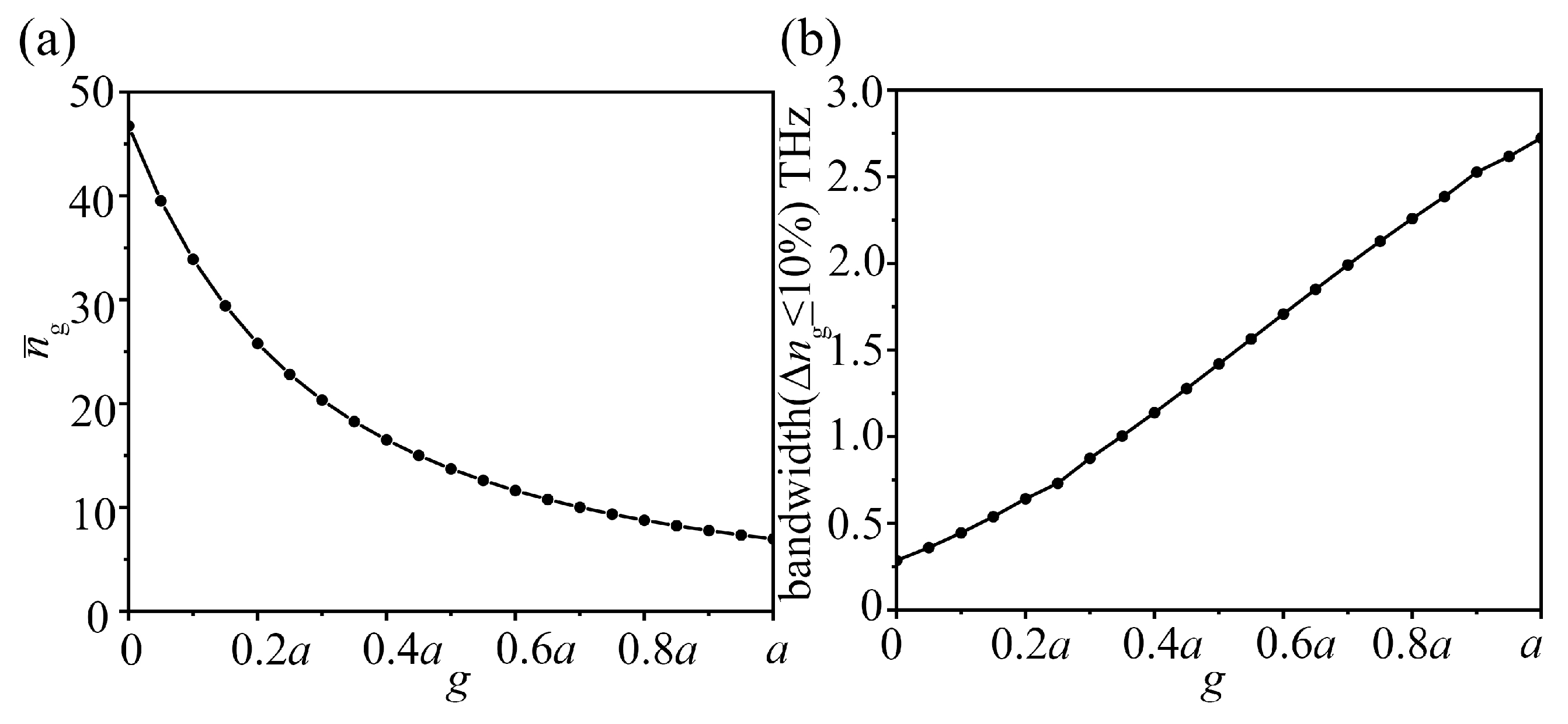
Appendix B. Chiral Validation Calculations of PhC Waveguide for More g Parameters
References
- Haldane, F.D.M.; Raghu, S. Photonic topological insulators. Nat. Photonics 2013, 6, 58–62. [Google Scholar] [CrossRef]
- Maczewsky, L.J.; Zeuner, J.M.; Nolte, S.; Szameit, A. Observation of photonic anomalous Floquet topological insulators. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photonics 2017, 11, 763–773. [Google Scholar] [CrossRef]
- Lu, C.; Sun, Y.Z.; Wang, C.; Zhang, H.; Zhao, W.; Hu, X.; Xiao, M.; Ding, W.; Liu, Y.-C.; Chan, C.T. On-chip nanophotonic topological rainbow. Nat. Commun. 2022, 13, 20236. [Google Scholar] [CrossRef]
- Regnault, N.; Xu, Y.; Li, M.R.; Ma, D.S.; Jovanovic, M.; Yazdani, A.; Parkin, S.S.P.; Felser, C.; Schoop, L.M.; Ong, N.P.; et al. Catalogue of flat-band stoichiometric materials. Nature 2022, 603, 824–828. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.D.; Gao, Z.X.; Cui, X.; Mo, H.C.; Chen, W.J.; Zhang, R.Y.; Chan, C.T.; Dong, J.-W. Realization of Time-Reversal Invariant Photonic Topological Anderson Insulators. Phys. Rev. Lett. 2024, 133, 133802. [Google Scholar] [CrossRef]
- Zhu, W.; Li, L. A brief review of hybrid skin-topological effect. J. Phys. Condens. Matter 2024, 36, 253003. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Jiang, J.; Jiang, H.; Sun, Y.; Yang, Y.; Chen, H.; Guo, Z. Observation of robust polarization conversion via topological edge states in dimer chains. J. Opt. 2025, 27, 045401. [Google Scholar] [CrossRef]
- Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Experiment. Science 2018, 359, 4003. [Google Scholar] [CrossRef]
- Alù, A.; Pilozzi, L.; Xu, H.; Fan, J. Topological photonics and beyond: Introduction. Photonic Res. 2021, 9, TPB1–TPB2. [Google Scholar] [CrossRef]
- Wu, H.C.; Xu, H.S.; Xie, L.C.; Jin, L. Edge State, Band Topology, and Time Boundary Effect in the Fine-Grained Categorization of Chern Insulators. Phys. Rev. Lett. 2024, 132, 083801. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Rechtsman, M.C.; Chong, Y.D. Anomalous Topological Phases and Unpaired Dirac Cones in Photonic Floquet Topological Insulators. Phys. Rev. Lett. 2016, 117, 013902. [Google Scholar] [CrossRef] [PubMed]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.-K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2012, 6, 158–163. [Google Scholar] [CrossRef]
- Wu, L.H.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Kang, Y.; Ni, X.; Cheng, X.; Khanikaev, A.B.; Genack, A.Z. Pseudo-spin–valley coupled edge states in a photonic topological insulator. Nat. Commun. 2018, 9, 3029. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Purtseladze, D.; Smirnova, D.A.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Spin- and valley-polarized one-way Klein tunneling in photonic topological insulators. Sci. Adv. 2018, 4, 8802. [Google Scholar] [CrossRef]
- Bower, E.; Giles, R.F.L.; Martin, A.M. The effects of substrate temperature on the properties of pulsed laser deposited YBCO films. New J. Phys. 2016, 18, 025012. [Google Scholar] [CrossRef]
- He, X.-T.; Liang, E.-T.; Yuan, J.-J.; Qiu, H.-Y.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.-X.; Liang, L.; Zhu, W.; Fan, L.; Lin, Z.-K.; Li, F.; Zhang, X.; Luan, P.-G.; Poo, Y.; et al. Hybrid topological photonic crystals. Nat. Commun. 2023, 14, 4457. [Google Scholar] [CrossRef]
- Cheng, X.; Genack, A.Z.; Khanikaev, A.B. Photonic Topological Insulators: A New Route to Unidirectional Waveguides. Adv. Opt. Mater. 2017, 5, 1700357. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Zhang, Y.Z.; Xiao, S.; Cheshkov, A.; Merai, A.; Shvets, G. Nonlinear light generation in topological nanostructures. Nat. Nanotechnol. 2018, 14, 126. [Google Scholar] [CrossRef]
- Cheng, X.; Genack, A.Z.; Khanikaev, A.B. Nonlinear light generation in topological nanostructures. Appl. Phys. Lett. 2018, 112, 233106. [Google Scholar] [CrossRef]
- Kirsch, M.S.; Zhang, Y.; Kremer, M.; Maczewsky, L.J.; Ivanov, S.K.; Kartashov, Y.V.; Torner, L.; Bauer, D.; Szameit, A.; Heinrich, M. Nonlinear second-order photonic topological insulators. Nat. Phys. 2021, 17, 995–1000. [Google Scholar] [CrossRef]
- Barik, S.; Karasahin, A.; Flower, C.; Cai, T.; Miyake, H.; DeGottardi, W.; Hafezi, M.; Waks, E. A topological quantum optical interface. Science 2018, 359, 666–668. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Z.; Ivanov, S.K.; Kartashov, Y.V.; Torner, L. Nonlinear higher-order polariton topological insulator. Phys. Rev. Lett. 2020, 124, 083603. [Google Scholar] [CrossRef]
- Chen, X.-D.; Deng, W.-M.; Shi, F.-L.; Zhao, F.-L.; Chen, M.; Dong, J.-W. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys. Rev. Lett. 2019, 122, 233902. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Du, L.; Li, P.; Dong, Y.; Tao, L.; Li, Z.; Guo, Y.; Song, K.; Zhao, X. Ultrabroadband valley transmission and corner states in valley photonic crystals with dendritic structure. Commun. Phys. 2024, 7, 214. [Google Scholar] [CrossRef]
- Canyellas, R.; Liu, C.; Arouca, R.; Eek, L.; Wang, G.; Yin, Y.; Guan, D.; Li, Y.; Wang, S.; Zheng, H.; et al. Topological edge and corner states in bismuth fractal nanostructures. Nat. Phys. 2024, 20, 1421–1428. [Google Scholar] [CrossRef]
- Barone, A.; Clementi, M.; Poempool, T.; Marcia, A.; Bajoni, D.; Liscidini, M.; Gerace, D.; Fromherz, T.; Galli, M. Generation of entangled photon pairs from a silicon bichromatic photonic crystal cavity. APL Photonics 2024, 9, 016110. [Google Scholar] [CrossRef]
- Gao, Y.F.; He, Y.H.; Li, Y.; Rouzi, S.; Jin, M.C.; He, Y.; Zhou, S.Y. Topological waveguide-cavity coupling system based on valley photonic crystals. Opt. Laser Technol. 2024, 175, 110799. [Google Scholar] [CrossRef]
- Rechtsman, M.C. Reciprocal topological photonic crystals allow backscattering. Nat. Photonics 2023, 17, 383–384. [Google Scholar] [CrossRef]
- Rosiek, C.A.; Arregui, G.; Vladimirova, A.; Albrechtsen, M.; Vosoughi Lahijani, B.; Christiansen, R.E.; Stobbe, S. Observation of strong backscattering in valley-Hall photonic topological interface modes. Nat. Photonics 2023, 17, 386–392. [Google Scholar] [CrossRef]
- Liu, G.G.; Gao, Z.; Wang, Q.; Xi, X.; Hu, Y.H.; Wang, M.; Liu, C.; Lin, X.; Deng, L.; Yang, S.A.; et al. Topological Chern vectors in three-dimensional photonic crystals. Nature 2023, 609, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liang, W.; Li, Z.Y. Broadband dispersionless topological slow light. Opt. Lett. 2020, 45, 4964–4967. [Google Scholar] [CrossRef]
- Yoshimi, H.; Yamaguchi, T.; Ota, Y.; Arakawa, Y.; Iwamoto, S. Slow light waveguides in topological valley photonic crystals. Opt. Lett. 2020, 45, 2648–2651. [Google Scholar] [CrossRef]
- Chen, Yafeng and Lan, Zhihao and Li, Jensen and Zhu, Jie Topologically protected second harmonic generation via doubly resonant high-order photonic modes. Phys. Rev. B 2021, 104, 155421. [CrossRef]
- Luo, H.; Sohn, S.S.; Lu, W.; Li, L.; Li, X.; Soundararajan, C.K.; Krieger, W.; Li, Z.; Raabe, D. A strong and ductile medium-entropy alloy resists hydrogen embrittlement and corrosion. Nat. Commun. 2020, 11, 3081. [Google Scholar] [CrossRef]
- Kumar, A.; Tan, Y.J.; Navaratna, N.; Gupta, M.; Pitchappa, P.; Singh, R. Slow light topological photonics with counter-propagating waves and its active control on a chip. Nat. Commun. 2024, 15, 926. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Ding, D.S.; Zhang, W.; Zhou, Z.Y.; Shi, S.; Xiang, G.Y.; Wang, X.S.; Jiang, Y.K.; Shi, B.S.; Guo, G.C. Quantum Storage of Orbital Angular Momentum Entanglement in an Atomic Ensemble. Phys. Rev. Lett. 2015, 114, 050502. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Arregui, G.; Gomis-Bresco, J.; Sotomayor-Torres, C.M.; Garcia, P.D. Quantifying the Robustness of Topological Slow Light. Phys. Rev. Lett. 2021, 126, 027403. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Wang, Y. Topological slow light waveguide in photonic valley-locked heterostructures. Phys. Scripta 2023, 98, 065508. [Google Scholar] [CrossRef]
- Luan, E.; Shoman, H.; Ratner, D.M.; Cheung, K.C.; Chrostowski, L. Silicon Photonic Biosensors Using Label-Free Detection. Sensors 2018, 18, 3519. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface Micro/Nano-Optical Sensors: Principles and Applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef] [PubMed]
- Barik, S.; Karasahin, A.; Mittal, S.; Waks, E.; Hafezi, M. Chiral quantum optics using a topological resonator. Phys. Rev. B 2020, 101, 205303. [Google Scholar] [CrossRef]
- Ji, K.; Zhong, Q.; Ge, L.; Beaudoin, G.; Sagnes, I.; Raineri, F.; El-Ganainy, R.; Yacomotti, A.M. Tracking exceptional points above the lasing threshold. Nat. Commun. 2023, 14, 8304. [Google Scholar] [CrossRef]
- Kuramochi, E.; Nozaki, K.; Shinya, A.; Takeda, K.; Sato, T.; Matsuo, S.; Taniyama, H.; Sumikura, H.; Notomi, M. Large-scale integration of wavelength-addressable all-optical memories on a photonic crystal chip. Nat. Photonics 2014, 8, 474–481. [Google Scholar] [CrossRef]
- Zhong, T.; Kindem, J.M.; Bartholomew, J.G.; Rochman, J.; Craiciu, I.; Miyazono, E.; Bettinelli, M.; Cavalli, E.; Verma, V.; Nam, S.W.; et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 2017, 357, 1392–1395. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Wang, Y.; Fei, H.; Lin, H.; Bai, J.; Zhang, M.; Liu, X.; Cao, B.; Tian, Y.; Xiao, L. Ultra-compact electro-optic phase modulator based on a lithium niobate topological slow light waveguide. Opt. Express 2024, 32, 3980. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.D.; Zhao, F.L.; Chen, M.; Dong, J.W. Valley-contrasting physics in all-dielectric photonic crystals: Orbital angular momentum and topological propagation. Phys. Rev. B 2017, 96, 020202. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Yuan, H.; Zhong, J.; Lu, C. Universal numerical calculation method for the Berry curvature and Chern numbers of typical topological photonic crystals. Front. Optoelectron. 2020, 13, 73–88. [Google Scholar] [CrossRef]
- Zhao, R.; Xie, G.-D.; Chen, M.L.N.; Lan, Z.; Huang, Z.; Sha, W.E.I. First-principle calculation of Chern number in gyrotropic photonic crystals. Opt. Express 2020, 28, 4638–4649. [Google Scholar] [CrossRef]
- Hughes, S.; Ramunno, L.; Young, J.F.; Sipe, J.E. Extrinsic optical scattering loss in photonic crystal waveguides: Role of fabrication disorder and photon group velocity. Phys. Rev. Lett. 2005, 94, 033903. [Google Scholar] [CrossRef]
- Mori, D.; Baba, T. Wideband and low dispersion slow light by chirped photonic crystal coupled waveguide. Opt. Express 2005, 13, 9398–9408. [Google Scholar] [CrossRef]
- Liu, S.; Lu, W.; Lin, Z.; Chui, S.T. Magnetically controllable unidirectional electromagnetic waveguiding devices designed with metamaterials. Appl. Phys. Lett. 2010, 97, 201113. [Google Scholar] [CrossRef]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; O’Boyle, M.; Hamann, H.F.; McNab, S.J. Active control of slow light on a chip with photonic crystal waveguides. Nature 2005, 438, 65–69. [Google Scholar] [CrossRef]
- Liang, Y.; Peng, C.; Sakai, K.; Iwahashi, S.; Noda, S. Three-dimensional coupled-wave analysis for square-lattice photonic crystal surface emitting lasers with transverse-electric polarization: Finite-size effects. Opt. Express 2012, 20, 15945. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.J.; Chen, X.D.; Sun, L.; Guo, C.H.; Li, M.Y.; Tian, Z.T.; Chen, H.H.; Wang, H.W.; Sun, Q.Y.; Pan, Y.D.; et al. Broadband and fabrication-tolerant 3-dB couplers with topological valley edge modes. Light. Sci. Appl. 2024, 13, 166. [Google Scholar] [CrossRef]
- Jalali Mehrabad, M.; Foster, A.P.; Martin, N.J.; Dost, R.; Clarke, E.; Patil, P.K.; Skolnick, M.S.; Wilson, L.R. Chiral topological add–drop filter for integrated quantum photonic circuits. Optica 2023, 10, 415. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, M.; Pitchappa, P.; Wang, N.; Szriftgiser, P.; Ducournau, G.; Singh, R. Phototunable chip-scale topological photonics: 160 Gbps waveguide and demultiplexer for THz 6G communication. Nat. Commun. 2022, 13, 5404. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Ji, H.Y.; Wang, Y.J.; Zhang, X.D. Topologically protected beam splitters and logic gates based on two-dimensional silicon photonic crystal slabs. Opt. Express 2020, 28, 34015. [Google Scholar] [CrossRef]
- Wang, H.; Sun, L.; He, Y.; Tang, G.; An, S.; Wang, Z.; Du, Y.; Zhang, Y.; Yuan, L.; He, X.; et al. Asymmetric Topological Valley Edge States on Silicon-On-Insulator Platform. Laser Photonics Rev. 2022, 16, 2100631. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, J.; Gu, L.; Fang, L.; Zhang, Y.; Zhao, J.; Gan, X. Compact on-chip power splitter based on topological photonic crystal. Opt. Mater. Express 2024, 14, 1390. [Google Scholar] [CrossRef]
- Shao, H.; Wang, Y.; Yang, G.; Sang, T. Topological transport in heterostructure of valley photonic crystals. Opt. Express 2023, 31, 32393. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, C.; Li, G.; Yang, J.; Ma, C.; Qi, X. Tunable Slow Light in Valley-Locked Topological Photonic Crystal Waveguide. Photonics 2025, 12, 332. https://doi.org/10.3390/photonics12040332
Peng C, Li G, Yang J, Ma C, Qi X. Tunable Slow Light in Valley-Locked Topological Photonic Crystal Waveguide. Photonics. 2025; 12(4):332. https://doi.org/10.3390/photonics12040332
Chicago/Turabian StylePeng, Chenyang, Gang Li, Junhao Yang, Chunlin Ma, and Xinyuan Qi. 2025. "Tunable Slow Light in Valley-Locked Topological Photonic Crystal Waveguide" Photonics 12, no. 4: 332. https://doi.org/10.3390/photonics12040332
APA StylePeng, C., Li, G., Yang, J., Ma, C., & Qi, X. (2025). Tunable Slow Light in Valley-Locked Topological Photonic Crystal Waveguide. Photonics, 12(4), 332. https://doi.org/10.3390/photonics12040332




