Quantum Entanglement of the Final Particles in the Resonant Trident Pair Production Process in a Strong Electromagnetic Wave
Abstract
1. Introduction
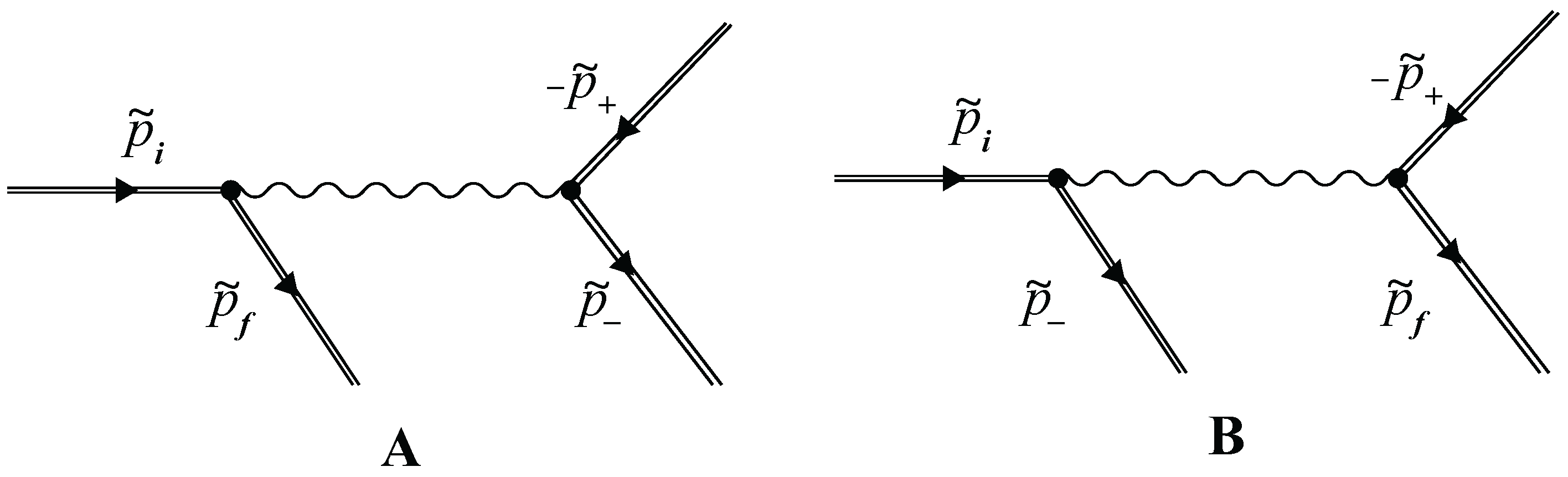
2. Process Amplitude
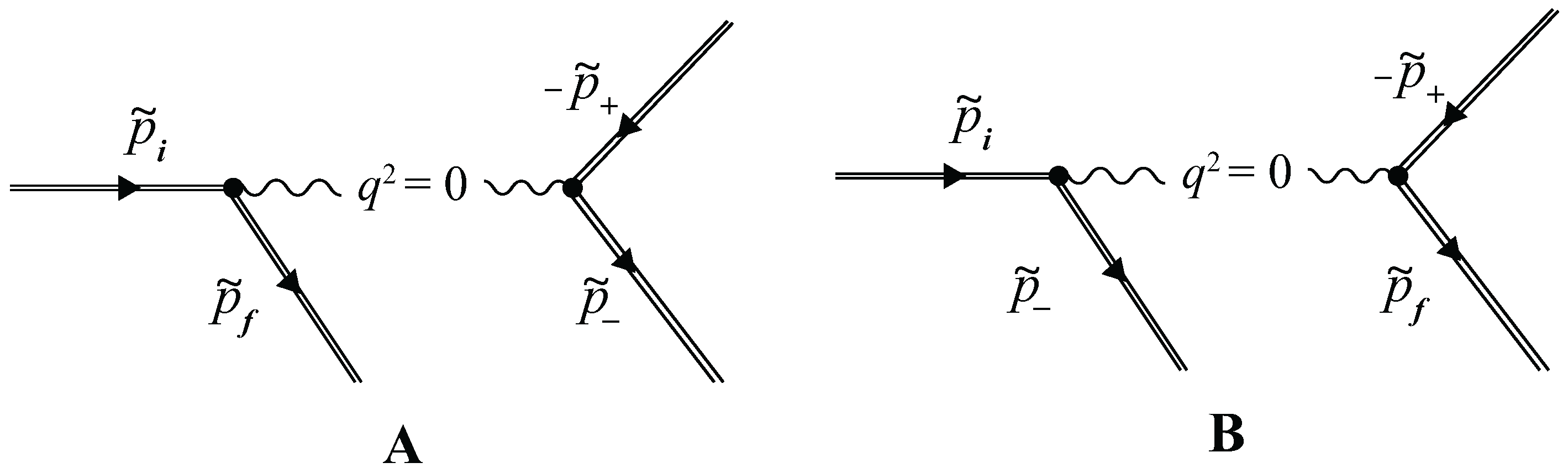
3. Resonant Kinematics
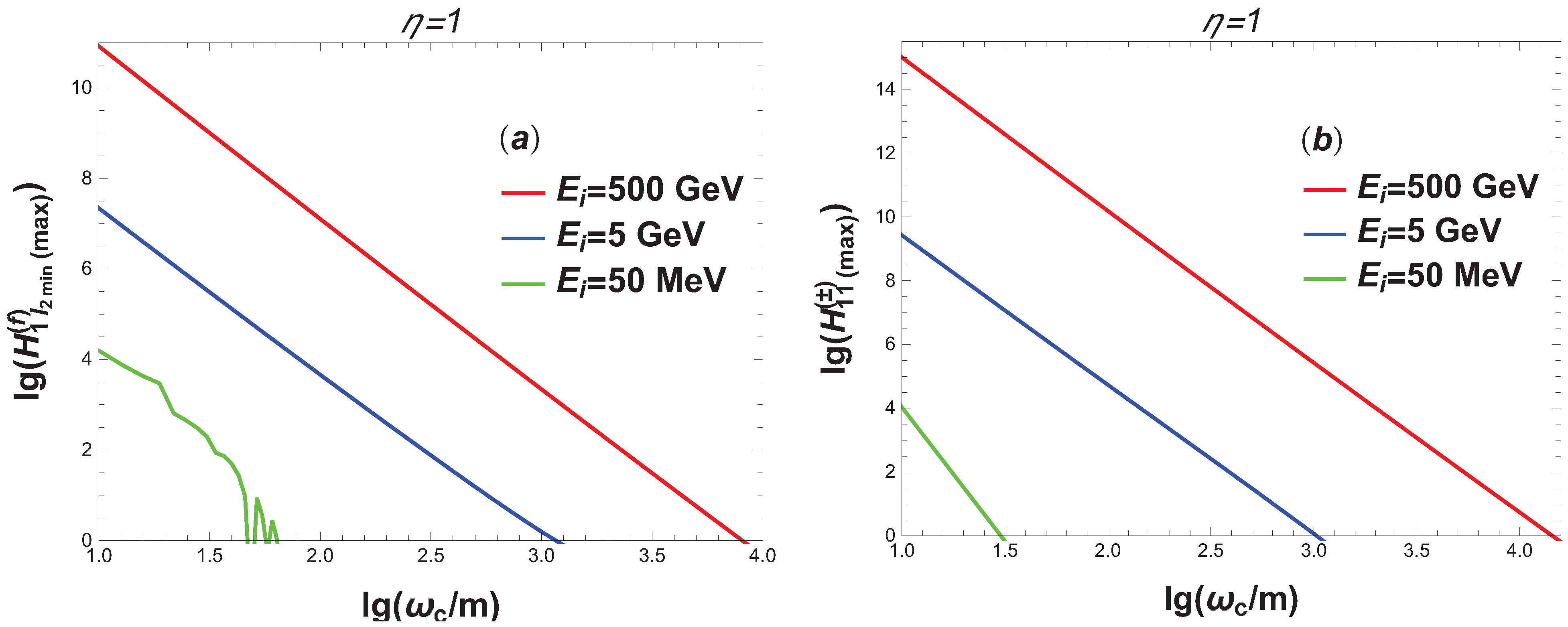
4. Resonant Differential Probability
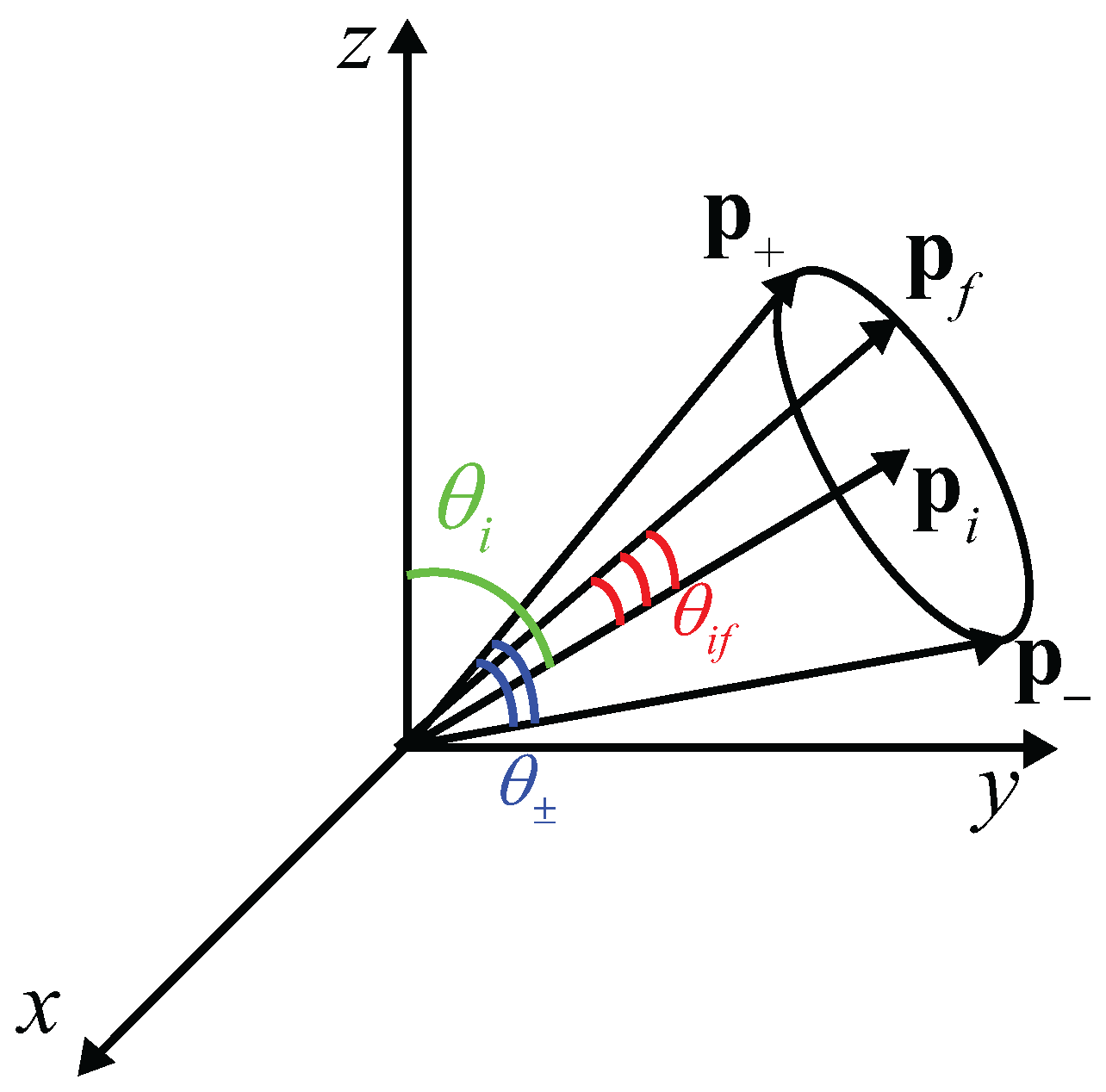
- If the final electron energy on the lower branch and the angle between momenta of the pair on the upper branch are simultaneously recorded :
- If the outgoing angle of the final electron on the lower branch and the outgoing angle of the electron–positron pair on the upper branch are simultaneously recorded :
- If the energy of the electron–positron pair on the lower branch and the outgoing angle of the elecron on the upper branch are simultaneously recorded :
- If the outgoing angle of the electron–positron pair on the lower branch and the outgoing angle of the final electron on the upper branch are simultaneously recorded :
5. Discussion
- Under resonant conditions, the intermediate virtual gamma-quantum becomes real. As a result, the initial second-order process by the fine structure constant in the wave field effectively splits into two first-order processes. In the first vertex, the Compton effect stimulated by an external field occurs, and, in the second vertex, the Breit–Wheeler process stimulated by an external field takes place.
- Due to the laws of the conservation of energy and momentum, the RTPP process can take place in two cases. In the first case, the energies and outgoing angles of the final particles are determined by the Compton effect stimulated by an external field. In the second case, the energies and outgoing angles of the final particles are determined by the Breit–Wheeler process stimulated by an external field. It is important to note that in the RTPP process, electrons and positrons of the pair are generated with equal energies.
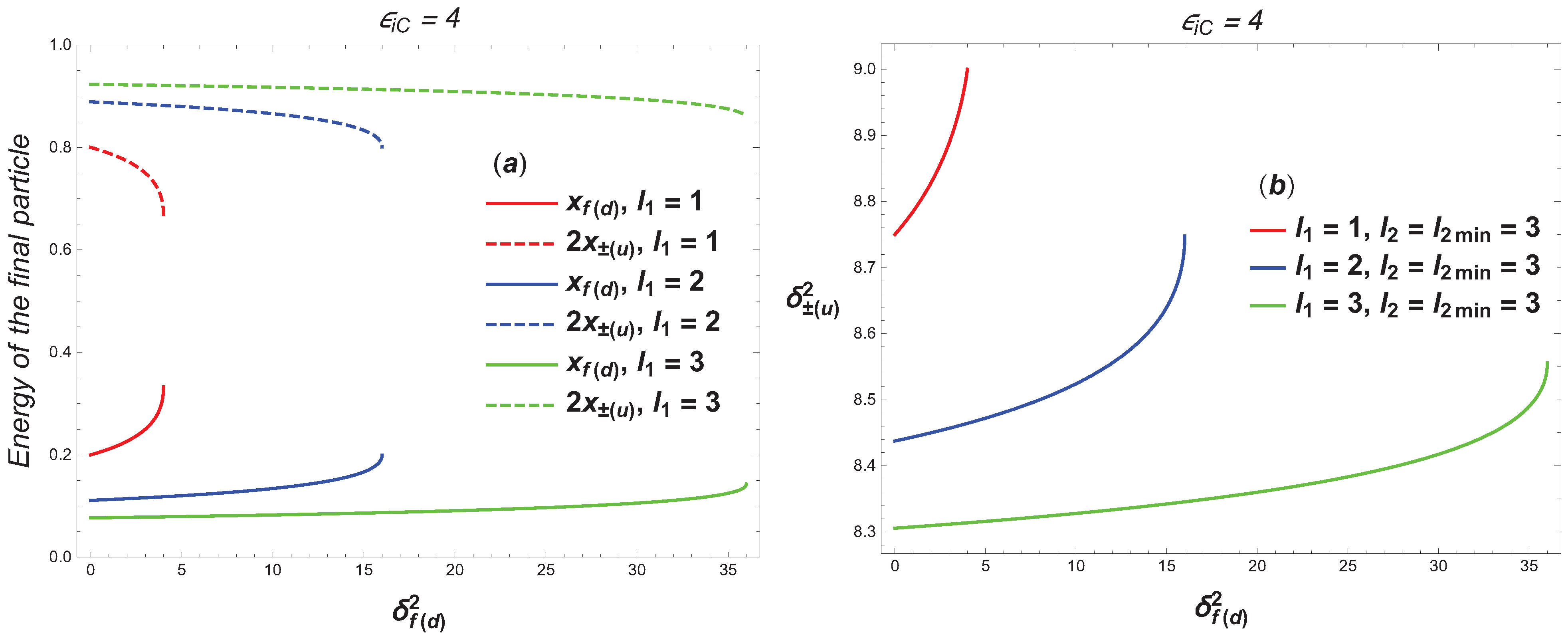
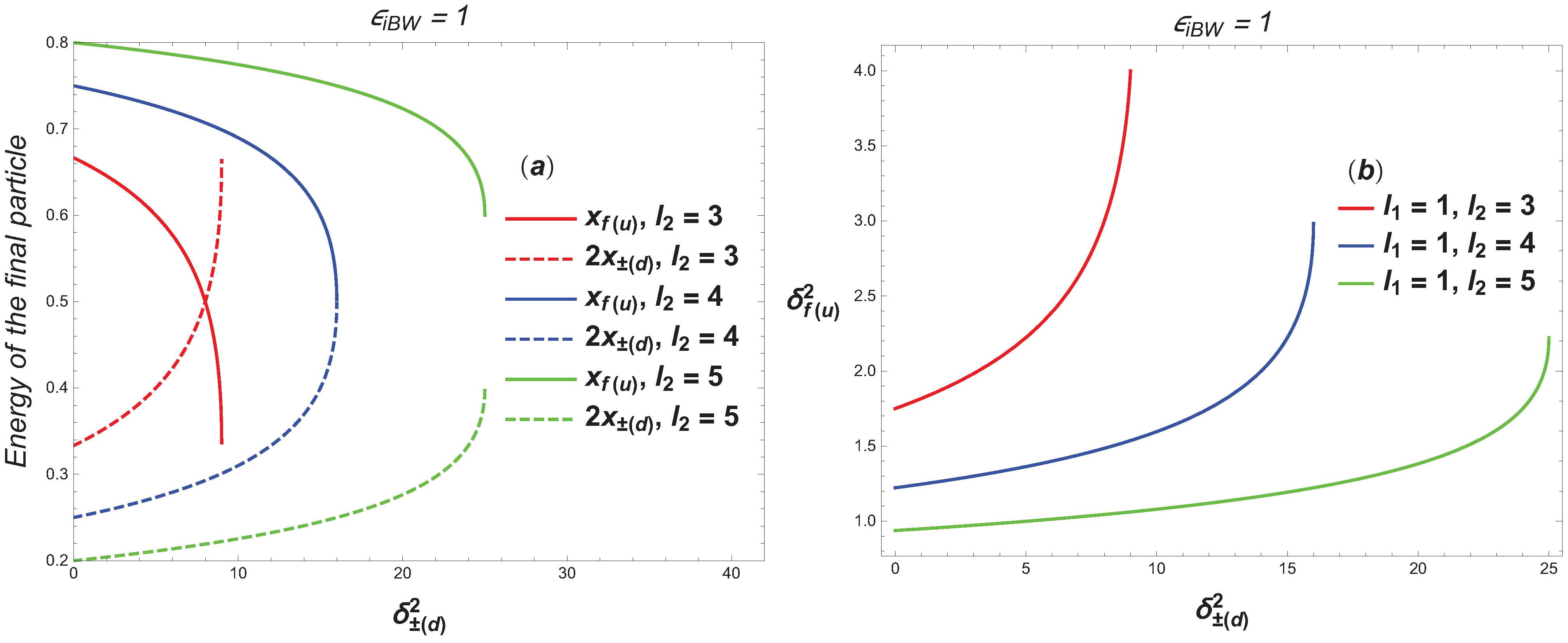
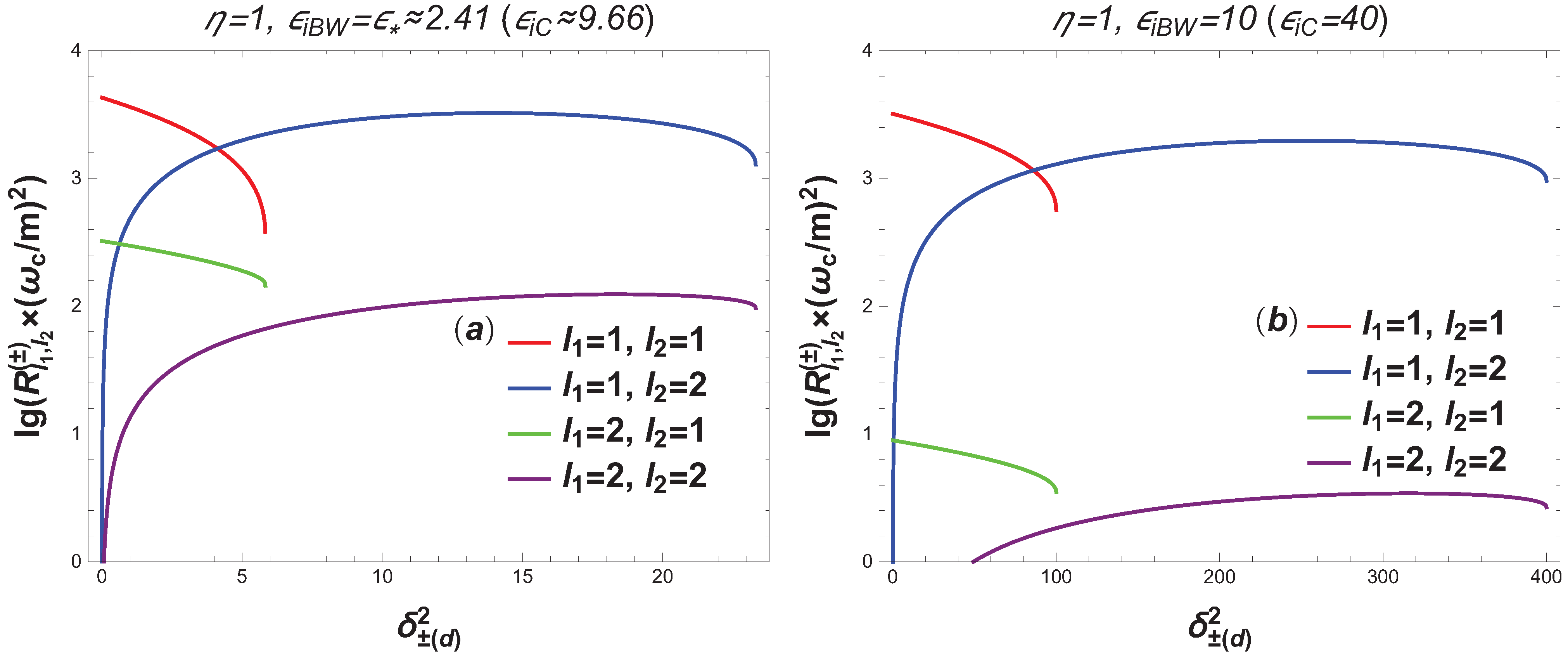
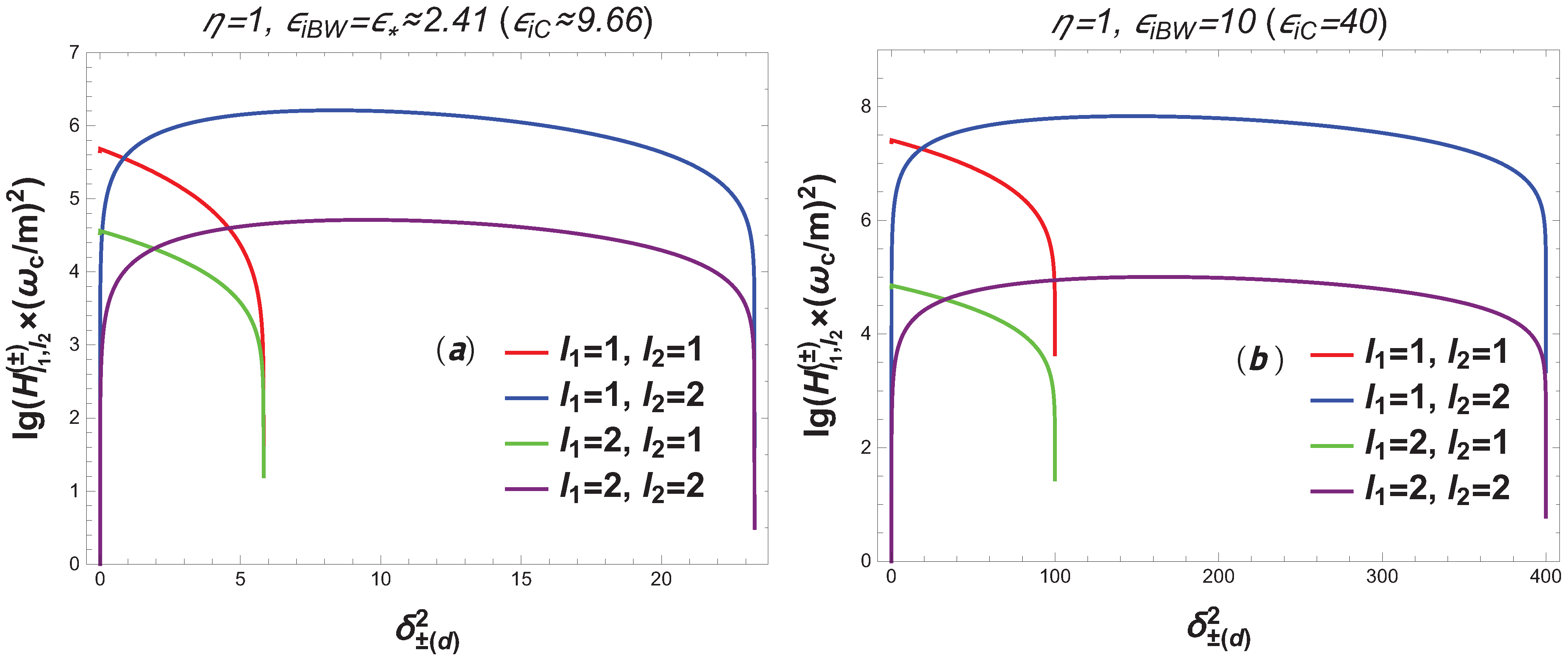
- In the first case, the outgoing angle of the final electron (ultrarelativistic parameter ), the quantum parameter of the Compton effect , and the number of absorbed photons of the wave at the first vertex determine the outgoing angle of the electron–positron pair (ultrarelativistic parameter ), as well as the energies of the electron (on the lower branch), electron–positron pair (on the upper branch), and the number of absorbed photons of the wave at the second vertex . In this case, if the quantum parameter , then the energy of the initial electron basically transforms into the energy of the electron–positron pair.
- In the second case, the outgoing angle of the electron–positron pair (an ultrarelativistic parameter ), as well as the quantum parameter of the Breit–Wheeler process and the number of absorbed photons of the wave at the second vertex , determine the outgoing angle of the electron (an ultrarelativistic parameter ), as well as the energies of the electron–positron pair (on the lower branch) and the electron (on the upper branches). In this case, if the quantum parameter , then the energy of the initial electron transforms to the energy of the final electron.
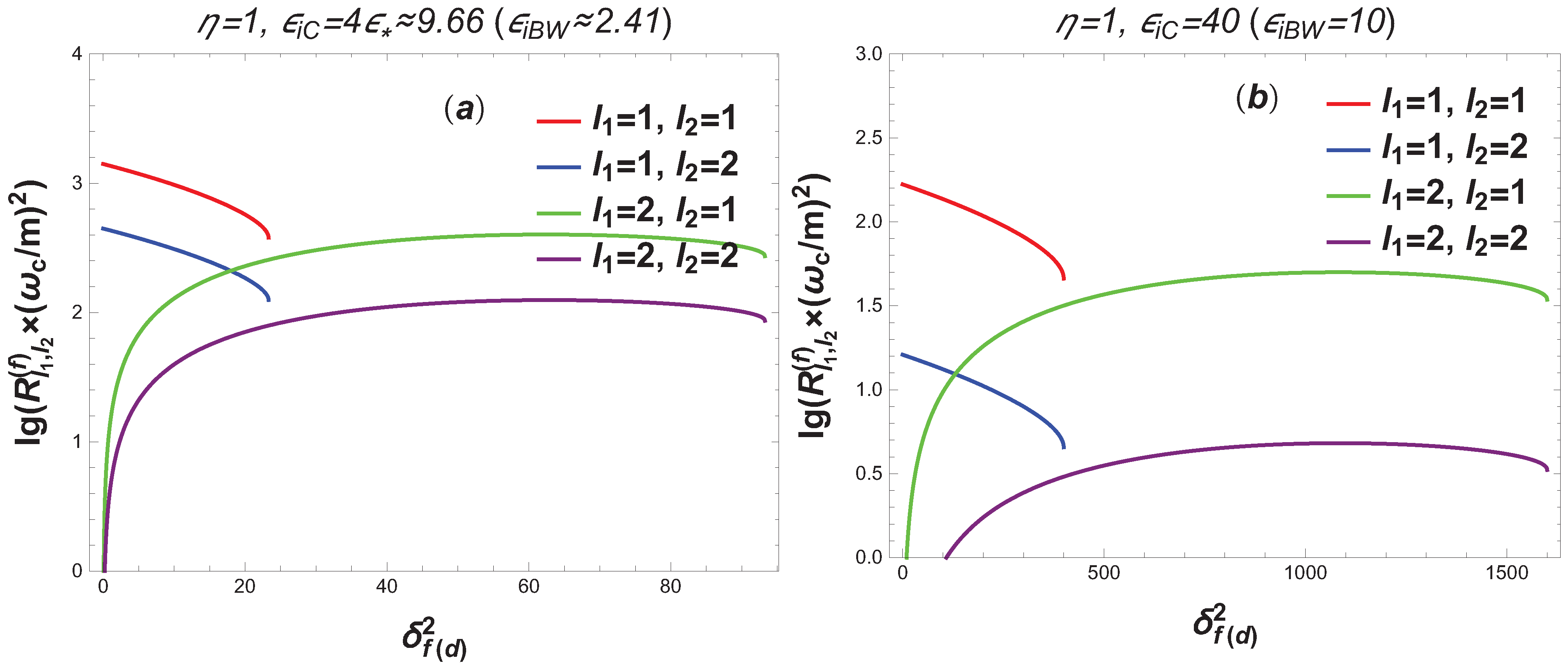
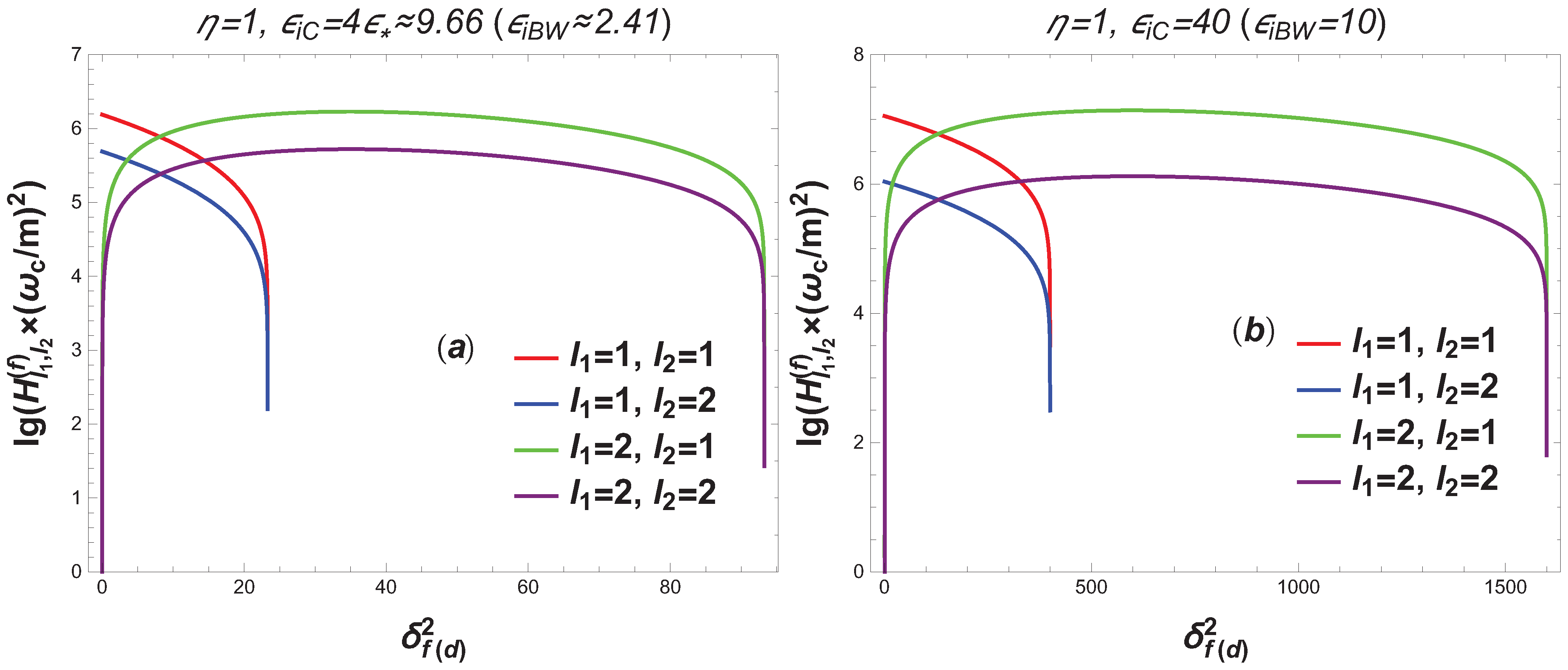
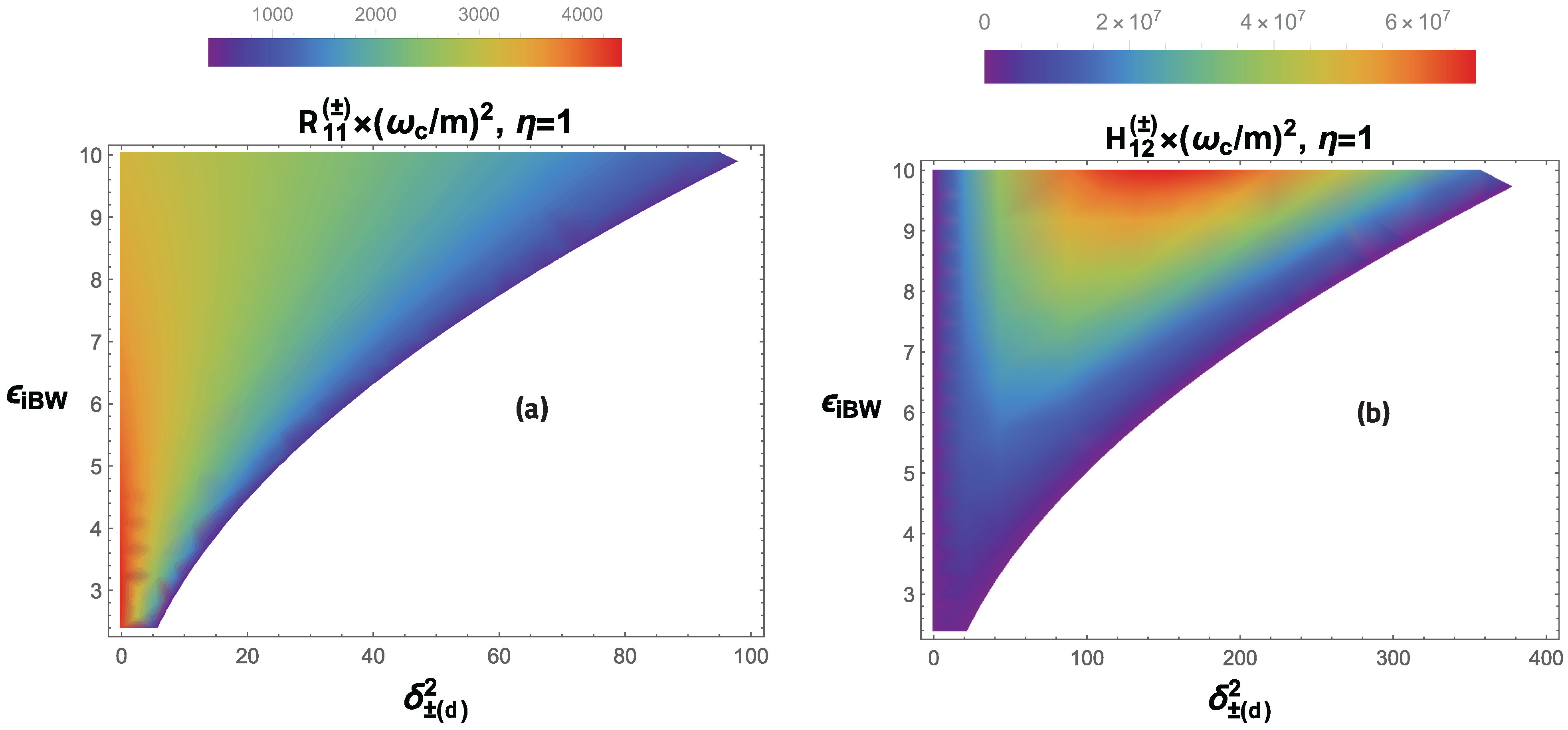
- The value of the differential probability of the RTPP process essentially depends on the quantum parameters of the Compton effect and the Breit–Wheeler process , the characteristic energy of the Compton effect , and the number of photons absorbed at the first and second vertices of the wave.
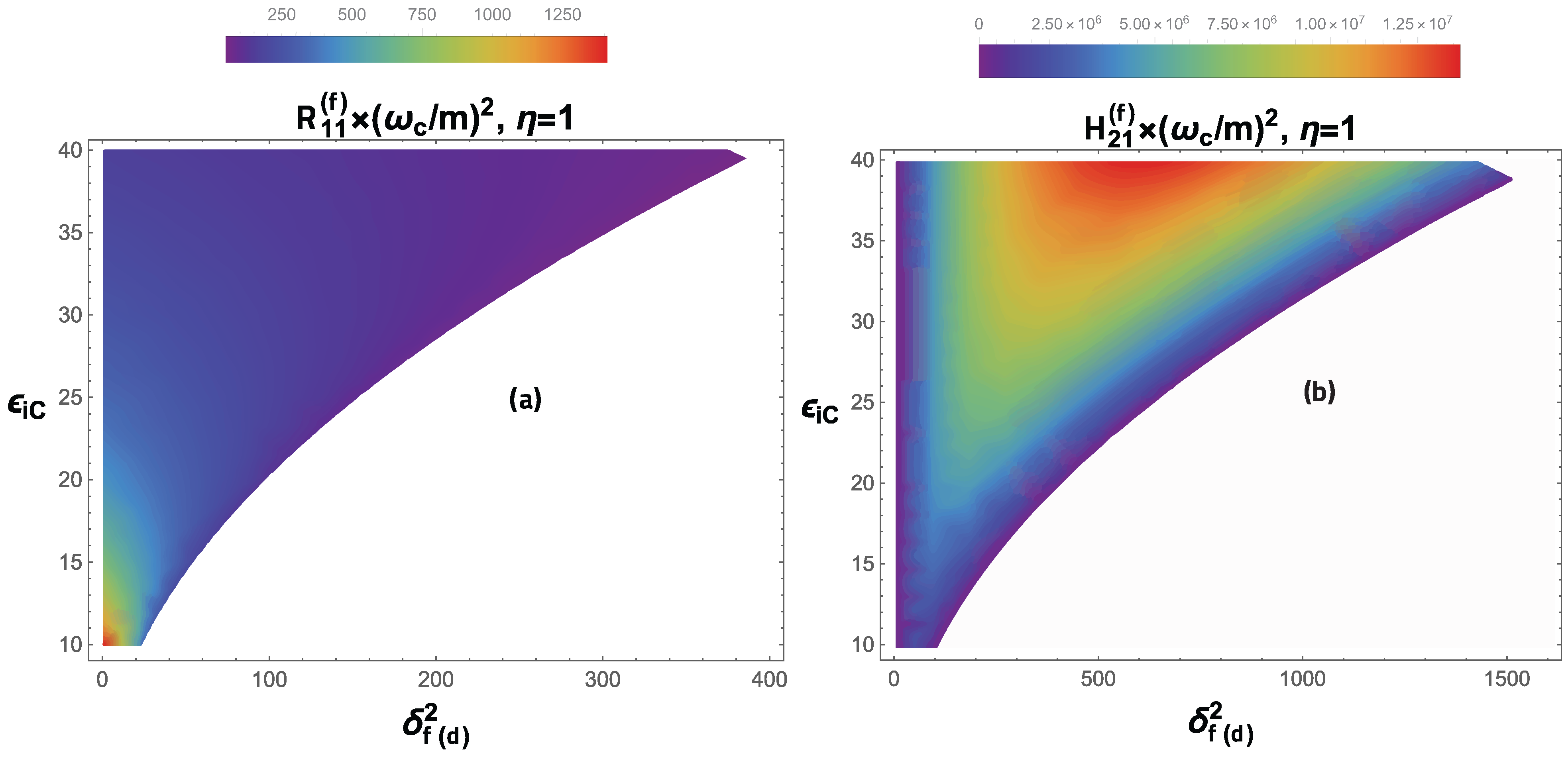
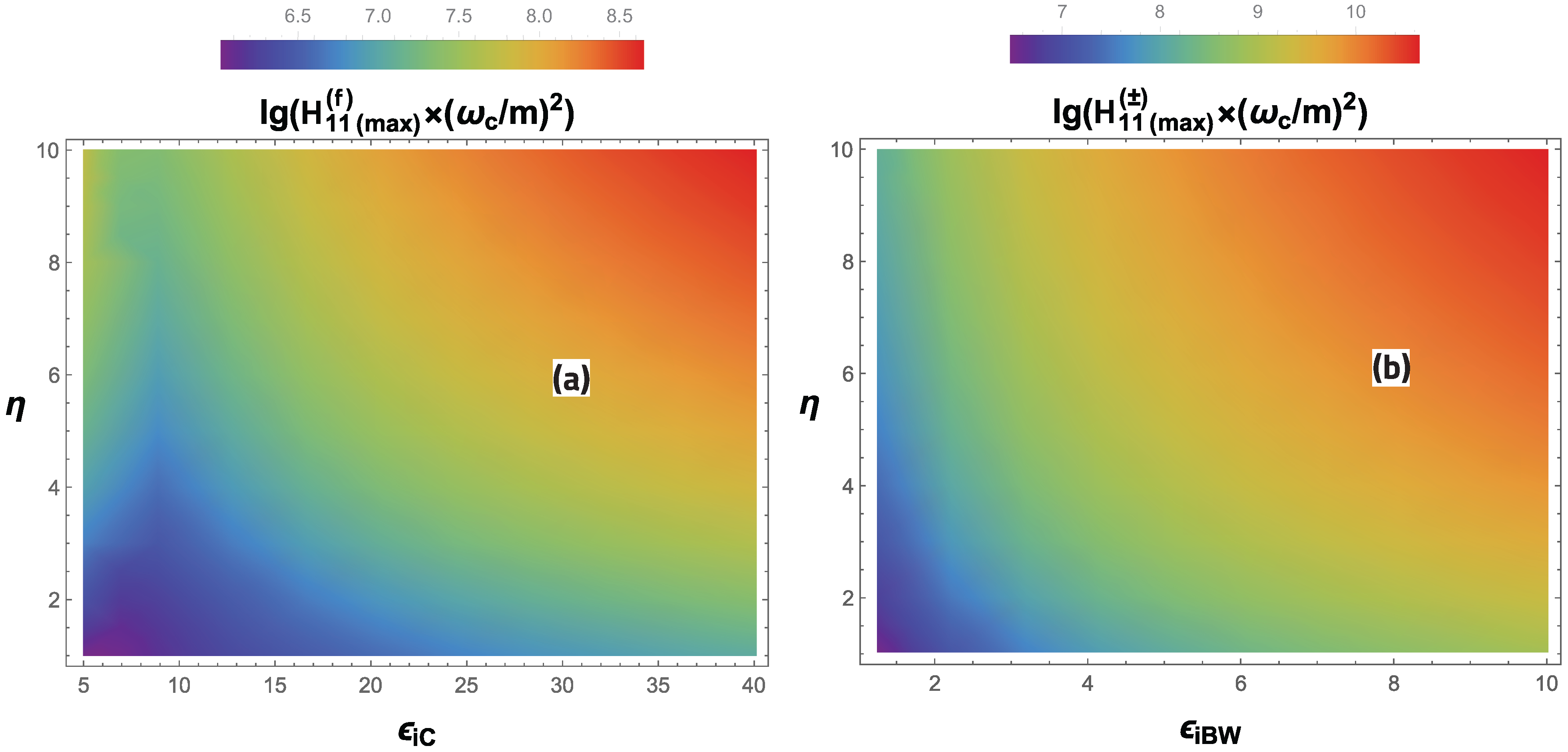
- In the region of optical frequencies and small electromagnetic wave intensities (), the relative differential probability of the RTPP process (in units of the total probability of the Compton effect stimulated by an external field) exceeds unity for sufficiently large initial electron energies . For very high initial electron energies , the RTPP process becomes dominant (see Figure 12 and Figure 13, as well as Table 6).
- In a sufficiently wide range of frequencies and intensities of a strong X-ray wave from to , as well as in a wide range of the initial electron energies , the RTPP process becomes dominant and can exceed the total probability of the Compton effect stimulated by an external field by many orders of magnitude (see Figure 14).
- In the RTPP process, quantum entanglement of the final particles occurs when the measurement of the electron (electron–positron pair) outgoing angle uniquely determines the energies of the final particles and the electron–positron pair (electron) outgoing angle. Moreover, this effect can significantly (by many orders of magnitude) exceed the corresponding Compton effect stimulated by an external field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bula, C.; McDonald, K.T.; Prebys, E.J.; Bamber, C.; Boege, S.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Ragg, W.; Burke, D.L.; et al. Observation of Nonlinear Effects in Compton Scattering. Phys. Rev. Lett. 1996, 76, 3116–3119. [Google Scholar] [CrossRef] [PubMed]
- Turcu, E.; Balascuta, S.; Negoita, F.; Jaroszynski, D.; McKenna, P. Strong field physics and QED experiments with ELI-NP 2×10PW laser beams. AIP Conf. Proc. 2015, 1645, 416–420. [Google Scholar] [CrossRef]
- Popovici, M.A.; Mitu, I.O.; Cata-Danil, G.; Negoita, F.; Ivan, C. Shielding assessment of high field (QED) experiments at the ELI-NP 10PW laser system. J. Radiol. Prot. 2017, 37, 176–188. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; Lee, S.K.; Nam, C.H. Realization of laser intensity over 1023 w/cm2. Optica 2021, 8, 630. [Google Scholar] [CrossRef]
- Turcu, I.C.E.; Shen, B.; Neely, D.; Sarri, G.; Tanaka, K.A.; McKenna, P.; Mangles, S.P.D.; Yu, T.P.; Luo, W.; Zhu, X.L.; et al. Quantum electrodynamics experiments with colliding petawatt laser pulses. High Power Laser Sci. Eng. 2019, 7, e10. [Google Scholar] [CrossRef]
- Tanaka, K.; Spohr, K.; Balabanski, D.; Balascuta, S.; Capponi, L.; Cernaianu, M.; Cuciuc, M.; Cucoanes, A.; Dancus, I.; Dhal, A.; et al. Current status and highlights of the ELI-NP research program. Matter Radiat. Extrem. 2020, 5, 024402. [Google Scholar] [CrossRef]
- Weber, S.; Bechet, S.; Borneis, S.; Brabec, L.; Bucka, M.; Chacon-Golcher, E.; Ciappina, M.; DeMarco, M.; Fajstavr, A.; Falk, K.; et al. P3: An installation for high-energy density plasma physics and ultra-high intensity laser matter interaction at ELI-Beamlines. Matter Radiat. Extrem. 2017, 2, 149–176. [Google Scholar] [CrossRef]
- Papadopoulos, D.; Zou, J.; Le Blanc, C.; Cheriaux, G.; Georges, P.; Druon, F.; Mennerat, G.; Ramirez, P.; Martin, L.; Freneaux, A.; et al. The Apollon 10 PW laser: Experimental and theoretical investigation of the temporal characteristics. High Power Laser Sci. Eng. 2016, 4, e34. [Google Scholar] [CrossRef]
- Bromage, J.; Bahk, S.W.; Begishev, I.; Dorrer, C.; Guardalben, M.; Hoffman, B.; Oliver, J.; Roides, R.; Schiesser, E.; Shoup, M.; et al. Technology development for ultraintense all-OPCPA systems. High Power Laser Sci. Eng. 2019, 7, e4. [Google Scholar] [CrossRef]
- Rossbach, J.; Schneider, J.; Wurth, W. 10 years of pioneering X-ray science at the Free-Electron Laser FLASH at DESY. Phys. Rep. 2019, 808, 1–74. [Google Scholar] [CrossRef]
- Gonoskov, A.; Bashinov, A.; Bastrakov, S.; Efimenko, E.; Ilderton, A.; Kim, A.; Marklund, M.; Meyerov, I.; Muraviev, A.; Sergeev, A. Ultrabright GeV Photon Source via Controlled Electromagnetic Cascades in Laser-Dipole Waves. Phys. Rev. X 2017, 7, 041003. [Google Scholar] [CrossRef]
- Magnusson, J.; Gonoskov, A.; Marklund, M.; Esirkepov, T.Z.; Koga, J.K.; Kondo, K.; Bulanov, S.; Korn, G.; Bulanov, S.S. Laser-Particle Collider for Multi-GeV Photon Production. Phys. Rev. Lett. 2019, 122, 254801. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.L.; Yu, T.P.; Chen, M.; Weng, S.M.; Sheng, Z.M. Generation of GeV positron and γ-photon beams with controllable angular momentum by intense lasers. New J. Phys. 2018, 20, 083013. [Google Scholar] [CrossRef]
- Xu, H.; Padilla, O.; Wang, D.; Li, M. Changepoints: A Collection of Change-Point Detection Methods. 2021. Available online: https://github.com/HaotianXu/changepoints (accessed on 3 December 2024).
- Alejo, A.; Samarin, G.M.; Warwick, J.R.; Sarri, G. Laser-Wakefield Electron Beams as Drivers of High-Quality Positron Beams and Inverse-Compton-Scattered Photon Beams. Front. Phys. 2019, 7, 49. [Google Scholar] [CrossRef]
- Long, T.Y.; Zhou, C.T.; Huang, T.W.; Jiang, K.; Ju, L.B.; Zhang, H.; Cai, T.X.; Yu, M.Y.; Qiao, B.; Ruan, S.C.; et al. All-optical generation of petawatt gamma radiation via inverse Compton scattering from laser interaction with tube target. Plasma Phys. Control. Fusion 2019, 61, 085002. [Google Scholar] [CrossRef]
- Terzic, B.; Mckaig, J.; Johnson, E.; Dharanikota, T.; Krafft, G. Laser chirping in inverse Compton sources at high electron beam energies and high laser intensities. Phys. Rev. Accel. Beams 2021, 94, 094401. [Google Scholar] [CrossRef]
- Gunther, B. Overview on Inverse Compton X-ray Sources; Springer: Berlin/Heidelberg, Germany, 2023; pp. 117–147. [Google Scholar] [CrossRef]
- Nielsen, C.F.; Holtzapple, R.; Lund, M.M.; Surrow, J.H.; Sørensen, A.H.; Sørensen, M.B.; Uggerhøj, U.I. Differential measurement of trident production in strong electromagnetic fields. Phys. Rev. D 2023, 108, 052013. [Google Scholar] [CrossRef]
- Macleod, A.; Hadjisolomou, P.; Jeong, T.M.; Bulanov, S.V. All-optical nonlinear Breit-Wheeler pair production with gamma-flash photons (Conference Presentation). In Proceedings of the Research Using Extreme Light: Entering New Frontiers with Petawatt-Class Lasers V, Prague, Czech Republic, 24–28 April 2023; Bulanov, S.V., Silva, L.O., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 2. [Google Scholar] [CrossRef]
- Powell, J.; Jolly, S.; Vallieres, S.; Fillion-Gourdeau, F.; Payeur, S.; Fourmaux, S.; Lytova, M.; Piche, M.; Ibrahim, H.; MacLean, S.; et al. Relativistic Electrons from Vacuum Laser Acceleration Using Tightly Focused Radially Polarized Beams. Phys. Rev. Lett. 2024, 133, 155001. [Google Scholar] [CrossRef]
- Nikishov, A.I.; Ritus, V.I. Interaction of Electrons and Photons with a Very Strong Electromagnetic Field. Phys. Usp. 1970, 13, 303–305. [Google Scholar] [CrossRef]
- Nikishov, A.I.; Ritus, V.I. Quantum Electrodynamics Phenomena in the Intense Field; Nauka: Moscow, Russia, 1979. [Google Scholar]
- Nikishov, A.I. Quantum electrodynamics of strong fields. Sov. Phys. Uspekhi 1987, 30, 551–552. [Google Scholar] [CrossRef]
- Roshchupkin, S.P. Resonant effects in collisions of relativistic electrons in the field of a light wave. Laser Phys. 1996, 6, 837–858. [Google Scholar]
- Roshchupkin, S.; Tsybul’nik, V.; Chmirev, A. The probability of multiphoton processes in quantum-electrodynamic phenomena in a strong light field. Laser Phys. 2000, 10, 1256–1272. [Google Scholar]
- Ehlotzky, F.; Krajewska, K.; Kaminski, J.Z. Fundamental processes of quantum electrodynamics in laser fields of relativistic power. Rep. Prog. Phys. 2009, 72, 046401. [Google Scholar]
- Ruffini, R.; Vereshchagin, G.; Xue, S.S. Electron–positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2009, 487, 1–140. [Google Scholar] [CrossRef]
- Piazza, A.; Muller, C.; Hatsagortsyan, K.; Keitel, C. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2011, 84, 1177. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Lebedev, A.A.; Padusenko, E.A.; Voroshilo, A.I. Quantum electrodynamics resonances in a pulsed laser field. Laser Phys. 2012, 22, 1113–1144. [Google Scholar] [CrossRef]
- Hartin, A. Strong field QED in lepton colliders and electron/laser interactions. Int. J. Mod. Phys. A 2018, 33, 1830011. [Google Scholar] [CrossRef]
- Mironov, A.; Meuren, S.; Fedotov, A. Resummation of QED radiative corrections in a strong constant crossed field. Phys. Rev. D 2020, 102, 053005. [Google Scholar] [CrossRef]
- Gonoskov, A.; Blackburn, T.G.; Marklund, M.; Bulanov, S.S. Charged particle motion and radiation in strong electromagnetic fields. Rev. Mod. Phys. 2022, 94, 045001. [Google Scholar] [CrossRef]
- Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, H.; Torgrimsson, G. Advances in QED with intense background fields. Phys. Rep. 2023, 1010, 1–138. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Voroshilo, A. Resonant and Coherent Effects of Quantum Electrodynamics in the Light Field; Naukova Dumka: Kiev, Ukraine, 2008. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Lebed’, A. Effects of Quantum Electrodynamics in Strong Impulse Laser Fieldsd; Naukova Dumka: Kiev, Ukraine, 2013. [Google Scholar]
- Greiner, W.; Müller, B.; Rafelski, J. Quantum Electrodynamics of Strong Fields: With an Introduction into Modern Relativistic Quantum Mechanics; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Narozhny, N.B.; Fofanov, M.S. Photon Emission by an Electron Colliding with a Short Focused Laser Pulse. In Super-Intense Laser-Atom Physics IV; Springer: Dordrecht, The Netherlands, 1996; pp. 411–420. [Google Scholar] [CrossRef]
- Narozhny, N.B.; Fofanov, M.S. Scattering of relativistic electrons by a focused laser pulse. J. Exp. Theor. Phys. 2000, 90, 753–768. [Google Scholar] [CrossRef]
- Harvey, C.; Heinzl, T.; Ilderton, A. Signatures of high-intensity Compton scattering. Phys. Rev. A 2009, 79, 063407. [Google Scholar] [CrossRef]
- Boca, M.; Florescu, V. Nonlinear Compton scattering with a laser pulse. Phys. Rev. A 2009, 80, 053403. [Google Scholar] [CrossRef]
- Mackenroth, F.; Di Piazza, A. Nonlinear Compton scattering in ultrashort laser pulses. Phys. Rev. A 2011, 83, 032106. [Google Scholar] [CrossRef]
- Seipt, D.; Kampfer, B. Nonlinear Compton scattering of ultrashort intense laser pulses. Phys. Rev. A 2011, 83, 022101. [Google Scholar] [CrossRef]
- Mackenroth, F.; Di Piazza, A. Nonlinear Double Compton Scattering in the Ultrarelativistic Quantum Regime. Phys. Rev. Lett. 2013, 110, 070402. [Google Scholar] [CrossRef]
- Seipt, D.; Kampfer, B. Two-photon Compton process in pulsed intense laser fields. Phys. Rev. D 2012, 85, 101701. [Google Scholar] [CrossRef]
- Boca, M.; Dinu, V.; Florescu, V. Electron distributions in nonlinear Compton scattering. Phys. Rev. A 2012, 86, 013414. [Google Scholar] [CrossRef]
- Dai, Y.N.; Jiang, J.J.; Jiang, Y.H.; Shaisultanov, R.; Chen, Y.Y. Effects of angular spread in nonlinear Compton scattering. Phys. Rev. D 2023, 108, 056025. [Google Scholar] [CrossRef]
- Khalaf, M.; Kaminer, I. Compton scattering driven by intense quantum light. Sci. Adv. 2023, 9, eade0932. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, R.; Ioka, K. Collective Thomson scattering in magnetized electron and positron pair plasma and the application to induced Compton scattering. Phys. Rev. D 2024, 109, 043048. [Google Scholar] [CrossRef]
- Podszus, T.; Dinu, V.; Di Piazza, A. Nonlinear Compton scattering and nonlinear Breit-Wheeler pair production including the damping of particle states (Conference Presentation). In Proceedings of the Research Using Extreme Light: Entering New Frontiers with Petawatt-Class Lasers V, Prague, Czech Republic, 24–28 April 2023; Bulanov, S.V., Silva, L.O., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 3. [Google Scholar] [CrossRef]
- Titov, A.I. Effects of Photon Polarizations in Non-Linear Compton Process. Phys. Part. Nucl. 2024, 55, 920–928. [Google Scholar] [CrossRef]
- Li, Y.F.; Chen, Y.Y.; Hatsagortsyan, K.Z.; Di Piazza, A.; Tamburini, M.; Keitel, C.H. Strong signature of one-loop self-energy in polarization resolved nonlinear Compton scattering. Phys. Rev. D 2023, 107, 116020. [Google Scholar] [CrossRef]
- Gelfer, E.G.; Fedotov, A.M.; Mironov, A.A.; Weber, S. Nonlinear Compton scattering in time-dependent electric fields beyond the locally constant crossed field approximation. Phys. Rev. D 2022, 106, 056013. [Google Scholar] [CrossRef]
- Song, H.H.; Wang, W.M.; Chen, M.; Sheng, Z.M. From linear to nonlinear Breit-Wheeler pair production in laser-solid interactions. Phys. Rev. E 2024, 109, 035204. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Tang, S. Optimal photon polarization toward the observation of the nonlinear Breit-Wheeler pair production. Phys. Rev. D 2022, 106, 056003. [Google Scholar] [CrossRef]
- Golub, A.; Villalba-Chavez, S.; Muller, C. Strong-field Breit-Wheeler pair production in QED 2 + 1. Phys. Rev. D 2021, 103, 096002. [Google Scholar] [CrossRef]
- Tang, S.; King, B. Pulse envelope effects in nonlinear Breit-Wheeler pair creation. Phys. Rev. D 2021, 104, 096019. [Google Scholar] [CrossRef]
- Degli Esposti, G.; Torgrimsson, G. Worldline instantons for nonlinear Breit-Wheeler pair production and Compton scattering. Phys. Rev. D 2022, 105, 096036. [Google Scholar] [CrossRef]
- Blackburn, T.G.; King, B. Higher fidelity simulations of nonlinear Breit–Wheeler pair creation in intense laser pulses. Eur. Phys. J. C 2022, 82, 44. [Google Scholar] [CrossRef]
- Dai, Y.N.; Shen, B.F.; Li, J.X.; Shaisultanov, R.; Hatsagortsyan, K.Z.; Keitel, C.H.; Chen, Y.Y. Photon polarization effects in polarized electron-positron pair production in a strong laser field. Matter Radiat. Extrem. 2022, 7, 014401. [Google Scholar] [CrossRef]
- Hafizi, B.; Gordon, D.F.; Kaganovich, D. Pair Creation with Strong Laser Fields, Compton Scale X Rays, and Heavy Nuclei. Phys. Rev. Lett. 2019, 122, 233201. [Google Scholar] [CrossRef]
- MacLeod, A.J.; Hadjisolomou, P.; Jeong, T.M.; Bulanov, S.V. All-optical nonlinear Breit-Wheeler pair production with gamma-flash photons. Phys. Rev. A 2023, 107, 012215. [Google Scholar] [CrossRef]
- Mahlin, N.; Villalba-Chavez, S.; Muller, C. Dynamically assisted nonlinear Breit-Wheeler pair production in bichromatic laser fields of circular polarization. Phys. Rev. D 2023, 108, 096023. [Google Scholar] [CrossRef]
- Eckey, A.; Golub, A.; Salgado, F.C.; Villalba-Chavez, S.; Voitkiv, A.B.; Zepf, M.; Muller, C. Impact of laser focusing and radiation reaction on particle spectra from nonlinear Breit-Wheeler pair production in the nonperturbative regime. Phys. Rev. A 2024, 110, 043113. [Google Scholar] [CrossRef]
- Seipt, D.; Samuelsson, M.; Blackburn, T. Nonlinear Breit–Wheeler pair production using polarized photons from inverse Compton scattering. Plasma Phys. Control. Fusion 2025, 67, 035002. [Google Scholar] [CrossRef]
- Oleinik, V.P. Resonance Effects in the Field of an Intense Laser Beam. J. Exp. Theor. Phys. 1967, 25, 697. [Google Scholar]
- Oleinik, V.P. Resonance Effects in the Field of an Intense Laser Ray. J. Exp. Theor. Phys. 1968, 26, 1132. [Google Scholar]
- Sizykh, G.K.; Roshchupkin, S.P.; Dubov, V.V. Resonant Effect of High-Energy Electron-Positron Pairs Production in Collision of Ultrarelativistic Electrons with an X-ray Electromagnetic Wave. Universe 2021, 7, 210. [Google Scholar] [CrossRef]
- Titov, A.I.; Acosta, U.H.; Kampfer, B. Positron energy distribution in a factorized trident process. Phys. Rev. A 2021, 104, 062811. [Google Scholar] [CrossRef]
- Kaminski, J.Z.; Krajewska, K. Trident pair creation by a train of laser pulses: Resonance, threshold, and carrier envelope phase effects. arXiv 2022, arXiv:2211.04716. [Google Scholar]
- Roshchupkin, S.P.; Larin, N.R.; Dubov, V.V. Resonant photoproduction of ultrarelativistic electron-positron pairs on a nucleus in moderate and strong monochromatic light fields. Phys. Rev. D 2021, 104, 116011. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Dubov, A.V.; Dubov, V.V.; Starodub, S.S. Fundamental physical features of resonant spontaneous bremsstrahlung radiation of ultrarelativistic electrons on nuclei in strong laser fields. New J. Phys. 2022, 24, 013020. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Serov, V.D.; Dubov, V.V. Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit-Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave. Photonics 2023, 10, 949. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Makarov, S.B. Generation of Narrow Beams of Super High-Energy Gamma Quanta in the Resonant Compton Effect in the Field of a Strong X-ray Wave. Photonics 2024, 11, 597. [Google Scholar] [CrossRef]
- King, B.; Ruhl, H. Trident pair production in a constant crossed field. Phys. Rev. D 2013, 88, 013005. [Google Scholar] [CrossRef][Green Version]
- Tang, S.; King, B. Locally monochromatic two-step nonlinear trident process in a plane wave. Phys. Rev. D 2023, 107, 096004. [Google Scholar] [CrossRef]
- Hu, H.; Muller, C.; Keitel, C.H. Complete QED Theory of Multiphoton Trident Pair Production in Strong Laser Fields. Phys. Rev. Lett. 2010, 105, 080401. [Google Scholar] [CrossRef]
- Dinu, V.; Torgrimsson, G. Trident pair production in plane waves: Coherence, exchange, and spacetime inhomogeneity. Phys. Rev. D 2018, 97, 036021. [Google Scholar] [CrossRef]
- Ilderton, A. Trident Pair Production in Strong Laser Pulses. Phys. Rev. Lett. 2011, 106, 020404. [Google Scholar] [CrossRef]
- King, B.; Fedotov, A.M. Effect of interference on the trident process in a constant crossed field. Phys. Rev. D 2018, 98, 016005. [Google Scholar] [CrossRef]
- Mackenroth, F.; Di Piazza, A. Nonlinear trident pair production in an arbitrary plane wave: A focus on the properties of the transition amplitude. Phys. Rev. D 2018, 98, 116002. [Google Scholar] [CrossRef]
- Yaghjian, A.D. Lorentz-Abraham-Dirac and Landau-Lifshitz equations of motion and the solution to a relativistic electron in a counterpropagating laser beam. Phys. Rev. Accel. Beams 2021, 24, 114002. [Google Scholar] [CrossRef]
- Lv, Q.Z.; Raicher, E.; Keitel, C.; Hatsagortsyan, K.Z. High-Brilliance Ultranarrow-Band X Rays via Electron Radiation in Colliding Laser Pulses. Phys. Rev. Lett. 2022, 128, 024801. [Google Scholar] [CrossRef]
- Schulze, K.S.; Grabiger, B.; Loetzsch, R.; Marx-Glowna, B.; Schmitt, A.T.; Garcia, A.L.; Hippler, W.; Huang, L.; Karbstein, F.; Konôpková, Z.; et al. Towards perfectly linearly polarized x-rays. Phys. Rev. Res. 2022, 4, 013220. [Google Scholar] [CrossRef]
- Salgado, F.; Cavanagh, N.; Tamburini, M.; Storey, D.; Beyer, R.; Bucksbaum, P.; Chen, Z.; Piazza, A.; Gerstmayr, E.; Harsh; et al. Single Particle Detection System for Strong-Field QED Experiments. New J. Phys. 2022, 24, 015002. [Google Scholar] [CrossRef]
- Borneis, S.; Lastovicka, T.; Sokol, M.; Jeong, T.M.; Condamine, F.; Renner, O.; Bohlin, H.; Fajstavr, A.; Hernandez, J.C.; Jourdain, N.; et al. Design, installation and commissioning of the ELI-Beamlines high-power, high-repetition rate HAPLS laser beam transport system to P3. High Power Laser Sci. Eng. 2021, 9, e30. [Google Scholar] [CrossRef]
- Di Piazza, A.; Fronimos, F.P. Quasiclassical representation of the Volkov propagator and the tadpole diagram in a plane wave. Phys. Rev. D 2022, 105, 116019. [Google Scholar] [CrossRef]
- Jirka, M.; Sasorov, P.; Bulanov, S.V. New and old physics in the interaction of a radiating electron with the extreme electromagnetic field. Phys. Rev. D 2022, 105, 113004. [Google Scholar] [CrossRef]
- Di Piazza, A.; Patuleanu, T. Electron mass shift in an intense plane wave. Phys. Rev. D 2021, 104, 076003. [Google Scholar] [CrossRef]
- Muller, C.; Voitkiv, A.B.; Grun, N. Differential rates for multiphoton pair production by an ultrarelativistic nucleus colliding with an intense laser beam. Phys. Rev. A 2003, 67, 063407. [Google Scholar] [CrossRef]
- Krachkov, P.; Di Piazza, A.; Milstein, A. High-energy bremsstrahlung on atoms in a laser field. Phys. Lett. B 2019, 797, 134814. [Google Scholar] [CrossRef]
- Habibi, M.; Arefiev, A.; Toncian, T. High field suppression of bremsstrahlung emission in high-intensity laser–plasma interactions. Phys. Plasmas 2023, 30, 103108. [Google Scholar] [CrossRef]
- Gong, Z.; Hatsagortsyan, K.Z.; Keitel, C.H. Electron Polarization in Ultrarelativistic Plasma Current Filamentation Instabilities. Phys. Rev. Lett. 2023, 130, 015101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhang, Z.M.; Zhou, W.M. Quantum splitting of electron peaks in ultra-strong fields. Matter Radiat. Extrem. 2023, 8, 054003. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Hatsagortsyan, K.Z.; Keitel, C.H.; Shaisultanov, R. Electron spin- and photon polarization-resolved probabilities of strong-field QED processes. Phys. Rev. D 2022, 105, 116013. [Google Scholar] [CrossRef]
- Ruf, M.; Mocken, G.R.; Muller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Pair Production in Laser Fields Oscillating in Space and Time. Phys. Rev. Lett. 2009, 102, 080402. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Plunien, G.; Shabaev, V.M. Momentum distribution of particles created in space-time-dependent colliding laser pulses. Phys. Rev. D 2017, 96, 076006. [Google Scholar] [CrossRef]
- Wondrak, M.F.; van Suijlekom, W.D.; Falcke, H. Gravitational Pair Production and Black Hole Evaporation. Phys. Rev. Lett. 2023, 130, 221502. [Google Scholar] [CrossRef]
- Wollert, A.; Bauke, H.; Keitel, C.H. Spin polarized electron-positron pair production via elliptical polarized laser fields. Phys. Rev. D 2015, 91, 125026. [Google Scholar] [CrossRef]
- Lv, Q.Z.; Dong, S.; Li, Y.T.; Sheng, Z.M.; Su, Q.; Grobe, R. Role of the spatial inhomogeneity on the laser-induced vacuum decay. Phys. Rev. A 2018, 97, 022515. [Google Scholar] [CrossRef]
- Aleksandrov, I.; Kohlfurst, C. Pair production in temporally and spatially oscillating fields. Phys. Rev. D 2020, 101, 096009. [Google Scholar] [CrossRef]
- Adamo, T.; Ilderton, A.; MacLeod, A.J. Particle-beam scattering from strong-field QED. Phys. Rev. D 2021, 104, 116013. [Google Scholar] [CrossRef]
- MacLeod, A.J.; King, B. Fundamental constants from photon-photon scattering in three-beam collisions. Phys. Rev. A 2024, 110, 032216. [Google Scholar] [CrossRef]
- Dahiri, I.; Baouahi, M.; Jakha, M.; Mouslih, S.; Manaut, B.; Taj, S. Effect of electron spin polarization in laser-assisted electron–proton scattering. Chin. J. Phys. 2022, 77, 1691–1700. [Google Scholar] [CrossRef]
- Karlovets, D.V.; Serbo, V.G.; Surzhykov, A. Wave function of a photon produced in the resonant scattering of twisted light by relativistic ions. Phys. Rev. A 2021, 104, 023101. [Google Scholar] [CrossRef]
- Mendonca, J.T. Penrose Scattering in Quantum Vacuum. Photonics 2024, 11, 448. [Google Scholar] [CrossRef]
- Gies, H.; Karbstein, F.; Klar, L. All-optical quantum vacuum signals in two-beam collisions. Phys. Rev. D 2022, 106, 116005. [Google Scholar] [CrossRef]
- Li, X.B.; Gan, L.F.; Wang, J.; Jiao, J.L.; Jin, S.; Zhuo, H.B.; Zhou, C.T.; Zhu, S.P.; He, X.T.; Qiao, B. Identify spin property of relativistic electrons in fully relativistic laser fields. New J. Phys. 2021, 23, 123043. [Google Scholar] [CrossRef]
- Krajewska, K.; Kaminski, J.Z.; Muller, C. Pulse shape effects in high-field Bethe-Heitler pair production. New J. Phys. 2021, 23, 095012. [Google Scholar] [CrossRef]
- Pastor, I.; Alvarez-Estrada, R.F.; Roso, L.; Castejon, F. Classical Scattering of High-Energy Electrons off Ultra-Intense Laser Beams Taking into Account Radiation Reaction. Photonics 2024, 11, 113. [Google Scholar] [CrossRef]
- El Asri, S.; Mouslih, S.; Jakha, M.; Manaut, B.; Attaourti, Y.; Taj, S.; Benbrik, R. Elastic scattering of a muon neutrino by an electron in the presence of a circularly polarized laser field. Phys. Rev. D 2021, 104, 113001. [Google Scholar] [CrossRef]
- Ouali, M.; Ouhammou, M.; Taj, S.; Benbrik, R.; Manaut, B.; El Idrissi, M. Muon pair production via e+e annihilation in the presence of a circularly polarized laser field. Laser Phys. 2022, 32, 106002. [Google Scholar] [CrossRef]
- Dai, Y.N.; Hatsagortsyan, K.Z.; Keitel, C.H.; Chen, Y.Y. Fermionic signal of vacuum polarization in strong laser fields. Phys. Rev. D 2024, 110, 012008. [Google Scholar] [CrossRef]
- Olofsson, C.; Gonoskov, A. Attaining a strong-field QED signal at laser-electron colliders with optimized focusing. Phys. Rev. A 2022, 106, 063512. [Google Scholar] [CrossRef]
- Zaim, N.; Sainte-Marie, A.; Fedeli, L.; Bartoli, P.; Huebl, A.; Leblanc, A.; Vay, J.L.; Vincenti, H. Light-Matter Interaction near the Schwinger Limit Using Tightly Focused Doppler-Boosted Lasers. Phys. Rev. Lett. 2024, 132, 175002. [Google Scholar] [CrossRef]
- Martinez, B.; Barbosa, B.; Vranic, M. Creation and direct laser acceleration of positrons in a single stage. Phys. Rev. Accel. Beams 2023, 26, 011301. [Google Scholar] [CrossRef]
- Volkov, D.M. On a class of solutions of the Dirac equation. Z. Phys. 1935, 94, 250. [Google Scholar]
- Berestetskii, V.; Lifshitz, E.; Pitaevskii, L. Quantum Electrodynamics: Volume 4; Course of theoretical physics; Elsevier Science: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Breit, G.; Wigner, E. Capture of Slow Neutrons. Phys. Rev. 1936, 49, 519–531. [Google Scholar] [CrossRef]
- Deng, Z.L.; Gao, Z.F.; Li, X.D.; Shao, Y. On the Formation of PSR J1640+2224: A Neutron Star Born Massive? Astrophys. J. 2020, 892, 4. [Google Scholar] [CrossRef]
- Deng, Z.L.; Li, X.D.; Gao, Z.F.; Shao, Y. Evolution of LMXBs under Different Magnetic Braking Prescriptions. Astrophys. J. 2021, 909, 174. [Google Scholar] [CrossRef]
- Gao, Z.F.; Wang, N.; Shan, H.; Li, X.D.; Wang, W. The Dipole Magnetic Field and Spin-down Evolutions of the High Braking Index Pulsar PSR J1640-4631. Astrophys. J. 2017, 849, 19. [Google Scholar] [CrossRef]
- Wang, H.; Gao, Z.F.; Jia, H.Y.; Wang, N.; Li, X.D. Estimation of Electrical Conductivity and Magnetization Parameter of Neutron Star Crusts and Applied to the High-Braking-Index Pulsar PSR J1640-4631. Universe 2020, 6, 63. [Google Scholar] [CrossRef]
- Gao, Z.F.; Li, X.D.; Wang, N.; Yuan, J.P.; Wang, P.; Peng, Q.H.; Du, Y.J. Constraining the braking indices of magnetars. Mon. Not. R. Astron. Soc. 2015, 456, 55–65. [Google Scholar] [CrossRef]
- Yan, F.Z.; Gao, Z.F.; Yang, W.S.; Dong, A.J. Explaining high braking indices of magnetars SGR 0501+4516 and 1E 2259+586 using the double magnetic-dipole model. Astron. Nachrichten 2021, 342, 249–254. [Google Scholar] [CrossRef]

| 1, 1 | 0 | 5.79 | 0.09 | 0.91 | ||
| 1, 2 | 0 | 16.44 | 0.09 | 0.91 | ||
| 2, 1 | 62.40 | 5.75 | 0.06 | 0.94 | ||
| 2, 2 | 62.84 | 16.04 | 0.06 | 0.94 | 125 | |
| 1, 1 | 0 | 36.80 | 0.02 | 0.98 | 167 | |
| 1, 2 | 0 | 77.80 | 0.02 | 0.98 | ||
| 2, 1 | 1083 | 36.51 | 0.02 | 0.98 | 50 | |
| 2, 2 | 1086 | 77.15 | 0.02 | 0.98 |
| 1, 1 | 0 | 5.79 | 0.09 | 0.91 | ||
| 1, 2 | 0 | 16.44 | 0.09 | 0.91 | ||
| 2, 1 | 34.95 | 5.74 | 0.05 | 0.95 | ||
| 2, 2 | 35.05 | 15.95 | 0.05 | 0.95 | ||
| 1, 1 | 0 | 36.80 | 0.02 | 0.98 | ||
| 1, 2 | 0 | 77.80 | 0.02 | 0.98 | ||
| 2, 1 | 597.61 | 36.45 | 0.01 | 0.99 | ||
| 2, 2 | 598.34 | 77.00 | 0.01 | 0.99 |
| 1, 1 | 6.33 | 0 | 0.59 | 0.41 | ||
| 1, 2 | 3.17 | 13.98 | 0.75 | 0.25 | ||
| 2, 1 | 13.16 | 0 | 0.59 | 0.41 | ||
| 2, 2 | 7.48 | 18.34 | 0.72 | 0.28 | ||
| 1, 1 | 4.43 | 0 | 0.90 | 0.10 | ||
| 1, 2 | 2.65 | 253.18 | 0.94 | 0.06 | ||
| 2, 1 | 8.88 | 0 | 0.90 | 0.10 | ||
| 2, 2 | 5.88 | 315.62 | 0.93 | 0,07 |
| 1, 1 | 6.33 | 0 | 0.59 | 0.41 | ||
| 1, 2 | 2.79 | 8.35 | 0.77 | 0.23 | ||
| 2, 1 | 13.16 | 0 | 0.59 | 0.41 | ||
| 2, 2 | 5.80 | 9.47 | 0.77 | 0.23 | ||
| 1, 1 | 4.43 | 0 | 0.90 | 0.10 | ||
| 1, 2 | 2.36 | 146.94 | 0.94 | 0.06 | ||
| 2, 1 | 8.88 | 0 | 0.90 | 0.10 | ||
| 2, 2 | 4.79 | 162.89 | 0.94 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roshchupkin, S.P.; Shakhov, M.V. Quantum Entanglement of the Final Particles in the Resonant Trident Pair Production Process in a Strong Electromagnetic Wave. Photonics 2025, 12, 307. https://doi.org/10.3390/photonics12040307
Roshchupkin SP, Shakhov MV. Quantum Entanglement of the Final Particles in the Resonant Trident Pair Production Process in a Strong Electromagnetic Wave. Photonics. 2025; 12(4):307. https://doi.org/10.3390/photonics12040307
Chicago/Turabian StyleRoshchupkin, Sergei P., and Mikhail V. Shakhov. 2025. "Quantum Entanglement of the Final Particles in the Resonant Trident Pair Production Process in a Strong Electromagnetic Wave" Photonics 12, no. 4: 307. https://doi.org/10.3390/photonics12040307
APA StyleRoshchupkin, S. P., & Shakhov, M. V. (2025). Quantum Entanglement of the Final Particles in the Resonant Trident Pair Production Process in a Strong Electromagnetic Wave. Photonics, 12(4), 307. https://doi.org/10.3390/photonics12040307






