Single-Path Spatial Polarization Modulation for Vector Transmission Matrix Measurement and Polarization Control in Scattering Media
Abstract
1. Introduction
2. Experimental Setup
3. VTM Retrieval and Measurement Procedure
4. Experimental Results and Polarization Control
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VTM | Vector transmission matrix |
| SLM | Spatial light modulator |
| FSPM | Full-Stokes polarimetry module |
| LCVR | Liquid-crystal variable retarder |
| QWP | Quarter-wave plate |
| AoLP | Angle of linear polarization |
| DoLP | Degree of linear polarization |
Appendix A. Input Polarization Mapping by the LCVR and Linear Independence of Two Settings
Appendix B. Derivation of Input Coupling (Single Retardance) and Full VTM Recovery with Two Retardance Settings
Appendix C. Optical Components
| Component | Details |
|---|---|
| Laser | Manufacturer: Changchun New Industries Optoelectronics Technology Model: MSL-U-532, Single Lognitudinal Mode Laser Key Specifications: Wavelength: 532 nm Polarization Ratio: >100:1, Vertical Max Output power: 1 W factor: |
| SLM | Manufacturer: Meadowlark Optics Model: HSP1K, Spatial Light Modulator Key Specifications: Type: Liquid Crystal on Silicon (LCoS) Optical Axis Direction: Horizontal Color Coding: Raw 8 bit Resolution: 1024 × 1024 Pixel pitch: 17 × 17 m |
| LCVR | Manufacturer: Meadowlark Optics Model: D5020-HS, HLC-200-VIS, Liquid Crystal Variable Retarder Key Specifications: Fundamental Drive Waveform: 2 kHz AC square wave Retardance: −50–425 nm Voltage Range: 0–20 Vrms Beam Deviation: ≤2 arc min |
| Polarization Camera | Manufacturer: Alkeria Model: Celera C5S-MP Key Specifications: Sensor Type: Mono Polarized Sensor Model: SONY Pregius IMX250MZR Sensor resolution: 2464 × 2056 Sensor technology: CMOS, global shutter Polarization Configuration: On-pixel filters in a 2 × 2 calculation unit with orientations of 0°, 45°, 90°, and 135°. |

| Polarization | |||
|---|---|---|---|
| H | 0.989 | −0.028 | −0.014 |
| V | −0.999 | 0.010 | 0.034 |
| 0.049 | 0.998 | 0.014 | |
| −0.042 | −0.994 | −0.094 | |
| R | −0.010 | 0.000 | 0.999 |
| L | 0.035 | −0.179 | −0.983 |
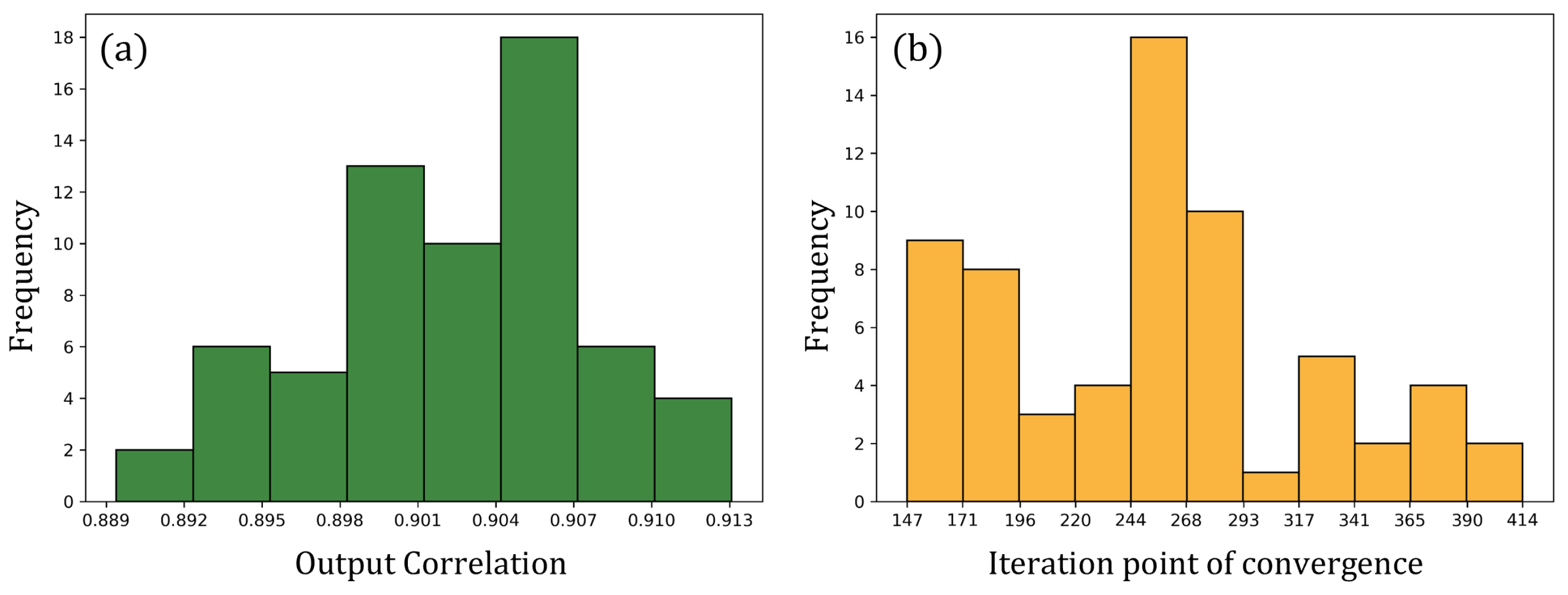
Appendix D. Statistical Analysis of Retrieval Algorithm
References
- Bicout, D.; Brosseau, C.; Martinez, A.S.; Schmitt, J.M. Depolarization of multiply scattered waves by spherical diffusers: Influence of the size parameter. Phys. Rev. E 1994, 49, 1767. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Alfano, R.R. Random walk of polarized light in turbid media. Phys. Rev. Lett. 2005, 95, 213901. [Google Scholar] [CrossRef]
- Brasselet, S. Polarization-resolved nonlinear microscopy: Application to structural molecular and biological imaging. Adv. Opt. Photonics 2011, 3, 205. [Google Scholar] [CrossRef]
- Rotter, S.; Gigan, S. Light fields in complex media: Mesoscopic scattering meets wave control. Rev. Mod. Phys. 2017, 89, 015005. [Google Scholar] [CrossRef]
- Gigan, S.; Katz, O.; De Aguiar, H.B.; Andresen, E.R.; Aubry, A.; Bertolotti, J.; Bossy, E.; Bouchet, D.; Brake, J.; Brasselet, S.; et al. Roadmap on wavefront shaping and deep imaging in complex media. J. Phys. Photonics 2022, 4, 042501. [Google Scholar] [CrossRef]
- Yu, Z.; Li, H.; Zhong, T.; Park, J.H.; Cheng, S.; Woo, C.M.; Zhao, Q.; Yao, J.; Zhou, Y.; Huang, X.; et al. Wavefront shaping: A versatile tool to conquer multiple scattering in multidisciplinary fields. Innovation 2022, 3, 100292. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Allan, B.; Anand, V.; Arnon, S.; Arockiaraj, F.G.; Art, J.; Bai, B.; Balasubramaniam, G.M.; Birnbaum, T.; et al. Roadmap on computational methods in optical imaging and holography. Appl. Phys. B 2024, 130, 166. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, L.; Qi, P.; Zhang, X.; Li, X.; Huang, Y.; Zhao, Y.; Hu, H. Polarimetric binocular three-dimensional imaging in turbid water with multi-feature self-supervised learning. PhotoniX 2025, 6, 24. [Google Scholar] [CrossRef]
- Mosk, A.P.; Lagendijk, A.; Lerosey, G.; Fink, M. Controlling waves in disordered media: Current state of the art. Nat. Photonics 2012, 6, 283–292. [Google Scholar] [CrossRef]
- Freund, I. Correlation functions of random wave fields. Phys. A Stat. Mech. Its Appl. 1990, 168, 49–62. [Google Scholar] [CrossRef]
- Webster, M.A.; Gerke, T.D.; Weiner, A.M.; Webb, K.J. Polarization-sensitive optical coherence tomography for tissue imaging. Opt. Lett. 2004, 29, 1491–1493. [Google Scholar] [CrossRef]
- Tripathi, S.; Paxman, R.; Bifano, T.; Toussaint, K.C., Jr. Vector transmission matrix for the polarization behavior of light propagation in highly scattering media. Opt. Express 2012, 20, 16067–16076. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Focusing light through an opaque scattering medium. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [PubMed]
- Vellekoop, I.M.; Lagendijk, A.; Mosk, A. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef]
- Katz, O.; Small, E.; Bromberg, Y.; Silberberg, Y. Controlling light in time and space through a complex medium. Nat. Photonics 2011, 5, 372–377. [Google Scholar] [CrossRef]
- Aulbach, J.; Gjonaj, B.; Johnson, P.M.; Mosk, A.P.; Lagendijk, A. Control of the spectral intensity of light transmitted through a disordered medium. Phys. Rev. Lett. 2011, 106, 103901. [Google Scholar] [PubMed]
- McCabe, D.J.; Tajalli, A.; Austin, D.R.; Bondareff, P.; Walmsley, I.A.; Gigan, S.; Chatel, B. Spatio-temporal focusing of light through a multiple scattering medium. Nat. Commun. 2011, 2, 447. [Google Scholar]
- Small, E.; Katz, O.; Guan, Y.; Silberberg, Y. Focusing light through a scattering medium with a digital mirror device. Opt. Lett. 2012, 37, 3429–3431. [Google Scholar] [CrossRef]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the Transmission Matrix in Optics: An Approach to the Study and Control of Light Propagation in Disordered Media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef]
- Guan, Y.; Katz, O.; Small, E.; Zhou, J.; Silberberg, Y. Polarization control of multiply scattered light through random media by wavefront shaping. Opt. Lett. 2012, 37, 4663–4665. [Google Scholar] [CrossRef]
- Galstian, T.; Gauvin, F.; Larochelle, P. Local Electrooptic Enhancement of the Degree of Linear Polarization of Coherently Scattered Light. Opt. Commun. 2025, 596, 132412. [Google Scholar] [CrossRef]
- Park, J.; Park, J.H.; Yu, H.; Park, Y. Focusing through turbid media by polarization modulation. Opt. Lett. 2015, 40, 1667–1670. [Google Scholar] [CrossRef]
- Tripathi, S. Optical Polarization Control in Free Space and Through Random Media Using Wavefront Shaping. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2014. [Google Scholar]
- Xiong, W.; Hsu, C.W.; Bromberg, Y.; Antonio-Lopez, J.E.; Amezcua Correa, R.; Cao, H. Complete polarization control in multimode fibers with polarization and mode coupling. Light Sci. Appl. 2018, 7, 54. [Google Scholar] [CrossRef]
- de Aguiar, H.B.; Gigan, S.; Brasselet, S. Polarization recovery through scattering media. Sci. Adv. 2017, 3, e1600743. [Google Scholar] [CrossRef]
- Huang, G.; Wu, D.; Luo, J.; Lu, L.; Li, F.; Shen, Y.; Li, Z. Generalizing the Gerchberg–Saxton algorithm for retrieving complex optical transmission matrices. Photonics Res. 2020, 9, 34–42. [Google Scholar] [CrossRef]
- Vector Transmission Matrix Retrieval and Input Shaping for Focusing. 2025. Available online: https://github.com/photonics-ai-lab/vector-tm-retrieval-and-input-shaping (accessed on 12 November 2025).
- Šverko, Z.; Vrankić, M.; Vlahinić, S.; Rogelj, P. Complex Pearson correlation coefficient for EEG connectivity analysis. Sensors 2022, 22, 1477. [Google Scholar] [CrossRef] [PubMed]
- Marčenko, V.A.; Pastur, L.A. Distribution of eigenvalues for some sets of random matrices. Math. USSR-Sb. 1967, 1, 457. [Google Scholar] [CrossRef]
- Drémeau, A.; Liutkus, A.; Martina, D.; Katz, O.; Schülke, C.; Krzakala, F.; Gigan, S.; Daudet, L. Reference-less measurement of the transmission matrix of a highly scattering material using a DMD and phase retrieval techniques. Opt. Express 2015, 23, 11898–11911. [Google Scholar] [CrossRef]
- Zhao, T.; Ourselin, S.; Vercauteren, T.; Xia, W. Seeing through multimode fibers with real-valued intensity transmission matrices. Opt. Express 2020, 28, 20978–20991. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoryan, E.; Sargsyan, A.; Sarukhanyan, T.; Rafayelyan, M. Single-Path Spatial Polarization Modulation for Vector Transmission Matrix Measurement and Polarization Control in Scattering Media. Photonics 2025, 12, 1145. https://doi.org/10.3390/photonics12111145
Grigoryan E, Sargsyan A, Sarukhanyan T, Rafayelyan M. Single-Path Spatial Polarization Modulation for Vector Transmission Matrix Measurement and Polarization Control in Scattering Media. Photonics. 2025; 12(11):1145. https://doi.org/10.3390/photonics12111145
Chicago/Turabian StyleGrigoryan, Edvard, Aram Sargsyan, Tatevik Sarukhanyan, and Mushegh Rafayelyan. 2025. "Single-Path Spatial Polarization Modulation for Vector Transmission Matrix Measurement and Polarization Control in Scattering Media" Photonics 12, no. 11: 1145. https://doi.org/10.3390/photonics12111145
APA StyleGrigoryan, E., Sargsyan, A., Sarukhanyan, T., & Rafayelyan, M. (2025). Single-Path Spatial Polarization Modulation for Vector Transmission Matrix Measurement and Polarization Control in Scattering Media. Photonics, 12(11), 1145. https://doi.org/10.3390/photonics12111145






