Coherent Perfect Absorption in a Parametric Cavity-Ensemble System
Abstract
1. Introduction
2. Model and Steady-State Solution
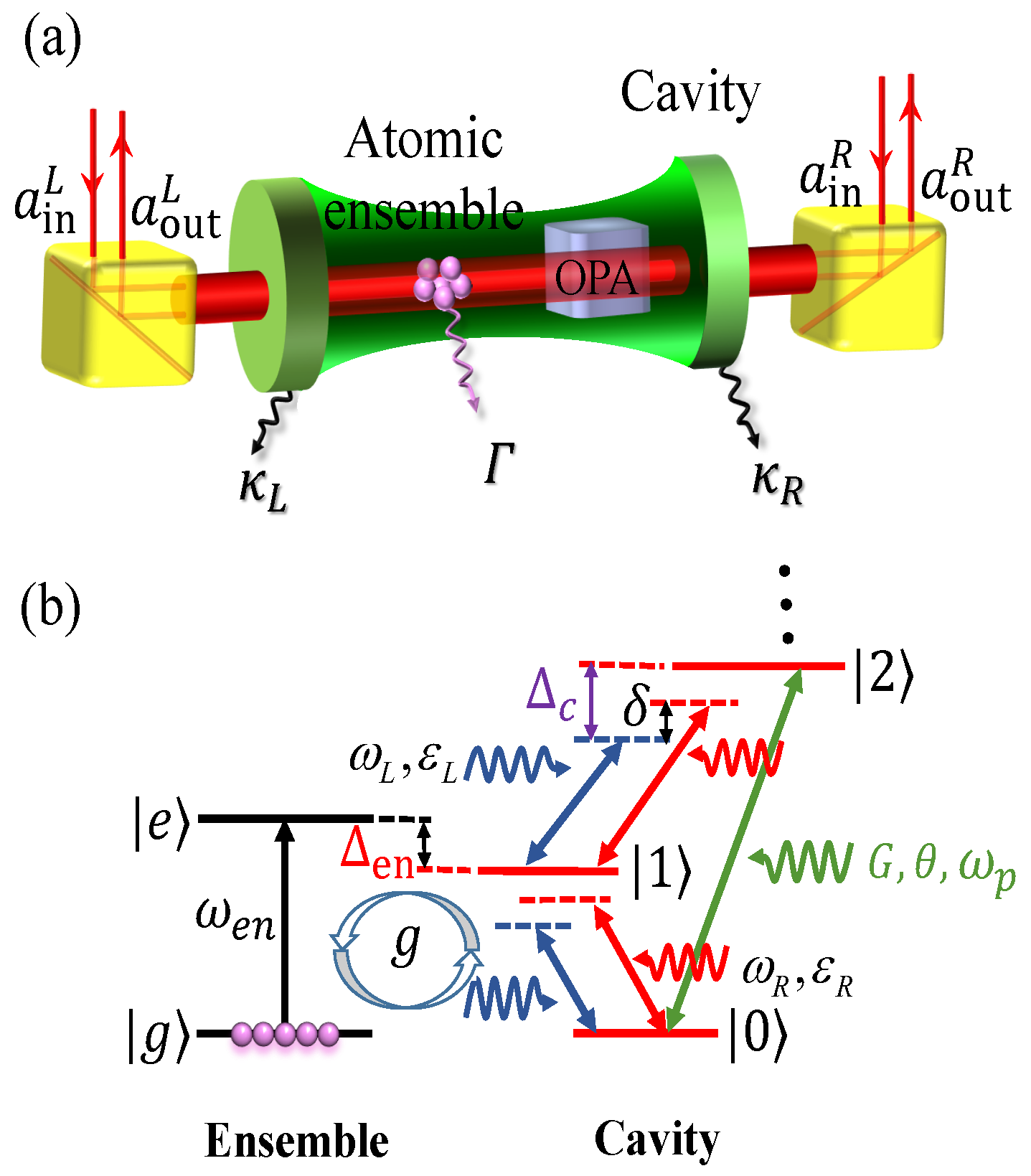
2.1. Model
2.2. Steady-State Solution
3. CPA Condition
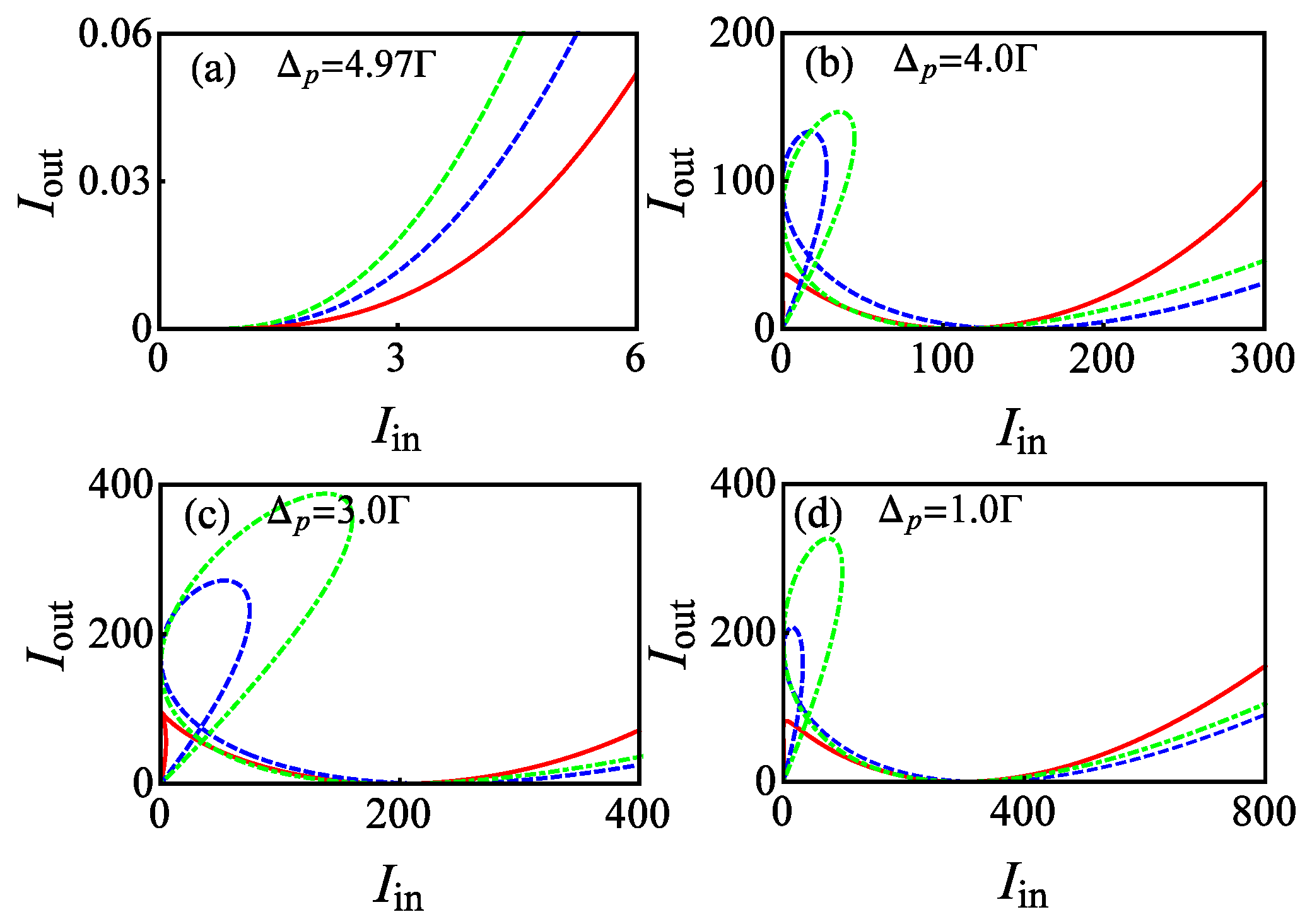
4. CPA
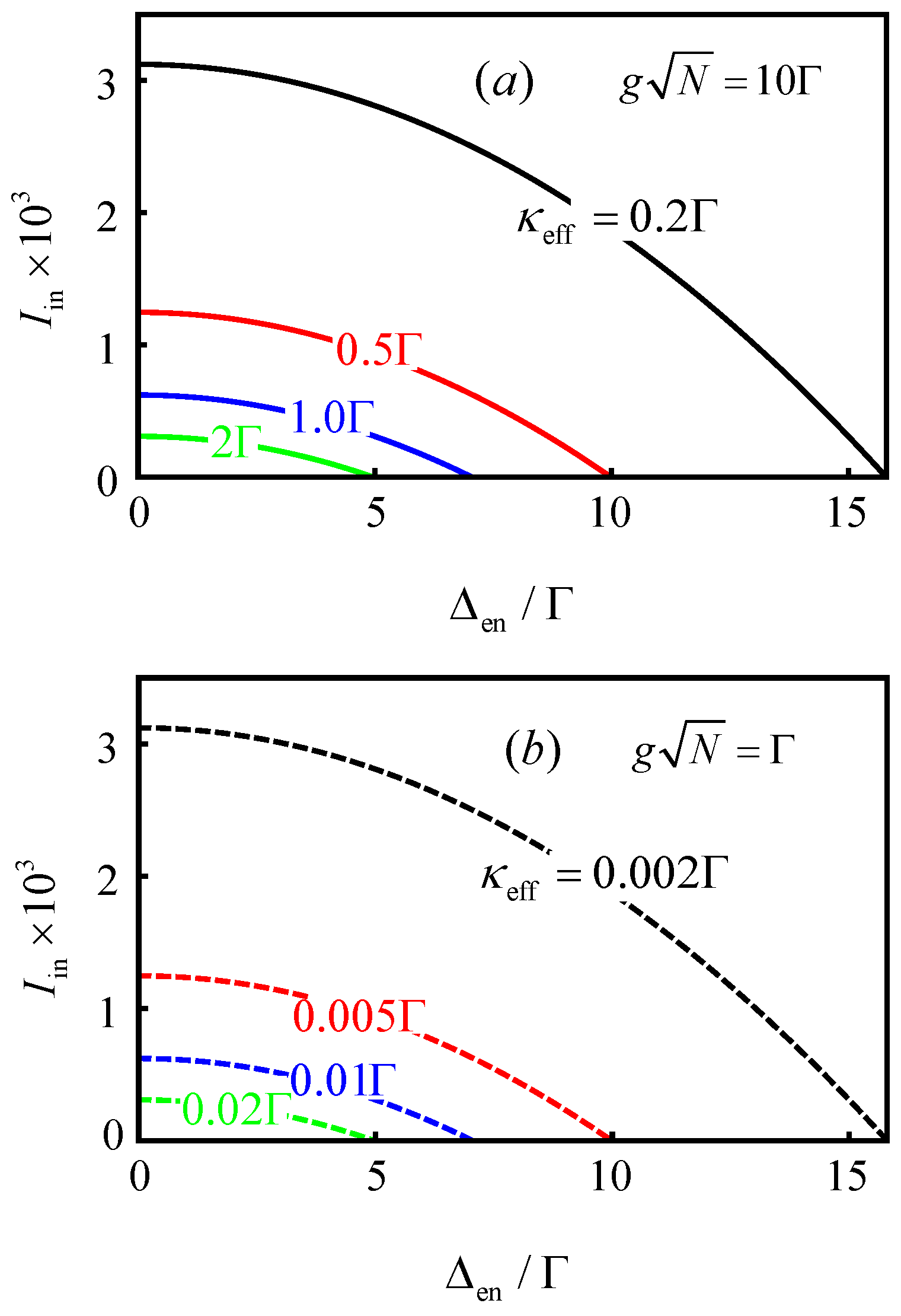
4.1. Strong Coupling
4.2. Weak Coupling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Julsgaard, B.; Sherson, J.; Cirac, J.; Fiurášek, J.; Polzik, E.S. Experimental demonstration of quantum memory for light. Nature 2004, 432, 482. [Google Scholar] [CrossRef]
- Reithmaier, J.P.; Sęk, G.; Löffler, A.; Hofmann, C.; Kuhn, S.; Reitzenstein, S.; Keldysh, L.V.; Kulakovskii, V.D.; Reinecke, T.L.; Forchel, A. Strong coupling in a single quantum dot–semiconductor microcavity system. Nature 2004, 432, 197. [Google Scholar] [CrossRef] [PubMed]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.M.; Rupper, G.; Ell, C.; Shchekin, O.B.; Deppe, D.G. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200. [Google Scholar] [CrossRef] [PubMed]
- Almeida, V.R.; Barrios, C.A.; Panepucci, R.R.; Lipson, M. All-optical control of light on a silicon chip. Nature 2004, 431, 1081. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, T.; Notomi, M.; Mitsugi, S.; Shinya, A.; Kuramochi, E. Fast all-optical switching using ion-implanted silicon photonic crystal nanocavities. Appl. Phys. Lett. 2005, 87, 151112. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon blockade in an optical cavity with one trapped atom. Nature 2005, 436, 87. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Wang, Y.; Xiong, W. Detection sensitivity enhancement of magnon Kerr nonlinearity in cavity magnonics induced by coherent perfect absorption. Phys. Rev. B 2023, 107, 064417. [Google Scholar] [CrossRef]
- Shen, R.C.; Li, J.; Sun, Y.M.; Wu, W.J.; Zuo, X.; Wang, Y.P.; Zhu, S.Y.; You, J.Q. Cavity-magnon polaritons strongly coupled to phonons. Nat. Commun. 2025, 16, 5652. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, X.Q.; Wang, Y.P.; Li, T.F.; You, J.Q. Observation of the exceptional point in cavity magnon–polaritons. Nat. Commun. 2017, 8, 1368. [Google Scholar] [CrossRef]
- Xiong, W.; Chen, J.; Fang, B.; Lam, C.H.; You, J.Q. Coherent perfect absorption in a weakly coupled atom-cavity system. Phys. Rev. A 2020, 101, 063822. [Google Scholar] [CrossRef]
- Wiersma, D.S.; Bartolini, P.; Lagendijk, A.; Righini, R. Localization of light in a disordered medium. Nature 1997, 390, 671. [Google Scholar] [CrossRef]
- Störzer, M.; Gross, P.; Aegerter, C.M.; Maret, G. Observation of the critical regime near Anderson localization of light. Phys. Rev. Lett. 2006, 96, 063904. [Google Scholar] [CrossRef]
- Jović, D.M.; Denz, C.; Belić, M.R. Anderson localization of light in PT-symmetric optical lattices. Opt. Lett. 2012, 37, 4455. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594. [Google Scholar] [CrossRef]
- Melentiev, P.N.; Afanasiev, A.E.; Kuzin, A.A.; Baturin, A.S.; Balykin, V.I. Subwavelength light localization based on optical nonlinearity and light polarization. Opt. Lett. 2013, 38, 2274. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Lukin, M.D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 2000, 84, 5094. [Google Scholar] [CrossRef]
- Zanotto, S.; Mezzapesa, F.P.; Bianco, F.; Biasiol, G.; Baldacci, L.; Vitiello, M.S.; Sorba, L.; Colombelli, R.; Tredicucci, A. Perfect energy-feeding into strongly coupled systems and interferometric control of polariton absorption. Nat. Phys. 2014, 10, 830. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Cao, H.; Stone, A.D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Chong, Y.; Ge, L.; Noh, H.; Stone, A.D.; Cao, H. Time-reversed lasing and interferometric control of absorption. Science 2011, 331, 889. [Google Scholar] [CrossRef] [PubMed]
- Dutta, G.S. Strong-interaction-mediated critical coupling at two distinct frequencies. Opt. Lett. 2007, 32, 1483. [Google Scholar] [CrossRef]
- Gmachl, C.F. Suckers for light. Nature 2010, 467, 37. [Google Scholar] [CrossRef] [PubMed]
- Dutta-Gupta, S.; Deshmukh, R.; Gopal, A.V.; Martin, O.J.F.; Gupta, S.D. Coherent perfect absorption mediated anomalous reflection and refraction. Opt. Lett. 2012, 37, 4452. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.W.; Koh, G.M.; Song, S.H.; Magnusson, R. Measurement and modeling of a complete optical absorption and scattering by coherent surface plasmon-polariton excitation using a silver thin-film grating. Phys. Rev. Lett. 2012, 109, 257402. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Agarwal, G.S. Coherent perfect absorption of path entangled single photons. Opt. Express 2014, 22, 20936. [Google Scholar] [CrossRef]
- Roger, T.; Vezzoli, S.; Bolduc, E.; Valente, J.; Heitz, J.J.F.; Jeffers, J.; Soci, C.; Leach, J.; Couteau, C.; Zheludev, N.I.; et al. Coherent perfect absorption in deeply subwavelength films in the single-photon regime. Nat. Commun. 2015, 6, 7031. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Zhu, Y. Photon trapping in cavity quantum electrodynamics. Phys. Rev. A 2015, 92, 023824. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Di, K.; Wang, L.; Zhu, Y. Perfect photon absorption in the nonlinear regime of cavity quantum electrodynamics. Phys. Rev. A 2016, 93, 063805. [Google Scholar] [CrossRef]
- Wang, L.; Di, K.; Zhu, Y.; Agarwal, G.S. Interference control of perfect photon absorption in cavity quantum electrodynamics. Phys. Rev. A 2017, 95, 013841. [Google Scholar] [CrossRef]
- Agarwal, G.S. Vacuum-field Rabi splittings in microwave absorption by Rydberg atoms in a cavity. Phys. Rev. Lett. 1984, 53, 1732. [Google Scholar] [CrossRef]
- Raizen, M.G.; Thompson, R.J.; Brecha, R.J.; Kimble, H.J.; Carmichael, H.J. Normal-mode splitting and linewidth averaging for two-state atoms in an optical cavity. Phys. Rev. Lett. 1989, 63, 240. [Google Scholar] [CrossRef]
- Zhu, Y.; Gauthier, D.J.; Morin, S.E.; Wu, Q.; Carmichael, H.J.; Mossberg, T.W. Vacuum Rabi splitting as a feature of linear-dispersion theory: Analysis and experimental observations. Phys. Rev. Lett. 1990, 64, 2499. [Google Scholar] [CrossRef] [PubMed]
- Law, C.K. Vacuum Rabi oscillation induced by virtual photons in the ultrastrong-coupling regime. Phys. Rev. A 2013, 87, 045804. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 2014, 113, 083603. [Google Scholar] [CrossRef] [PubMed]
- Abdurakhimov, L.V.; Bunkov, Y.M.; Konstantinov, D. Normal-mode splitting in the coupled system of hybridized nuclear magnons and microwave photons. Phys. Rev. Lett. 2015, 114, 226402. [Google Scholar] [CrossRef]
- Yang, G.; Gu, W.J.; Li, G.; Zou, B.; Zhu, Y. Quantum nonlinear cavity quantum electrodynamics with coherently prepared atoms. Phys. Rev. A 2015, 92, 033822. [Google Scholar] [CrossRef]
- Zhang, Y.; Sohail, A.; Yu, C. Perfect photon absorption in hybrid atom-optomechanical system. Europhys. Lett. 2016, 115, 64002. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Nanomechanical inverse electromagnetically induced transparency and confinement of light in normal modes. New J. Phys. 2014, 16, 033023. [Google Scholar] [CrossRef]
- Colombe, Y.; Steinmetz, T.; Dubois, G.; Linke, F.; Hunger, D.; Reichel, J. Strong atom–field coupling for Bose–Einstein condensates in an optical cavity on a chip. Nature 2007, 450, 272. [Google Scholar] [CrossRef]
- Kubo, Y.; Ong, F.R.; Bertet, P.; Vion, D.; Jacques, V.; Zheng, D.; Dréau, A.; Roch, J.-F.; Auffeves, A.; Jelezko, F.; et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys. Rev. Lett. 2010, 105, 140502. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photonics 2011, 5, 397. [Google Scholar] [CrossRef]
- Hu, X.; Liu, Y.; Nori, F. Strong coupling of a spin qubit to a superconducting stripline cavity. Phys. Rev. B 2012, 86, 035314. [Google Scholar] [CrossRef]
- Mercurio, A.; Abo, S.; Mauceri, F.; Russo, E.; Macrì, V.; Miranowicz, A.; Savasta, S.; Stefano, O.D. Pure dephasing of light-matter systems in the ultrastrong and deep-strong coupling regimes. Phys. Rev. Lett. 2023, 130, 123601. [Google Scholar] [CrossRef] [PubMed]
- Macrì, V.; Mercurio, A.; Nori, F.; Savasta, S.; Sánchez, C. Spontaneous scattering of Raman photons from cavity-QED systems in the ultrastrong coupling regime. Phys. Rev. Lett. 2022, 129, 273602. [Google Scholar] [CrossRef] [PubMed]
- Macrì, V.; Minganti, F.; Kockum, A.F.; Ridolfo, A.; Savasta, S.; Nori, F. Revealing higher-order light and matter energy exchanges using quantum trajectories in ultrastrong coupling. Phys. Rev. A 2022, 105, 023720. [Google Scholar] [CrossRef]
- Minganti, F.; Macrì, V.; Settineri, A.; Savasta, S.; Nori, F. Dissipative state transfer and Maxwell’s demon in single quantum trajectories: Excitation transfer between two noninteracting qubits via unbalanced dissipation rates. Phys. Rev. A 2021, 103, 052201. [Google Scholar] [CrossRef]
- Mollow, B.R.; Glauber, R.J. Quantum theory of parametric amplification. I. Phys. Rev. 1967, 160, 1076. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-W.; Cheng, Y.-X.; Wu, Y.-X.; Chen, J.; Xiong, W. Coherent Perfect Absorption in a Parametric Cavity-Ensemble System. Photonics 2025, 12, 1135. https://doi.org/10.3390/photonics12111135
Li Z-W, Cheng Y-X, Wu Y-X, Chen J, Xiong W. Coherent Perfect Absorption in a Parametric Cavity-Ensemble System. Photonics. 2025; 12(11):1135. https://doi.org/10.3390/photonics12111135
Chicago/Turabian StyleLi, Zi-Wei, Yan-Xue Cheng, Ying-Xia Wu, Jiaojiao Chen, and Wei Xiong. 2025. "Coherent Perfect Absorption in a Parametric Cavity-Ensemble System" Photonics 12, no. 11: 1135. https://doi.org/10.3390/photonics12111135
APA StyleLi, Z.-W., Cheng, Y.-X., Wu, Y.-X., Chen, J., & Xiong, W. (2025). Coherent Perfect Absorption in a Parametric Cavity-Ensemble System. Photonics, 12(11), 1135. https://doi.org/10.3390/photonics12111135




