Numerical Investigation of Idler Pulse Generation by Four-Wave Mixing in Nonlinear Optical Ring Resonator

Abstract

Generation of idler pulses via the four-wave mixing (FWM) effect in a nonlinear optical ring resonator (NORR) was investigated numerically. It was found that the relative delay $\tau$ between input pump pulses significantly affects both the energy and temporal–spectral characteristics of generated idler pulses. Specifically, idler pulse energy decreases with increasing $\tau$ due to phase-matching conditions in FWM. Maximum energy transfer occurs for $\tau$ = 0, where optimal phase alignment among pump, signal, and idler waves is achieved. Temporal and spectral analysis at different relative delays reveals a change from a symmetric, multi-subpulse structure with a comb-like spectrum (for $\tau$ = 0) to a near-single-pulse form with a single-comb-line spectrum (for $\tau$ = 9 ps). These findings demonstrate the critical dependence of FWM efficiency on pump pulse synchronization. Therefore, precise control of the relative delay is essential for optimizing idler pulse generation in NORRs.

1. Introduction

Nonlinear optical ring resonators (NORRs) are a class of photonic devices that exploit the nonlinear optical properties of materials to enable a variety of functionalities. These devices consist of a closed-loop waveguide, typically in the form of a circular or racetrack geometry, which acts as an optical resonator [1]. When pump light is coupled into the ring resonator, it can circulate multiple times within the loop, leading to the buildup of optical intensity. The high intensity, combined with the nonlinear optical properties of the materials utilized to create the resonator, can give rise to a range of nonlinear optical effects, such as four-wave mixing, the Kerr effect, and parametric amplification [2]. Its performance is critically reliant on the design parameters, such as the resonator geometry, the choice of materials, and the coupling conditions. Careful optimization of these parameters is decisive to achieve the desired nonlinear optical effects and device functionality [3].

Four-wave mixing (FWM) is a nonlinear optical process that occurs in materials with a third-order nonlinear susceptibility, ${\chi }^3$. In this process, three input waves at frequencies ${\omega }_1$, ${\omega }_2$ (known as the frequencies of the pump), and ${\omega }_3$ (signal) interact to generate a fourth wave at a frequency ${\omega }_4$ (idler) that satisfies the energy conservation condition: ${\omega }_4$ = ${\omega }_1$ ± ${\omega }_2$ ± ${\omega }_3$ [2]. When FWM occurs in an NORR, the circulating waves can experience significant enhancement due to the resonant nature of the cavity. This can lead to efficient generation of new frequency components and the potential for applications such as wavelength conversion, parametric amplification, and optical frequency comb generation [4,5]. The dynamics of FWM are governed by a set of coupled-mode equations that take into account the dispersion, nonlinearity, and coupling of the various frequency components. Analytical and numerical models have been developed to study FWM process in these materials [6,7].

In several experiments, researchers have demonstrated the use of silicon ring resonators to generate entangled photon pairs via spontaneous FWM, which is excited by a pulsed pump laser [8,9]. These photons are produced at wavelengths around 1550 nm—the standard wavelength for conventional fiber-optic communication. This wavelength is chosen because optical fibers are most transparent to it, minimizing signal loss over long distances [10], a feature essential for building a practical quantum network.

The objective of this study is to present a numerical investigation of idler pulse generation by degenerate FWM in an NORR. Through simulations of a set of nonlinear coupled-mode equations, it is analyzed how the relative delay between the pump pulses affects the energy and temporal–spectral characteristics of the generated idler pulses. It is found that variations in relative delay strongly impact FWM efficiency by altering phase-matching conditions. As a consequence, the generated idler pulses evolve toward a near-single-pulse profile with a single-comb-line spectrum. These findings demonstrate the importance of pump pulse synchronization in controlling FWM efficiency and customizing idler pulse characteristics for applications in the fields of integrated photonics and optical technology [11,12].

2. Theoretical Model and Numerical Procedure

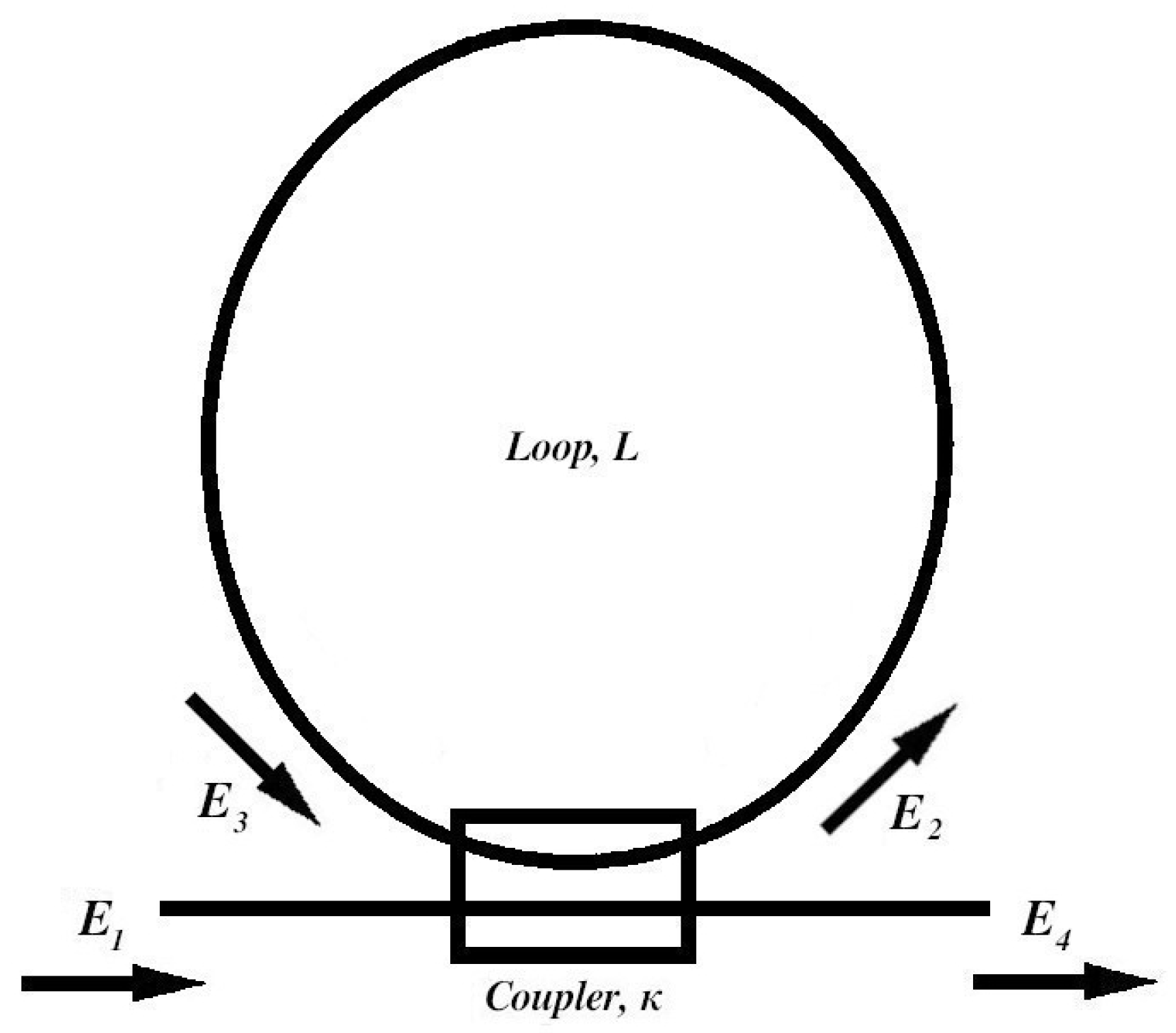
The basic configuration of an NORR is shown in Figure 1. Two ports of a low-loss single-mode directional coupler are joined by a loop of a monomode waveguide and the other two ports are used for power input and output. The equations connecting the input and output fields shown in Figure 1 for an X coupler are given by [13]

$$\begin{array}{ccc}\hfill E_2& =& i{(1-\kappa )}^{1/2}{E}_1+{\kappa }^{1/2}{E}_3,\hfill \end{array}$$

(1a)

$$\begin{array}{ccc}\hfill E_4& =& {\kappa }^{1/2}{E}_1+i{(1-\kappa )}^{1/2}{E}_3,\hfill \end{array}$$

(1b)

where $\kappa$ is the coupling coefficient.

After the coupled-mode interaction, the dynamics of FWM along the fiber ring from $z=0$ to $z=L$ can be described using the nonlinear coupled-mode equations for the pump $E_p$, signal $E_s$, and idler $E_i$. These differential equations may be expressed as [2,14]

$${\displaystyle \frac{\partial E_p}{\partial z}}+{\displaystyle \frac{i}{2}}{\beta }_2{\displaystyle \frac{{\partial }^2{E}_p}{\partial t^2}}+{\displaystyle \frac{1}{2}}\alpha E_p=i\gamma [(|E_p{|}^2+2|E_s{|}^2+2|E_i{|}^2)E_p+2E_p^{\ast }{E}_s{E}_i{e}^{i\Delta kz}],$$

(2)

$${\displaystyle \frac{\partial E_s}{\partial z}}+{\displaystyle \frac{i}{2}}{\beta }_2{\displaystyle \frac{{\partial }^2{E}_s}{\partial t^2}}+{\displaystyle \frac{1}{2}}\alpha E_s=i\gamma [(|E_s{|}^2+2|E_i{|}^2+2|E_p{|}^2)E_s+2E_i^{\ast }{E}_p^2{e}^{-i\Delta kz}],$$

(3)

$${\displaystyle \frac{\partial E_i}{\partial z}}+{\displaystyle \frac{i}{2}}{\beta }_2{\displaystyle \frac{{\partial }^2{E}_i}{\partial t^2}}+{\displaystyle \frac{1}{2}}\alpha E_i=i\gamma [(|E_i{|}^2+2|E_p{|}^2+2|E_s{|}^2)E_i+2E_s^{\ast }{E}_p^2{e}^{-i\Delta kz}],$$

(4)

where z and t are space and time coordinates. The parameters ${\beta }_2$ and $\alpha$ are the second-order chromatic dispersion and loss rate, respectively. The parameter $\gamma$ represents the Kerr nonlinearity and is proportional to the nonlinear refraction index $n_2$ [2]. The term $\Delta k$ is the magnitude of the wave-vector mismatch and may be defined as

$$\Delta k=k_s+k_i-2k_p,$$

(5)

where $k_j=\overline{n}{\omega }_j/c$$(j=p,s,i)$ is the propagation constant, $\overline{n}$ is the average refractive index change of the fiber mode, ${\omega }_j$ is the carrier frequency at which the pulse spectrum is centered, and c is the speed of light in vacuum.

Now, assuming the undepleted pump field approximation [2], the fiber loss and the second-order chromatic dispersion are neglected in Equations (2)–(4). The pumping power is taken to be so large as to be dominant. Therefore, the pumping light is not subject to FWM-induced reaction. The signal light and the idler light are of about the same magnitude and interact together through FWM. Under these simplifying conditions, and introducing one more equation for a second pump field, we obtain the following nonlinear coupled-mode equations:

$${\displaystyle \frac{\partial E_{p_1}}{\partial z}}=i\gamma (|E_{p_1}{|}^2+2|E_{p_2}{|}^2)E_{p_1},$$

(6)

$${\displaystyle \frac{\partial E_{p_2}}{\partial z}}=i\gamma (|E_{p_2}{|}^2+2|E_{p_1}{|}^2)E_{p_2},$$

(7)

$${\displaystyle \frac{\partial E_s}{\partial z}}=2i\gamma (|E_{p_1}{|}^2+|E_{p_2}{|}^2)E_s+2i\gamma E_{p_1}{E}_{p_2}{E}_i^{\ast }{e}^{-i\Delta kz},$$

(8)

$${\displaystyle \frac{\partial E_i}{\partial z}}=2i\gamma (|E_{p_1}{|}^2+|E_{p_2}{|}^2)E_i+2i\gamma E_{p_1}{E}_{p_2}{E}_s^{\ast }{e}^{-i\Delta kz},$$

(9)

where $E_{p_1}$ and $E_{p_1}$ denote electric-field amplitudes for the input pump pulses.

Equations (6)–(9) form the mathematical model for our numerical simulation. It is assumed that the input pulses to NORR are Gaussian pulses given by

$$E_{p_1}(0,t)=E_{0}exp\left(-{\displaystyle \frac{t^2}{2T_0^2}}\right),$$

(10)

$$E_{p_2}(0,t)=E_{0}exp\left[-{\displaystyle \frac{{(t-\tau )}^2}{2T_0^2}}\right],$$

(11)

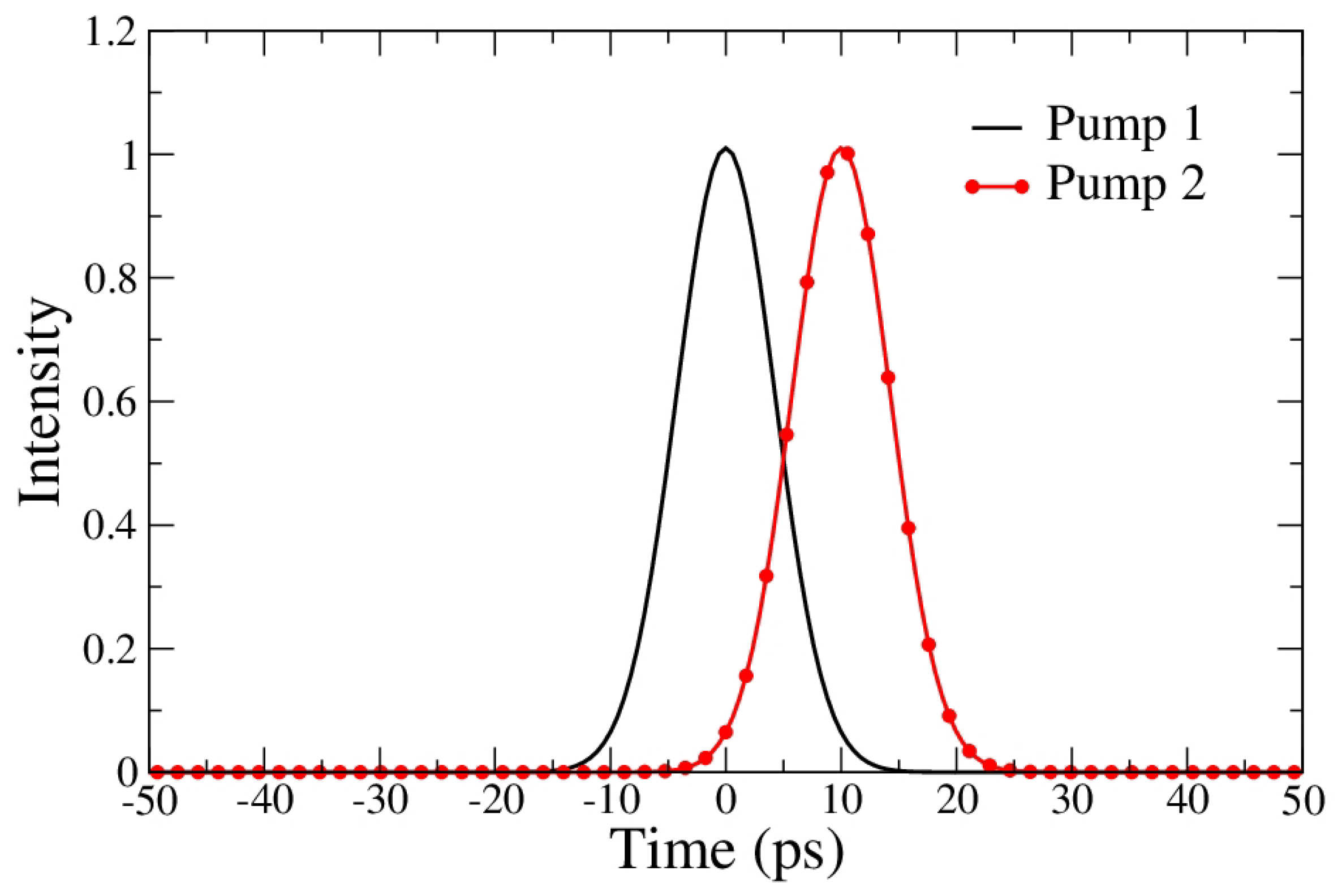
where $E_0$ is the initial electric-field amplitude, $T_0$ is the initial pulsewidth, and $\tau$ is the relative delay between the two input pump pulses. Figure 2 shows the temporal shapes of the input pump pulses for $\tau$ = 10 ps. As in Equation (10), Gaussian pulses were also assumed for the signal $E_s$ and idler $E_i$. The output pulse energy can be evaluated by

$$U_{out}={\int }_{-\infty }^{\infty }{|E(nL,t)|}^{2}dt,$$

(12)

where E is the output amplitude and n is the number of times the pulses propagate within the loop L.

The NORR interferometer is considered to have a fiber waveguide of length L = 20 cm and a coupling coefficient $\kappa$ = 0.5. The fiber parameter $\gamma$ = 20/Wkm has been used in Equations (6)–(9), as well as the initial phase-matching condition, $\Delta k$ = 0, in order to obtain efficient FWM [15]. The input pump pulses have initial $T_{FWHM}$ = 10 ps ($T_{FWHM}=1.66T_0$ is the full width at half maximum) at 1550 nm and the signal pulse has also an initial $T_{FWHM}$ of 10 ps but at 1547 nm, while the initial idler pulse is set at $E_i(0,t)$ = 0. The set of coupled Equations (6)–(9) was numerically solved by using the fourth-order Runge–Kutta method [16] for n = 112.

3. Results and Discussion

The energy of the idler pulse generated in an NORR as a function of the relative delay between the input pump pulses is shown in Figure 3. It is noted that the energy decreases as the relative delay increases, reaching a minimum value when $\tau \approx$ 6.7 ps, revealing the great influence of the relative delay. This influence stems from the phase-matching conditions necessary for effective FWM to take place. In fact, in the process of FWM, energy is transferred from the pump pulses to create new frequency components, including the idler pulses. For this energy transfer to be efficient, the phase velocities of the pump, signal, and idler waves must be aligned. Hence, this phasematching is particularly sensitive to the relative delay between the pump pulses. When $\tau$ is adjusted to meet the phase-matching condition, the energy transfer to the idler pulses reaches its maximum ($\tau$ = 0 according to Figure 3). On the other hand, if the relative delay is not aligned correctly, the phase-matching could be suboptimal, leading to a significant decrease in the energy of the generated idler pulses. Therefore, optimizing this relative delay is essential for achieving efficient idler pulse generation in NORRs.

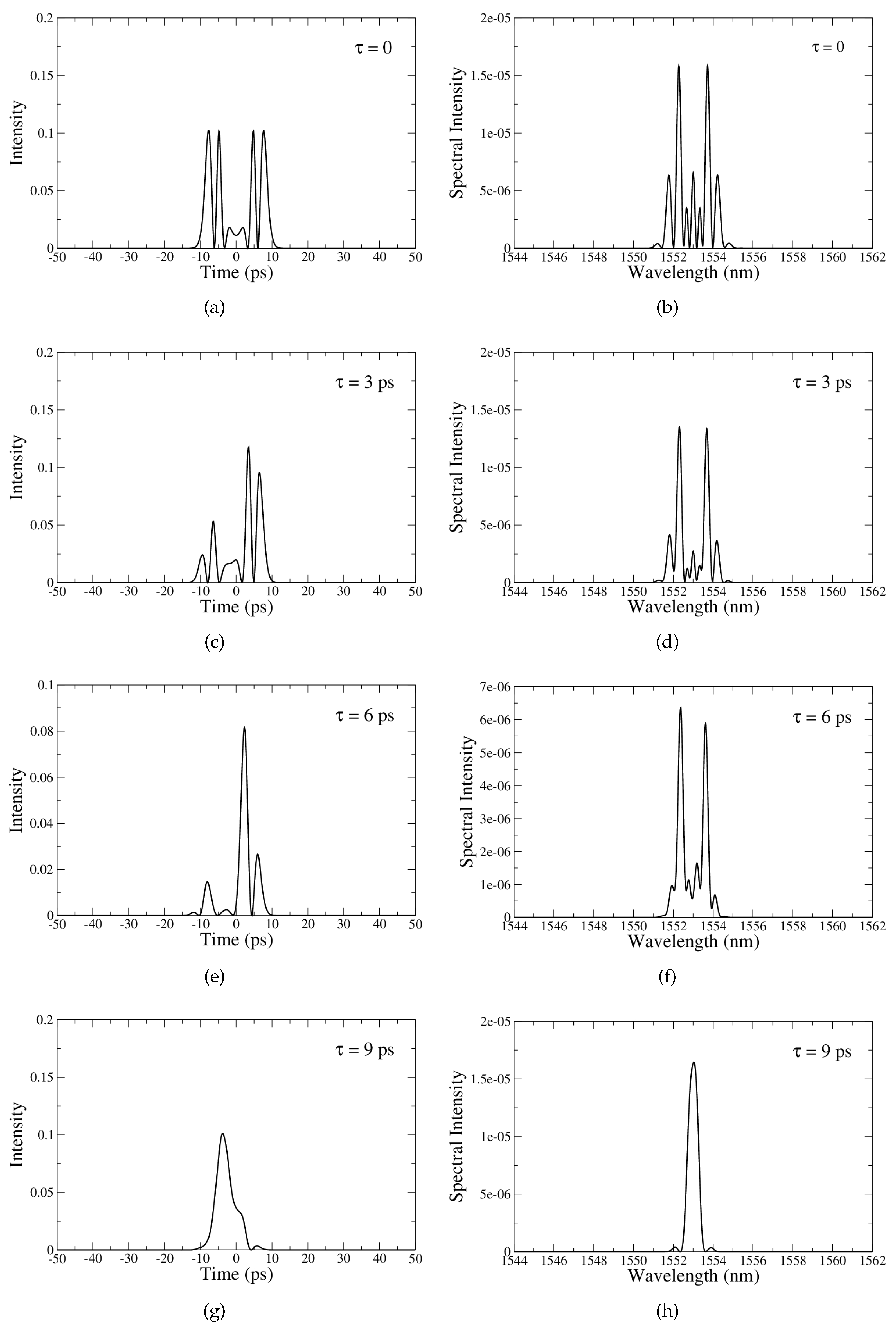
In order to gain an understanding of the idler pulse dependence of the relative delay between input pump pulses in NORRs, the temporal shapes and spectra of the generated idler pulses are plotted in Figure 4 for $\tau$ = 0, 3, 6, and 9 ps. It can be seen in Figure 4a that the idler pulse consists of a central subpulse followed by four side subpulses in the time domain for $\tau$ = 0, exhibiting a symmetric temporal profile. The subpulses have approximately the same width and the same amplitude, except for the central subpulse. The corresponding spectrum, shown in Figure 4b, exhibits a comb-like spectrum owing to the nonlinear effect of FWM, as expected [5]. The comb lines are equally spaced and have a very narrow linewidth (excluding resonant modes near the boundary that are still in the generation process).

The temporal shape of the generated idler pulse for $\tau$ = 3 ps is shown in Figure 4c. The qualitative feature is that the temporal shape of the pulse becomes asymmetric. This asymmetry has its origin in the phase-matching conditions. The leading edge of the pulse ($t<0$) experiences a greater decrease in intensity than the trailing edge once the energy decreases. The corresponding spectrum in Figure 4d still shows a comb-like structure, but with diminished comb line intensity due to the energy reduction. Figure 4e and Figure 4f show the temporal shape and spectrum of the generated idler pulse for $\tau$ = 6 ps, respectively. A comparison of pulse shapes in Figure 4a,e reveals a dramatic difference as $\tau$ increases. Both the intensity and number of subpulses show a decreasing trend. Similarly, comparative analysis of the spectra in Figure 4b,f demonstrates significant changes in both the intensity and number of comb lines, showing a decreasing trend. Finally, Figure 4g and Figure 4h show the temporal shape and spectrum of the generated idler pulse for $\tau$ = 9 ps, respectively. In this case, the generated idler pulse manifests as a single pulse with slight pedestal formation in the time domain, while the corresponding spectrum exhibits a single comb line (again excluding boundary resonant modes).

Therefore, according to numerical simulations, a remarkable transformation occurs in the generated idler pulse structure as $\tau$ increases. For $\tau$ = 0, the generated idler pulse has a symmetric, multi-subpulse temporal profile with a comb-like spectrum. However, for $\tau$ = 9 ps, it changes to a nearly single-pulse profile with a single-comb-line spectrum. These observations indicate that precise synchronization of the input pump pulses is essential to control FWM efficiency and tailor idler pulse characteristics.

4. Conclusions

A numerical simulation of the idler pulse generation in an NORR by the FWM effect was presented. This study demonstrates that the energy and characteristics of the generated idler pulse are highly dependent on the relative delay ($\tau$) between the input pump pulses. The energy of the idler pulse decreases as $\tau$ increases, reaching a minimum at $\tau \approx$ 6.7 ps, emphasizing the importance of phase-matching conditions in the FWM process. Optimal energy transfer occurs when $\tau$ = 0, ensuring proper phase alignment between the pump, signal, and idler waves. Any deviations from this ideal condition can lead to reduced efficiency and asymmetric temporal profiles in the idler pulses.

Further analysis of temporal shapes and spectra at different relative delays ($\tau$ = 0, 3, 6, and 9 ps) reveals that the idler pulse changes from a symmetric, multi-subpulse structure with a comb-like spectrum for $\tau$ = 0 to a nearly single-pulse profile with a significantly diminished spectrum for $\tau$ = 9 ps. This change occurs due to the sensitivity of FWM efficiency to pump pulse synchronization. Therefore, precise control over the relative delay is essential for optimizing idler pulse generation in NORRs, providing high efficiency and desired spectral properties for practical applications in nonlinear optics.