Nonparaxial Exploding Cylindrical Vector Beams
Abstract
1. Introduction
2. Theory and Methods
2.1. Paraxial Exploding Vortex Beam
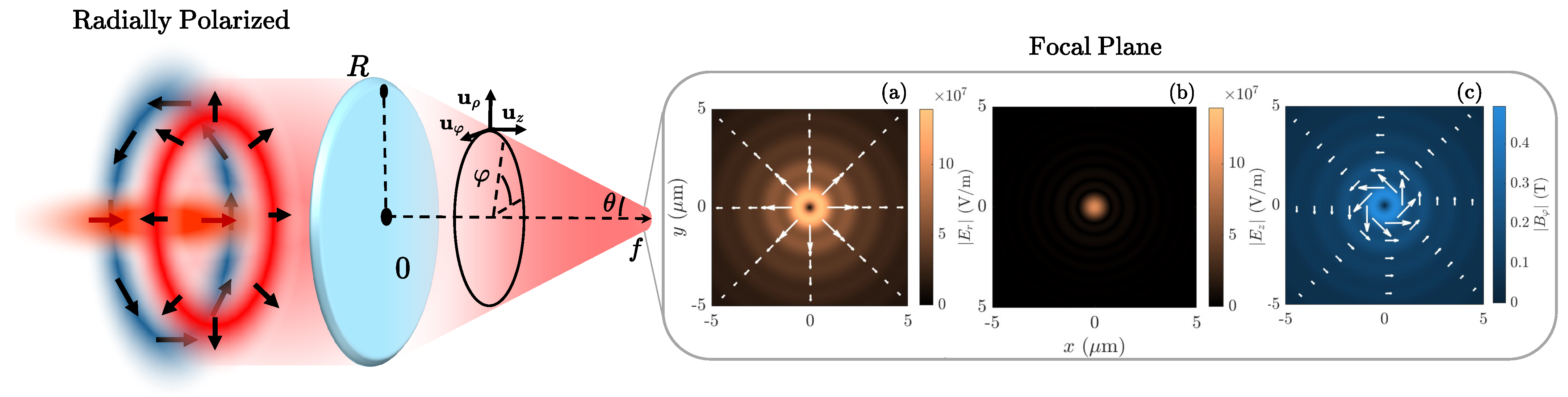
2.2. Tightly Focused Exploding Cylindrical Vector Beams
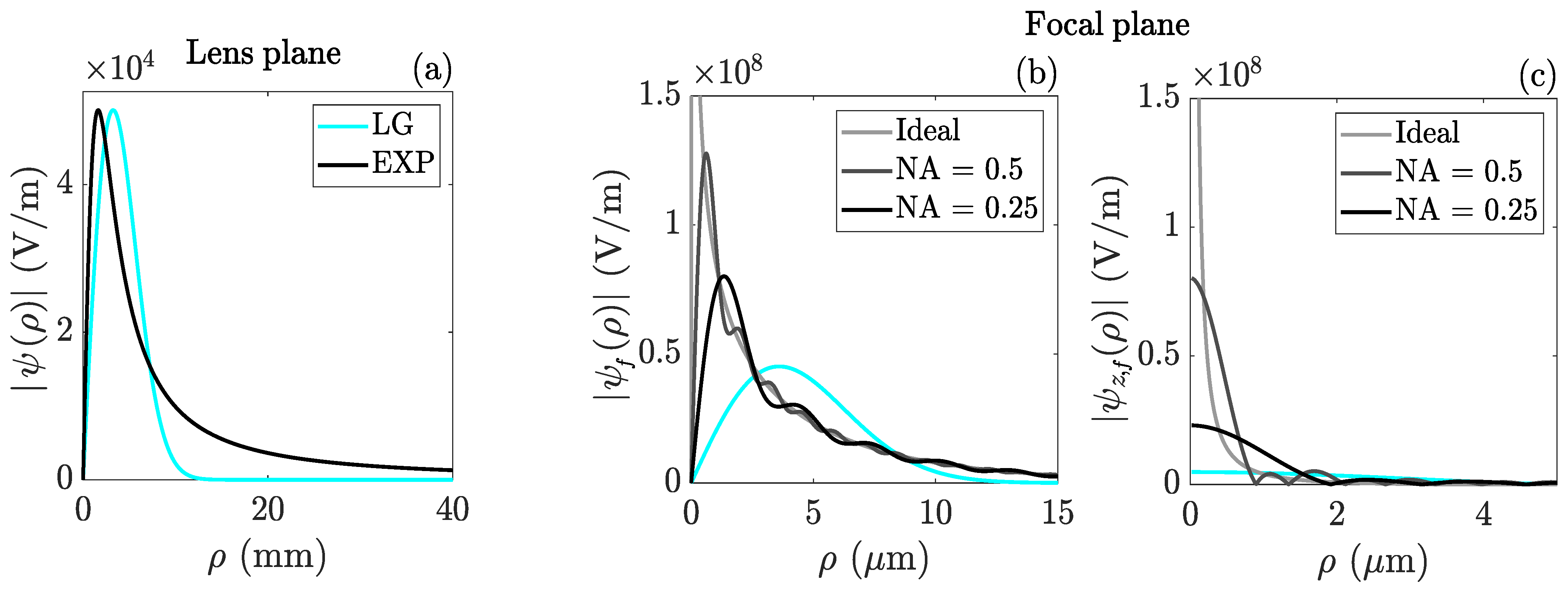
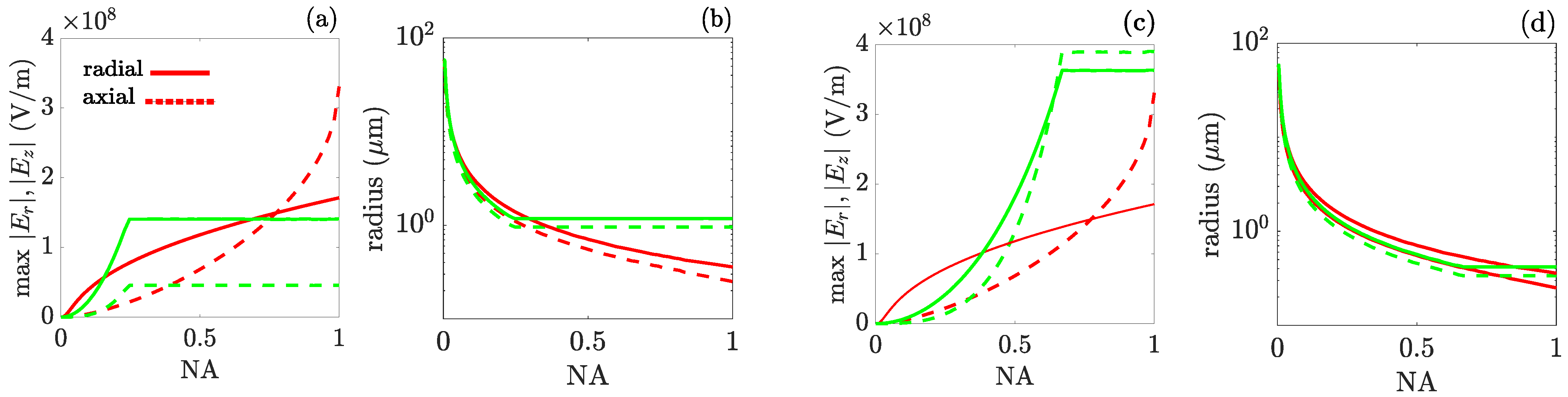
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Optical Vortices and Polarization Singularities. Prog. Opt. 2009, 53, 293–363. [Google Scholar]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. A 1974, 336, 165–190. [Google Scholar]
- Berry, M.V.; Upstill, C. IV catastrophe optics: Morphologies of caustics and their diffraction patterns. Prog. Opt. 1980, 18, 257–346. [Google Scholar]
- Zeng, L.; Zeng, J. Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities. Commun. Phys. 2020, 3, 26. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A. Beam nonparaxiality, filament formation, and beam breakup in the self-focusing of optical beams. J. Opt. Soc. Am. B 1988, 5, 633–640. [Google Scholar] [CrossRef]
- Peres, A. Quantum Theory: Concepts and Methods, 5th ed.; Kluwer Academic Publishers: San Diego, CA, USA, 1994. [Google Scholar]
- Aiello, A. Spontaneous generation of singularities in paraxial optical fields. Opt. Lett. 2016, 41, 1668–1671. [Google Scholar] [CrossRef]
- Porras, M.A. Exploding paraxial beams, vortex beams, and cylindrical beams of light with finite power in linear media, and their enhanced longitudinal field. Phys. Rev. A 2021, 103, 033506. [Google Scholar] [CrossRef]
- Barriopedro, M.G.; Holguín, M.; de Lara-Montoya, P.; Mata-Cervera, N.; Porras, M.A. Three-Dimensional Exploding Light Wave Packets. Photonics 2024, 11, 652. [Google Scholar] [CrossRef]
- Aiello, A.; Paúr, M.; Stoklasa, B.; Hradil, Z.; Řeháček, J.; Sánchez-Soto, L.L. Observation of concentrating paraxial beams. Osa Contin. 2020, 3, 2387–2394. [Google Scholar] [CrossRef]
- Mata-Cervera, N.; Sharma, D.K.; Maruthiyodan Veetil, R.; Mass, T.W.W.; Porras, M.A.; Paniagua-Domínguez, R. Observation of Exploding Vortex Beams Generated by Amplitude and Phase All-Dielectric Metasurfaces. ACS Photonics 2024, 11, 2713–2721. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper Focus for a Radially Polarized Light Beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef]
- Chen, Y.F.; Lu, T.H.; Huang, K.F. Hyperboloid Structures Formed by Polarization Singularities in Coherent Vector Fields with Longitudinal-Transverse Coupling. Phys. Rev. Lett. 2006, 97, 233903. [Google Scholar] [CrossRef]
- Burresi, M.; Engelen, R.J.P.; Opheij, A.; van Oosten, D.; Mori, D.; Baba, T.; Kuipers, L. Observation of Polarization Singularities at the Nanoscale. Phys. Rev. Lett. 2009, 102, 033902. [Google Scholar] [CrossRef]
- Zhen, W.; Ren, Z.C.; Wang, X.L.; Ding, J.; Wang, H.T. Polarization structure transition of C-point singularities upon reflection. Sci. China Phys. Mech. Astron. 2025, 68, 244211. [Google Scholar] [CrossRef]
- Zeng, Y.; Hu, G.; Liu, K.; Tang, Z.; Qiu, C.W. Dynamics of Topological Polarization Singularity in Momentum Space. Phys. Rev. Lett. 2021, 127, 176101. [Google Scholar] [CrossRef]
- Gao, S.; Speirits, F.C.; Castellucci, F.; Franke-Arnold, S.; Barnett, S.M.; Götte, J.B. Paraxial skyrmionic beams. Phys. Rev. A 2020, 102, 053513. [Google Scholar] [CrossRef]
- Lax, M.; Louisell, W.H.; McKnight, W.B. From Maxwell to paraxial wave optics. Phys. Rev. A 1975, 11, 1365. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Wen, M.; Salamin, Y.I.; Keitel, C.H. Electron acceleration by a radially-polarized laser pulse in a plasma micro-channel. Opt. Express 2019, 27, 557–566. [Google Scholar] [CrossRef]
- Zurita-Sánchez, J.R.; Novotny, L. Multipolar interband absorption in a semiconductor quantum dot. II. Magnetic dipole enhancement. J. Opt. Soc. Am. B 2002, 19, 2722–2726. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barriopedro, M.G.; Holguín, M.; Porras, M.A. Nonparaxial Exploding Cylindrical Vector Beams. Photonics 2025, 12, 1083. https://doi.org/10.3390/photonics12111083
Barriopedro MG, Holguín M, Porras MA. Nonparaxial Exploding Cylindrical Vector Beams. Photonics. 2025; 12(11):1083. https://doi.org/10.3390/photonics12111083
Chicago/Turabian StyleBarriopedro, Marcos G., Manuel Holguín, and Miguel A. Porras. 2025. "Nonparaxial Exploding Cylindrical Vector Beams" Photonics 12, no. 11: 1083. https://doi.org/10.3390/photonics12111083
APA StyleBarriopedro, M. G., Holguín, M., & Porras, M. A. (2025). Nonparaxial Exploding Cylindrical Vector Beams. Photonics, 12(11), 1083. https://doi.org/10.3390/photonics12111083




