Abstract
With the rapid advancement of infrared detection technology, the development of infrared stealth materials has become a pressing need. The study of optical micro/nano infrared stealth materials, which possess selective infrared radiation properties and precise structural features, is of significant importance. By integrating deep reinforcement learning with a multilayer perceptron, we have framed the design of radiation-selective films as a reinforcement learning problem. This approach led to the creation of a Ge/Ag/Ge/Ag multilayer micro/nano optical film that exhibits infrared stealth characteristics. During the design process, the agent continuously adjusts the thickness parameters of the optical film, exploring and learning within the defined design space. Upon completion of the training, the agent outputs the optimized thickness parameters. The results demonstrate that the film structure, optimized by the agent, exhibits a low average emissivities of 0.086 and 0.147 in the 3∼5 µm and 8∼14 µm atmospheric windows, respectively, meeting the infrared stealth requirements in terms of radiation characteristics. Additionally, the film demonstrates a high average emissivity of 0.75 in the 5∼8 µm range, making it effective for thermal radiation management. Furthermore, we coated the Si surface with the designed thin film and conducted experimental validation. The results show that the coated material exhibits excellent infrared stealth properties.
1. Introduction
Infrared stealth technology involves reducing or modifying the infrared radiation characteristics of a target to decrease its detectability, which is of significant importance in modern military applications [1,2]. According to the Stefan–Boltzmann law, reducing the emissivity of a target and controlling its surface temperature are fundamental methods for achieving infrared stealth. Due to constraints such as environmental conditions, altering the surface temperature of an object is often challenging, making the control of spectral emissivity a more feasible approach. However, achieving a balance between low emissivity and effective thermal management through heat dissipation is challenging. Therefore, the current requirements for low emissivity infrared stealth materials are as follows: (1) low emissivity in the 3∼5 µm and 8∼14 µm atmospheric window bands to evade infrared detection; (2) high emissivity in the 5∼8 µm non-atmospheric window bands to facilitate thermal radiation management [3,4]. Zhang et al. fabricated one-dimensional Ge/ZnS photonic crystals, achieving average emissivities as low as 0.046 and 0.190 in the atmospheric windows of 3∼5 µm and 8∼14 µm, respectively, and an average emissivity as high as 0.579 in the non-atmospheric window of 5∼8 µm [5]. Zhu et al. combined Ge/ZnS photonic crystals with the thermal insulating material silica aerogel to achieve infrared stealth at high temperatures [6].
At present, various methods have been developed to achieve emissivity regulation on target surfaces, including metamaterials [7,8,9,10], phase change materials [11,12], photonic crystals [5,13], and multilayer films [14]. Among these, multilayer films control the reflection, transmission, and absorption characteristics of incident light by alternately stacking different materials. Due to their simple structure and ease of large-scale manufacturing, they have become prominent in the field of infrared stealth materials in recent years. Peng et al. proposed a simple Ge/Ag/Ge/Ag four-layer metal film structure that balances strong infrared stealth performance and high thermal dissipation [15]. Zhu et al. proposed a structure composed of ZnS/Ge multilayer films and Cu-ITO-Cu metasurface to achieve multispectral camouflage across visible light, infrared, laser, and microwave ranges [16]. Unlike the previously mentioned four-layer Ge/Ag multilayer film, the Ge/ZnS multilayer film adopts an eleven-layer structure. This structure not only integrates infrared stealth capabilities in the MWIR and LWIR bands and laser stealth at 1.55 µm and 10.6 µm but also achieves visible-light stealth through the top ZnS layer.
In recent research on multilayer film design, beyond intuitive methods based on human experience and intuition, there has been a growing focus on using efficient and intelligent approaches for inverse design [17]. The inverse design method generates the corresponding sample structure based on the target spectral properties. Classic optimization algorithms include genetic algorithms [18,19], evolutionary strategy [20], simulated annealing [21], particle swarm optimization [22,23], and topology optimization [24]. However, a limitation of these algorithms is that their computational complexity increases exponentially with the number of parameters. An alternative approach is using neural networks for the inverse design of material structures [25,26]. Liu et al. proposed using tandem neural networks in micro-nano photonic structure design to address the non-uniqueness problem encountered in the inverse design of photonic devices using deep neural networks [27]. Guan et al. applied tandem neural networks to the design of film colors in colored radiative cooling films, successfully identifying the bottom nano-cavity structures corresponding to arbitrary colors, thereby minimizing color matching errors [28]. Wang et al. introduced tandem neural networks into the design of circular hole metamaterials for infrared stealth, achieving multi-band compatible infrared stealth [29]. However, these deep neural network-based design methods can be labor-intensive, often requiring substantial amounts of training data and extensive data preprocessing.
Reinforcement learning is a prominent artificial-intelligence algorithm that, unlike deep neural networks, does not require a pre-existing dataset. Instead, it learns and completes complex tasks through exploration and interaction with the environment. Deep reinforcement learning algorithms combine reinforcement learning with deep neural networks (DNNs), enabling agents to develop a more robust understanding of complex environments. These algorithms have been increasingly applied to the design of multilayer films and metamaterials in recent years. Jiang et al. employed Deep Q-Network (DQN) for the design of multilayer optical films, optimizing a solar absorber without any human intervention [30]. Liao et al. combined deep neural networks and the Proximal Policy Optimization algorithm for the intelligent design of flexible target chiral meta-surfaces, achieving optimal absolute circular dichroism values with high time efficiency in the training results [31]. Yu et al. proposed a general framework for emissivity engineering using DQN, which can be widely applied in the design of thermal metamaterials [32]. However, this method requires real-time computation of transmission matrices during intelligent design, leading to high computational costs.
Research on the intelligent design of materials with both infrared stealth and thermal radiation management properties is limited, and the advantages of reinforcement learning have yet to be fully applied to the design and optimization of infrared stealth materials. In this work, we apply the Deep Q-Network (DQN) algorithm to adjust the thickness of a multilayer Ge/Ag/Ge/Ag micro-nano film structure. A virtual design environment based on a multilayer perceptron is established, where the process of adjusting the film thickness is treated as a Markov decision process, enabling automated adjustment and design of the film. Benefiting from a pre-trained MLP, the agent can rapidly generate spectral responses based on the current state, thereby replacing complex electromagnetic computations. This significantly enhances the learning efficiency of the DQN during exploration. Compared to the previously proposed four-layer Ge/Ag structure [15], the design obtained through machine exploration achieves an average absorption reduction of 0.1 in the 3∼5 µm and 8∼14 µm bands, a higher absorption peak in the 5∼8 µm band, and it is observed that the fourth Ag layer has no significant effect on the absorption spectrum. The results show that the agent can efficiently explore and learn the design environment, with the automatically designed structures demonstrating excellent performance.
2. Model and Method
2.1. Setting Up the Design Environment
As shown in Figure 1, the design space for the target problem consists of a four-layer Ge/Ag/Ge/Ag structure. The thickness parameters for these layers, from top to bottom, are represented as l1, l2, l3, and l4, with the surrounding environment considered as air. Even small changes in the thickness of each layer can significantly affect the absorption spectrum, making it challenging to identify the correct set of four thickness values within this design space. Our goal is to enable the agent to automatically adjust these thicknesses, designing a structure that meets the target spectral characteristics. To frame this problem as a reinforcement learning challenge, we define the state space as the thicknesses of the four layers and the action space as the adjustments to the thicknesses that the agent can make. In this scenario, we specify the range of parameters for the different layers and allow the agent to learn and design structures within these predefined limits. Specifically, the thickness ranges are set as follows: l1 ranges from 250 nm to 750 nm, l2 from 5 nm to 45 nm, l3 from 250 nm to 750 nm, and l4 from 5 nm to 45 nm. This formulation enables a structured exploration and learning process where the agent iteratively adjusts the layer thicknesses to optimize the desired optical properties. To reduce training time and enable real-time acquisition of electromagnetic responses under current conditions, we use a multilayer perceptron (MLP), as shown in Figure 2. This MLP serves as the surrogate model for electromagnetic computation. Through this multilayer perceptron model, we can provide real-time absorption spectra for the current state while the agent explores the environment. These spectra are used to formulate the reinforcement learning reward and penalty functions, enabling timely updates to the agent’s network. The multilayer perceptron consists of an input layer, hidden layers, and an output layer. The input layer corresponds to the thickness of various layers of the film. The hidden layers consist of four fully connected layers, each containing 500 nodes. The output layer represents the absorption spectrum of the membrane in the 3 to 14 µm range. In this case, predictions are made at 0.5 µm wavelength intervals, corresponding to 23 output values. The ReLU [33] activation function is chosen for the layers, and the mean squared error (MSE) function is selected as the loss function:
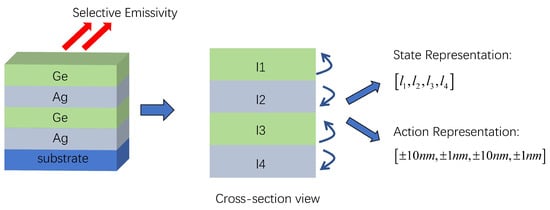
Figure 1.
Design environment.
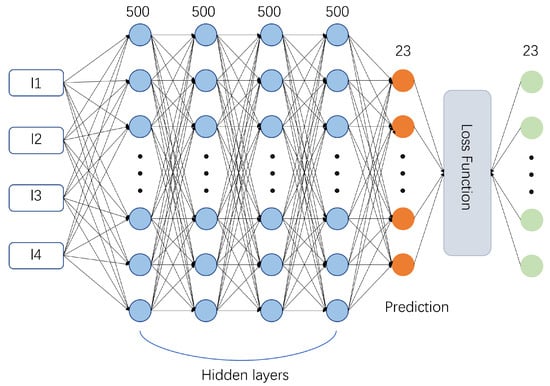
Figure 2.
Multilayer perceptron.
In the formula, N represents the number of discrete points in the absorption spectrum, which is 23, refers to the predicted values of the absorption spectrum outputted by the MLP, while corresponds to the actual values of the absorption spectrum from the dataset.
We obtained the dataset required for training the MLP using COMSOL Multiphysics 6.0. In data collection, build the model with reference to Figure 1. Apply periodic boundary conditions on the x–y plane, and let the light be incident along the negative z-axis. Treat l1, l2, l3, and l4 as parameters and perform parametric sweeps to obtain the absorption. The thicknesses l1 and l3 varied from 250 nm to 750 nm in increments of 50 nm, while l2 and l4 ranged from 5 nm to 45 nm in 5 nm increments. For the Ge layer, we perform a scan with a 50 nm step size, and for the Ag layer we use a 5 nm step size. This ensures that the resulting data uniformly cover the design space, thereby allowing more effective learning of the electromagnetic spectra within the parameter domain. In the subsequent design process, the design resolution for each layer is set to one-fifth of the scanning step size, thus maintaining design accuracy while making effective use of the MLP’s predictive capabilities. A total of 9801 sets of absorption spectrum data for different structures were collected. Of these, 80% were used for the training set and 20% for the test set. The data were then input into the MLP model for training, resulting in a well-trained spectral prediction surrogate model.
2.2. DQN Design Process
Figure 3 illustrates how we transform the film design problem into the Markov Decision Process (MDP) framework required for reinforcement learning. The MDP is defined as , where S is the set of finite states, A is the set of finite actions, P represents the state transition probabilities, R is the reward function, and is the discount factor used to calculate the cumulative reward. At time t, the state of the environment is denoted as , which represents the thickness of each layer of the film at that moment, where belongs to the set S of all possible states. The action taken by the agent at time t is , which involves adjusting the thickness of the Ge layer by increments or decrements of 10 nm, and the Ag layer by increments or decrements of 1 nm, with belonging to the set A of possible actions. After the agent executes action , the environment transitions to the next state, . The environment then utilizes a well-trained multilayer perceptron (MLP) model to predict the absorption spectrum at the new state, . Based on this predicted absorption spectrum and a predefined reward function, the reward is calculated and returned to the agent. Based on the described process, the sequence from moment 0 to time t forms a Markov Decision Process (MDP). To design absorption spectra that closely approximate the ideal absorption spectra for infrared stealth, which ideally has very low absorption rates in the 3∼5 µm and 8∼14 µm ranges and high absorption rates in the 5∼8 µm range, and to guide the proper design process, a reward function is required. The deviation between the design outcome and the expectation can be evaluated based on RMSD [34]:
where and are the simulated and ideal spectral emissivities, respectively, within the wavelength range of 3∼14 µm, and N is the total number of wavelengths considered.
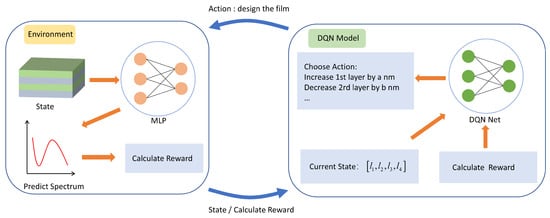
Figure 3.
DQN network interacts with the design environment.
Since the reward needs to be set as a positive value, and the ideal emissivity in the 5∼8 µm range can be considered as 1, while the ideal emissivity in the 3∼5 µm and 8∼14 µm ranges is considered as 0, the following preliminary reward function can be formulated.
where R represents the reward value and is the emissivity at wavelength .
In this design environment, there are a total of 23 discrete points in the 3∼14 µm range. Considering the relatively fewer data points in the 5∼8 µm range, their weights need to be increased to achieve more significant training results. Finally, the reward function is specified as follows:
Formula (4) omits the two critical points at 5 µm and 8 µm. In the formula, R represents the reward value, represents the absorption values at the five discrete points between 5 µm and 8 µm, and represents the absorption values at the sixteen discrete points between 3∼5 µm and 8∼14 µm.
Based on the aforementioned MDP process, the agent explores and learns within the environment, which provides timely feedback to the agent. During this interactive process, the agent needs a strategy to guide its actions, referred to as . The objective of the reinforcement learning process is to find the optimal policy, , that maximizes cumulative rewards. The formula for cumulative rewards is as follows:
where represents the cumulative return starting at time step t, is the discount factor that determines the present value of future rewards, is the reward received by taking action in state , and the summation accounts for the accumulated rewards over all time steps. Based on Equation (5) and the agent’s policy, , we can introduce the action–value function, which represents the expected return from taking a certain action in a given state, as follows:
If the optimal policy, , has been obtained, according to the Bellman equation, the action–value function can be expressed in terms of the action–value function at the next time step:
where represents the action–value function under policy , denotes the expected value, is the reward received after taking action a in state s, is the discount factor that determines the importance of future rewards, and represents the maximum action–value for the next state, , under the optimal action, . The equation captures the expected cumulative reward starting from state s and action a under policy . In Equation (7), the optimal policy is defined as choosing the action with the highest action–value function, . However, for an initial problem, we need a formula to iteratively update Q in order to obtain the desired optimal policy. In the Q-learning algorithm, this formula is defined as:
In the formula, represents the learning rate. The Deep Q-Network (DQN) algorithm builds upon the Q-learning algorithm by introducing a neural network to approximate the Q-function, addressing the challenge of updating and converging in a high-dimensional state space that Q-learning faces. To enhance the stability of training, the DQN algorithm incorporates another network, known as Q_target. The update formula for DQN is defined as:
In the formula, represents the target network, represents the parameters of the target network, and represents the current parameters of the DQN network. In this specific problem, the DQN network consists of an input layer corresponding to the film thickness, a hidden layer with 50 nodes, and an output layer corresponding to the actions.
2.3. Training Process
To prevent convergence to local optima, the DQN algorithm utilizes an -greedy mechanism to select actions. Here, is a parameter within the range [0, 1], representing the probability of selecting the action with the highest Q-value in the current state. With a probability of 1-, an action is selected randomly, ensuring the exploration of the unknown environment. In this study, is set to 0.9, indicating a 90% probability of selecting the best-known action and a 10% probability of exploring by choosing an action at random. After an agent selects an action based on the DQN network, it utilizes a mechanism known as the experience replay buffer to collect experiences. This involves storing tuples of the form in the replay buffer. During the update process, the DQN network retrieves batches of these tuples from the buffer to update itself. The capacity of the replay buffer is set to 2000. During the update phase, the DQN network begins updating once the capacity of the replay buffer is full. In each update, it selects a batch of size, typically referred to as batch-size, from the replay buffer for processing. The loss function used is the mean squared error (MSE), and the network parameters are updated using the Adam optimizer. Furthermore, every n steps, the parameters of the DQN network are copied to the target network , to gradually integrate learned behaviors into the more stable target model. In this specific setup, the batch-size is set at 32 and n is set at 100, indicating that the update of the target network’s parameters from the DQN’s occurs every 100 steps. This process helps stabilize learning by smoothing out fluctuations in the estimated values.
3. Result
The method was validated on a personal computer equipped with an i7-13700K 3.40 GHz processor and 32GB of RAM. During the training phase of the multilayer perceptron (MLP) model, the learning rate was set to 0.001. The loss functions for both the training and test sets, as depicted in Figure 4, indicate that the MLP model effectively learns from the spectral data in the dataset. To demonstrate the accuracy of the MLP prediction, we randomly sampled 1296 structures within the design space and evaluated their mean absolute error to quantify the prediction error.
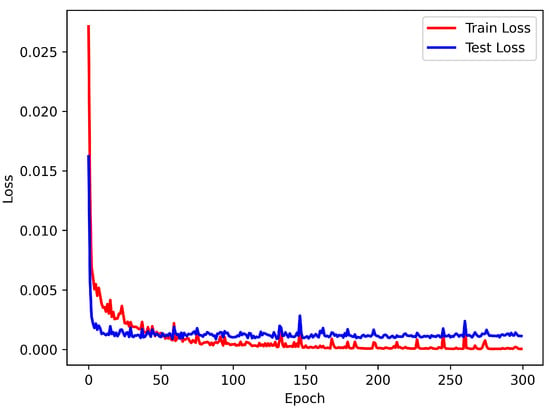
Figure 4.
The traing and test loss of MLP.
As shown in Figure 5, if an MAE < 0.01 is defined as accurate, then 97.61% of the predicted data meet this criterion, demonstrating that the MLP can effectively replace electromagnetic simulations within the design space. For a more intuitive explanation, the network was tested by inputting random thickness parameters. The predicted absorption spectra and the simulated absorption spectra, shown in Figure 6a–d, confirm that the MLP model achieves a good fit for the absorption spectra within the designed space. The DQN model was configured to explore the designated environment by storing experiences in the replay buffer and sampling from it during learning iterations. The number of episodes was set to 600, with each episode consisting of 150 adjustment steps. The learning rate was set at 0.005. To ensure complete exploration of the agent and the design space, the four thickness parameters were initialized to random values within their parameter domain at the start of each exploration round. If any thickness parameter exceeded its domain boundaries, it was reset to the opposite boundary. The reward values over the episodes are depicted in Figure 7, showing an increase from an initial −2000 to a final 8000, indicating that the DQN model effectively learns from the design environment. The trained model was retained for further adjustments to the four thickness parameters, and trajectories for 10 sets of parameter changes were plotted. The changes in each layer’s thickness across the adjustment steps are shown in Figure 8a–d. Specifically, l1 converged to 330 nm, l2 to 10 nm, and l3 to 600 nm, while l4 did not converge, indicating that the thickness of the bottom Ag layer does not significantly impact the target absorption spectra.
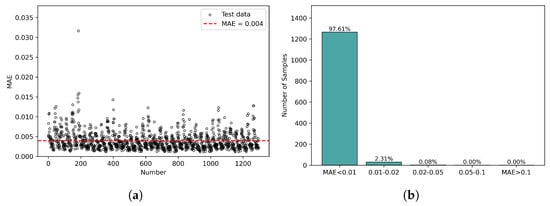
Figure 5.
The MAE between the MLP-predicted values and the actual simulation results. (a) Scatter plot; (b) Statistical distribution histogram.
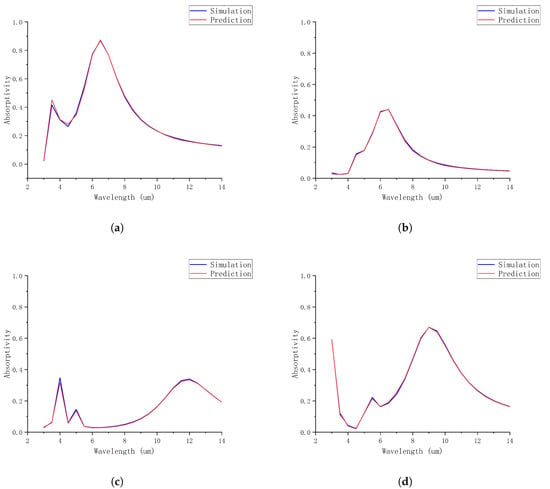
Figure 6.
Comparison of MLP-predicted and simulated absorptivity for four cases of random thicknesses. (a) l1 = 300, l2 = 5, l3 = 350, l4 = 10; (b) l1 = 350, l2 = 20, l3 = 450, l4 = 25; (c) l1 = 690, l2 = 28, l3 = 550, l4 = 38; (d) l1 = 500, l2 = 10, l3 = 550, l4 = 40.
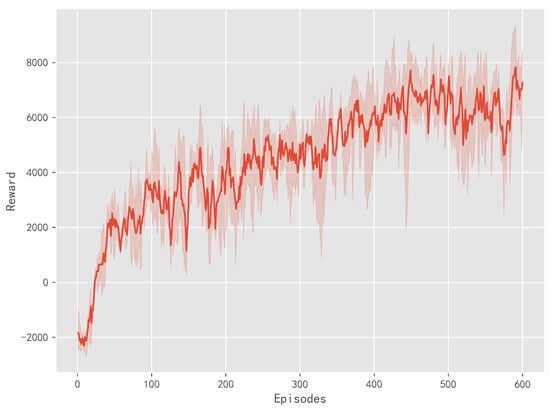
Figure 7.
Reward curves of DQN across three different training runs. The dark lines represent the mean values and the shaded areas indicate the standard deviations of the means.
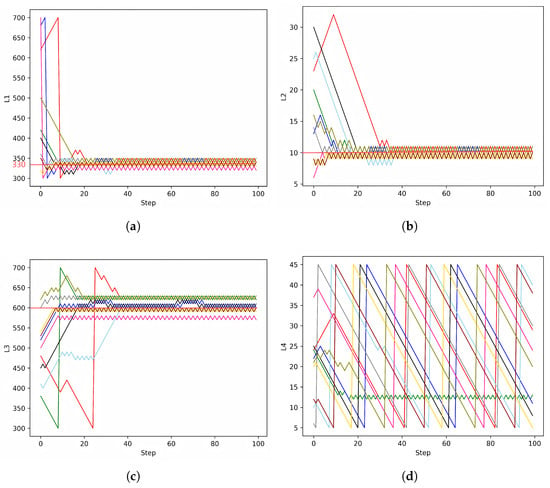
Figure 8.
Convergence of the thickness of each layer under DQN conditioning. (a) Layer 1; (b) Layer 2; (c) Layer 3; (d) Layer 4.
Based on the results, the final automatic design configuration determined by the DQN model is as follows: l1 = 330 nm, l2 = 10 nm, l3 = 600 nm, and l4 = 25 nm. This structure was then subjected to electromagnetic simulation to validate its performance. The absorption spectra, as depicted in Figure 9, show that, in the atmospheric windows of 3∼5 µm and 8∼14 µm, the average emissivity is low, at 0.086 and 0.147, respectively. Meanwhile, in the main radiative cooling band of 5.5∼7.5 µm, the average emissivity reaches as high as 0.75. These characteristics meet the requirements for infrared stealth and thermal radiation management.
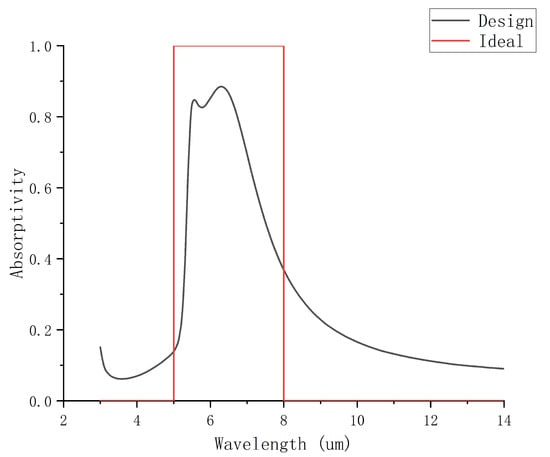
Figure 9.
Absorption spectra of design and ideal results.
4. Experiment
Following the designed film parameters, we deposited the film on a silicon wafer using a coating process to produce a physical sample. The coating process utilizes electron beam evaporation. The equipment employed is the SKY system from Shenyang Scientific Instruments, featuring a temperature control precision of ±0.2 °C and temperature uniformity within ±2 °C. For Ge sputtering, the pressure is maintained at 0.4 Pa, with a radio frequency power of 60 W. Ag sputtering is conducted at a pressure of 0.4 Pa using a direct current power of 50W. Both the coated silicon wafer and a bare silicon wafer were placed on a heating stage, and images were captured using an infrared thermal imager for comparative analysis. The heating stage was set to three different temperatures: 30 °C, 50 °C, and 70 °C. Measurements were conducted after heating to the target temperature was stabilized, with a heating duration of approximately 30 minutes. The results, as shown in Figure 10, indicate that the coated silicon wafer appears significantly darker in the infrared thermal imager compared to the uncoated silicon wafer, showing lower temperatures by 1.8 °C, 8.9 °C, and 12.2 °C at the respective heating temperatures. We also measured the emissivity of the two specimens, and the results are shown in Figure 11. The figure indicates that the emissivity of the silicon wafer significantly decreases in the 3∼5 µm and 8∼14 µm ranges after coating, while it increases in the 5∼8 µm range. This result is generally consistent with our simulation outcomes; however, some discrepancies do exist. These errors may be attributed to the following factors: inaccuracies in the actual coating process, leading to slight differences between the fabricated layer thicknesses and those used in the simulations; variations in the material parameters employed in practice compared to those in the simulations, as the optical properties of materials can differ under varying conditions; and minor contamination or oxidation of the materials during the processing or measurement stages. The experimental measurements presented above demonstrate that the designed thin film effectively regulates the emissivity of the silicon wafer within the infrared detection wavelength range, thereby validating its effectiveness for infrared stealth applications.

Figure 10.
Infrared images of two materials at three different temperatures. (a) Heating stage set to 30 °C; (b) Heating stage set to 50 °C; (c) Heating stage set to 70 °C.
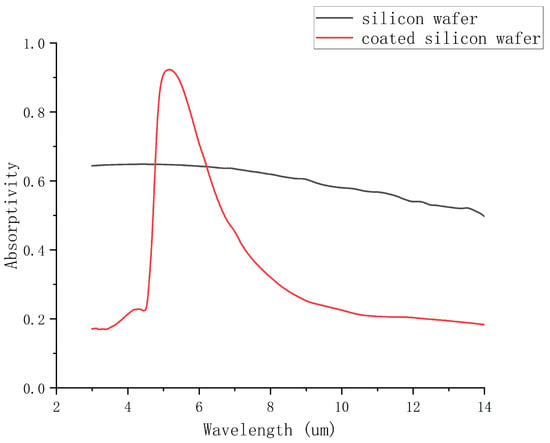
Figure 11.
Emissivity measurement of silicon wafers and coated silicon wafers.
5. Discussion
Tandem neural networks and genetic algorithms are classic methods in inverse design. This chapter discusses and compares the performance differences of the MLP-DQN method proposed in this paper, the tandem neural network method, and the genetic algorithm within the context of infrared stealth film design. The structure of the tandem neural network is illustrated in Figure 12. The forward network utilizes a previously trained MLP and is trained using the previously generated 9801 datasets for the inverse network. During the training of the inverse network, the forward network is kept fixed, and the output of the inverse network is used as the input to the forward network to obtain the forward network’s prediction. The error between the forward network’s output and the inverse network’s input is set as the loss function, thereby addressing the one-to-many problem inherent in spectral inverse design. The MSE is shown in Figure 13, and the convergence of the training and testing errors indicates the successful training of the inverse network. After training, the expected absorption spectrum is input, and the inverse network outputs the thicknesses of the four-layer film. Compared to the RL method previously used, the uncertainty in the network’s output may result in unreasonable structures (such as thickness values outside the design range or negative values). Therefore, it is necessary to generate several plausible absorption spectra using the Gaussian formula and select structural parameters with better performance from these spectra.
where a is the baseline absorptivity. The parameter b is the height of the Gaussian peak above the baseline, making the peak value . The term is the center wavelength of the peak, and determines the width and sharpness of the peak.
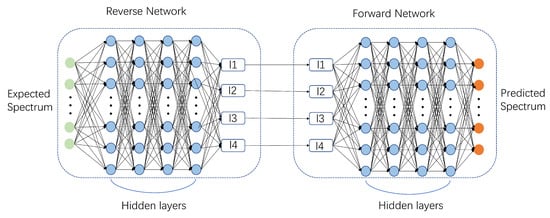
Figure 12.
Tandem neural networks.
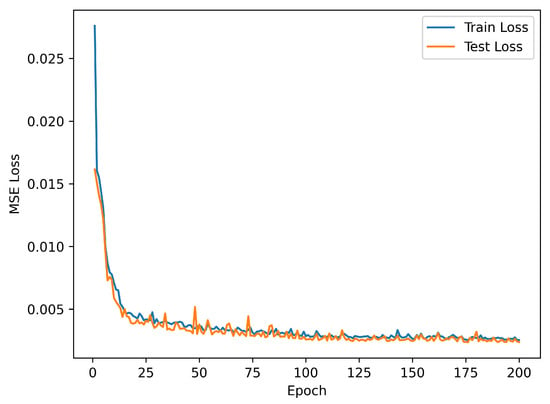
Figure 13.
The training and test loss of tandem neural networks.
The genetic algorithm is also implemented based on the previously trained MLP. The initialization phase is similar to the earlier DQN environment, with the ranges for l1 and l3 set between 250 and 750 nm, and l2 and l4 set between 5nm and 45 nm. The target absorption spectrum is set to 0 in the ranges of 3∼5 µm and 8∼14 µm, and to 1 in the range of 5∼8 µm. The MSE between the predicted spectrum and the target spectrum is calculated, and its negative value is used as the fitness function for the genetic algorithm. The fitness improvement with the number of iterations is shown in Figure 14, and the optimal film thickness for each layer is ultimately output.
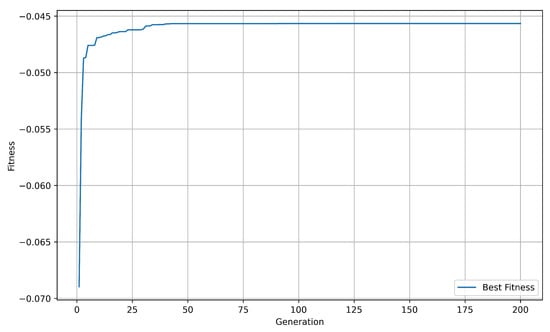
Figure 14.
Iterative performance of the genetic algorithm.
The design results from the three algorithms were subjected to electromagnetic simulations, yielding absorption spectra as shown in Figure 15a. To accurately assess the infrared stealth performance of the structures produced by the three algorithms, the following MAE calculation formula was established, and the performance of the design results was defined as 1-MAE. The performance of the design results from the three algorithms is presented in Figure 15b.
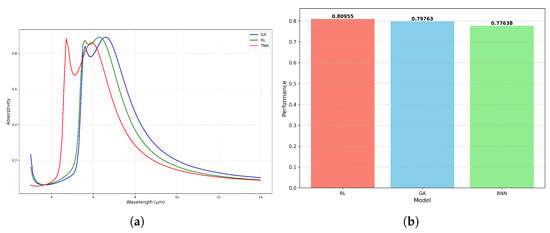
Figure 15.
Comparison of the design results of three algorithms. (a) Absorption spectra of the design results; (b) performance comparison of the design results.
In summary, the proposed MLP-DQN method in this paper exhibits the best performance in designing infrared stealth thin films as shown in Table 1. The results of the genetic algorithm are comparable to those of the DQN method. However, the disadvantage of the genetic algorithm lies in its inability to flexibly respond to design objectives, as it requires re-iteration for each design spectrum. In contrast, the other two methods, RL and TNN, can retain network parameters and achieve flexible design objectives by adjusting the input spectrum without the need for retraining. The design results of the tandem neural networks are not as good as those of DQN. Moreover, due to the uncertainty of the network outputs, it may produce values that exceed the design region or negative values, necessitating the generation of multiple absorption spectra using Gaussian formulas for the design. On the other hand, DQN fully leverages RL’s exploration mechanism of the design environment, enabling it to directly output results that meet expectations.

Table 1.
Comparison of methods in inverse design.
6. Conclusions
We propose a method for designing infrared stealth films utilizing deep reinforcement learning and a multilayer perceptron (MLP). The MLP maps the design space, facilitating real-time interaction between the agent and the design environment. This configuration enables the agent to autonomously learn and design film structures that meet the spectral characteristics necessary for infrared stealth. The performance of the resulting structures was validated experimentally. In addition, we compared the MLP-DQN algorithm proposed in this paper with several classical inverse design algorithms within the given design scenario. The results indicate that the MLP-DQN algorithm yields superior design outcomes and offers greater efficiency and stability. This method is characterized by short optimization times and high scalability, making it applicable to the design of other micro- and nano-structured devices.
Author Contributions
Conceptualization, K.Z. and D.L.; methodology, K.Z. and D.L.; software, K.Z.; validation, D.L. and S.Y.; investigation, K.Z. and D.L.; resources, K.Z., D.L. and S.Y.; data curation, K.Z.; writing—original draft preparation, K.Z.; writing—review and editing, K.Z., D.L. and S.Y.; visualization, K.Z.; supervision, K.Z., D.L. and S.Y.; project administration, D.L.; funding acquisition, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (grant nos. 62274124 and 61774120).
Data Availability Statement
All data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, J.; Zhang, X.; Zhang, X.; Wang, L.; Feng, W.; Li, Q. Beyond the visible: Bioinspired infrared adaptive materials. Adv. Mater. 2021, 33, 2004754. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, W.; Han, T.; Zheng, X.; Li, J.; Li, B.; Fan, S.; Qiu, C.W. Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 2021, 6, 488–507. [Google Scholar] [CrossRef]
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef]
- Bhatia, B.; Leroy, A.; Shen, Y.; Zhao, L.; Gianello, M.; Li, D.; Gu, T.; Hu, J.; Soljačić, M.; Wang, E.N. Passive directional sub-ambient daytime radiative cooling. Nat. Commun. 2018, 9, 5001. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, G.; Zhang, J.; Wang, H.; Hou, H. Infrared spectrally selective low emissivity from Ge/ZnS one-dimensional heterostructure photonic crystal. Opt. Mater. 2014, 37, 343–346. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Q.; Zheng, C.; Hong, Y.; Xu, Z.; Wang, H.; Shen, W.; Kaur, S.; Ghosh, P.; Qiu, M. High-temperature infrared camouflage with efficient thermal management. Light. Sci. Appl. 2020, 9, 60. [Google Scholar] [CrossRef]
- Hu, R.; Xi, W.; Liu, Y.; Tang, K.; Song, J.; Luo, X.; Wu, J.; Qiu, C.W. Thermal camouflaging metamaterials. Mater. Today 2021, 45, 120–141. [Google Scholar] [CrossRef]
- Zouhdi, S.; Sihvola, A.; Vinogradov, A.P. Metamaterials and Plasmonics: Fundamentals, Modelling, Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar] [CrossRef]
- Zayats, A.V.; Maier, S. Active Plasmonics and Tuneable Plasmonic Metamaterials; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Z.; Ma, H.; Du, T.; Luo, M.; Liu, D.; Yang, J. Tunable mid-infrared selective emitter based on inverse design metasurface for infrared stealth with thermal management. Opt. Express 2022, 30, 18250–18263. [Google Scholar] [CrossRef] [PubMed]
- Du, K.K.; Li, Q.; Lyu, Y.B.; Ding, J.C.; Lu, Y.; Cheng, Z.Y.; Qiu, M. Control over emissivity of zero-static-power thermal emitters based on phase-changing material GST. Light. Sci. Appl. 2017, 6, e16194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.K.; Shi, J.M.; Zhao, D.P.; Wang, Q.C.; Wang, C.M. Realization of compatible stealth material for infrared, laser and radar based on one-dimensional doping-structure photonic crystals. Infrared Phys. Technol. 2017, 85, 62–65. [Google Scholar] [CrossRef]
- Liu, M.; Xia, S.; Wan, W.; Qin, J.; Li, H.; Zhao, C.; Bi, L.; Qiu, C.W. Broadband mid-infrared non-reciprocal absorption using magnetized gradient epsilon-near-zero thin films. Nat. Mater. 2023, 22, 1196–1202. [Google Scholar] [CrossRef]
- Peng, L.; Liu, D.; Cheng, H.; Zhou, S.; Zu, M. A multilayer film based selective thermal emitter for infrared stealth technology. Adv. Opt. Mater. 2018, 6, 1801006. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Q.; Tao, C.; Hong, Y.; Xu, Z.; Shen, W.; Kaur, S.; Ghosh, P.; Qiu, M. Multispectral camouflage for infrared, visible, lasers and microwave with radiative cooling. Nat. Commun. 2021, 12, 1805. [Google Scholar] [CrossRef] [PubMed]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Liu, C.; Maier, S.A.; Li, G. Genetic-algorithm-aided meta-atom multiplication for improved absorption and coloration in nanophotonics. ACS Photonics 2020, 7, 1716–1722. [Google Scholar] [CrossRef]
- Martin, S.; Rivory, J.; Schoenauer, M. Synthesis of optical multilayer systems using genetic algorithms. Appl. Opt. 1995, 34, 2247–2254. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Li, Z.; Liu, W.; Geng, G.; Cheng, H.; Li, J.; Tian, J.; Chen, S. Deep-learning enabled multicolor meta-holography. Adv. Opt. Mater. 2022, 10, 2102628. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Forestiere, C.; Donelli, M.; Walsh, G.F.; Zeni, E.; Miano, G.; Dal Negro, L. Particle-swarm optimization of broadband nanoplasmonic arrays. Opt. Lett. 2010, 35, 133–135. [Google Scholar] [CrossRef]
- Yang, C.; Hong, L.; Shen, W.; Zhang, Y.; Liu, X.; Zhen, H. Design of reflective color filters with high angular tolerance by particle swarm optimization method. Opt. Express 2013, 21, 9315–9323. [Google Scholar] [CrossRef] [PubMed]
- Christiansen, R.E.; Sigmund, O. Inverse design in photonics by topology optimization: Tutorial. J. Opt. Soc. Am. B 2021, 38, 496–509. [Google Scholar] [CrossRef]
- Peurifoy, J.; Shen, Y.; Jing, L.; Yang, Y.; Cano-Renteria, F.; DeLacy, B.G.; Joannopoulos, J.D.; Tegmark, M.; Soljačić, M. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv. 2018, 4, eaar4206. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.T.; Cai, W. Generative model for the inverse design of metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Tan, Y.; Khoram, E.; Yu, Z. Training deep neural networks for the inverse design of nanophotonic structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef]
- Guan, Q.; Raza, A.; Mao, S.S.; Vega, L.F.; Zhang, T. Machine learning-enabled inverse design of radiative cooling film with on-demand transmissive color. ACS Photonics 2023, 10, 715–726. [Google Scholar] [CrossRef]
- Wang, L.; Dong, J.; Zhang, W.; Zheng, C.; Liu, L. Deep learning assisted optimization of metasurface for multi-band compatible infrared stealth and radiative thermal management. Nanomaterials 2023, 13, 1030. [Google Scholar] [CrossRef] [PubMed]
- Jiang, A.; Osamu, Y.; Chen, L. Multilayer optical thin film design with deep Q learning. Sci. Rep. 2020, 10, 12780. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Gui, L.; Gao, A.; Yu, Z.; Xu, K. Intelligent design of the chiral metasurfaces for flexible targets: Combining a deep neural network with a policy proximal optimization algorithm. Opt. Express 2022, 30, 39582–39596. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Zhou, P.; Xi, W.; Chen, Z.; Deng, Y.; Luo, X.; Li, W.; Shiomi, J.; Hu, R. General deep learning framework for emissivity engineering. Light. Sci. Appl. 2023, 12, 291. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Yu, D.; Wang, X.; Ma, Y.; Chen, M.; Shen, J.; Li, Y.; Wu, X. Dual-dielectric Fabry-Perot film for visible-infrared compatible stealth and radiative heat dissipation. Opt. Commun. 2025, 574, 131173. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).