Joint Constellation and Reflectance Optimization for Tunable Intelligent Reflecting Surface-Aided VLC Systems
Abstract
1. Introduction
- A newly IRS-aided SISO VLC system under dimming constraints is investigated with a metasurface-based IRS for which its reflectance can be synchronously tuned with the LED’s emitting signals.
- The joint PAM constellation and reflectance optimization problem is formulated by maximizing the minimum distance between any two adjacent received constellation points to achieve better BER performance.
- The optimization problem is solved in two steps. In step one, we solve a convex optimization problem for the optimal received constellation. In step two, a feasible problem is decomposed into two alternative optimizing sub-problems to find the transmit constellation and IRSs’ reflectances corresponding to the optimal received constellation.
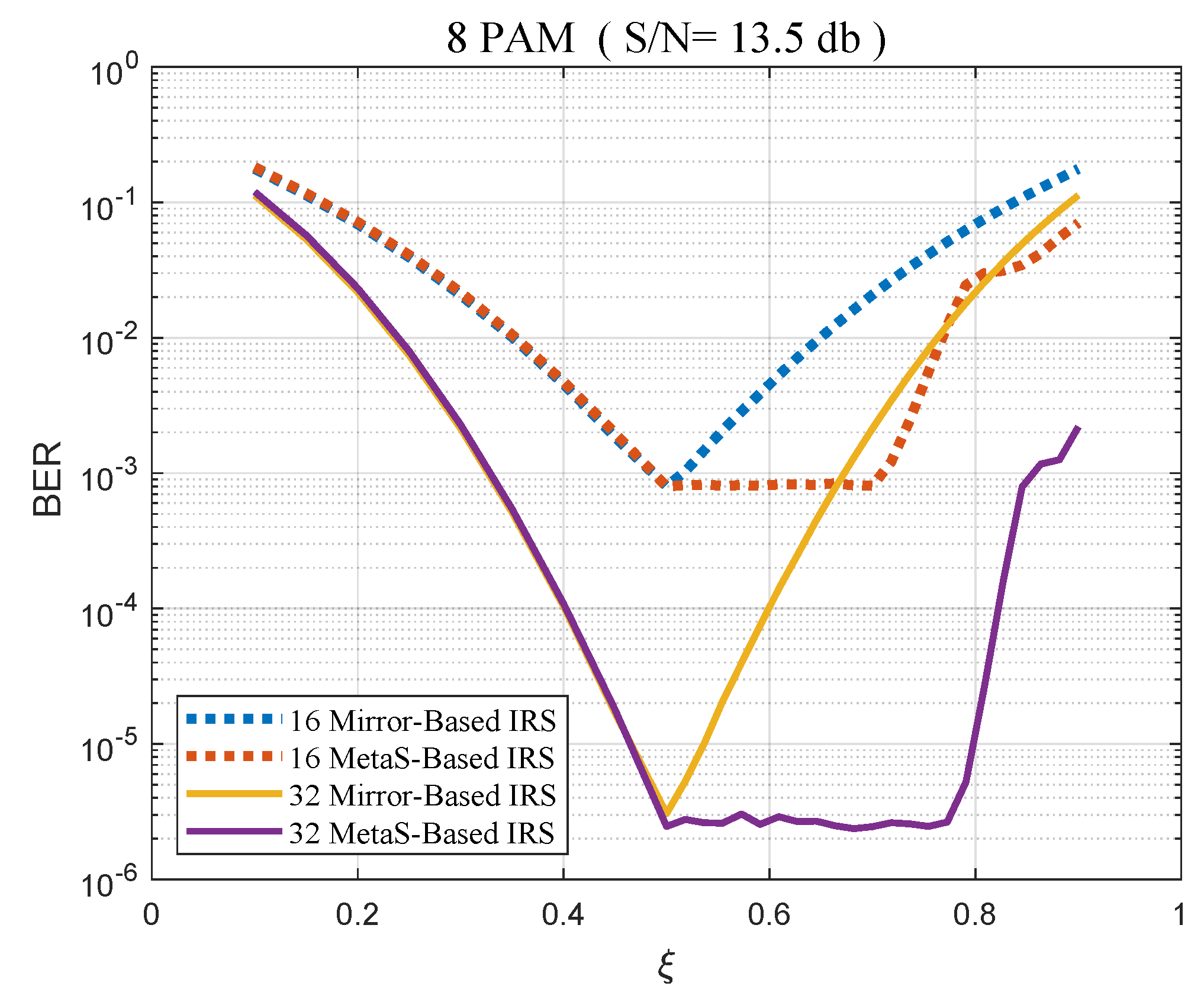
- The BER performance is shown and analyzed in terms of the BER curves and the constellation distributions. The extra dimming constraint relaxation benefit of the tunable IRS are illustrated compared with the mirror-based IRS.
2. System Model and Problem Formulation
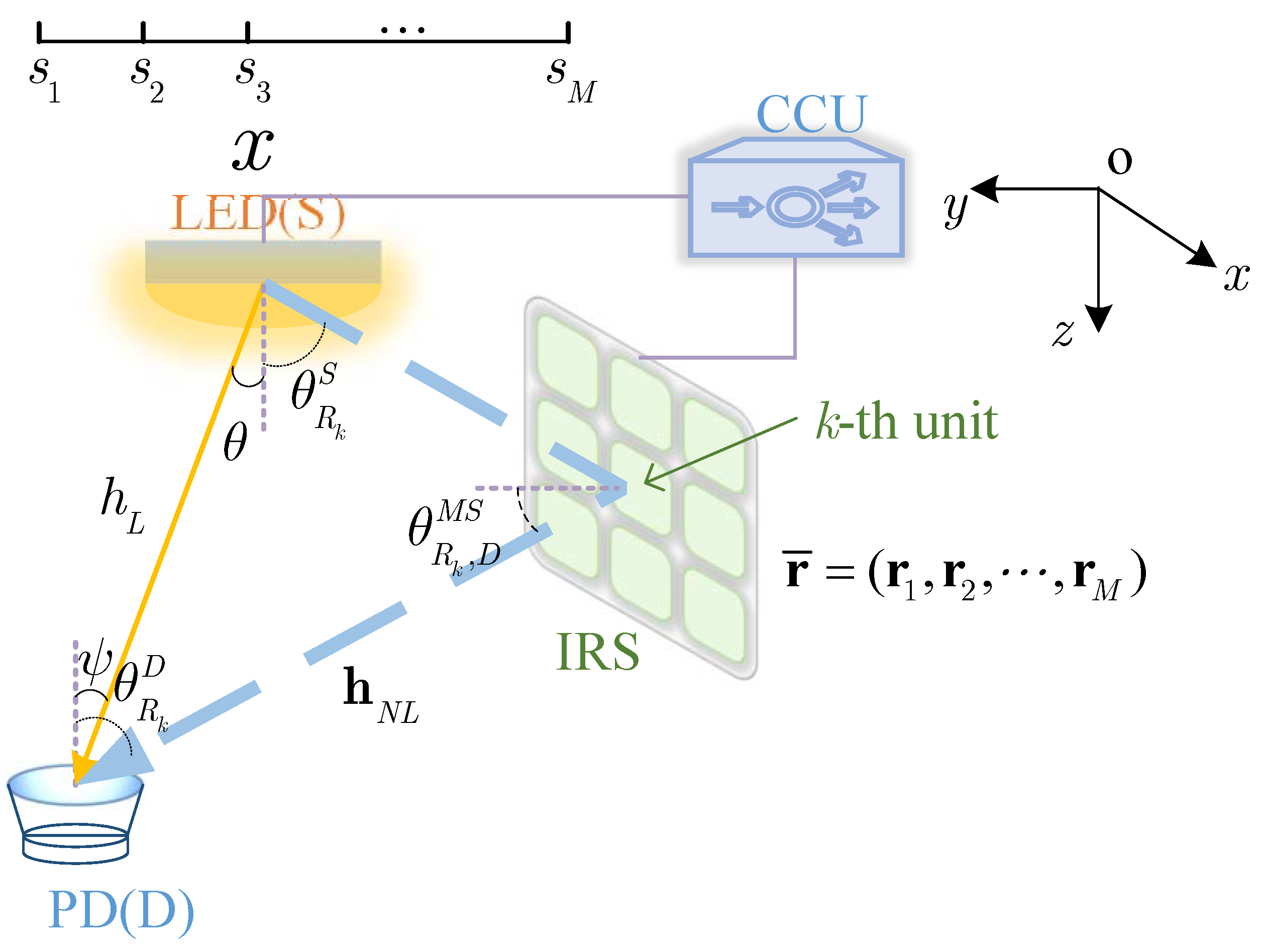
2.1. System Model
2.2. Problem Motiviation
3. Proposed Optimization Algorithm
- Solve for the optimal received signal constellation .
- Find the transmit constellation points and the coherent reflectance vector corresponding to the optimal received constellation points.
3.1. Received Constellation Optimization
3.2. Joint Transmit Constellation and Reflectance Optimization
| Algorithm 1 Joint Constellation and Reflectance Optimization Algorithm |
| Input: Step1: Slove for by (P1) Step2: While: 1 Initialize: s satisfying (9), (10), and (11). Do: Calculate by (P2aR); Calculate by (P2bR); Until: and are converged if: The converged (, ) is a feasible solution of (P2); Break; endif End While Return: , , |
4. Numerical Results
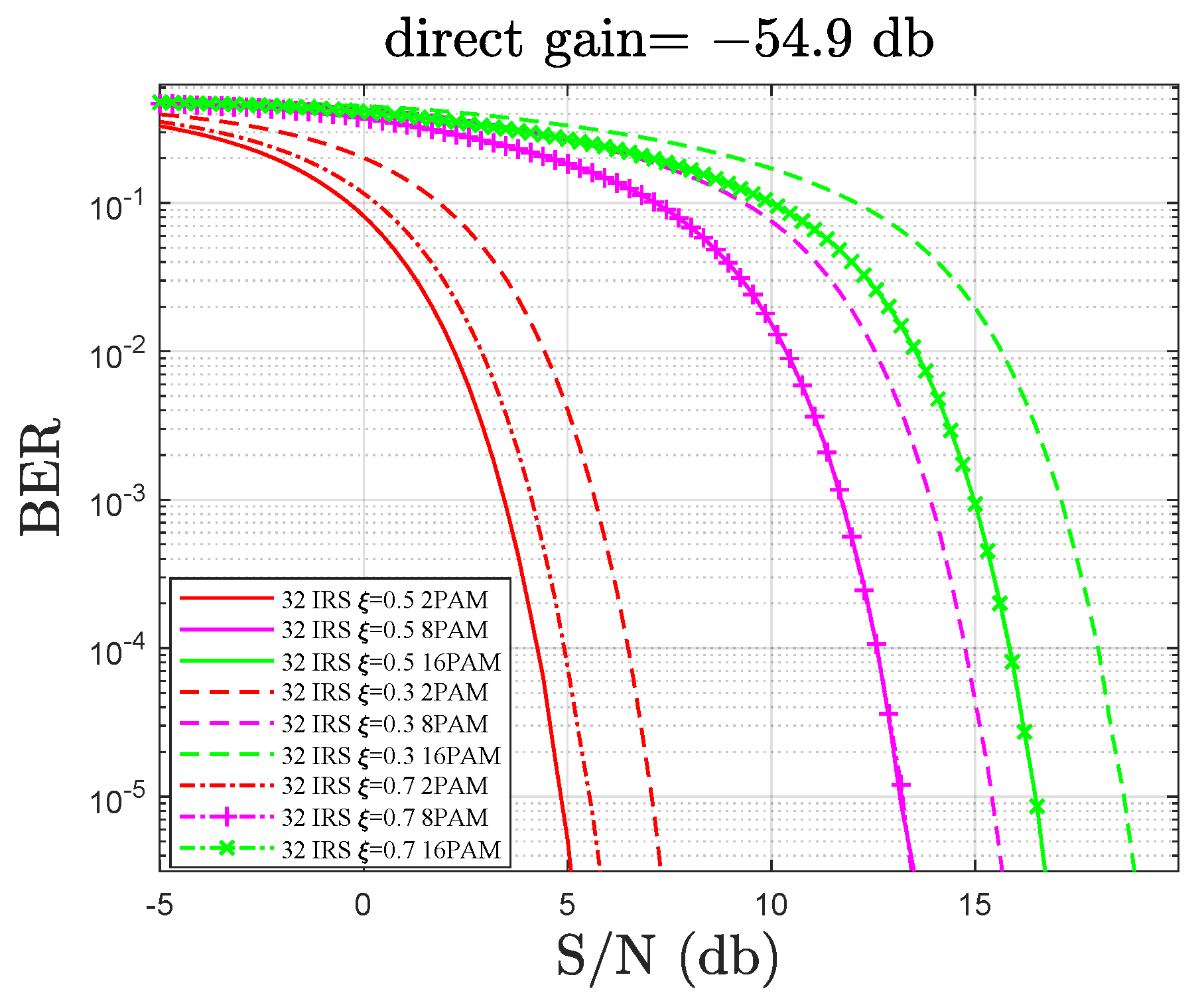
4.1. Simulation Scenarios
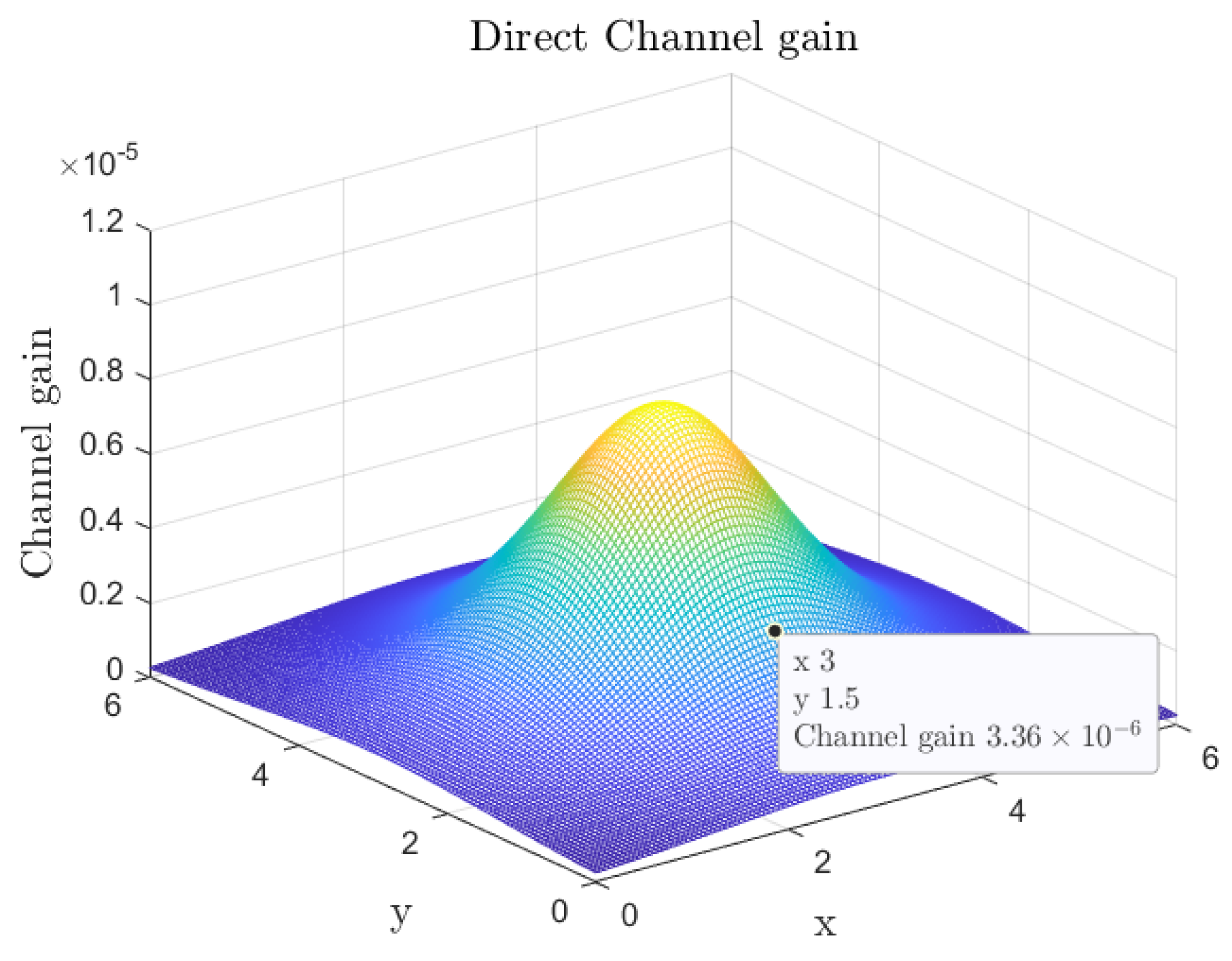
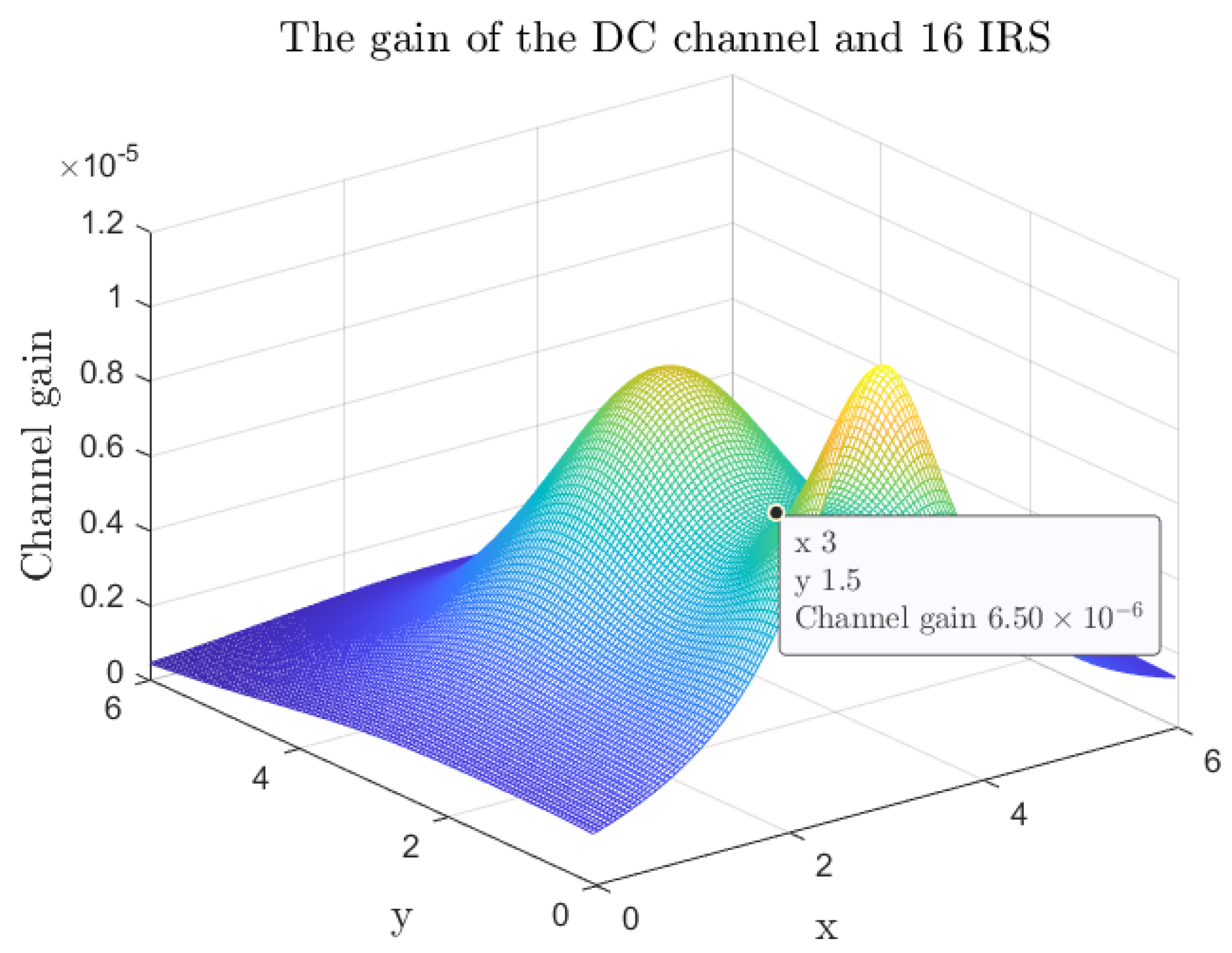
4.2. Channel Gain
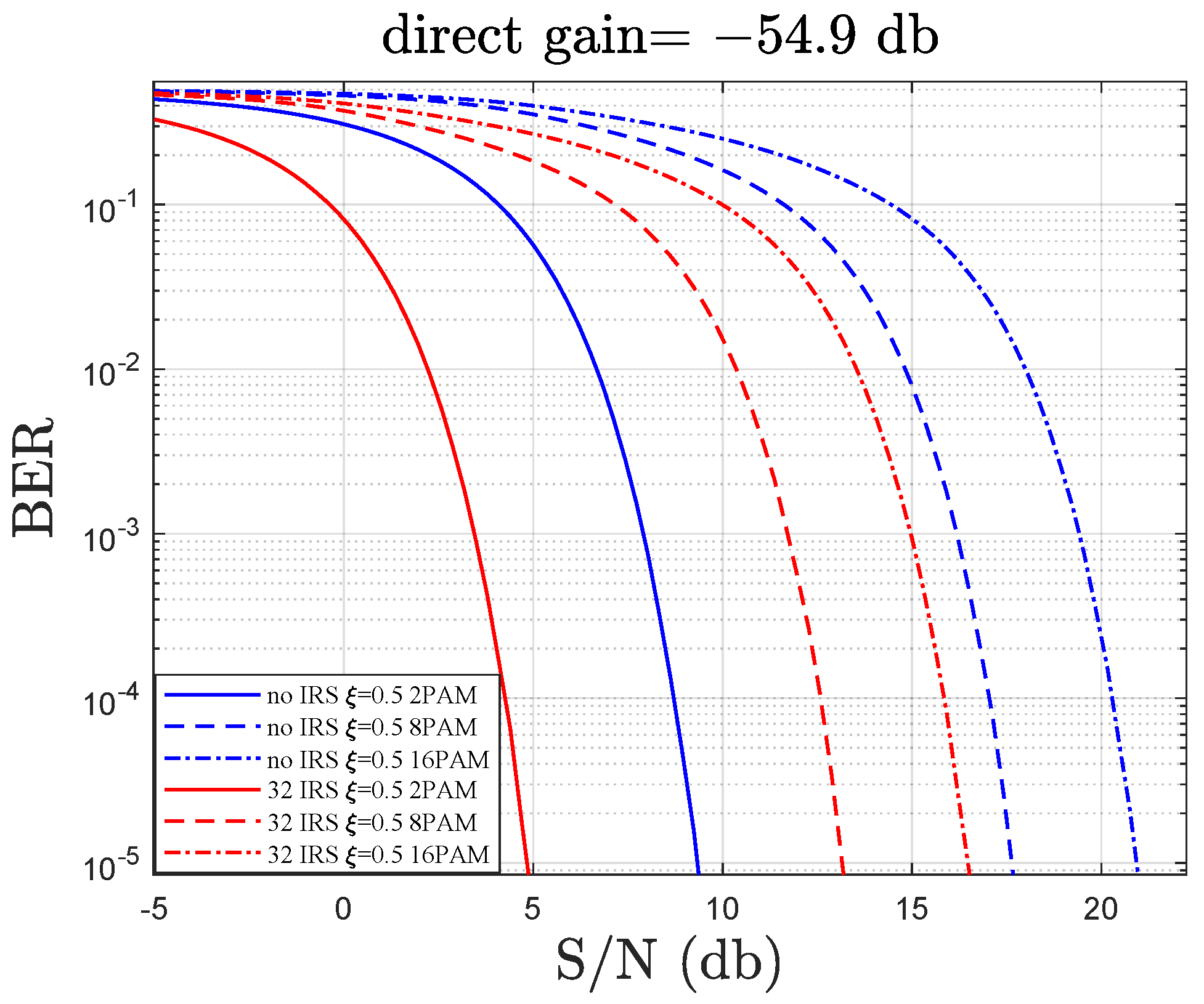
4.3. BER Performance
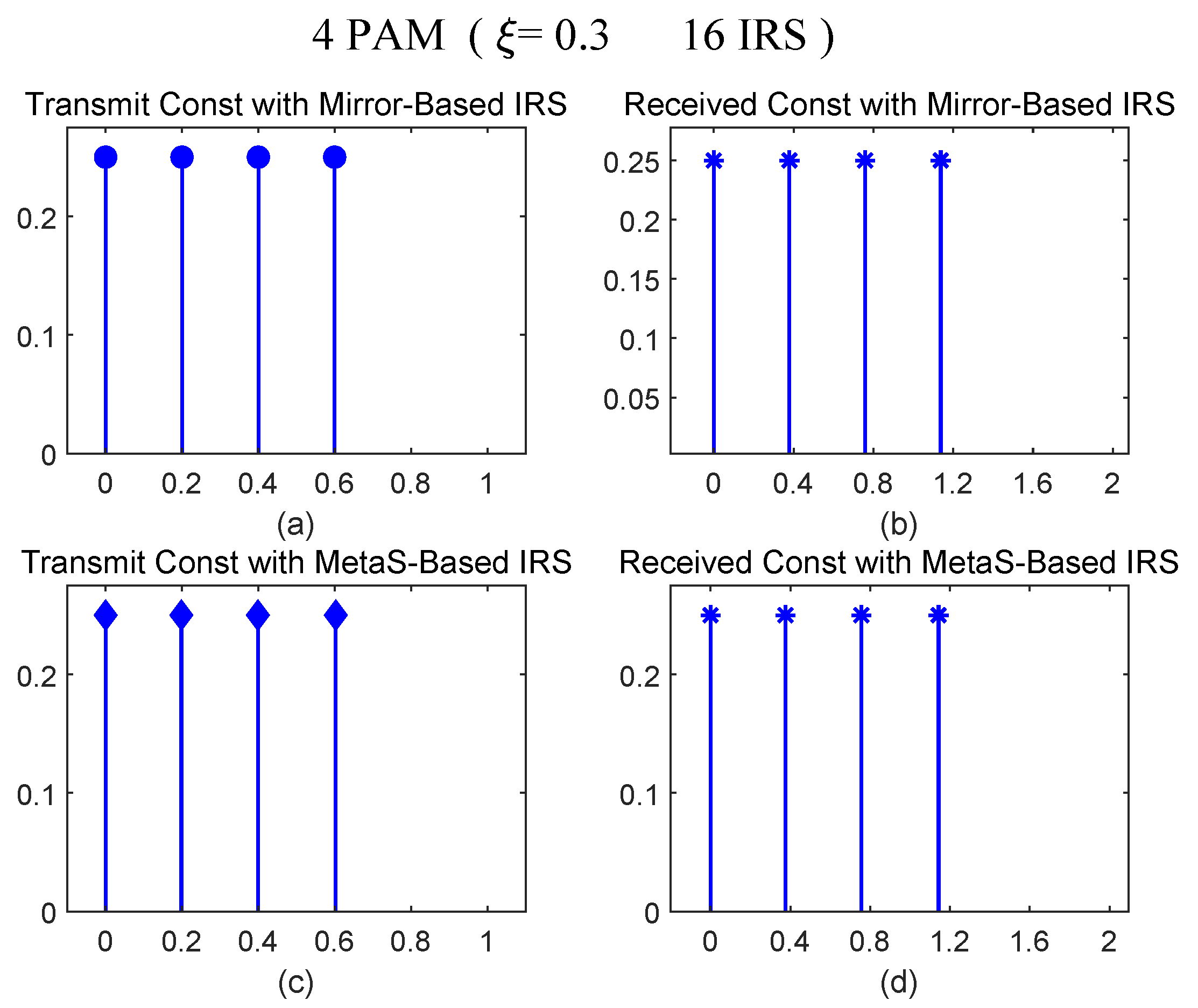
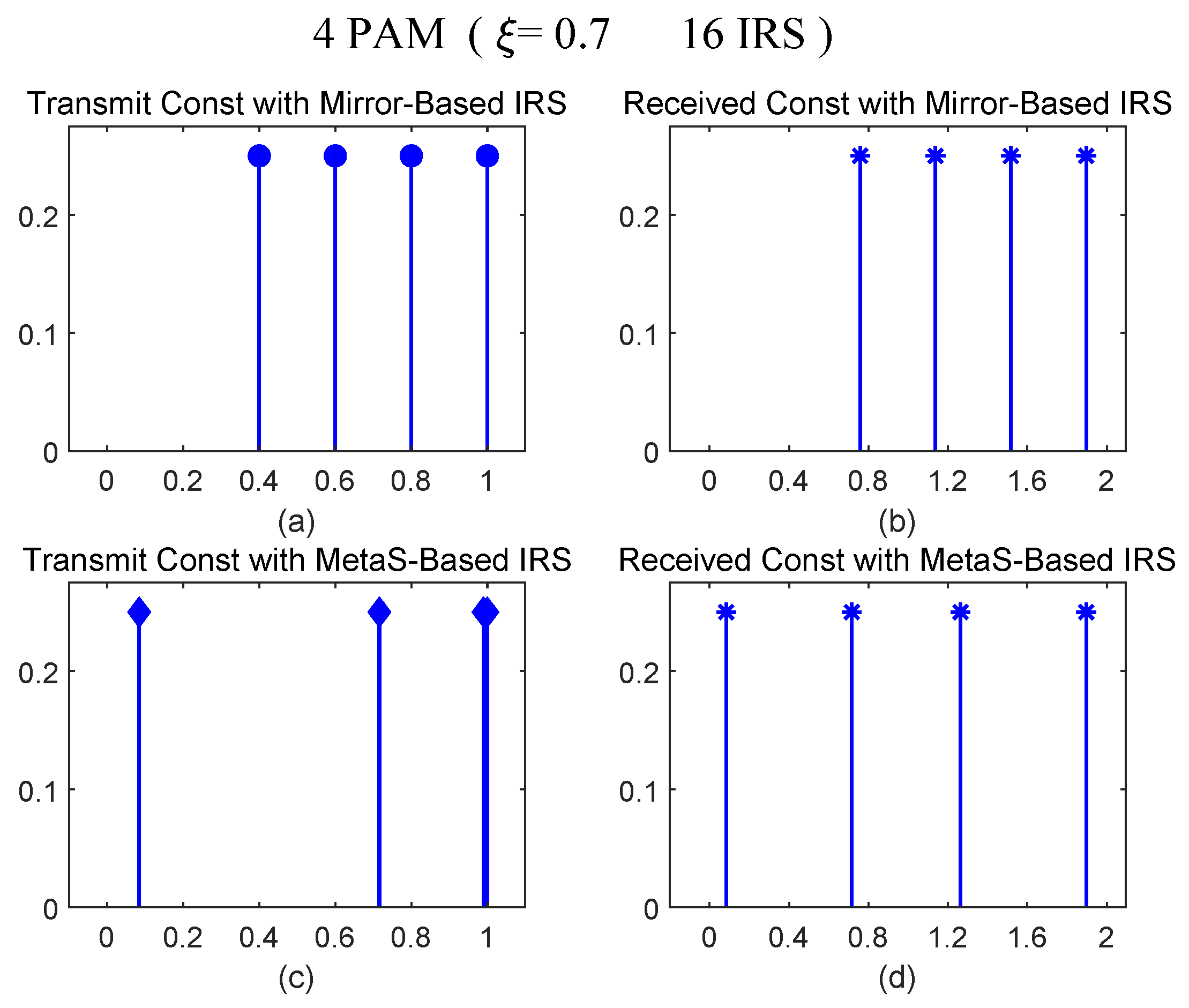
4.4. Constellations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VLC | Visible light communication; |
| IRS | Intelligent reflecting surface; |
| LoS | Line of sight; |
| NLoS | Non-light of sight; |
| SISO | Single-input single-output; |
| BER | Bit error rate; |
| 6G | Sixth-generation; |
| LED | Light-emitting diode; |
| RF | Radio frequency; |
| MIMO | Multiple-input multiple-output; |
| DPC | Dirty-paper coding; |
| IM/DD | Intensity modulation and direct detection; |
| PAM | Pulse amplitude modulation; |
| CCU | Central control unit; |
| PD | Photo-detector; |
| DC | Direct channel; |
| FoV | Field of view; |
| LD | Laser diode; |
| OOK | On–Off keying; |
| PPM | Pulse position modulation; |
| SER | Symbol error rate; |
| ML | Maximum likelihood; |
| SNR | Signal-to-noise ratio. |
Appendix A
References
- Sun, S.; Yang, F.; Song, J.; Han, Z. Joint Resource Management for Intelligent Reflecting Surface–Aided Visible Light Communications. IEEE Trans. Wirel. Commun. 2022, 21, 6508–6522. [Google Scholar] [CrossRef]
- Sun, S.; Wang, T.; Yang, F.; Song, J.; Han, Z. Intelligent Reflecting Surface-Aided Visible Light Communications: Potentials and Challenges. IEEE Veh. Technol. Mag. 2022, 17, 47–56. [Google Scholar] [CrossRef]
- Abumarshoud, H.; Mohjazi, L.; Dobre, O.A.; Di Renzo, M.; Imran, M.A.; Haas, H. LiFi through Reconfigurable Intelligent Surfaces: A New Frontier for 6G? IEEE Veh. Technol. Mag. 2022, 17, 37–46. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, G.; Zhi, K.; Hong, S.; Wu, T.; Pan, Y.; Ren, H.; Renzo, M.D.; Lee Swindlehurst, A.; Zhang, R.; et al. An Overview of Signal Processing Techniques for RIS/IRS-Aided Wireless Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 883–917. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, X.; Zhang, Y.J.A. Matrix-Calibration-Based Cascaded Channel Estimation for Reconfigurable Intelligent Surface Assisted Multiuser MIMO. IEEE J. Sel. Areas Commun. 2020, 38, 2621–2636. [Google Scholar] [CrossRef]
- Elmossallamy, M.A.; Sultan, R.; Seddik, K.G.; Li, G.Y.; Han, Z. Maximizing dirty-paper coding rate of RIS-assisted multi-user MIMO broadcast channels. Intell. Converg. Netw. 2022, 3, 64–73. [Google Scholar] [CrossRef]
- Abdelhady, A.M.; Salem, A.K.S.; Amin, O.; Shihada, B.; Alouini, M.S. Visible Light Communications via Intelligent Reflecting Surfaces: Metasurfaces vs Mirror Arrays. IEEE Open J. Commun. Soc. 2021, 2, 1–20. [Google Scholar] [CrossRef]
- Sun, S.; Yang, F.; Song, J.; Zhang, R. Intelligent Reflecting Surface for MIMO VLC: Joint Design of Surface Configuration and Transceiver Signal Processing. IEEE Trans. Wirel. Commun. 2023, 22, 5785–5799. [Google Scholar] [CrossRef]
- Sun, S.; Yang, F.; Song, J. Sum Rate Maximization for Intelligent Reflecting Surface-Aided Visible Light Communications. IEEE Commun. Lett. 2021, 25, 3619–3623. [Google Scholar] [CrossRef]
- Aboagye, S.; Ngatched, T.M.N.; Dobre, O.A.; Ndjiongue, A.R. Intelligent Reflecting Surface-Aided Indoor Visible Light Communication Systems. IEEE Commun. Lett. 2021, 25, 3913–3917. [Google Scholar] [CrossRef]
- Zhi, K.; Pan, C.; Ren, H.; Chai, K.K.; Elkashlan, M. Active RIS Versus Passive RIS: Which is Superior with the Same Power Budget? IEEE Commun. Lett. 2022, 26, 1150–1154. [Google Scholar] [CrossRef]
- Bhowmik, T.; Chowdhary, A.K.; Sikdar, D. Polarization- and Angle-Insensitive Tunable Metasurface for Electro-Optic Modulation. IEEE Photonics Technol. Lett. 2023, 35, 879–882. [Google Scholar] [CrossRef]
- Lee, K.; Park, H. Modulations for Visible Light Communications with Dimming Control. IEEE Photonics Technol. Lett. 2011, 23, 1136–1138. [Google Scholar] [CrossRef]
- Wang, T.; Yang, F.; Song, J.; Han, Z. Dimming Techniques of Visible Light Communications for Human-Centric Illumination Networks: State-of-the-Art, Challenges, and Trends. IEEE Wirel. Commun. 2020, 27, 88–95. [Google Scholar] [CrossRef]
- Drost, R.J.; Sadler, B.M. Constellation Design for Channel Precompensation in Multi-Wavelength Visible Light Communications. IEEE Trans. Commun. 2014, 62, 1995–2005. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Jia, L.; Shu, F.; Huang, N.; Chen, M.; Wang, J. Capacity and Optimum Signal Constellations for VLC Systems. J. Light. Technol. 2020, 38, 2180–2189. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| The number of IRS units K | 16, 32 |
| The modulation order M | 2, 4, 8, 16 |
| The dimming coefficient | 0.1∼0.9 |
| The Lambertian index m | 1 |
| The PD area | |
| The FoV of the concentrator | |
| The optical filter gain | 1 |
| The refractive index n | |
| 100 | |
| The maximum reflectance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Wang, Q.; Zhang, Y. Joint Constellation and Reflectance Optimization for Tunable Intelligent Reflecting Surface-Aided VLC Systems. Photonics 2024, 11, 840. https://doi.org/10.3390/photonics11090840
Jia L, Wang Q, Zhang Y. Joint Constellation and Reflectance Optimization for Tunable Intelligent Reflecting Surface-Aided VLC Systems. Photonics. 2024; 11(9):840. https://doi.org/10.3390/photonics11090840
Chicago/Turabian StyleJia, Linqiong, Qikai Wang, and Yijin Zhang. 2024. "Joint Constellation and Reflectance Optimization for Tunable Intelligent Reflecting Surface-Aided VLC Systems" Photonics 11, no. 9: 840. https://doi.org/10.3390/photonics11090840
APA StyleJia, L., Wang, Q., & Zhang, Y. (2024). Joint Constellation and Reflectance Optimization for Tunable Intelligent Reflecting Surface-Aided VLC Systems. Photonics, 11(9), 840. https://doi.org/10.3390/photonics11090840





