Abstract
This two-part work develops a comprehensive toolbox for the statistical characterization of nonlinear distortions of DAC-generated signal constellations to be transmitted over communication links, be they electronic (wireline, wireless) or photonic, Mach–Zehnder modulator (MZM)-based optical interconnects in particular. The all-analytic toolbox developed here delivers closed-form expressions for the second-order statistics (means, variances) of all relevant constellation metrics of the DACs’ building blocks and of DAC-driven MZM-based optical transmitters, all the way to the slicer in the optical receivers over a linear channel with coherent detection. The key impairment targeted by the model is the random current mismatch of the ASIC devices implementing the DAC drivers. In particular the (skew-)centrosymmetry of the DAC metrics is formally derived and explored. A key applicative insight is that the conventional INL/DNL (Integral NonLinearity/Differential NonLinearity) constellation metrics, widely adopted in the electronic devices and circuits community, are not quite useful in the context of communication systems, since these metrics are ill-suited to predict communication link statistical performance. To rectify this deficiency of existing electronic DAC metrics, we introduce modified variants of the INL|DNL, namely the integral error vector (IEV) and the differential error vector (DEV) constellation metrics. The new IEV|DEV represent straightforward predictors of relevant communication-minded metrics: error vector magnitude (EVM) treated here in Part I, and Symbol/Bit Error-Rates (SER, BER) treated in the upcoming Part II of this paper.
1. Introduction
The DAC and ADC interfaces pose significant bottlenecks in broadband communication systems at large, and in next-gen optical transmission systems in particular. The incessant generational evolution of optical communication networks calls for ever higher baud rates, in conjunction with ever higher D/A and A/D precision (effective resolution). This paper is devoted to “all-analytic” stochastic modeling of the DAC building block and exploration of its impact on end-to-end performance of communication systems, ultra-high speed coherent optical or wireless/wireline links in particular.
Note: the readers are referred to Section 1.1 listing the abbreviations used in this introduction and throughout this paper as well as the mathematical notation and abbreviations.
We develop a toolbox of closed-form formulas modeling the second-order statistics (the mean and variance vectors) of the source current arrays and output constellations generated by current-steering eDACs, and the ensuing impact on communication systems performance. The eDAC random impairments are assumed to be induced by the stochastic mismatch errors of the transistors implementing the current sources.
Our applicative interest is in particular in optical communication interconnects based on MZMs driven by ultra-high-speed eDACs [1]. However, the results are meaningful for electrical (wireless, wireline) electrical communication at large as we elucidate here the impact of eDAC nonlinearity metrics on error vector magnitude (EVM). The analytic-statistical eDAC foundations developed in this paper will enable, in our planned sequel publication (Part II), developing an analytic model the nonlinear propagation of the eDAC current mismatch impairment statistics via the MZM nonlinear sine-shaped TC, as well as modeling optical DACs (oDAC).
Random device variations are identified as a key factor limiting the performance of high-resolution CMOS current steering D/A converters used as drivers in ultra-high-speed electronic and optical Tx-s. For high-end ultra-high-speed energy-efficient applications, current-steering eDACs are the drivers of choice [2]. In eDACs, the transistor mismatch of current sources is often the predominant error determining the nonlinearity of the static eDAC transfer characteristic. This paper provides in-depth analytic statistical treatment of electronic mismatch in eDACs, albeit not at the device level but at the sub-system level.
The stochastic effect of “devices mismatch” (the inevitable variability in identically designed devices) is the most fundamental of the eDAC impairments, irreducible (for any given device structure) by technological advances, in fact becoming progressively worse along Moore’s law evolutionary path, as the CMOS technology node is reduced. Despite a formidable amount of research having addressed device-level mismatch, e.g., [3,4], knowledge is still insufficient on the propagation of random contributions from the stochastic mismatch sources on the eDAC chip via the Tx, channel and Rx sub-systems, collectively affecting the attainable precision of the Tx output, as well as the signal detected in the Rx at the far end of the link. In historical terms, Pelgrom et al. [5] pioneered rigorous device-level modeling of the mismatch impairment of CMOS transistors. Some 16 years later, he insightfully commented on the significance of mismatch statistical analysis, providing the following perspective [6]: “As dimensions shrink, the granularity of the silicon device will play a more and more dominant role … It seems inevitable that we are now entering an era where statistical design is the rule not the exception… We will see many more papers exploring the statistical behavior of the devices and their interaction with technology”.
Our paper may well be one of those contemplated by Pelgrom in 2005, with some distinctions: granted, numerous papers have been published ever since on the impact of mismatch modeled by Monte Carlo simulation. However, to the best of our knowledge, far fewer papers [7,8,9] approached the statistical problem in an all-analytic mindset. Moreover, our paper is differentiated by its particular (optical) communication orientation, analytically tracing the mismatch statistics of the eDAC current source devices all the way along the chain of subsystems in the (optical) transmission link to obtain communication performance figures of merit such as EVM (in the current paper Part I), SER and BER (in the upcoming Part II), of direct interest to optical or wireless communication engineers designing eDAC drivers into their transmitters.
This paper maps device-level statistics into subsystem-level statistics, developing an all-analytic stochastic model enabling deeper intuition into the propagation mechanisms of the mismatch impairment via the eDAC and the subsequent modules in the end-to-end transmission chain comprising the eDAC, the (optical) Tx, a linear channel and the Rx.
Particular attention is given to formally proving and exploring the symmetries of the various eDAC random variates and performance metrics. As in most areas of physics, it is beneficial to reveal and explore the symmetries hidden in the structures and interactions Moreover, the normalization of various physical quantities by judicious selection of suitable units of measurement, is an investment worth making upfront, enabling to simplify and streamline physical models. For current-steering eDACs, it is highly beneficial to normalize all currents by the so-called unary current and to explore the symmetries implied by the block diagrammatic structure of the eDACs and the mathematical nature of the eDAC codes.
In the context of optical communication, to be addressed in the upcoming Part II of this paper, the eDAC output mismatch will be tracked across the electrical-to-optical interface in the Tx, accounting for the MZM nonlinearity, all the way to the input of the decision circuit in the optical Rx, enabling to relate useful communication performance parameters such as received constellation EVM and SER at the optical Rx, to the fundamental current mismatch impairment of the eDAC drivers in the optical Tx.
Our novel all-analytic behavioral statistical modeling toolset may turn useful in the early stage of eDAC and/or wireless|optical Tx design cycle, to enable a grasp on the fundamentals of the design, providing insight into main features of the solution, as useful addition to Monte Carlo simulations, e.g., [10,11,12] which are useful but are best deferred to fine-tuning and final verification in the later stages of eDAC + Tx design cycle, once all-analytic pre-design (enabled by our new toolset) has been completed.
Our analytical stochastic analysis framework pertains to performance metrics such as EVM, SER and BER, important to any communication engineer, regardless of the physical nature of the transmission channel (EVM is directly addressed in this paper, SER/BER are addressed in Part II). Since the electrical DAC is an essential building block in any type of digital communication system at large, it follows that most of this paper may be found useful for readers with no interest in optical communication, but rather oriented to wireless or wireline transmission (e.g., to model EVM|SER|BER of wireless links, quantifying the impairments due to electronic mismatch propagation via the nonlinearities of power amplifiers).
To preview some of the highlights of the paper by way of graphic visualization (which we suggest skimming ahead of delving into the gradual mathematical modeling construction), the matrix models we develop for the eDACs are mapped in Figure 1 and Figure 2 into behavioral block diagrams for generation of Unipolar (UNIP) and Bipolar (BIP) eDACs of orders 4, 8 and 16 (e.g., a UNIP ePAM4 constellation is of the form {0, Iu, 2Iu, 3Iu}, all non-negative, whereas a BIP ePAM4 constellation is of the form {−3Iu, −Iu, Iu, 3Iu}/2, containing ± levels).
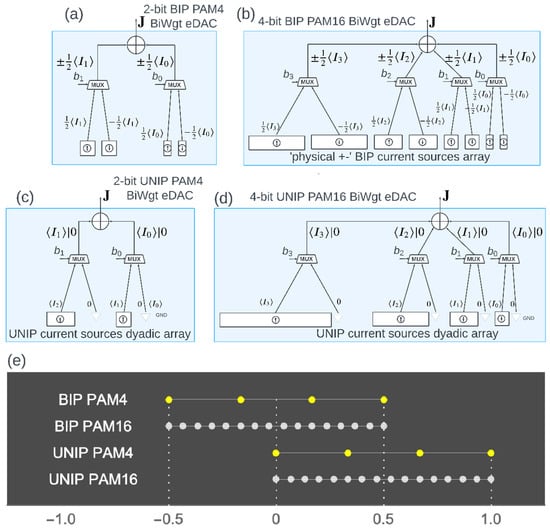
Figure 1.
Behavioral models and generated constellation diagrams of PAM4|16 BiWgt eDACs of the UNIP|BIP polarities: conceptual block diagrams, implemented using current source arrays, combined via a switching matrix implemented by MUX selectors and a currents summer. Circuit implementations may differ from these conceptual structures. The (31) models are “behaviorally implemented” by the depicted flow diagrams (the superscripts UNIP|BIP on the various currents are omitted in the figures, for brevity). (a,b): BIP-PAM4|16 BiWgt eDACs. The s-th mux (for s = 0, 1 in (a), s = 0, 1, 2, 3 in (b)), controlled by bit bs, selects between antipodal source currents, . In (a), the four mean output currents, obtained by summing the MUX outputs, are . A dyadic sources array satisfying yields . In (b), the 16 resulting mean output currents are given by . A dyadic array satisfying yields . (c,d): UNIP-PAM4|16 BiWgt eDACs. The s-th control bit now switches between . In (c), the mean output currents of the UNIP-PAM4 constellation are . If , then . In (d), the mean output currents of the UNIP-PAM16 constellation are given by . The dyadic array satisfying yields . (e): Generated constellation diagrams of PAM4|16 BiWgt UNIP|BIP eDACs. Note that the full scales of the constellations are all equal (taken as unity here).
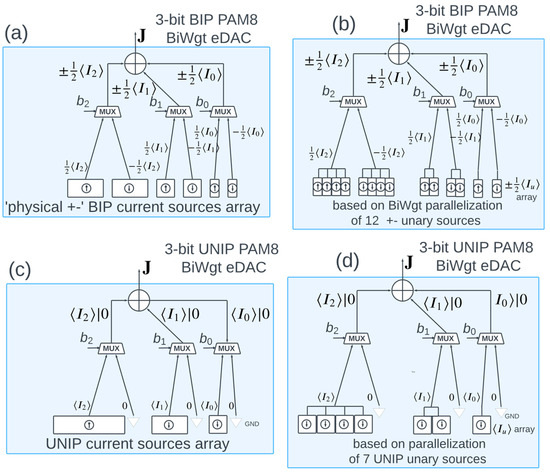
Figure 2.
Behavioral models of PAM8 BiWgt eDACs of the UNIP|BIP polarities, using dyadic source current arrays, possibly synthesized (in (b,d)) by parallelizing subsets of unary current sources. (a,b): BIP-PAM8 BiWgt eDACs. The s-th mux (for s = 0, 1, 2), is actuated by the eDAC input bit bs to select one of the two antipodal source currents, . The 8 mean output currents, obtained by summing all possible outputs of the three MUXes, are . Whenever the dyadic current sources condition is satisfied, we obtain a “perfect” BIP-PAM8 constellation . Note that (b) is functionally equivalent to (a), but in (b) the three source currents are synthesized using a “uniform” array of 7 nominally identical “half-unary” current sources of means , partitioned in subsets of 1, 2, 4 elements, respectively, i.e., . The half-unary sources in the 2nd and 3rd subsets are parallelized as in (b), to form the triplet of dyadic source currents . (c,d): UNIP-PAM8 BiWgt eDACs. The s-th control bit now switches between , for s = 0,1,2. The resulting 8 mean output currents in both (c,d), are .
This paper is concerned with the statistics of the mismatch-induced variations in the eDAC output levels. The statistics turns Gaussian to an excellent approximation, determined solely by the means and variances. Figure 3 and Figure 4 are also worth previewing as they illustrate some striking statistical properties of the output constellations, the statistics of which is derived from the statistics of the independent current sources. Figure 3c and Figure 4c depict the histograms of three current sources, nominally in 1:2:4 ratios, combined to generate the eight levels of UNIP and BIP constellations, respectively.
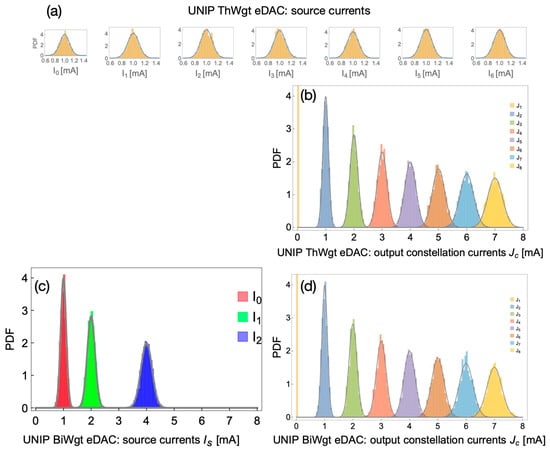
Figure 3.
Monte Carlo simulations of the distributions of the source currents and output constellation currents for 3-bit (PAM8) UNIP eDACs, both ThWgt and BiWgt, overlayed with the corresponding analytic PDFs. (a): ThWgt UNIP eDAC: Distributions of the 7 independent random source currents, labeled I0, I1, …, I6. (b): ThWgt UNIP eDAC: Distributions of the corresponding output currents J1, J2, …, J8, of the output constellation, obtained by accumulating the 7 IID ThWgt source currents of part (a). (c): BiWgt UNIP eDAC: Distributions of the 3 independent random source currents, labeled I2, I1, I0, synthesized from the ThWgt source current array of seven 1500-vectors displayed in Figure 3a, based on the “BiWgt structuring of an ThWgt current sources array” construction introduced in (249) of Section 2.8. (d): UNIP BiWgt eDAC: Distributions of the corresponding output currents obtained by passing the 3 IID BiWgt source currents of (c) via the UNIP code matrix modeling the switching-in|out of 0, 1, 2 or 3 of the three sources and the summation of their currents.
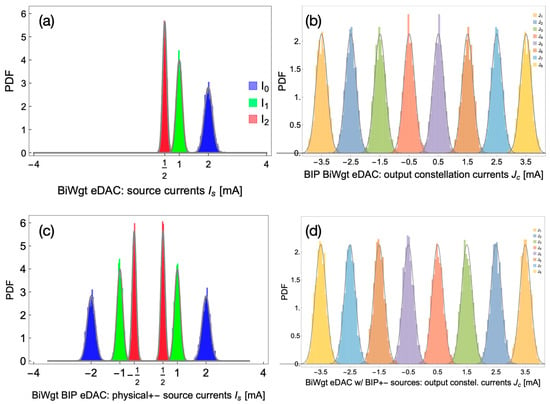
Figure 4.
Monte Carlo simulations of the distributions of the source currents and output constellation currents for BiWgt BIP (PAM8, i.e., 3-bit) eDACs, overlayed by the corresponding analytic PDFs. (a): The “mathematical” source currents. (b): The resulting output levels currents. (c): The “physical±” source currents (that (b) is an equivalent mathematical representation thereof). (d): The resulting output levels currents (seen to have identical distributions, as in (b)).
The actual histograms of the resulting eight levels are depicted in Figure 3d and Figure 4d, respectively, and they are very different. In the BIP case (Figure 4d), all constellation levels have identical statistics, which is not intuitive at all. In the UNIP case (Figure 3d), the constellation levels experience gradually higher statistical spreads, as the level magnitudes increase. In fact, the induced standard deviations with regard to the regular nominal positions of the levels are in the ratios . We hope that the preview of these results provides some motivation for staying the path along our systematic analytical development of the statistics of mismatch of current steering eDACs, all derived as stemming from nothing more than Pelgrom’s seminal transistor mismatch statistics model [5].
1.1. Overview of the Paper Structure
This subsection presents this paper’s roadmap. Section 2 systematically develops the all-analytic statistical model, starting from simple device statistical physics assumptions. The taken approach is to postulate the mismatch statistical model of Pelgrom’s groundbreaking paper [5], retaining the lead term of the mismatch expansion therein, simply modeling the relative mismatch (relative STD (RSTD)) of the MOS transistor current source level as inversely proportional to the square root of the device active area. From Pelgrom’s RSTD formula, we infer that the variances of the current sources must be proportional to their mean currents. Everything at the subsystem level then stems from this simple device-level posit on the variances of uncorrelated source currents. We proceed to model the electrical switching matrix of the eDAC by means of a matrix-based linear model accounting for the formation of the eDAC output current constellation, modeling the linear eDAC just using no more than elementary random signals theory, generalizing a matrix approach by Crippa et al. [7], as well as on our own matrix-based earlier formulation [13] (originally developed for oDACs but analogously applicable to eDACs). We derive closed-form formulas for the second-order statistics of the mismatch perturbations of the eDAC output current levels, as well as corresponding statistics for the constellation “steps”, defined as the separations between neighboring levels. A novel feature of our linear-algebraic models of the eDAC is the formal derivation and explorations of the (skew-)centrosymmetry of the DAC random variates and statistical metrics, as taken up in Section 2.6.
In Section 3, we relate the second-order statistical edifice constructed in Section 2, to the conventional definitions of the INL and DNL—the most prevalent DAC specifications. A key observation is that the INL|DNL eDAC metrics are inappropriate for statistical modeling in communication applications. To address this deficiency, we introduce simpler yet more suitable variants of INL|DNL, referred to as IEV|DEV. These proposed eDAC metrics are directly relevant to transmission link modeling. The IEV describes the deviations of the actual constellation from a nominal (nominal) constellation (with its end-points taken subtly different than those of the reference constellation in the INL definition). The DEV quantifies the “eye-opening” between adjacent traces in an eye diagram. We present simple, yet elegant derivations of the second-order statistics of the IEV|DEV random vectors, in the wake of mismatch errors of the array of eDAC current sources, based on our matrix-based approach. The mismatch-induced statistics of our new IEV|DEV metrics are much simpler to model statistically than those of the original INL|DNL. Fortunately, as readily derived using no more than elementary random signals analysis, the IEV|DEV are normally distributed (whenever the mismatch perturbations are). In contrast, the statistical distribution of INL|DNL is non-Gaussian, requiring sophisticated Brownian Bridge stochastic analysis methods, as seen in the work of Radulov et al. [8,9].
The study of eDAC random variates symmetry, commenced in Section 2.6, is extended to the INL|DNL metrics.
Section 3 culminates in Section 3.9 aggregating the I and Q components into complex-valued IEV|DEV, suitable for the full characterization of the QAM constellation generated by a pair of eDACs used as I and Q tributaries in a QAM Tx. It is the complex-valued IEV that directly determines the QAM constellation EVM, whereas the SER is evaluated from the Re&Im parts of complex-DEV. We mention that no such no such “complexification” seems possible with the INL|DNL. Closed-form formulas are developed for the EVM transmission metrics for bipolar PAM and QAM constellations generated by eDAC-based communication transmitters, directly relevant to communication engineers, expressing the EVM in terms of the IEV|DEV statistical behavioral model of the eDAC. Operationally, the constellation EVM is simply obtained in closed form by linearly scaling the IEV, then evaluating its RAMS-type average.
The analytical statistical eDAC models developed in Section 2 are developed in Section 2.7 and Section 2.8 for the specific example of 3-bit PAM8 UNIP|BIP, ThWgt|BiWgt eDACs.
The eDAC random characteristics and metrics developed in Section 2 and Section 3 are numerically verified by means of Monte Carlo simulations in Section 2.9 and Section 3.10, confirming that the analytic statistical models and metrics of eDAC current arrays and output constellations are indeed consistent with our underlying device-level Proposition 1.
Section 3.11 presents Monte Carlo simulations of the newly introduced (IEV, DEV) vs. incumbent (INL, DN)L eDAC metrics.
Appendix A and Appendix B detail most of the proofs of the multiple theorems, lemmas and corollaries developed in this paper. Appendix C assembles the specific math notations and abbreviations used throughout this paper.
2. Second-Order Statistical Modeling of Current-Steering Electronic DACs (eDAC)
2.1. Matrix-Based Modeling of Current-Steering eDACs: From Current Sources to Output Levels
The two types of DACs of interest to us (be they eDAC or oDAC) may be described by matrix techniques [13], as partially introduced in [14] for oDACs modeling, ported and adapted here for the first time to eDAC modeling, in preparation of developing an all-analytic approach suitable for statistical modeling of all eDAC types.
In this work, we assume current-steering eDACs (most suitable for high-speed communication applications) of the UNIP and BIP type, with more attention on BIP eDACs as used in coherent (optical) communication applications, albeit without neglecting to address UNIP eDACs as well.
Note: BIP eDACs, such as those used for generating I or Q tributaries in QAM transmission, generate symmetric constellations, having bipolar antipodal values, around the origin of the output current or voltage domain axis.
Fundamentally, random fabrication and material imperfections dictate that the electrical current sources, realized as MOS transistors, in current-steering eDAC ASICs cannot be fabricated to precisely operate at their nominal designed values, but are subject to inevitable statistical variations. The elementary current sources are modeled as independently drawn from a statistical distribution (typically a normal distribution). The relative deviations of the current values of the independent elementary sources relative to a nominal expected common value are referred to as “current mismatch errors”, or in short “mismatch”. In fact, mismatch is a fundamental, inevitable eDAC impairment, statistically modeled here using analytic methods.
In this paper, all eDAC currents are viewed as random variables perturbed around their nominal values (typically their means) due to the electronic mismatch errors. Other types of eDAC errors such as systematic errors are not addressed in this paper, with the exception of bias (static) errors. Our probabilistic mismatch model then pertains to an ensemble of eDAC chips, exhibiting fundamentally stochastic variations in their physical parameters, chip-to-chip. We aim to develop analytical tools enabling us to assess the quality of the output constellations of electronic or optical transmitters (e.g., based on MZM modulators or on compound oDACs). The communication links of interest use higher-order transmission constellations (e.g., QAM); hence, the Tx-s are to be electronically driven by eDACs. Electronic mismatch errors inherently affecting the eDAC drivers of the (electronic or optical) Tx-s are the key transmitter impairments modeled in this paper. Fortunately, eDACs of the BiWgt and ThWgt type are linear devices, enabling a streamlined matrix-based model developed in the sequel.
Consider a stochastic ensemble of nominally identical current-steering eDACs. Each eDAC comprises S current sources, generating currents , with S the number of current sources. The source currents, , are RVs, collected into a random vector . Note the unusual reverse indexing for the elements of from S − 1 down to 0. Moreover, the source currents means are assumed to be positive means, even for bipolar eDACs, since antipodal negative sources are assumed to be effectively generated by switching circuits, modeled by means of a switching matrix, also known as code matrix, C, of size , with elements all for BIP eDACs, 0|1 for UNIP eDACs:
where (a column vector) is the output C-levels current constellation generated by the eDAC. The transposes of the rows of the code matrix are denoted where is the c-th row of (and is a column vector corresponding to the transpose of the c-th row of ).
The rows of are referred to as the “eDAC codewords”, and the set of codewords is called the “eDAC code”. The elements of each code vector , as arrayed along the c-th row of , are the linear combination weights applied to the source currents in order to generate the c-th output current level .
Note: the code matrix of the eDAC (see (1)) is in fact similar to the code matrix for the SEMZM-oDACs and MP-oDACs, as introduced in [14], except that in that work the domain and co-domain of the linear transformation are not current-domains, as in (1), but are rather different physical (photonic) quantities. Nevertheless, both matrices for BIP oDACs in [14] and for BIP eDACs here are valued, notwithstanding the different interpretations of the input and output of the respective linear transformations.
The linear transformation (1), applied to the source currents S-vector, , yields the c-th output current level
where the matrix elements are 0|1 for UNIP, ±1 for BIP. For UNIP and BIP eDACs, respectively, the output current of the c-th level is then given by
where for BIP eDACs, the signs of the source currents additive contributions are determined by the ±1 values in the c-th row of the matrix CBIP, i.e., the bipolar bits of the c-th BIP codeword, whereas for UNIP eDACs, the 0 or 1 selection of the source currents additive contributions are determined by the bit values in the c-th row of the matrix CUNIP, i.e., the binary bits of the c-th UNIP codeword.
For a Thermometer Weighted (ThWgt) BIP|UNIP eDAC, the size S of the source current array (and the length of each codeword vector), equals S = C − 1 (with C the length of the codewords—C is also the output current constellation order). Successive BIP and UNIP codewords have the following forms for ThWgt|BiWgt eDAC topologies of the UNIP|BIP polarities:
For a BiWgt BIP eDAC, the size S of the source current array (and the length of each codeword vector), equals S = B, with B = log2C the minimal number of bits specifying the order C of the output constellation, which is assumed an integer power of 2 (i.e., B is the eDAC “nominal-number-of-bits”, e.g., a 3-bit eDAC features C = 8 levels).
The C = 2B BiWgt codewords are B-bit bitstrings forming a “counting code”, i.e., counting 0, 1, 2, 3, …, albeit in binary base:
where denotes the binary representation (bitstring) of the integer n. The successive codewords are 0|1-valued bitstrings corresponding to the base-2 representations of the successive integers 0, 1, 2, …, C − 1). The counting code (5) satisfies
Introducing the notation
for the B-element dyadic sequence, (a geometric sequence with ratio ½ ending in 1), (6) is then rewritten as
For a BIP eDAC (be it ThWgt|BiWgt), (1) is specialized to ; taking the mean (or expectation, denoted per Section 1.1) of both sides, yields a linear relation between the means of the source currents and of the output current levels:
As an example, consider a BiWgt BIP-PAM4 eDAC with C = 4, B = 2,
For BiWgt BIP-PAM4 eDACs, the linear transformation of mean currents, (9) reduces to
Conceptual block diagrams implementing the behavioral model of BIP|UNIP-PAM4|16 BiWgt eDACs are depicted in Figure 1. These concrete examples are worth carefully inspecting, to gain insight into our abstract mathematical models of BiWgt eDACs.
The behavioral model of Figure 1 need not implement multiplications by matrices with generic elements—for our purposes it suffices to consider code matrices with weights ±1 for UNIP and 1|0 for UNIP, which amounts to sign flips of source currents and inclusion/exclusion of source currents. We now explain how the behavioral model seen in Figure 1a for BIP-PAM4, based on electronic MUXes, implements the signed-sums linear transformation (11), concisely written as
(with distinct combinations of ± signs for each of the output level indices, c = 1, 2, 3, 4). Recall the functionality of each of the two MUXes as selector of one of its two inputs, as determined by the control bit, : when (, the RSH (LHS) input to the mux is passed to the mux output. Since the pair of inputs to each mux have been designed to be antipodal, , then the mux controlled by bit generates at its output. Finally, the two mux outputs and are summed up to generate one of the four signed sums (12) amounting to the linear transformation (11) corresponding to the code matrix in (10). As the two MUXes are controlled by a pair of bits, , if these two Boolean variables take values in the set {±1} instead of {1,0}, then the vector , with the control bit combinations referred to as “codewords” coincide with the rows of the code matrix in (10).
As for the behavioral model of Figure 1b for UNIP-PAM4, we now return to using binary codewords (corresponding to the rows of in (10)). For UNIP, the RHS input of each of the two MUXes is null (grounded). Thus, the mean output of the s-th mux is , with the first (second) outcome for (). Summing up the two mux outputs yields the four possible combinations
Having justified the correspondence of the behavioral models of Figure 1a,c with our code matrix-based linear transformations, the remaining Figure 1b,d pertaining to BIP and UNIP ePAM16 are evident generalizations, as further detailed in the figure caption.
Note: In Figure 1, factors of ½ appear in the BIP formulations; such factors are absent in the UNIP formulations. The factors of ½ are justified in (29)–(32) in Section 2.2 in the following. For now, these factors should be accepted as an ad hoc convention.
For higher-order PAM constellations, the coding matrices become larger, e.g., for C = 8:
PAM8 eDACs examples are elaborated in Section 2.7 and Section 2.8. See in particular Figure 2 in Section 2.7 for the block diagrams of the behavioral models for PAM8 eDACs. Behavioral models for a BIP-PAM16 are depicted here in Figure 1b,d. For ePAM8, refer to Figure 2 below. The totality of sub-figures in Figure 1 and Figure 2 then covers the gamut of ePAM4|8|16 UNIP|BIP BiWgt eDACs.
Let us now consider the outermost levels in the 1D output constellation of an eDAC.
- BiWgt vs. ThWgt mean source and output currents
BiWgt eDACs are driven in parallel by B = S actuation bits, where , is the number of bits and S is the number of current sources. In our model, BiWgt eDACs of either UNIP|BIP polarities conceptually use just S = B nominal current sources, , arrayed in the current sources vector in reverse order, with (at s = 0 index) in the last element of , (s = 1 index) ahead of it, in the first element of .
The B current sources in our model for BiWgt eDACs (be they UNIP|BIP) form a so-called “dyadic sequence”, defined as a geometric sequence with ratio 2,
where we note that the first element, indexed s = 0, , of the increasing geometric sequence is the least element, and it is also the GCD of the dyadic sequence of elements.
In UNIP BiWgt eDACs, the B current sources are weighted by 0|1 values, to form the linear combination representing the eDAC output, implemented by having the switching matrix either include or exclude (either steer-in or block, divert away) some or all of the current sources in the binary linear combination:
The level-index, c, determines the 0|1 weights of the sources, per the bitstring specified in the c-th UNIP codeword, , which embodies a “counting code”.
The codewords (and coding matrix) of BIP BiWgt eDACs are obtained from the UNIP ones by the replacements 0 → −1, 1 → 1. Thus, BIP BiWgt eDACs, the B current sources (15) are weighted by “bipolar bits”, namely ±1 values, generating the following linear combination, having the code matrix either add up or subtract the current sources, flipping or not flipping the polarity of each of the contributing current sources in the bipolar linear combination:
Here, the output level index, c, determines the particular signs used for weighting each current source, as listed in the c-th BIP codeword, .
For BiWgt UNIP|BIP eDACs, the total mean source current (applicable to both UNIP|BIP BiWgt eDACs) is obtained by summing up the elements of dyadic sequence (15), yielding
To recapitulate, for BiWgt eDACs, be they UNIP|BIP,
Let us now introduce some as useful eDAC parameters: the eDAC most/least significant level, full scale and full-scale range:
Definition 1.
The Least-Significant-Level (LSL) and the Most-Significant-Level (MSL), of an eDAC current constellation, , are the first and the last element , respectively. The “Full-Scale” (FS) of an eDAC is defined as the difference between the MSL and LSL:
Evidently, the FS is an RV and so are the MSL and LSL. A useful metric is the mean FS,
The segment of the real axis is referred to as the Full-Scale Range (FSR). Its length equals the mean-FS. The C constellation levels (points) partition the FSR into C − 1 constellation “steps” also known as “increments” also known as nearest-neighbor (NN) intervals.
- eDAC constellation steps (increments)
We now proceed to define and model the steps (increments) of the eDAC constellation levels, i.e., the separations between successive output levels of the constellation.
Definition 2.
The “Steps”, , of a 1D constellation of levels are defined as the lengths of the intervals between pairs of adjacent levels of the constellation:
The sequence of constellation steps is arrayed into a “steps vector” .
The steps-operator, , alternatively called first-difference operator, is the linear mapping
Lemma 1.
The c-th level, of a constellation is obtained by accumulating the first c − 1 steps of the given sequence, having them added to the initial element, :
Formula (23) for the c-th level of the output constellation, in terms of the steps, is formally obtained as the solution of the recursion,
The full scale of the constellation is then given by the accumulation of all C − 1 steps:
The (arithmetic) “average step” is obtained by scaling the FS (25) by the factor:
Taking the (stochastic) mean of the average step yields the “mean-average-step”:
The mean-average-step coincides with the fixed mean step of a deterministic “nominal” uniform reference constellation specified to have its LSL and MSL, respectively, coinciding with the mean LSL and mean MSL of the given constellation:
Note: The “nominal” (reference) constellation is random whenever the original constellation is, since is defined to satisfy the “boundary conditions” , i.e., have the same LSL and MSL. However, is always a uniform constellation, consistent with the convex linear combination (28), specifying its inner levels.
2.2. UNIP vs. BIP Source Currents Convention
The last subsection explored the linear transformation mapping the eDAC source currents into the eDAC output current levels. This subsection addresses the relative scaling of the source currents used in UNIP vs. BIP eDACs, such as to facilitate meaningful performance comparison between the ThWgt|BiWgt polarities for a given eDAC topology.
We introduce a convention specifying the ratio of UNIP vs. BIP source currents under the constraint of a given total of the mean “physical” source currents (equivalently, for a given chip area of the “physical” current sources) for either of the two polarities (UNIP|BIP):
Note: Recall that, for a UNIP BiWgt eDAC, there as are many effective current sources, , as the number of bits, B, determining the codewords or levels. In contrast, the UNIP ThWgt eDAC topology uses S = C − 1 = 2B − 1 sources.
Henceforth, denoting simply as , then our UNIP|BIP convention (29) may be equivalently formulated as
The corresponding eDAC output currents and their means are then given by
Note: operationally, a factor of ½ appears in the BIP formulations; this factor is absent in the UNIP formulations.
Component-wise, we have (with the notation ) the “switch & sum” models,
Note: the simple linear combination (32) of source currents model with either ±1 or 0|1 coefficients renders the evaluation of the second-order statistics of relatively straightforward, given the second-order statistics of the source current vector , of which statistics is about to be derived in Section 2.4.
At this point, let us clarify what we mean by “physical” source currents, as opposed to the “mathematical” source currents, heretofore used in our linear models, assumed to consist of all-positive-valued vectors. In our BIP “mathematical” linear model, negative current contributions are generated by means of multiplication the −1 elements of the C-matrix, rather than by means of defining current sources of negative polarity. However, in the “physical” behavioral model of Figure 1, bipolar current sources are employed. Evidently, the “physical” and “mathematical” eDAC models are equivalent, but we need to calibrate the relative magnitudes of the “mathematical” source currents used in the two eDAC variants of different polarities.
For UNIP eDACs, the two types of source currents (mathematical vs. physical) coincide. However, for BIP eDACs, the “physical±“ current sources used in BIP circuits are bipolar; half of the current sources are of negative polarity, as made evident in Figure 1. We may array the source currents in each eDAC depicted in Figure 1 into a “physical±” mean vector of BIP source currents, comprising 2B elements, consisting of a permuted version of the vector . Inspecting the eDAC examples, in Figure 1a, for B = 2, the respective “mathematical” and “physical±” sources are (with the BIP superscripts discarded, for brevity):
whereas in Figure 1b, for B = 4,
Note: the positive-valued elements of coincide with , whereas the negative valued elements of coincide with , but the two sub-vectors are interspersed.
Our UNIP|BIP-convention stipulates the constraint of fixed total mean “physical” source currents for either BIP|UNIP. This constraint is formulated for a BiWgt eDAC as
We now verify that our UNIP|BIP-convention (29) satisfies “fixed-total” constraint (35): since the positive-valued elements of coincide with , whereas the negative-valued elements of coincide with ; therefore, it is evident that
The factor-of-two in the last equality is compensated by the factor of in our UNIP|BIP convention (29):
.
Note: Yet another equivalent, intuitive, statement: the “physical” BIP array also uses mirror-image sources; therefore, it comprises twice as many current sources; to have a fixed total current, we must half all source currents upon transitioning from UNIP to BIP. Having twice as many sources for BIP compensates for scaling the mean amplitude of the BIP sources by a factor of , relative to the UNIP case.
As a simple example of the UNIP|BIP “fixed-total” constraint (35), consider the BIP PAM4 BiWgt eDAC of Figure 1a, implementing the switch-and-sum operation , using four physical current sources having means . The sum of the absolute values of the four mean source currents of this BIP-PAM4 BiWgt eDAC equals
A UNIP-PAM4 eDAC may use just the pair of current sources , having them combined as per . The sum total of all currents here may also yield
Thus, this example validates fixed total current constraint (35).
The UNIP|BIP PAM4 example is readily generalized to higher-order BIP PAM constellations utilizing multiple current sources. Most generally, the physical array of S bipolar currents (the generalization of Figure 1) comprises the following bipolar source currents:
These are the source currents, each consisting of its mean + perturbation. Thus, in the “physical± model”, there are now 2S current sources, having means S of which are positive and S of which are negative. In contrast, in the “math model”,
onto which the matrix is to act in order to generate the output current of the eDAC, as per , we just have S current sources, , all having positive means (negative currents are effectively provided by −1 elements of the switching matrix C). In fact, these S positive-mean current sources of have means, respectively, equal to those of the currents in (40) with positive means:
Thus, for UNIP eDACs, the “mathematical” and “physical±” source arrays coincide, both consist of , whereas for BIP, the “physical±” array has twice as many sources (2S), compared to the “math model” array comprising S positive-currents. The “physical±” array, , comprises S positive-mean currents coinciding in-the-mean with the elements of and S positive-mean currents antipodal in-the-mean to the elements of .
Note 1: we have seen that “physical±” circuits of BIP BiWgt eDACs practically use twice as many sources: viewing the BIP sources as paired up in antipodal pairs (assigning to each current level both signs), we would have their antipodal source currents generated by two separate effective current sources (possibly the two halves of a current mirror cell) rather than being derived from a single source. In contrast, in our mathematically convenient model, J = CI, wherein I comprises B non-negative source currents, and this effect is attained by a linear transformation entailing a ±1-valued code matrix, such that the bipolar sign flips ±1 in the linear combinations forming the currents be conceptually provided by ±1-valued codewords. As a result, our simple matrix-based model does not correctly predict cross-correlations between eDAC output levels. Nevertheless, for the purpose of statistical modeling of variances, which is our specific target, our “mathematical” construction, based on B non-negative source currents, is indistinguishable from a circuit-model based on 2B independent bipolar source currents for BIP eDACs, 2B − 1 independent unipolar sources currents for UNIP eDACs, though, as discussed earlier, with the proviso of imposing the condition onto the respective source currents.
Note 2: The scaling by the factor-of-half relation, , holds only in-the-mean. Generally, , since , may be additively decomposed into means + perturbations; it is only the means that are in a factor-of-half relation, the perturbations are not. Writing (without wrapping the means around both sides) may lead to erroneous statistical results, inconsistent with the correct statistical model to be developed in Section 2.4, e.g., implies but this relation between the variances is incorrect. We preview that the actual consequence of Proposition 1 developed in Section 2.4 is .
Note 3: It will be shown in the sequel that the UNIP|BIP “fixed-total” constraint (35) is consistent with having identical chip areas of the source currents aboard the BIP and UNIP eDACs ASICs; thus, the performance comparison of BIP vs. UNIP eDACs is consistently carried out under the constraint of identical investments of the salient design resource of chip area (the current sources chip area is the primary resource determining the quality of the eDAC in the wake of currents mismatch). Moreover, our UNIP|BIP convention renders the mean full scales of corresponding UNIP and BIP eDACs equal, and we show that the “unary current” metrics (defined in Section 2.4) are equal.
We now proceed to explore the impact of our UNIP|BIP convention on the comparative characteristics of the output current constellations of BIP vs. UNIP. We first explore the relations between BIP vs. UNIP BiWgt codewords which are B-bit bitstrings obtained from per the mapping 0 → −1 and 1 → +1, formalized in vector notation as the following affine transformation taking UNIP codewords into BIP ones,
where we recall the all-ones vector notation introduced in Appendix C. Now, (32) yields
Now plugging
into the last expression in (43) yields
Thus, the BIP mean output current constellation is obtained from the UNIP one by a down-shift by half the mean UNIP MSL (or 1/2 the total mean current of the UNIP sources):
Note: More concisely, the last result is viewed as the BIP mean output constellation being obtained by centering the one-sided UNIP mean output constellation, which spans the FSR , yielding the FSR for the BIP mean output constellation. Note that both constellations have identical full-scale, .
- The UNIP|BIP convention amounts to design constraints on eDAC full scales and chip areas.
Considering the shift transformation (45), plug in c := 1 and use , yielding the relation between the LSLs of UNIP vs. BIP; similarly, plug in c := C to obtain the relation between the MSLs of UNIP vs. BIP. The two relations may be compactly recapped by stating the FSRs of BIP and UNIP, respectively (consistent with the last note above):
The FSR of BIP (a segment of the real line) may be obtained as a rigid shift of the FSR of UNIP. The lengths of the two FSR segments are evidently equal. BIP and UNIP are seen to share a common mean full scale (FS):
which is readily verified as follows:
Thus, UNIP and BIP constellations have the same “extents” (<FS>), under our UNIP|BIP convention (29). It is just that the mean FSR of BIP is relatively shifted by with respect to that of UNIP, resulting in the MSL of BIP being half that of UNIP.
In addition to calibrating the UNIP|BIP polarities comparison, we ought to further compare the two eDAC topologies, namely the ThWgt and BiWgt ones. For ThWgt-BIP eDACs, we should take S = C − 1 in (40). For BiWgt-BIP eDACs, we should take S = B (as many positive current sources as the number of bits, B; thus, the total number of positive and negative current sources should be 2B:
where the superscript +− and the superscripts remind us that the 2S signed physical source currents set may be partitioned into pairs with antipodal means . The “physical source currents” should be distinguished from the “mathematical source currents”, which are just the positive currents , forming our formal source currents vector, I.
For our communication applications purposes, the BiWgt-BIP topology is of higher interest to us than the ThWgt-BIP one is; hence, the structure (51) of the current sources is our main focus, in the treatment of the “physical±” model of eDAC current sources arrays. In fact, to fully propound the “physical±” model, we ought to specify the first- and second-order statistics of the random current sources (51): the mean of (53) yields
whereas, per Proposition 1 to be developed in Section 2.3 below, the variances of the source currents in (51) will be shown proportional to the respective means of the source currents.
Note: For ThWgt-BIP eDACs, we should set S = C − 1 in (40). For BiWgt-BIP eDACs, we should set S = B, using as many positive current sources as the number of bits, B; thus, the total number of positive and negative current sources is now 2B:
In fact, the means of the positive sources in the signed physical array coincide with the elements of , whereas the negative sources in coincide with the elements of . It is then evident that
thus, we have verified that the “absolute total” (meaning the sum of the absolute values of) the physical source currents is the same for UNIP and BIP by virtue of our source currents convention, i.e., generally holds for either UNIP|BIP constellations of the same size, as already formally proven in (35) above.
We are about to show, in the discussion around Proposition 1 below, that the source currents (ignoring their signs, i.e., taking absolute values) are proportional to the areas of the MOS transistors implementing the current sources, namely , with the total area of the active sources. The equality of absolute totals of source currents, for BIP|UNIP, amounts to a corresponding equality of the total areas of the current sources:
This convention enables a unified treatment fairly comparing BiWgt|ThWgt eDAC topologies of both UNIP|BIP polarities. is regarded as a key design constraint to be equally assigned to various alternative designs. We then recapitulate the following equivalences:
Note: In communication links the span (full-scale) of the transmitted constellation is a key transmission resource, since over linear transmission channels the received constellation is proportional to the transmitted one. The larger the FSR (span) of the received constellation is, the better the link BER performance. Thus, is a useful criterion for comparison of communication scenarios using BIP vs. UNIP constellations.
Our meaningful comparison of performance for the UNIP|BIP polarity will henceforth assume the UNIP vs. BIP current-sources convention (29) and (30), whereby the BIP and UNIP mathematical source currents, in-the-mean, are in a ratio of 1:2, (to be shown to amount to equality of total source current areas and to equality of the full scales for UNIP and BIP):
To recapitulate the key idea to recall regarding our UNIP|BIP convention: there are twice as many “physical±” sources for BIP (arranged in antipodal pairs), than there are for UNIP; therefore, it follows that, at identical full scales, we can afford to halve all UNIP positive source currents (in-the-mean) to obtain the BIP positive physical sources, since we also have BIP negative physical sources at our disposal.
2.3. All eDAC Currents Are Normalized by the (Mean) Unary Current
As in most areas of physics, the normalization of various physical quantities by judicious selection of suitable units of measurement is an advantageous approach worth adopting upfront, making it possible to simplify and streamline physical models. eDAC theory is no exception. In this subsection, we introduce “unary normalizations” for deterministic and stochastic modeling of eDACs.
For a given chip, batch or production lot of eDACs, it is useful to measure all current sources in units of the mean of a conveniently specified reference current, , referred to as “unary current” (the subscript u stands for “unit” or “unary”). The nominal value of the RV , i.e., its mean, , is going to be used as the unit of measurement to peg all current sources and all output currents aboard the chip; this normalization makes it possible to most compactly formulate the first and second-order statistical metrics of the array of eDAC current sources. The choice of the current level constituting the mean unary current is in principle arbitrary—smart selection of the unary current is guided by eDAC modeling convenience, such as to yield easiest-to-handle expressions in terms of normalized currents on the eDAC chip.
A useful choice of “unary current” is to designate the eDAC source current having the least mean as the unary current. This works well for BiWgt|ThWgt eDACs but turns out unsuitable for more general (non-uniform) constellation generation, e.g., as arising in optical transmission. We thus adopt a more versatile unary current specification, applicable to arbitrarily shaped constellations, in particular applicable to non-uniformly spaced constellations, such as predistorted ones, wherein the current sources, , are required to depart from the standard ThWgt or BiWgt uniform designs (which, respectively, feature equal mean current sources and dyadic currents sources). To encompass eDACs generating uniform output constellations, as well as extend the model to non-uniform output eDAC constellations, we introduce the following generalized definition for (yet reducing to conventional definitions, once the constellation is taken uniform):
Definition 3.
Unary random current, : the unary current is defined as the random current of a fictitious current source, conceptually constructed on the same eDAC chip, equal to the “average step” of the output current constellation of the eDAC:
The unary current is evidently an RV, since the FS is random; its mean value, namely , is equal to the “mean-average step” of the given (generally nonuniform) constellation,
“mean-average” meaning here that the stochastic mean is applied to the arithmetic average (58). The “mean-average” applied to the sequence of constellation steps yields
The mean-average step (i.e., ) is seen to be C − 1 times smaller than the FS of the eDAC.
Note 1: the unary current (equal to the “average step”) was seen to be an RV. In contrast, the mean unary current (equal to the “mean-average step”) is deterministic.
Note 2: upon evaluating the “mean-average”, the orders of arithmetic averaging and stochastic mean (expectation) may be commuted, .
In the special case that the mean output current constellation is uniform (e.g., for UNIP|BIP BiWgt|ThWgt eDACs), the definition above for coincides with the fixed nearest-neighbors (NN) separation of the given uniform constellation. For BIP eDACs, be they BiWgt|ThWgt, we have
with the least source current. The fixed NN-spacing of this arithmetic sequence is
The BIP unary current is twice the least source current for BiWgt|ThWgt BIP eDACs,
It is useful to also list the expressions for the LSL and MSL and the FS of the BIP eDAC:
where in the last equality we used
Note: (64) is consistent with , in fact holding for any eDAC.
For UNIP BiWgt|ThWgt eDACs,
The corresponding results for the UNIP eDACs are then
The UNIP unary current equals the least source current for BiWgt|ThWgt UNIP eDACs,
It is useful to also list the expressions for the LSL and MSL and the FS of UNIP eDAC:
The FS of either UNIP|BIP is given by a common expression
but from (63) and (67) it seems that the unary currents for UNIP|BIP C-level eDACs differ by a factor-of-two (below denotes the least source current)
but we made the convention that the all-positive source mean currents of BIP and UNIP are in 1:2 ratio as per ; thus, evidently, so are the least source currents:
It then follows from the last two equations that the respective unary currents of the UNIP|BIP constellations come out equal, which is convenient, as so are the corresponding full scales, and so are the two total areas of the source current arrays in the eDAC chips
Henceforth, we no longer distinguish between denoting the common value of either of these quantities as . Likewise, we no longer distinguish between denoting the common value of either of these quantities as .
Note: the result (72) stems from our “physical” BIP source currents array comprising mirror antipodal currents, despite our usage of only all-positive current arrays, mathematically.
For any eDAC topology (BiWgt|ThWgt) and/or polarity (BIP|UNIP), as soon as the pertinent unary current is determined, it is useful to have it put to use, in order to obtain normalized representations of all current quantities in our statistical model, simply having all current quantities divided by . This will be seen to render the statistical model formulation simpler and more elegant. All amplitude-domain quantities, be they random variables or deterministic metrics (mean, STD), are normalized by the mean unary current, . Any current RV or amplitude-domain statistical metric of the eDAC is then expressed in units of Normalized scalars/vectors are denoted by over-crescents .
Here are three examples of normalized current quantities:
where denotes the standard-deviation of a random variable (RV), X.
At times, we shall also use the alternative compact superscript notation, ⟨⟩ to designate the mean (expectation) for any random object (equivalent to wrapping by ⟨⟩),
The following are additional examples of normalized mean currents or current vectors:
where and reflect the commutativity of the normalization and mean (expectation) operations. We mainly reserve the alternative notation ⟨⟩ for designating the mean in the context of mean-normalized (or normalized-mean) currents:
The normalized mean source currents of UNIP BiWgt eDACs are given by
generated by simply dividing (69) by .
For BIP, using , the normalized currents are half those of UNIP:
For UNIP|BIP ThWgt eDACs, the corresponding results are
It is worth reiterating that, in our convention , the all-positive source current vectors (be they unnormalized, or normalized, ) do depend on the eDAC polarity (UNIP|BIP), but they are determined by the eDAC topology (ThWgt|BiWgt). The eDAC polarity (UNIP|BIP) determines the code matrices, C, (having either 0|1 or ±1 elements for UNIP|BIP, respectively).
In the case of the BIP BiWgt eDAC, wherein (see (63)), we have
The normalized output current levels of BIP BiWgt|ThWgt eDACs are obtained by dividing by :
For UNIP BiWgt|ThWgt eDACs, for which , we have
The normalized output current levels of UNIP BiWgt|ThWgt eDACs are simply obtained by dividing by :
The results are summarized in the following.
Corollary 1.
The UNIP and BIP mean normalized constellations (be they BiWgt|ThWgt) are arithmetic sequences with increment 1:
Equivalently, , .
The mean normalized full scale (FS) of both is C − 1 (with C the constellation size):
The FSs for UNIP vs. BIP are identical; however, the mean MSLs differ by a factor-of-two:
Proof.
The simple derivation, based on (81) and (82), is omitted.□
Defining the “total positive source current” of BIP as the sum of the all-positive source currents,
we notice that the physical BIP source current vector, denoted , has an “absolute total”, namely total of the absolute values of its elements (L1-norm), which is double (since the negative antipodal currents feature the same absolute sum as the positive currents do):
It is useful to normalize the total source current as well, since for either UNIP|BIP BiWgt|ThWgt eDACs, and then dividing by yields . However, for UNIP|BIP eDACs, the MSL current levels are given (using and ) by
Normalizing by division through as well as normalizing by division through yields
But since for either UNIP|BIP BiWgt|ThWgt eDACs (with the sum of the positive source currents only, not accounting for the absolute values of the negative current sources), then
To recapitulate, a UNIP normalized constellation comprises C normalized constellation levels ranging over the [0, C − 1] FSR, whereas a BIP normalized constellation ranges over the FSR , both in increments of unity (1 = the unary step normalized by itself).
2.4. Second-Order Statistics of Electronic Mismatch Errors in Current-Steering eDACs
Equipped with these mathematical preliminaries, we now address the all-analytic statistical modeling of mismatch errors.
Electronic mismatch errors of the current sources of a current-steering eDAC have been extensively modeled in the electronic DAC literature, initiated by the pioneering work of Pelgrom et al. [5], followed by a flurry of later works refining the MOS mismatch models.
Previewing our approach, we assume nothing more than the principle, in [5], according to which the stochastic spread of any current source on the eDAC chip is inversely proportional to the square root of the transistor area that generates it,
(see Appendix A), augmented by the reasonable assumption that individual source currents are statistically independent (provided the source transistors are sufficiently separated, spatially, on the chip).
Mismatch errors, referred to here as (mismatch-induced) perturbations, are defined as the random deviations of the source currents from their means, denoted as follows:
As per [5], we assume that the source currents, , of the current-steering eDAC are statistically independent (hence uncorrelated). To advance, we must relate the individual source current variances to the current source structural (physical) parameters. For all current-steering eDACs of interest, the variances of the S source currents are modeled in this paper by the following key.
Proposition 1.
The eDAC current sources, , are statistically independent, have variances that are proportional to their means, and are Gaussian distributed
with a proportionality factor (in [Ampere] units) relating means and variances for all current sources on the eDAC chip, wafer or batch of wafers, assuming statistical spatial homogeneity of the chip/wafer/batch, barring systematic mismatch errors:
Proof of Proposition 1.
Relegated to Appendix A.
Note: reviewing the proof is highly recommended, as it distills the physical basis of the underlying device physics [5] into a statistical formulation used as “anchor” for our entire development of an all-analytic model of eDACs and oDACs.
Our first use of this proposition is to derive the relative variances of the source currents, defined as the variance, , divided by the square of the mean, :
It follows from (95) that the “relative variance” of any eDAC current source, say the s-th one, is inversely proportional to the mean current of that source:
The “relative-standard-deviation” of the s-th current source, also known as “coefficient of variation” (defined as the standard deviation, , normalized by the mean, ),
is then given for the s-th eDAC current source by
In the eDAC literature, this ratio, , between the current STD and the current mean value, is referred to as the “relative matching” of the current source, shown below to directly determine its needed silicon area. Proposition 1 implies that current source transistors of larger areas (wider lateral dimension, higher conductance) generate proportionally higher mean currents and proportionally higher variances (per (95)), yet their relative variances become smaller in inverse proportion to the mean source currents, as per (98).
Note: it is apparent that larger mean source currents are noisier in absolute terms, yet less noisy in relative terms (compared to the larger means). The larger the mean source currents are, the more precise (featuring lower relative fluctuations) the current sources are. Thus, despite stronger current sources aboard the eDAC chip featuring larger variances, the stronger sources are relatively “quieter”, manifesting the weak-law-of-large-numbers.
Using Proposition 1, the currents vector variance is expressed as being proportional to the mean currents vector:
Given the coefficient of proportionality characteristic of the eDAC chip/wafer/batch, and given the mean source currents, of the particular current sources array on the chip, the variances of all current sources are uniquely determined, as per (99). Equivalently, specifying the mean and variance (or relative variance) of any particular current source aboard the chip amounts to specifying as the ratio of the variance and mean for that given current source, which is applicable to any other current source on the chip. Equivalently, the relative variance in any single particular current source on the chip uniquely determines the second-order statistics of all current sources on the chip. It is this observation that suggests selecting a convenient reference current on the chip, referred to as “unary current” (see (58) in Definition 3), then specifying its (relative) variance, subsequently making it possible to evaluate the second-order statistics (means and variances) for any of the current sources and subsequently for all current output levels aboard the eDAC. Moreover, it is useful to normalize all means and STDs of the current sources and current output levels by the mean of the unary current, expressing all currents and their STDs in units of the “unary current” as introduced in Section 2.2. The unary-current based normalizations streamline and simplify the all-analytic statistical model of eDACs.
- eDAC statistics compactly reformulated using normalizations by the unary current.
We now show that specifying the mean and relative variance (or relative STD) of the unary current determines the joint statistics of the array of eDAC current sources.
We start by noting that the unary current, , is an RV, whereas the mean unary current is a deterministic scalar; as such, is decomposed into mean-plus-perturbation:
any given eDAC chip will then be statistically characterized by identifying its unary current distribution (and in particular, the mean unary current and its variance, STD and RSTD metrics). The same distribution of unary current may pertain not only to a particular eDAC chip but to the entire wafer or production lot carrying the eDAC device replicas, provided the “statistical conditions” of the material and fabrication be invariant across the wafer and over the production process. It is useful to adopt the relative standard deviation (RSTD) of the unary current RV, , as the metric parameterizing the mismatch of current sources (transistors) on the chip, waver or production lot, denoting the relative variance in the unary current, , by (referred to as “relative mismatch”) as customary in the literature.
Definition 4.
“Relative mismatch”, of an eDAC chip, wafer or production lot (assuming statistical homogeneity, i.e., spatial stationarity) is defined as the relative standard deviation (RSTD) (also known as “coefficient of variation”) of the selected unary current, , for that chip, wafer or production lot:
Squaring the relative mismatch (101) yields the relative variance in the unary current synonymously referred to as “squared-relative-mismatch”:
Note: The relative mismatch and the relative variance are dimensionless quantities. Those are essentially the STD and variance in the random unary current, , albeit measured in units of and , respectively,
Conversely, the STD and variance in the eDAC unary current source, , are expressed in terms of , as fractions of and , respectively:
Given an eDAC chip, its mean unary current, , and its relative mismatch, , fully specify the second-order statistics of any current sources on that chip. Indeed, for any particular eDAC chip, wafer or batch, consider an actual or fictitious reference source current having the mean (e.g., for a UNIP eDAC, this may be the least mean current). Let the associated random current (mean + perturbation) be . The unary current, like any other current on the eDAC chip, satisfies the proportionality property (95), per Proposition 1: the variance in is proportional to its mean, the two quantities being related by the proportionality constant, , characteristic of the chip:
Solving this equation for the proportionality constant, (namely the constant ratio of variance and mean for any current on the chip, which is solely characteristic of the eDAC chip material and fabrication), yields
Note that is not to be confused with the unary relative variance, . In fact, we readily relate the var-over-mean proportionality constant to the relative mismatch . Substituting (103) into (105) yields
The two constants are seen as proportional, multiplicatively related by a factor
We now have two related eDAC chip characterizations, at our disposal, as alternative characteristic figures of the statistical quality of an eDAC chip/wafer/batch.
For a given fabrication process (assumed homogeneous across the chip/wafer/batch), is uniquely determined by the material and fabrication process (irrespective of the DAC current sources statistical parameters), whereas is set by both the material fabrication process and the mean of the current source adopted as unary current reference (thus, also depends on the current sources structure, determining the unary current).
The following result then follows for the second-order statistics of eDAC source currents.
Corollary 2.
Variance and relative variance in all eDAC current sources in terms of the parameters:
It is useful to compare the relative mismatches of UNIP and BIP eDACs (assuming the same sources chip area, i.e., the same absolute total current of the ± sources on the eDAC chip, implying that the BIP and UNIP peak output currents (the eDAC MSLs) are in a ratio of 1:2). As shown in (72), the BIP and UNIP eDACs then have equal full scales and they also have equal unary currents, . In conjunction with (107), this implies that (under the stated conditions) the UNIP|BIP unary mismatches are equal:
Thus, the mismatch, , pertains to the BIP|UNIP eDAC polarity. Nor does mismatch depend on the eDAC topology, BiWgt|ThWgt (as the mismatch is a property of the chip, not of its layout).
- Normalized second-order statistics of eDAC source currents and output currents.
It is useful to normalize the standard deviations of the eDAC source and output currents by the mean unary current. Thus, we have the STD of the current fluctuations measured in units of , as indicated by crescents over the STD symbols:
Correspondingly, all squared-current quantities (in particular, variances) are normalized by the squared mean unary current, :
It then follows that the normalized variances are proportional to the corresponding normalized means (with (108) used in the fourth equality below):
Indeed, per Proposition 1, the unnormalized variance is proportional to the unnormalized mean, and the normalizations of the variance and mean are proportional to the two proportional quantities, and are hence proportional to each other.
Corollary 3.
The normalized representations (defined as ) of the eDAC current sources are independent Gaussian distributed RVs. The variance and relative variance in the s-th normalized current source, , are, respectively, proportional and inversely proportional to the normalized mean current, :
The (unnormalized) variances and relative variances of the unnormalized source currents, , are expressed in terms of the normalized mean current as follows:
Proof.
Outlined above the corollary statement. □
Note: Comparing the two in the mean-to-variance linear maps, namely the unnormalized, , and normalized, , it is apparent that the proportionality constant is replaced by the proportionality constant (squared “relative mismatch”).
Likewise, comparing the unnormalized, , and normalized proportionality versions for the mean to relative variance linear maps.
Heretofore, we have studied the statistics of the source currents vector, I. We now derive the statistics of the eDAC output vector, J, assisted by the following generic result:
Lemma 2.
Given a random vector, , with independent components, its variance propagation rule via a linear transformation represented by a compatible matrix, T, is given by
Note: Recall the Shur-square definition in 1.1: is obtained from by squaring its matrix elements: .
Proof (Outline).
Let T have dimensions (with C and S arbitrary integers, not necessarily related to eDACs). Then, is a random C-vector. Have its c-th component, , decomposed into mean and random perturbation, . Evaluate using the additivity of variances for a sum of independent components.□
Theorem 1.
Output variance vector of any eDAC described by the linear model :
Proof.
Apply Lemma 2 to the eDAC linear model (1), by substituting in (118), yielding the variance vector (119) at the eDAC output.□
Note: Theorem 1 yields the variance vector at the linear eDAC output, Evidently, the mean output vector is . However, are an incomplete description of the output statistics; for a full description the cross-correlations between the output levels of the eDAC, the covariance matrix, , must also be specified. The components of are generally statistically correlated whenever the rows of the C matrix (the codewords) are non-orthogonal, which is actually the case for the matrices. The full covariance matrix is readily obtained from the source current variances:
In fact, Formula (119) of Theorem 1 provides the diagonal of the covariance matrix, (120), ignoring the off-diagonal elements of . It is to be noted that, although our statistical models account just for output variances (the diagonal terms in (120)) but not for cross-correlations (off-diagonal terms), the variances nevertheless suffice for modeling symbol-by-symbol optical detection scenarios, not accounting for inter-symbol-interference effects.
We now apply Theorem 1 to UNIP|BIP eDACs (be they ThWgt|BiWgt).
The output variance vector (119) is generated by linearly transforming the input variance vector through a matrix consisting of the squares of the elements of the code matrix, C. For UNIP eDACs, the elements of C are 0|1, still valued 0|1, invariant when squared. For BIP eDACs, the elements of C are ±1; thus, their squares are always 1-s. It follows that
Specializing (121) to UNIP and BIP eDACs, be they BiWgt|ThWgt, yields
where (109) and were specialized to UNIP. In fact, the result above most generally pertains to UNIP eDACs with non-uniform constellations.
Dividing (122) by yields a result (generally valid for non-uniform constellations) featuring the proportionality of the UNIP normalized variance vector and the normalized current constellation vector:
In the special case of a UNIP eDAC with a uniform output constellation, (122) reduces to
Dividing (124) by yields a result (valid for uniform constellations):
As for , in the most general case of a non-uniform constellation, we have
where equality #2 above made use of (121); #3 made use of (99); #5 made use of matrix-vector multiplication identity
#6 made use of the notation for the total of the all-positive mean current vector (here labeled as BIP); #7 made use of (109).
In the special case of a UNIP eDAC with a uniform output constellation, (122) reduces to
where the first equality above made use of
We note that, under our unary currents convention, (72), the BIP and UNIP eDACs have equal full scales and equal unary currents, ; thus, the BIP and UNIP labels may be dropped off the mean unary currents, writing for either.
Moreover, as the unary relative mismatch, (101), is solely determined by our choice of unary current and since we have the UNIP and BIP unary currents as equal, it follows that is identical for UNIP and BIP; thus, there is no need to label as UNIP|BIP-specific. However, we should not drop the BIP label off since the total of the vector of all-positive mean currents does depend on the eDAC polarity (UNIP|BIP), there appearing a factor of ½ in the BIP case. With this proviso, we recapitulate the output variance vectors of UNIP and BIP, while also listing the output current levels:
Those are the unnormalized output variances. Corresponding normalized versions of the output current variances are readily obtained by dividing the variances through the normalizing factor . The results above are recapped and normalized and further extended in the following:
Corollary 4.
For ThWgt|BiWgt eDACs impaired by electronic mismatch perturbations, generating uniform mean constellations, the (normalized) eDAC output currents are given, for the respective UNIP|BIP polarities, by
Moreover, the BIP variance results in (132) hold not just for uniform constellations with C equispaced mean levels over the FSR . More generally, they hold for any BIP mean constellation , be it uniform or non-uniform and for either BiWgt|ThWt BIP eDACs, we have
However, the UNIP variance vector stated in (132) exclusively holds for any UNIP eDAC generating a uniform mean constellation:
For any BiWgt eDAC, be it UNIP|BIP, be its output constellation unif/non-unif, the following result holds for the (arithmetic) average variance of the C constellation levels (with arithmetic averages denoted by overbars),
To recapitulate for either BIP eDACs of any topology (BiWgt|ThWgt) or for UNIP BiWgt eDACs, both categories featuring generally non-uniform constellations (uniform constellations as special cases), the average variance is given by
Note 1: the eDACs that (135) does not hold for are “non-unif UNIP-ThWgt” ones.
For all other types of eDACs, (135) does hold (e.g., it holds for unif UNIP eDACs of any topology; it holds for unif/non-unif BIP eDACs of any topology).
Note 2: “non-uniform” eDAC constellations are equivalently referred to in Section 3.4 as “biased” constellations.
Proof of Corollary 4.
The result (132) was proven in the text above the corollary. To prove (133), namely the surprising property that the variances of all output currents attain a common value, and moreover, the variance is the same even for non-uniform BIP output constellations, the most intuitive derivation inspects Formula (3) for BIP eDACs, namely , takes its mean,
and uses Proposition 1 to evaluate the variance of the c-th output level as follows:
where factor of ½ for the means in the BIP case, , in equality #6, is justified by our convention of halving the mean values of the positive source currents in the case of BIP relative to UNIP, to ensure the physical constraint that the absolute total of the BIP current sources of both signs equals that of the UNIP current sources; in #8 (107) was used. The equalities chain (137) provides the most intuitive derivation of the BIP variance formula in Corollary 4, this derivation holding even for non-uniform constellations, as we note that no assumption has been made on the mean values of the constellation output levels.
Next, consider the even more surprising result (134) on the (arithmetic) average of the variances of the C levels irrespective of the topology of the eDAC (ThWgt|BiWgt), its polarity (UNIP|BIP), the (non-)uniformity of its constellation. The derivation of (134) for BIP eDACs (of any topology and (non-)uniformity) trivially follows from the trivial result (132) for BIP eDACs, namely
since the average of a constant sequence equals the constant itself. However, the proof of (134) for generally non-unif BiWgt UNIP eDACs is a bit tricky, essentially stemming from a property of the code matrix of a BiWgt UNIP eDAC of any order, C, namely that each of the code matrix columns has half its elements (C/2 elements) consisting of ones—the detailed derivation (134) is relegated to the proof of Corollary 4 in Appendix B.2. □
2.5. Second-Order Statistics of the Steps of the Output Constellation—Matrix-Based Evaluation
We now develop a matrix-based methodology for evaluating the second-order-statistics of the output current constellation steps vector, with elements (the “steps”) defined in (21). The steps vector, , is obtained from the constellation vector, , by applying the first-difference linear transformation, (called “Del”), introduced in
The linear transformation is viewed below as a matrix, with −1 s on its main diagonal, 1 s in all entries right above the diagonal, zeros in all other entries, e.g., for C = 8:
Relating the output levels to the source currents, as per (1), yields
where associativity of matrix multiplication was used for this matrix triple product, is ; for a ThWgt eDAC, S = C − 1; for a BiWgt eDAC . is viewed as a matrix, of size :
Once the matrix product is evaluated for the given code matrix, , then the output steps vector (140) is readily obtained by left-multiplying the eDAC current sources vector, , by the matrix: The rows of the matrix are obtained by taking differences of the successive rows of ,
Recalling that the eDAC codewords (viewed as rows) are the rows of the C matrix, then the rows of (given by the differences of the successive rows of C) are obtained as the first-differences of the list of successive row-codewords. We refer to the differences of successive rows of the C matrix as the “code-steps”:
The code-steps are readily evaluated for any code matrix, C. Arraying the code-steps as rows in a matrix yields the matrix. In particular, the c-th element of the steps-vector (140) may be evaluated as follows, directly from the eDAC source currents:
The output current constellation steps are obtained as the inner products of the successive code-steps, , with the source currents vector, .
For a given eDAC, of order C and given topology ThWgt|BiWgt, it is worth tabulating the code-steps, , in advance (or equivalently tabulating , the rows of which are the code-steps). Note that, for the BIP eDAC polarity of interest, all code-steps (elements of the matrix) are tri-level-valued, (since for BIP eDACs, the elements of the C matrix are ±1; hence, (±1) − (±1) = 0|±2), whereas for UNIP polarity the elements of the C matrix are 0|1; thus, the UNIP code-steps (elements of ) matrix are obtained as (0|1) − (0|1) = 0|±1); thus, assume the values .
For the purpose of steps variance evaluation, we require the Shur-square of or equivalently the Shur-squares of its rows, , readily obtained by XORing the successive eDAC codewords of the eDAC code For the next lemma, we define the XOR of a pair of Boolean vectors, i.e., vectors with elements restricted to one of a pair of values (in our case of interest, the two possible values being 0|1 for UNIP and ±1 for BIP):
Definition 5.
For a pair of length-C Boolean vectors, , with elements with (e.g., | for UNIP|BIP) the XOR of the vectors, , is defined as the binary-valued S-vector
thus, the XOR of two Boolean vectors is defined elementwise and in turn the XOR of two bits, , is defined as 1 if , 0 if a definition valid even for BIP, in which case are not binary-valued but rather ±1-valued.
Lemma 3.
Shur-squares of the code-steps, expressed as XOR of successive codewords:
Thus, the elements of are 0|1 valued for UNIP and 0|4 valued for BIP.
Proof of Lemma 3.
Relegated to Appendix B.1. A key observation is that the elements of were seen to be ; thus, the elements of are . As for the elements of , those were seen to be ; thus, the elements of are ; in fact, 1 is only obtained when the corresponding bits in the s-th locations in the two codewords are different.□
For the purpose of evaluating eDAC statistical metrics such as the DNL and our own DEV metric (introduced in Section 3), the variance of the steps vector, , is to be evaluated.
Since is obtained from the vector of independent current sources, , by the linear transformation (140), the variance propagation rule (118) is applicable upon plugging , yielding .
Theorem 2.
Variance vector of the steps at the current output of a linear UNIP|BIP eDAC, of the BiWgt|ThWgt type:
the variancesof the eDAC output steps are expressed component-wise as
where we recall that is defined as and we have
and the c-th XOR vector was defined as c-th row of the steps code matrix :
Specializing now to the BiWgt eDAC topology (for the UNIP|BIP cases, respectively),
The vector form of (152) consists of matrix-times-column-vector multiplications,
where we introduced a “steps-XOR matrix” , having (151) in its c-th row:
Component-wise, the corresponding steps variances for BIP BiWgt eDACs are
The steps vector variance is then given by
Proof of Theorem 2.
Relegated to Appendix B.1. □
Theorem 2 establishes that the source-currents-mismatch-induced variance vector of the steps of the BIP constellation is twice that of UNIP (under our normalizations for the source currents in the two cases). To put this in perspective, in the context of optical communication links, we note that UNIP eDACs are used in Tx-s for direct detection (DD), whereas BIP eDACs are used in Tx-s for coherent detection, which is more sensitive than DD, and it is apparent that the BIP disadvantage of twice mismatch variance for the constellation steps is offset by the large sensitivity advantage enabled by coherent detection of BIP constellations with regard to the direct detection of UNIP constellations.
The compact key result (152) expresses the doubly normalized variance for UNIP as an inner product of the XOR vector, (151) of successive code-steps with the dyadic sequence . Operationally, the inner product scales the bits of the XOR bitstring by the respective dyadic weights then sums up the binary weighted bit values to yield the doubly normalized variance of the steps (with a factor of 2 applied in the BIP case relative to the UNIP one).
The (corresponding) bit positions in contributing to the DNL are those where becomes unity; the heavier contributors are bits where is unity (indicative of corresponding bit flips at those positions, upon transitioning from to ) with more significant position (having indices s, farther to the left along the rows ). In particular, the heaviest contributors are the most significant bit-flip location, , , which are the farthest to the left, as we recall that the index s increases from right to left (but only if the bits at the corresponding locations (same s) in the two successive codewords are different, ).
Let us now formally derive the index of “worst” codeword of the BiWgt topology, using (155) of Theorem 2, for the case of a 4-bit 16-level BiWgt eDAC, featuring , a behavioral block diagram which is depicted in Figure 1b. For this eDAC example, Table 1 presents the full BiWgt code, the XORs of successive codewords and twice the inner products between the XOR vectors in the third column and the {8, 4, 2, 1} weights, yielding the (doubly normalized) steps variance stated in the fourth column “Steps VAR”.

Table 1.
BiWgt code for BIP 16-PAM eDAC, the 16 codewords, the XORs of successive codewords and the doubly normalized steps variances of the 15 steps. The code (succession of codewords) in the 2nd column is a “counting code” (imagine replacing −1-s by 0-s in the “Codeword” column: the successive rows are then seen to count in binary starting at zero). The 3rd column lists the bitwise XOR of consecutive codewords, with XOR being defined for “bipolar bits” as . To form the 4th column, the XOR bits are weighted by {8, 4, 2, 1} and summed up, then doubled, implementing Formula (155). This amounts to expressing the XOR binary string entries in decimal and doubling. This column, labeled “steps VAR”, lists the doubly normalized variance of each step, (for the last equality see (376) in the sequel, with the differential error vector (DEV) metric introduced in Section 3.7 below, as a variant of the conventional DNL metric better suited for transmission modeling). The steps VAR column is then given by The most perturbed step of the BiWgt eDAC output is the one at “mid-code”, between the 8th and 9th level, wherein the doubly normalized step variance peaks to 30 units (30 times the mismatch variance ). The impact of the steps variances onto the performance of communication links, optical interconnects in particular, is explored below.
Table 1 pertains to the BIP PAM16 BiWgt eDAC. A similar table for the UNIP PAM16 BiWgt eDAC (not presented) would be obtained by replacing all occurrences of −1 in the BIP code by a 0 bit, and by halving all entries of the “Step VARs” column (the variances):
This result for STEP variances for an UNIP 16-level BiWgt eDAC is generally known (up to different notations). Our analysis, as summarized in Table 1, extends those known UNIP results to the case of PAM16 BIP BiWgt eDACs, wherein, as per Table 1, we have
Most generally, the second-order statistics of the steps for PAM-C BiWgt eDACs may be modeled using Theorem 2.
Inspection of Table 1 indicates that the “worst offender” (the entry with the highest mismatch variance) is located “mid-code” i.e., at the transition of the eighth level to the ninth level. In a similar table, made for a UNIP eDAC, the “worst offender” would still occur at the eighth to ninth level transition, from codeword to codeword , wherein all bits at corresponding locations flip upon the transition from c = 8 to c = 9, i.e., is one’s-complement of . The XOR of these two codewords is 1111 (indicating that all corresponding bits differ) and the mismatch variance comes out 15 units for UNIP, two times that, i.e., 30, for BIP (see the entry at the fourth column and eighth row in Table 1),
reducing (155) to
For UNIP BiWgt eDACs , whereas for BIP BiWgt eDACs
Generalizing the example, to a -levels BiWgt code, the worst-offender successive UNIP codewords are now , yielding
Substituting the index and the XOR into (155) yields for the inner product expression,
such that (155) reduces to the following (for B = 4 the factors of 15 and 30 correctly arise):
The UNIP BiWgt result is familiar to eDAC practitioners (barring normalizing factors and notation to reconcile) as it enters into the evaluation of the worst variance of the DNL metric. Here, our main interest is in modulated optical sources for coherent detection, requiring BIP eDACs to drive MZMs, for which we shall use the expression eDAC, per the second line in (163).
For the unnormalized worst step variance, multiply both sides of (163) by :
Consistent with the results obtained here, the DNL and DEV eDAC metrics will be shown in Section 3 to peak at the “mid-code” step as well, indicative of the most “vigorous” perturbation occurring for that transition. In a coherent communication applications context, with relatively high probability, some eDAC devices in the ASIC fab batch have their constellation mid-code step significantly reduced, e.g., for BIP PAM16 (as used in 256QAM transmission), the eighth and ninth constellation levels (those with means ) tend to crowd together the most, i.e., the separation tends to be reduced for a larger fraction of the eDAC devices out of the batch (reducing the yield). Therefore, Rx decision errors mistaking the eighth level for the ninth one (or vice-versa) tend to dominate the symbol and bit error rates (as is going to be treated in part II of this paper). The next largest variance contributions are attributed to the transitions at a quarter (fourth to fifth) and three-quarters (twelfth to thirteenth) along the code (the corresponding step variances are ). Next in line, there are steps contributing 6 units of variance. The least steps perturbation is 2 units of variance. All these perturbations are reflected in the EVM of the constellation (refer to Section 3.8 and Section 3.9 for treatment of the EVM of eDACs). This discussion indicates that the second-order statistics of the constellation steps emerges as a significant factor affecting communication link performance, to be explored below.
The analysis above for the step variances of BiWgt eDACs is readily adapted to ThWgt eDACs, albeit with normalized source current (79), yielding . Moreover, the XORs now yield sparse C-1-vectors, each of which with a lone-one element. The sum of bits, , for each sparse XOR vector with a single one element, is simply unity, , yielding,
yielding for UNIP ThWgt eDACs, the minimal possible step variance. It is well-known by eDAC practitioners that nothing surpasses the low DNL of a ThWgt eDAC, if one can afford one. Unfortunately, ThWgt designs incur the energy inefficiency of the power-hungry digital encoder required to map bits to codewords at the full baud rate. For next-gen optical communication, the exorbitant power consumption of the digital encoders of ThWgt eDACs precludes having them adopted as optical modulator drivers. This motivates us to focus on BiWgt eDACs in the following work. Moreover, since our main interest is in coherent optical detection, calling for BIP constellations for the QAM tributaries, we mainly focus on BIP PAM-C constellation generation with BiWgt eDACs.
2.6. Symmetries of Codewords, Output Levels and Steps in ThWgt|BiWgt UNIP|BIP eDACs
We start by defining the “reverse” operator and (skew) centrosymmetric properties of vectors, exploring these symmetries in Corollary 5. This enables formulating and formally proving a key Theorem 3 on the symmetries arising in analytic eDAC models.
Definition 6.
The “reverse” of a vector in is the operator , defined for any as the following linear transformation, listing the elements in reverse order:
e.g., .
For the integer indices, c = 1, 2, 3, …, C, define the “image-indices”, given by , respectively:
i.e., given index c, the associated “image-index” , is the C + 1-complement of c, i.e., the “reflection” of the given index relative to the “mid-point” of the list {1, 2, 3, …, C}:
Definition 7.
A “centrosymmetric” vector is one satisfying
A “skew-centrosymmetric” vector is one satisfying
Thus, a (skew-)centrosymmetric vector remains invariant (flips sign) under a reversion of its elements, i.e., such a vector displays even (odd) symmetry around its center.
Definition 8.
(i) The “center” (also known as “center-of-mass”) of a vector is defined as the (arithmetic) average of its elements, denoted (with the sum of elements of )
(ii) A “balanced vector”, sometimes denoted, , is a vector with zero center, i.e., satisfying . An “imbalanced” vector, , is a vector with non-zero center, .
Lemma 4.
Any C-vector, , is expressible as the sum of a balanced vector and a constant vector:
Moreover, t is unique, given by the average of , , i.e., , and so is the “balanced component” unique for any given v; hence, it may be denoted by .
The unique decomposition into additive balanced and constant components is then written in the form
Conversely, any C-vector, , may be translated by to yield a balanced vector,
uniquely associated with , referred to as the “balancing of ” (also known as the “centering of ”).
If then is a balanced vector to begin with.
Definition 9.
A vector is referred to as “raised-skew-centrosymmetric”, if it may be expressed as a non-zero translation, by a constant vector , of a skew-centrosymmetric vector:
Corollary 5.
Some properties of (skew)centrosymmetries.
- (i)
- Any skew-centrosymmetric vector is balanced.
- (ii)
- Any raised-skew centrosymmetric vector is imbalanced.
- (iii)
- Any raised-skew centrosymmetric vector may be translated to yield a skew-centrosymmetric vector.
- (iv)
- Not all balanced vectors are skew-centrosymmetric.
- (v)
- The elements of a raised-skew-centrosymmetric vector satisfyi.e., the centers of all pairs of mirror-image elements coincide with one another and with the center of the given vector. Equivalently, the balanced elements satisfyConversely, if the elements of a vector satisfy either (176) or (177), then must be raised-skew-centrosymmetric.
- (vi)
- Given a C-vector, , if there exists a translation by a constant vector such that is skew-centrosymmetric, then necessarily ; thus, the only translation, by a constant vector, of the given vector into a centrosymmetric one is the translation by the constant vector .
- (vii)
- Equivalently, if the elements of a vector satisfythen is raised-skew-centrosymmetric, and its center is .Thus, for the vector satisfying the averages (centers) of each of the mirror-image elements of for any c, are all equal to the center (average) of :
- (viii)
- Given a pair of raised-skew-centrosymmetric C-vectors, u, v, if their FSRs are equal, i.e., (in other words, their LSLs are equal and their LSLs are equal) that implies , i.e., the two vectors have the same center.
- (ix)
- The difference of two raised-skew-centrosymmetric C-vectors, u, v, generally yields a raised-skew-centrosymmetric vector.More strongly, the difference is skew-centrosymmetric, provided that either have equal centers, , or have equal full-scale ranges (FSRs), (i.e., u, v have same LSL, , and same MSL, )
- (x)
- The first-difference (steps-vector), , of a raised-skew-centrosymmetric vector, , always yields a centrosymmetric vector:
- (xi)
- If a C-vector v is centrosymmetric, an affine transformation of the formyields a centrosymmetric vector .
If the C-vector is skew-centrosymmetric, the affine transformation of the form (181) generates a raised-skew-centrosymmetric vector, .
Proof of Corollary 5.
relegated to Appendix B.1□
As in all areas of physics and engineering, symmetries are useful to enable insight into eDACs as well. We proceed to apply the (skew-)centro-symmetry formalism above to explore new properties and points of view for various eDAC parameters and metrics.
Theorem 3.
Centrosymmetries of codewords, output levels and steps of possibly non-uniform eDACs having the ThWgt|BiWgt eDAC topologies and the UNIP|BIP polarities:
- (i)
- For a UNIP ThWgt|BiWgt eDAC, the c-th row of and its -th row, namely the codewords, and at mirror-image indices, (with ), are in a one’s-complement relation, i.e., the bits of are related to the corresponding bits of by the substitutions ,where is the all-ones vector (for ThWgt: ; for BiWgt: ):The second line in (182), equivalent to the one’s complement relation between the mirror-image codewords.
- (ii)
- For a BIP ThWgt|BiWgt eDAC, the two codewords and , at mirror indices, are in a zero’s-complement relation, i.e., the two codewords sum up to zero; the “bipolar bits” of are obtained from those of by the substitutions . Equivalently, the two mirror-image BIP codewords are antipodal:
- (iii)
- For either eDAC topology|polarity (ThWgt|BiWgt, UNIP|BIP), the sequence of code-word-steps, satisfies
- (iv)
- The C-levels of the eDAC output constellation, , satisfy, irrespective of the source current vector , the following complementarity properties.For UNIP eDACs (be they BiWgt|ThWgt):i.e., the eDAC output current levels at mirror-image indices complement each other to the total source current,Any UNIP eDAC output current constellation, , is always raised-skew-centrosymmetric, with center given by half the total current,For BIP eDACs (BiWgt|ThWgt), the output current constellations are skew-centrosymmetric with zero center, i.e., are antisymmetric,
- (v)
- For either eDAC topology/polarity, and for any source current, I, the steps vector is always centrosymmetric, i.e., steps paired to have mirror-image indices are equal:
Note: For a C-level eDAC, the steps vector is a length-C-1 sequence. Its “center” is now rather that for the original C-levels constellation. The definition of image-index (167) now changes to as specified in (185).
Proof of Theorem 3.
The derivation is somewhat long; hence, it is relegated to Appendix B. □
Note 1: the symmetry properties in the theorem above assume neither that the ThWgt sources are all equal, nor that the BiWgt sources are dyadic, i.e., in ratios 1:2:4:,... The theorem stems from the symmetry of the codewords, albeit requiring no particular symmetry of the current sources array.
Definitions (169), (170) of (skew-)centrosymmetry of a vector in may be generalized to a sequence of vectors, i.e., an indexed set, of vectors, :
The vectors need not be (skew-)centrosymmetric themselves.
Per this extended definition of (skew)centrosymmetry, the property (185) in Theorem 3, may be compactly expressed as the following equivalent statement:
The sequence of codeword-steps is centrosymmetric:
We now exemplify Theorem 3 for a BiWgt UNIP 16-PAM oDAC (C = 8, B = 3), the code matrix of which was stated in (14).
Abbreviating the one’s-complement as 1’c, the key property in (i) is readily verified,
The positions of the -pairs are seen as symmetric around the center of the sequence.
- Pairs with indices that are mirror-images around the center are one’s-complementary.
As for (iii), in the case of a UNIP BiWgt eDAC, let us evaluate the codeword-steps at indices c = 1, 2, 3, and at the corresponding mirror-image indices :
where all six vector differences in the three equalities are seen to be equal .
To validate the complementarity of currents (iv) for the UNIP BiWgt eDAC:
As for (v), the centrosymmetry of the steps, we expect,
readily validated using for c = 1, 2, 3, as well as (193):
This example is a “sanity check” for the Theorem, in the particular in the BiWgt UNIP case.
An important application of Theorem 3 is the ready derivation of the centrosymmetries of the eDAC metrics discussed in Section 3 below, namely the INL, DNL, IEV and DEV.
2.7. Example: Analytic Models for 3-Bit (PAM8) eDACs of the ThWgt|BiWgt UNIP|BIP Types
In this section, we specialize the heretofore developed analytic models of first-order and second-order statistical performance to the special cases of ThWgt|BiWgt UNIP|BIP eDACs with of B = 3 bits, i.e., C = 8 levels (PAM8).
A total mean current budget of is assumed. The unary current is taken as for both UNIP and BIP. The relative mismatch is taken as , excessive in practical terms, yet useful to highlight the random mismatch variations for all currents—see the figures in Section 2.9––validating the analytic models of this subsection by Monte Carlo simulations. To recapitulate our specifications for the modelled eDAC instances:
ThWgt UNIP: use C-1 = 7 independent normally distributed current sources all of mean current :(consistent with )
The resulting eight output levels distributions are shown in Figure 2b, evaluated by accumulating the seven source currents, , yielding:
The means, variances and STDs of the output levels vector are then
The C = eighth level (the MSL) is the noisiest, having the largest STD:
The Gaussian distributions of the outputs current levels have the following PDFs:
We now model a B = 3-bits (C = 8 levels) BiWgt UNIP eDAC, with source currents vector
The mean source currents are in binary ratios, forming a three-element dyadic sequence:
In our special case, ; thus,
For a generic , the mean output currents of this BIP 3-bit BiWgt eDAC are given by
thus, in our special case, , the eDAC generates the output constellation
The analytic model for the variances and the STDs of the three BIP BiWgt source currents is obtained using (109) with as per (204):
or finally,
i.e., using (206) and (209), the distribution of the source currents vector is
Let us now model the case of a 3-bit BiWgt BIP eDAC, with currents array
Per our convention for UNIP vs. BIP source currents, we must now scale the mean source currents by factors of , taking BiWgt BIP eDAC source currents half as large as their BiWgt UNIP counterparts:
The mean output currents generated by the BIP 3-bit BiWgt eDAC are then
Note that the mean full scale (FS) of this eDAC is
coinciding with the mean FS of the ThWgt UNIP eDAC simulated above:
The variances of the three BIP BiWgt source currents are obtained using (109), yielding the following prediction of our analytic modeling:
The variances of the eight output current levels of the 3-bit BiWgt BIP eDAC were also derived in of Corollary 4, specialized here to yield
Thus, all eight levels of the BiWgt eDAC feature identical variances and identical STDs:
The resulting Gaussian distributions are then identical for all eight output levels:
Using a dyadic array satisfying yields the perfect UNIP-PAM8 constellation . (d) is functionally equivalent to (c), but in (d), the three currents are synthesized using a “uniform” array of nominally seven current sources of identical means , partitioned in subsets of 1, 2, 4 elements, respectively, . The unary sources in the second and third subsets are electrically parallelized as shown in (d), generating the triplet of dyadic currents . It is readily verified, in all four diagrams, that the total of all mean currents of the elements of the sources array (current absolute-values in the BIP case), equals , whereas the mean full scales, , of the J-constellations come out equal, for UNIP|BIP eDACs, both given by
At this point, let us consider an equivalent model of the BiWgt BIP eDAC based on the “physical±” bipolar current sources (53) that are arrayed in pairs in each of three current-mirror cells implementing 1-bit controlled MUXEDs switching in either a positive source current or its antipodal counterpart. Thus, taking B = 3, the six random source currents (each consisting of its mean + perturbation) are denoted as
Taking B = 3 in (53), the six current sources have means three of which are positive and three of which are negative,
The physical bipolar ± array operation, generating the eight output current levels of the BiWgt BIP eDAC, may be modeled by eight equations in six unknowns, compactly expressed as
e.g., the sixth equation represented by this matrix–vector multiplication is
i.e., we switch-in the negative third source, the positive second source, the negative first source.
All eight equations may be compactly written as
where 2±[c], 1±[c], 0±[c] are ±1-valued, determined by the c-index (for c = 1, 2, 3, …, 8).
The linear transformation (222) is an alternative description of the BiWgt-BIP eDAC, equivalent to our earlier developed linear transformation (1), which, upon being specialized for the 3-bit BiWgt-BIP eDAC, reads
The relation between the “mathematical” all-positive three source currents (211) and the “physical±” source currents (220), respectively, driving the two models (222) and (225) is
Our “physical±” six-vector current array, (220) (to be propagated through the switching linear transformation (222)) is characterized by the stipulation that its six ± current sources be statistically independent and have means of forming the dyadic sequence
and thus have variances proportional to the means, per Proposition 1. The variances may be explicitly evaluated using (109), the notation meaning , to account for negative current sources:
i.e., the six “physical±” current sources have STDs given by
Once the source current variances are known, as per (228), we are ready to have them propagated via the switching matrix (222). This may be effectively accomplished by considering the individual linear equations corresponding to (222), observing that the summation (224) of three independent currents implies that the variance of the c-th output current level is given by the sum of variances of the three participating current sources that are switched in:
This alternative derivation of the (equal) variances of the output levels of 3-bit BiWgt BIP eDAC, pertaining to the “physical±” BiWgt BIP eDAC structure, retrieves our earlier obtained result (218), which assumed the “math model” of positive-valued current sources modulated by the signs of the code (switching) matrix, .
Note: a third alternative derivation of the output variances would be based on (119) with (see (222)); details are omitted.
In Section 2.5, we derived the second-order statistics of the steps of a BiWgt BIP eDAC. In particular, Table 1 addressed the 4-bit (BiWgt BIP PAM16) case. We now specialize (155) of theorem II to the B = 3-bit (BiWgt BIP-PAM8) eDAC case of interest here:
where the “XOR-steps matrix” (154) was evaluated for the 3-bit BiWgt BIP eDAC:
Using our specifications (196) we have , and the steps variance vector (231) results in
The worst-case variance, , occurs mid-code at the fourth-to-fifth level transition.
It is also useful to derive the mean output steps in this special 3-bits BiWgt BIP case:
Evidently, all mean output constellation steps are equal to ; thus, the mean constellation points are equispaced by .
Note that an alternative derivation would take the mean of (140),
where the last equality above used verified using the explicit form of in (232).
In this subsection, we have analytically obtained the means and variances of the output levels and steps for the example of the 3-bit BiWgt BIP eDAC. These analytic predictions are going to be numerically verified in Section 2.9 by means of Monte Carlo simulations.
2.8. BiWgt-Parallelization of a Unary Array of Current Sources
In ASIC layout designs of B-bits BiWgt UNIP eDACs, the B current sources to be switched and additively combined are often obtained by a structure implementing an array of nominally identical “unary” current sources (hence, having IID statistical distributions), referred to here as the “sub-sources”, all sharing a common mean , as if this is a ThWgt UNIP eDAC with S = C − 1 = 2B − 1 levels. However, sub-sources of this “unary array” are partitioned into B subsets to form B effective sources. The B subsets of unary sub-sources, respectively, comprise unary sources (consistent with ). The “unary” sub-sources within each subset are electrically combined in parallel, to effectively yield the B binary-weighted current sources, featuring mean currents forming a dyadic sequence,
We refer to this construction as “BiWgt-parallelization of a ThWgt unary sources array”.
Let us exemplify this construction for 3-bit (eight levels) BiWgt UNIP and BIP eDAC. Staring with the 3-bit BiWgt UNIP eDAC case, the task is to synthesize its three random sources
To this end, an array of seven IID ThWgt UNIP sub-sources is formed
and conceptually partitioned into three subsets comprising 4, 2, 1 ThWgt sub-sources:
The sub-sources within each of the three subsets are then parallel-connected (denoted ):
Note: evidently, upon parallel connection of current sources, the currents are added up.
The resulting array of three BiWgt BIP current sources is
The means of these three current sources are readily verified to form a dyadic sequence,
wherein, in the last line, we used the fact that the sub-sources array consists of unary currents,
Moreover, since the seven RVs of the underlying ThWgt UNIP sub-sources array (238) are statistically independent, it is readily seen that so are the three BiWgt UNIP sources (240). The variances of the three source current RVs, synthesized by this construction, are readily obtained using the additivity of variances of independent RVs:
For completeness, (241) is also restated
The first- and second-order statistics (244) and (243) of the source currents vector (240) based on “BiWgt-parallelization of the unary array” is seen as consistent with our earlier derived (205) and (209) in Section 2.7, wherein the source current array was assumed to satisfy Proposition 1.
We now develop a similar synthesis for the current sources of a 3-bit BiWgt BIP eDAC.
Our BIP vs. UNIP current sources convention (57), indicates that BiWgt-BIP current sources synthesis should essentially follow the BiWgt-UNIP construction, albeit with all mean currents scaled by a factor of .
Thus, to synthesize the “mathematical” random sources of the 3-bit BiWgt BIP eDAC,
an array of seven IID ThWgt UNIP sub-sources is first formed,
such that the mean source currents in this array of sub-sources be half the mean source currents of the ThWgt-UNIP array (238):
The sub-sources array is then partitioned into three subsets comprising 4, 2, 1 ThWgt sub-sources, respectively:
The sub-sources within each of the three subsets are finally parallel-connected:
The resulting array (245) of three BiWgt BIP current sources synthesized this way has the means of its three sources forming a dyadic sequence,
where (247) was used in the third equality.
Note: Compared with (241), we have, as expected, .
Moreover, since the seven RVs of the underlying ThWgt BIP sub-sources array (238) are statistically independent, then so are the three resulting BiWgt UNIP sources (240). The variances of the three source current RVs are readily obtained using the additivity of variances of independent RVs, yielding
where in #2 (249) was used; in #3, notation such as means that the variances of the sources labeled by s = 6, 5, 4, 3 are identical:
Equalities #4,#5,#6 readily follow from the three variance formulas above. Finally, in #7 and #8, we plugged in the specifications (196) pertinent to all our 3-bit eDAC examples in Section 2.7–2.9. To recapitulate,
The result (253) retrieves our earlier result (216). For completeness, we also recapitulate (250)
The first- and second-order statistics, (209) and (251) of the source currents vector (245) based on the “BiWgt-parallelization of a unary array” synthesis, is consistent with our earlier derived (212) and (216), in Section 2.6, wherein the source current array was simply designed with mean source currents in ratios of 4:2:1 (thus requiring the widths of the three current sources to be in ratios 4:2:1). Proposition 1 was used to predict the variances of the three source currents. This example then shows that BiWgt- parallelization of the unary array synthesis is consistent with Proposition 1, in terms of its resulting second-order statistics.
Consider now, still for the 3-bit BiWgt-BIP eDAC current sources array, the “physical±” version of the “BiWgt parallelization of ThWgt unary current sources” constructions, as depicted in Figure 2b,d. Inspecting the array of seven IID ThWgt UNIP positive-valued sub-sources, this array is now augmented by an array of nominally antipodal sub-sources, consisting of seven IID ThWgt UNIP positive-valued sub-sources (in fact, the two sub-sources arrays are drawn interspersed in Figure 2b,d, such as to reduce the complexities of interconnects upon sub-sources partitioning and parallel-connections). Mathematically, the 2 × 7 = 14 sources are partitioned and grouped as follows, with the lowest (inner-most parenthesized) levels in the hierarchy comprising sub-sources to be electrically parallel-connected, the next higher level comprising pairs of nominally antipodal, nominally dyadic-sized, current sources to be applied to the multiplexers which select either positive or negative source currents:
Mapping this vector of current sub-sources to the vector of corresponding means yields
where the factor of ½ being due to the UNIP vs. BIP scaling. Upon parallel-connecting (summing) the sub-source currents at the inner-most levels in (255), we obtain the array of six current sources entering the three MUXes:
The correspondence of this mathematical representation to Figure 2b,d is evident, as we have a quad of positive currents and a quad of negative currents, each parallel-connected, to be switched in the left-hand mux, a pair of positive currents and a pair of negative currents each parallel-connected to be switched in the mid mux, a singlet positive currents and a singlet negative current, to be switched in the right-hand mux.
The second-order statistics of (257) is readily derived (to be compared with our earlier results for the statistics). The mean of is obtained by summing up the identical means within the inner-most parenthesized levels in (256) (corresponding to the summations of 4, 2, 1 currents due to the parallel connections in (257)). The summations of 3, 2, 1 mean currents simply scale up the common mean by factors of 4, 2, 1, yielding
To recapitulate, the six means of the source currents entering the three MUXes are
The corresponding variances are readily evaluated using (109) (the notation meaning , to account for negative sources):
where the numerical expressions in each of the three lines were obtained by substituting the parameters (196) for the example at hand.
The output current is the summation of the three mux outputs, written as
where there are 2 × 2 × 2 = 8 combinations depending on the signs of .
The three RVs are mutually independent (each being a summation of parallel-connected sub-source RV, from subsets (comprising 4, 2, 1 elements) of the 14 sub-sources are which are themselves mutually independent (as they are spatially distinct sources on the chip). As are independent, their variances are then additive:
where #3 was obtained by substituting the variances (260); #5 was obtained by substituting the parameters (196) for the example at hand. Rewardingly, the current variance results (260) and (262) are consistent with (228) and (230), respectively.
2.9. Monte Carlo Simulations for PAM8 eDACs Verifying Key Analytic Statistics of This Section
In this subsection, we validate, by means of Monte Carlo simulations (MC-sims), the statistical analytic model derived heretofore. All simulations refer to the 3-bit 8 level eDAC examples analytically modeled in the last two subsections, the parameters of which were specified in (196), namely . Specifically, we Monte Carlo simulate ThWgt|BiWgt, UNIP|BIP eDACs with these parameters.
Figure 3, Figure 4, Figure 5 and Figure 6 below verify Proposition 1 and Theorems 1 and 2 of this section, by means of MC-sims. In Figure 3, Figure 4 and Figure 6, histograms of various current RVs are plotted overlaid with the Gaussian analytic PDFs stemming from our analytic models. In all cases, we effectively verify the analytic models over an effective ensemble of 1500 3-bit BiWgt|ThWgt BIP|UNIP eDACs, all sharing the parameters specified in (196). The number of drawn realizations of each of the independent RVs for each of the considered currents or current metrics (e.g., the steps of the output levels of the currents) is then 1500. This is then the total number of points accumulated within each of the displayed histograms. Inspecting the multiple (sub)figures, it is apparent that, for each of the RVs of interest, at this sample size, the histograms well approximate the theoretical PDFs overlayed onto the respective histograms, validating the analytic models by means of the MC-sims presented here, which fit the theory.
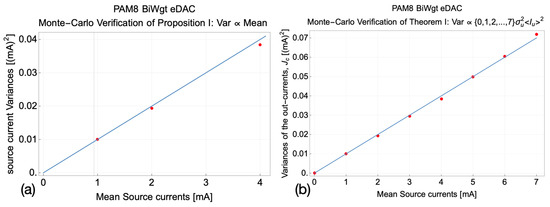
Figure 5.
“Regression-like” linear fits for the (Mean, Var) pairs (the red points) as evaluated for the 1500 randomly drawn values out of the current distributions of a PAM8 UNIP BiWgt eDAC, parameterized by unary current and by relative mismatch , overlayed by the linear fits (the blue lines through the origin) numerically confirming key analytic results of this section. (a): Verification of Proposition 1 for the three UNIP BiWgt source currents . (b): Verification of Corollary 4 (132) for the 8 output currents
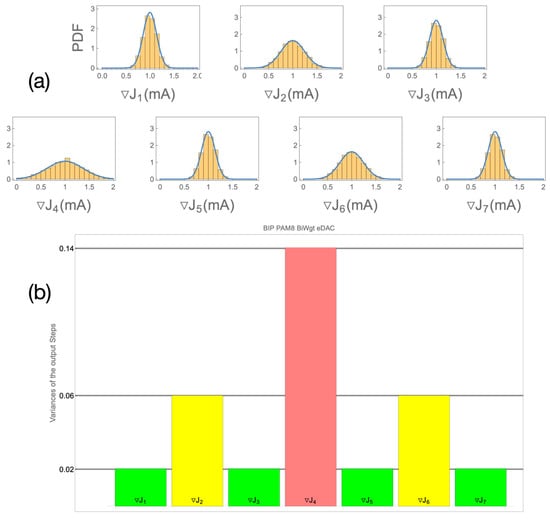
Figure 6.
Monte Carlo verification of the statistics of the BIP PAM8 BiWgt eDAC output current steps (namely the differences between successive output constellation levels), evaluated for the same Monte Carlo simulation as in Figure 2 and Figure 3 (1500 sample values drawn for each of the three source currents). (a): Histograms of the 7 output steps, overlaid with the Gaussian analytic PDFs corresponding to the mean steps and variances predicted by Theorem 2 for C = 8 constellation points, namely where the parameters in our Monte Carlo simulation are . (b): Corresponding empirical variances of the output steps (“measured” for the random samples forming the histograms displayed in (top)). The empirical output level variances are represented as the heights of the bars, seen to closely approximate the expected analytic variance values {0.02, 0.06, 0.14}. The variance of the step at the “mid-code” location is the worst one (~0.14), consistent with the analysis in Section 2.5.
Figure 3 simulates 3-bit (PAM8) UNIP eDACs, of the ThWgt and BiWgt topologies. The current sources in the ThWgt UNIP case of Figure 3a are drawn IID, all S = C − 1 = 7 of them normally distributed as the unary current, , namely (with ):
The 1500 instances of the randomly drawn 7-vector are then propagated via the C-matrix, yielding 1500 instances of the output currents vector of the eDAC:
Equivalently, the resulting eight output level distributions, shown in Figure 3b, are evaluated by accumulating the seven source currents, :
The eight histograms of the 1500 elements (output current levels) for c = 1, 2, …, 8 are displayed in Figure 3b along with the eight analytic Gaussian PDF overlays (202):
The good fit between PDFs and the histogram plots, in all subfigures, verifies the analytics.
The visuals of Figure 3b are consistent with the expected results, e.g., the spreads (STDs) of the UNIP ThWgt eDAC output levels are seen to monotonically progress as the square roots of an arithmetic sequence (see last line of (200)). Thus, Figure 3b verifies Theorem 1 for a UNIP ThWgt eDAC.
Figure 3c takes up the BiWgt UNIP case, displaying the three empirical distributions (histograms) of the current sources, overlayed by the analytic Gaussian PDFs of the current sources, showing excellent fit with the analytic prediction (210). To obtain Figure 3d, the vector of the three current sources (203), drawn 1500 from the Gaussian IID distribution (210), is propagated via the 8 × 3 BiWgt-BIP C-matrix, yielding 1500 instances of the output currents vector of the eDAC:
Operationally, this amounts to a single matrix multiplication
using the extended 7 × 1500 and 8 × 1500 matrices formed in terms of their columns.
The eight histograms of the 1500 elements (output current levels) for c = 1, 2, …, 8 are displayed in Figure 3d, along with their analytic Gaussian PDF overlays. Comparing Figure 3b,d, it is apparent that the respective distributions of the eight output levels fit the same eight analytic Gaussian PDFs, irrespective of the type of ThWgt source currents (and corresponding C-matrix), namely the sources Figure 3a to obtain Figure 3b, vs. the sources of Figure 3c to obtain Figure 3d.Thus, in terms of output level variances, UNIP ThWgt|BiWgt eDACs are statistically equivalent.
Qualitatively, it is seen that any of the displayed currents in Figure 3b,d have their spreads (STDs) increase from left to right, essentially consistent with Proposition 1, as the means of the distributions monotonically increase. Concurrently, since PDF-like histograms are displayed, the histogram heights are reduced in inverse proportion.
Figure 4 addresses a BiWgt BIP eDAC. Figure 4a depicts the histograms of the three “mathematical” (all-positive) current sources. Those are akin to those of the BiWgt UNIP eDAC of Figure 3c, except that the means of the three BiWgt BIP sources of Figure 4a are scaled by a factor of ½ relative to those of the BiWgt UNIP sources of Figure 3c, as per the conventions in Section 2.2. The means can be read off in Figure 4a at positions {2,1, ½} mA as compared to {4, 2, 1} mA in Figure 3c.
The STDs of the three BiWgt BIP current sources of Figure 4a are roughly visualized to correspond to the rule according to which the STDs are proportional to the square-roots of the means.
In Figure 4b, the resulting BIP BiWgt eDAC outputs, are simulated for each of the 1500 randomly drawn realizations of the sources triplet ,
with the signs selected for each c according to the c-th row of the BIP-ThWgt code matrix. The eight histograms of Figure 4b indicate that the output currents are identically distributed, fitting the common theoretical PDF per (219).
In fact, this feature of the BIP BiWgt eDACs is surprising, since for a UNIP BiWgt eDAC the output current levels are quite differently distributed than depicted in Figure 3d. This statistical property of the BIP BiWgt eDACs may be traced to the current sources just flipping signs (see (269)), as the output linear combination of statistically independent current sources is formed by the switching electrical network to generate the output constellation.
To Monte Carlo simulate vector (203) of the three current sources, independently drawn 1500 times from the Gaussian IID distribution (210), is propagated via the 8 × 3 BiWgt-BIP C-matrix, yielding 1500 instances of the output currents vector of the eDAC: . Operationally, the repeated random drawing amounts to a single matrix multiplication,
using extended 7 × 1500 and 8 × 1500 random matrices for the source and output currents, respectively, with these matrices formed by stacking their columns as indicated.
One may compare the visual mean full-scale range (FSR) , as obtained from Figure 4a with the FSR obtained from Figure 3d (the mean LSL and MSL may be read-off in the two sub-figures). The mean FSRs are seen as identical, 3.5 − (−3.5) = 7 − 0 = 7, consistent with the conventions for UNIP vs. BIP BiWgt eDACs, as introduced in Section 2.2.
Figure 4c,d pertain to the alternative BIP BiWgt source currents “physical±” model developed in (220)–(222) for the 3-bit BIP BiWgt eDAC. There are now six “physical±” sources
as depicted in Figure 4c. Comparison with the three “physical±” sources Figure 4a indicates that the positive sources of Figure 4c, and the three “mathematical” sources of Figure 4a, coincide in their respective distributions. The three new negative sources in (271) have means that are mirror images of the means of the positive sources, whereas the variances of “±”-mirror pairs are, respectively, identical. The current sources vector (271) is propagated via a different switching matrix than usual, namely the 8x6 matrix in (222):
The eight histograms corresponding to resulting 1500 output current vectors, namely
are displayed in Figure 4d along with the analytic Gaussian PDF overlays. Visual inspection of this figure indicates that it features essentially identical respective distributions as those of Figure 4b, verifying that the “mathematical” sources of Figure 4a are equivalent to the “physical±” sources of Figure 4b.
Figure 5 proceeds to directly verify the foundational second-order statistical results of this section, namely Proposition 1 and Corollary 4, respectively, exemplified in parts (a), (b) of Figure 5. The linear fits in Figure 4a empirically corroborates the proportionality of the BiWgt source current variances and their respective means, as per Proposition 1. The linear fit in Figure 5b verifies Corollary 4 by showing that the output mean currents and the output variances form proportional arithmetic sequences, to an excellent approximation, as per (132). The datapoints in Figure 5b were evaluated by passing each of the 1500 realizations of the triplets of UNIP BiWgt sources via the 3 × 8 UNIP BiWgt code matrix, to generate the eight output currents realizations (1500 random values each), then evaluating their sample means and variances.
Figure 6 verifies the result (155) of Theorem 2 on the second-order statistics of the seven steps of the BIP PAM8 BiWgt eDAC. The histograms and PDF fits of the output steps are presented Figure 6a, whereas the output variances of the steps are illustrated in the bars diagram of Figure 6b. Additional detail is provided in the caption of Figure 6. Excellent fit is displayed in Figure 6a between the histograms and the theoretical Gaussian PDFs for the steps, validating the statistical analysis of Section 2.3. The most-spread, worst-quality step, having the highest variance is seen to be the “mid-code” step ––the mid-step in the list of seven steps. The step variances are seen as closely approaching the theoretically predicted values. In fact, the empirical variances of the steps, as displayed in Figure 6b, so closely approach the theoretical variances {0.02, 0.06, 0.14} that the seven bars representing the empirical variances appear “right-on” (given the “law-of-large-numbers, at 1500 IID drawings), since the relative deviations, namely {1.21%, 0.07%, 0.29%} are barely distinguishable.
To recapitulate the entire Section 2, let us highlight its conceptual foundation: Proposition 1, for the second-order statistics of the eDAC current sources, which enabled Theorems 1 and 2 for the statistics of the eDAC output current levels and steps, laying a solid analytical foundation for the remainder of this paper as well as for the sequel paper (upcoming Part II). The validity of these key results was just verified by means of Monte Carlo simulations.
3. DAC Integral/Differential Nonlinearities—New Normalized Error Vector Metrics
In the first two subsections of this section, we review the conventional INL and DNL eDAC metrics, albeit seeking a deeper perspective into these somewhat elusive conventional concepts, attained by leveraging on our analytic models. In Section 3.3, we systematically derive and explore the symmetries of the INL and DNL. In Section 3.4, we model the statistics of INL|DNL. In Section 3.5, Section 3.6, Section 3.7 and Section 3.8, we introduce and explore our novel IEV and DEV eDAC metrics, shown to be “relatives” of the INL and DNL conventional metrics, albeit more suitable for modeling communication-oriented eDAC applications. In Section 3.9 and Section 3.10, the IEV is applied to evaluation of the EVM of a communication link. Finally, in Section 3.11, Monte Carlo simulations verify the theory of this section.
3.1. Conventional INL Review (in Our Notation)
In the context of constellations generated by DACs in communication transmitters, the term “nonlinearity” refers the deviation of the levels’ constellation from an ideal set of corresponding uniformly spaced levels. More precisely, the eDAC “nonlinearity” is quantified in terms of the actual levels deviations relative to nominal, also known as reference, constellation , which is uniform, i.e., has its levels equispaced, separated by steps , and has its end levels coinciding with those of the given constellation.
Definition 10.
The “nominal-referred error vector (EV)” of the C-levels constellation at eDAC output is defined as the vector of deviations of the constellation levels with regard to the nominal (reference, intended, ideal) positions of the levels,
where the nominal constellation, , is a uniform reference constellation with LSL and MSL coinciding with the respective MSL and LSL of (see (28) and the note below it):
The LSL and MSL of the given constellation are adopted as those of the nominal constellation. Thus, is a uniform interpolation between the two end-points of .
The EV, , corresponding to a given constellation, , is the deviation of the given constellation with regard to the reference uniform constellation, .
Note: as are generally RVs, so are and so are and random for all c (the underlying randomness stems from the current sources mismatch). Thus, the nominal constellation is a random vector (or finite sequence); nevertheless, all its sample sequences are uniform, though the fixed step in each of the uniform sample constellations is random.
The conventional Integral NonLinearity (INL) metric is essentially a normalized version of the EV, (322). The normalizer in the conventional INL definition is taken as the “average-step” or “average-LSB”, a generally random scalar designated here as , , or as , defined as the arithmetic average (58) of the given constellation steps (increments),
Identifying the average step of the constellation as the unary current , as per (58), provides new insight into the INL definition, as will be seen presently.
The INL samples, (elements of the INL vector, ) are defined below as fractional deviations of the constellation levels: the elements of the vector of the deviations of the levels (relative to the nominal levels) are simply measured in units of (referred to as “average-step” also known as “average-LSB” or average-increment”).
Definition 11.
The (conventional) INL vector of a constellation is a random vector obtained as a normalized version of the EV, , essentially the EV divided by the avg-step, (276):
with the first line in (277) introducing the vector version of the INL, whereas the second line above specifies the elements of the INL vector for c = 1, 2, …, C (the “INL samples”).
The equispaced levels of the nominal reference constellation featuring in the INL definition are uniformly spaced at the (generally random) average step, , (for c = 1, 2, …, C):
This relation stems from the defined uniformity of the constellation, and from the end-point matching constraints (275), implying that and have the same average step and the same full scales (these quantities generally being RV):
The average-step is then a fraction of the common FS of , equal to the constant steps of the nominal reference constellation, :
Note: In light of our definition of the unary current, , as the arithmetic average (random) step of the constellation (see (58) now repeated as (276) above), the first equation in the first line of the INL conventional definition (277) may be written as
Moreover, the nominal (reference) levels (278) may now be written in terms of :
For the c-th nominal level, just shift the first (nominal or actual) level by c − 1 steps of .
Noting that the c-th INL sample is evaluated in as the random vector divided by the random variable , and that both and are Gaussian (dependent) RVs, the evaluation of the statistics of the INL samples turns out rather difficult in the case of stochastic constellation deviations stemming from electronic mismatch errors, since the INL samples are the ratios of two Gaussian RVs; thus, they are not Gaussian themselves.
Note: an evaluation of the distribution of the ratio of two Gaussian RVs calls for advanced statistical analytic tools, e.g., the “Brownian Bridge” [8,9]. In Section 3.5, we introduce a simpler yet highly useful variant of the INL, namely the IEV, bypassing the need to work out the distribution of the ratio of two Gaussian RVs.
It is useful to solve the INL defining Equation (281) for , expressing the constellation vector and its levels in terms of the INL vector, :
or component-wise,
where for #2, the second equality in (278) was substituted for . To recapitulate,
indicating that the constellation levels are determined by initial condition along with the INL vector.
3.2. Conventional DNL Review (in Our Notation)
The DNL is the second well-known eDAC metric complementing the INL. The DNL as an affine transformation of the sequence of constellation steps (for c = 1, 2, …, C-1), working out the steps deviations with regard to the average step, , finally having these deviations expressed in units of the average step (same normalizer reference as used in the conventional INL definition). Comparing the INL and DNL definitions, the INL is a normalized version of the sequence of deviations of the eDAC output levels (with regard to the nominal levels), whereas the DNL is a normalized version of the sequence of deviations of the output steps (with regard to the average step). The conventional INL and DNL definitions are both based on a common normalization: both metrics divide their respective deviations sequences by the average step, , measuring both the levels deviations sequence (for the INL) and the steps deviations sequence (for the DNL) in average-step units.
Definition 12.
The (conventional) DNL vector of an eDAC constellation, J, is obtained from the output steps vector, . (22) is as follows. First, the deviations of the steps with regard to their average, are evaluated, forming the “steps-deviation” sequence
with (276) the “average-step” of the constellation, generally an RV.
Finally, the steps-deviations vector (286) is normalized (divided) by the average step:
The last equality in each of the two lines in (287), is an alternative DNL formulation, dividing each of the steps, , by the average step, , then subtracting unity (as opposed to subtracting off the average-step, then normalizing).
Conversely, solving the equation for yields a formula for unnormalized steps of the constellation, as an affine transformation of the DNL samples:
This formula highlights the interpretation of the c-th DNL sample as the fractional deviation of the c-th step relative to the average-step .
Note 1: all statements made, in the INL context, regarding the construction of as a uniform random sequence interpolation stretching between the LSL and MSL end-levels of the given , also apply here, in the DNL context.
Note 2: when the intended constellation is evident from the context superscript, J is discarded, writing for and for the c-th sample of DNL.
The constellation levels were expressed formula (23) as accumulations of the steps. This relation carries over to obtaining the INL samples as accumulations of the DNL samples. To see this, let us express the levels in terms of the DNL (and the initial level ) plugging Formula (288) for the steps into (23) and simplifying:
where in the last line above (278) was used.
To recapitulate, (289) expresses the constellation levels in terms (average-step-scaled) of accumulations of the DNL samples:
This equation is equivalent to
But the LHS of (291) is identified as (277). Replacing the LSH of (291) by (as per (277)) then yields a compact result: . This result is restated below in a corollary.
Now, recalling (58), we observe that: the DNL vector of an eDAC constellation could be alternatively expressed as the deviation in the eDAC steps from the (random) unary step, , measured in “mean-unary-current” units:
Note: equality #4 above simply expresses the DNL as the deviation in the unary-normalized steps of the constellation with regard to unity:
Conversely, the unary-normalized steps (i.e., the steps measured in units of ) simply equal one-plus-the-DNL samples.
We end this subsection with an explicit formulation of the two-way linear transformations relating the two INL and DNL metrics.
Corollary 6.
The DNL and INL metrics are linked by linear transformations: accumulating the DNL yields the INL; conversely, first-differencing the INL yields the DNL:
Proof of Corollary 6.
Relegated to Appendix B. □
Note 1: the linear transformations (294), relating the INL and DNL vectors, are not invertible (are not inverses of each other), consistent with the DNL and INL vectors of a given eDAC having different dimensions (DNL has C-1 elements, whereas INL has C elements).
Note 2: it is possible to have eDACs sharing the same INL statistics, yet having DNLs of different variances, eDACs are topology-dependent. This is the case for the ThWgt, BiWgt and Seg eDAC, which may be designed for same INL, though their DNLs generally differ.
3.3. INL, DNL Relations and Symmetries
In this subsection we provide, for the first time, to the best of our knowledge, formal derivations of the (skew)-centrosymmetries of the INL and DNL metrics. Those symmetries will be found useful in the sequel.
We start by introducing a streamlined notation for uniform constellations:
Definition 13.
Uniform C-point constellation with endpoints :
Note: are convex combinations of the LSL and MSL, ( ).
As an application of this definition of uniform constellations, the INL definition (277) may be rephrased by leveraging the fact that our earlier introduced nominal constellation is a uniform one:
Definition 14.
A general affine transformation is a map
given by
with
a
matrix and
a D-vector. In eDAC theory, we often encounter a particular subclass of affine transformations, having the following form parameterized by a pair scalar coefficients a, b, representing isotropic scaling and translation:
Note 1: the definition (287) of the DNL vector is essentially the image of affine transformation of the form (301) acting on the output constellation steps vector :
Note 2: the generation of the INL vector from cannot be viewed as an affine transformation of the form (301), but it is rather a more general affine transformation of the form (300), albeit with reduced to a diagonal matrix, , and using a non-constant translation vector, .
Lemma 5.
- (i)
- An affine transformation of the form (301), acting on a uniform constellation, yields a uniform vector, with end-points that are the images of the original endpoints under the same transformation:
- (ii)
- Any uniform constellation (297) is generally raised-skew-centrosymmetric.
Proof of Lemma 5.
Relegated to Appendix B.2. □
Thus, affine transformations of the form (301) acting on eDAC constellations preserve constellation uniformity.
Corollary 7.
- (i)
- Both the INL vector and the DNL vector are invariant under any affine transformation of the form (301), acting on the current vector, namely :
- (ii)
- For any given eDAC topology (or equivalently code matrix), eDACs of the UNIP and BIP polarities have identical INL vectors, and also have identical DNL vectors, whenever these eDACs are driven by identical source current vectors, I. Thus, the INL and DNL metrics do not depend on eDAC polarity (UNIP|BIP); however, they generally do depend on eDAC topology or equivalently on the code matrix (BiWgt|ThWgt). Formally,
Proof of Corollary 7.
The derivation of property (i) is relegated to Appendix B.2. □
Note 1: a more verbose (and informative yet more cumbersome) notation for , above would be .
Note 2: for BiWgt|ThWgt eDACs (irrespective of polarity), the DNLs are different, whereas the INLs come out the same:
Moreover, in light of Corollary 7 (ii), the values of the INL|DNL quantities in (306) do not change upon transitioning any eDAC (be it BiWgt|ThWgt) from UNIP to BIP, the transformation of the output constellation of which may be expressed in the affine form (301).
Note 3: as a special case of the affine transformation (301), an isotropic scaling transformation of the current just leaves the INL and DNL invariant. This is easy to make sense of, as the linear scaling of the INL amounts to amplifying the numerator and denominator in the INL and DNL definitions by the factor a, which cancels out. Likewise, the translation by any constant vector (a vector with equal elements) keeps the INL and DNL invariant.
We finally state some usage additional properties of the INL and DNL metrics:
Corollary 8.
For a UNIP|BIP BiWgt|ThWgt eDAC (irrespective of its source currents):
- (i)
- The first and last elements of the INL vector are always zero:
- (ii)
- The sum of the elements of the DNL vector is always zero:
- (iii)
- The DNL vector is “centrosymmetric”:
- (iv)
- The INL vector is “skew-centrosymmetric”:
Proof.
The detailed derivation is relegated to Appendix B. □
The Monte Carlo simulations of INL|DNL presented in Section 3.11 below verify Corollary 7.
3.4. Modeling of Statistical Properties of the INL|DNL Metrics for (un)Biased eDACs
The INL|DNL vectors are typically inferred for each measured eDAC experimental realization, but it is useful to consider a large ensemble of eDACs subject to the mismatch statistics. For randomly perturbed constellation levels, the INL|DNL vectors are evidently random; thus, it is useful to evaluate their first- and second-order mismatch statistics. It turns out that the statistics of eDAC constellations may be compactly described by the probability distributions of the INL and DNL vectors. We first address features common to the statistical descriptions of both INL and DNL metrics. To abbreviate notation, we pair up structurally identical statements pertaining to both INL and DNL, introducing the *NL metric notation to stand for either of INL|DNL. A concise second-order statistical description of both *NL metrics consists of the mean and variance vectors (the sequences of means and variances of the samples):
Equivalently, the second-order statistics of the *NL metrics is specified by the mean and RMS values of the *NL samples: . Such alternative description is equivalent to (311), since from elementary probability .
Generally, INL|DNL vectors are viewed as random ones; however, they become deterministic whenever the eDAC output constellation is itself deterministic. Examples for which the *NL is deterministic:
- (i)
- Experimentally measured stochastic realizations of the random constellation vector, for one particular eDAC at a time.
- (ii)
- Deterministic nominal uniform eDAC constellations driving memoryless nonlinearities such as an MZM. The MZM output constellation is also deterministic but non-uniform. For deterministic constellations, the value of max{INL|DNL} (most positive sample of *NL) and the value of min{DNL} (most negative sample) are often stated as concise *NL-derived figures of merit. Alternatively, the max of the absolute values of the INL samples is specified, an important specification making it possible to evaluate the “yield”—the fraction of the manufactured chips having their max-INL under any specified threshold, evaluation of which calls for the statistical sophistication of Brownian–Bridge methods [8,9].
The eDAC output constellation deviation sequence, , may often be viewed as a superposition of two (non-zero) components: a deterministic deviations sequence referred to as “deviations; bias and a random mismatch-induced zero-mean perturbation sequence. Examples of constellations with deviations decomposed into bias + zero-mean mismatch:
- i.
- eDAC chips with systematic fabrication structural errors (systematic bias + mismatch).
- ii.
- eDAC feeding an MZM—joint effect of the static nonlinearity of the MZM sine TC and the eDAC electronic-mismatch induced perturbations of the MZM optical output field.
For deterministic eDAC constellations, the uniformity of the constellation or lack thereof is the key characteristic. The “non-uniformity” of a deterministic constellation is synonymously referred to as the “bias” of the constellation. Ideal uniform constellations are referred to as “unbiased”.
An important sub-class of eDACs features zero-mean random perturbation mechanisms with regard to the nominal output constellation, yielding constellation deviations, , free of systematic error (zero-bias), thus satisfying . In this “bias-free” case, taking the mean of the definition (322) yields
i.e., the mean of the given perturbed constellation coincides with mean of the associated nominal uniform constellation.
Note: conversely, a “biased”, also known as non-uniform constellation features, by definition, .
In fact, the “bias-free” eDAC condition pertains to the fundamental physical mechanism of electronic mismatch underlying Proposition 1, which ignored systematic bias errors on the eDAC chip. The fundamental mismatch perturbations at the eDAC output are then zero-mean, which is equivalent to having zero-mean *NL (i.e., INL, DNL) vector metrics.
Having defined (mismatch-induced) perturbations of the source currents as deviations of the source currents from their means, it follows that . Invoking the linear transformation model of source currents to output currents, , we then have
But since the means for BiWgt|ThWgt UNIP|BIP eDACs were shown to be uniform, it is readily shown that .
Lemma 6.
For “unbiased eDACs” featuring “bias-free zero-mean perturbations”,
It is only for such eDACs that the means of the INL and DNL come out null:
Proof.
Relegated to Appendix B. □
Note: “unbiased” eDACs, to which Lemma 6 pertains, are essentially uniform eDACs perturbed by zero-mean current mismatch. If the mismatch were hypothetically nulled out, the resulting eDACs would be uniform. Conversely, eDACs which are non-uniform under the hypothetical mismatch-free assumption are “biased”.
To recapitulate, Lemma 6 may be compactly restated as a chain of equivalences:
Often, rather than specifying all components of the INL|DNL variance vectors, a single characteristic aggregate scalar summarizing the entire vector is extracted. One such concise metric is defined as the root average mean square (RAMS), as defined in Section 1.1, evaluated as the square root of the average of the means of squares of the INL|DNL samples:
Another concise scalar metric is the peak of the sequence of RMS values of the INL|DNL samples, stated as representative of the entire INL|DNL random vector:
The scalar metrics and pertain to either biased or bias-free eDACs. For bias-free eDACs, we have ; thus, the mean-square vector coincides with the variance vector, reducing (317) to the root average square (RAS) (defined in Section 1.1) of the STD-INL|DNL vector:
Therefore, for bias-free eDACs (affected by mismatch but no biases), the concise RAMS scalar metric may be replaced by the RAS of the standard deviations vector, :
Alternatively, the maximum of all standard deviations of the INL|DNL samples is stated, as alternative concise scalar metric summarizing the entire INL|DNL random vector:
A scalar eDAC specification states an upper bound on either of the aforementioned scalar metrics. In the case of the MAX-STD specification, none of standard deviations of the DNL samples should exceed the given value.
It is useful to analytically derive the STD in terms of the Gaussian statistics of the zero-mean current components. Unfortunately, as INL|DNL is generally non-Gaussian, which implies an intricate statistical endeavor, requiring advanced Brownian–Bridge concepts as modeled by Radulov et al. [8]. Moreover, the utility of the metrics (INL and DNL) for communication performance analysis has never been demonstrated.
In the next two subsections, we introduce modified INL and DNL metrics, respectively, referred to as the integral error vector (IEV) and differential error vector (DEV), which are conveniently Gaussian distributed and are amenable to relatively elementary analytic statistical evaluation. Part II of this paper proceeds to establish the direct relevance and utility of the IEV|DEV eDAC descriptions to evaluating transmission metrics of interest in optical or wireless communication, such as the constellation probability of error. In Section 3.9 of this paper, the EVM transmission metric is expressed in terms of the newly defined IEV.
3.5. Integral Error Vector (IEV) as INL Variant Better Suited for Communication Modeling
We proceed to introduce alternative DAC constellation metrics, namely the IEV and DEV, akin to and inspired by the INL and DNL metrics, yet more suitable for communication systems modeling, optical transmission links modeling in particular.
In a nutshell, the modified IEV|DEV metrics may be obtained from their conventional INL|DNL counterparts by replacing in the INL|DNL definitions by its mean . This simple yet subtle change makes all the difference, as is it presently going to become apparent.
Let us start with an auxiliary definition, introducing a modified form of the error vector:
- Mean-nominal-referred error vector (EV).
Definition 15.
“Mean-nominal-referred error vector (EV)” of a C-levels constellation, :
defined as the vector of deviations of the constellation levels with regard to the means of the nominal positions of the levels. The “mean-nominal” constellation,, is now used as reference Its LSL and MSL coincide with the means of the respective (random) MSL and LSL of the given constellation :
Note: Comparing the definition of our original nom-referred EV (274) with the new “mean-nom-referred” definition (322), it is apparent that the “reference” or “nominal” samples are now replaced by their means,
- “Integral Error Vector” (IEV)
Definition 16.
“Integral Error Vector” (IEV) is our communication-oriented modified INL metric, defined as a normalized version of (322), obtained by dividing the mean-nominal-referred deviations, , by the “mean-average step” (325) of the constellation:
Note 1: comparing the new “mean-nominal-referred EV” definition (322) with the “nominal-referred EV” definition (274) used in the INL, the random reference in (274) is now replaced by its mean , a deterministic sequence. Consistent with having been defined as a uniform random constellation satisfying (275), the new reference satisfies (323).
Hence, the mean-nominal-referred EV, , describes the deviation of the actual constellation from a deterministic reference uniform constellation fitting the means of the random end-points LSL and MSL of the given constellation, .
Note 2: In fact, both and are both uniform references, but is random (its sample sequences have random FS and end-points, yet the inner levels of any of its sample sequences are uniformly spaced), whereas is a deterministic uniform sequence with fixed end-points (323) and fixed FS.
Note 3: our IEV is essentially a modification of the conventional INL definition (277), obtained by adopting in lieu of in the numerator and in lieu of in denominator, i.e., replacing the “average-step” random denominator in the INL definition (277) by a deterministic numerator
referred to as “mean-average-step”. The order of the arithmetic averaging, the mean and first-difference operations may be commuted, , which accounts for the alternative expressions in (325) for the “mean-average-step” normalizer of the IEV.
Note 4: we reiterate that the normalizer (325) adopted in the IEV definition (324) is obtained by applying both arithmetic averaging and mean (expectation) functionals (in either order) to the random sequence of steps of the given constellation. The new “mean-average step” (also known as “average-mean step”) normalizer (325), is a deterministic scalar, whereas the “average-step” normalizer used in the INL is an RV (which appreciably complicates the evaluation of the distribution of the INL in mismatch statistical modeling, calling for advanced methods such as the Brownian–Bridge [8]; in contrast, the distribution of the IEV simply comes out Gaussian, since the IEV is proportional to its numerator , which is modeled as Gaussian in eDAC mismatch models.
Note 5: the random sequence appearing in the IEV definition (324) is actually the same one as adopted in (278) for the INL definition, yet that reference sequence is not directly used but we rather use the sequence of its means ,
The deterministic mean nominal levels form a uniform sequence, with regard to which the level deviations , featuring in the IEV numerator, are evaluated.
Note 6: the normalizer is sometimes referred as the “LSB” of the IEV, as is for the INL, but more precisely is the mean-average-LSB. The is dimensionless, but it is said to be measured in “LSB” units, e.g., 0.04 LSB. The same “LSB” language is used for the conventional INL, but it is more problematic there, since in the conventional INL definition the “LSB” (the denominator) is random, whereas in the IEV it is deterministic.
Inspecting (59), it is apparent that the normalizer in the denominator of the IEV definition (324) coincides with the unary current, , as defined in (59). An alternative definition of the IEV leverages this fact, recalling that unary-normalization (division) by is denoted by a round-hat (as per (73)).
Definition 17.
The IEV of an eDAC constellation is defined as a unary-normalized version of . The IEV is given by the mean-nominal-referred deviation vector measured in “mean-unary-current” units:
Corollary 9.
IEV as mean-nominal referred deviation of the normalized current :
In brief, the deviations operator and the unary-normalizer operator commute:
The constellation levels expressed in terms of the nominal constellation levels and the IEV:
The constellation levels expressed in terms of the initial level (the LSL) and the IEV:
Proof of Corollary 9.
Relegated to Appendix B.2. □
Note 1: The second line in (331) is readily obtained from the first one by dividing the first line by .
Specializing (331) to c:= 1 and taking means:
Specializing (331) to c:= C, and taking means:
Solving the last equation in (333) for yields
but , which is plugged into (334), yielding .
To recapitulate, by virtue of the IEV definition, we have the interesting property that the first sample of the IEV (the IEV of the LSL level) and the last sample of the IEV (the IEV of the MSL level) are always null:
Note: the LSL and MSL IEV null out only in the mean, over the entire ensemble of eDACs, i.e., generally the RVs are non-zero. In fact, property (335) is the counterpart of the INL property (307). However, for the INL metrics, each realization of the ensemble of eDACs satisfies (307), whereas for the IEV metrics, (335) only holds in the mean, over the entire ensemble.
An important observation regarding the IEV|DEV metrics is that they can only be evaluated when an entire ensemble is specified, as the IEV|DEV definitions require the mean unary current . Given an individual eDAC, without specifying which eDAC ensemble it has been drawn from, and what its first-order statistics is, the IEV|DEV metrics remain undefined.
Not so with the INL|DNL metrics, which are well defined for any given sample of an eDAC regardless of its batch or lot.
3.6. IEV of Biased eDACs—Decomposed into Deterministic and Random Zero-Mean Components
Biased eDACs are those either affected by systematic errors or inherently designed to yield non-uniform output constellations. For biased eDACs, the IEV has non-zero mean, and the mean eDAC output constellation is now non-uniform (the mean constellation, , does not coincide with the uniform reference constellation ):
In biased eDACs, besides the mismatch-induced random errors, there are also present deterministic level offsets (systematic errors), i.e., built-in departures from the uniform nominal grid. For “biased” eDACs, it is useful to decompose the total mean-nom deviations vector (322) into the sum of a fixed, deterministic, static component (the bias vector), , plus a zero-mean random perturbation, .
Formally, the mean-nominal-referred deviation is processed by subtracting and adding , yielding a decomposition of into a zero-mean (ZM) component + a deterministic (DET) component:
where the definition of perturbation,
is recalled.
The key result (337) is restated in the following
Lemma 7.
DET + ZM decomposition of mean-nominal-referred deviations and the IEV:
where the nonlinear DET and random ZM respective additive components are given by
Proof of Lemma 7.
In (339), the additive component is a ZM perturbation, , whereas the component is DET, essentially the non-zero mean of with the first equality in (340) obtained by the substitution into the definition of , and the last equality in (340) obtained by applying the mean operator onto both sides of □.
Unary-normalizing the DET + ZM decomposition (339) of yields the following.
Theorem 4.
IEV decomposition into deterministic IEV-of-the-mean component and unary-normalized zero-mean mismatch-induced current perturbation:
The two additive components of in (342) are alternatively expressed as
The DET + ZM additive decomposition of the IEV may be written in two alternative forms:
The mean-square IEV vector is accordingly additively decomposed into a pair of partial MS terms, respectively, associated with the DET and ZM components of the IEV, as follows:
The RAMS-IEV scalar metric is expressed as a root-sum-of-squares of the DET and ZM components,
In the special case of unbiased (nominally uniform) eDACs,
thus, the mean-square IEV vector (345) and the RAMS-IEV (346) yield
For either biased BIP BiWgt|ThWgt eDACs or for biased UNIP BiWgt eDACs:
Proof of Theorem 4.
Relegated to Appendix B.2.□
But for those interested to reconstruct the derivation of some “punch-line” formulas, we provide some hints. To show (348), use
To prove (349), use (135), repeated below, for evaluating :
Note 1: Result (349) is incorrect in the case of biased (non-uniform) ThWgt UNIP eDACs.
Note 2: The IEV properties just proven above are extended in Part II of this paper to eDACs terminated in memoryless nonlinearities, with application to an optical communication Tx consisting of an MZM fed by a nominally uniform eDAC driver.
Since the INL amounts to the ratio of two dependent, generally non-zero-mean, Gaussian RVs, it is more difficult to handle, statistically, than handling IEV which is plain Gaussian. One problem with ratios of Gaussians is that they are usually heavy-tailed. Further investigating the statistical properties of the ratio distribution of the INL is outside the scope of the current paper, but we note that another approach, namely the Gaussian-Bridge, was used in [8,9] to model the distribution of the INL as well as the distribution of the yield.
The handling of normal (Gaussian) statistics of the IEV is much simpler than that of the non-normal statistics of the INL, e.g., the IEV yield, defined as the probability that the maximum element of the IEV vector be under a given threshold (percentage of devices in the fab run meeting a threshold specification for the max-IEV) may be readily obtained by order statistics methods for dependent normal RVs.
3.7. Differential Error Vector (DEV) as DNL Variant Better Suited for Communication Models
In analogy with the transition from conventional to , we now introduce a variant of the vector, namely the “Differential Error Vector”, , more suitable for communication-oriented eDAC applications than the conventional DNL metric is. Our proposed modification of the DNL definition (287) simply replaces the average-step normalizer (an RV) by its mean: the mean-average-step (325) (a deterministic scalar characteristic of a batch or lot of eDAC chips):
Definition 18.
The “Differential Error Vector” (DEV) vector, , of an eDAC current constellation, , is obtained from the steps vector, (22) as follows: first, the deviations of the steps from the “mean-average step”, are evaluated, forming the random “steps-deviation” sequence
where, as seen in (325),
is the “mean-average-step” of the constellation, a scalar metric used as normalizer in both our IEV and DEV, obtained by taking the (stochastic) mean of the (arithmetic) average step (276) used in the conventional DNL definition (the order of the mean and average may be reversed as in the second equality in (353)).
Finally, the DEV vector is obtained by normalizing (dividing) the “steps-deviation” sequence (286) by the mean-average step, :
Note 1: an alternative notation for the “mean-average-step” normalizer, , sometimes referred to as “LSB”, is (reminding us that it is a joint property of all mean steps of the constellation—their arithmetic average).
Note 2: although the metric is dimensionless, it is said to be measured in “LSB” units, e.g., 0.04 LSB. The same language is used for the conventional DNL, but it is more problematic there, as in the DNL definition the “LSB” the normalizer, , is random, whereas in our DEV definition the “LSB” normalizer is deterministic, being more naturally referred to as “LSB”.
Since the definition (354) is effectively obtained from the conventional DNL one, (287), simply by replacing by everywhere in the defining formulas for the conventional DNL, the same replacement may be made in all corollaries stemming the original definition, as derived in Section 3.2. In particular formulas (288), (290) and (294) may now be retrofitted with the substitutions INL:= IEV, DNL:= DEV,, and , yielding five useful formulas listed next:
Corollary 10.
Mapping vectors to step-vectors, , and to constellation levels, :
Back-and-forth transformations between and :
Proof.
This corollary may be directly derived from the DEV definition (354), paraphrasing the derivation of similar formulas pertaining to INL and DNL in Section 3.1, Section 3.2 and Section 3.3. □
At this point, as we have done with the IEV, we may view the DEV as a “unary-normalization”, providing a useful alternative point of view, simply making the substitutions in the DEV definition (354), yielding the following alternative definition.
Definition 19.
The DEV of an eDAC constellation, , is evaluated from the constellation steps in equivalent forms, by having them “unary-normalized” (expressed in units of ) to yield , then subtracting off , i.e., subtracting unity from all C-1 elements of :
Conversely, solving (358) for the normalized steps, , yields the useful relation:
In case the eDAC is “perfect”, then and the normalized steps are all unity.
Note: it is instructive to verify that this alt def of the DEV metric is consistent with the alt def (328) of the IEV metric. Taking the means of (328) and of (359):
Let us verify the consistency of the two equations in (361), based on (357). Taking the mean and commuting it with , yields
Applying on both sides of the first eq. in (361), , yields
where in #3 the property (85) was used. The equalities chain above verifies the consistency of the alternative definitions (328) and (359) of the IEV and DEV with (362).
Now, more generally, from (357), any DEV vector may be obtained by taking the steps of the corresponding IEV vector, .
Equipped with the compact alt def (359) of the DEV metric, formulas (356), (357) may now be derived even more readily.
3.8. DEV Statistics of (un)Biased eDACs—Deterministic and Random Zero-Mean components
Lemma 8.
eDAC (unary-normalized) steps and their perturbations expressed in terms of the constellation DEV:
Consider the normalized and unnormalized eDAC constellation steps:
The following random zero-mean perturbations and derived quantities are all equal: the perturbations of the DEV of the constellation, ; the perturbations of the normalized steps ; the steps of the normalized perturbations, ; the DEV, , of the constellation perturbations, :
where we recall the definition (A97) of the perturbation operator .
Proof of Lemma 8.
Relegated to Appendix B.2. □
Note: the particular result in (365) may be justified as equivalent to , which is a special case of (360) under the substitution .
For “biased” eDACs impaired by systematic biases, in addition to zero-mean mismatch effects we have non-zero “biases”, . The second-order statistics of the DEV vectors of biased eDACs is worked out by leveraging our earlier results on the statistics of We start from the IEV result (342), applying the operator onto both sides of the equality yielding
where in the last equality (357) was used.
Now, in the last expression in (367) may be equated with as per (365); thus, is substituted into the last equality in (367), yielding:
Hence, we have obtained a DET + ZM decomposition for the DEV metric, akin to that earlier obtained in (344) for the IEV metric:
Theorem 5.
IEV|DEV DET + ZM decompositions for generally biased eDACs and their first-order and second-order statistics.
The IEV and DEV are, respectively, decomposed into DET + ZM components as follows:
The IEV and DEV vectors are Gaussian distributed, since is Gaussian distributed. First-order statistics of the IEV|DEV vectors:
Second-order statistics of the IEV|DEV vectors,
In the case of unbiased eDACs with uniform constellations, consistent with (132) we have:
As for the steps statistics as captured in the DEV metric, , we have,
, per (151)
The max-variance component of (using (163)) occurs “mid-code” and is given b:
RAMS scalar metrics concisely representing the IEV|DEV vectors,
yielding, for either BIP BiWgt|ThWgt biased eDACs or for UNIP BiWgt biased eDACs, the following RAMS scalar metrics:
Proof of Theorem 5.
Relegated to Appendix B.2. □
3.9. EVM Communication Constellation Metric—Evaluated from Our IEV eDAC Metric
Communication engineers do not typically use INL|DNL metrics customarily utilized in the eDAC community, to assist in characterizing the transmission performance of BIP|UNIP PAM transmission constellations. Communication practitioners typically assess and specify the quality of the transmitted constellations based on distinct constellation quality measures tailored to the communication context, such as error vector magnitude (EVM) and Symbol|Bit Error Rate (SER|BER).
In this subsection we show how IEV|DEV metrics, as introduced in this paper for eDAC characterization, facilitate immediate evaluation of the EVM in wireless|optical transmission applications.
We start by reviewing the conventional definition of the EVM metric for any given randomly perturbed and/or non-uniform 1D PAM constellation.
Note: we distinguish between 1D (UNIP|BIP) PAM constellations and 2D constellations such as QAM. 1D|2D then refer to the dimensionality of the real-axis and the IQ-plane.
For 1D communication constellations, the “mean-nominal constellation” is taken as the “perfect” perturbation-free uniformly-spaced (unbiased) target constellation we ideally aim to have, whereas the actually generated imperfect constellation, perturbed by electronic mismatch and distorted by static bias, is represented by the random vector .
The conventional EVM formulation [15,16,17], characterizing the quality of the eDAC-generated 1D constellation in a communication transmitter, is cast in the formalism of our paper, viewed as a functional extracting a scalar (the EVM) summarizing the random vector (322), namely the “mean-nominal-referred error vector (EV)”.
Definition 20.
The error vector magnitude (EVM) of an eDAC output constellation, , is given by a functional acting on the constellation Error-Vector (EV),
where the RAMS, RoG and RAS functionals were defined in Section 1.1.
Note: recall that a functional is a mapping .
In words, the deviations (322) of the levels of the actual constellation , with regard to the ideal levels of a “nominal” uniform constellation, , are concisely represented by a single scalar metric, the Root-Average-Mean-Square (RAMS) of the nominal-referred deviations, albeit normalized by the Radius-of-Gyration (A103) of the “perfect” constellation.
Note: the normalization by the denominator of the EVM in (381) ensures such that at a given target EVM, larger extent constellations may tolerate larger RAMS-deviations.
Conventionally, expressions equivalent to those in the second line in (381) are used to define EVM [15,16,17], but here we structure the EVM definition in terms of our streamlined notation (322) of this paper. In the second equality in (381) (A103) was used in order to evaluate the RoG of the mean-nominal reference constellation, as the Root-Average-Square of the distances of the ideal constellation points from their center-of-mass.
We now present our key findings positing our IEV metric as a preferred tool for express EVM evaluation. We essentially show that the EVM is nothing but a scaled version of the RAMS of our IEV vector.
Theorem 6.
The EVM of a 1D PAM-C constellation is proportional to the Root-Average-Mean-Square (RAMS) of the IEV vector of the given constellation,
with proportionality constant, , given by the inverse of the radius-of-gyration of the normalized constellation, parameterized by the constellation size, C as follows:
expressing , for any our 1D constellations of interest, as proportional to the Root-Average-Mean-Square :
This result is obtained by plugging (383) into (382) and simplifying.
For DACs impaired by deterministic (static) bias + mismatch errors, we plug our formula (349) yielding
These formulas for the EVM of non-uniform PAM-C are parameterized by the STD, of the relative mismatch, by the DET IEV bias vector, and by the constellation size, C of the DAC.
In particular, for unbiased DACs (e.g., conventional linear eDACs), the bias component nulls out, , reducing (385) to simple expressions proportional to the mismatch relative STD, , with coefficients of proportionality parameterized by C:
Proof of Theorem 6.
Relegated to Appendix B.2. □
The bottom line of Theorem 6, just proven, is that once having evaluated the Root-Average-Mean-Square (RAMS) of the IEV vector, , the conventional EVM metric may be immediately obtained, by simply scaling by the multiplicative factor for UNIP|BIP (this factor is given by the inverse RoG of the nominal PAM).
To recapitulate, the IEV (and its complex plane extension) is simply proportional to the error-vector used to work out the EVM constellation metric by Root-Average-Mean-Squaring. Thus, evaluating EVM is a simple matter of scaling the IEV and calculating its RAMS.
Our IEV eDAC description is seen to provide an “express track” to EVM evaluation.
Note 1: in fact, we may think of our introduced RAMS-IEV as the IEV, up to a multiplicative constant .
Note 2: here we solely account for the component of EVM due to the eDAC mismatch. The EVM due to additive white Gaussian noise, for example, is not treated here. Thus, the EVM evaluated here is an upper bound to the actual EVM, attained in the noiseless case.
3.10. EVM of QAM Constellations Readily Evaluated from the IEV Metrics of the IQ eDACs
In this subsection, we extend the EVM-RMS definition from the real-axis (1D) to the complex plane (2D(, aggregating the EVs and EVMs of the I and Q tributaries into corresponding complex-valued metrics, to enable modeling QAM constellations in wireless|optical communication links, accounting for the impairments of the driver eDACs.
EVM for QAM is a known metric, but a new aspect is that the IEV and DEV eDAC metrics are complexified here for the first time and the complex IEV is related to the QAM EVM.
For a QAM transmitter nesting a pair of I and Q tributaries, each with its own eDAC driver, we aggregate the EV, IEV and DEV metrics of the two I and Q tributaries into corresponding complex-valued metrics.
Definition 21.
Complex-valued EV, IEV, DEV for a QAM Tx IQ-nesting a pair of eDACs:
Let denote the actual constellations of I and Q tributary eDACs, and let denote their corresponding “mean-nominal” reference constellation.
Then, the corresponding complex constellations (labeled by over-tildes) are defined as
and the corresponding complex mean-nominal-referred Error Vectors are defined as
The IEV|DEV of the complex constellation (in brief complex-*EV) are defined as
Corollary 11.
Complex EV and IEV in terms of (normalized) I and Q constellations:
“Complexifying” the IEV alt def (327) yields
“Complexifying” the DEV alt def (358) yields
Proof.
The simple derivations of the formulas of this corollary are omitted. □
The complexified EV and enable the extension of the concept of EVM from a real-valued constellation to a complex-valued constellation, paraphrasing def (381) of real-valued EVM, simply by replacing all real-valued quantities by complex ones:
Definition.
EVM of complex constellation, :
It is useful to relate the EVM of a complex QAM constellation to the EVMs of the I and Q tributary constellations. Here we assume the statistical “symmetry” of the QAM constellation, the technical term being the “circularity” of the complex random vector , amounting here to being IID vectors. Thus, per this definition, is circular.
We shall need the generic properties of the RAMS and RoG for complex (circular) vectors.
Lemma 9.
For any complex random vector with independent Re&Im parts has its I and Q components adding on an root-sum-of-squares basis:
Now assuming the complex random vector is circular (i.e., are IID),
For a deterministic real vector with identical Re&Im components, , the RoG of the complex vector, , is times the RoG of the real component:
Proof of Lemma 9.
The derivation is omitted, but it essentially stems from the RAMS (A102) and RoG (A103) definitions. □
Lemma 10.
For a QAM constellation with IID mismatch statistics of its IQ components, the EVM of the complex constellation, equals the EVM of either of the I|Q tributary constellations:
This means that having evaluated the EVM of the I|Q PAM-C tributaries we are done—we immediately have the EVM of the C2-QAM complex constellation. Specifically, since the results (382)–(386) for the EVM of a real-valued constellation, in terms of the IEV, carry over to I|Q component constellation, they also yield the EVM of the complex QAM constellation. E.g., for a biased “complex DAC”, i.e., a pair of nominally identical statistically independent, identically biased DACs generating the IQ tributaries, from (385) and (398) it follows that EVM of the complex C2-QAM constellation may be evaluated by this formula, determined by the deterministic IEV of the identically biased I|Q DACs, by the identical electronic mismatch of the two DACs and by the constellation size:
Proof of Lemma 10.
The derivation follows from the definitions of real-valued and complex valued EVM and the assumed circularity of the IQ component statistics. Applying Lemma 10 to the complex random vector , assumed circular, and to the complex deterministic vector with identical Re&Im parts (as behooves a well-behaved QAM constellation), the EVM of the complex constellation may be expressed as follows in terms of the RAMS and RoG of the Re&Im parts:
□
A key take from this subsection is that our newly introduced IEV|DEV are readily extended to the complex plane in order to model QAM constellations, but no such meaningful “complexification” seems feasible with the INL|DNL conventional metrics.
3.11. Monte Carlo Simulations of Key Properties of the INL, DNL, IEV, DEV eDAC Metrics
In this subsection we verify essential features of the INL, DNL, IEV, DEV eDAC metrics theoretically treated heretofore in Section 3, presenting Monte Carlo simulations based on the same ensemble of 1500 BiWgt UNIP PAM4 eDACs with B = 3, C = 8, as already used in the simulations in 2.9. Here we randomly extract five eDACs out of the 1500 eDACs ensemble, drawing five random realizations of the corresponding source vectors, , satisfying Proposition 1, (five mutually independent Gaussian random vectors, each with independent components with means and variances per (94), with parameters as defined in the simulations in Section 2.9). We then work out the five resulting output currents by acting onto the five drawn vectors with the UNIP BiWgt code matrix. For each of the resulting five output UNIP constellations, we evaluate the INL, DNL, IEV, DEV vectors, and have these vector metrics depicted in Figure 7, Figure 8, Figure 9 and Figure 10.
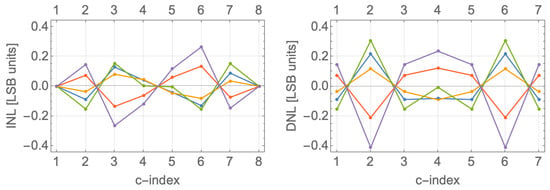
Figure 7.
Monte Carlo simulations of (left) INL, (right) DNL for five eDACs with randomly drawn source currents, verifying the symmetries of the INL and DNL metrics. The colors of the various jagged lines represent distinct sample paths of the random process.
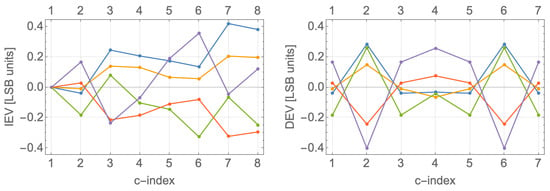
Figure 8.
Monte Carlo simulations (left) IEV, (right) DEV for five UNIP BiWgt eDACs with randomly drawn source currents, verifying the symmetries of the IEV and DEV metrics.
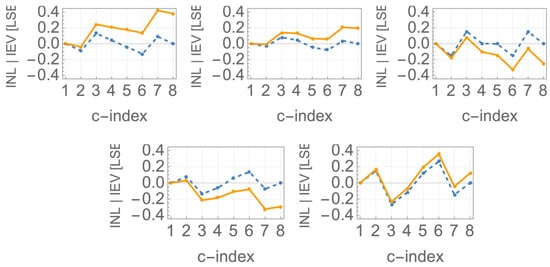
Figure 9.
Monte Carlo simulations of the INL (dashed, blue curves) and IEV (solid, orange curves) of each of the 5 BiWgt UNIP PAM8 eDACs (randomly selected out of the eDACs ensemble) the 5 INL curves of which were already plotted in Figure 7(left). Here, plotting the INL and IEV together for each of the five eDACs enables discerning the distinct qualities of these metrics, in particular the pinning to zero of the INL at the two extreme samples (the LSL and MSL) vs. a trend of increased deviation of the INL from zero, as the index c increases, consistent with the variance of the eDAC zero-mean output current component actually linearly increasing with the index c (Theorem 4).
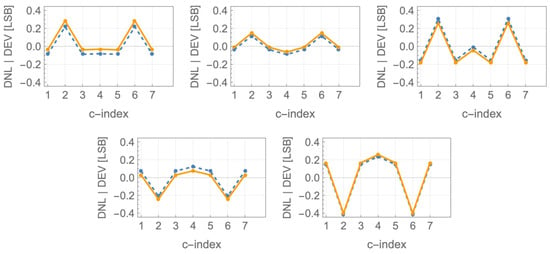
Figure 10.
Monte Carlo simulations of the DNL (dashed, blue curves) and DEV (solid, orange curves) for each of the 5 BiWgt UNIP PAM8 eDACs (randomly selected out of the eDACs ensemble), pertaining to the DNL curves plotted in Figure 7(right).
Overviewing the four figures presented in Figure 7, 5 INL curves are assembled together and so are 5 DNL curves. Figure 8 piles 5 IEV curves together and 5 DEV curves together. Figure 9 associates each of the five INLs with its corresponding IEV. Figure 10 associates each of the five DNLs with its corresponding DEV.
Elaborating, Figure 7 verifies Corollary 8, visualizing the skew-centrosymmetry of the INL, the centrosymmetry of the DNL and the fact that the INL is “pinned” to zero values at its two extreme (LSL and MSL) samples.
Next transitioning from the INL, DNL to the corresponding IEV, DEV metrics, Figure 8 is the counterpart of Figure 7, presenting the respective IEV and DEV for the same five randomly drawn BiWgt UNIP PAM4 eDACs. Visually comparing the INL and IEV graphs (Figure 7(left) vs. Figure 8(left)) it is apparent that the UNIP IEV is no longer skew-centrosymmetric, and in particular it is no longer pinned to zero at the MSL index (c = 8) (though it is pinned to zero at the LSL index (c = 1). In fact, the general statistical trend of the IEV is to rise in absolute value as the index c increases, consistent with our analytical model in Theorem 4 indicating that for unbiased UNIP eDACs as the index c increases, the variance of the IEV linearly increases. Evidently, these are just 5 IEV realizations out of the entire statistical ensemble but the variance growth tread trend is already visible. In contrast, the pinning at zero of the INL at the two extremities (as in Figure 7(left)) is not a faithful physical representation of eDACs mismatch statistics, since it fails to capture that the noisiest sample (the output current sample likely to have the largest absolute value) of an UNIP eDAC is actually the last one, the MSL (here at c = 8)—thus, the pinning the last INL sample to zero suppresses information about the most pronounced noisiness of the MSL sample. In contrast, the advantage of the IEV metric is that its absolute value does provide a faithful indication of the actual noisiness (or biasing distortion) of the sample.
The UNIP INL is visibly skew-centrosymmetric, as may be seen by inspecting the five INL cures in (Figure 7(left)).The IEV metric (Figure 8(left)) does not possess (skew-)centrosymmetry properties. In contrast the DEV metric (Figure 8(right)) is seen to retain the centrosymmetry of the DNL metric (Figure 7(right)). Both the DNL an DEV are centrosymmetric, and in fact their respective graphs are nearly identical, with only minute differences between the DEV and DNL for each of the five eDACs (this observation is also apparent in Figure 10).
The fact that the DNL and DEV are almost identical, yet the INL and IEV are so different is accounted for by the INL, IEV being accumulations of the DNL, DEV, respectively. Thus, small differences between the DEV and DNL (as apparent in Figure 10) accumulateto a gradual runoff between the IEV and INL (as apparent in Figure 9 as well as in Figure 7(left)).
Figure 9 overlays in each of its five frames, the plots of the INL and IEV of five UNIP eDACs. Again, it is visible that the INL (dashed, blue) curves are pinned to zero at their two extremities (at indices 1 and 8), whereas for the IEV curves (solid, orange) are pinned to zero just on their LHS (at c = 1), tending to run off to higher absolute values as the index c increases. The other visible effect is the lack of skew-centrosymmetry of the IEV—which is a positive aspect as such centrosymmetry is “unphysical”, inconsistent with the second-order statistics of the output current vectors, J.
Figure 10 superposes in each of its five frames the plots of the DNL and DEV of five UNIP eDACs. It is again apparent that there are just small differences (small vertical discrepancies) between the DEV and DNL vectors. Moreover, the centro-symmetry of the DEV is seen to be holding just like that of the DNL in Figure 8(right). We note that since the DEV vector is essentially an affine transformation on the current vector, J, and the physical reality is that the levels of J do form out a centrosymmetric sequence for BiWgt eDACs, then so should the DEV samples.
Figure 11 verifies the second-order statistical properties of the IEV according to Theorem 4 (albeit for unbiased eDACs affected solely by electronic mismatch errors, no systematic errors). The empirical Standard Deviation (STD) of the c = 1, 2, 3, …, 8 IEV samples is calculated over the entire ensemble of 1500 eDACs for each of the C = 8 IEV samples, plotted as 8 red blue dots in the figure. The orange curve, represents the stochastic STD of the IEV samples, plotted in the figure as ideal reference for the empirical STD points. Actually, this function of c is discrete-valued as it is only defined at discrete indices, c = 1, 2, 3, …, 8, though, for visualization purposes, we had it plotted as continuous-valued graph (as if c is a real-valued index defined over the closed segment with endpoints 1, 8). The expected stochastic STD values are the intersection points between the orange curve and the 8 vertical gridlines at c = 1, 2, 3, …, 8. It is apparent that the blue dots representing the empirical STDs of the IEV over the ensemble of 1500 eDACs deviate only minutely from the expected stochastic STD values. The size of 1500 points yields excellent accuracy of the empirical STD, which becomes a highly accurate estimate of the expected stochastic STD. The correspondence of the empirical and stochastic STDs, provides verification for the Theorem 4 result paraphrased here,
since taking the square-root of this formula yields
where we recall that in our drawn ensemble of 1500 eDACs, we have selected .
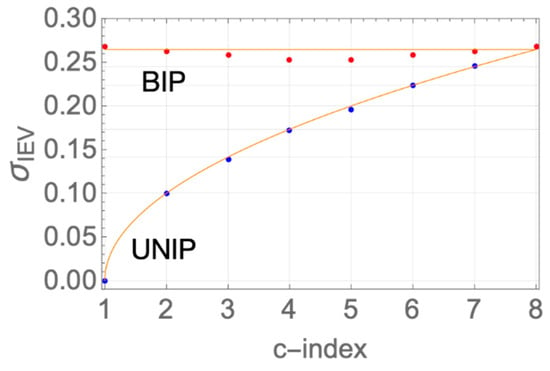
Figure 11.
Verification of Theorem 4 in Section 3.6, for the ensemble of 1500 UNIP|BIP eDACs, comparing the 8 blue dots of the empirical STD of the IEV (based on the 1500 UNIP eDACs drawn ensemble) with the theoretical prediction of (402). The orange curve, representing the theoretical IEV STD as the function for , is made continuous just for visualization purposes, as is actually defined only for integer indices, c = 1, 2, 3, …, 8 (thus, it should have been presented as 8 discrete points, the intersections of the continuous curve with 8 vertical grid lines at abscissae c = 1, 2, 3, …, 8). The UNIP empirical STD essentially follows this functional dependence on the level index, c, whereas the BIP empirical STD is essential constant, close to the value .
We recall that the theoretical STD of the IEV is constant, given by formula the following formula of Theorem 4:
This expected constant level of the STD of the IEV of BIP eDACs is plotted as a continuous curve in Figure 11, along with the 8 discrete red dots representing the empirical STDs of the IEV samples for c = 1, 2, 3, …, C. The deviations of the red dots from the expected flat level are reasonable, since the relative mismatch, is relatively pronounced.
This completes the Monte Carlo verification of Theorem 4 for the statistics of the IEV.
Finally, we aim to verify the key Formula (376) of Theorem 5, stating the STD of the DEV vector, paraphrased here:
Here, are the XORs of successive codewords as per (151):
The resulting list of XOR vectors for the UNIP PAM8 eDAC, i.e., for C = 8, B = 3, is as follows: {{0, 0, 1}, {0, 1, 1}, {0, 0, 1}, {1, 1, 1}, {0, 0, 1}, {0, 1, 1}, {0, 0, 1}} as may be readily verified for the BiWgt counting code, {{0, 0, 0}, {0, 0, 1}, {0, 1, 0}, {0, 1, 1}, {1, 0, 0}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1}}.
The dyadic vector in (404) reduces for B = 3 to {4, 2, 1}, and the inner products in (404), respectively, yield
where the three distinct elements in the list in braces were obtained as follows:
Taking the square root of (406) yields our final formulas for PAM4 UNIP eDACs:
For the simulated eDAC ensemble, , yielding
The last vector is the theoretical DEV STD plotted in Figure 12 as the orange curve slightly above the blue curve (representing the “empirical STD”, i.e., the root average mean square (RAMS) of each of the IEV samples for c = 1, 2, 3, …, 8. The empirical STD is seen to be an excellent estimate for the theoretical STD, validating the key Formula (376) of Theorem 5.
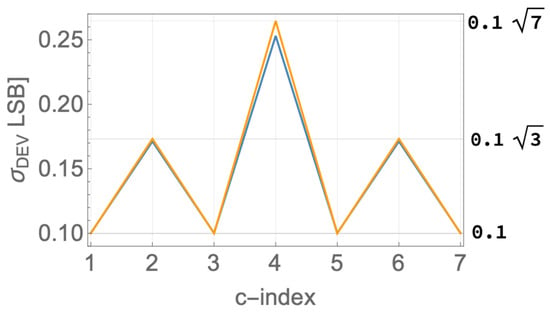
Figure 12.
Verification of Theorem 5 in Section 3.8, for the ensemble of 1500 UNIP eDACs, indicating excellent fit between the empirical standard deviation vector of the new DEV metric, and its analytically derived (as in (376) of Theorem 5) theoretical expected standard deviation vector. The analytic STD is the orange curve which is slightly higher than the blue curve, which in turn is the graph of the empirical STD of the array of 1500 eDACs, i.e., the Root-Average-Mean-Square (RAMS) of the 1500 realizations of each of the 8 samples of the IEV vector, evaluated for each of the Monte Carlo simulated 1500 eDACs.
4. Conclusions
This work developed a comprehensive analytical toolbox for the statistical characterization of nonlinear distortions of eDAC-generated signal constellations to be transmitted over communication links. The emerging rigorous all-analytic statistical model for the UNIP|BIP ThWgt|BiWgt eDACs pertains to the propagation of electronic mismatch random variations in current-steering eDAC. The all-analytic toolbox, derived and explored here, consists of closed-form expressions for the second-order statistics (means, variances, STD) of all relevant quantities in the current-steering eDACs building blocks impacting communication transmitters.
A key insight emerging from our eDAC statistical modeling is that conventional INL|DNL constellation metrics, routinely used in the electronic devices and circuits community, are ineffective characterizations in the context of communication links performance. Unfortunately, the INL|DNL metrics of an eDAC in a communication transmitter are not amenable to being translated into the statistical performance of transmission links, for which communication engineers resort to other metrics, e.g., SER, BER and constellation error vector magnitude (EVM). To rectify this disconnect between the modeling methodologies used in the respective devices and circuits [4,5,6] vs. communication [15,16,17,18,19] domains, this paper introduced modified variants of the INL|DNL, namely the IEV|DEV constellation metrics, from which statistical transmission performance metrics are readily inferred, relevant to communication engineers in their designs of wireless, wireline or optical channels, especially with Rx-s using coherent detection (for which BIP eDACs are needed). In Part I of this paper, we have established the IEV|DEV as straightforward predictors of EVM. Nevertheless, INL|DNL withstand as useful metrics for experimental characterization of individual eDAC specimens, whereas IEV|DEV are best suited for modeling communication links performance on an aggregate basis, across statistical ensembles of eDACs, inevitably affected by random current mismatch variations.
Our upcoming Part II, building upon the current Part I foundations, is going to explore the impact of the various eDAC metrics (INL|DNL|IEV|DEV) onto the SER|BER characteristics of data transmission links. Our all-analytic model of the second-order statistics of electronic mismatch, impairing the eDAC driver in the (wireless/wireline/optical) Tx, will be propagated all the way to the Tx output and then via the linear AWG channel, to the Rx. In particular, we shall treat MZM-based coherent optical interconnects, using the BIP BiWgt eDAC topology for the I|Q tributaries of QAM transmitters.
Space limitations also precluded us from addressing the extension of the current statistical all-analytic modeling toolbox from the UNIP|BIP ThWgt|BiWgt eDAC topologies, extensively modeled here, to linear segmented (Seg) DACs. We note here that optical DACs such as our MP-oDACs [14,20,21] may be interpreted as a form of DAC segmentation in the optical domain. The analytic modeling of the Seg-eDAC|MP-oDAC topologies is deferred to upcoming publications.
It is our hope that the analytical toolbox developed here may serve as a common-modeling-language bridging between the devices and circuits and the wireless/optical communication tech-communities.
Author Contributions
Conceptualization, M.N.; methodology, M.N.; software, M.N.; validation, M.N. and I.T.; formal analysis, M.N.; investigation, M.N.; resources, I.T.; data curation, M.N.; writing—original draft preparation, M.N. and I.T.; writing—review and editing, I.T. and M.N.; visualization, M.N.; supervision, I.T.; project administration, I.T.; funding acquisition, I.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work has received funding from the EU’s Horizon Europe SNS programme under FLEX-SCALE project, Grant Agreement No. 101096909.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. “Anchor” Proposition 1 Derived from Pelgrom’s Transistor Mismatch Model
Proof of Proposition 1.
A paramount insight stemming from Pelgrom et al. [5] is that for any current source on the chip, say , (for s = 0, 1, 2, …, S − 1), its “relative variance” is inversely proportional to the MOS transistor active area (sometimes equivalently restated that “relative STD” is inversely proportional to the square root of the MOS transistor active area),
to first-order (barring higher-order corrections), assuming that all MOS transistors are of equal length and subject to a fixed potential drop. The MOS transistors active areas of the current sources arrays are modeled rectangular, with the current sources of various widths , sharing a common length and a common depth. Since It then follows from Pelgrom’s model (A1) that the relative variance (A1) is inversely proportional to the transistor width:
Equivalently, the relative standard deviation of each current source is inversely proportional to the square root its active area, hence also inversely proportional to the square root of the transistor active region width:
The higher-order refined current mismatch models which followed Pelgrom et al. seminal work [5], provided refined additive corrections to the dominant term , but in this work we assume just the dominant term as described by the transistor models above.
Noting that is taken constant, and so is the depth of all active areas constant, it follows that the MOS transistor on-state conductances are proportional to the device widths, , (since the conduction of a surface resistor is proportional to its transverse (cross-sectional) area, and given a fixed depth, this area is proportional to the width, ). And since all MOS transistor active areas are assumed subject to a common voltage drop, then, by Ohm’s law, each mean source current is proportional to the respective source active region conduction, which is turn is proportional to the width, ; thus, so are mean source currents proportional to the active widths (thus proportional to the respective active areas):
To intuitively make this conclusion plausible, note that increasing the transistor width n-fold, amounts (neglecting boundary effects) to side-wise stacking n transistors in parallel, evidently yielding an n-fold increase in current.
Our key assertion (95) in Proposition 1 (the inverse proportionality of the relative variance and the mean for each current source) then logically stems from (A2) as well as from (A4), yielding . To recapitulate, . Now, denoting the coefficient of inverse proportionality between the relative variance and the mean current by , yields
which amounts to the inverse proportionality formulation (97). Multiplying both sides of the second equality in (A5) by and cancelling then establishes the validity of the key rule (95) in Proposition 1 (the proportionality of the source current variances and means):
□
An even simpler derivation of Proposition 1 is possible in the special case of current steering eDACs of the BiWgt type, in which the currents form a geometric sequence with ratio 2, i.e., and wherein the various source currents are realized by parallel connection of nominally identical unary currents sources, , , , , with all having a common same mean. In this case as the currents are IID random variables, it is seen that
and the mean of is also the sum of the means:
Taking the ratio of the variance and the mean we see that for all s = 0, 1, 2, …, S − 1 we have:
i.e., we conclude that in BiWgt eDAC current sources structures wherein there is built a large array of unary sources which are bunched up in subsets of 1, 2, 4, … and are connected in parallel within each subset, then
Remarkably, this derivation holds irrespective of the dependence on the mismatch variance on the area of the transistor (i.e., the formula need not hold for (A10) to be true in this case, as the derivation of (A10) made no assumption except that the unary sources have identical means and are independent; in fact, any other formula for the relative variance as a function of area would have worked all the same.
Appendix B. Detailed Longer Proofs of Theorems, Lemmas and Corollaries
Appendix B.1. Proofs for Section 2
Proof of Corollary 4.
Some of the results were proven in the text above. What remains to complete here is the proof of (134) for UNIP eDACs (of any topology and (non-)uniformity):
Let be the S mean source currents of a UNIP eDAC of any of the considered types. In (122) we have seen that for a generally non-uniform UNIP eDAC,
Let us now evaluate the (arithmetic) average of this variance vector,
where #1 is an evident way to describe the mean of a vector as an inner product of the vector with ; #2 casts the inner product as matrix left-product by the corresponding row vector; #3 has (A11) substituted in for ; #4 is a matrix manipulation bringing the row inside the mean, past the multiplicative scalar.
At this point we may verify the following property of BiWgt UNIP code matrices:
In fact, the left-multiplication of by the row vector amounts to summing up the elements in each of successive columns of ; the sums are then tallied in an 1 × S row vector. But since the elements of are 0|1, summing up the elements in any column yields the #-of-ones in each column of . But for each of the BiWgt code matrices of dimension , it may be verified that half the elements in each column are 1 s (the rest are zeros). The property that there are C/2 ones in each column is readily verified for the UNIP PAM4 code matrix (10) and for the UNIP PAM8 code matrix (14). The general case may be formally proven by induction starting with PAM4 case.
Thus, the sum of elements in each column of the code matrix equals , yielding the S = B elements row vector
Substitution of the last result into equality #4 yields equality #5; equality #6 is a trivial algebraic manipulation; finally, #7 expresses the inner product of with an all-ones vector as a sum of all elements of the vector: . □
Proof of Lemma 3.
have elements 0|1 for UNIP, ±1 for BIB; has elements −1|0|1 for UNIP (indeed, 0 − 0 = 0, 0 − 1 = −1, 1 − 0 = 1, 1 − 0 = 1), elements −2|0|2 for BIP (indeed, (−1) − (−1) = 0, (−1) −1 = −2, 1 − (−1) = 2, 1 − 1 = 0); has elements (−1|0|1)2 = 0|1 for UNIP, elements (−2|0|2)2 = 0|4 for BIP. For UNIP, we have just shown that , the s-th bit of is given by
with the last equality obtained from the last piecewise definition for in (147). It is apparent that a XOR of the two vectors yields :
A derivation similar to that in (A15) for BIP yields
establishing that
. □
Proof of Theorem 2.
Use (117) to obtain the second equality in (148), namely . Divide both sides of this equality by :
where to obtain the c-th component of both sides, the c-th row of on the RHS was identified as . Then substitute the XOR form of (147) for .
The last equality in (152) is obtained by using (77) for the normalized BiWgt UNIP source current vector and (78) for the normalized BiWgt BIP source current.
Finally, (155) elaborates on the BiWgt BIP case of (152). □
Proof of Corollary 5.
- (i)
- (ii)
- using (175):
- (iii)
- using (175):Thus, the translation generated a skew-centrosymmetric vector.
- (iv)
- to construct an example of balanced non-skew-centrosymmetric vectors, start with a skew-centrosymmetric vector and perform any permutation upon it, changing the order of its elements. All permutations will preserve the balancing property (as the sum of elements will not change) but will break the skew-centrosymmetry. The simplest such permutation is a transposition of two elements both in either the first half of the vector or in the second half.
- (v)
- as is specified raised-skew-centrosymmetric, there is a translation generating a skew-antisymmetric balanced vector ; its elements then satisfy:
- (vi)
- assume there exists a translation by yielding skew-centrosymmetricAn alternative elementwise derivation:i.e., we have shown that (or equivalently ).
- (vii)
- as it is given that , for c = 1, 2, 3, …, C, thenThe vector is recognized as a translation by of the vector , and it is apparent that this translation yielded a vector which is skew-centrosymmetric. Thus, it follows that the original vector v must be raised-skew-centrosymmetric, and since the constant shift -t of each element is identified as that implies, that . Then, since , per (176), then it follows that
- (viii)
- as u, v are raised-skew-centrosymmetric it follows thatin particular, for c = 1 and for c = C we have (with second equalities stemming from ):Then, as the FSRs of u, v are specified to be equal, then , ; together with (A24) this implies .
- (ix)
- in light of (viii) it suffices to assume for the two given raised-skew-centrosymmetric vectors, then show that that implies that be skew-centrosymmetric, i.e.,From (A23) (implied by assumed raised-skew-centrosymmetric) along with , it follows that . Then
- (x)
- derivation of (180) for a raised-skew-centrosymmetric vector, v:where the first line stems from (ii); the first equivalence in the second line uses the fact that the ordering of indices reverses under reverse-operator reflections (proven using definition (167)):In the last line in (A27), the mirror-image index definitions were recalibrated from a C-vector to a C − 1-vector (with C − 1 is the length of the step vectors, ), based on the following identities, stemming from definition (167) of mirror-image index:The last expression in (A27) is our sought result.
- (xi)
- inspecting the vector when is (skew)-centrosymmetric it is readily seen that is (skew)-centrosymmetric, respectively. If is centrosymmetric, then so is and adding the constant vector (which is centrosymmetric) preserves centrosymmetry (as centrosymmetry is readily seen to be additive). If is skew-centrosymmetric, then so is centrosymmetric and adding the constant vector yields a raised-centrosymmetric vector. □
Proof of Theorem 3.
- (i)
- let us first present the derivation for a BiWgt UNIP eDAC. Using (5) and (8),where the last equality is readily verified by evaluating the inner product of the dyadic sequence (7) with the all-ones vector,An alternative derivation of (A31) uses as well as (8), as follows:To recapitulate (A31),But the equation , where are Boolean vectors (i.e., have elements 0|1), is readily shown to be equivalent to (this amounts to the radix-number representation being unique), i.e., may be formally “cancelled” from both sides (A33), yielding , (182) elementwise amounting toThus, if , respectively, then , i.e., we have established the sought one’s-complement relation. Now given two bitstrings in one’s-complement relation, their XOR is the all-ones bitstring. This proves (182) for BiWgt UNIP.Proceeding to prove (i) for a ThWgt UNIP eDAC, it suffices to inspect the ThWgt UNIP code matrix and verify that the bitstrings (codewords) in and rows are in one’s-complement relation, , from which remainder of the properties in (182) follow. Thus, for either ThWgt|BiWgt eDACs we have
- (ii)
- to prove the “zero’s complement” property (184) for BIP eDACs, let the generic codeword of a BIP eDAC (be it of the ThWgt|BiWgt topology) be denoted and that of a UNIP eDAC be denoted . Resorting to the UNIP-BIP affine transformation (42), we evaluate the sum :where in the third equality we used the already established one’s complementarity of UNIP eDACs.
- (iii)
- The proof (185) stems from the result (ii) (182), which in turn impliesThe last line is equivalent to following lines:where in the second line in (A38) we used the fact that the ordering of indices reverses under reverse-operator reflections (proven using definition (167)):In the third line we rearranged the equation. In the fourth line the mirror-image index definitions were recalibrated from a C-vector to a C − 1-vector (with C − 1 is the length of the step vectors, ), based on the following identities, stemming from definition (167) of mirror-image index:The last line in (A38) is our sought result (185) on centrosymmetry of the codeword steps.
- (iv)
- write the mirror-image currents, using (2), and add up the two currents:To recapitulate,Using Corollary V-(vii) the constancy of implies that is a raised-skew-centrosymmetric vector with center
- (v)
- Specialize (145) to indices c and , yieldingwhich together with (185) imply , proving the sought steps centrosymmetry (v). □
Appendix B.2. Proofs for Section 3
Proof of Corollary 6.
Result (294) is obtained by interpreting the LSH of (291) as Next, (295) is derived by plugging in the accumulations of DNL samples for and for (per first line in (294)) and simplifying the difference of sums. Finally, (296) is derived by induction. Plugging c = 1 into (296) yields the first step of the induction:
The second equivalent equality is a special case of (295) with c = C 1. Now assuming (296) is true for index c, it is readily shown that it must also be true for index c + 1, i.e., we must prove :
□
Proof of Corollary 7.
(i) Affine transformations leave the INL, DNL invariant:
where first equality (the substitution ) used the fact that depends on J only via the endpoints of J; in the third equality we used the result of Lemma 5, and also used
As for the DNL invariance under affine transformations:
A one-liner alternative proof of the DNL invariance under affine transformations leverages the invariance of the INL under affine transformations, using (295):
We next prove property (ii) the invariance of eDACs of any topology under transitioning from UNIP to BIP polarity:
Thus, we have shown that the output current in the BIP case is obtained from that in the UNIP case by a translation, viewed as an affine transformation of the form (301):
Then, the affine mapping preserves INL, and also preserves DNL.□
Proof of Corollary 8.
- (i)
- from (277) it follows that
- (ii)
- where and (i) were used.
- (iii)
- from (287) it follows that . Since was shown centrosymmetric in (190), , it then follows using the linearity of the inverse operator:An alternative derivation: to show that the DNL vector is centrosymmetric use the observation (302) that the DNL is nothing but a certain affine transformation of the form (181) or (301), acting on the eDAC output steps vector, . Having shown in Theorem 3 (v) (190) that the steps vector of the eDAC output constellation is centrosymmetric, and having shown in Corollary 5 (xi) that centrosymmetry is preserved under an affine transformation of the form (181), it then follows that the DNL must be centrosymmetric.
- (iv)
- to show that the INL vector is skew-centrosymmetric, recall def (299) of INL:It suffices to show that is skew-centrosymmetric (as any proportionality transformation, here scaling by , preserves skew-centrosymmetry). We observe that are both raised-skew-centrosymmetric ( is by Theorem 3 (iv), and is by Lemma 5 (ii)); we next invoke Corollary 5 (ix) which states that when two vectors are both raised-skew-centro-symmetric and they satisfy , , then their difference is skew-centrosymmetric. Here are taken as , which were both seen to be raised-skew-centro-symmetric and they do satisfy ; it then follows from Theorem 3 that is skew-centrosymmetric, then so is INL in (A54).An alternative less abstract but more cumbersome proof follows:From (294), (307) , and (296) we haveFor c = 1 the last two equations reduce to but since the length-C-1 DNL vector is centrosymmetric; thus, i.e., we have established , the first step of an inductive proof.We may continue the inductive proof of , assuming be true. Then, □
Proof of Lemma 6.
To show the equivalence of (314) with , take the mean of definition (277) of the INL, which in light of (314) must come out zero:
Now taking the means of the two Formulas (294) yields
from which it readily follows that □
Proof of Corollary 9.
To show (330) solve the equation for , yielding .
Next recall Formula (326) for the elements of the mean-nominal constellation,
Now, using the last formula is recast as
Using this formula proves (331):
□
Proof of Lemma 5
- (i)
- (ii)
- .The convex coefficients mirror-images at the mirror-image indices are readily evaluated: . To recap:Using Corollary 5 (vii) (178) it follows that the vector is raised-skew-centrosymmetric, and its center is . □
Proof of Theorem 4.
The following three lines (top, mid, bottom lines) are now shown equivalent:
where we recall the definition of perturbation .
The bottom line here reproduces (342) to be proven, assuming the top line (339) of Lemma 7. The mid line is obtained by unary-normalizing (applying rounded hats) onto the top line, and using the linearity and commutativity of the round-hat with the mean and nominal mappings. By commutativity of and nom we mean the property , where the nominal mapping, nom, fits a uniform constellation between two end-points equal to the mean LSL and MSL of a given constellation. The order of the two operations (fitting of a uniform constellation between the end-points, vs. unary-normalization, ) is immaterial since is a discrete convex combination of the endpoints of , which is a linear operation.
Formula (342) is derived from the second line by using the Alt Def of IEV (327). Therefore, in (342) is now established. Taking the mean of the last equation and using in #3 below being deterministic whereas is zero-mean, i.e., , proves :
Note: an alternative derivation of uses
Now, (344) follows from and substituting :
To derive in (343),
with #1 being the definition (see (A64)), and #2 using used the second equality in (342).
To derive the MS additive decomposition (345), use the generic property (A99), making the identifications
The first equality in the IEV-RAMS Formula (346) is directly obtained by arithmetic-averaging both sides of (345) and taking the square root. We also use the following averages
The second equality in (346) is obtained from the first equality in (346) factoring out of the square roots. □
Proof of Lemma 8.
Solving the alternative defining eq. (359), for proves that . The second eq. is derived by scaling both sides of the first one by . Now start with the following two equalities stemming from the commutativity of the three linear operators :
Now apply the perturbation operator (see (A69)) onto both sides of (359):
Now evaluate :
where the last equality in (A71) is justified by (360), under the substitution . Now equating the first and last expressions in (A71) yields the non-intuitive result:
The chain of equalities
is then proven. Formula for the steps perturbation is obtained by scaling both sides of by □
Proof of Theorem 5.
Equation (369) restates (344) for the IEV. The first equality in Equation (370), namely was proven in (368) above. An instructive alternative rederivation of this decomposition of is based on the alt-def (359) of ,
with equivalence #1 obtained by cancelling out the all-ones vectors in the two sides of the first eq., . Note that #3 is not an equivalence but it is rather a one-way implication; thus, the logical flow stems backward from the identity . Derivation of the first-order statistic in (371):
with #1 per first eq. in (369); #2 per linearity of the mean; #3 per (perturbation RVs are ZM); #4 since is deterministic, given by #5 by making the substitution in (328), yielding equality #1 in the chain
with #2 due to being deterministic, i.e., equal its own mean; #3 stems from the commutativity of the mean, nom, operations; #4 stems from definition (274) by plugging in and using commutativity .
Derivation of the first-order statistic in (372):
#1 per alt def (359) of DEV; #2 per linearity of the mean; #3 per commutation of and mean; #4 again per alt def (359) of DEV, albeit under the substitution .
The Mean-Square IEV (373) and DEV (374) are derived, using the IEV and DEV variances
with the DEV variance (expressed in units of ) derived using the alternative definitions of IEV (328) and DEV (359), the invariance (A98) of the variance of any RV under a deterministic shift and the XOR expressions for evaluating . The mean square IEV is then
with #2 using (A99); #3 using (328); #4 using (A98).
The MS DEV is similarly derived,
with #2 using (A99); #3 using (359); #4 using (A98).
The RAMS-IEV results (379) have already been derived in (346).
The RAMS scalar metrics, (378) for the IEV|DEV vectors may be derived in a unified way, from the definition (A102) of RAMS, using and a similar chain of equalities for , finally plugging these results into Itemized IEV-RAMS scalar metrics (379), (380) follow from (378) plugging-in the arithmetic-averaged variances (135):
□
Proof of Theorem 6.
To derive the first equality in (382), recall alt def (327) for the IEV, solving it for the deviation vector , seen proportional to the IEV:
We then have the EVM expressed in terms of the IEV:
with #1 from the EVM def (381); #3 by using the homogeneity of the RAMS functional (A102), for any constant, c; to show #4, use the homogeneity of the generic RoG functional (A103), :
In the last equality the unary-normalization def (see (73)) was used.
The chain of equalities above proves the first equality in (382). The second equality in (382) stems from the Root-Average-Mean Square (RAMS) definition (A102).
To derive the itemized formulas (383) for the proportionality constant , UNIP eDACs (be they ThWgt|BiWgt) generate integer-valued normalized UNIP-PAM-C,
The “center of mass” (arithmetic-average) of this UNIP constellation is readily worked out:
The radius-of-gyration, , of the mean-nominal reference constellation is
BIP eDACs (be they ThWgt |BiWgt) generate the following normalized BIP-PAM-C,
The BIP constellation center of mass is zero (as evident from the anti-symmetry of the nominal BIP constellation),
yielding for the RoG of the normalized mean-nominal reference constellation, :
Remarkably, the RoGs of the normalized UNIP and BIP constellations are identical:
Formulas (383) for as a function of C, then follow.
Now just plug the proportionality constant (383) into (382), yielding,
and simplify by combining the square-roots.
Recalling our Formula (346) for the metric, repeated here,
Use this formula to prove (385).
Formula (386) for unbiased DACs follows by plugging into (385), then simplifying by combining the square-roots: , □
Appendix C. Abbreviations and Notations Used throughout the Paper
The most prevalent abbreviations well as the main mathematical notations used throughout the paper are listed in this subsection:
- n.m, with n,m, integers, is used to denote subsection n.m.
- Mach-Zehnder-Modulator (MZM); Transfer Characteristic (TC) (a sine for the MZM).
- Transmitter (Tx). Receiver (Rx). Direct Digital Drive (DDD).
- Digital to Analog Converter (DAC); Electrical DAC (eDAC);
- Thermometer-Weighted (ThWgt); Binary-Weighted (BiWgt); Segmented (Seg)
- Optical DAC (oDAC). Multi-Parallel oDAC (MPoDAC). Segmented-MZM (SEMZM).
- Trans-Impedance Amplifier (TIA);
- Pulse Amplitude Modulation (PAM). electrical PAM (ePAM); optical PAM (oPAM).
- Unipolar (UNIP)—all constellation levels are non-negative; Bipolar (BIP)—± levels.
- Quadrature Amplitude Modulation (QAM). In-Phase and Quadrature (IQ).
- Integral Nonlinearity (INL); Differential Nonlinearity (DNL)—known eDAC metrics.
- Integral Error Vector (IEV); Differential Error Vector (IEV)—our eDAC metrics.
- Standard Deviation (STD); Relative STD (RSTD). Random Variable (RV).
- Least Significant Level (LSL); Most Significant Level (MSL).
- Full-Scale (FS): FS = MSL − LSL. Full-Scale-Range (FSR): defined as the segment [LSL, MSL].
- Building Block (BB); With Regard To (WRT). Real and Imaginary (Re&Im).
- Equation (eq.). Definition (Def). Independent Identically Distributed (IID).
- Monte Carlo (MC); Symbol Error Rate (SER); Bit Error Rate (BER).
- | denotes OR, e.g., 4|2 means 4 OR 2; a|b|c denotes a OR b OR c for any objects a, b, c.
- v = {a, b, …, z} denotes a column vector with elements a, b, …, z.
- denotes the all-ones column m-vector: .
- m-vector means a vector with m elements.
- denotes an all-ones matrix of dimensions .
- designates the m-th row (n-th colon) of the matrix , as per [13].
- is a diagonal matrix with the elements of arrayed along its diagonal.
- is the sum of elements of the m-vector , and when is a column, .
- denotes the Shur (elementwise) product, , of compatible vectors.
- is the Shur-square: for .
- For any function , and vector , is defined elementwise, e.g., the sine of a vector is the vector of the sines of the elements of the vector.
- means substitute Y for X; means .
- denotes the (stochastic) Mean (expectation) of an RV, R, and more compactly we also use an alternative superscript notation: .
- The mappingis called the “perturbation operator”.
- Any generic RV, , is decomposed as mean, + perturbation, : .
- The variance of R is denoted, and we always have .
- Let be a real-valued random vector. Its variance vector is defined as the vector of variances of its components: . A random vector, , is called “independent” when its elements are independent RVs.
- For any deterministic M-vector, ,denotes the Mean-Square (second-moment element-wise) of a random vector:is the Root-Mean-Square (RMS) of a vector, element-wise (take the Squares of the components, the (stochastic) Means and the (square) Roots).
- denotes the (arithmetic) Average of the sequence .is the Root-Average-Square (RMS) of a vector (Square the components, eval their (arithmetic) Mean and then (square) Root).
- The last RMS and RAS operations may be merged into a single operation extracting a scalar metric representing the random vector, the Root-Average-Mean-Square (RAMS):(take the Squares of the components, the (stochastic) Means, their (arithmetic) Average, and the (square) Root).denotes the Radius-of-Gyration (RoG) of a deterministic vector, essentially its centralized RAS (subtract the average off all components of then evaluate the RAS).
- denotes “it follows that” or “to recapitulate”; Completion of a proof (q.e.d.) is denoted □.
- Other less frequent abbreviations and notations are introduced in the text as needed.
References
- Laperle, C.; O’Sullivan, M. Advances in high-speed DACs, ADCs, and DSP for optical coherent transceivers. J. Light. Technol. 2014, 32, 629–643. [Google Scholar] [CrossRef]
- Chacón, M.O.; Wikner, J.J.; Svensson, C.; Siek, L.; Alvandpour, A. Analysis of energy consumption bounds in CMOS current-steering digital-to-analog converters. Analog. Integr. Circuits Signal Process 2022, 111, 339–351. [Google Scholar] [CrossRef]
- Bosch, A.; Steyaert, M.; Sansen, W. Static and Dynamic Performance Limitations for High Speed D/A Converters, 1st ed.; Springer: Boston, MA, USA, 2004. [Google Scholar] [CrossRef]
- Pelgrom, M.J.M. Analog-to-Digital Conversion; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Pelgrom, M.J.M.; Duinmaijer, A.C.J.; Welbers, A.P.G. Matching properties of MOS transistors. IEEE J. Solid State Circuits 1989, 24, 1433–1439. [Google Scholar] [CrossRef]
- Pelgrom, M. A JSSC classic paper: Matching properties of MOS transistors. IEEE Solid-State Circuits Soc. Newsl. 2005, 10, 6–7. [Google Scholar] [CrossRef]
- Crippa, P.; Turchetti, C.; Conti, M. A statistical methodology for the design of high-performance CMOS current-steering digital-to-analog converters. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2002, 21, 377–394. [Google Scholar] [CrossRef]
- Radulov, G.I.; Heydenreich, M.; van der Hofstad, R.W.; Hegt, J.A.; van Roermund, A.H.M. Brownian-bridge-based statistical analysis of the DAC INL caused by current mismatch. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 146–150. [Google Scholar] [CrossRef]
- Heydenreich, M.; van der Hofstad, R.; Radulov, G. Functionals of brownian bridges arising in the current mismatch in D/A converters. Probab. Eng. Inf. Sci. 2009, 23, 149–172. [Google Scholar] [CrossRef]
- Dumitru, F.S.; Ilie, C.R.; Enachescu, M. Exploring the Effect of Segmentation on INL and DNL for a 10-bit DAC. In Proceedings of the 2020 International Semiconductor Conference CAS, Sinaia, Romania, 7–9 October 2020; pp. 161–164. [Google Scholar] [CrossRef]
- Conroy, C.S.G.; Lane, W.A.; Moran, M.A. Statistical Design Techniques for D/A Converters. IEEE J. Solid State Circuits 1989, 24, 1118–1128. [Google Scholar] [CrossRef]
- Cijan, G.; Tuma, T.; Arpad, B. Modeling and simulation of MOS transistor mismatch. In Proceedings of the 6th Eurosim, Ljubljana, Slovenia, 9–13 September 2007; pp. 1–8. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Introduction to Applied Linear Algebra—Vectors, Matrices, and Least Squares; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Nazarathy, M.; Tomkos, I. Accurate Power-Efficient Format-Scalable Multi-Parallel Optical Digital-to-Analogue Conversion. Photonics 2021, 8, 38. [Google Scholar] [CrossRef]
- Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; Koos, C.; et al. Error vector magnitude as a performance measure for advanced modulation formats. IEEE Photonics Technol. Lett. 2012, 24, 61–63. [Google Scholar] [CrossRef]
- Freude, W.; Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; et al. Quality Metrics for Optical Signals: Eye Diagram, Q-factor, OSNR, EVM and BER. In Proceedings of the ICTON 2012: 14th Int’l Conference on Transparent Optical Networks, Coventry, UK, 2–5 July 2012; p. 1. [Google Scholar]
- Shafik, R.A.; Rahman, M.S.; Islam, A.R.; Korea, S. On the Extended Relationships Among EVM, BER and SNR as Performance Metrics. Available online: https://ieeexplore.ieee.org/document/4178493 (accessed on 29 July 2024).
- Barry, J.; Lee, E.; Messerschmitt, D. Digital Communication, 3rd ed.; Kluwer Academic Publishers: New York, NY, USA, 2004. [Google Scholar]
- Simon, M.; Hinedi, S.; Lindsey, W. Digital Communication Techniques; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Nazarathy, M.; Tomkos, I. Perfect’ PAM4 Serial Digital-Optical Conversion. IEEE Photonics Technol. Lett. 2021, 33, 475–478. [Google Scholar] [CrossRef]
- Nazarathy, M.; Tomkos, I. Energy-Efficient Reconfigurable 4|16|64|256-QAM Transmitter Based on PAM2|4-Driven Optical DACs. IEEE Photonics Technol. Lett. 2022, 34, 1159–1162. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).