A Numerical Study of Microwave Frequency Comb Generation in a Semiconductor Laser Subject to Modulated Optical Injection and Optoelectronic Feedback
Abstract
1. Introduction
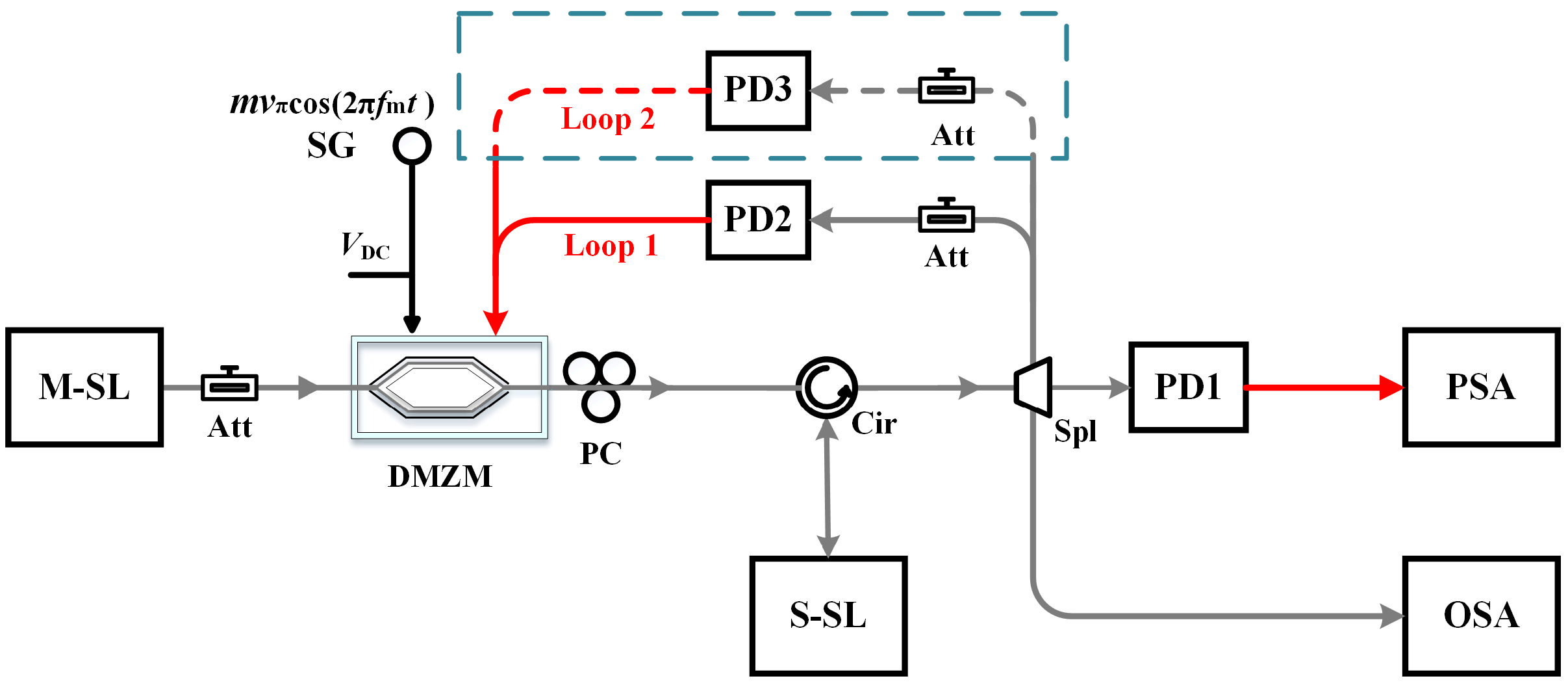
2. Theoretical Model
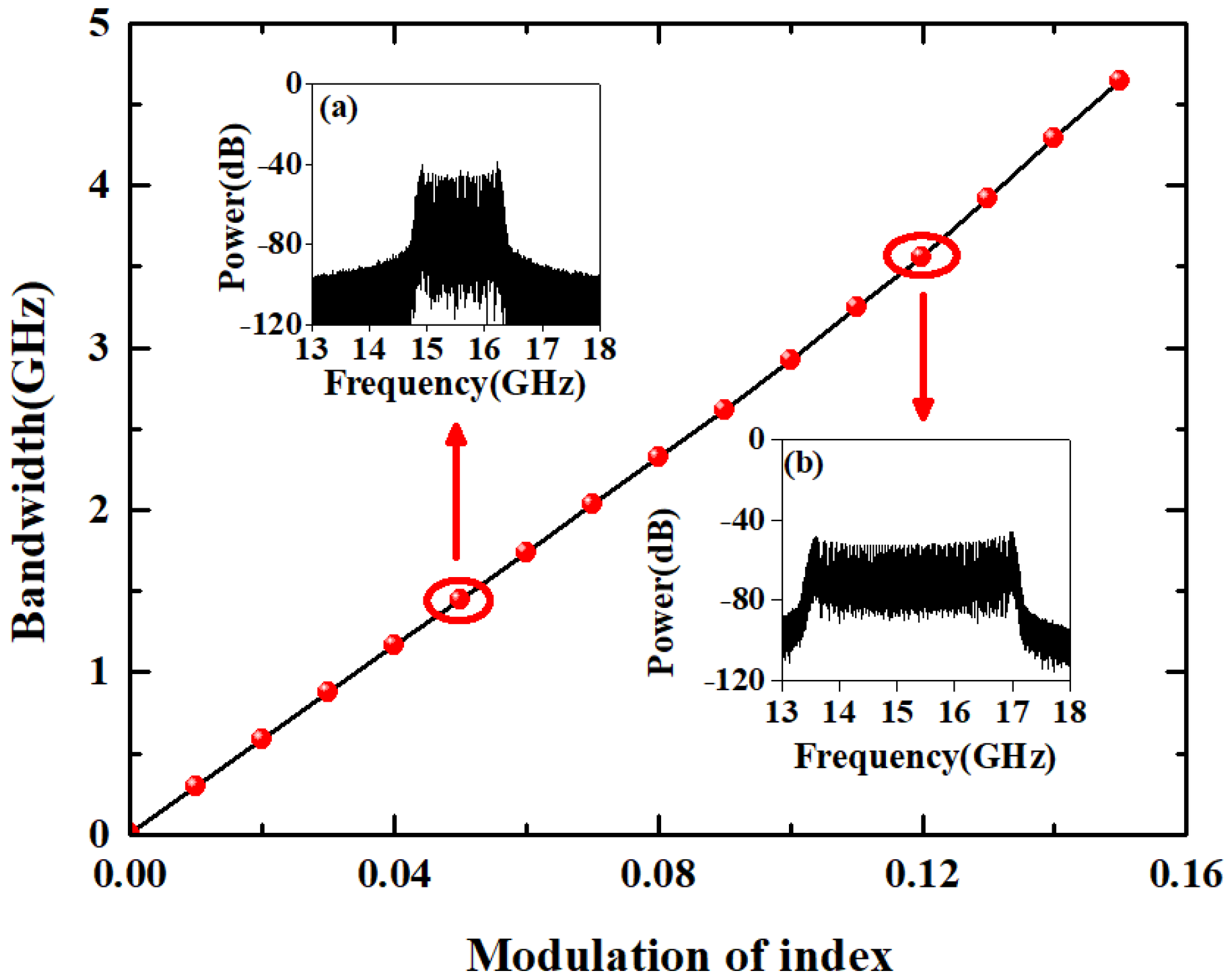
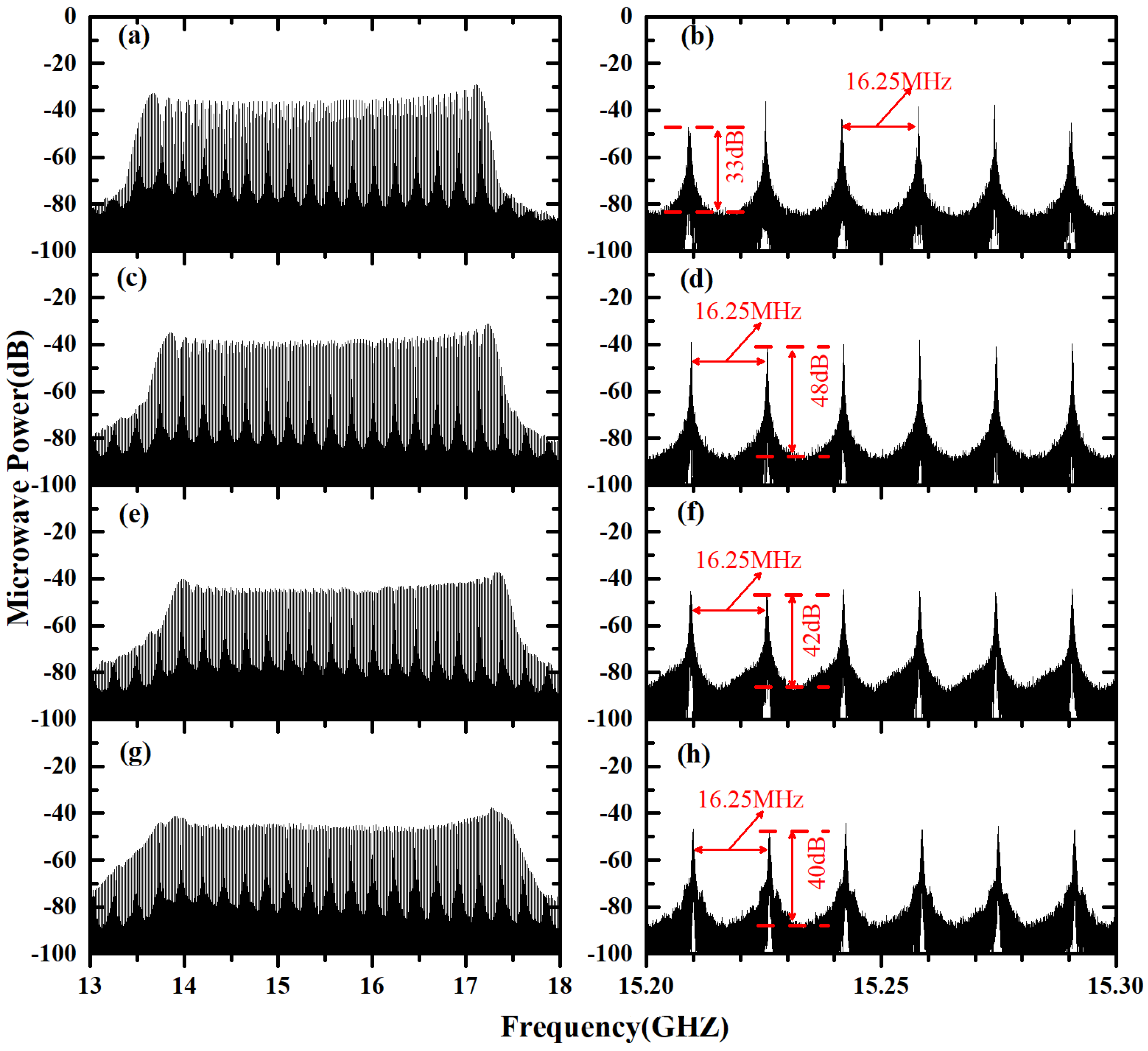
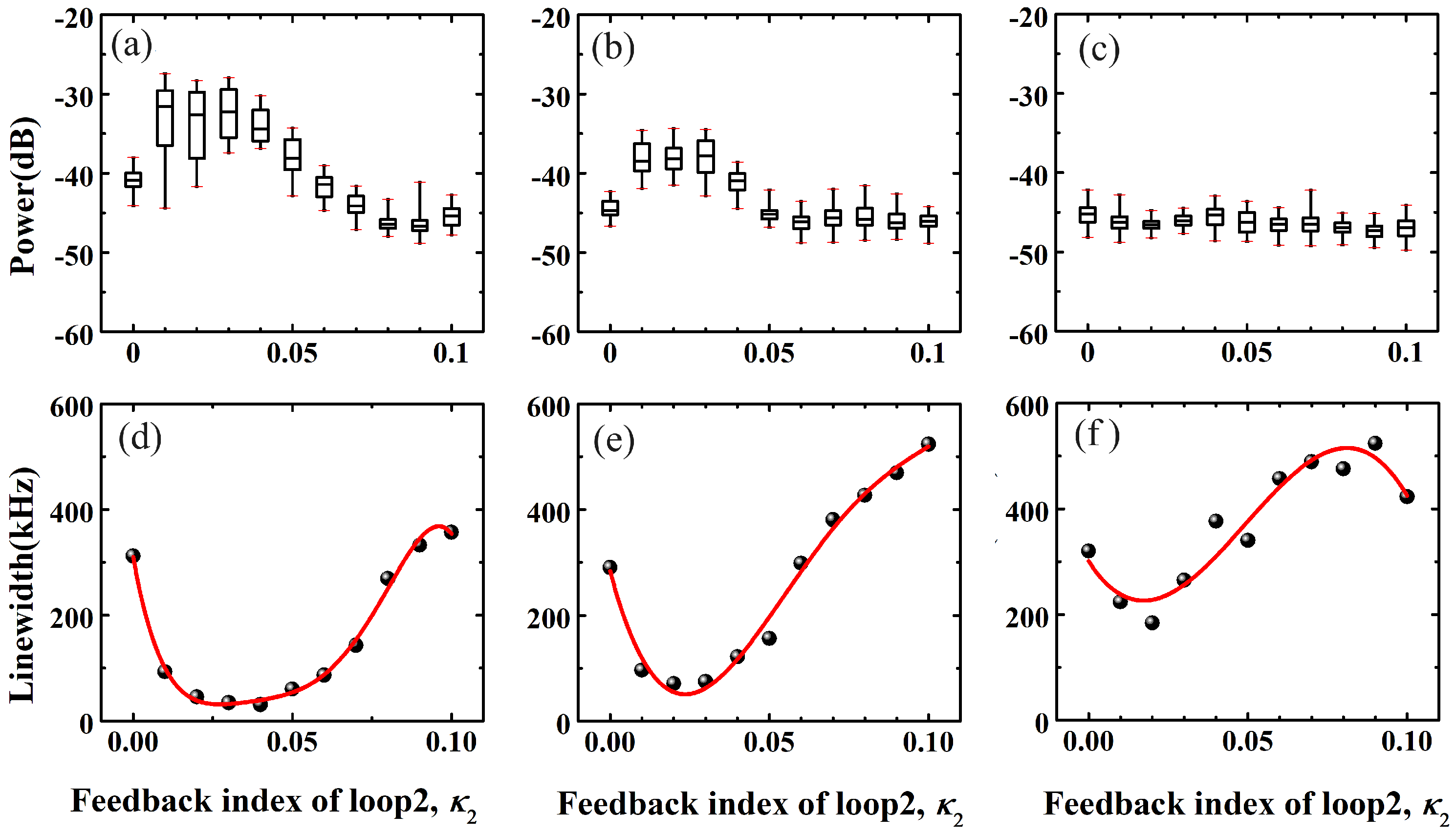
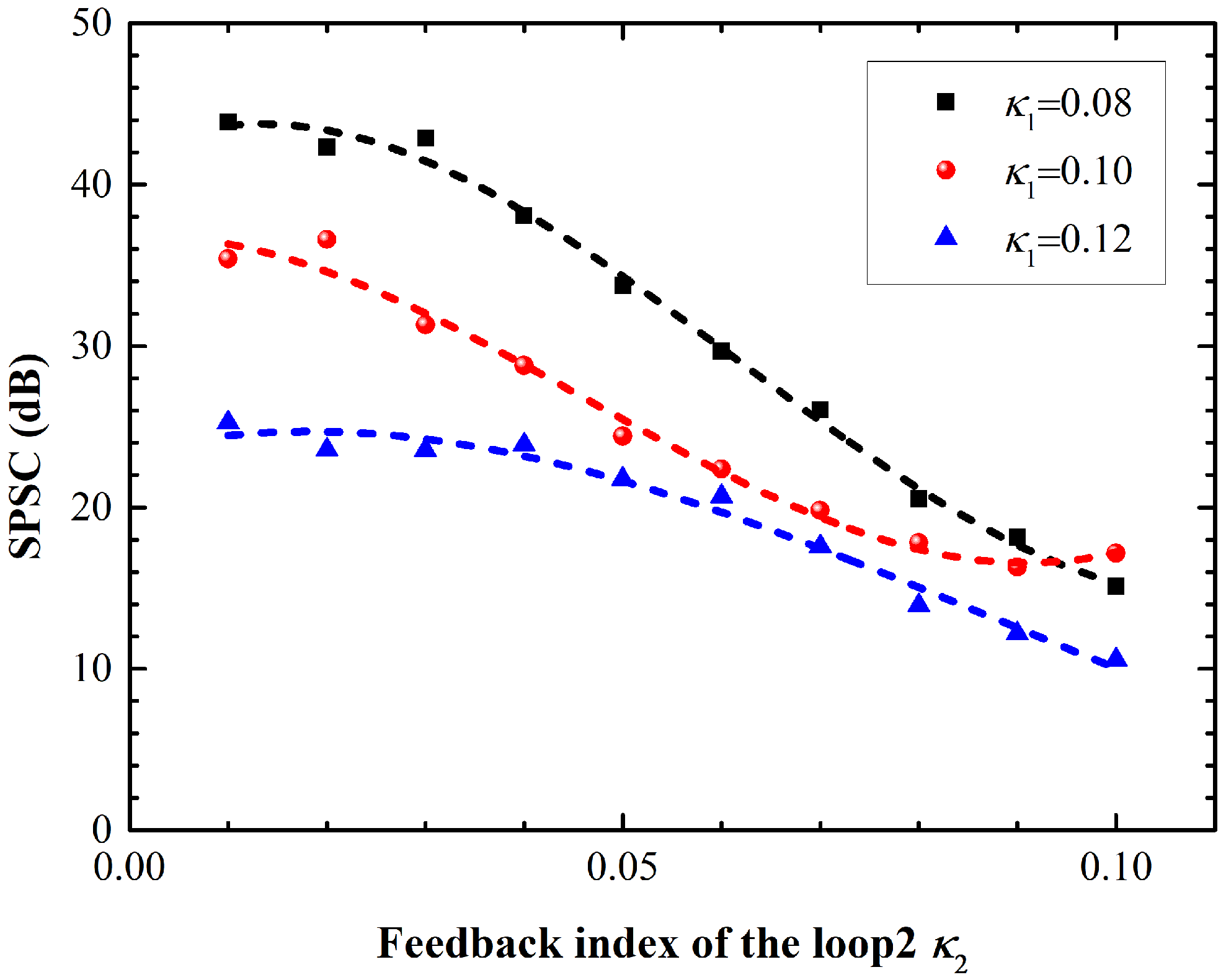
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, F.Y.; Liu, J.M. Diverse waveform generation using semiconductor lasers for radar and microwave applications. IEEE J. Quantum Electron. 2004, 40, 682–689. [Google Scholar] [CrossRef]
- Xu, Z.; Shu, X. Fiber Optic Sensor Based on Vernier Microwave Frequency Comb. J. Lightw. Technol. 2019, 37, 3503–3509. [Google Scholar] [CrossRef]
- Yasui, T.; Yokoyama, S.; Inaba, H.; Minoshima, K.; Nagatsuma, T.; Araki, T. Terahertz Frequency Metrology Based on Frequency Comb. IEEE J. Sel. Topics Quantum Electron. 2011, 17, 191–201. [Google Scholar] [CrossRef]
- Ng’oma, A.; Fortusini, D.; Parekh, D.; Yang, W.; Sauer, M.; Benjamin, S.D.; Hofmann, W.H.E.; Amann, M.C.; Chang-Hasnain, C.J. Performance of a Multi-Gb/s 60 GHz Radio Over Fiber System Employing a Directly Modulated Optically Injection-Locked VCSEL. J. Lightw. Technol. 2010, 28, 2436–2444. [Google Scholar] [CrossRef]
- Hagmann, M.J.; Stenger, F.S.; Yarotski, D.A. Linewidth of the harmonics in a microwave frequency comb generated by focusing a mode-locked ultrafast laser on a tunneling junction. J. Appl. Phys. 2013, 114, 223107. [Google Scholar] [CrossRef]
- Hagmann, M.J.; Efimov, A.; Taylor, A.J.; Yarotski, D.A. Microwave frequency-comb generation in a tunneling junction by intermode mixing of ultrafast laser pulses. Appl. Phys. Lett. 2011, 99, 011112. [Google Scholar] [CrossRef]
- Chan, S.C.; Xia, G.; Liu, J.M. Optical generation of a precise microwave frequency comb by harmonic frequency locking. Opt. lett. 2007, 32, 1917–1919. [Google Scholar] [CrossRef] [PubMed]
- Quirce, A.; de Dios, C.; Valle, A.; Acedo, P. VCSEL-Based Optical Frequency Combs Expansion Induced by Polarized Optical Injection. IEEE J. Sel. Topics Quantum Electron. 2019, 25, 1–9. [Google Scholar] [CrossRef]
- AlMulla, M. Microwave frequency comb generation through optical double-locked semiconductor lasers. Optik 2020, 223, 165506. [Google Scholar] [CrossRef]
- Rosado, A.; Martin, E.P.; Pérez-Serrano, A.; Tijero, J.M.G.; Esquivias, I.; Anandarajah, P.M. Optical frequency comb generation via pulsed gain-switching in externally-injected semiconductor lasers using step-recovery diodes. Opt. Laser Technol. 2020, 131, 106392. [Google Scholar] [CrossRef]
- Doumbia, Y.; Wolfersberger, D.; Panajotov, K.; Sciamanna, M. Tailoring frequency combs through VCSEL polarization dynamics. Opt. Express 2021, 29, 33976–33991. [Google Scholar] [CrossRef] [PubMed]
- Jain, G.; Gutierrez-Pascual, D.; Wallace, M.J.; Donegan, J.F.; Anandarajah, P.M. Experimental Investigation of External Optical Injection and its Application in Gain-Switched Wavelength Tunable Optical Frequency Comb Generation. J. Lightw. Technol. 2021, 39, 5884–5895. [Google Scholar] [CrossRef]
- Wu, B.; Zhao, Q. Research on Optical Mutual Injection to Generate Tunable Microwave Frequency Combs. Photonics 2024, 11, 195. [Google Scholar] [CrossRef]
- Li, W.; Yao, J. Investigation of Photonically Assisted Microwave Frequency Multiplication Based on External Modulation. IEEE Trans. Microw. Theory Tech. 2010, 58, 3259–3268. [Google Scholar] [CrossRef]
- Juan, Y.S.; Lin, F.Y. Ultra broadband microwave frequency combs generated by an optical pulse-injected semiconductor laser. Opt. Express 2009, 17, 18596–18605. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Xia, G.; Tang, X.; Deng, T.; Chen, J.J.; Lin, X.; Li, Y.N.; Wu, Z. Tunable Ultra-Broadband Microwave Frequency Combs Generation Based on a Current Modulated Semiconductor Laser Under Optical Injection. IEEE Access 2017, 5, 17764–17771. [Google Scholar] [CrossRef]
- Xu, X.Q.; Fan, L.; Xia, G.; Wu, Z. Numerical Investigation on Ultra-Broadband Tunable Microwave Frequency Comb Generation Using a Semiconductor Laser under Regular Pulse Injection. IEEE Access 2018, 6, 55284–55290. [Google Scholar] [CrossRef]
- Shen, Z.; Jin, C.; Yang, J.; Zhang, S.; Tang, M.; Wang, K. Method for the generation of microwave frequency combs based on a Vernier optoelectronic feedback loop. Opt. Express 2020, 28, 35118–35127. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, M.; Gao, P.; Zhang, J.; Yin, B.; Wang, C.; Fan, G. Tunable Microwave Frequency Comb Generation Based on Actively Mode-Locked OEO. IEEE Photon. Technol. Lett. 2023, 35, 221–224. [Google Scholar] [CrossRef]
- Zhao, W.; Mao, Y.; Li, Y.; Chen, G.; Lu, D.; Kan, Q.; Zhao, L. Frequency-Tunable Broadband Microwave Comb Generation Using an Integrated Mutually Coupled DFB Laser. IEEE Photon. Technol. Lett. 2020, 32, 1407–1410. [Google Scholar] [CrossRef]
- Lo, K.H.; Hwang, S.K.; Donati, S. Optical feedback stabilization of photonic microwave generation using period-one nonlinear dynamics of semiconductor lasers. Opt. Express 2014, 22, 18648–18661. [Google Scholar] [CrossRef]
- Zhuang, J.; Chan, S.C. Tunable photonic microwave generation using optically injected semiconductor laser dynamics with optical feedback stabilization. Opt. Lett. 2013, 38, 344–346. [Google Scholar] [CrossRef]
- Ji, S.; Hong, Y.; Spencer, P.S.; Benedikt, J.; Davies, I. Broad tunable photonic microwave generation based on period-one dynamics of optical injection vertical-cavity surface-emitting lasers. Opt. Express 2017, 25, 19863–19871. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, J.; Chan, S.C. Phase noise characteristics of microwave signals generated by semiconductor laser dynamics. Opt. Express 2015, 23, 2777–2797. [Google Scholar] [CrossRef] [PubMed]
- Alharthi, S.S. Broad tunable photonic microwave signal generation using optically-injected 1310 nm spin-VCSELs. Results Phys. 2022, 44, 106007. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, P.; Li, K.; Bao, H.; Li, N. Photonic generation of high-performance microwave frequency combs using an optically injected semiconductor laser with dual-loop optoelectronic feedback. Opt. Lett. 2021, 46, 4622–4625. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Zhang, F.; Guo, Q.; Li, S.; Pan, S. Reconfigurable Radar Waveform Generation Based on an Optically Injected Semiconductor Laser. IEEE J. Sel. Topics Quantum Electron. 2017, 23, 1–9. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, F.; Pan, S. Generation of Linear Frequency-Modulated Waveforms by a Frequency-Sweeping Optoelectronic Oscillator. J. Lightw. Technol. 2018, 36, 3927–3934. [Google Scholar] [CrossRef]
- Zhuang, J.; Li, X.Z.; Li, S.; Chan, S.C. Frequency-modulated microwave generation with feedback stabilization using an optically injected semiconductor laser. Opt. Lett. 2016, 41, 5764–5767. [Google Scholar] [CrossRef]
- Xue, C.; Ji, S.; Hong, Y.; Jiang, N.; Li, H.; Qiu, K. Numerical investigation of photonic microwave generation in an optically injected semiconductor laser subject to filtered optical feedback. Opt. Express 2019, 27, 5065–5082. [Google Scholar] [CrossRef]
- Kim, H.; Gnauck, A.H. Chirp characteristics of dual-drive. Mach-Zehnder modulator with a finite DC extinction ratio. IEEE Photon. Technol. Lett. 2002, 14, 298–300. [Google Scholar]
- Simpson, T.B.; Liu, J.M.; Huang, K.F.; Tai, K. Nonlinear dynamics induced by external optical injection in semiconductor lasers. Quantum Semiclass. Opt. 1997, 9, 765–784. [Google Scholar] [CrossRef]
- Ji, S.; Xue, C.; Valle, A.; Spencer, P.S.; Li, H.; Hong, Y. Stabilization of Photonic Microwave Generation in Vertical-Cavity Surface-Emitting Lasers with Optical Injection and Feedback. J. Lightw. Technol. 2018, 36, 4347–4353. [Google Scholar] [CrossRef]
- Xue, C.; Chang, D.S.; Fan, Y.; Ji, S.; Zhang, Z.; Lin, H.; Spencer, P.S.; Hong, Y. Characteristics of microwave photonic signal generation using vertical-cavity surface-emitting lasers with optical injection and feedback. J. Opt. Soc. Am. B 2020, 37, 1394–1400. [Google Scholar] [CrossRef]
- Brunel, M.; Vallet, M. Pulse-to-pulse coherent beat note generated by a passively Q-switched two-frequency laser. Opt. Lett. 2008, 33, 2524–2526. [Google Scholar] [CrossRef]




| Parameters | Symbol | Value |
|---|---|---|
| The cavity decay rate | 0.536 ps−1 | |
| The nonlinear carrier relaxation rate | 19.1 ns−1 | |
| The differential carrier relaxation rate | 7.53 ns−1 | |
| The spontaneous carrier relaxation rate | 5.96 ns−1 | |
| Linewidth enhancement factor | b | 3.2 |
| Frequency detuning of the optical injection | 7 GHz | |
| Injection strength | 0.13 | |
| FWHM of the free-running slave SL | 30 MHz | |
| Half-wave voltage of the DMZM | 1 V | |
| DC bias voltage | ||
| Normalized bias current | J | 1.222 |
| Modulation index of the upper arm | m | 0.12 |
| Modulation frequency of the upper arm | 16.25 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Chen, W.; Zhu, B.; Zhang, Z.; Hong, Y. A Numerical Study of Microwave Frequency Comb Generation in a Semiconductor Laser Subject to Modulated Optical Injection and Optoelectronic Feedback. Photonics 2024, 11, 741. https://doi.org/10.3390/photonics11080741
Xue C, Chen W, Zhu B, Zhang Z, Hong Y. A Numerical Study of Microwave Frequency Comb Generation in a Semiconductor Laser Subject to Modulated Optical Injection and Optoelectronic Feedback. Photonics. 2024; 11(8):741. https://doi.org/10.3390/photonics11080741
Chicago/Turabian StyleXue, Chenpeng, Wei Chen, Beibei Zhu, Zuxing Zhang, and Yanhua Hong. 2024. "A Numerical Study of Microwave Frequency Comb Generation in a Semiconductor Laser Subject to Modulated Optical Injection and Optoelectronic Feedback" Photonics 11, no. 8: 741. https://doi.org/10.3390/photonics11080741
APA StyleXue, C., Chen, W., Zhu, B., Zhang, Z., & Hong, Y. (2024). A Numerical Study of Microwave Frequency Comb Generation in a Semiconductor Laser Subject to Modulated Optical Injection and Optoelectronic Feedback. Photonics, 11(8), 741. https://doi.org/10.3390/photonics11080741







