Abstract
Optical fiber sensors consist of multiple Mach–Zehnder (MZ) interferometers and are common in the protection of different compounds. These sensors are very sensitive to any intrusion or threat. However, the spatial resolution is proportional to the number of MZ interferometers along the sensor. Consequently, a long sensor with a high resolution can be costly. In this paper, we suggest replacing the cascaded MZ interferometers with a couple of adjacent fibers, each of which have a harmonically varying refractive index. In this theoretical study, it is shown that two fibers with varying refractive indices demonstrate a sensitivity equivalent to that of multiple MZ interferometers. Furthermore, when the coupling coefficient between the fibers is weak, an analytical expression can be derived for the transmission between the fibers. This transmission reveals a quantization rule for which the light coupling between the two fibers vanishes.
1. Introduction
Optical fiber sensors are used in numerous applications, such as detecting building, bridge, and airplane fractures [1,2,3,4,5]. They are also effective for detecting intrusions in protected areas like fences, walls, and military or government compounds (see, for example [6,7,8,9]).
The methods vary depending on the specific application. For example, Brillouin optical fiber sensors are suitable for covering long perimeters where high detection resolution is not required [9,10]. However, for higher sensitivity, fiber Mach–Zehnder interferometers can be strategically placed along the sensor [11,12]. If the spatial resolution is not critical, a single interferometer may suffice (see Figure 1a). When a perturbation occurs within the interferometer’s domain, the interference signal can be detected at the opposite ends of both fibers.
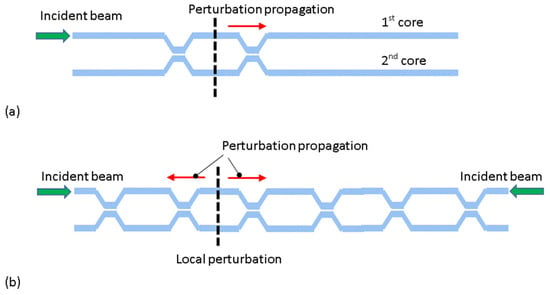
Figure 1.
The optical fiber sensor consists of a couple of fibers with integrated MZ interferometers. (a) A single interferometer, (b) multiple interferometers.
To enhance spatial resolution, multiple interferometers can be incorporated along the sensor. In this case, counter-propagating beams should be launched into the sensing device (see Figure 1b). This configuration allows the interference signal to propagate in both directions, enabling the exact location of the perturbation to be determined by measuring the delay (using correlation) between the two signals at both ends of the fibers.
While these types of sensors can be highly sensitive and perform well, their main disadvantage is their cost due to the need to integrate multiple couplers. Consequently, high-definition sensors can be prohibitively expensive. Clearly, the couplers are the Achilles’ heel of this device [13]. Typically, the couplers are constructed by attaching the two fibers at a specific distance to achieve the required coupling ratio, usually 50:50. As Figure 1b suggests, the spatial resolution is determined by the length of the MZ arms. The shorter the arms, the better the resolution.
There are other methods to create coupling points between adjacent fibers, but not all couplers are efficient, and achieving a precise 50:50 coupling ratio is not always possible. However, since these couplers are used for sensing rather than power transmission, the exact coupling ratio is not critical. It is possible, for example, to connect alternately single mode fiber sections to multi-mode fiber ones (see, for example, other sensing applications using these fibers in Refs. [14,15]). However, this configuration requires time-consuming (and therefore costly) splicing techniques.
This paper proposes controlling the coupling between the two fibers by varying the refractive index along the fibers instead of changing the distance between them. In this configuration, the distance between the fibers can remain fixed.
A two-fiber system, where the refractive index changes, has a mathematically analogous system in Quantum Mechanics. In this analogy, the longitudinal dimension of the fibers corresponds to time in the quantum system, and the two fibers represent a double-well potential. Thus, the process in which beam power oscillates between two fibers (with homogeneous refractive index) is analogous to the process where the probability of finding a particle in one of the (unvarying) wells oscillates over time [16]. It should be stressed that the analogy is purely mathematical since the quantum Schrödinger equation resembles the paraxial approximation of Maxwell’s wave equation mathematically.
Therefore, studies conducted on the quantum system can be applied to the optical fiber system. Specifically, if the refractive index difference between the fibers varies linearly along the propagation direction, then the power transmission coefficient between the two fibers (i.e., the amount of power that crosses from one fiber to the next) is equivalent to the probability of jumping from one well to the next in the quantum analog, provided the energy gap between the wells varies linearly with time. This quantum problem has been well-studied in the literature (see Refs. [17,18] and references therein). To date, this is the only temporal scenario of the two-coupling state for which an analytical solution has been derived. However, it was found numerically in the 90s that if the energy difference between the two wells is modified harmonically, the transmission between the wells can be completely suppressed [19,20,21]. Despite the barrier between the wells remaining unchanged, at certain frequencies, the particle can be localized on one side of the barrier, effectively remaining in one of the wells. In these cases, tunneling between the varying wells is completely suppressed.
A related phenomenon was discovered for an oscillating delta function. It was found that while the transmission through a stationary delta function cannot be zero, if the delta function oscillates, the transmission can be completely suppressed at a certain frequency [22]. At the same time, it was conjectured that a temporally varying narrow potential well inside an opaque potential barrier could facilitate tunneling through several effects (e.g., the elevator effect) [23,24]. However, numerical solutions revealed that the system is more complex than initially thought. In most cases, the incoming particle is excited and exits the barrier with energy close to the barrier’s potential height. Yet, at certain incoming energy levels, this activation is highly suppressed [25,26].
It was realized that this effect is more generic, caused by destructive interference between temporal events, and is not restricted to harmonic changes [27]. Consequently, a quantization rule was formulated, where the energies at which suppression occurs depend on a quantum number. Moreover, it was found that under certain conditions, the current can be not only suppressed but can vanish completely [28].
The propagation of wave packets in fibers is governed by the paraxial approximation of Maxwell’s wave equation [29]. Since the Schrödinger equation is mathematically equivalent to the paraxial approximation, a similar quantization rule should appear in the optical analogy of transmission between adjacent fibers. In fact, zero transmission in the optical regime due to harmonic changes in the refractive index has been demonstrated in a waveguide with a temporally varying dielectric constant [30] and even in dielectric grating [31]. In both cases, the effect exists even for arbitrarily weak modulation amplitudes.
Returning to the optical analogy of the double-well scenario, there should be a specific criterion where the transmission between adjacent fibers can be suppressed, provided the refractive index varies harmonically along the propagation direction.
The main objective of this theoretical study is to analyze this effect and leverage its high sensitivity to modulation frequency to develop a highly sensitive optical sensor.
2. The Model under Study
The system is governed by the Paraxial approximation of the Maxwell’s wave equation [29]
where is the slowly varying (in the propagation z-direction) amplitude of the electromagnetic field , is the transverse Laplacian, is the propagation direction, is the mean wavenumber in the fiber’s cores ( is the mean refractive index in the cores and is the electromagnetic field’s wavelength in Vacuum), and . For simplicity, we can use the Schrödinger notation, i.e., we define an optical analogy of a potential , and then (1) reads
In the case under study, there are two fiber’s cores (see Figure 2) , and therefore V(r) can be written as a superposition of the left (“1”) and the right (“2”) cores, i.e.,
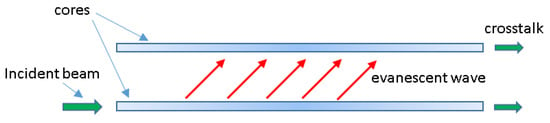
Figure 2.
Two adjacent fiber cores, where evanescent waves (symbolized by the red arrows) cause crosstalk between them.
Furthermore, we adopt the quantum mechanical notation of the propagation modes (states in the quantum terminology): propagation in core “1” and “2” will be denoted by the kets and , with the propagation coefficients and , respectively, i.e.,
Similarly, the electromagnetic field can be written as a superposition of the two solutions at the different fibers
and are the coefficients of the propagation state in the first and second fiber, respectively.
Substituting this solution in (2), the Shrödinger dynamics turn into coupled linear differential equations
and are the overlap integrals between the different modes in the presence of the fiber. Consequently, they decrease exponentially with the distance between the fibers.
It is useful to adopt the dimensionless parameters , and to reformulate (6) into
To calculate the crosstalk between the two fiber’s cores, one can start with the initial condition
This initial condition represents the fact that initially the beam is restricted to the first fiber.
Equation (7) can be solved numerically. For some analytical insight, these equations can be simplified by adding a phase to the coefficients, i.e.,
yielding the following simple set of equations
In case the two fibers are similar on average, then (10) can be rewritten as
where and are the coupling coefficient between the fiber’s cores (the overlapping integral).
3. Exactly Solvable Case (I): Linear Profile
Equation (11) is generic for any profile of refractive index difference , provided it is slowly varying (its spatial derivative is considerably smaller than the beam’s wavenumber). The simplest, and the only exactly solvable case, is when the profile varies linearly, i.e.,
As was said above, this scenario was well studied in the quantum mechanical context.
Originally, the Landau–Zener formula [17,18] calculates the probability for a particle, initially located in one well, to be transmitted to the second well. In the optical analogy, this formula calculates the amplitude transmission coefficient from one fiber to the next [32]:
and therefore the power transmission is
Since depends exponentially on the distance between the fibers, this configuration can be used as a sensitive sensor device, provided . However, in this case, the transferred power is exponentially small. Therefore, since we already focused on the weak transmission regime, we can formulate a generic formula for any profile—not necessarily a linear one. Consequently, we can find profiles that show higher sensitivity.
4. Generic Formula for Weak Transmission Coefficient
When the transmission between the two cores is suppressed at the vicinity of the suppression point, then . Therefore, one can take the approximation , yielding the following solution for any
For long fibers (in comparison to the reciprocal of the refraction index change), the total transmission coefficient between the cores can be approximated by
Therefore, the transmission coefficient at the end of the fiber is approximately
Moreover, from (17), one can calculate the criterion for suppressed transmission, in which case
Equation (18) has the exact solutions only in special scenarios. In general, these integrals have no analytical solutions.
5. Analytically Solvable Approximations
5.1. Case II: Parabolic Profile
Let us begin with the simplest scenario, in the case where the refractive index changes gradually in a parabolic shape (see Figure 3a), i.e.,
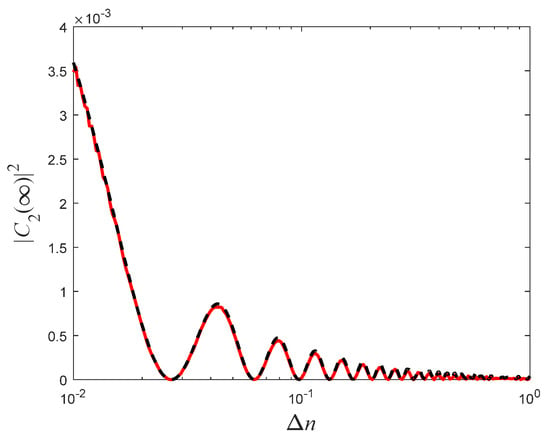
Figure 3.
Transmission coefficient as a function of . The solid (red) curve represents the exact numerical solution, while the dashed (black) curve represents the analytical approximation. The simulation was taken for the parameters , , and .
In this case, the integral (17) reads
where Ai(x) stands for the Airy function (see Formula 10.4.32 in Ref. [33]).
Therefore, unlike the linear profile, when the profile is parabolic, the transmission coefficient is much more sensitive to the distance (Z in this case). The transmission coefficient vanishes when
where is the nth zero of the Airy function .
In the case where , then Equation (20) can be approximated by the function (see formula 10.4.60 in Ref. [33])
Equation (22) vanishes for , which satisfies
Qualitatively, Equation (22) shows similar behavior to the transmission coefficient of a MZ interferometer. The main difference is that the maxima, which is proportional to , is considerably smaller than the MZ case; nevertheless, the minima in both cases is zero. Therefore, in the vicinity of these minima, where the transmission coefficient can be approximated by
the sensor sensitivity can be very high.
As can be seen in Figure 3 and Figure 4, the analytical expression (20) shows high agreement with the exact numerical analysis, as long as the transmission coefficient is small enough, which is a requisite condition for the validity of the derivation.
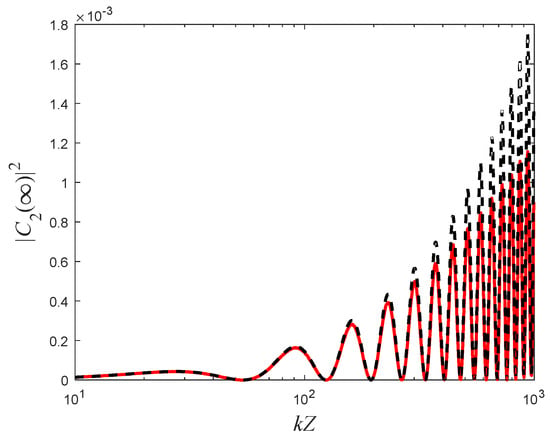
Figure 4.
Transmission coefficient as a function of . The solid (red) curve represents the exact numerical solution, while the dashed (black) curve represents the analytical approximation. The simulation was taken for the parameters , , and .
5.2. Case III: Harmonic Profile
In the previous section, it was shown that when the difference in the refractive index between the fibers follows a parabolic profile, the transmission from one fiber to the next exhibits sensitivity similar to that of an MZ interferometer. Therefore, to improve spatial resolution, the refractive index profile can be harmonic instead of parabolic. Specifically, each fiber core would have a harmonic refractive index profile, e.g., one with a profile
, while the other has its out-of-phase counterpart, i.e., (see Figure 5). Therefore, the refractive index difference reads
where , and is the wavelength of the harmonic profile (see Figure 5).
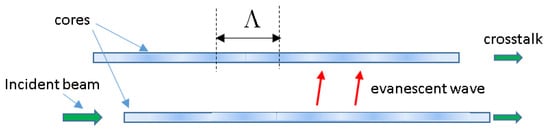
Figure 5.
Coupled fibers’ cores with out-of-phase harmonic profiles.
In this case, the integral in Equation (17) should be limited to an integer number of periods. In this case, using Equation (9.1.18) of Ref. [33], the transmission coefficient at the end of a fiber of length reads
In Figure 6, we see again that the interference pattern is maintained, and that the approximation (26) shows high agreement with the exact numerical solution.
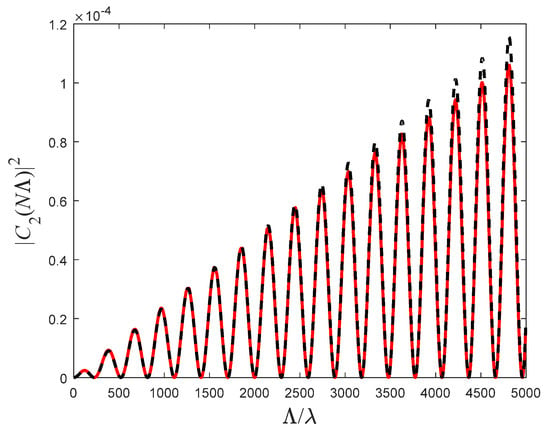
Figure 6.
The transmission coefficient as a function of the period for periods. The solid (red) curve represents the exact numerical solution, while the dashed (black) curve represents the analytical approximation (26). The simulation was taken for the parameters , , and .
In the regime where , the periodicity reappears. Using Equation (9.2.1) of Ref. [33]
Therefore, a similar quantization rule for suppression appears
and at the vicinity of these zero transmission points
Consider the similarity between Equations (27) and (28) and their MZ counterpart: and , respectively, (where in the MZ case represents the MZ’s arm’s length and stands for the refraction index difference between the two arms). Therefore, the sensitivity and behavior are very similar. Moreover, as in the MZ case, the spatial resolution is determined by the wavelength ; the shorter the wavelength, the better the spatial resolution.
Equations (26)–(28) teach that the main experimental results depend on a single parameter , which is a product of the relative change in refractive index and the ratio between the wavelengths . All the other parameters of the system, such as the distance between the fiber’s cores, the diameter of the cores, the absolute values of the refractive index, and even the specific propagation mode, are all encapsulated in the single parameter . Therefore, different systems with different parameters will exhibit similar behavior (up to a prefactor ) provided they have the same .
It should be emphasized that these optical fiber sensors can be applied to any sensing scenario where cascaded MZ interferometers are currently used, such as strain-sensitive applications. For instance, they can detect subtle strains caused by mechanical vibrations or thermal changes.
The key distinction between these sensors (Figure 5) and conventional MZ interferometers (Figure 1b) lies in sensitivity mechanisms. MZ interferometers are highly sensitive to differences between their two arms, whereas these sensors detect variations in the harmonic pattern period. Therefore, these sensors can be more compact than MZ counterparts.
The best ways to fabricate these fibers require more detailed research. However, in principle, the Bragg grating technology can be adopted, i.e., gradually changing the refractive index by applying UV light. Since the UV illumination can take place in the transverse direction, the profile fabrication can be automated completely (see, for example, Refs. [34,35,36,37]). Moreover, the two fiber cores can be illuminated simultaneously using different beams or a tunable mask. The automated fabrication eliminates the need for expensive splicing. Initially, this technology will be costly due to the need for new fabrication devices. However, as the technology matures, the fabrication cost can be reduced to nearly that of an ordinary fiber, i.e., less than USD 1 per meter. This is 100 times lower than the cost of a Mach–Zehnder-based optical fiber sensor with a 1 m spatial resolution. Currently, there is no simple method to automate the placement of couplers between the two fibers every meter, which is required for the MZ case. Additionally, the couplers themselves increase the cost by at least a factor of 10, and the work required for their integration is even more expensive.
It should be noted that the fibers do not need to be identical. The difference between two harmonic profiles is harmonic regardless of their specific amplitudes and phases. Even the periodicity does not have to be the same. Furthermore, since the main effect is independent of the coupling coefficient, it can vary along the fiber without affecting the device’s sensitivity.
6. Summary
Cascaded MZ interferometer optical fiber sensors are highly sensitive to strains within the fibers, making them suitable for applications requiring high sensitivity. However, achieving improved spatial resolution typically necessitates multiple interferometers, significantly increasing sensor costs. This paper introduces a more cost-effective optical fiber sensor design where the distance between coupled fibers remains constant, while the refractive index profile along the fibers varies harmonically in the propagation direction.
It is demonstrated that sensor sensitivity is influenced by the period of this harmonic variation, analogous to how MZ sensors depend on the relative distance between interferometer arms. Therefore, the proposed sensors not only offer affordability but also potential compactness.
Furthermore, it is shown that in scenarios with very weak coupling between the fibers, an analytical expression can be derived for the transmission coefficient between them.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study (numerical analysis is included) are included in the article. The numerical parameters are specified under the figures. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mhdi, B.R.; Aljaber, N.A.; Aljwas, S.M.; Khalid, A.H. Design and Construction Optical Fiber Sensor System for Detection the Stress and Fine Motion. Int. J. Nano Devices Sens. Syst. (IJ-Nano) 2012, 1, 25–33. [Google Scholar] [CrossRef]
- Vargas-Silva, G.; Hernández, R. Fiber optic sensor network for monitoring new building cladding systems. In Fourth European Workshop on Optical Fibre Sensors; SPIE: Bellingham, WA, USA, 2010; Volume 7653, pp. 548–551. [Google Scholar]
- Kressel, I.; Balter, J.; Evenhaim, S.; Leibovich, H. Health and usage monitoring of aging helicopter structure using fiber Bragg grating sensor net. In Proceedings of the 51st Israel Annual Conference on Aerospace Sciences, Tel-Aviv and Haifa, Israel, 23–24 February 2011; Volume 1, pp. 144–145. [Google Scholar]
- Sengupta, S.; Basumallick, N.; Bhattacharya, S.; Biswas, P.; Bhattacharya, S.; Bandyopadhyay, S. Athermal Fiber Bragg Grating Strain Sensor Packages for Health Monitoring of Railway Pantograph. In Proceedings of the 12th International Conference on Fiber Optics and Photonics, Delhi, India, 13–16 December 2014; OSA Technical Digest (Online) Paper S5A.16. Optica Publishing Group: Washington, DC, USA, 2014. [Google Scholar]
- Hill, W.D.; Williams, J.J.; Lees, G. Fiber-Optic Sensing: Smart Fiber-Optic Sensing Systems Enhance Physical Border Walls and Fences; Laser Focus World: Nashua, NH, USA, 2013. [Google Scholar]
- Bryson, C.; Hawkes, I. Interferometric sensor system for security applications. In Proceedings of the SPIE Tenth International Conference on Optical Fibre Sensors, Glasgow, Scotland, 11–13 October 1994; SPIE: Bellingham, WA, USA, 1994; Volume 2360, pp. 485–488. [Google Scholar]
- Bryson, C.; Hawkes, I. Fibre optic sensor system for integrated perimeter protection. In Proceedings of the IEEE European Convention on Security and Detection, Brigton, UK, 16–18 May 1995; Volume 408, pp. 188–192. [Google Scholar]
- Allwood, G.; Wild, G.; Hinckley, S. Optical Fiber Sensors in Physical Intrusion Detection Systems: A Review. IEEE Sens. J. 2016, 16, 5497–5509. [Google Scholar] [CrossRef]
- Galíndez, C.; López-Higuera, J.M. Brillouin Distributed Fiber Sensors: An Overview and Applications. J. Sens. Hindawi Publ. Corp. 2012, 2012, 204121. [Google Scholar]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Kirkendall, C.K.; Dandridge, A. Overview of high performance fibre-optic sensing. J. Phys. D Appl. Phys. 2004, 37, R197–R216. [Google Scholar] [CrossRef]
- Wild, G.; Hinckley, S. Acousto-ultrasonic optical fiber sensors: Overview and state-of-the-art. IEEE Sens. J. 2008, 8, 1184–1193. [Google Scholar] [CrossRef]
- Kashima, N. Passive Optical Componenets for Optical Fiber Transmission; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Leung, C.Y.; Chang, I.F. Optical fiber line-sensor based on intermodal interference. In Proceedings SPIE 14th International Congress of the International Commission for Optics, QC, Canada, 24–28 August 1987; SPIE: Bellingham, WA, USA, 1987; Volume 813, pp. 365–366. [Google Scholar]
- Pan, K.; Uang, C.-M.; Cheng, F.; Yu, F.T. Multimode fiber sensing by using mean-absolute speckle-intensity variation. Appl. Opt. 1994, 33, 2095–2098. [Google Scholar] [CrossRef]
- Bohm, D. Quantum Theory; Dover Publications: New York, NY, USA, 1979. [Google Scholar]
- Vutha, A.C. A simple approach to the Landau–Zener formula. Eur. J. Phys. 2010, 31, 389. [Google Scholar] [CrossRef]
- Wittig, C. The Landau−Zener Formula. J. Phys. Chem. B 2005, 109, 8428–8430. [Google Scholar] [CrossRef]
- Kayanuma, Y. Role of phase coherence in the transition dynamics of a periodically driven two-level system. Phys. Rev. A 1994, 50, 843. [Google Scholar] [CrossRef]
- Kayanuma, Y. Stokes phase and geometrical phase in a driven two-level system. Phys. Rev. A 1997, 55, 2495. [Google Scholar] [CrossRef]
- del Campo, A.; García-Calderón, G.; Muga, J.G. Quantum transients. Phys. Rep. 2009, 476, 1–50. [Google Scholar] [CrossRef]
- Bagwell, P.F.; Lake, R.K. Resonances in transmission through an oscillating barrier. Phys. Rev. B 1992, 46, 15329. [Google Scholar] [CrossRef] [PubMed]
- Azbel, M.Y. Elevator resonance activation. Europhys. Lett. 1992, 18, 537. [Google Scholar] [CrossRef]
- Azbel, M.Y. Eigenstate Assisted Activation. Phys. Rev. Lett. 1992, 68, 98. [Google Scholar] [CrossRef] [PubMed]
- Granot, E. Selected elevation in quantum tunneling. Europhys. Lett. 2003, 61, 817. [Google Scholar] [CrossRef]
- Granot, E. The Tunneling Current through Oscillating Resonance and the Sisyphus Effect. Adv. Cond. Matter Phys. 2017, 2017, 2435857. [Google Scholar]
- Zangwil, G.; Granot, E. Eigenstate suppressed activation. Phys. B 2015, 461, 140–146. [Google Scholar] [CrossRef]
- Granot, E.; Zangwill, G. Generic temporal quantization criterion in Dynamic Resonant Tunneling for Current Suppression. Phys. B 2023, 669, 415332. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Granot, E. Total Reflection of Optical Beams by Weakly Oscillating Dielectric Scatterers. Phys. Rev. A 2016, 94, 063828. [Google Scholar] [CrossRef]
- Granot, E. Derivation of analytical expressions for anomalous reflection in the limit of zero thickness and weakly modulated dielectric grating. J. Opt. Soc. Am. A 2022, 39, 2205–2213. [Google Scholar]
- Glasbrenner, E.P.; Schleich, W.P. The Landau-Zener formula made simple. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 104001. [Google Scholar]
- Abramowitz, M.; Stegun, A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Delmdahl, R.; Buchwald, K. Optics Fabrication: Fiber Bragg Grating Fabrication System Is Automated; Laser Focus World: Nashua, NH, USA, 2016; pp. 31–34. [Google Scholar]
- Stepanov, D.Y.; Corena, L. Bragg grating fabrication with wide range coarse and fine wavelength control. Opt. Express 2014, 22, 27309–27320. [Google Scholar] [CrossRef] [PubMed]
- Othonos, A.; Kalli, K. Fiber Bragg Grating Fundamentals and Applications in Telecommunications and Sensing; Artech House Boston: MA, USA, 1999. [Google Scholar]
- Kashyup, R. Fiber Bragg Gratings; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).