1. Introduction
Quantum non-destructive measurement schemes are diversifying in current research areas, including particle motion tracking in biology [
1], position stabilization between satellites in astronomy [
2], optical image detection [
3], and optical precision measurements [
4]. These schemes play a vital role in various research fields. Quantum communication, in particular, is an emerging interdisciplinary field that combines classical communication with quantum mechanics. It utilizes quantum principles to encode information in quantum states, often referred to as photons, ensuring that information is transmitted in a completely secure manner. Any attempt to intercept the information is likely to be detected and destroyed.
Since the proposal of the BB84 protocol [
5] for quantum key distribution (QKD), numerous theoretical research efforts and experimental simulations have been conducted in the field of quantum information processing for secure communication between remote parties [
6,
7,
8]. Subsequently, several notable QKD protocols have been introduced, such as E91 [
9], which is based on quantum entanglement, and B92 [
10], which employs two nonorthogonal quantum states. Additionally, other quantum cryptographic schemes based on previous work have been suggested, using bright entangled beams [
11] or squeezed states [
12]. In recent studies, the high-dimensional, high-speed QKD protocol is one of the current research foci [
13,
14,
15], which could achieve a high communication rate over a long transmission distance. Also, the asynchronous measurement-device-independent quantum key distribution (asynchronous-MDIQKD) [
16] protocol was presented through time multiplexing. Even further applied in e-commerce scenarios by proposing an efficient quantum e-commerce scheme [
17], this presents a promising solution for providing information-theoretic security for e-commerce.
Building upon the research on the chained Zeno effect [
18], Salih, Li, Alamri, and Zubairy introduced the SLAZ protocol, in which the information could be directly exchanged between Alice and Bob with no physical particles traveling in the transmission channel, thus achieving complete counterfactual measurement [
19]. This protocol is demonstrated using equivalent Mach–Zehnder interferometers (MZIs), where the switch’s performance as a logic gate on one of the interconnected MZI arms is deduced from measurements of two outputs. Importantly, this measurement is, in principle, interaction-free [
20], as any photons in the transmission channel will not be detected due to destructive interference. The earlier quantum mechanical protocol of interaction-free measurement (IFM) was demonstrated using down-conversion photon pairs in a Michelson interferometer [
21], achieving an experimental efficiency of nearly 50%. Subsequently, a polarization-based Mach–Zehnder interferometer structure was considered for semitransparent objects, showing that +the IFM detection efficiency can approach 1 when system losses are negligible [
22]. Building on IFM and the quantum Zeno effect [
23], a completely different scheme for implementing key distribution was proposed by Noh (N09) based on counterfactual quantum cryptography (CQC) [
24]. This scheme offers the possibility, in principle, of transmitting secret information without actually sending a particle through the quantum communication channel. In contrast to the traditional quantum key distribution (QKD) method, G. C. Guo et al. proved the unconditional security of the CQC protocol by employing a perfect single-photon source with well-controlled single-photon detectors in an ideal case [
25]. Then, quantum secure direct communication (QSDC) attracts much attention for enabling secure transmission of messages without prior key encryption [
26,
27], G. L. Long and Y. B. Sheng et al. propose a one-step QSDC protocol that could provide unconditionally secure communication over arbitrarily long distances [
28,
29]. The first proof-in-principal demonstration of CQC was conducted in experiments, with no information carriers passing through the quantum channel [
30]. Additionally, utilizing the quantum Zeno effect, the concept of IFM based on an unstable many-particle system was also proposed in ultracold atoms [
31], single-atom experiments [
32], and electron measurements [
33].
The direct communication system consists of Alice and Bob parts in the SLAZ protocol [
19]. Firstly, Alice sends a stream of horizontally polarized photons into a setup with two tandem Michelson interferometers. This setup allows the signal photons to circulate within Alice’s part using controllable mirrors. Meanwhile, Bob sends a stream of random logic 1 (which transforms horizontally polarized photons into vertically polarized photons) or logic 0 (which conserves the polarization for propagating photons). The measurement result of the logic information code is obtained from detectors D
1 or D
2 based on Bob’s choices.
The measurement system has been demonstrated through a similar structure, which consists of M − 1 big series MZIs and N − 1 small series MZIs in one arm of each big MZI. This setup ensures that the chance of photons leaking into the transmission channel approaches zero as M(N) approaches infinity, and the reflectivity of each beam splitter has been strictly limited to the value . However, the conclusions drawn from mathematical analysis are confined to the assumption that all operational processes are in the ideal case. In practical measuring devices, the impact of degradation caused by optical devices and the transport process will increase with the number of beam splitters. Therefore, the system’s balance must be considered to successfully implement this protocol.
In this paper, we describe the details of the optimized protocol based on counterfactual communication. The theoretical results are calculated to demonstrate the effects of degradation and the finite number of MZIs. Additionally, we propose an attenuation correction method to improve the reliability and efficiency of communication. We also provide experimental evidence for a high-reliability quantum communication protocol using this method to illustrate that practical implementation with a finite number of M and N beam splitters could be achievable.
2. Direct Communication Protocol with Degradation
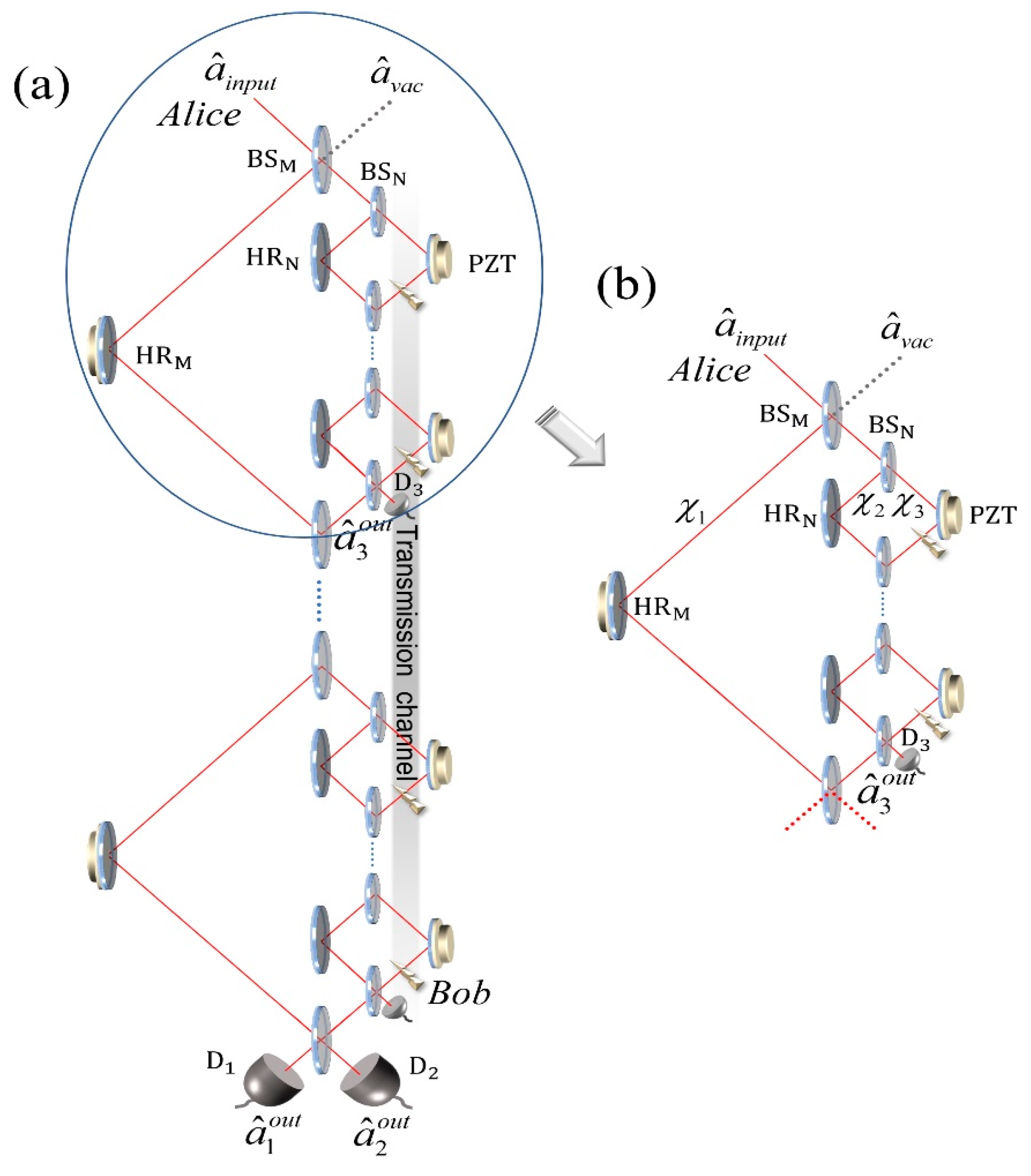
A setup similar to the SLAZ protocol is shown in
Figure 1, where the number of large MZIs and small MZIs is
M − 1 and
N − 1, respectively, with the chained small MZIs embedded in one of the arms of the large MZI.
M and
N represent the number of beam splitters, BS
N and BS
M. To achieve interaction-free transmission, all the beam splitters BS
M in the large MZIs are designed with the same reflectivity
, while the beam splitters BS
N in the small MZIs also have the same reflectivity
. The HR
M and HR
N, as shown in the saturated lens, are high reflection mirrors with 100% reflectivity. Information communication can be accomplished with the operation of Alice and Bob using a single photon (or coherent light). We define the input state incident into the first BS
M as an annihilation operator
, and the vacuum field incident into the other end of the first BS
M is defined as the annihilation operator
. The blocks indicated by the golden lightning symbols can be turned on (logic 0) or off (logic 1) to access any of the light fields through Bob’s choice in the transmission channel. The detectors, represented by D
1, D
2, and D
3, are used to receive signals from each output port of the system. Piezoelectric transducers (PZTs) are used to lock the phase difference in each MZI to zero. Theoretical derivation suggests that ideally, detector D
1 or D
2 will click with a 100% detection probability corresponding to logic 0 or logic 1, respectively. However, in our experimental system described in this section, we observed some deviations from the ideal system (
Figure 1a), where the signal inevitably degrades in actual experiments (indicated by
,
, and
, as shown in
Figure 1b). Through numerical simulation analysis, it is remarkable how such a small change can have a significant impact on the output results.
Here, we divide the paths of the communication system into three parts during the experiment, as shown in
Figure 1: the path on the left side of the BS
Ms, the path between the BS
Ms and BS
Ns, and the path on the right side of the BS
Ns. Concerning the actual application, the degradation in the three paths mentioned above is represented by
,
, and
, and the total degradation increases with the number of BS
M(N). We then describe the degradation effect using the transfer-matrix method, which can be expressed as follows:
where
is the transmissivity of the bottom arm of each big MZI,
is the transmissivity of the bottom arm of each small MZI (as a result,
is the transmissivity of the top arm of each big MZI), and
is the transmissivity of the top arm of each small MZI. The effect of the phase difference on the path of each big MZI or small MZI can be written in the form
where
is the phase difference in one MZI achieved by using a piezoelectric transducer to drive the corresponding HR. The location of
varies depending on where the corresponding PZT is positioned in the communication system’s path. There are two types of beam splitters, denoted as BS
M and BS
N, which can be represented by
in which
and
denote the reflection amplitudes of BS
M and BS
N, while
and
stand for the transmission amplitudes of BS
M and BS
N, respectively. By using a similar method, we obtain that the transfer matrix of inner free space between two adjacent BS
Ms, which is under the effect of the reflection of “
N”. BS
Ns can be represented as
Apparently, is approximately equal to one as N approaches infinity. Similarly, it is convenient to calculate that the free-space transfer matrix between two adjacent BSNs is an identity matrix. Subsequently, all kinds of transfer matrices corresponding to different parts of the communication system are acquired. Next, we will numerically simulate the reliability of communication with degradation and a finite number of MZIs in an actual direct communication application.
3. Numerically Simulated Reliability of Communication
There are two parameters that are extremely crucial for evaluating the quality of a good or bad communication system, as shown in
Figure 1b:
, representing the probability ratio
, and
, representing the probability ratio
under logic 1 and logic 0 for Bob. Here,
(or
) denotes the probability of a click on D
1 (or D
2). Consequently, the higher the values of
(or
), the closer the communication system is to perfection.
The efficiency of communication is independent of the input state, and if we can use the column vector to represent it, then the output state can be written as . is the whole transformation matrix of the communication device, which has a different form based on logic 1 or logic 0. The values of and can be calculated based on the modular square of the matrix element and .
3.1. Logic 1
In the case of logic 1 with blocks in the transmission channel, the interference of each small MZI is completely disrupted, and a series of reflected paths on the
N BS
N becomes one arm of the big MZI. Therefore, the whole transformation matrix can be expressed as
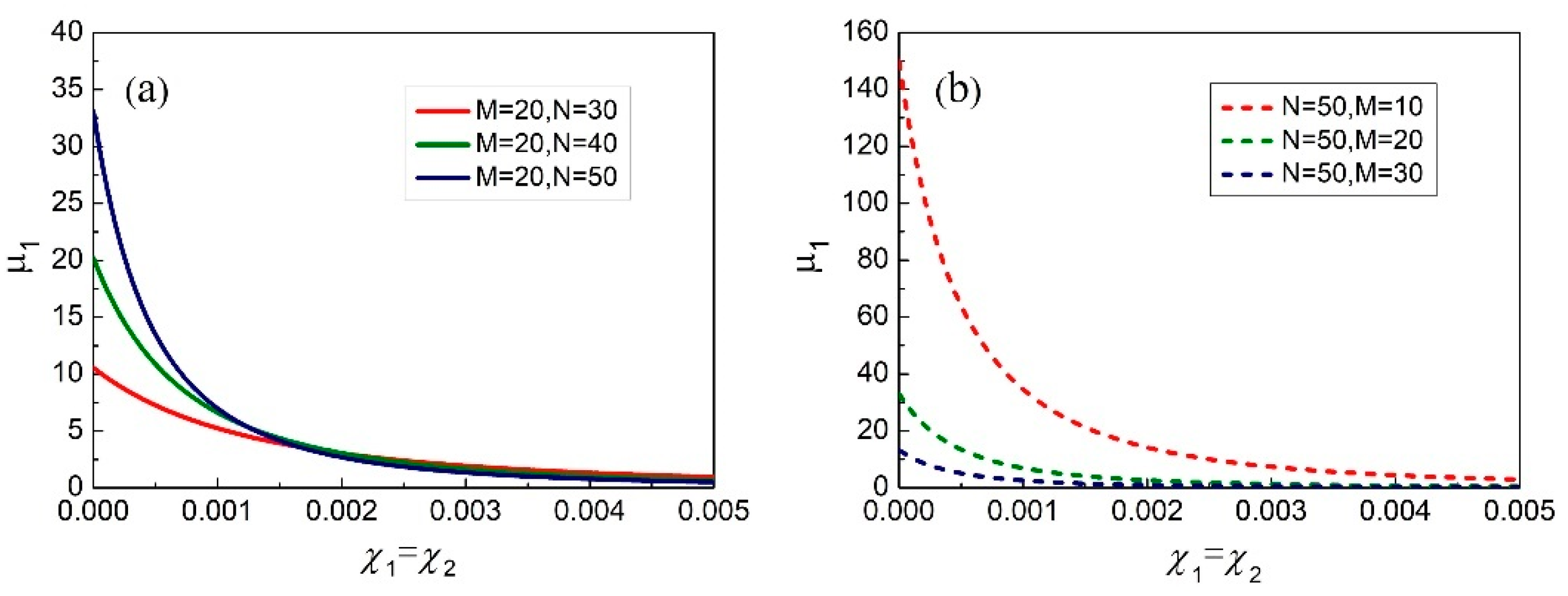
As shown in
Figure 1, when the phase difference in big MZI is set to be
, we plot the reliability
versus
with
M = 20,
N = 30, 40, 50, and with
N = 50,
M = 10, 20, 30, respectively. It shows that the reliability
decreases sharply and then decreases slightly as the degradation of the big MZI increases. Note that for fixed
M in
Figure 2a, the reliability
(solid curves) would increase with the number of BS
N and this relationship is more distinct for low degradation (
) than for high degradation (
). It could be explained that when there is a certain amount of degradation in actual measurement, each cycle brings constant losses, which finally lead to the breakdown of coherence with the addition of infinitely many
N numbers. On the other hand, the reliability
(dashed curves) would decrease with the number of BS
M for fixed
N in
Figure 2b. Accordingly, we can combine the suitable BS
N number and a small number of BS
M to achieve information transmission with higher reliability for logic 1, which is in the presence of degradation.
Note that not only the reliability
but also the value of
is important, as it serves as the benchmark for the communication system. In
Figure 3, we plot the reliability (the probability of a click at D
2 for logic 1) versus
M and
N using
, the data are simulated using Mathematica 11.0 software for numerical analysis. This is evident in the probability density plot, as the value of
does not tend to 1 with an increasing number of BS
N. Instead, each fixed number of BS
M corresponds to a specific number of BS
N, ensuring the highest efficiency for key encryption.
3.2. Logic 0
Firstly, considering only the inner transfer matrix
for
N tandem small MZIs of each group for the case of logic 0 without block, the total transfer matrix is expressed as
Here, we set the degradation
based on the symmetry of the interferometer structure and obtain the matrix elements of the
according to Equation (6). We obtain
, whose value is independent of the degradation and the number of BS
N and
, which can be seen from
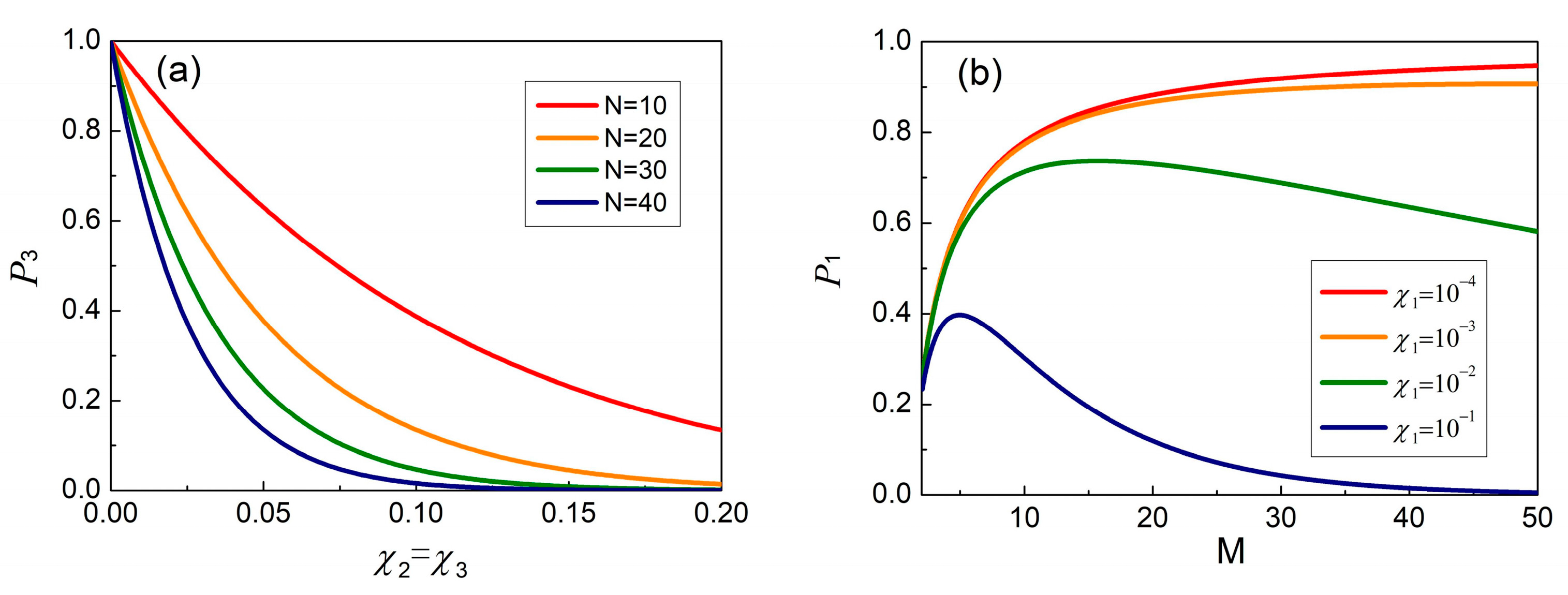
Figure 4a. Our calculations reveal that the light field will never enter the big MZI after the (
N − 1)th loop, regardless of the transmission channel it passes through. On the other hand, we plot
Figure 4a, which shows the probability
of the click of D
3 as a function of the degradation
. The probability decreases as the number of BS
Ns increases under the same degradation level, with the curve clearly declining as
N increases. This demonstrates that we can employ an appropriate number of small MZIs, rather than an infinite number, to complete the information transmission process.
Next, we consider the whole of the MZIs without blocks, as shown in
Figure 1, where the total transfer matrix can be represented as
where the degradation
could be written as 1 according to the interpretation of the inner transfer matrix mentioned above. As a result, we calculate the value of the reliability
, which is not only independent of the degradation
and the number of BS
N, but also an increasing function of
M. As important indexes of the communication protocol with degradation, the probability of the click at D
1 for logic 1 cannot be ignored. In
Figure 4b, we have plotted the probability
as a function of
M with
, There is an equilibrium distribution relationship between the degradation and the number of big MZI, the huge
M increase did not have a beneficial effect on the result and undermined the high probability of detection. For example, a maximum value below 40% with
M = 5 has been displayed for a large degradation
. Both cases (logic 1 and logic 0) partly treat the same subject, with the inevitable degradation, and reach a similar conclusion that the high reliability of direct communication can be obtained with imperfect interferometers of a finite number.
4. Improving Communication Reliability via Controllable-Signal Degradation
Based on the discussion above, we have determined that the unavoidable degradation imposes limits on the number of beam splitters that can be practically employed in measurements. Can we effectively address this issue? Can we improve communication reliability under current conditions or even achieve a relatively ideal control result ()? The disparity between big and small MZIs tends to result in differences in degradation. To rectify this, we can introduce attenuation correction in the path of each big MZI to balance both arms, similar to the tandem small MZI discussed in Equation (6).
We have obtained promising results in our experiment. To ensure continuous control over the degradation, we implemented a continuous-adjustable attenuator in one arm of each large MZI, as shown in
Figure 5b. Subsequently, we used a weak light source with a wavelength of 895 nm to assess whether we could improve reliability. The optical element representing corrective attenuation is denoted as
and the number of BSs is set to
M = 3,
N = 8. In the case of logic 1 with blocks in the transmission channel, the corrective attenuation effect in the inner free space between two adjacent BS
Ms can be expressed as
where
is the balanced attenuation including inherent and corrective attenuation in the arm of big MZI. The practical transmissivity
was about 90% after repeated measurement experiments and system debugging. Then, the whole transformation matrix can be expressed as
Here introduces the phase difference via the HRM, and we adjust the voltage at PZT via a computer-controlled system to obtain the maximum intensity at D2, while the minimum intensity is at D1. Then, the optimized reliability can be obtained when we lock the phase difference in two big MZIs to be .
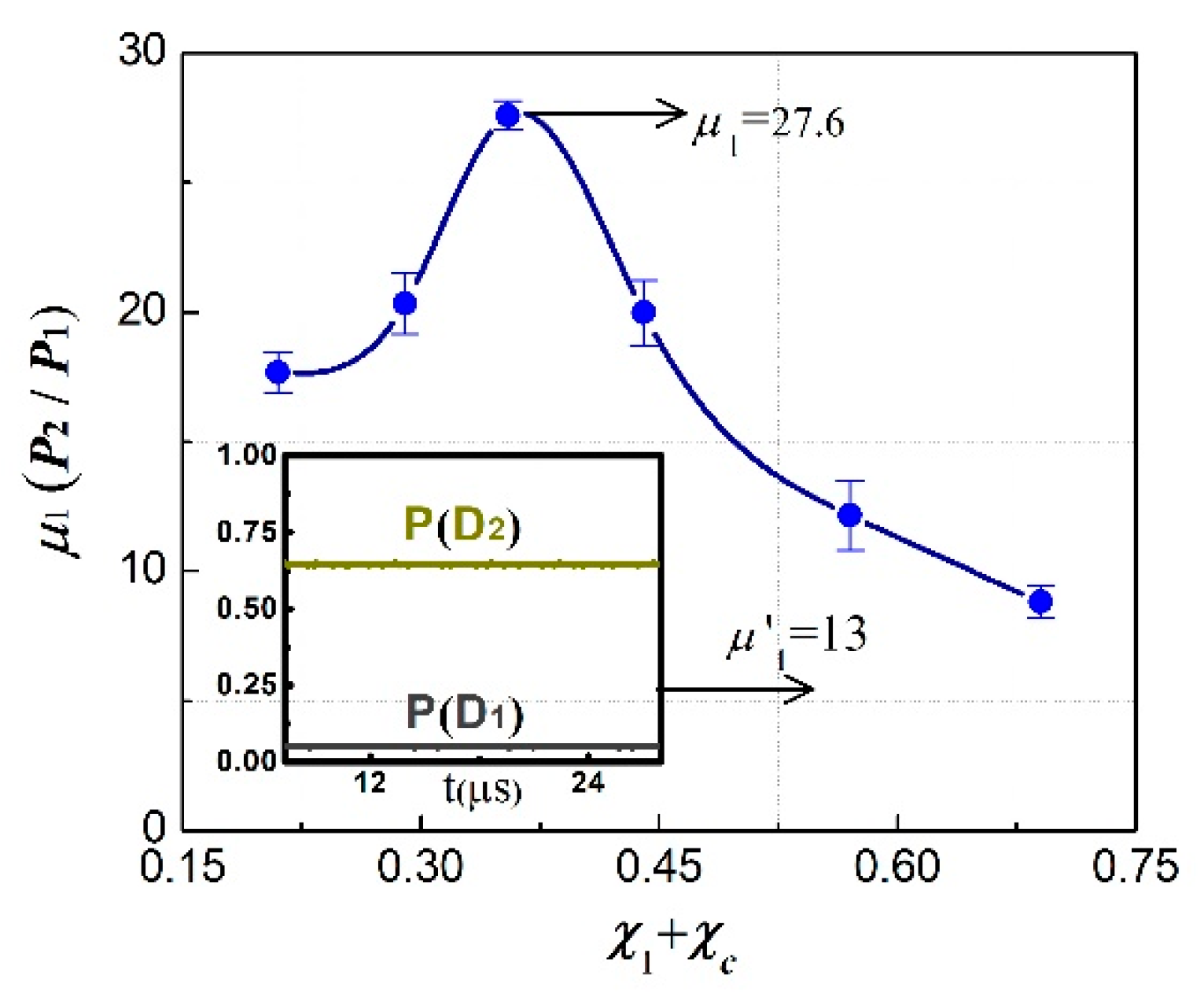
When the signal attenuation
on the left path of the BS
Ms is set to 0.340, the value of the reliability
= (
/
)
2 we calculated will be infinity. Note that the definite value represents the total actual attenuation on another arm of the large MZI, which is equal to
. The blue points in
Figure 6 represent experimental data showing the reliability
versus different
. The reliability exhibits an initial increase, followed by a subsequent decrease, with the peak reliability
occurring at
, which is higher than the non-controlled signal degradation (as shown in the small figure embedded in
Figure 6 with a value of
). As a result, the answer to the question posed earlier is affirmative. Communication reliability with an infinite number of beam splitters and degradation can theoretically reach 100%, and the measured results confirm high-reliability direct communication in the experiment. On the other hand, the results for logic 0 remain unaffected by the attenuation correction method after repeated measurement experiments. However, in the actual measurement process, there is a lot of uncertainty, such as the difference in the sensitivity and quantum efficiency of the detectors, the difference in the degradation of each path for MZIs, the difference in the losses of the optical components in each arm, phase fluctuation for the piezoelectric transducers, the frequency drift of the weak light source, and so on. This affects the reliability more or less. For the setup, the measuring reflectivity of beam splitters is obtained from the test report; the uncertainty is at 1% and 0.5%, respectively, and all beam splitters are selected strictly according to our theoretical result in the experiment; meanwhile, the random shifting of the phase in each MZI is suppressed through the assisted locking control system.