Deep Learning-Assisted High-Pass-Filter-Based Fixed-Threshold Decision for Free-Space Optical Communications

Abstract

This paper proposes a deep learning (DL)-assisted high-pass-filter (HPF)-based fixed-threshold decision (FTD) for free-space optical (FSO) communication. HPF is applied to reduce the scintillation effect by filtering out the low-frequency components of the received signal. However, the performance is limited owing to the signal distortion from HPF and remnant scintillation effect due to insufficient filtering. Therefore, the DL model is adopted to improve the performance of HPF-based scintillation effect compensation. The multilayer perceptron (MLP) model is used to adaptively select the peak frequency component of the received signal as the optimized cutoff frequency of HPF. Furthermore, recurrent neural network (RNN) and long short-term memory (LSTM) models are cascaded after HPF to compensate for the remnant scintillation effect and recover the signal distortion without the optimization of HPF cutoff frequency. The simulation was conducted under different turbulence channels and data rates. Simulation results showed that MLP-assisted adaptive optimized cutoff frequency and cascaded LSTM and HPF methods were close to the adaptive-threshold decision with precise channel state information under various turbulence channel degrees.

1. Introduction

Free-space optical (FSO) communication systems are widely used in space and terrestrial communication links. These systems have the features of ease of installation, free licensed spectrum, high data rates, high security, low cost, and low power consumption compared to conventional radio frequency communication systems [1]. However, FSO systems experience intensity fluctuations when optical signals traverse atmospheric turbulence channels, that is, the scintillation effect [2]. This phenomenon significantly degrades the performance of FSO communication systems and is a challenge for FSO technology. Regarding the on–off keying (OOK)-FSO communication system, the turbulence effect leads to fluctuations in the received OOK signal intensity [3]. Several studies have been conducted to mitigate the scintillation effects of OOK-FSO links. Adaptive optics systems have been studied to reduce the scintillation effect by detecting and correcting wavefront distortions [4]. However, this method is only effective in the context of weak turbulence channels. In [5], an adaptive channel coding technique has been proposed to pre-compensate the scintillation effect under the estimation of imperfect channel state information (CSI) at the transmitter. However, the periodic CSI estimation process leads to the hardware overhead increasing and time delay. The aperture averaging method has been discussed to mitigate the scintillation effect by employing a large aperture in the receiver end [6]. Nonetheless, challenges remain in deploying a large aperture in practice.

Fixed-threshold detection (FTD) and adaptive-threshold detection (ATD) are widely utilized in FSO systems [7]. The traditional FTD method employs the mean value of the received signal intensity as the decision threshold. However, it becomes ineffective under a stronger turbulence effect [8]. ATD can mitigate the scintillation effect through symbol-by-symbol decision threshold estimation [9]. However, the optimal decision-making process requires an accurate CSI. The instantaneous CSI is filtered by a low-pass filter (LPF) with optimization of the cutoff frequency [10]. However, with respect to the low transmission speed, the performance of the ATD is degraded owing to the severe signal distortion caused by the LPF. In [11], researchers integrate a dual-transmitter system with an adaptive-threshold receiver, which can mitigate the adverse effects of turbulence and improve system performance without the need for expensive adaptive optics. However, their effectiveness may be limited in scenarios of intense turbulence. Recently, deep learning (DL) techniques have been introduced into FSO communication in order to improve the system performance [12,13]. A convolutional neural network (CNN) has been employed to identify the intensity image categories of Laguerre Gaussian beams transmitted through free-space channels under various turbulence conditions for the sake of simultaneously detecting turbulence intensity and orbital angular momentum modes [14]. Fully connected neural networks (FCNNs) have been studied to compensate for the turbulence effects by extracting turbulence channel features from the received signal through element-wise multiplication and summation [15]. In [16], a feed-forward de-noising convolutional neural network (DnCNN) scheme has been proposed to implicitly remove potential clean images from the hidden layers through a residual learning strategy. The high-pass filter (HPF) has been applied to achieve FTD by blocking atmospheric turbulence caused by low-frequency fluctuations [17]. However, the low-frequency components of the signal are truncated by HPF as well, which decreases the performance of FTD. Therefore, the DL method is studied to improve the performance of HPF-based scintillation effect compensation.

In this study, a fixed-threshold OOK detection technique based on the HPF and DL is proposed for the FSO system. The HPF was used to block the low-frequency components of the OOK signal to reduce the scintillation effect. A multilayer perceptron (MLP) model was introduced to adaptively select the peak frequency component of the received signal as the optimized cutoff frequency of the HPF. Furthermore, recurrent neural networks (RNN) and long short-term memory (LSTM) models are cascaded to the HPF to compensate for the remnant scintillation effect and recover signal distortion without the optimized cutoff frequency of the HPF. The proposed method was evaluated through a simulation. Simulation results illustrated that the performance of the proposed MLP-assisted adaptive optimized cutoff frequency, cascaded LSTM and HPF were close to that of the traditional ATD with precise CSI.

The outline of this paper is as follows: In Section 2, we describe the principle of the proposed DL-assisted HPF-based FTD technique. In Section 3, we describe the turbulence channel analysis and simulation parameter setup. The simulation results are given in Section 4. In Section 5, we describe the conclusion of this paper.

2. Operation Principle

The principle of HPF-based FTD, MLP-assisted adaptive optimized cutoff frequency, and cascaded HPF and DL-based FTD without the optimization of HPF cutoff frequency was discussed in this section.

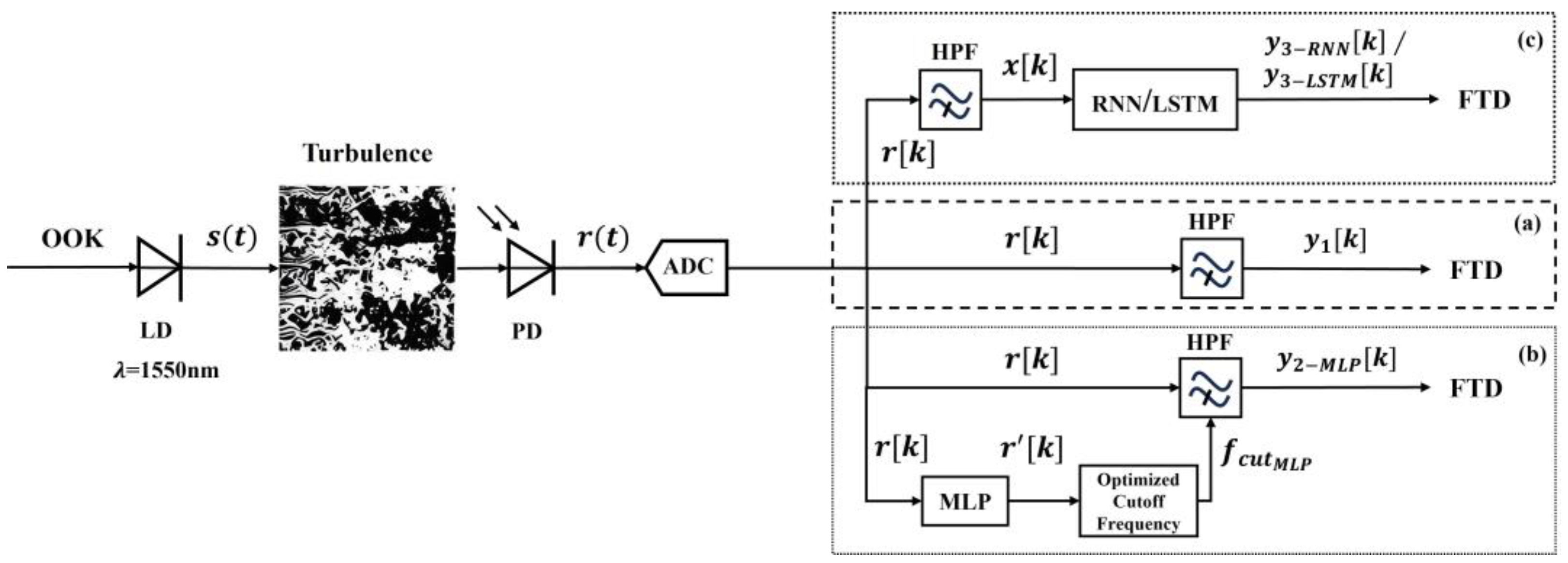
A block diagram of the proposed HPF-based FTD OOK detection technique is shown in Figure 1. A 1550 nm laser diode (LD) was directly modulated with the OOK signal. The modulated laser beam propagates through the FSO link and experiences turbulence-induced scintillation effects. The strength of the scintillation effect is assessed by the scintillation index ${\sigma }_I^2$, and it is given by

$${\sigma }_I^2=\frac{〈I^2〉}{{〈I〉}^2}-1,$$

(1)

where $I$ denotes the intensity fluctuation and 〈∙〉 denotes the ensemble average [1]. At the receiver end, the received optical signal is converted into an electrical signal using a photodiode (PD). The PD-received signal is converted into a digital signal $r[k]$ using an analog-to-digital converter (ADC), and it is expressed as

$$r\left[k\right]=I\left[k\right]s\left[k\right]+n\left[k\right],$$

(2)

where $s[k]\in \left\{\left.0,1\right\}\right.$ denotes the symbol information, $n[k]$ represents signal-independent additive white Gaussian noise from the PD and background [18].

A.

HPF-based FTD

In Figure 1a, the received signal passes through the HPF, and the scintillation-caused signal-intensity fluctuation is compensated for via low-frequency blocking. The frequency components of the received signal $r\left[k\right]$ are calculated using Discrete Fourier Transform (DFT) as follows [19]

$$R(f)={\displaystyle \sum _{n=0}^{N-1}r[k]·e^{(-j2\pi fn/N)}},$$

(3)

where $R(f)$ is the DFT of the output $r\left[k\right]$, $n$ denotes a discrete time point in the time domain, and $N$ is the signal length. The frequency characteristics of the received signal are then calculated using the power spectral density (PSD), which is given as follows [19]

$$S(f)=\frac{1}{N}|R(f){|}^2,$$

(4)

where $S(f)$ is the PSD of the $r\left[k\right]$. The frequency spectrum characteristics and PSD of the received signal are analyzed to determine the cutoff frequency $f_{cut}$ of the HPF. The cutoff frequency of the HPF is calculated as [20]

$${\omega }_{cut}=\frac{2\pi f_{index}}{N{f}_s},$$

(5)

where $f_{index}$ denotes the index of the selected cutoff frequency $f_{cut}$ in PSD, while ${\omega }_{cut}$ represents the angular frequency from $f_{cut}$, and $f_s$ is the sampling rate. The output signal $y_1[k]$ at the HPF is expressed as [20]

$$y_1[k]=\tan \left({\omega }_{cut}\left(r[k]-2{\tan }^{-1}(\frac{{\omega }_{cut}{f}_s}{N})\right)\right).$$

(6)

The mean value of $y_1[k]$ is calculated as the decision threshold $I_{th}$ of the received OOK signal to distinguish bits “1” and “0”. The performance of the proposed technique is assessed by analyzing bit error rate (BER), and the BER is calculated by [21]

$$BER=\frac{1}{2}\left[\frac{1}{2}erfc\left(\frac{I_{th}}{\sqrt{2{\sigma }_n^2}}\right)+{\displaystyle {\int }_0^{\infty }\frac{1}{2}erfc\left(\frac{I-I_{th}}{\sqrt{2{\sigma }_n^2}}\right)}f\left(I\right)\mathrm{d}I\right],$$

(7)

where ${\sigma }_n^2$ is the variance of $n[k]$, and $erfc\left(·\right)$ is the complementary error function.

B.

MLP-assisted adaptive optimized cutoff frequency

The optimized cutoff frequency of the HPF is dependent on the data rates and turbulence degrees. Thus, a dynamic cutoff frequency is required to support the variation in data rates and turbulence channels. The DL technique is applied to adaptively select the optimized cutoff frequency of the HPF to effectively compensate for the scintillation effect. In Figure 1b, the digital signal is split into two branches, and the lower branch is used to learn the frequency characteristics of the received signal and adaptively select the appropriate cutoff frequency of the HPF using DL. 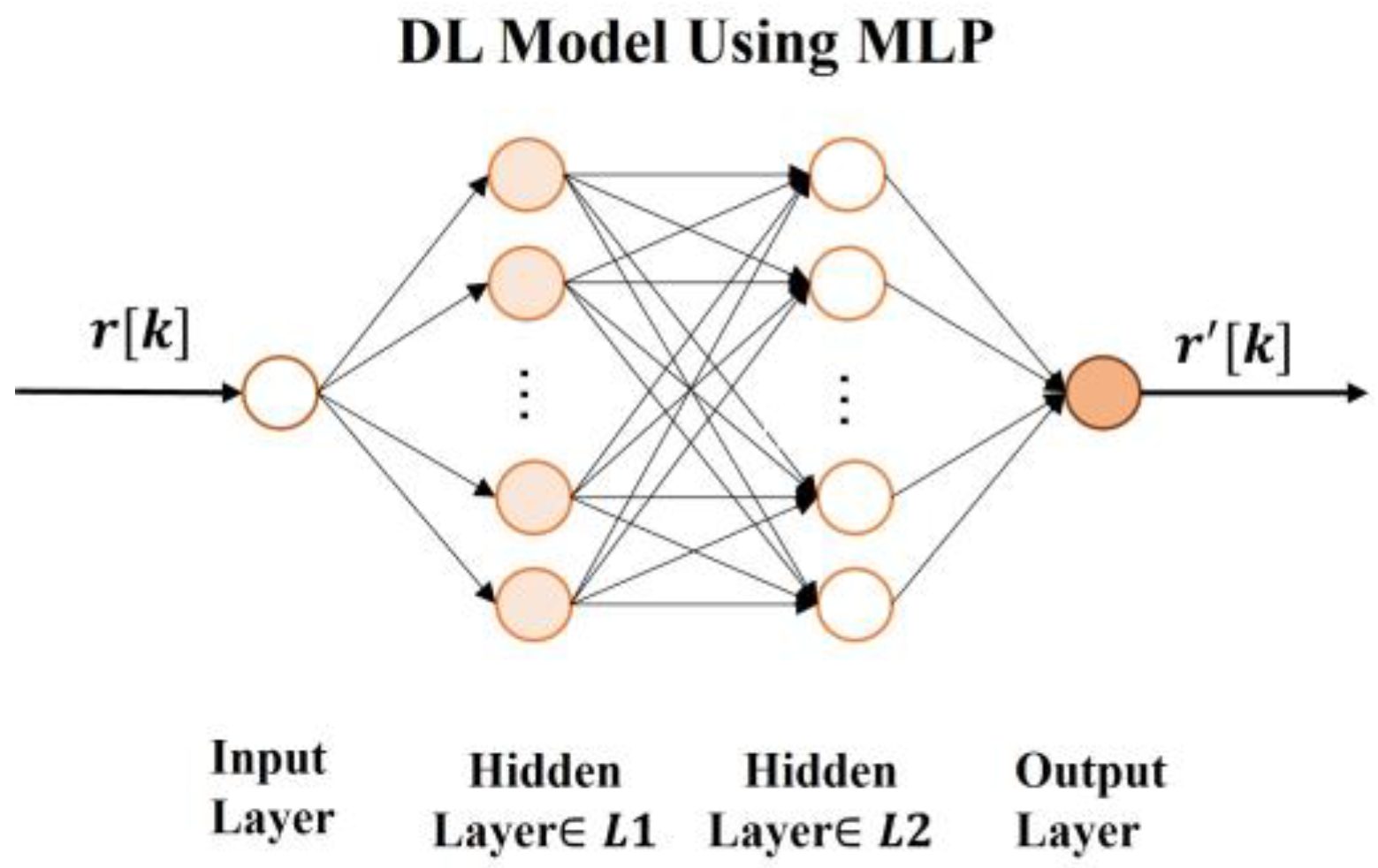Figure 2 illustrates the proposed DL model employing MLP, including two fully connected layers with 64 neurons and an output layer [22]. In the MLP model, the modified input layer only delivers the input signal $r[k]$ into the hidden layers first. The ReLU activation function $R\{·\}$ learns the feature representation of $r[k]$ due to the nonlinear transformations. Then, the output layer reconstructs the spectrum of $r^{\prime }[k]$ using the learned feature representation. Finally, the optimal cutoff frequency $f_{cu{t}_{MLP}}$ is determined by identifying the main components of the received signal through the analysis of the $r^{\prime }[k]$ spectrum. The processes of input and output layers are defined as follows

$$\begin{array}{l}{n}_1[k]=w_{1}r[k]+b_1\\ n_2[k]=R\left(w_2\left(R\left(w_{1}r[k]+b_1\right)\right)+b_2\right)\\ r^{\prime }[k]=R\left(w_3{n}_2[k]+b_3\right),\end{array}$$

(8)

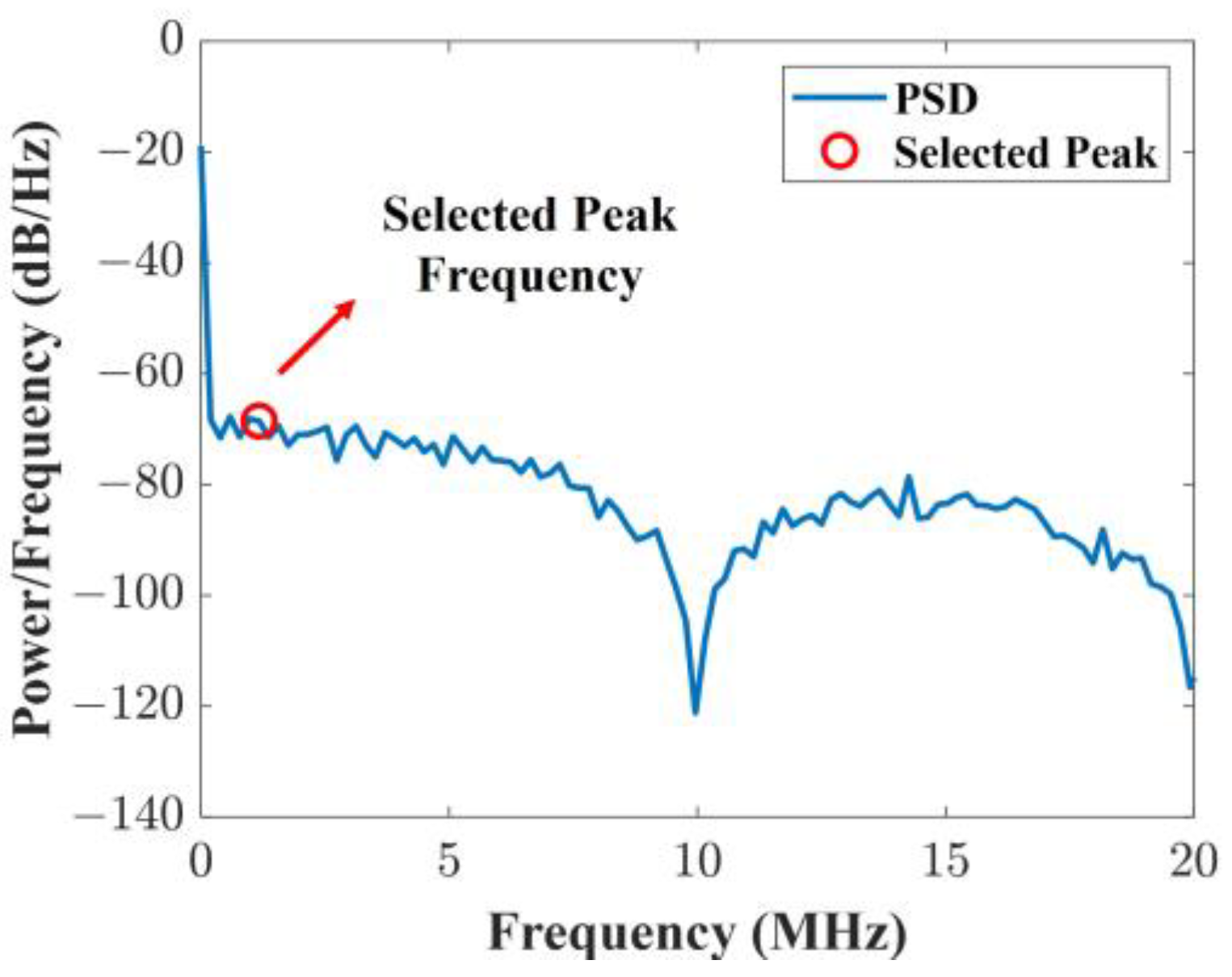
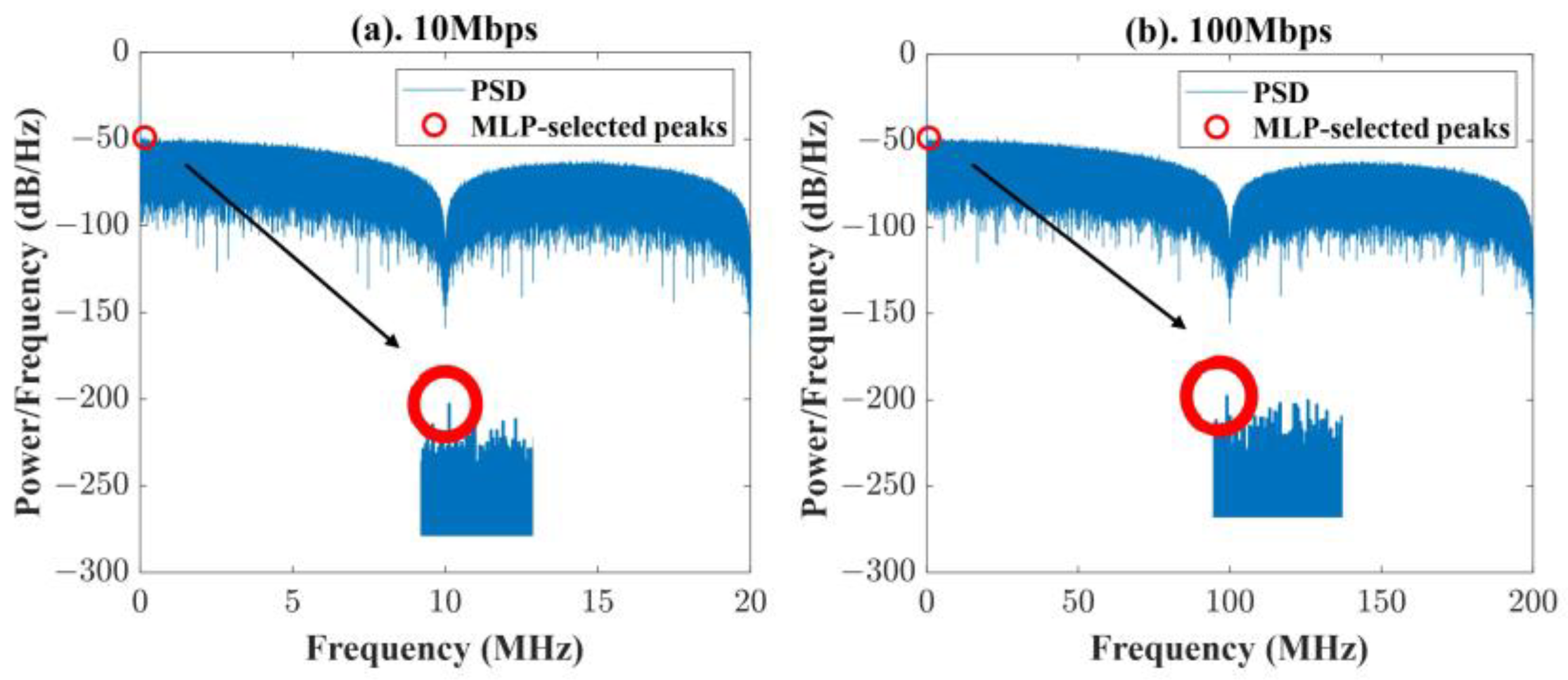
where $w_i$ is the weight matrix of the layer $i$, $b_i$ is the bias term of the layer $i$, $n_1$ is the input layer, $n_2$ represents a neural network structure composed by two hidden layers, and $r^{\prime }$ is the output layer. Figure 3 shows the PSD of the OOK signal after the turbulence channel with a ${\sigma }_I^2$ of 0.4286 at 10 Mbps. MLP model adaptively selects the peak frequency component in the PSD of the OOK signal, excluding the DC component. Then, the selected frequency is set to the optimized cutoff frequency of the HPF under various data rates and turbulence degrees.

C.

Cascaded DL and HPF

RNN and LSTM are employed after HPF to further suppress the scintillation effect and recover signal distortion from the HPF without optimizing the HPF cutoff frequency, as shown in Figure 1c. Figure 4 illustrates a DL-based detector model utilizing RNN [23], characterized by a hidden layer comprising 64 neurons and an output layer. The filtered signal $x[k]$ is imported into the RNN model, and it captures the temporal dependencies using the recurrent structure by learning the features and patterns of $x[k]$. Ultimately, it utilizes the learned features and temporal information to achieve the turbulence effect compensation. The formula of the hidden state $h[k]$ is given by

$$h[k]=\tanh \left\{W_{ih}\ast x[k]+b_{ih}+W_{hh}\ast h[k-1]+b_{hh}\right\},$$

(9)

where $W_{ih}$ is the weight matrix between input and hidden layers, $W_{hh}$ is the weight matrix between hidden and hidden layers, $b_{ih}$ and $b_{hh}$ are the bias terms between input and hidden layers, and $\tanh$ is the activation function. The RNN adjusts its parameters through backpropagation to improve the accuracy of turbulence prediction and compensation. Based on the hidden state $h[k]$, the output $y_{3-RNN}[k]$ is calculated as follows

$$y_{3-RNN}[k]=\mathrm{softmax}\left\{W_{hy}\ast h[k]+b_{hy}\right\},$$

(10)

where $W_{hy}$ denotes the weight matrix from hidden to output layers. The RNN structure can be used to process sequential data. However, it has the issue of gradient vanishing and gradient explosion for long sequential data processing, which leads to difficulties in capturing the long-range dependencies. LSTM with complex variants can handle the longer sequence dependencies by using additional gating mechanisms [23]. 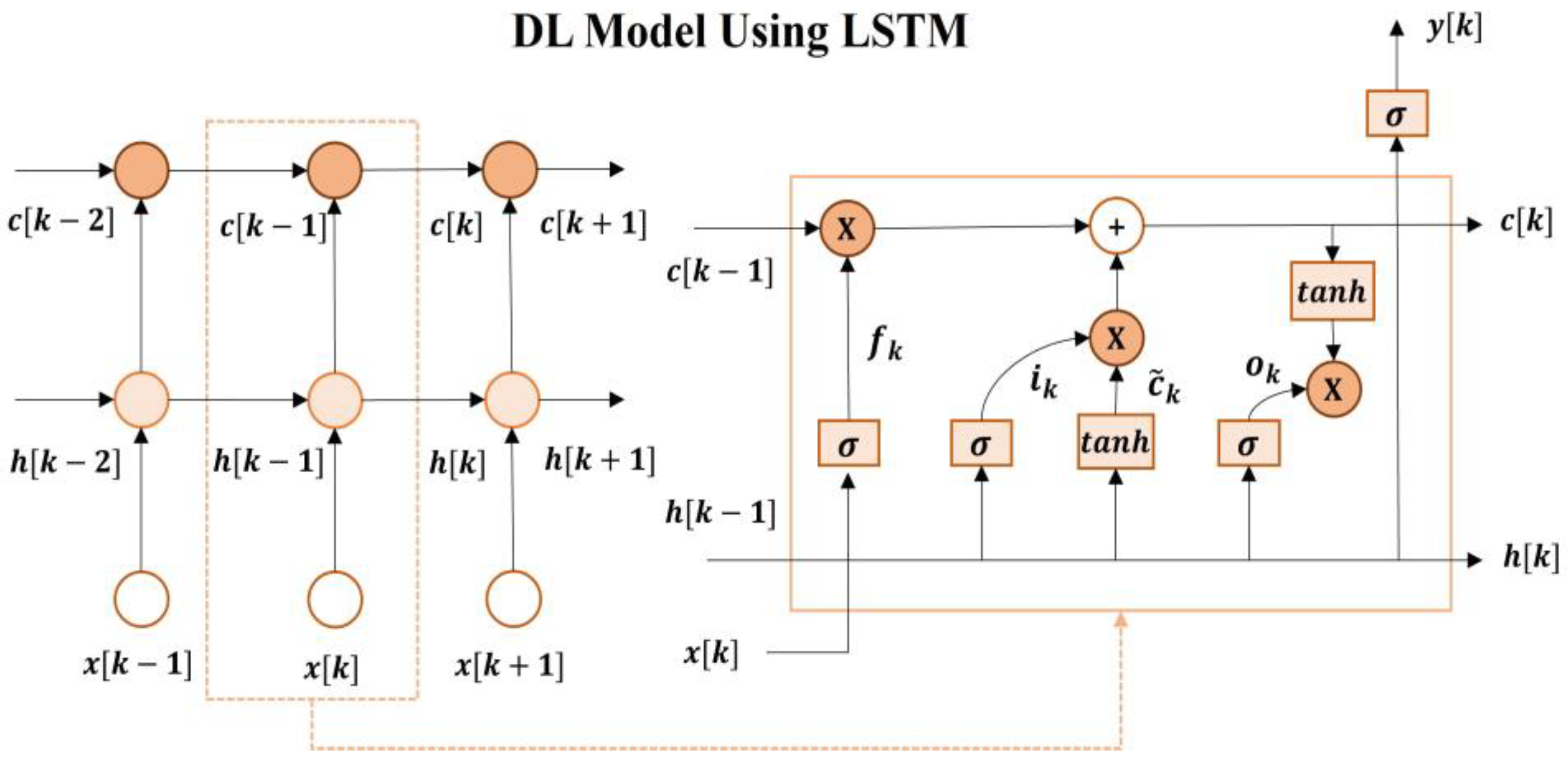Figure 5 illustrates the proposed DL-based detector model using LSTM. The input gate, forget gate, cell state, and output gate of LSTM collectively aid the network in capturing and adapting to the signal intensity variations [24]. The input gate adjusts the cell state $c[k]$ of the current time step to reflect the current input signal $x[k]$ and the previous hidden state $h[k-1]$. The signal with serious intensity fluctuations is prioritized by the input gate. The calculation formula of the input gate is as follows

$$i[k]=\sigma \left\{W_{xi}\ast x[k]+W_{hi}\ast h[k-1]+b_i\right\},$$

(11)

where $i[k]$ is the output of the input gate, and $\sigma$ is the sigmoid activation function. The forget gate reduces the interference and noise to ensure the cell state $c[k]$ can capture the intensity fluctuations caused by the turbulence effect. The calculation formula of the forget gate is as follows

$$f[k]=\sigma \left\{W_{xf}\ast x[k]+W_{hf}\ast h[k-1]+b_f\right\}.$$

(12)

The cell state $c[k]$ is updated based on the information from the input gate and the forget gate in order to integrate the features of the $x[k]$. The specific process is as follows

$$\begin{array}{l}\tilde{c}[k]=\tanh \left\{W_{xc}\ast x[k]+W_{hc}\ast h[k-1]+b_c\right\},\\ c[k]=f[k]\ast c[k-1]+i[k]\ast \tilde{c}[k],\end{array}$$

(13)

where $\tilde{c}[k]$ represents the updated candidate cell state. The output gate determines the information delivered to the output layer according to the features learned at the current time step.

$$o[k]=\sigma \left\{W_{xo}\ast x[k]+W_{ho}\ast h[k-1]+b_o\right\}.$$

(14)

The final output layer implements a turbulence compensation process based on the features learned by the network, and the output signal $y_{3-LSTM}[k]$ is obtained as

$$y_{3-LSTM}[k]=\sigma \left\{W_{hy}\ast o[k]\ast \tanh \odot c[k]\right\},$$

(15)

where ⨀ denotes the dot product between the vectors. Finally, FTD is achieved for RNN and LSTM-based methods by using the mean values of $y_{3-RNN}[k]$ and $y_{3-LSTM}[k]$ as decision thresholds, respectively. The BERs can be calculated using Equation (7) to assess the performance of the two models. Consequently, the scintillation effect is compensated for by the proposed DL-assisted HPF-based FTD technique under different turbulence channels and data rates.

3. Channel Analysis and Simulation Parameters

A.

Channel analysis

The atmospheric turbulence effect encompasses beam wandering, beam spreading, and beam scintillation effects. Among these effects, the scintillation effect causes significant temporal and spatial fluctuations in received signal intensity, which is the major concern in intensity modulation/direct detection FSO systems. Thus, this study focuses on the performance degradation induced by scintillation effects. The lognormal model, a widely recognized and simple approach, was used for modeling weak turbulence channels. The probability density function (PDF) is calculated by [25,26]

$$f\left(I\right)=1/\sqrt{2\pi {\sigma }_I^{2}I}\hspace{0.33em}\exp \left[-{\left(\ln \left(I\right)-\mu \right)}^2/\left(2{\sigma }_I^2\right)\right],$$

(16)

where $\mu$ is the mean of $\ln \left(I\right)$ [1]. The turbulence channel was modeled through phase modulation, inverse Fourier transform, and the first-order Rytov approximation. Figure 6 shows the turbulence channel modeled by employing parameters in

Table 1. Parameters of the turbulence channel.

Parameters	Values
Link distance	10 km
Wavelength	1550 nm
Aperture diameter	10 cm
Wind velocity	5 m/s
$C_n^2$	$1.5\times {10}^{-11}$
Divergence angle	10 urad
Visibility	30 km

. The modeled turbulence channel exhibits time-varying signal intensity features as illustrated in Figure 6a, and it has a low-frequency dominant spectrum as demonstrated in Figure 6b. In Figure 6c, the PDF of the modeled turbulence channel fits well with the lognormal distribution. Therefore, the turbulence channel was modeled effectively, and it was used as the dataset in this study. Turbulence channels modeled with gamma–gamma distribution, Weibull distribution, K-distribution, and negative exponential distribution will be discussed in further works.

B.

Simulation parameters

The standard parameters of the DL model are outlined in

Table 2. The tuned hyperparameters.

Hyperparameters	Value
Size of dataset-10 Mbps	$1\times {10}^7$
Size of training dataset-10 Mbps	$8\times {10}^6$
Size of test dataset-10 Mbps	$2\times {10}^6$
Size of dataset-100 Mbps	$1\times {10}^8$
Size of training dataset-100 Mbps	$8\times {10}^7$
Size of test dataset-100 Mbps	$2\times {10}^7$
Loss function	MSE
Epoch	20
Batch size	$2^{16}$
Learning rate	0.005
Turbulence channel	${\sigma }_I^2$ = 0.6850, 0.4286, 0.1256, 0.0596

. Simulations were conducted using MATLAB 2021b and PyCharm 2021.3.2. The test platform employed an NVIDIA GeForce RTX 4070 Laptop GPU. Throughout the training process, the output signals were used as the dataset. In total, 80% of the dataset was used for training, and 20% of the dataset was used for testing. The DL detector was trained using labeled training data with one-hot vector labels representing the transmitted symbols.

4. Simulations and Results

The proposed OOK detection method using the DL-assisted HPF-based FTD was evaluated via simulation. The BER performance of the ATD with precise CSI, HPF-based FTD under different cutoff frequencies, MLP-assisted adaptive optimized cutoff frequency, and cascaded HPF and DL-based FTD without the optimization of HPF cutoff frequency techniques were compared. Additionally, the accuracy and computational complexity of the proposed DL-assisted HPF techniques were analyzed. The average signal-to-noise ratio (SNR) was used in this work due to the signal intensity variation, and it is calculated as $E\left[I^2\right]/2{\sigma }_n^2$ [27].

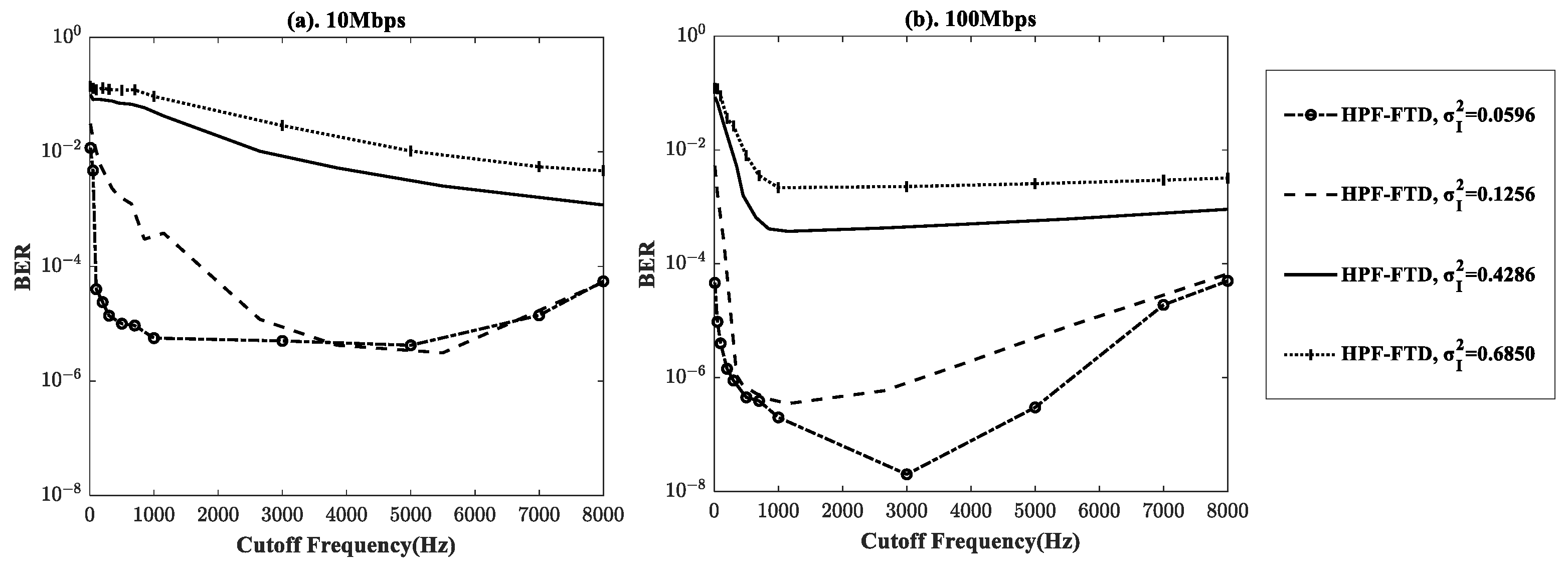
Figure 7 illustrates the BER performance of the proposed OOK detection method at different cutoff frequencies of HPF. Turbulence channels with ${\sigma }_I^2$ values of 0.0596, 0.1256, 0.4286, and 0.6850 were adopted in the simulation. The data rates were set to 10 Mbps and 100 Mbps, and the average signal-to-noise ratio (SNR) was set to 28 dB for PD and background noise reduction. The cutoff frequency of the HPF was set to 10 Hz-0.8 MHz due to the low-frequency features of the turbulence channel. At a data rate of 10 Mbps, the BER was initially improved by increasing the cutoff frequency of the HPF, because a much larger proportion of turbulence frequency was removed from the received signal by HPF. When the cutoff frequency of the HPF exceeded a critical value, the BER was degraded due to a severe signal distortion from HPF. A similar performance was observed in the case of 100 Mbps. Therefore, an optimization process is required for HPF under various ${\sigma }_I^2$ and data rates.

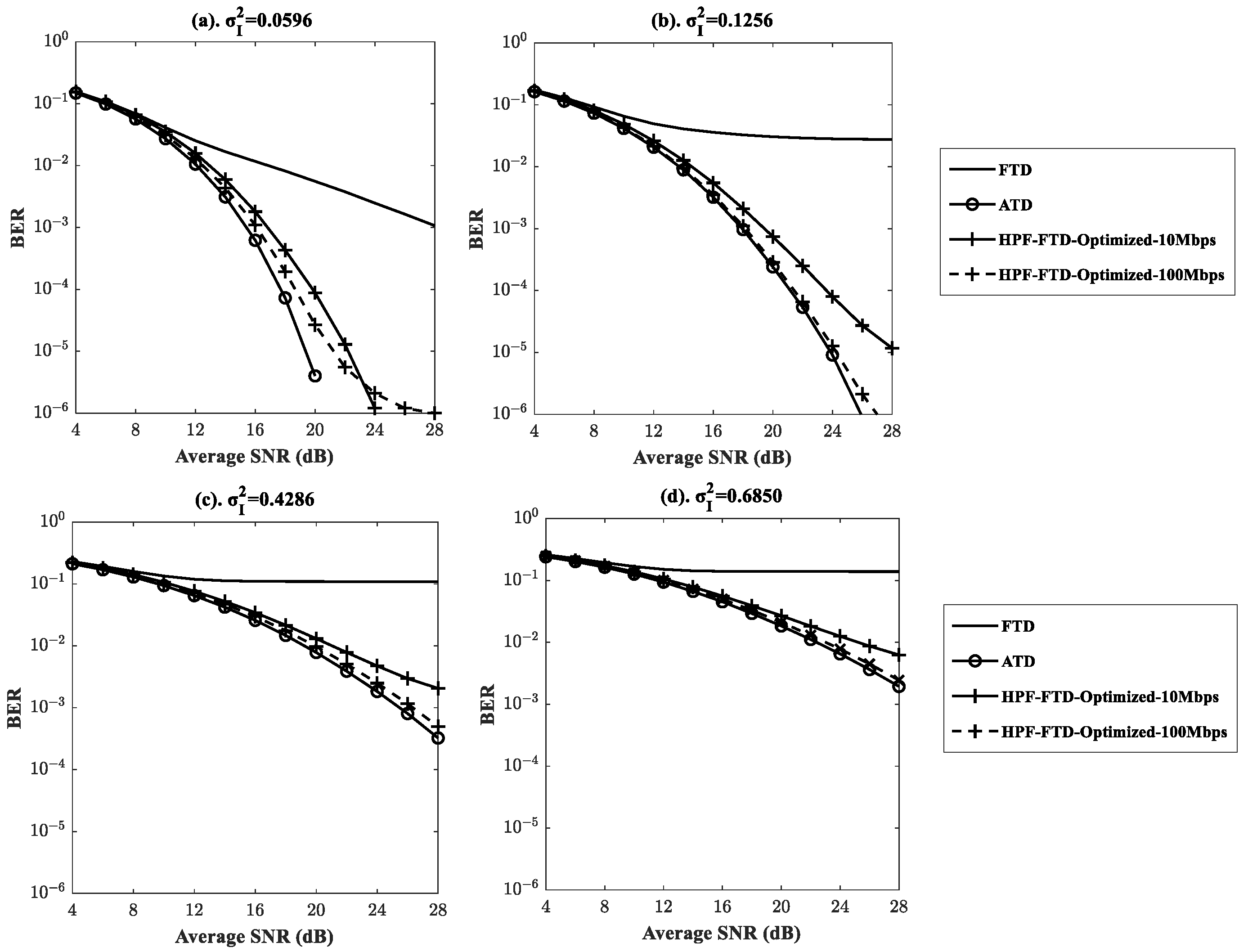
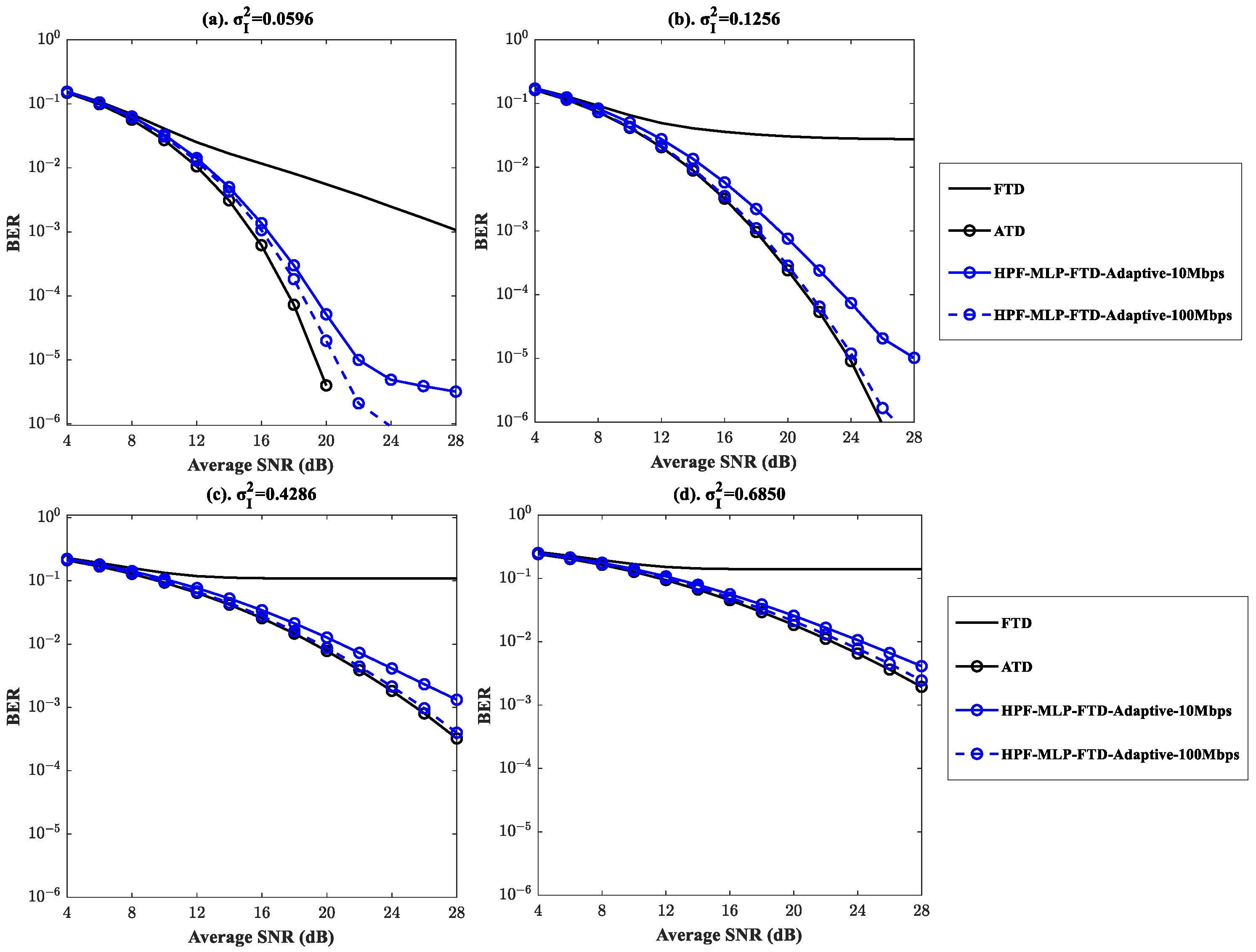
Figure 8 illustrates the BER performance of HPF-based FTD with the optimized HPF cutoff frequency at data rates of 10 Mbps and 100 Mbps. The optimized cutoff frequency was set according to the results from Figure 7. A similar BER performance was achieved by HPF-based FTD with the optimized cutoff frequency compared to ATD with precise CSI due to an effective turbulence effect mitigation. Figure 9 depicts the BER performance of fixed-threshold OOK detection with the MLP-assisted adaptive optimized cutoff frequency of HPF at data rates of 10 Mbps and 100 Mbps. The cutoff frequency of HPF was optimized under various turbulence channels and data rates by selecting the peak frequency component in the PSD of the OOK signal excluding the DC component, as illustrated in Figure 10. The BER performance of the proposed MLP-assisted adaptive method is similar to that of the HPF-based FTD with the optimized cutoff frequencies of the HPF, as shown in Figure 8.

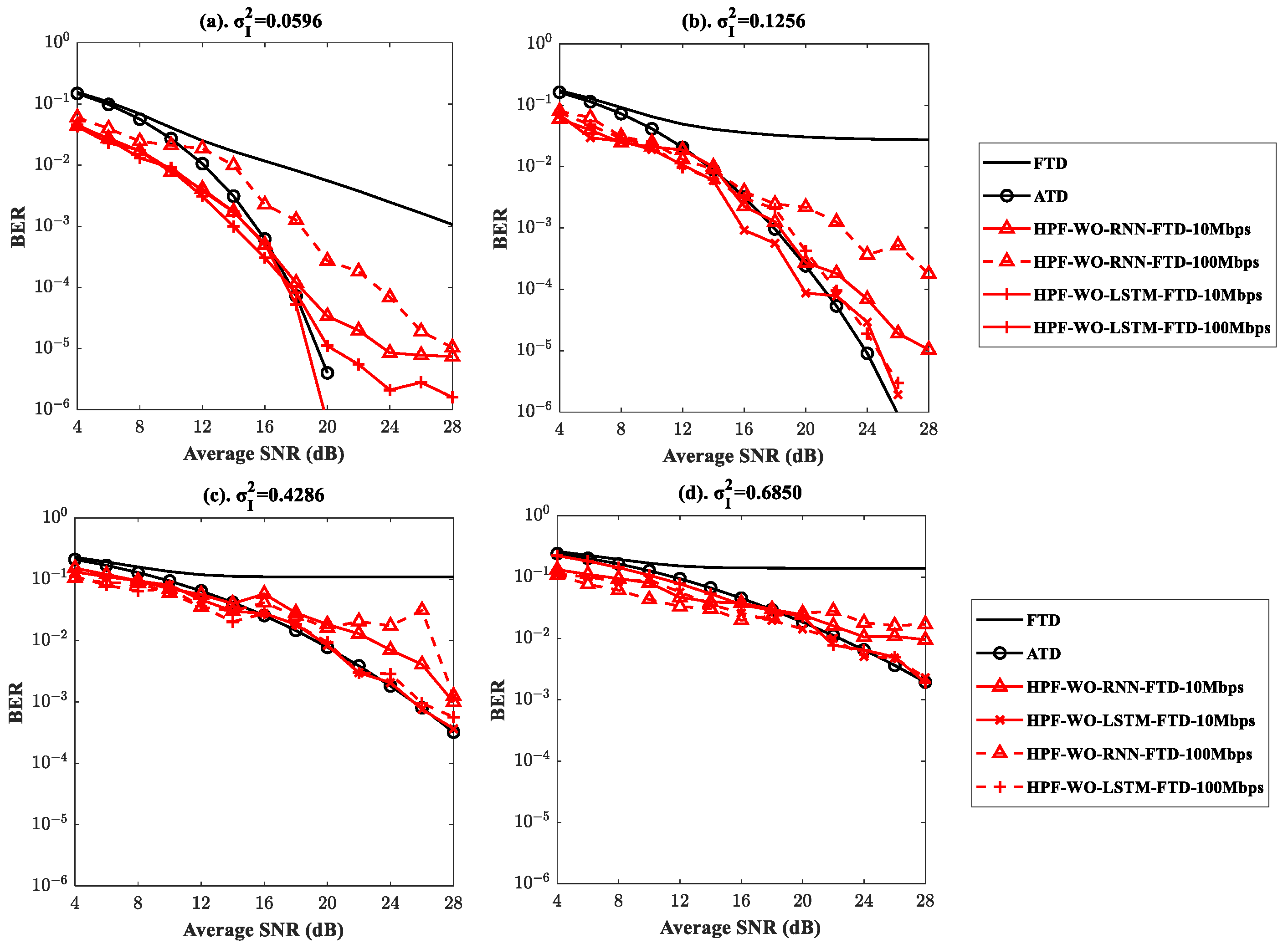
Figure 11 shows the BER performance of the proposed cascaded HPF and DL-based FTD without optimization of the HPF cutoff frequency under various turbulent channels and data rates. The RNN and LSTM models were used to recover the signal distortion from the HPF and mitigate the remnant scintillation effect without the optimized cutoff frequency of HPF. The cutoff frequency of the HPF was fixed at 1 kHz. Vanishing and exploding gradient BERs were observed by the proposed cascaded HPF and RNN methods at high SNR values because of the difficulty of capturing long-term dependency. The BER performance of the proposed cascaded HPF and LSTM methods was close to that of the ATD technique owing to the introduction of gating mechanisms. These gating mechanisms control the information flow and filter unimportant information; thus, the LSTM-based method can mitigate the effect of gradient explosions. Therefore, the proposed cascaded HPF and LSTM without optimization of the cutoff frequency technique can effectively compensate for the turbulence effect and recover the signal distortion.

Table 3. Accuracy and computational complexity of MLP-based adaptive cutoff frequency of HPF under ${\sigma }_I^2$ of 0.4286.

Data Rate	Training Data	Accuracy Rate	Training Time
10 Mbps	$1\times {10}^5$	91.22%	57 s
100 Mbps	$1\times {10}^6$	95.94%	747 s

shows the accuracy and computational complexity of MLP-based adaptive cutoff frequency of HPF under ${\sigma }_I^2$ of 0.4286 at data rates of 10 Mbps and 100 Mbps. Longer training times and higher accuracy were observed by higher data rate signal transmission due to the application of larger training datasets.

Table 4. Accuracy and computational complexity of cascaded HPF and DL-based FTD without optimized cutoff frequency under ${\sigma }_I^2$ of 0.4286.

DL Model	Data Rate	Training Data	Accuracy Rate	Training Time
RNN	10 Mbps	$1\times {10}^5$	92.67%	61 s
	100 Mbps	$1\times {10}^6$	89.75%	793 s
LSTM	10 Mbps	$1\times {10}^5$	96.63%	76 s
	100 Mbps	$1\times {10}^6$	94.23%	859 s

illustrates the computational complexity and accuracy of cascaded HPF and DL-based FTD without optimized cutoff frequency under ${\sigma }_I^2$ of 0.4286. A shorter training time was obtained by using the RNN model compared to the LSTM model owing to its simpler structure and lower computational complexity. However, a higher accuracy was achieved by applying the LSTM model due to the strong memory capabilities and flexibility, which has the capability of handling long-term dependencies. The accuracy and computational complexity of MLP-based adaptive cutoff frequency of HPF and cascaded HPF and DL-based FTD without optimized cutoff frequency were analyzed under ${\sigma }_I^2$ of 0.0596, 0.1256 and 0.6850, as shown in

Table 5. Accuracy and computational complexity of MLP-based adaptive cutoff frequency of HPF under various ${\sigma }_I^2$.

Atmospheric Turbulence	Data Rate	Training Data	Accuracy Rate	Training Time
0.0596	10 Mbps	$1\times {10}^5$	91.37%	59 s
	100 Mbps	$1\times {10}^6$	96.10%	740 s
0.1256	10 Mbps	$1\times {10}^5$	92.48%	54 s
	100 Mbps	$1\times {10}^6$	96.45%	763 s
0.6850	10 Mbps	$1\times {10}^5$	92.23%	61 s
	100 Mbps	$1\times {10}^6$	96.90%	803 s

,

Table 6. Accuracy and computational complexity of cascaded HPF and RNN-based FTD without optimized cutoff frequency under various ${\sigma }_I^2$.

Atmospheric Turbulence	Data Rate	Training Data	Accuracy Rate	Training Time
0.0596	10 Mbps	$1\times {10}^5$	89.52%	64 s
	100 Mbps	$1\times {10}^6$	87.90%	826 s
0.1256	10 Mbps	$1\times {10}^5$	87.34%	62 s
	100 Mbps	$1\times {10}^6$	87.12%	880 s
0.6850	10 Mbps	$1\times {10}^5$	90.24%	68 s
	100 Mbps	$1\times {10}^6$	89.42%	893 s

and

Table 7. Accuracy and computational complexity of cascaded HPF and LSTM-based FTD without optimized cutoff frequency under various ${\sigma }_I^2$.

Atmospheric Turbulence	Data Rate	Training Data	Accuracy Rate	Training Time
0.0596	10 Mbps	$1\times {10}^5$	97.31%	78 s
	100 Mbps	$1\times {10}^6$	94.90%	788 s
0.1256	10 Mbps	$1\times {10}^5$	96.12%	76 s
	100 Mbps	$1\times {10}^6$	95.23%	808 s
0.6850	10 Mbps	$1\times {10}^5$	97.12%	81 s
	100 Mbps	$1\times {10}^6$	96.81%	910 s

. A similar accuracy and computational complexity performance was obtained compared to these methods under ${\sigma }_I^2$ of 0.4286. Therefore, the proposed cascaded HPF and LSTM methods can effectively compensate for the turbulence effects under different data rates and turbulent channel conditions with relatively longer computational times. The application of other DL models, accuracy improvement of the RNN model, and computational complexity reduction in the LSTM model will be conducted in our future work.

5. Conclusions

In conclusion, we have proposed a DL-assisted HPF-based FTD for FSO communication systems. The performance of HPF-based FTD under different cutoff frequencies, MLP-assisted adaptive optimized cutoff frequency, and cascaded HPF and DL-based FTD without the optimization of cutoff frequency techniques were analyzed and compared to the conventional FTD and ATD with precise CSI under various scintillation effects and data rates. The proposed technique was evaluated via simulation. The simulation results demonstrated that the proposed MLP-assisted adaptive optimized cutoff frequency and cascaded LSTM and HPF methods were close to the ATD with precise CSI under various turbulent channels and data rates. Therefore, it provides a promising solution to address the scintillation effect in FSO communication systems.