Impact of Motion Characteristics of Airborne Platforms on the Performance of Space Laser Communication Links
Abstract
1. Introduction
2. Atmospheric Laser Communication Link Model
3. Simulations and Data Analysis
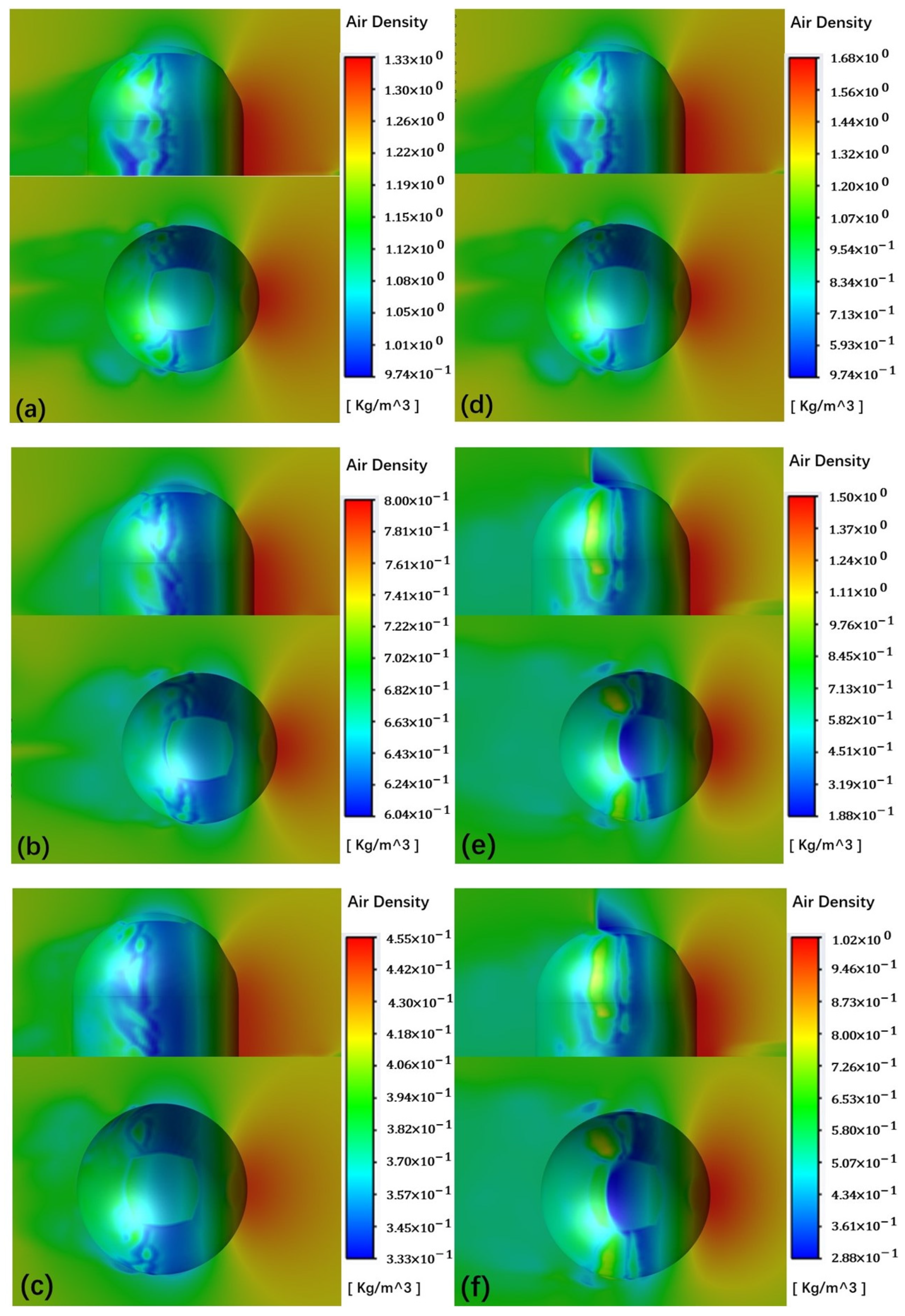
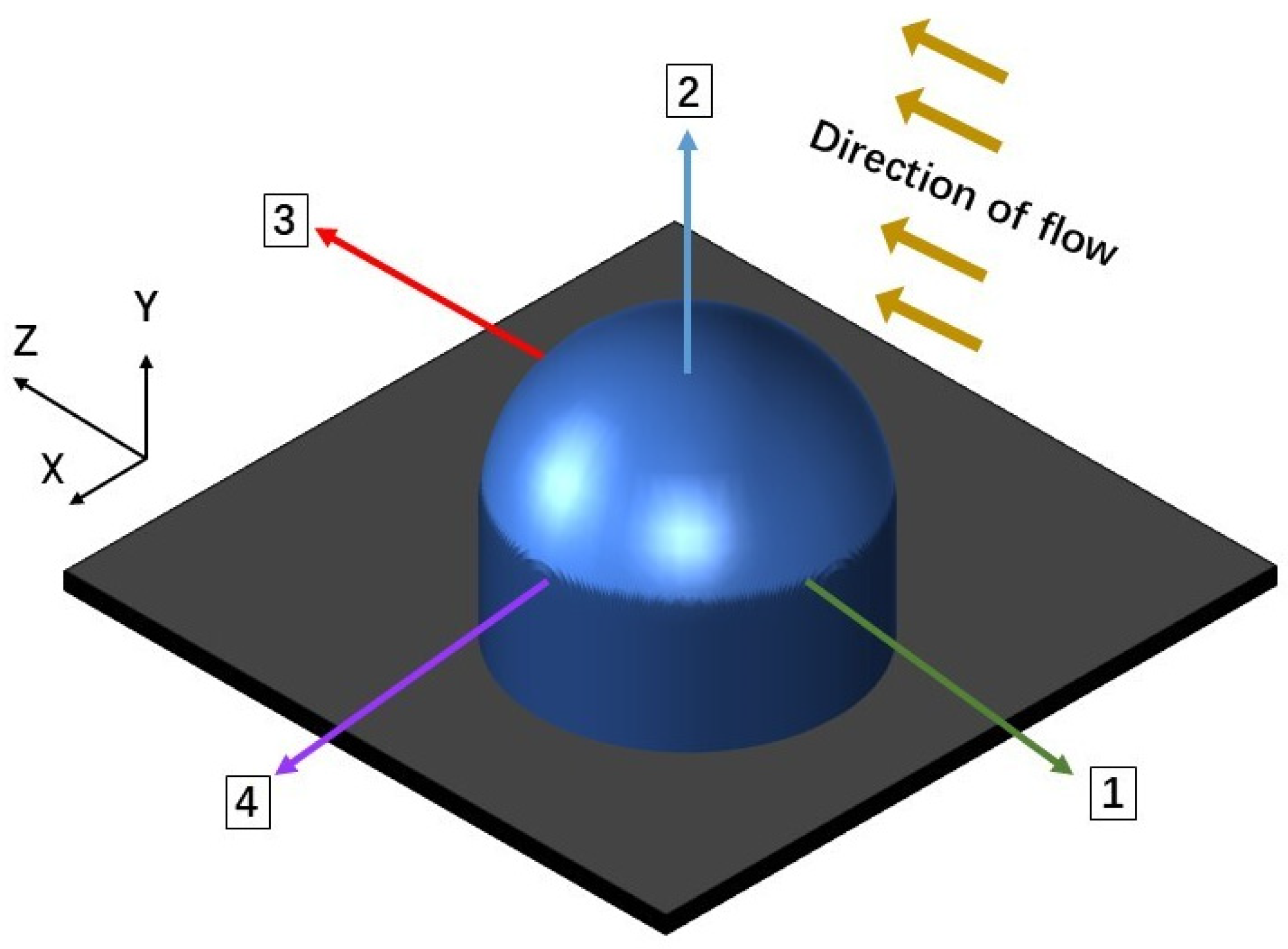
Simulation of Flow Fields and Beam Propagation
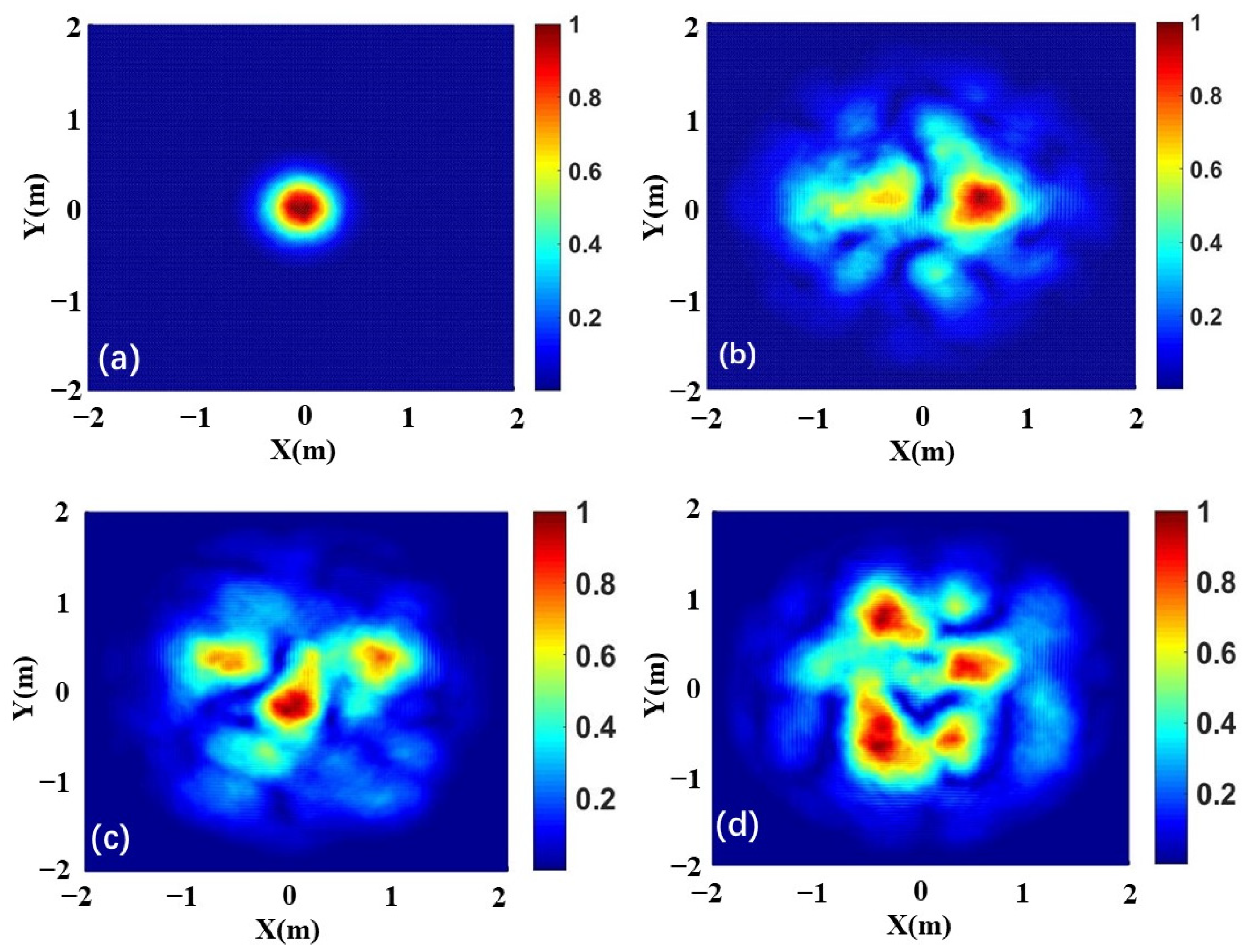
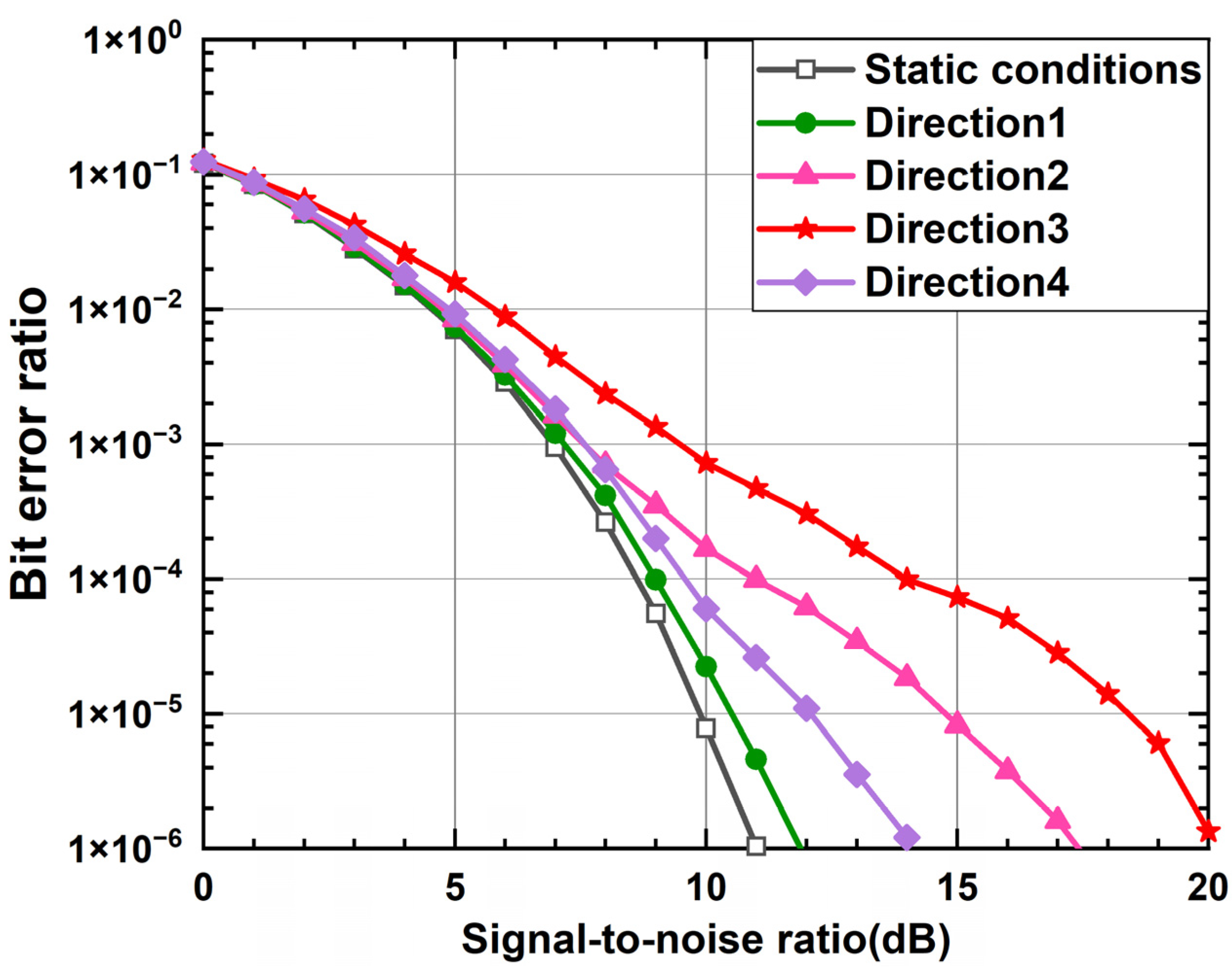
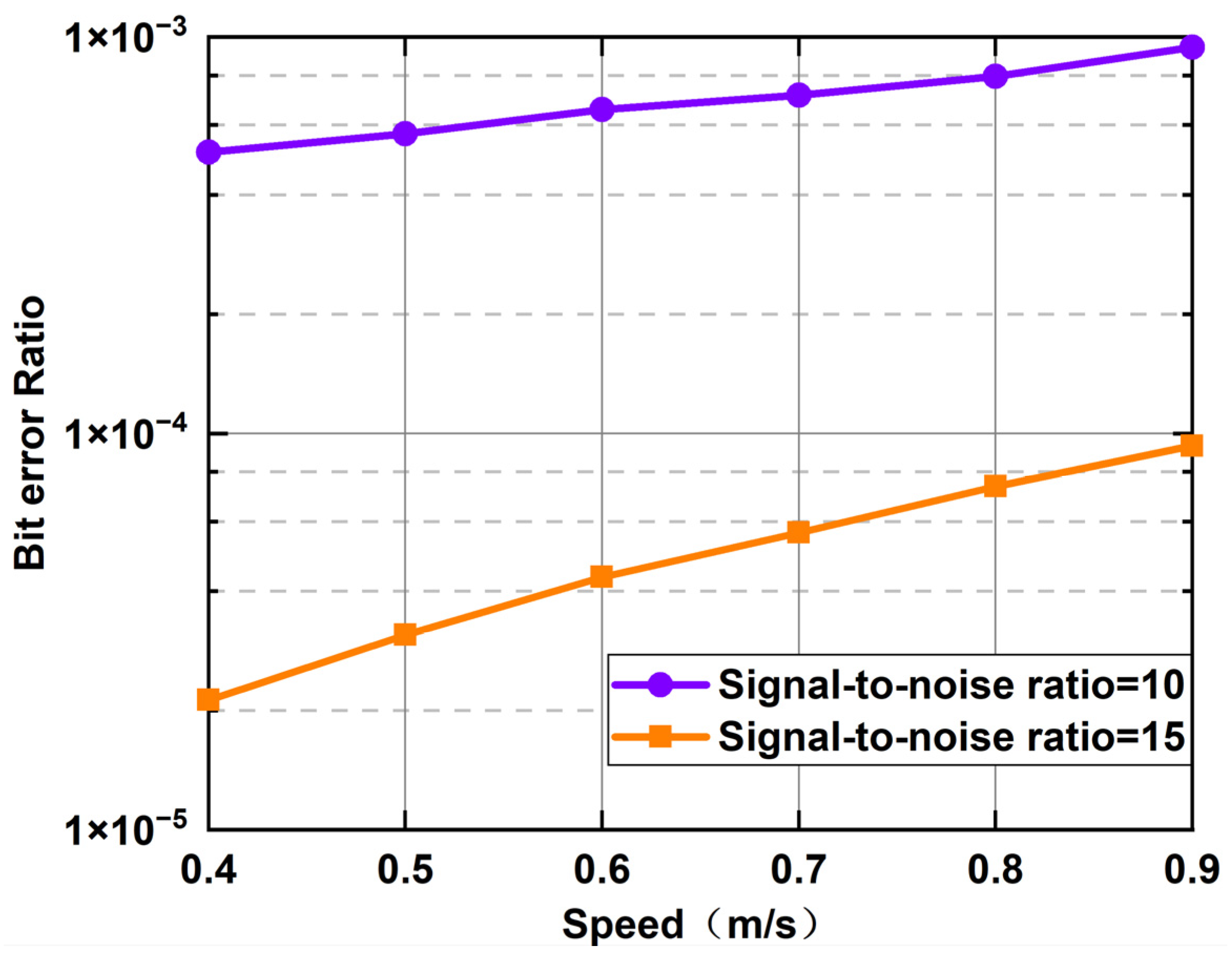
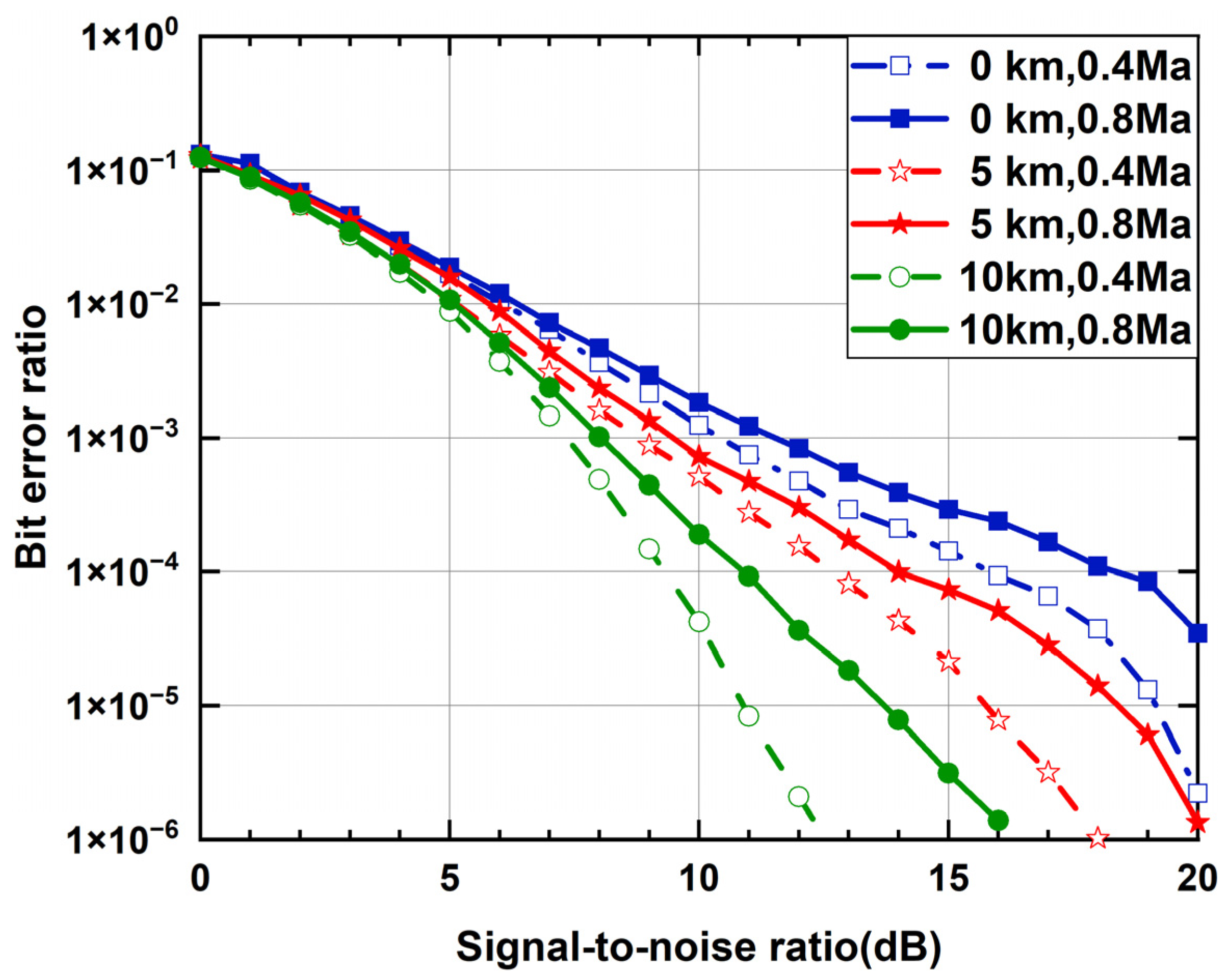
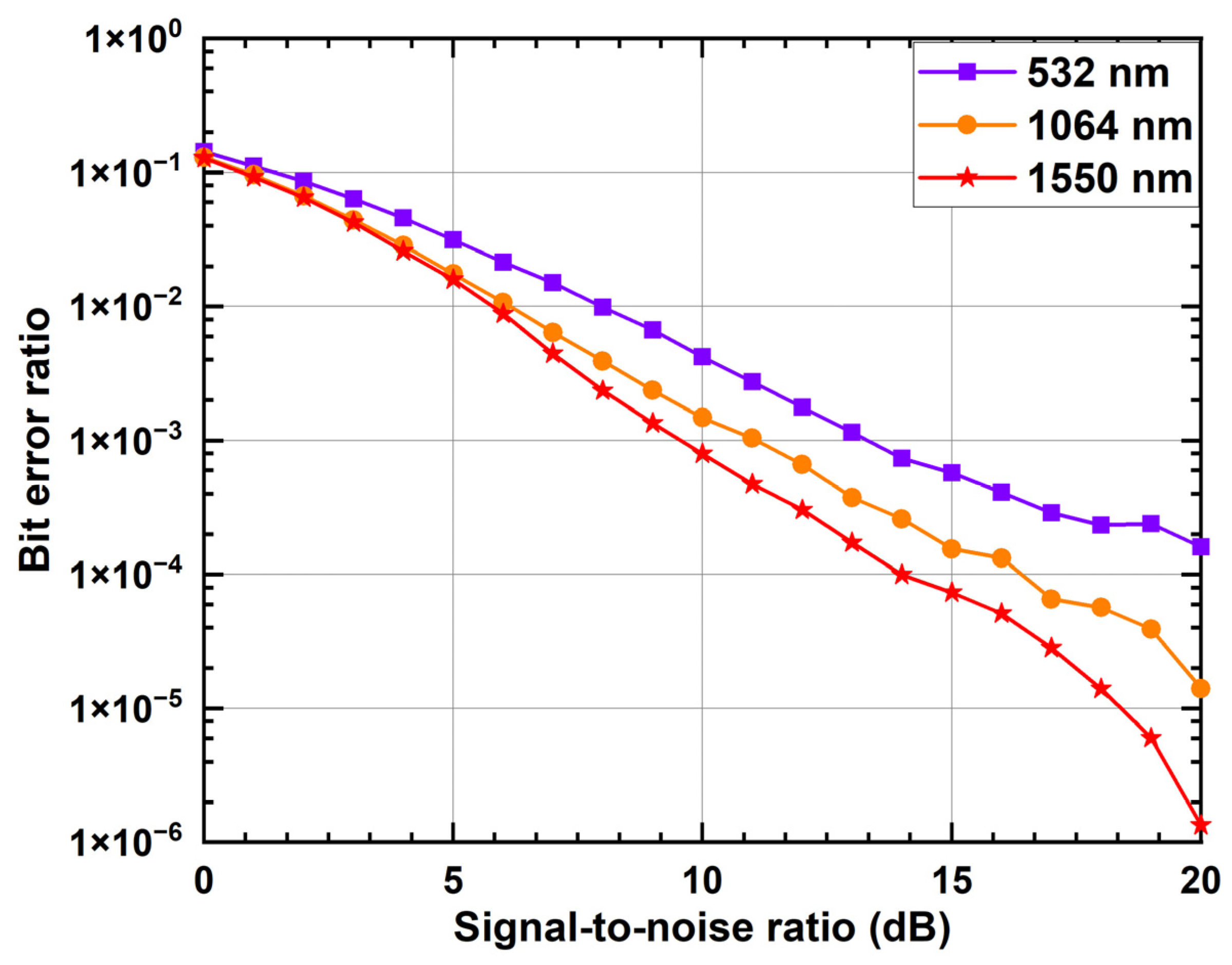
4. Simulation of Communication Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Tan, X.; Jia, J.; Dong, B.; Huang, C.; Luo, P.; Shi, J.; Chi, N.; Zhang, J. A Hybrid Millimeter-Wave and Free-Space-Optics Communication Architecture with Adaptive Diversity Combining and HARQ Techniques. Photonics 2023, 10, 1320. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Y.; Cai, R.; Zheng, A.; Yu, Z.; Wang, T.; Liu, Z.; Gao, S. Free-space communication turbulence compensation by optical phase conjugation. IEEE Photonics J. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Bai, J.; Wan, X.; Arslan, E.; Zong, X. Global Solar Radiation and Its Interactions with Atmospheric Substances and Their Effects on Air Temperature Change in Ankara Province. Climate 2024, 12, 35. [Google Scholar] [CrossRef]
- Wang, K.; Meng, W. Computational Analysis of Aero-Optical Distortions by Flow over a Cylindrical Turret. AIAA J. 2016, 54, 1461–1471. [Google Scholar] [CrossRef]
- Jumper, E.J.; Fitzgerald, E.J. Recent advances in aero-optics. Prog. Aerosp. Sci. 2001, 37, 299–339. [Google Scholar] [CrossRef]
- Jiang, L.; Yu, X.; Wang, C.; Dai, T.; Dai, Z.; Tong, S. Analysis of imaging quality of new laser communication system on missile in the aerodynamic environment. J. Russ. Laser Res. 2021, 42, 210–218. [Google Scholar] [CrossRef]
- Zheng, A.R.; Huang, Y.; Gao, S.M. Modeling and spatial diversity-based receiving improvement of in-flight UAV FSO communication links. Appl. Sci. 2021, 11, 6365. [Google Scholar] [CrossRef]
- Dabiri, M.T.; Sadough, S.M.S.; Khalighi, M.A. Channel modeling and parameter optimization for hovering UAV-based free-space optical links. IEEE J. Sel. Areas Commun. 2018, 36, 2104–2113. [Google Scholar] [CrossRef]
- Lyke, S.D.; Voelz, D.G.; Roggemann, M.C. Probability density of aperture-averaged irradiance fluctuations for long range free space optical communication links. Appl. Opt. 2009, 48, 6511–6527. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Mei, H.; Ye, S.; Tao, Z.; Deng, H.; Wu, X.; Rao, R. Spatial Fluctuations of Optical Turbulence Strength in a Laboratory Turbulence Simulator. Photonics 2024, 11, 229. [Google Scholar] [CrossRef]
- Ding, H.; Yi, S.; Zhu, Y.; He, L. Experimental investigation on aero-optics of supersonic turbulent boundary layers. Appl. Opt. 2017, 56, 7604–7610. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Yu, H.; Yao, X. Passive fluidic control on aero-optics of transonic flow over turrets with rough walls. Phys. Fluids 2022, 34, 109–115. [Google Scholar] [CrossRef]
- Jacob, M.; Stanislav, G.; Nicholas, D.L.; Jumper, E.J. Shock-related effects on aero-optical environment for hemisphere-on-cylinder turrets at transonic speeds. Appl. Opt. 2017, 56, 4814–4824. [Google Scholar]
- Pond, J.E.; Sutton, G.W. Aero-Optic Performance of an Aircraft Forward-Facing Optical Turret. J. Aircr. 2006, 43, 600–607. [Google Scholar] [CrossRef]
- Beauchamp, R.L.; Fiorino, S.T. Propagation of laser light through aero-optic flow: Dry air at 0.4 Mach with three-dimensional turret. In Proceedings of the SPIE—The International Society for Optical Engineering, Baltimore, MD, USA, 23–27 April 2012; Volume 8380, p. 18. [Google Scholar]
- Yang, B.; Yu, H.; Liu, C.; Wei, X.; Fan, Z.; Miao, J. An Aero-Optical Effect Analysis Method in Hypersonic Turbulence Based on Photon Monte Carlo Simulation. Photonics 2023, 10, 172. [Google Scholar] [CrossRef]
- Kalensk, M.; Gordeyev, S.; Jumper, E.J. In-flight studies of aero optical distortions around AAOL-BC. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; AIAA: Reston, VA, USA, 2019; p. 3253. [Google Scholar]
- Wayne, D.T.; Phillips, R.L.; Andrews, L.C.; Leclerc, T.; Sauer, P. Observation and Analysis of Aero-Optic Effects on the ORCA Laser Communication System. In Proceedings of the Atmospheric Propagation VIII, Orlando, FL, USA, 25–29 April 2011; SPIE: Bellingham, WA, USA, 2011; Volume 8038, pp. 101–112. [Google Scholar]
- Phillips, R.L.; Andrews, L.C. FSO communications: Atmospheric effects for an airborne backbone. In Proceedings of the Atmospheric Propagation V, Orlando, FL, USA, 16–20 March 2008; SPIE: Bellingham, WA, USA, 2008; Volume 6951, pp. 11–21. [Google Scholar]
- Zhao, J.; Zhao, S.; Zhao, W.; Cai, J.; Liu, Y.; Li, X. Probability of fade for airborne laser communication system over exponentiated Weibull distribution under aperture averaging. Opt. Rev. 2018, 25, 487–492. [Google Scholar]
- Sun, X.W.; Yang, X.L.; Liu, W. Aero-optical suppression for supersonic turbulent boundary layer. J. Turbul. 2021, 22, 1–25. [Google Scholar] [CrossRef]
- Ninos, M.P.; Nistazakis, H.E.; Sandalidis, H.G.; Stassinakis, A.N.; Tombras, G.S. Block error rate performance of OOK free-space optical links over gamma–gamma turbulence channels with generalized non-zero boresight pointing error. IET Optoelectron. 2018, 12, 269–272. [Google Scholar] [CrossRef]
- Chang, Y.; Liu, Z.; Yao, H.; Gao, S.; Dong, K.; Liu, S. Performance Analysis of Multi-Hop FSOC over Gamma-Gamma Turbulence and Random Fog with Generalized Pointing Errors. Photonics 2023, 10, 1240. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, S.H.; Zhao, W.H.; Cai, J.; Liu, Y.; Li, X. BER performance analysis of M-ary PPM over exponentiated Weibull distribution for airborne laser communications. J. Opt. Technol. 2017, 84, 658–663. [Google Scholar] [CrossRef]


| Altitude/km | Temperature/K | Static Pressure/Pa |
|---|---|---|
| 0 | 288.15 | 101,325 |
| 5 | 255.67 | 54,048 |
| 10 | 223.25 | 26,499 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Gao, S.; Liu, Z.; Jiang, Q.; Meng, L.; Wang, H.; Dong, K. Impact of Motion Characteristics of Airborne Platforms on the Performance of Space Laser Communication Links. Photonics 2024, 11, 378. https://doi.org/10.3390/photonics11040378
Zhang X, Gao S, Liu Z, Jiang Q, Meng L, Wang H, Dong K. Impact of Motion Characteristics of Airborne Platforms on the Performance of Space Laser Communication Links. Photonics. 2024; 11(4):378. https://doi.org/10.3390/photonics11040378
Chicago/Turabian StyleZhang, Xin, Shiming Gao, Zhi Liu, Qingfang Jiang, Lixin Meng, Helong Wang, and Keyan Dong. 2024. "Impact of Motion Characteristics of Airborne Platforms on the Performance of Space Laser Communication Links" Photonics 11, no. 4: 378. https://doi.org/10.3390/photonics11040378
APA StyleZhang, X., Gao, S., Liu, Z., Jiang, Q., Meng, L., Wang, H., & Dong, K. (2024). Impact of Motion Characteristics of Airborne Platforms on the Performance of Space Laser Communication Links. Photonics, 11(4), 378. https://doi.org/10.3390/photonics11040378





