Abstract
Based on the two-dimensional (2D) nonlinear Schrödinger equation, we investigate the collapse dynamics of a vector vortex optical field (VVOF) in nonlinear Kerr media with parity–time (PT)-symmetric modulation. The critical power for the collapse of a VVOF in a Kerr-ROLP medium (Kerr medium with a real optical lattice potential) is derived. Numerical simulations indicate that the number, position, propagation distance, and collapse profile of the collapse of a VVOF in sine and cosine parity–time-symmetric potential (SCPT) Kerr media are closely related to the modulation depth, initial powers, and the topological charge number of a VVOF. The VVOF collapses into symmetric shapes during propagation in a Kerr-ROLP medium, and collapse shapes are sensitively related to the density of the PT-symmetric optical lattice potential. In addition, due to gain–loss, the VVOF will be distorted during propagation in the Kerr-SCPT medium, forming an asymmetric shape of collapse. The power evolution of the VVOF in a Kerr-SCPT medium as a function of the transmission distance with different modulating parameters and topological numbers is analyzed in detail. The introduction of PT-symmetric optical lattice potentials into nonlinear Kerr materials may provide a new approach to manipulate the collapse of the VVOF.
1. Introduction
In the past few decades, light field manipulation has been extensively studied, leading to many breakthroughs in research [1,2,3,4,5,6]. The nonlinear collapse phenomenon of a structured beam in nonlinear optical media has attracted much attention due to its fundamental interest and potential applications [7,8,9,10]. The collapse dynamics refer to a phenomenon in optics that the intensity of the optical field rapidly increases due to the nonlinear self-focusing effect of the medium, leading to localized concentration phenomena. In a medium undergoing self-focusing, the collapse of beams occurs once the input power surpasses a critical threshold. The local intensity of the optical field increases to a level where the nonlinear self-focusing effect can no longer sustain it, resulting in collapse. Following by other nonlinear phenomena like multiple photon absorption, plasma generation, or higher-order defocusing effects could inhibit the collapse of the beam. As a result, the beam can propagate and self-focus in filaments over a long range when the power exceeds the critical power [8,9,11,12,13,14,15]. Some typical applications include aerosol detection, plasma physics research, and the generation of sub-THz radiation [16,17,18,19]. Therefore, the dynamic manipulation of the collapse of a structured optical field is an important topic in nonlinear optics, such as the position of collapse, the critical power of collapse, and the suppression of collapse.
Recently, the concept of PT symmetry originated from the study of quantum mechanics and has been introduced into optical systems [20,21,22,23,24,25,26]. It is worth noting that the parity–time (PT)-symmetric lattice, as an interesting periodic structure, has been extensively studied in nonlinear optics and soliton physics [27,28,29,30]; in particular, the study of the stabilization mechanisms of various solitons in PT-symmetric systems has obtained fruitful achievements [31,32,33,34,35]. Many novel applications in linear and nonlinear PT symmetry optics systems have been demonstrated, such as the localization of light, unidirectional transmission, and information encryption [36,37,38,39,40]. The nonlinear collapse and evolution of different types of beams in PT-symmetrically modulated nonlinear media have recently been studied [10,41,42,43]. The PT-symmetric potential mainly affects the collapse of light beams through two mechanisms. On one hand, the propagation and focusing of the beam are manipulated by the modulation of the refractive index distribution of the lattice (the real part of the parity–time-symmetric potential). On the other hand, the energy distribution of the light beams is controlled through the gain–loss modulation of the lattice (the imaginary part of the parity–time symmetric potential). When the scalar vortex beams propagate in the PT-symmetric Kerr medium, the beams will collapse into a symmetrical or distorted shape under different modulation factors of the PT potential [10]. In addition, the state of the collapse of the light field is also affected by the vortex topological charge and the initial powers [10]. This work studies the collapse dynamics of vector vortex beams in Kerr media with PT-symmetric lattice modulation. Compared with scalar vortex beams, the collapse dynamics of the VVOF in PT-symmetrical Kerr media proceed with more complex evolution due to the involvement of different polarization components. In particular, the effect of the PT symmetry modulation of the complex refraction index on the collapse dynamics of vector vortex beams in the Kerr medium under different polarization topological charges is studied in detail. It is found that the collapse number, collapse location, and propagation distance for the collapse occurrence of the target beam are closely related to the modulation depth of the PT symmetry structure and the parameters of the initial vector vortex beam. When the vector vortex beams propagate in the Kerr medium with real optical lattices, the collapse positions are sensitively dependent on the density of the PT-symmetric optical lattice potential, initial powers, and polarization state of the light field. For the Kerr-SCPT medium with the gain–loss modulation, the VVOF distorts during propagation in the sine and cosine parity–time-symmetric potential (SCPT) Kerr (hereafter, we denote as the Kerr-SCPT) medium due to the existence of gain–loss, forming an asymmetric shape of collapse. These results provide a new means and a deeper understanding of manipulating the collapse of a VVOF in a PT-symmetric Kerr medium.
2. Theoretical Model
The optical lattice potential, Q(X, Y), with PT operator characteristics, is expressed in the form of a complex function as follows [44]:
Here, the real part V(X, Y) of Q(X, Y), even in X and Y, represents the refractive index modulation in optics, while the imaginary part function W(X, Y), odd in X and Y, represents the gain–loss; X = x/w0 and Y = y/w0 are the dimensionless transverse coordinates with w0 representing the beam waist width; V0 and W0 represent the modulation depth of V(X, Y) and W(X, Y), respectively. V(X, Y) and W(X, Y) can be expressed in SCPT forms V(X, Y) = cos2(X/d) + cos2(Y/d), W(X, Y) = sin(2X/d) + sin(2Y/d) [23], where d represents the modulator factor for the PT-symmetric lattice density. In particular, when V0 ≠ 0 and W0 = 0, Q(X, Y) = V0V(X, Y) degenerates the ROLP (real optical lattice potential). The refractive index and gain–loss distributions with different modulator factors d for the PT-symmetric lattice are shown in Figure 1.
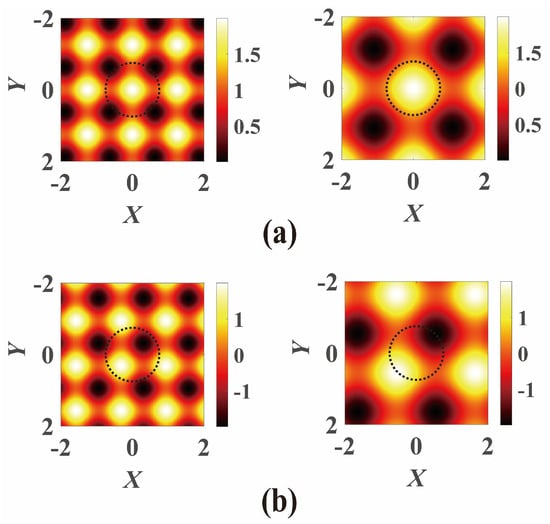
Figure 1.
The refractive index and gain–loss distributions with different modulator factors for the PT-symmetric lattice: (a) refractive index, (b) gain–loss. The left- and right-hand side figures are set as d = 0.4 and d = 0.7, respectively. The black dotted circle represents the width of the initial beam with n = 1 and m = 1.
The propagation dynamic behavior of a structured beam in the Kerr-SCPT medium is expressed by the following two-dimensional coupled nonlinear Schrodinger (NLS) equation [18]:
where the first term on the left of the equation represents the diffraction term of the light field, represents the Laplace operator, and the second term denotes the propagation term of the light field. The third term indicates the third-order Kerr nonlinear effect, and the fourth term denotes the modulation action term of the PT-symmetric optical lattice potential. and represent the left- and right-hand circular polarization components. The normalized two-dimensional coupled nonlinear Schrodinger (NLS) equation (Equation (1)) is obtained from the two-dimensional coupled nonlinear Schrödinger (NLS) equations [18,19,20], by setting X = x/w0, Y = y/w0, Z = z/(2kw02), and E(x, y) = kw0(2n2/n0)1/2A(x, y), where n2 is the third-order nonlinear coefficient, n0 is the linear refraction index of the medium, w0 is the beam width, and k is the linear wave number.
A vector vortex optical field (VVOF) can be expressed as follows:
where A0 is the amplitude of the VVOF, r is the normalized polar coordinates to w0, and φ and φ0 are the azimuth coordinates and the initial phase. ex and ey are the unit vectors in the x-direction and the y-direction. m and n represent the polarization and the vortex topological charges, respectively.
When propagating in the Kerr-ROLP medium (Kerr medium with a real optical lattice potential), the beam has two important physical quantities, namely, the beam power and the Hamiltonian. Let us define four quantities as follows [45,46]:
where I1 is the beam power, I2 the beam’s root-mean-square width, I3 the momentum, and I4 the Hamiltonian, which separately satisfy the evolution relations: dI1/dz = 0, dI2/dz = 0, dI3/dz = 0, and dI4/dz = 0. There is an important propagation invariant Q = 2I2(Z)I4(Z) − I32(Z)/4 that is related to the root-mean-square width I2 via the relation as follows [47]:
The general solution of Equation (5) with the VVOF as an initial field distribution can be given [42] as follows:
where
where , is a hypergeometric function. is the gamma function. Equation (6) describes the variation in the root-mean-square beam width of the VVOF in a Kerr-ROLP medium. When the Hamiltonian I4 = 0, the root-mean-square beam width became constant, and a balance was reached between the self-focus effect and the diffraction defocus effect [7,47]. Therefore, the critical amplitude A0 of the vector vortex beam can be calculated by setting I4 = 0, and then the critical power Pcr is obtained by the beam power :
The critical power of the collapse of scalar vortex beams in a Kerr medium can be given by assuming a topological charge of m = 0 and a modulation depth of V0 = 0 in Equation (8): , where the normalized critical power of a Gaussian beam in a Kerr medium PG = 4π [48,49].
The critical powers of the VVOF in a Kerr-ROLP medium with different V0 and d for various topological numbers are shown in Figure 2. The critical power in Equation (8) is determined by the parameters of the medium and beam, V0, d, n, and m. This critical power in Equation (8) indicates the total balance between the self-focusing, the diffraction, and the PT-symmetric lattice refractive index modulation during a vector vortex beam propagating in the PT-symmetry Kerr medium. The root-mean-square beam width remains constant when the input power is Pin = Pcr [50]. When the input power exceeds the threshold Pcr, the beam evolves into a global collapse, and the beam width decreases to zero over a finite distance. Notably, through numerical simulation, we found that the critical power of the vector vortex beam when it collapses is often smaller than the theoretical critical power. The critical power mentioned here is the upper threshold of the power when the beam collapses [8,50,51]. When the initial powers Pin = αPG (α is any positive value) are given, the initial amplitude of the vector vortex optical field E0 can be obtained by Pin = πE02n!/2n+1.
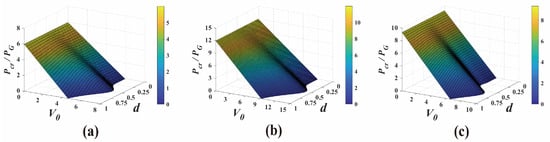
Figure 2.
The critical powers of the VVOF in a Kerr-ROLP medium with different V0 and d for various topological numbers: (a) n = 1, m = 1; (b) n = 1, m = 2; and (c) n = 2, m = 1.
3. Numerical Results and Analysis
Numerical calculations with split-step finite difference are carried out to further explore the collapse dynamics of a VVOF in a PT-symmetric Kerr medium, here λ = 0.53 μm and w0 = 10 μm. The evolution of the polarization state of a VVOF in a Kerr-SCPT can be described by the Stokes parameters: S0 = |EX|2 + |EY|2, S1 = |EX|2 − |EY|2, S2 = EXEY* + EYEX*, and S3 = i(EXEY* − EYEX*), where S0 denotes the light intensity and S1 represents the linear polarization component (its positive and negative values correspond to the horizontal and vertical directions, respectively). Similarly, positive and negative S2 represent the linear polarization components in the 45° and 135° directions, respectively, and the positive and negative values of S3 denote the left and right circular polarization components, respectively.
First, we investigate the collapse evolution of the VVOF in Kerr-ROLP media for m = 1, n = 1. The initial intensity profiles (Z = 0) of the optical field in Figure 3 are shown in the corresponding plots below. It can be seen from Figure 3a that when the VVOF propagates in the Kerr-ROLP medium with V0 = 0, the beam collapses at four points. These four points correspond to the positions of the four linear polarizations in the target beam, because the nonlinear refractive index of linearly polarized light is greater than that of circularly polarized light [18], thus the energy of the beam tends to be concentrated at the linearly polarized position. With the increase in V0 (the modulation depth of the real optical lattice potential), the four points that initially collapsed outside the axis gradually converge toward the center of the beam, and the center of the beam forms a partial collapse. This is because when the VVOF propagates in the Kerr-ROLP medium, the interaction among the lens convergence effect of the refractive index distribution of the real optical lattice potential (see Figure 1), the self-focusing effect of the Kerr nonlinear medium, and the linear diffraction effect of the beam leads to the difference in collapse positions.
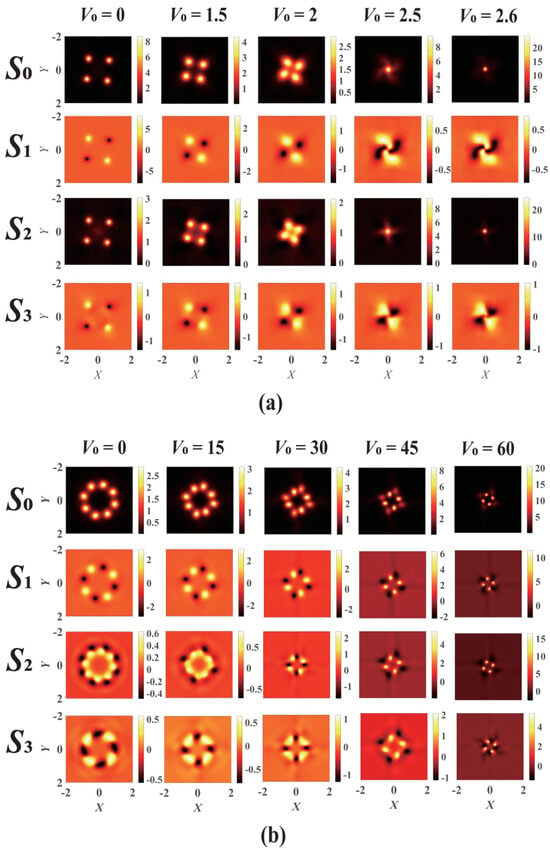
Figure 3.
The influence of different modulation depths on the evolution of the VVOF in a Kerr-ROLP medium with: (a) m = 1, n = 1, W0 = 0, d =0.75, Pin = 5.3 PG, Z = 1.305 and (b) m = 2, n = 1, W0 = 0, d = 0.75, Pin = 8.2 PG, Z = 0.34.
The collapse evolution of the VVOF with m = 1 and n = 1 in a Kerr-ROLP medium for different modulation depths V0 is shown in Figure 3b. With the increase in V0 (the optical lattice potential modulation depth), the eight collapse points outside the axis can be collapsed at four collapse positions where a higher refractive index is located. In addition, when m ≠ n, there is always an optical singularity located at the beam center (unlike the case of m = n, there can exist the optical field in the center of the beam such as m = n = 1); therefore, the beam never collapses at the beam center when m ≠ n.
The evolution of vector vortex beams in a Kerr-SCPT medium for different gain–loss modulations is shown in Figure 4. For the case m = 1 and n = 1, when W0 (the imaginary part gain–loss modulation depth) increases, three points of the original four collapse points gradually become darker, and finally there is only one collapse point, as seen in Figure 4a. On the other hand, for m = 2 and n = 1, the beam collapses into three or four collapse points with varying intensities instead of the original eight points as W0 increases, as shown in Figure 4b. The distortion and variation in the collapse positions are attributed to the modulation of the gain–loss distribution. The asymmetric collapse is attributed to the anti-centrosymmetric gain–loss modulation of the lattice.
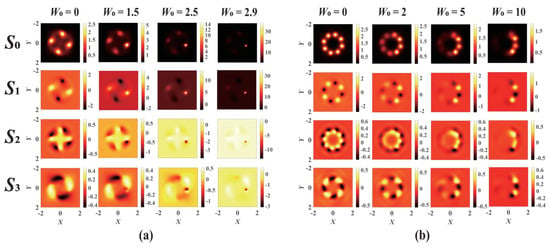
Figure 4.
The evolution of the VVOF in a Kerr-SCPT medium with different gain–loss modulations. (a) m = 1, n = 1, V0 = 4, d = 0.4, Pin = 2.6 Pcr, Z = 0.4 and (b) m = 2, n = 1, V0 = 0, d = 0.75, Pin = 8.2 PG, Z = 0.34.
The collapse distance of the VVOF as a function of the initial powers, modulation depth V0, and W0 is shown in Figure 5. The collapse distance is significantly shortened with increasing initial powers. The collapse distance of the light field is also shortened with increasing V0 and W0, which is consistent with our previous observations [8,9,10].
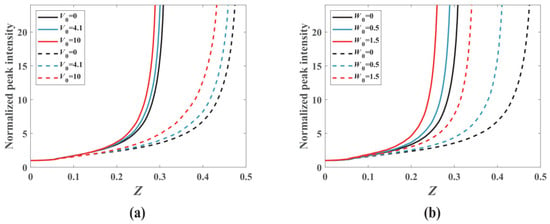
Figure 5.
The normalized peak intensity of the VVOF in a Kerr-SCPT medium as a function of the transmission distance. m = 2, n = 1, d = 0.4, the solid line indicates Pin = 11 PG, dotted line indicates Pin = 9.1 PG. (a) W0 = 0; (b) V0 = 0.
The effect of the variation in PT-symmetric optical lattice potential density on the propagation and collapse dynamics of the VVOF in a Kerr-ROLP medium is further intuitively described in 3-dimensional intensity evolutions, as shown in Figure 6, for the cases m = 1, n = 1 and m = 2, n = 1, respectively. The collapse positions of the beam are sensitively related to the optical lattice potential density. The main collapse positions of the VVOF with m = 2, n = 1 are 4 points for V0 = 4.1, W0 = 0, and Pin = 1.7 Pcr. It is worth noting that the collapse of the VVOF with d = 0.4 and d = 0.19 is at opposite positions, as shown in Figure 6b. This is because the refractive index distribution modulated by the potential density of the PT-symmetric optical lattice gradually turns the collapse point to a higher refractive index position. Therefore, the results confirm that the positions and number of collapses of the VVOF in the PT-symmetric optical lattice can be manipulated by the potential density, initial powers, topological charge number, and modulation depth.
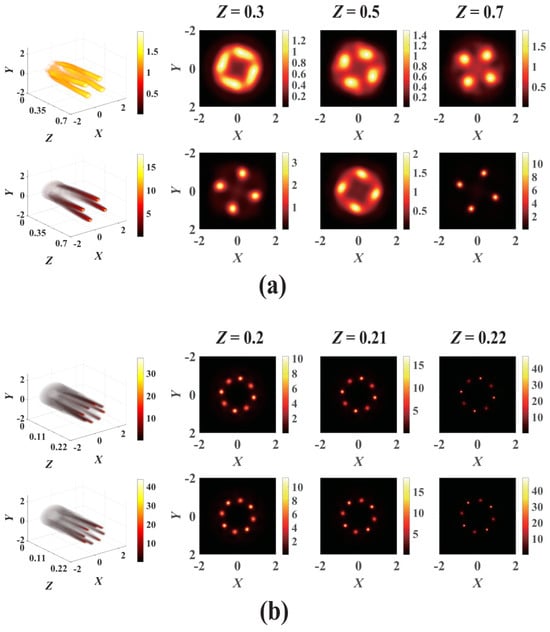
Figure 6.
The evolution of the VVOF in a Kerr-ROLP medium for different PT-symmetric lattice modulation densities; (a) m = 1, n = 1, V0 = 4, W0 = 0, Pin = 2.6 Pcr. The first line plot: d = 0.2, the second line plot: d = 0.4; (b) m = 2, n = 1, V0 = 4.1, W0 = 0, Pin = 1.7 Pcr, the first line plot: d = 0.19, the second line plot: d = 0.4.
For Kerr-SCPT media, the collapse points formed on the VVOF section present an asymmetric and non-uniform distribution due to the gain–loss modulation, as shown in Figure 7. Different from the Kerr-ROLP medium, the energy can be more concentrated on one point or side, whereas the intensity of a certain point or side of the beam is weakened. The number and positions of the final collapse points of the VVOF are significantly dependent on the modulation of gain–loss. It provides an effective means to manipulate the collapse of the VVOF in Kerr-SCPT media.
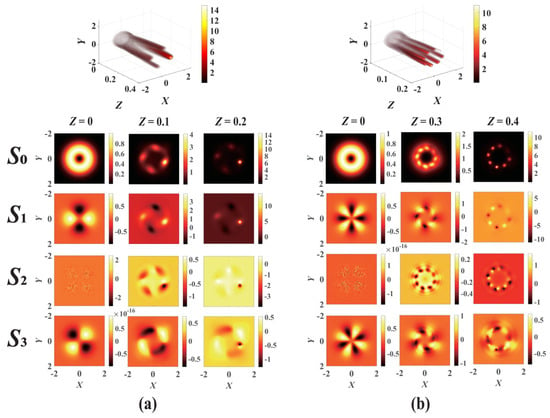
Figure 7.
The evolution of the VVOF in a Kerr-SCPT medium with different modulation depths and modulation factors: (a) m = 2, n = 1, V0 = 4.1, W0 = 4.5, d = 0.7, Pin = 1.7 Pcr; (b) m = 1, n = 1, V0 = 4, W0 = 2.5, d = 0.4, Pin = 2.6 Pcr.
When the VVOF propagates in the PT-Kerr medium, the field distribution and reshape of the VVOF vary due to the influence of the self-focusing of the Kerr medium, the real refractive index modulation, and optical diffraction in the PT lattice potential. Therefore, when the VVOF is modulated by gain–loss, the ratio of the gain–loss suffered by each point in the optical field is always changing. The proportion of the gain–loss modulation received by each point on the VVOF is closely dependent on the density of the PT optical lattice potential d, which determines the relative position of each point on the VVOF and the lattice potential.
The normalized powers of the VVOF in a Kerr-SCPT medium as a function of the transmission distance with different modulating parameters W0, V0, and d and topological numbers (m, n) are shown in Figure 8. The powers have been normalized to their initial powers. The powers remain invariant if W0 = 0 because of the conservation of energy. When d = 0.25, V0 = 0, and W0 ≠ 0, the powers of the VVOF increase during propagation in a Kerr-SCPT medium, indicating that the gain effect of the VVOF is greater than the loss effect. On the contrary, if d = 0.45, V0 = 0, and W0 ≠ 0, the power of the VVOF weakens with the extension of transmission distance, indicating that the gain effect of the VVOF is less than the loss effect, as shown in Figure 8a. When V0 ≠ 0 and W0 ≠ 0, the powers of the VVOF are influenced by the refractive index modulation of V0 due to its effect on the evolution of the VVOF. The influence of V0 on the power of the VVOF depends on the relative position of the PT lattice potential. When the VVOF is subjected to more gain for the values of V0, the power of the VVOF will be enhanced. In the contrary scenario, the power of the VVOF will be weakened. As shown in Figure 8b, when d = 0.95 and W0 = 12, the power of the VVOF increases with the extension of the transmission distance. It is worth noting that with the increase in V0, the power enhancement trend of the VVOF decreases. This is because the increase in V0 changes the refractive index of the Kerr-SCPT medium and the field distribution of the VVOF, resulting in the change in the relative position of the VVOF and PT lattice potential. However, due to the complex evolution of the VVOF in the Kerr-SCPT medium, the gain–loss ratio of the VVOF may have large fluctuations, as shown in Figure 8b. Especially when the value of W0 is large, the powers are sensitively related to the variation in V0, as shown by the solid lines in Figure 8b with d = 0.45, W0 = 90, and the power curves of the VVOF show large fluctuations during propagation. In addition, the power variations are also related to the initial powers and the topological charge number (m and n), as shown in Figure 8c,d. The reason for the power changes is that the nonlinear refraction index and gain–loss are related to the initial powers, as shown in Figure 8c, whereas the distributions of the VVOF are modulated by the topological charge number (m and n), as shown in Figure 8d. Therefore, the powers of the VVOF in a Kerr-SCPT medium can be dynamically manipulated with the modulation of the gain–loss (W0), the real refractive index modulation depth (V0), initial power (Pin), and topological charge number (m and n) when W0 ≠ 0.
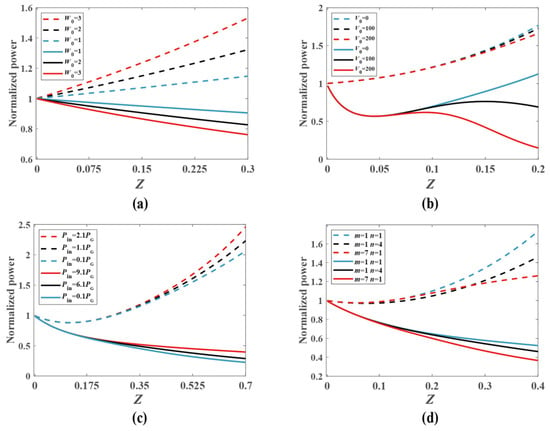
Figure 8.
The normalized power of the VVOF in a Kerr-SCPT medium as a function of the transmission distance with various modulating parameters: (a) m = 2, n = 1, V0 = 0, Pin = 5.2 PG, the solid line denotes d = 0.45, V0 = 0, dotted line indicates d = 0.25; (b) m = 2, n = 1, Pin = 5.2 PG, the solid line denotes d = 0.45, W0 = 90, dotted line indicates d = 0.95, W0 = 12; (c) m = 2, n = 1, V0 = 0, W0 = 12, the solid line denotes d = 0.4, dotted line indicates d = 0.9; (d) V0 = 0, W0 = 10, the solid line denotes d = 0.4, Pin = 8 PG, dotted line indicates d = 0.93, Pin = 2.1 PG.
4. Discussion
The nonlinear collapse of a structured light field and its control and manipulation have become a challenging research topic due to the rapid development of nonlinear optics and its wide application. The collapse properties of a VVOF in a PT-symmetry Kerr medium remain unexplored. With the introduction of PT-symmetric potential to a nonlinear Kerr medium, the collapse dynamics of a VVOF become more complex and provide a more flexible manipulation of a VVOF in nonlinear Kerr media due to the modulation of the symmetric distribution of the real part of the PT-symmetric potential (refraction index) and the asymmetric distribution of the imaginary part (gain–loss). In this work, the study of the collapse dynamics of a VVOF in nonlinear Kerr media with PT-symmetric modulation indicates that a VVOF collapses into symmetric shapes during propagation in a Kerr-ROLP medium, and collapse shapes are sensitively related to the density of the PT-symmetric optical lattice potential. In addition, due to the modulation of the asymmetric distribution of the gain–loss, the VVOF will be distorted during propagation in the Kerr-SCPT medium, forming an asymmetric shape of collapse. On the other hand, the power evolution of the VVOF in a Kerr-SCPT medium as a function of the transmission distance is closely related with different modulating parameters and topological charge numbers. The collapse dynamics of a VVOF propagating in a Kerr medium with a PT-symmetry complex refractive index distribution can extend our deeper understanding of the collapse dynamics in PT-symmetric Kerr media and provides a more flexible manipulation of the collapse of a VVOF in the Kerr-SCPT medium.
5. Conclusions
The collapse dynamics of a VVOF in PT-symmetric Kerr nonlinear media are demonstrated by using the 2D NLS equation. The critical power needed to keep the root-mean-square width of the beam constant during a VVOF propagating in the PT-symmetric Kerr nonlinear medium is derived theoretically. The numerical results indicate that the number, location, propagation distance for collapse, and profile of the collapse of the VVOF in SCPT Kerr media are closely related to the modulation depth, initial power, and the topological charge number of the VVOF. The VVOF collapses into symmetric shapes during propagation in a Kerr-ROLP medium, and collapse shapes are sensitively related to the density of the PT-symmetric optical lattice potential. In addition, due to gain–loss, the VVOF will be distorted during propagation in a Kerr-SCPT medium, forming an asymmetric shape of collapse. The power evolution of the VVOF in a Kerr-SCPT medium as a function of the transmission distance with different modulating parameters W0, V0, and d and topological numbers (m, n) is analyzed in detail.
Author Contributions
Conceptualization, R.-P.C.; methodology, R.-P.C., G.Y. and X.Z.; validation, R.-P.C. and K.-H.C.; investigation, X.Z., Y.W., Y.G. and R.-P.C.; data curation, X.Z., G.Y. and R.-P.C.; supervision, R.-P.C.; writing—original draft preparation, X.Z.; writing—review and editing, R.-P.C., Y.W., Y.G. and K.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Zhejiang Provincial Key Research and Development Program (No. 2022C04008) and the National Natural Science Foundation of China (No. 11874323).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Litchinitser, N.M. Structured Light Meets Structured Matter. Science 2012, 337, 1054–1055. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.P.; Dai, C.Q. Vortex solitons of the (3+1)-dimensional spatially modulated cubic-quintic nonlinear Schrodinger equation with the transverse modulation. Nonlinear Dyn. 2017, 90, 1563–1570. [Google Scholar] [CrossRef]
- Zhang, H.; Tzortzakis, S. Robust authentication through stochastic femtosecond laser filament induced scattering surfaces. Appl. Phys. Lett. 2016, 108, 211107. [Google Scholar] [CrossRef]
- Tan, C.; Li, N.; Xu, D.; Chen, Z. Spatial focusing of surface polaritons based on cross-phase modulation. Results Phys. 2021, 27, 104531. [Google Scholar] [CrossRef]
- Tian, X.; Duan, Y.; Liu, S.; Liu, Q.; Tan, C. Propagation and excitation properties of nonlinear surface plasmon polaritons in a rectangular barrier. Phys. E 2022, 144, 115417. [Google Scholar] [CrossRef]
- Liu, S.; Han, Z.; Li, D.; Tan, C. Analysis of Interference Effect in Double Optomechanically Induced Transparency System. Photonics 2024, 11, 289. [Google Scholar] [CrossRef]
- Chen, R.P.; Chew, K.H.; He, S.L. Dynamic Control of Collapse in a Vortex Airy Beam. Sci. Rep. 2013, 3, 1406. [Google Scholar] [CrossRef]
- Chen, R.P.; Chew, K.H.; Zhou, G.Q.; Dai, C.Q.; He, S.L. Vectorial effect of hybrid polarization states on the collapse dynamics of a structured optical field. Opt. Express 2016, 24, 28143–28153. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhong, L.X.; Chew, K.H.; Zhao, T.Y.; Zhang, X.B. Collapse dynamics of a vector vortex optical field with inhomogeneous states of polarization. Laser Phys. 2015, 25, 075401. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.H.; Chen, R.P. Collapse Dynamics of Vortex Beams in a Kerr Medium with Refractive Index Modulation and PT-Symmetric Lattices. Photonics 2022, 9, 249. [Google Scholar] [CrossRef]
- Kolesik, M.; Wright, E.M.; Moloney, J.V. Femtosecond filamentation in air and higher-order nonlinearities. Opt. Lett. 2010, 35, 2550–2552. [Google Scholar] [CrossRef]
- Trisorio, A.; Hauri, C.P. Control and characterization of multiple circularly polarized femtosecond filaments in argon. Opt. Lett. 2007, 32, 1650–1652. [Google Scholar] [CrossRef]
- Dubietis, A.; Tamosauskas, G.; Fibich, G.; Ilan, B. Multiple filamentation induced by input-beam ellipticity. Opt. Lett. 2004, 29, 1126–1128. [Google Scholar] [CrossRef]
- Bergé, L.; Gouédard, C.; Schjødt-Eriksen, J.; Ward, H. Filamentation patterns in Kerr media vs. beam shape robustness, nonlinear saturation and polarization states. Phys. D 2003, 176, 181–211. [Google Scholar] [CrossRef]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Robinson, P. Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 1997, 69, 507. [Google Scholar] [CrossRef]
- Kasparian, J.; Wolf, J.-P. Physics and applications of atmospheric nonlinear optics and filamentation. Opt. Express 2008, 16, 466–493. [Google Scholar] [CrossRef]
- Tao, H.; Lin, J.; Hao, Z.; Gao, X.; Song, X.; Sun, C.; Tan, X. Formation of strong light-trapping nano-and microscale structures on a spherical metal surface by femtosecond laser filament. Appl. Phys. Lett. 2012, 100, 201111. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, L.; Chu, W.; Zeng, B.; Gao, H.; Cheng, Y.; Liu, W. Simple method to enhance terahertz radiation from femtosecond laser filament array with a step phase plate. Opt. Lett. 2015, 40, 3838–3841. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex extension of quantum mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, S.; Guenther, U.; Moiseyev, N. Visualization of branch points in PT-symmetric waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef] [PubMed]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam dynamics in PT symmetric optical lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef] [PubMed]
- Ruter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Hu, S.; Ma, X.; Lu, D.; Yang, Z.; Zheng, Y.; Hu, W. Solitons supported by complex PT-symmetric Gaussian potentials. Phys. Rev. A 2011, 84, 043818. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, F.; Cao, S.; Xie, J.; He, Y. Multipole gap solitons in fractional Schrodinger equation with parity-time-symmetric optical lattices. Opt. Express 2020, 28, 1631–1639. [Google Scholar] [CrossRef] [PubMed]
- Konotop, V.V.; Yang, J.K.; Zezyulin, D.A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Zeng, L.W.; Zeng, J.H. Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities. Commun. Phys. 2020, 3, 26. [Google Scholar] [CrossRef]
- Tamilselvan, K.; Govindarajan, A.; Inbavalli, I.; Alagesan, T.; Lakshmanan, M. Modulational instability in PT-symmetric Bragg grating structures with saturable nonlinearity. Phys. Rev. A 2023, 107, 053510. [Google Scholar] [CrossRef]
- Thasneem, A.R.; Subha, P.A. One-dimensional PT-symmetric eigenmodes in k-wave number Scarf II potential with defocusing nonlinearity. Phys. Scr. 2023, 98, 035208. [Google Scholar] [CrossRef]
- Li, L.; Li, H.G.; Ruan, W.; Leng, F.C.; Luo, X.B. Gap solitons in parity-time-symmetric lattices with fractional-order diffraction. J. Opt. Soc. Am. B 2020, 37, 488–494. [Google Scholar] [CrossRef]
- Che, W.W.; Yang, F.W.; Cao, S.L.; Wu, Z.L.; Zhu, X.; He, Y.J. Gray solitons in parity-time-symmetric localized potentials with fractional-order diffraction. Phys. Lett. A 2021, 413, 127606. [Google Scholar] [CrossRef]
- Li, J.W.; Zhang, Y.P.; Zeng, J.H. Matter-wave gap solitons and vortices in three-dimensional parity-time-symmetric optical lattices. Iscience 2022, 25, 104026. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.J.; Hang, C.; Huang, G.X. Multidimensional optical solitons and their manipulation in a cold atomic gas with a parity-time-symmetric optical Bessel potential. Phys. Rev. A 2023, 107, 053501. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zeng, J.H. Gap solitons in parity-time symmetric moire optical lattices. Photonics Res. 2023, 11, 196–202. [Google Scholar] [CrossRef]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian photonics based on parity-time symmetry. Nat. Photonics 2017, 11, 752–762. [Google Scholar] [CrossRef]
- Musslimani, Z.H.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N. Optical solitons in PT periodic potentials. Phys. Rev. Lett. 2008, 100, 030402. [Google Scholar] [CrossRef]
- Zyablovsky, A.A.; Vinogradov, A.P.; Pukhov, A.A.; Dorofeenko, A.V.; Lisyansky, A.A. PT-symmetry in optics. Phys.-Uspekhi 2014, 57, 1063–1082. [Google Scholar] [CrossRef]
- Hang, C.; Zezyulin, D.A.; Huang, G.X.; Konotop, V.V.; Malomed, B.A. Tunable nonlinear double-core PT-symmetric waveguides. Opt. Lett. 2014, 39, 5387–5390. [Google Scholar] [CrossRef]
- Ramezani, H.; Kottos, T.; El-Ganainy, R.; Christodoulides, D.N. Unidirectional nonlinear PT-symmetric optical structures. Phys. Rev. A 2010, 82, 043803. [Google Scholar] [CrossRef]
- Yao, G.; Chew, K.H.; Wu, Y.; Li, Y.H.; Chen, R.P. Propagation dynamics of vector vortex beams in a strongly nonlocal nonlinear medium with parity-time-symmetric potentials. J. Opt. 2022, 24, 035606. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z.; Mihalache, D. Soliton formation and stability under the interplay between parity-time-symmetric generalized Scarf-II potentials and Kerr nonlinearity. Phys. Rev. E 2020, 102, 012216. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Malomed, B.A. Dynamical control of solitons in a parity-time-symmetric coupler by periodic management. Commun. Nonlinear Sci. Simul. 2019, 79, 104906. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Garcia-Ripoll, J.J.; Perez-Garcia, V.M.; Torres, P. Extended parametric resonances in nonlinear Schrödinger systems. Phys. Rev. lett 1999, 83, 1715. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Torres, P.J.; Montesinos, G.D. The method of moments for nonlinear Schrodinger equations:: Theory and applications. SIAM J. Appl. Math. 2007, 67, 990–1015. [Google Scholar] [CrossRef]
- Chen, R.-P.; Yin, C.-F.; Chu, X.-X.; Wang, H. Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 2010, 82, 043832. [Google Scholar] [CrossRef]
- Kruglov, V.; Logvin, Y.A.; Volkov, V. The theory of spiral laser beams in nonlinear media. J. Mod. Opt. 1992, 39, 2277–2291. [Google Scholar] [CrossRef]
- Fibich, G.; Gavish, N. Critical power of collapsing vortices. Phy. Rev. A 2008, 77, 045803. [Google Scholar] [CrossRef]
- Fibich, G.; Gaeta, A.L. Critical power for self-focusing in bulk media and in hollow waveguides. Opt. Lett. 2000, 25, 335–337. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-Trapping of Optical Beams. Phys. Rev. Lett. 1964, 13, 479. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).