Fundamental Limits on Earth-like Exoplanet Imaging with Large Telescopes Employing Laser Tomographic Adaptive Optics Systems: A Comparative Analysis of LGS AO and LTAO Systems
Abstract
1. Introduction
2. Assumptions
- We consider that the sensing wavelength is the same as the imaging wavelength, ignoring differential chromatic effects.
- Independent tip/tilt correction was performed.
- We do not consider the impacts of telescope characteristics, such as the central obscuration ratio, primary mirror segmentation, or secondary mirror supports, regarding the high-contrast imaging capabilities [22].
- The coronagraph is assumed to be a “perfect coronagraph”, which is used to suppress the diffraction pattern of stellar light [23].
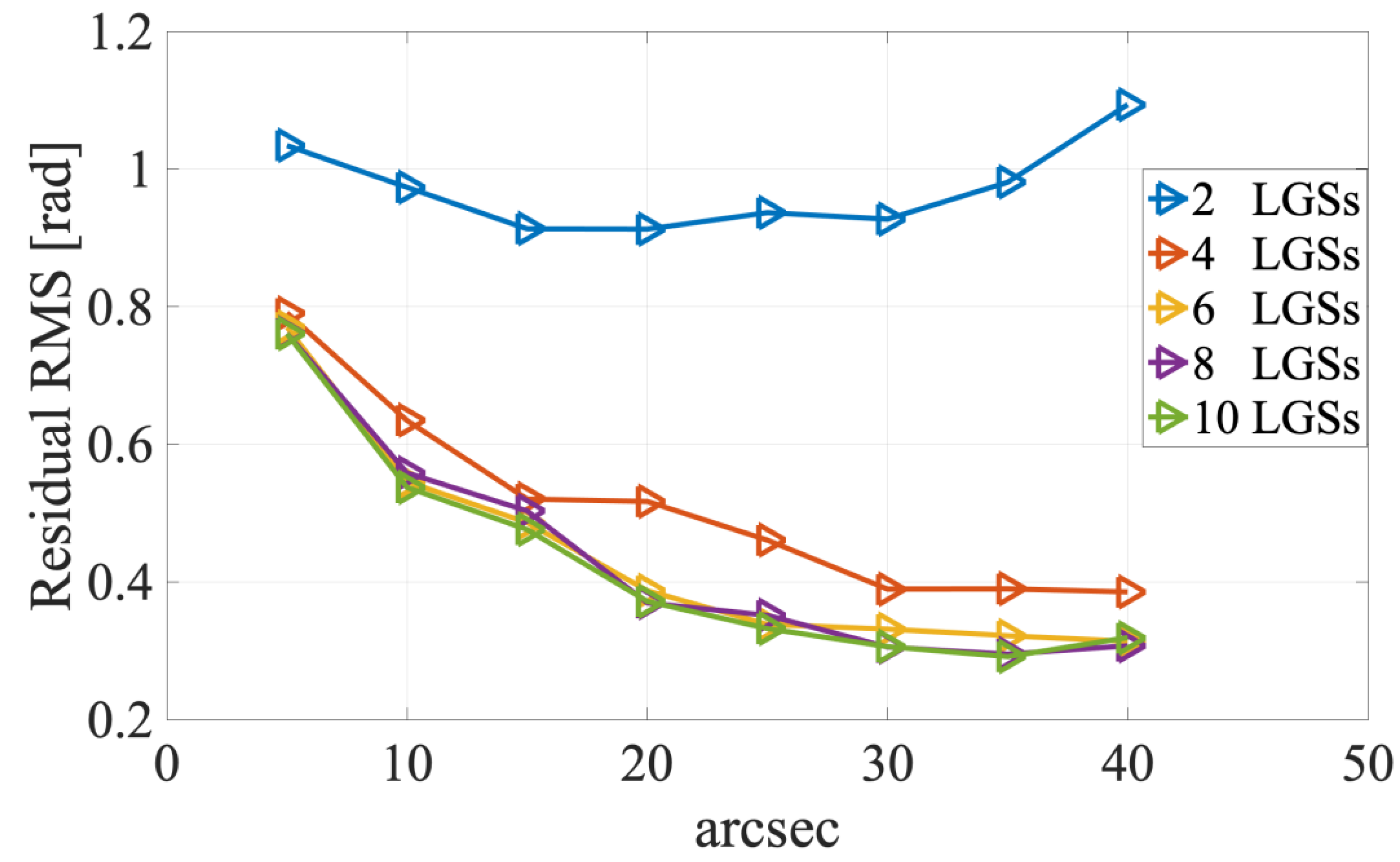
3. The Residual Phase Variance of Laser Tomographic Adaptive Optics and LGS Constellation Optimization
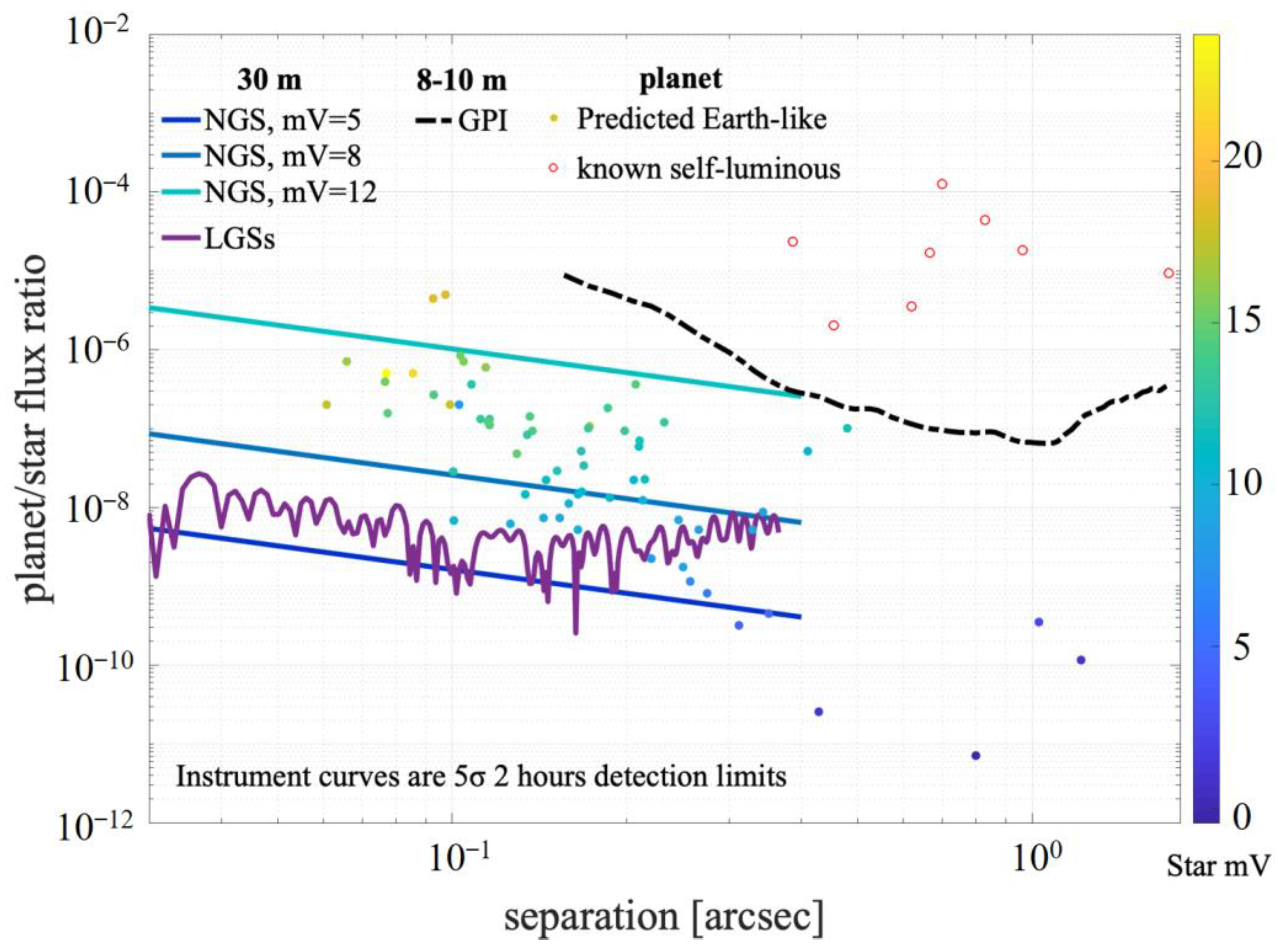
4. Limiting Post-Coronagraphic Contrast under Minimum Mean Square Error Control of Laser Tomographic Adaptive Optics
5. Discussion
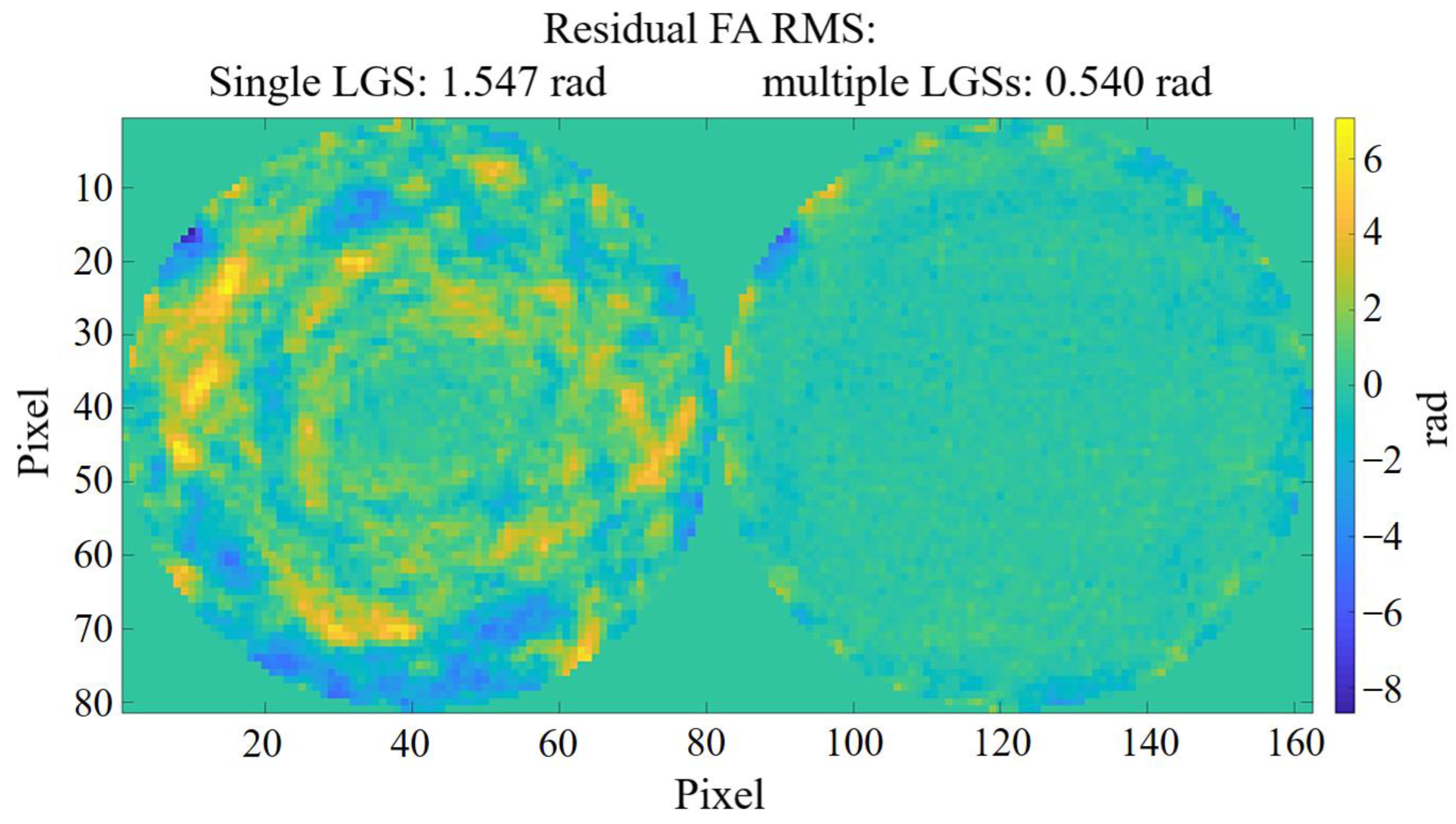
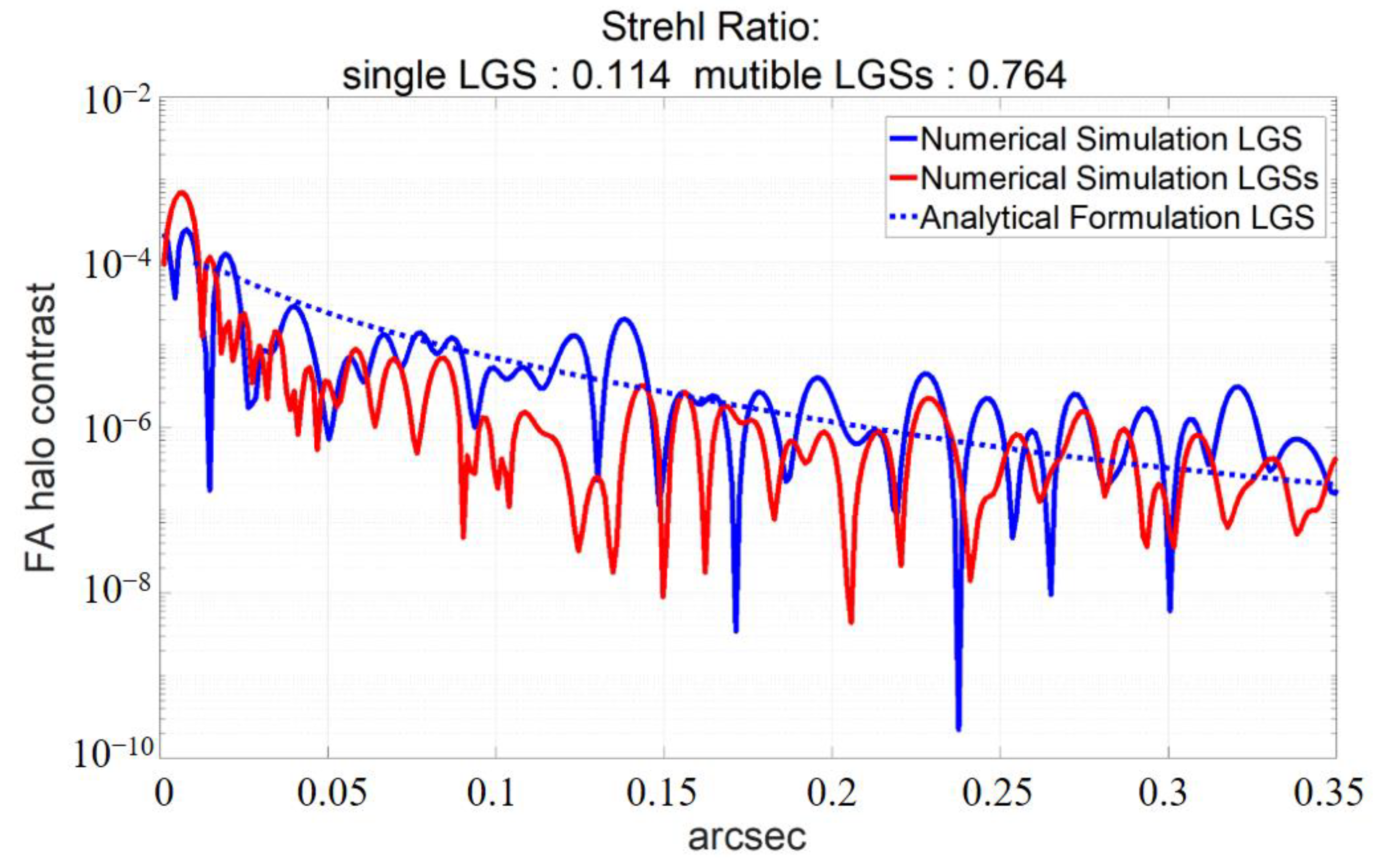
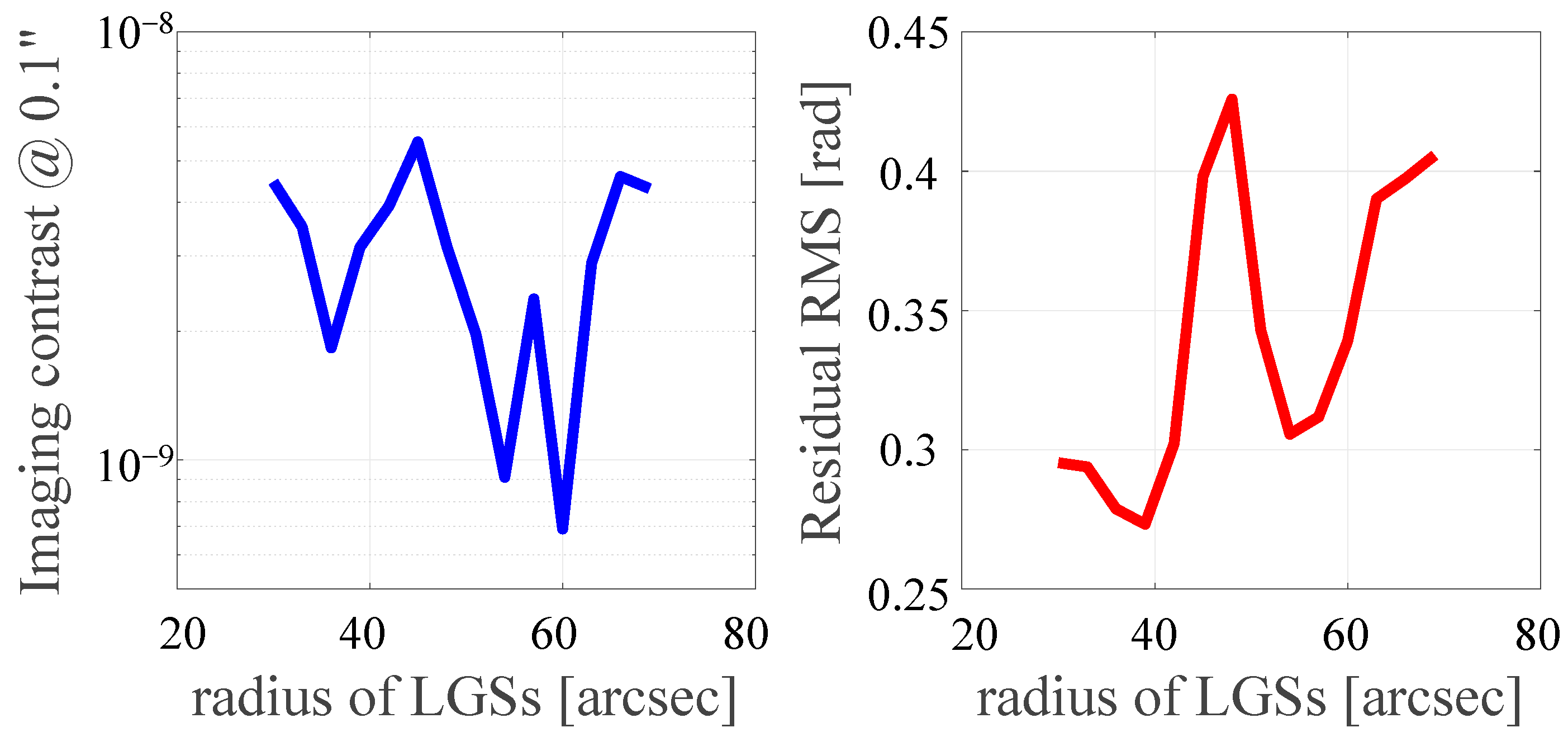
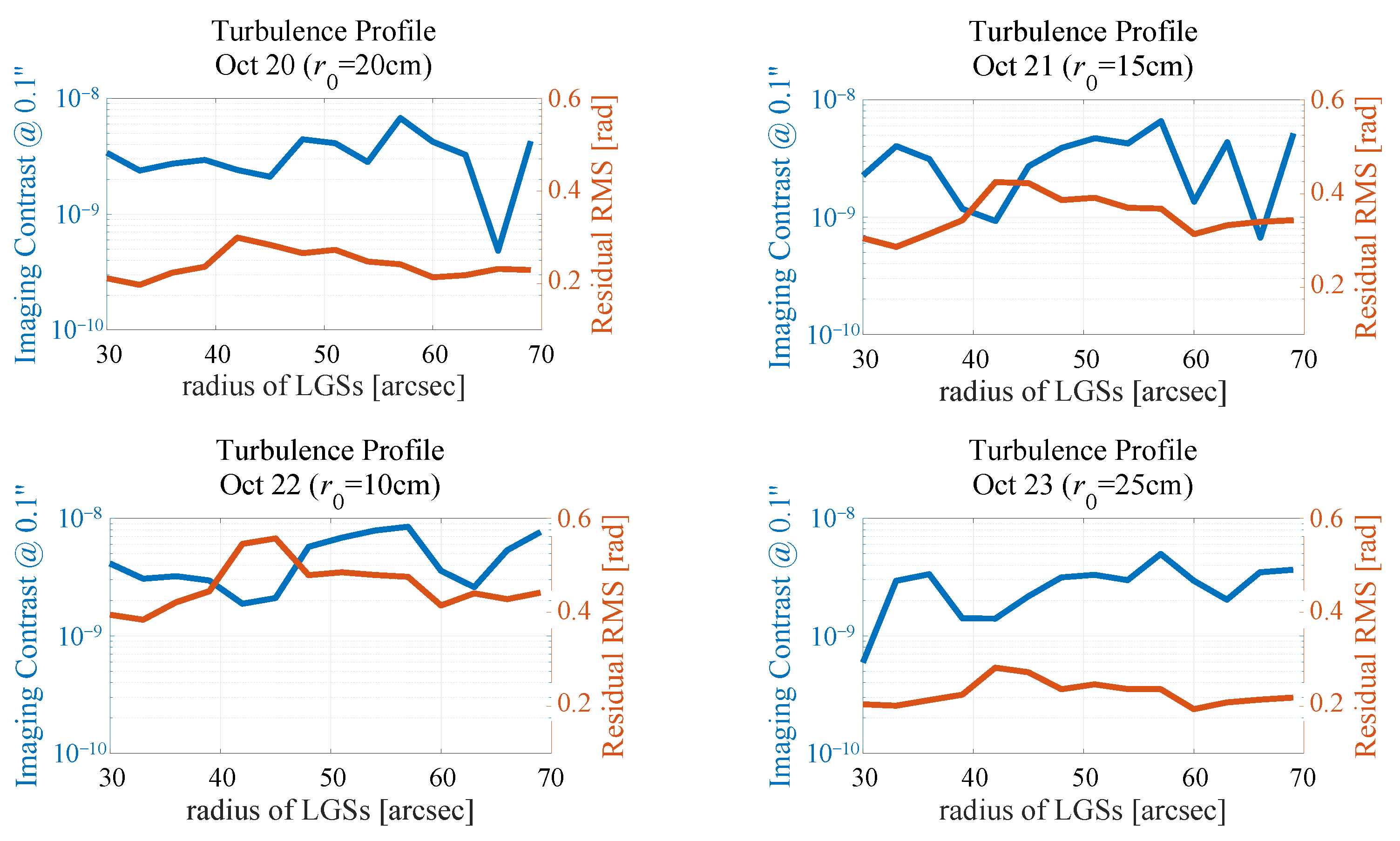
5.1. Comparison of Single LGS AO and LTAO Exoplanet Detection Capabilities
5.2. Analysis of the LTAO Unseen Spatial Frequency Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guyon, O. Extreme Adaptive Optics. Annu. Rev. Astron. Astrophys. 2018, 56, 315–355. [Google Scholar] [CrossRef]
- Follette, K.B. An introduction to high contrast differential imaging of exoplanets and disks. Publ. Astron. Soc. Pac. 2023, 135, 093001. [Google Scholar] [CrossRef]
- Dekany, R.; Roberts, J.; Burruss, R.; Bouchez, A.; Truong, T.; Baranec, C.; Guiwits, S.; Hale, D.; Angione, J.; Trinh, T.; et al. PALM-3000: Exoplanet adaptive optics for the 5 m Hale telescope. Astrophys. J. 2013, 776, 130. [Google Scholar] [CrossRef]
- Guyon, O. Imaging with Adaptive Optics and Coronographs for Exoplanet Research. In Handbook of Exoplanets; Springer: Cham, Switzerland, 2018; p. 112. [Google Scholar]
- Wizinowich, P.; Adkins, S.; Dekany, R.; Gavel, D.; Max, C.; Bartos, R.; Bell, J.; Bouchez, A.; Chin, J.; Conrad, A.; et al. WM Keck Observatory’s next-generation adaptive optics facility. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation 2010, San Diego, CA, USA, 27 June–2 July 2010; Volume 7736, pp. 229–240. [Google Scholar]
- Tatulli, E.; Ramaprakash, A.N. Laser tomography adaptive optics: A performance study. J. Opt. Soc. Am. A 2013, 30, 2482. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bouchez, A.H.; Acton, D.S.; Biasi, R.; Conan, R.; Espeland, B.; Esposito, S.; Filgueira, J.; Gallieni, D.; McLeod, B.A.; Pinna, E.; et al. The Giant Magellan telescope adaptive optics program. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation 2014, Montreal, QC, Canada, 22–27 June 2014; Volume 9148, pp. 300–318. [Google Scholar]
- Noecker, M.C.; Zhao, F.; Demers, R.; Trauger, J.; Guyon, O.; Kasdin, N.J. Coronagraph instrument for WFIRST-AFTA. J. Astron. Telesc. Instrum. Syst. 2016, 2, 011001. [Google Scholar] [CrossRef]
- Llop-Sayson, J.; Ruane, G.; Mawet, D.; Jovanovic, N.; Coker, C.T.; Delorme, J.-R.; Echeverri, D.; Fucik, J.; Riggs, A.J.E.; Wallace, J.K. High-contrast demonstration of an apodized vortex coronagraph. Astron. J. 2020, 159, 79. [Google Scholar] [CrossRef]
- Vidal, F.; Gendron, E.; Rousset, G. Tomography approach for multi-object adaptive optics. J. Opt. Soc. Am. A 2010, 27, A253–A264. [Google Scholar] [CrossRef] [PubMed]
- Neichel, B.; Fusco, T.; Conan, J.-M. Tomographic reconstruction for Wide-Field Adaptive Optics systems: Fourier domain analysis and fundamental limitations. J. Opt. Soc. Am. A 2008, 26, 219–235. [Google Scholar] [CrossRef]
- Farley, O.J.D.; Osborn, J.; Morris, T.; Fusco, T.; Neichel, B.; Correia, C.; Wilson, R.W. Limitations imposed by optical turbulence profile structure and evolution on tomographic reconstruction for the ELT. Mon. Not. R. Astron. Soc. 2020, 494, 2773–2784. [Google Scholar] [CrossRef]
- Nasedkin, E.; Mollière, P.; Wang, J.; Cantalloube, F.; Kreidberg, L.; Pueyo, L.; Stolker, T.; Vigan, A. Impacts of high-contrast image processing on atmospheric retrievals. Astron. Astrophys. 2023, 678, A41. [Google Scholar] [CrossRef]
- Cantalloube, F.; Farley, O.J.D.; Milli, J.; Bharmal, N.; Bradner, W.; Correia, C.; Dohlen, K.; Henning, T.; Osborn, J.; Por, E.; et al. Wind-driven halo in high-contrast images-I. Analysis of the focal-plane images of SPHERE. Astron. Astrophys. 2020, 638, A98. [Google Scholar] [CrossRef]
- Ahn, K.; Lee, S.H.; Park, I.K.; Yang, H.S. Simulation of a laser tomography adaptive optics with Rayleigh laser guide stars for the satellite imaging system. Curr. Opt. Photonics 2021, 5, 101–113. [Google Scholar]
- Fusco, T.; Agapito, G.; Neichel, B.; Oberti, S.; Correia, C.M.; Haguenauer, P.; Plantet, C.; Pedreros, F.; Ke, Z.; Costille, A.; et al. Key wavefront sensors features for laser-assisted tomographic adaptive optics systems on the Extremely Large Telescope. J. Astron. Telesc. Instrum. Syst. 2022, 8, 021514. [Google Scholar] [CrossRef]
- Farley, O.J.D.; Osborn, J.; Morris, T.; Fusco, T.; Neichel, B.; Correia, C.; Wilson, R.W. Identifying optical turbulence profiles for realistic tomographic error in adaptive optics. Mon. Not. R. Astron. Soc. 2019, 488, 213–221. [Google Scholar] [CrossRef]
- Fusco, T.; Rousset, G.; Sauvage, J.-F.; Petit, C.; Beuzit, J.-L.; Dohlen, K.; Mouillet, D.; Charton, J.; Nicolle, M.; Kasper, M.; et al. High-order adaptive optics requirements for direct detection of extrasolar planets: Application to the SPHERE instrument. Opt. Express 2006, 14, 7515–7534. [Google Scholar] [CrossRef]
- Rigaut, F.J.; Véran, J.P.; Lai, O. Analytical model for Shack-Hartmann-based adaptive optics systems. In Proceedings of the Astronomical Telescopes and Instrumentation 1998, Kona, HI, USA, 20–28 March 1998; Volume 3353, pp. 1038–1048. [Google Scholar]
- Guyon, O. Limits of adaptive optics for high-contrast imaging. Astrophys. J. 2005, 629, 592. [Google Scholar] [CrossRef]
- Girard, J.H.; Haffert, S.Y.; Bae, J.; Zeidler, P.; de Boer, J.; Bohn, A.J.; van Holstein, R.G.; Brinchmann, J.; Snellen, I.; Bacon, R.; et al. Planet formation with all flavors of adaptive optics: VLT/MUSE’s laser tomography adaptive optics to directly image young accreting exoplanets. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation 2020, Online, 14–18 December 2020; Volume 11448, p. 1144808. [Google Scholar]
- Martinez, P.; Boccaletti, A.; Kasper, M.; Cavarroc, C.; Yaitskova, N.; Fusco, T.; Vérinaud, C. Comparison of coronagraphs for high contrast imaging in the context of Extremely Large Telescopes. Astron. Astrophys. 2008, 492, 289–300. [Google Scholar] [CrossRef]
- Sauvage, J.-F.; Mugnier, L.M.; Rousset, G.; Fusco, T. Analytical expression of long-exposure adaptive-optics-corrected coronagraphic image. First application to exoplanet detection. J. Opt. Soc. Am. A 2010, 27, A157–A170. [Google Scholar] [CrossRef] [PubMed]
- Vérinaud, C.; Le Louarn, M.; Korkiakoski, V.; Carbillet, M. Adaptive optics for high-contrast imaging: Pyramid sensor versus spatially filtered shack—Hartmann sensor. Mon. Not. R. Astron. Soc. Lett. 2005, 357, L26–L30. [Google Scholar] [CrossRef]
- Poyneer, L.A.; Macintosh, B. Spatially filtered wave-front sensor for high-order adaptive optics. J. Opt. Soc. Am. A 2004, 21, 810–819. [Google Scholar] [CrossRef]
- Conan, R.; Correia, C. Object-oriented Matlab adaptive optics toolbox. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation 2014, Montreal, QC, Canada, 22–27 June 2014; Volume 9148, pp. 2066–2082. [Google Scholar]
- Fitzgerald, M.P.; Sallum, S.; Millar-Blanchaer, M.; Jensen-Clem, R.; Hinz, P.; Guyon, O.; Wang, J.; Mazin, B.A.; Skemer, A.J.; Chun, M.; et al. The Planetary Systems Imager for TMT: Overview and status. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation 2022, Montreal, QC, Canada, 17–23 July 2022; Volume 12184, pp. 736–743. [Google Scholar]
- Herscovici-Schiller, O.; Mugnier, L.M.; Sauvage, J.-F. An analytic expression for coronagraphic imaging through turbulence. Application to on-sky coronagraphic phase diversity. Mon. Not. R. Astron. Soc. Lett. 2017, 467, L105–L109. [Google Scholar] [CrossRef]
- Beichman, C.A.; Krist, J.; Trauger, J.T.; Greene, T.; Oppenheimer, B.; Sivaramakrishman, A.; Doyon, R.; Boccaletti, A.; Barman, T.S.; Rieke, M. Imaging young giant planets from ground and space. Publ. Astron. Soc. Pac. 2010, 122, 162. [Google Scholar] [CrossRef]
- Ruffio, J.-B.; Macintosh, B.; Wang, J.J.; Pueyo, L.; Nielsen, E.L.; De Rosa, R.J.; Czekala, I.; Marley, M.S.; Arriaga, P.; Bailey, V.P.; et al. Improving and assessing planet sensitivity of the GPI exoplanet survey with a forward model matched filter. Astrophys. J. 2017, 842, 14. [Google Scholar] [CrossRef]
- Tokovinin, A.; Vernin, J.; Ziad, A.; Chun, M. Optical turbulence profiles at Mauna Kea measured by MASS and SCIDAR. Publ. Astron. Soc. Pac. 2005, 117, 395. [Google Scholar] [CrossRef]

| Phase Screen | 1 | 2 | 3 |
| Height [m] | 300 | 5000 | 12,000 |
| Speed [m/s] | 10 | 5 | 2 |
| Cn2 fraction | 0.5 | 0.3 | 0.2 |
| r0 @ 500 nm [m] | 0.10 | ||
| Telescope diameter [m] | 1–30 | ||
| Guide star magnitude | 8 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, K.; Huang, J.; Wang, K. Fundamental Limits on Earth-like Exoplanet Imaging with Large Telescopes Employing Laser Tomographic Adaptive Optics Systems: A Comparative Analysis of LGS AO and LTAO Systems. Photonics 2024, 11, 338. https://doi.org/10.3390/photonics11040338
Deng K, Huang J, Wang K. Fundamental Limits on Earth-like Exoplanet Imaging with Large Telescopes Employing Laser Tomographic Adaptive Optics Systems: A Comparative Analysis of LGS AO and LTAO Systems. Photonics. 2024; 11(4):338. https://doi.org/10.3390/photonics11040338
Chicago/Turabian StyleDeng, Keran, Jian Huang, and Ke Wang. 2024. "Fundamental Limits on Earth-like Exoplanet Imaging with Large Telescopes Employing Laser Tomographic Adaptive Optics Systems: A Comparative Analysis of LGS AO and LTAO Systems" Photonics 11, no. 4: 338. https://doi.org/10.3390/photonics11040338
APA StyleDeng, K., Huang, J., & Wang, K. (2024). Fundamental Limits on Earth-like Exoplanet Imaging with Large Telescopes Employing Laser Tomographic Adaptive Optics Systems: A Comparative Analysis of LGS AO and LTAO Systems. Photonics, 11(4), 338. https://doi.org/10.3390/photonics11040338




