1. Introduction
In optical systems, optical zoom lenses are employed to change the focal length or magnification while keeping the image surface fixed [
1,
2]. They are widely used across diverse applications, including compact smartphone cameras [
3,
4,
5,
6], necessitating a mechanical structure to facilitate focal length adjustments in the cameras [
7,
8,
9]. However, the commercialization of optical zoom lenses mandates precise calculation of the movement of each lens group [
10,
11]. This movement, a continuous value, is typically computed via numerical analysis. Nonetheless, the movement of a lens group cannot be continuously expressed using numerical calculations [
12]. As a result, interpolation techniques have been utilized [
13,
14].
The linear interpolation method stands as a widely employed conventional estimation technique for constructing unknown discrete data through curve fitting [
14,
15,
16]. In contrast, nonlinear interpolation methods encompass spline and mimetic interpolation techniques [
17]. There is a limited body of prior research employing interpolation techniques in the field of optical systems. For instance, in a hexagonal microlens array, researchers utilized linear interpolation between adjacent points to create sharp edges at the boundaries of 0.75 mm [
18]. Another study introduced a hardwire interpolation technique aimed at distortion correction for effectively eliminating arbitrary distortion artifacts in geometric lenses at frame rates higher than 30 in 1024 × 768 pixels [
19]. An adaptive dispersion method was proposed with a maximum refraction error of 2.91 × 10
−6 for index interpolation [
20].
Spline interpolation utilizes polynomials between each point to smoothly determine unknown data, whereas mimetic interpolation helps estimate unknown field points using neighboring points (particularly useful for multidimensional vector fields) [
21,
22]. Moreover, to mitigate surface error in optical system design, one study utilized spline interpolation, proposing a B-spline method to produce free-form surfaces for optical lenses [
23]. Additionally, cubic spline interpolation was used to obtain expansion polynomials, effectively reducing distortion from 30% to 3.6% in wide-angle optical lenses [
24]. In the optical design software, the bi-cubic spline surface method was used to provide smooth freeform with C2 continuous points [
25]. Using the B-spline interpolation technique, the accuracy of the ray tracing with 10
−12 was achieved on the optical surface [
26]. Using the spline interpolation technique, the cam angle in the optical lens was calculated for a 10 MHz photoacoustic system [
27].
To determine the zoom locus in an optical system, numerous lens groups must navigate on specific positions discontinuously [
28]. Therefore, a certain interpolation technique is needed to be smoothly connected between these positions. Within optical zoom equations, certain undefined variables exist [
29]. To determine these variables, we need to utilize analytical techniques while moving the lens group. These methods help find the appropriate solutions for effective focal length (EFL) and back focal length (BFL) by employing either linear or nonlinear interpolation techniques [
30,
31,
32]. Deriving these unknown variables often involves iterative and matrix calculation methods, leading to complex mathematical computations. Even mathematical programs like Wolfram Mathematica or MATLAB require considerable time for these calculations [
33]. As an alternative, a displacement equation was proposed to solve the undefined variables in EFL and BFL equations in the first and second lens groups [
34]. However, this solution is limited to specific constricted discrete values. For precise positioning of the zoom locus at the minimum intervals in the optical system, the unknown variables in the zoom locus equations need to be calculated even for infinitely small interval ranges of up to seven lens groups [
35]. Due to the smoothness of the zoom locus and the scarcity of inflection points, it is possible to obtain a smooth zoom locus, even in an optical system with high zoom magnification. Consequently, the locus can be expressed as a function, and the distance between each locus can be determined accurately for some zoom positions.
To address this challenge, the locus was implemented in the form of a rational function utilizing Padé approximation. The Padé approximation expresses the function values as a rational function (the ratio of two polynomials) to solve for the narrow convergence radius, which is a drawback in the Taylor series [
34]. However, the shortcoming of this method lies in the requirement for equal separation of denominator and numerator degrees within the fractional function representing the zoom locus. The order of the denominator and numerator signifies the number of divisions from the wide-angle end to the telephoto end in the zoom optical system. Because the order of the denominator and numerator are equal, they can only be used if the optical system is even. The calculation of zoom locus in the optical systems is not limited to cases with an even number of segmented data points but is a requisite for all optical systems, regardless of the segment count.
To calculate the zoom locus, previous studies utilized MATLAB (MathWorks Inc., Natik, MA, USA) program’s built-in functions and the Code V (Synopsys, Inc., Sunnyvale, CA, USA) commercial optical system design software, employing an external data exchange method via an application programming interface (API). However, external software can lead to longer calculation times for the lockers, which can lead to execution problems caused by inconsistencies in graphical user interfaces (GUIs). To solve this problem, we sought to adjust the degree of the rational function (the ratio of two polynomials) to be used in any situation, regardless of the number of zoom data points. For faster processing and convenience, we focused only on Marco-Plus, the built-in language program of optical design software Code V (Ver. 2023.03).
Section 2 delineates the methodology for computing the zoom locus analysis of an optical zoom lens analytically, irrespective of the number of zoom data points.
Section 3 discusses the results of the proposed analytical interpolation method for the optical zoom lens system. This section details the utilization of additional node data and demonstrates how to obtain position changes in the principal plane. Finally,
Section 4 presents the conclusions of this study, summarizing the key findings and implications.
2. Materials and Methods
To address the constraints inherent in the zoom equations [
36], we previously proposed the technique employing nonlinear polynomial rational functions. The technique was aimed at calculating the zoom locus of each lens group. This was to ensure that the lens group moved continuously according to changes in focal length or magnification across all sections, spanning from the wide-angle end to the telephoto end.
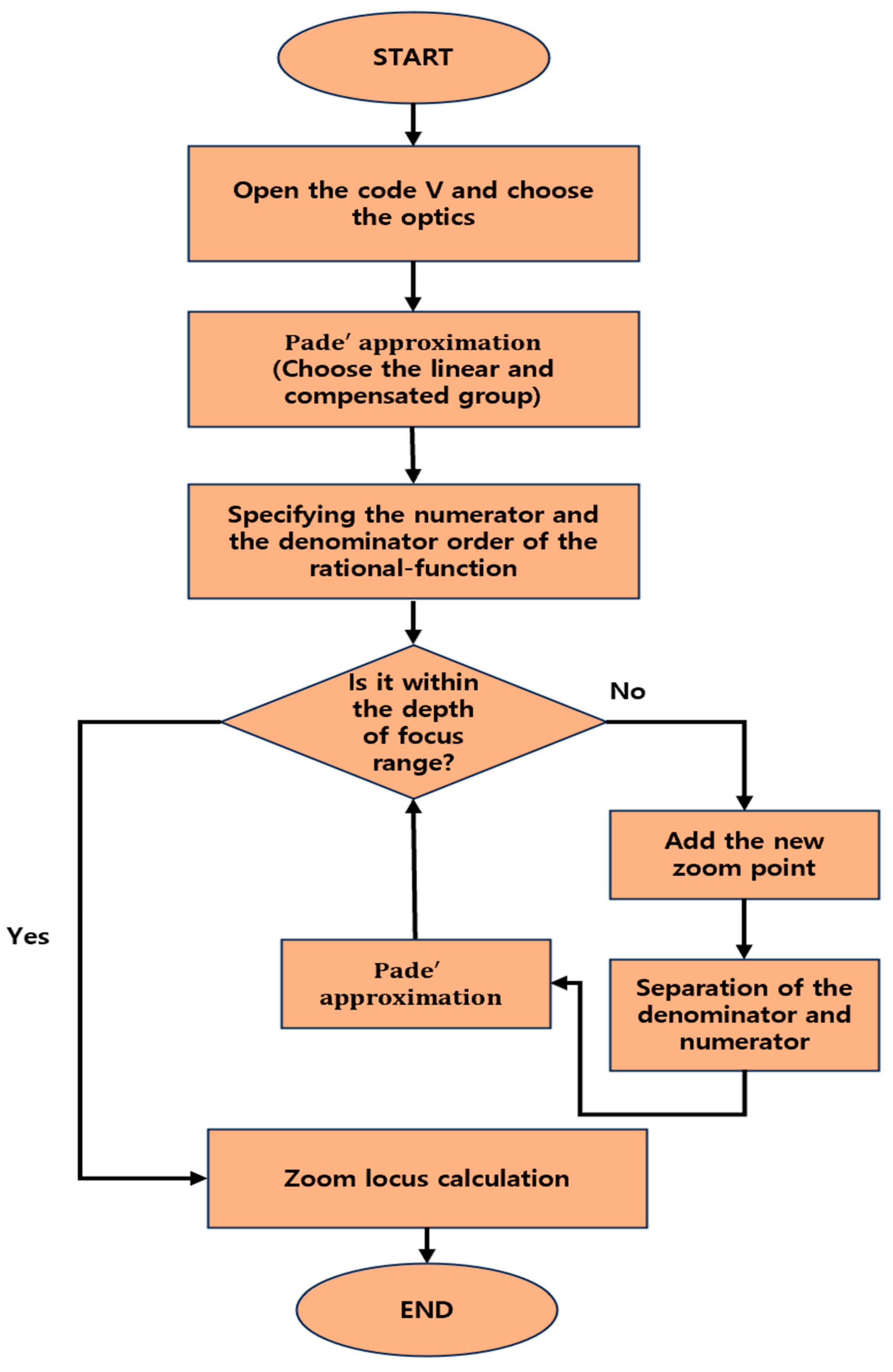
Figure 1 illustrates the algorithm adopted for computing the zoom locus.
Upon loading the optical system into the Code V design software, the zoom locus program was executed, and the linear and compensation groups were selected. Subsequently, the Padé approximation was applied to all lens groups to determine the lens group’s extent of movement using a rational function. If the zoom of the optical system is even, the same value is assigned to the numerator and denominator degrees of the rational function composed of two polynomials. Conversely, if the count is odd, the numerator’s degree is set to be one larger than the denominator’s degree before proceeding with the Padé approximation. If the Padé approximation is not possible with existing data, adjustments are made to the numerator and denominator orders to facilitate the approximation process. Notably, the presence of singularities must be considered when constructing a rational function. Thus, a program was implemented to ensure the absence of singularities within the movement section of the lens group through order adjustment.
If the position of the image surface obtained in this manner was within the depth of focus (DOF) range, the calculation was terminated. However, if it falls outside this range, additional steps are initiated. This involves adding zoom data, moving the compensation group, re-compensating, revisiting the order adjustment process, conducting Padé approximation iteratively, and recalculating until the value falls within the DOF range. Moreover, accessibility can be improved using the optical design software’s own internal program, eliminating the inconveniences associated with API usage. The absence of movement between data points enables efficient data acquisition without excessive time consumption, even if repeated calculations are conducted.
The zoom lens optical system typically comprises at least one middle section positioned between the wide-angle and telephoto ends. Equation (1) represents the zoom magnification of the optical system, which is the ratio of the focal lengths of the wide-angle end to those of the telephoto end:
where
EFLTele and
EFLWide are the EFLs of the telephoto and wide-angle ends, respectively.
Due to approximating intervals beyond the initial data using a function derived from the initial data, the image surface may remain uncorrected, potentially resulting in movement greater than the desired value [
37]. To move a specific group by solving the zoom equation via the Gaussian bracket method, the image surface must be moved by the desired amount [
38]. In optical system calculations, Gaussian brackets aid in computing the effective focal length (EFL) and back focal length (BFL) [
39,
40,
41]. Consequently, the Gaussian bracket finds extensive utilization for determining the movement of lens groups in zoom optical systems [
42].
Based on the corrected results, the Padé approximation can be repeated to establish a rational function for computing the zoom locus.
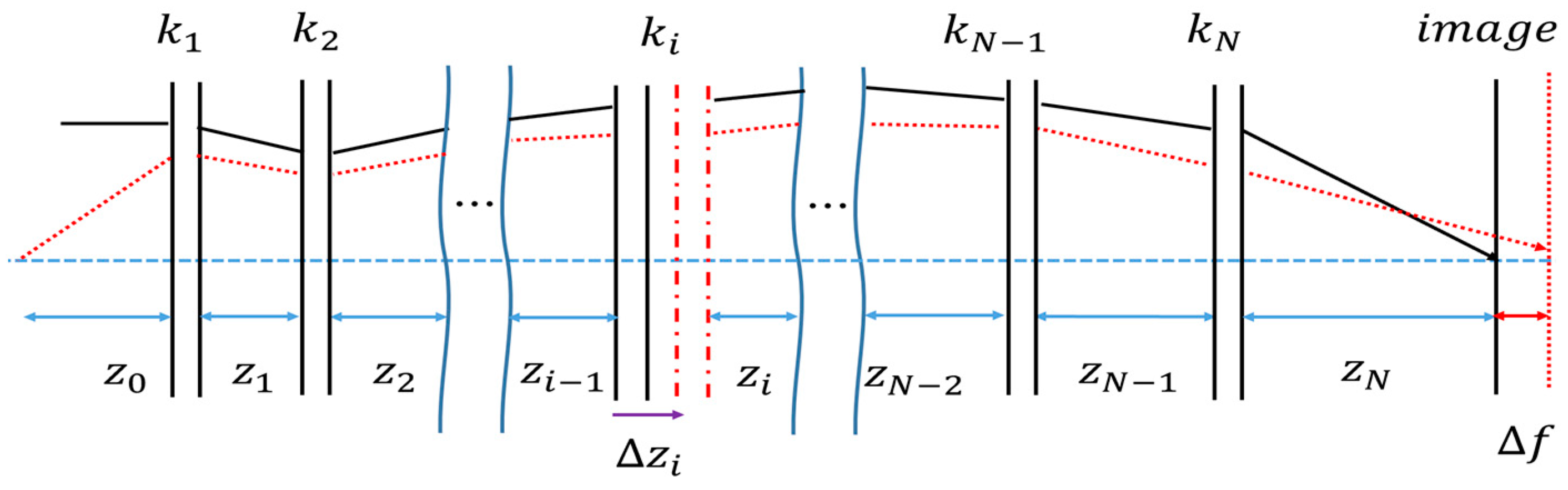
Figure 2 depicts the optical path representation when a specific
ith lens group moves by a distance ∆
zi in an optical system with an infinite object point [
43]. In this context,
k and
z denote the refractive power of each lens group and the distance between the main points of each lens group, respectively.
The zoom equation of correcting the top surface by moving the
ith lens group by ∆
zi can be expressed in Equations (2) and (3) [
44].
where
k denotes the refractive power of each lens group,
z represents the distance between the main points of each lens group, and
K is the refractive power of the entire optical system.
Equation (2) represents the inverse of the focal length of the entire optical system calculated using the zoom equation. Generally, the distance between the refractive power of the lens group and the main point is fixed because the zoom locus is calculated after the design is complete [
45]. Thus, the unknown parameter is ∆
zi, which indicates the extent of movement of the moving group. Equation (3) implies the height of the image surface of the optical system, wherein the height of the axial light on the image surface of the near-axis light tracking is zero. As shown in Equation (3), the unknown is ∆
zi, which signifies the extent of movement of the moving group.
The characteristics of Gaussian parentheses used for solving the zoom equations are expressed in Equations (4)–(6).
where
an is the
n-th unknown element in Gaussian parentheses.
If we solve Equation (3) using Equation (6), we obtain Equation (7):
If we extract ∆
zi from the parentheses in Equation (7) and rearrange it, it can be formulated as a quadratic equation for ∆
zi, as shown in Equation (8).
To simplify Equation (8), the variables (
A,
B,
C,
D, and
E) are defined in Equation (9).
Therefore, Equation (9) can be expressed with the variables (
A,
B,
C,
D, and
E) to obtain Equation (10).
By determining ∆
zi via solving Equation (9), it becomes possible to ascertain the required extent of movement of a specific lens group for correcting the image surface. Subsequently, the zoom locus can be calculated by employing the Padé approximation with the corrected data. The Padé approximation, a generalized form derived from the Taylor series, can be expressed as a ratio of polynomials and is defined by Equation (11) [
46].
The denominator and numerator
PM(
x) and
QN(
x) are composed of polynomials with highest-order terms of
M and
N, respectively. If the number of zooms in the optical system is even, the highest-order terms in the denominator and numerator are determined by dividing the number of zooms by two. However, if the number of zooms in the optical system is odd, the highest-order term
N in the numerator is set to be one larger than the highest-order term
M in the denominator. Each polynomial is expressed by Equations (12) and (13) as follows:
x0 signifies the parallel movement of the
x-value in the
x-axis coordinate.
where
α and
β are the coefficients of the numerator and denominator terms, respectively. Equations (14) and (15) represent the cases when the number of middle stages of the optical system is even and odd, respectively:
f0 represents the parallel movement along the
y-axis coordinate system; when calculating the zoom locus, we set it to zero.
To obtain the coefficients of the Padé approximation, Equation (15) is organized as shown in Equation (16):
Equation (16) can be expressed as the matrix in Equation (17) [
46].
In Equation (17), all values except the coefficients
α and
β are determined from design data, so the unknowns are the coefficients
α and
β. To separate the coefficients, we multiply both sides by the inverse matrix of the matrix in front of the coefficient, as shown in Equation (18).
The coefficient of Equation (18) was obtained using Macro-Plus, a built-in language program within the Code V optical design software. If the Padé approximation is possible using the initial optical system data, the degrees of the numerator and denominator are assigned based on the number of optical zoom data points, with Padé approximation performed using the assigned polynomial. However, in instances where Padé approximation cannot be performed with a polynomial, the degrees of the numerator and denominator were changed, with the approximation programmed to determine the degree to which it is possible. As the degree of the denominator increases, the number of polynomial solutions rises, thereby increasing the occurrence probability of a singular point. When adjusting the order of the numerator and denominator, a specific order was followed: For an optical system with an even number of zoom data points, the same order was assigned to the numerator and denominator. Conversely, if the zoom number was odd, the numerator order was assigned a value one unit larger than the denominator. As the degree of the denominator increases, the number of solutions increases, and the probability of a singular point occurring also rises. Therefore, the calculation is specifically set to increase the numerator’s order first, even when the Padé approximation does not proceed and an order adjustment is required.
3. Results and Discussion
We implemented a program that treats the distance between each group as unknown variables in the optical system data. It calculated the distance between each group as a locus according to the normalized cam angle. After loading the optical system data to compute the locus using the Code V commercial optical design software (Synopsis Inc., Sunnyvale, CA, USA), the Padé approximation program was executed.
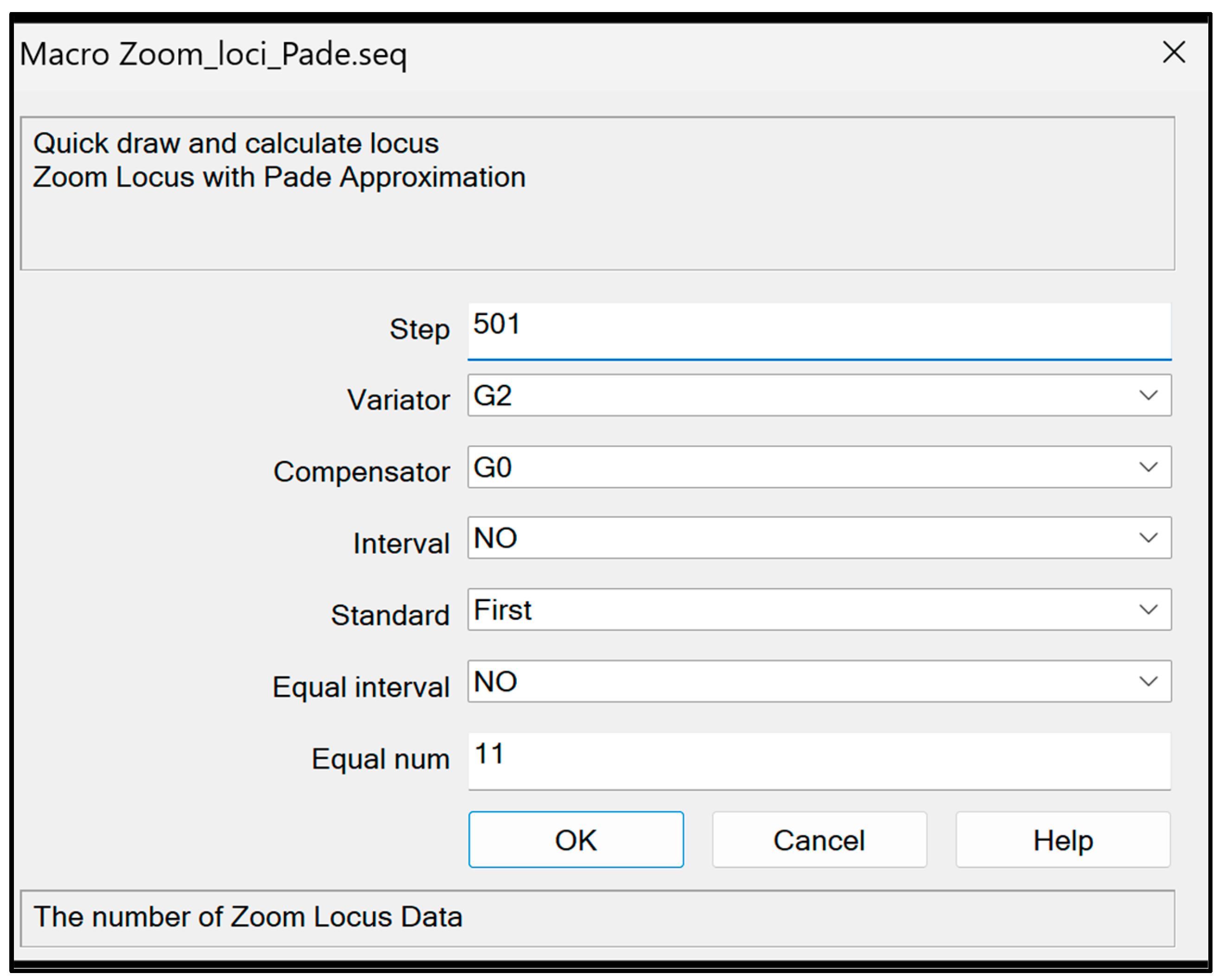
Figure 3 showcases a screen capture of the zoom locus calculation program executed in Code V.
The zoom-locus calculation program offers seven options. The first option, “Step”, determines the number of data points in the zoom locus, with a default value of 501, a minimum of 5, and a maximum of 1000. The second option, “Variator”, selects the linear group of the optical system. The third option, “Compensator”, chooses the compensation group of the optical system. The fourth option, “Interval”, delineates the step-by-step process through which the Padé approximation proceeds. The fifth option, “Standard”, specifies the reference point for calculating the Padé approximation, with the default value being “First”. The default reference point, “First”, designates the wide-angle, while selecting “Tele” sets the telephoto end as the reference point. Notably, the formula for the zoom locus varies depending on the reference point. The sixth option, “Equal interval”, provides fundamental data for the Padé approximation, while the seventh option, “Equal num”, sets the number of basic data points. The default value of “Equal interval” is “No”. In the default case, this was calculated as the initial zoom number of the loaded optical system data. If “Yes”, the number of data points can be set through “Equal num”. Both the sixth and seventh options facilitate obtaining evenly spaced fundamental data values created through spline interpolation. If we use these options, we can enable the Padé approximation, which cannot be calculated from the initial data in the optical system.
We aimed to compute the zoom locus using an example of an optical system wherein the zoom magnification is large and the total length is fixed.
Table 1 lists the zoom data for an optical system with a high zoom magnification of the EFL of 7–200 mm, comprising six optical lens groups. The zoomed data values were obtained through optimization. In
Table 1, Zoom 1 denotes the wide mode, while Zoom 2 to Zoom 6 represent the middle modes, and Zoom 7 signifies the tele mode (which comprises seven zooms). THI S7, S14, S22, S27, S30, and S32 denote the thicknesses of the 7th, 14th, 22nd, 27th, 30th, and 32nd sides, respectively. The BFL represents the distance between the cover glass and the image plane.
Table 2 displays the Padé approximation data value used for the zoom locus calculation, which is computed based on the wide-angle end. Cam represents the normalized value of the linear group’s movement from zero to one [
47]. G signifies the movement amount of each group, calculated by subtracting the value of the wide-angle end (Zoom 1) from the existing movement amount data. Additionally, CG denotes the cover glass, while BFL indicates the distance between the cover glass and the image plane. All data within the table are the values subtracted from the wide-mode values. Notably, the fixed groups G1, G3, G6, and CG have fixed values, demonstrating that the values subtracted from the standard wide mode equate to zero.
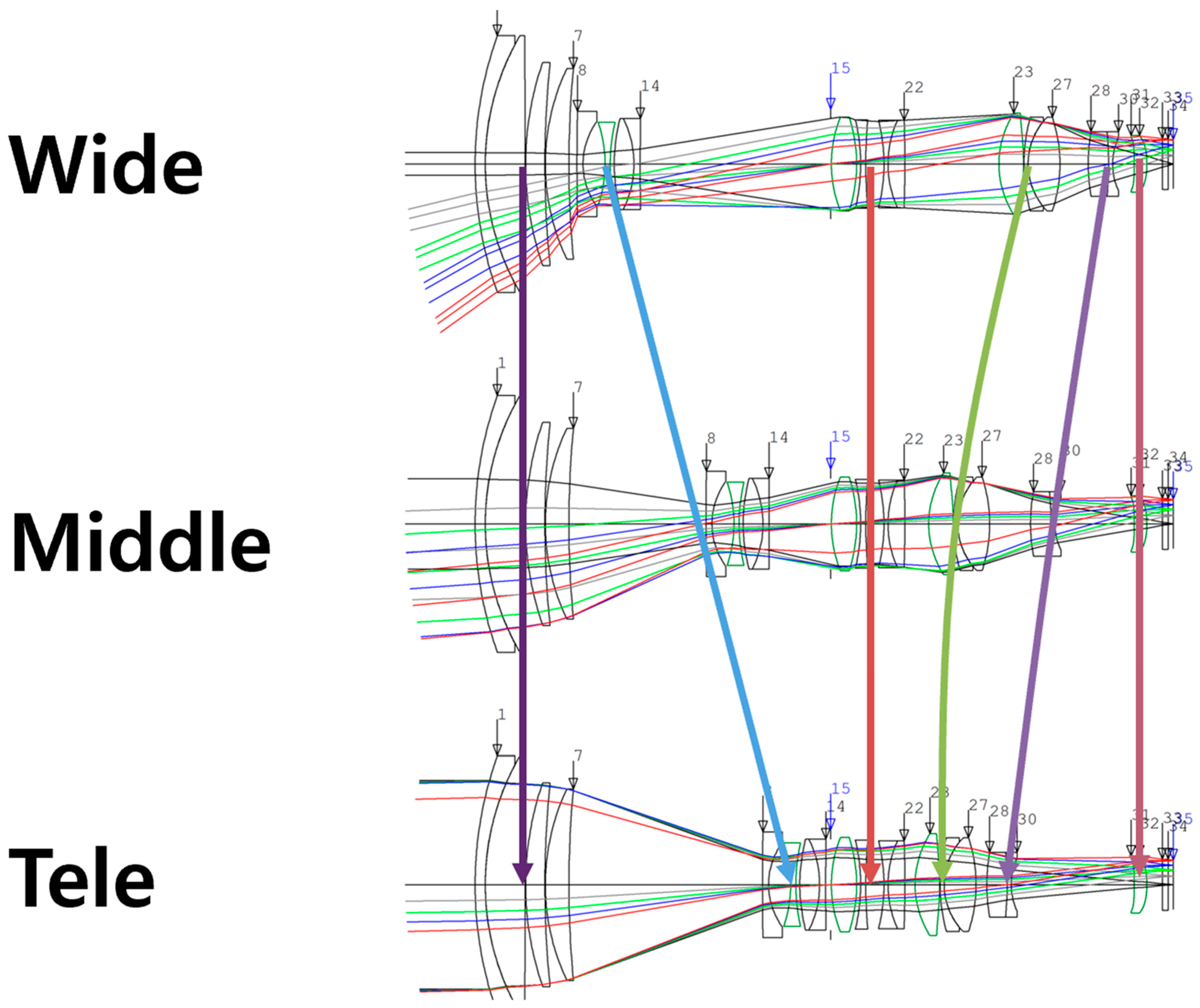
Figure 4 illustrates the optical layout of the high-magnification optical system. Excluding the cover glass, the optical system comprises six lens groups. In
Figure 4, the number and the arrow represent the surface number of the lens and the locus of moving from the wide mode to the tele mode, respectively. Among these, groups 1, 3, and 6 remain fixed, while groups 2, 4, and 5 were moved. The entire field length is a fixed optical system. The zoom locus was calculated using G2 for the linear group and G4 for the compensatory group. Notably, “Wide” and “Tele” signify the ends of the optical system, having Zoom 1 and Zoom 7, respectively. The “Middle” denotes the intermediate state of the optical system (Zoom 4 in the optical system). In designing a zoom lens, the resolution performance must be sufficient not only in the wide and tele states but also in the intermediate focal length range. Therefore, this “normal” state must also be incorporated into the zoom lens design. The optical designer determines the number of normal states that should be included, considering the resolution of the optical system [
48].
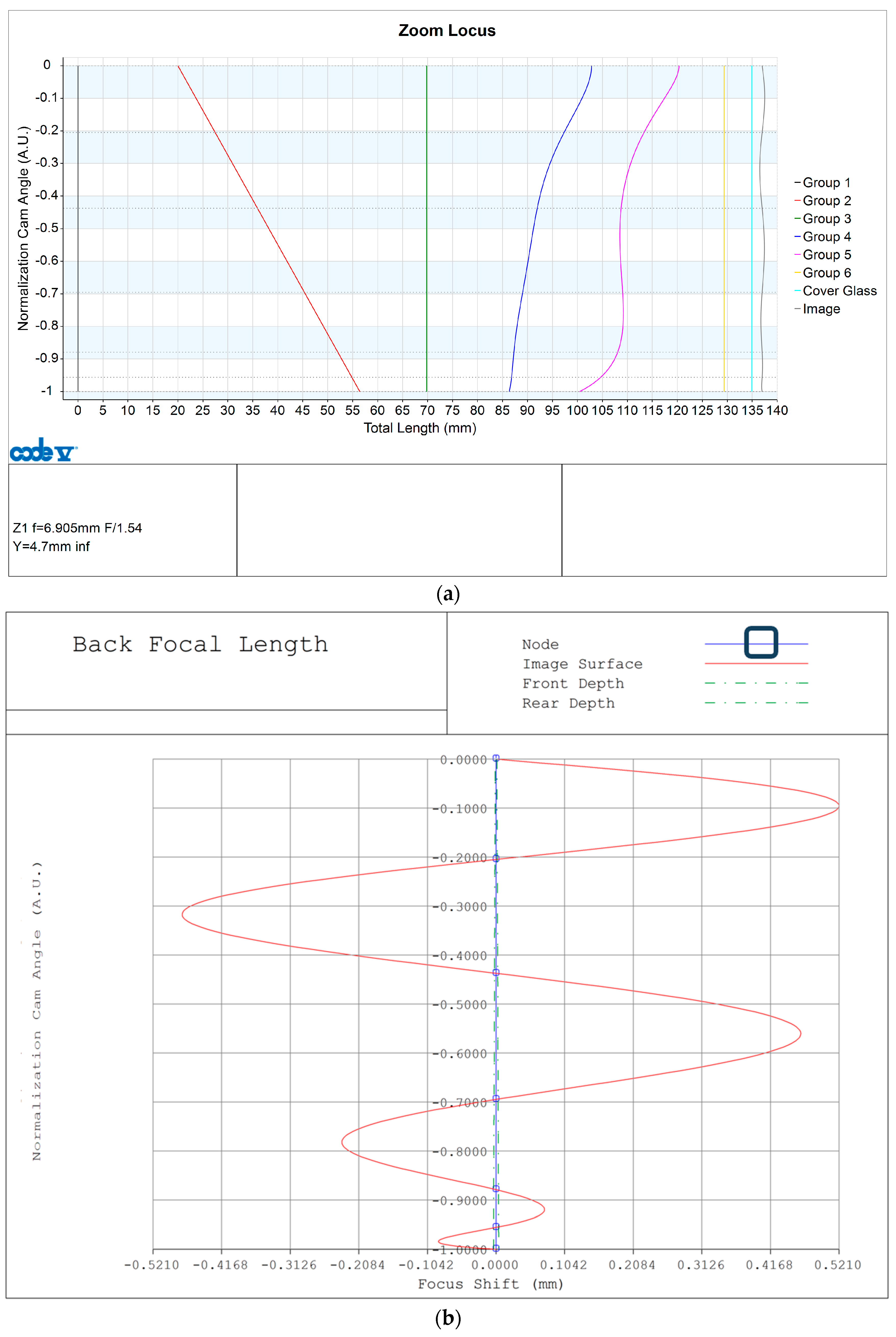
Figure 5a depicts the movement amount from the first side of each lens group to the image surface, forming the zoom locus of the optical system, as shown in
Figure 4. The
x-axis represents the amount of movement of each lens group, and the
y-axis represents a normalized value of the angle of the cam, a mechanism for moving the lens group. All zoom locus graphs in this study use the maximum cam angle normalized to one. Groups 1, 3, and 6 represent the movement amount from wide to tele of the first, third, and sixth lens groups, respectively. Groups 1, 3, and 6 are all fixed groups, so there is no movement. Group 2, as the Variator, has the largest movement amount. Groups 4 and 5 represent the movement amount of the compensator, and they play a role in correcting the BFL changed by the movement of the lens group. The cover glass plays a role in protecting the sensor in the optical system, and like groups 1, 3, and 6, it is a fixed group, so we can confirm that the amount of movement is zero. The image represents the movement amount of the image plane of the optical system. We can observe that the movement amount of the image plane is not fixed in areas other than the existing nodes interpolated by the Padé approximation.
Figure 5b is a separate diagram showing only BFL, which is the movement amount of the image plane, as shown in
Figure 5a. When the zoom locus is calculated numerically, the BFL is fixed to a set value. However, the BFL is not fixed in areas other than the existing node (blue color point) because this study expressed the position of each lens group in the form of a glass function using the Padé approximation. However, the image plane of the optical system must be located within the DOF (DOF consists of front depth and rear depth), which is the section where resolution does not change to prevent resolution changes due to assembly errors. As a result, at the current node, the BFL deviates from the front depth and rear depth, as shown in
Figure 5b. Therefore, we intend to introduce a new node in addition to the existing node of the currently designed optical system to ensure that the BFL is within the DOF in all sections. The added zoom node is determined by identifying areas exhibiting significant BFL changes.
Table 3 lists the coefficient values of the function that calculates the zoom locus using Padé approximation. The variables G, Alpha, and Beta represent the lens group of the optical system, numerator coefficient value, and denominator coefficient value, respectively. As shown in
Table 3, the fixed groups G1, G3, G6, and CG have the same coefficient values.
Upon analyzing the position change of the image surface in
Figure 5, it becomes evident that when computing the zoom locus using Padé approximation, the BFL deviates from the range of the dotted line, which is the DOF. This deviation occurs in areas beyond the scope of the existing zoom data. If the optical system is within the DOF range, the resolution performance does not change. Therefore, the BFL must be within the DOF range across all areas.
For this purpose, the zoom data (referred to as “Nodes”) were added, the compensation group was moved from the added data, and the locus was calculated again. The principle behind adding nodes involves recording the BFL values and determining the maximum value. In this case, the maximum value and the DOF were compared. If the maximum value exceeded the DOF value, a node was added to that location. This process was calculated sequentially from the wide-angle end to the telephoto end. It is iteratively repeated until the compensation group achieves a BFL within the DOF range. The desired outcome is to observe the results when a node is added once, utilizing the fourth option available in the zoom locus calculation program. This will provide insights into how this modification impacts the BFL and its alignment within the depth of the focus range.
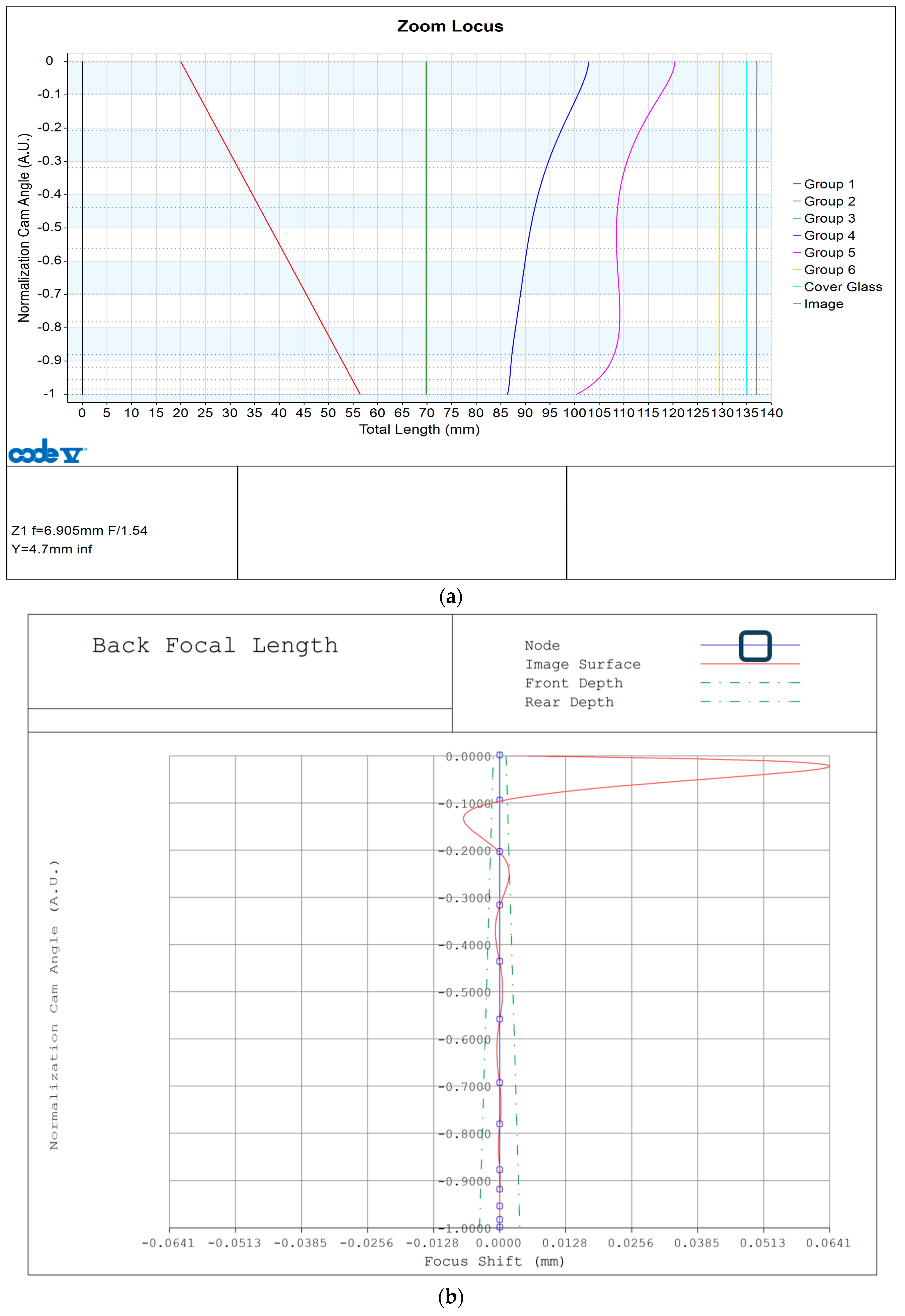
Figure 6 shows a zoom locus using a Padé approximation by adding a new node to an existing node once to hold the BFL within DOF.
Figure 6a shows the movement of the entire lens group, and
Figure 6b shows only BFL in
Figure 6a. Comparing
Figure 6b, which performed the Padé approximation by adding a new node, with
Figure 5b, which performed the Pade approximation at the existing node, the overall BFL movement was reduced through the
x-axis scale. However, near wide and zoom 1, we can still observe that the BFL does not come within DOF. Therefore, in all sections of the optical system, we would like to proceed with the process by adding nodes automatically until the BFL comes within DOF.
Table 4 lists the group data for the optical system when an additional node is added to the group of optical systems. Here, G represents a group of optical systems. All data are values subtracted from wide-mode values. We observed that all groups were fixed if the data value subtracted from the wide mode equated to zero.
Table 5 lists the coefficient values of the zoom locus function calculated using the Padé approximation after adding nodes. Variables G1–G6, alpha, beta, and order represent the lens group of the optical system, numerator coefficient value, denominator coefficient value, and order of the polynomial, respectively. The sum of the degrees of the compensation group denotes the total number of nodes. As shown in
Table 5, the fixed groups G1, G3, G6, and CG have the same coefficient values. When compared with the data in
Table 3, we observe that the values other than the coefficient values of compensation Group 4 are identical to those in
Table 3. This can be interpreted as only moving in Group 4 (the compensation group) to bring the BFL within the DOF.
To commercialize the designed optical system, the BFL must be located within the DOF.
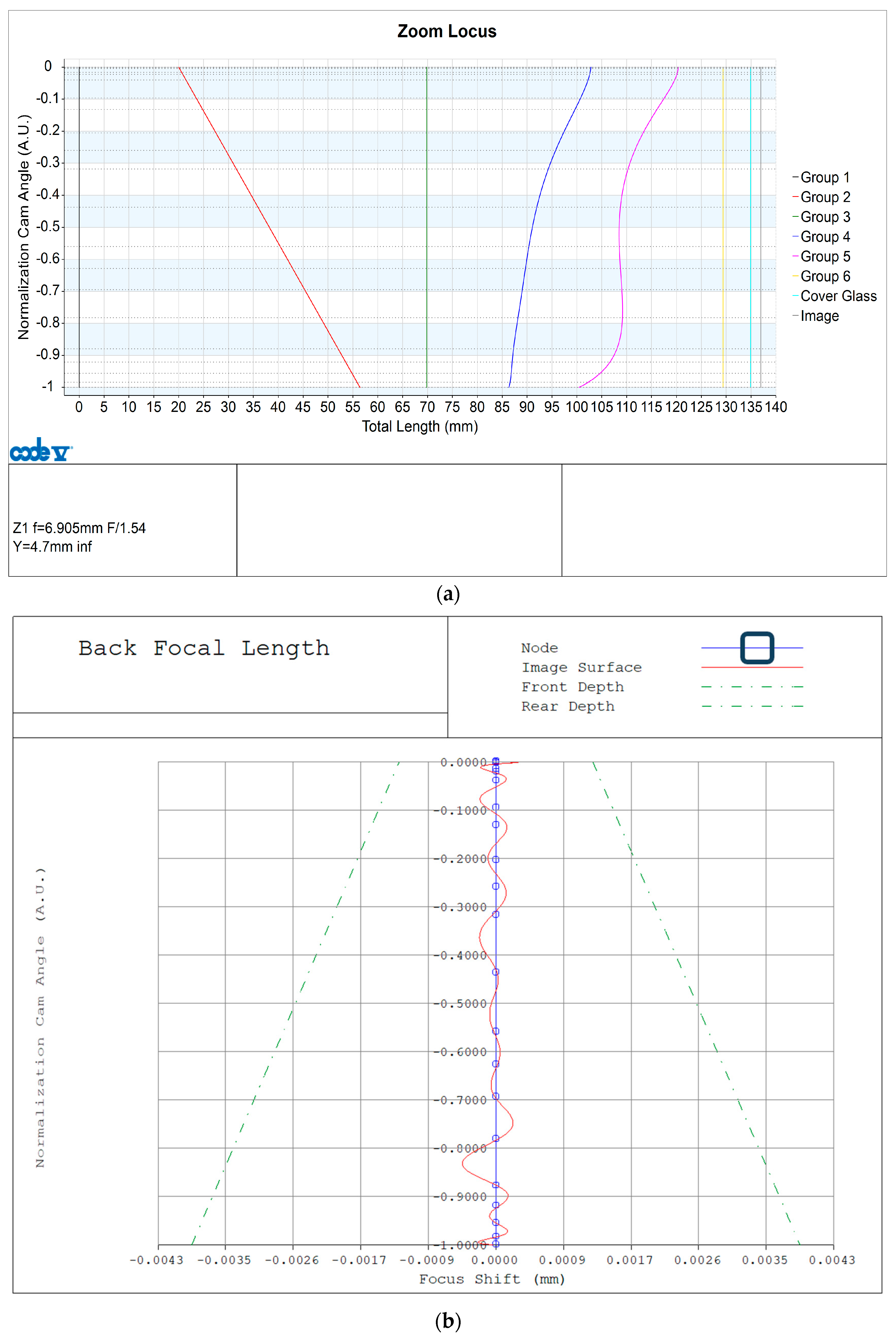
Figure 7 shows the process of adding a node automatically that allows the BFL to enter the DOF when the zoom locus is calculated through Padé approximation in all optical systems.
Figure 7a shows the movement of each lens group in all zooms when the BFL is located within the DOF.
Figure 7b shows only BFL in
Figure 7a. Compared to
Figure 5b, we can confirm that the BFL is located within DOF in all areas of the optical system.
Table 6 lists the final Padé approximation results for the high-magnification optical system, with the extent of movement of each group depending on the magnitude of cam movement. When the cam angle changed from zero to one, the compensation group (Group 4) varied from 0 to –16.47 mm. Since there was no change in the position of the fixed lens groups, we observed that the lens group’s extent of movement, according to the cam angle, was zero. The total number of nodes to shift to the compensation group was 21 if the position of the image surface was within the DOF range across all sections.
Table 7 presents the coefficient values of the final zoom locus function of the high-magnification optical system. Compared with the data in
Table 3, it is evident that all the data have the same coefficient values as
Table 3, except for the data of Group 4 (compensation group), which were used to correct the position of the image surface. This indicates that the position of the image surface of Group 4 moved within the DOF range. By substituting the alpha and beta coefficient values and orders obtained from
Table 7 into Equation (15), the locus of the compensation group can be expressed as an analytical rational function. In addition, we observed that the degrees of the numerator and denominator polynomials were 20° and 1°, respectively, with the sum of the two degrees being the total number of nodes. As the degree of the denominator increases, the probability of singularity also increases. Therefore, we confirmed that the program progressed in the direction of preferentially increasing the molecular order.
What we want to accomplish through the Padé approximation is to obtain the zoom locus. The Code V optimization and spline interpolation are both methods of obtaining loci. All of these methods can result in assembly errors due to curvature, thickness, and refractive index when tolerances are given [
12]. If such assembly errors occur, optical image resolution may decrease [
49]. Therefore, there is a stage of post-processing work based on tolerances during the production process. After the Padé approximation was performed, additional post-processing work is needed in the same way as the previously used Code V optimization and spline interpolation methods so the image quality in actual production needs to be considered.
From the actual production standpoint, fundamental reference data must first be provided for post-processing work [
50]. As one of the methods to create fundamental reference data, we propose the Padé approximation. It is useful for Padé approximation to represent the locus as a single function. For example, a total of 3500 pieces of data must be created if there are seven lens groups in the optical system, and 500 pieces of data are created when calculating the locus. These data are transmitted to the instrument designer during the manufacturing stage. However, we can create the data using the seven functions in the Padé approximation, which is advantageous when exchanging data during production. Therefore, we proposed a method to calculate the zoom locus with the Padé approximation.
The cam optimization in Code V only returns position data analytically, but the Padé approximation has the advantage of providing the locus function. Therefore, the function data can be passed on to the instrument designer during actual production. Additionally, the spline method calculates the locus by creating a different function for each node point. If we use the Padé approximation, the locus can be calculated with a single formula. In addition, the spline method can be calculated as a single formula if the Padé approximation is used to calculate the locus by creating a different function expression for each node point. With the spline method, the formula is different for each node. However, with the Padé approximation, the zoom trajectory can be expressed as a single function. In addition, the Padé approximation program can compute zoom trajectories by expressing polynomials in the form of rational functions. Therefore, we can expect that the Padé approximation program can be implemented in other programs that do not use Code V, such as MATLAB or Zemax software.
4. Conclusions
To meet specific conditions, earlier zoom locus computation methods typically involved obtaining a solution analytically by establishing simultaneous equations, employing the spline interpolation technique for mobile group movement calculation, and utilizing the Padé approximation for determining the extent of movement of certain lens groups. However, these prior methods encountered challenges where the formula became increasingly complex and time-consuming with an increase in optical system zoom data. In spline interpolation, problems arise due to variations in the formula for each section of the data. Moreover, the method of analytically calculating the locus using the Padé approximation was only possible when the number of zoom data points was even.
To address these issues, we developed a program utilizing the Padé approximation to compute the zoom locus for all optical systems and represent it as an analytical rational function. For the initial data, degrees were assigned to the two polynomials of the rational function, and the first Padé approximation was performed based on these assigned degrees. Subsequently, a node is added, and the process of assigning a degree to the added node is repeated if the BFL does not fall within the DOF.
In the final Padé approximation results for the high-magnification optical system, the compensation group (group 4) shifts from 0 to −16.47 mm when the cam angle progresses from zero to one. Notably, all values with zero were fixed in the optical system, and the BFL had the same value in all zooms. The total number of nodes required to move the compensation group (Group 4) was 21 when the position of the image surface was within the DOF range across all sections. By substituting the obtained coefficient alpha and beta values and the order recorded in Order into Equation (15), the locus of the compensation group can be expressed as an analytical rational function. Moreover, the degrees of the numerator and denominator polynomials were 20° and 1°, with the sum of the two degrees being the total number of nodes.
As the degree of the denominator increases during the degree assignment process, the likelihood of outliers also rises. Therefore, to minimize the occurrence of outliers, the degree of the numerator is set to increase first. By adding nodes and adjusting the order, we identified cases where the Padé approximation was feasible while ensuring the BFL remained within the DOF. By substituting the coefficients obtained through calculation into the formula, we confirmed that the zoom locus can be expressed in the form of an analytical rational function. Unlike the traditional calculation method, we can calculate complex and time-consuming previous zoom locus quickly. In addition, the locus of the compensated group could be expressed in a smooth form using the rational function, and the zoom locus could be expressed in one function form. However, splines change the function value at each node.