Performance of Orbital Angular Momentum Communication for a Non-Uniformly Correlated High-Order Bessel–Gaussian Beam in a Turbulent Atmosphere
Abstract
1. Introduction
2. Theory
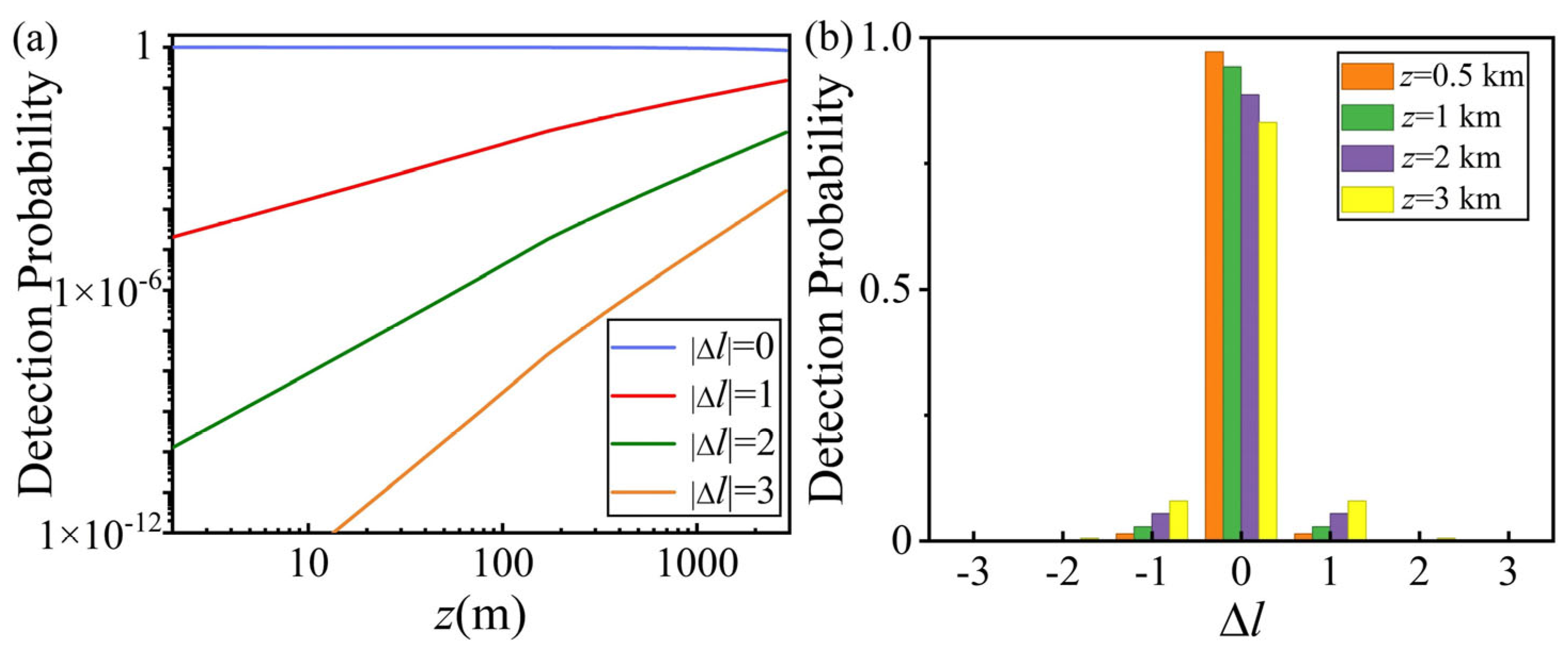
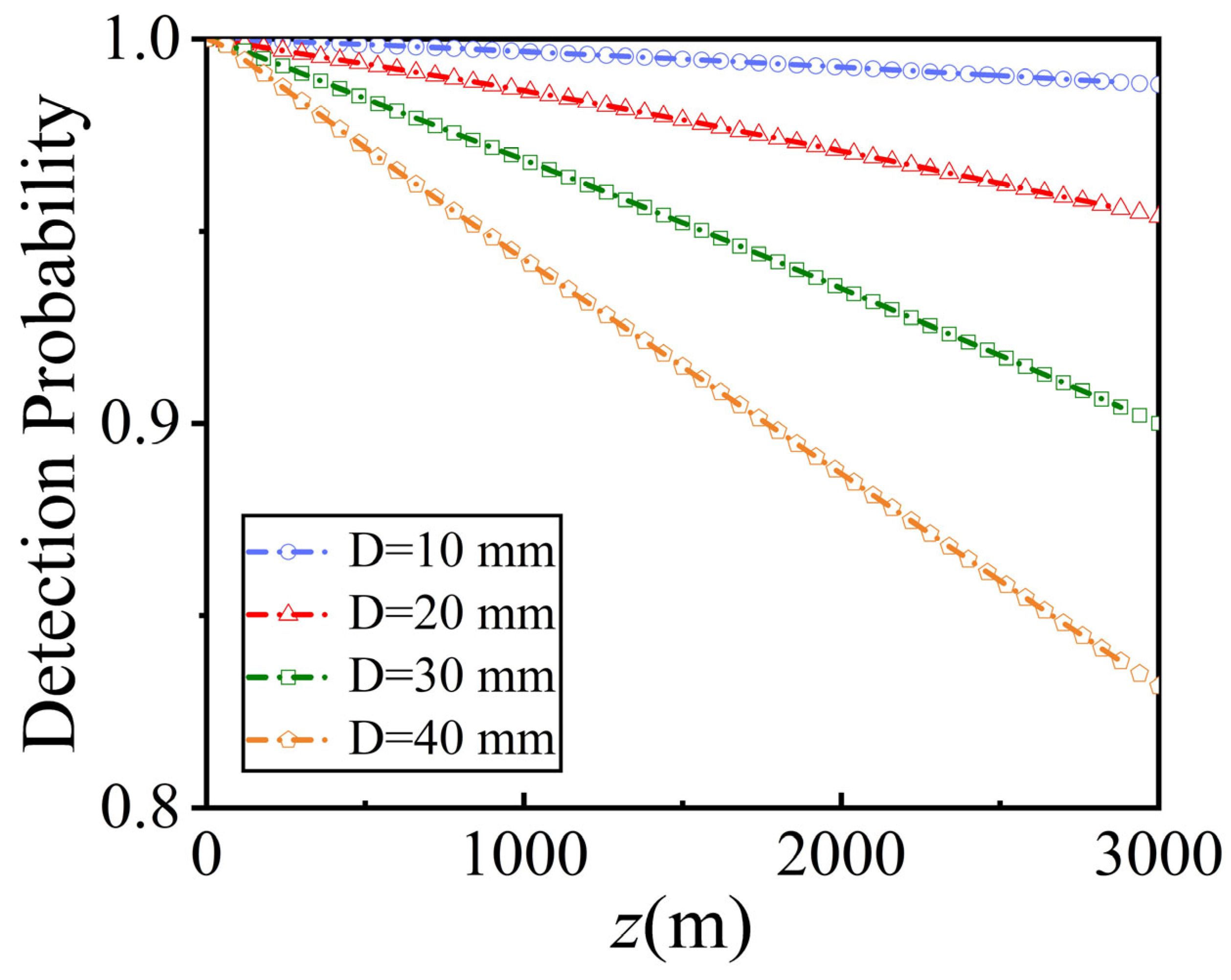
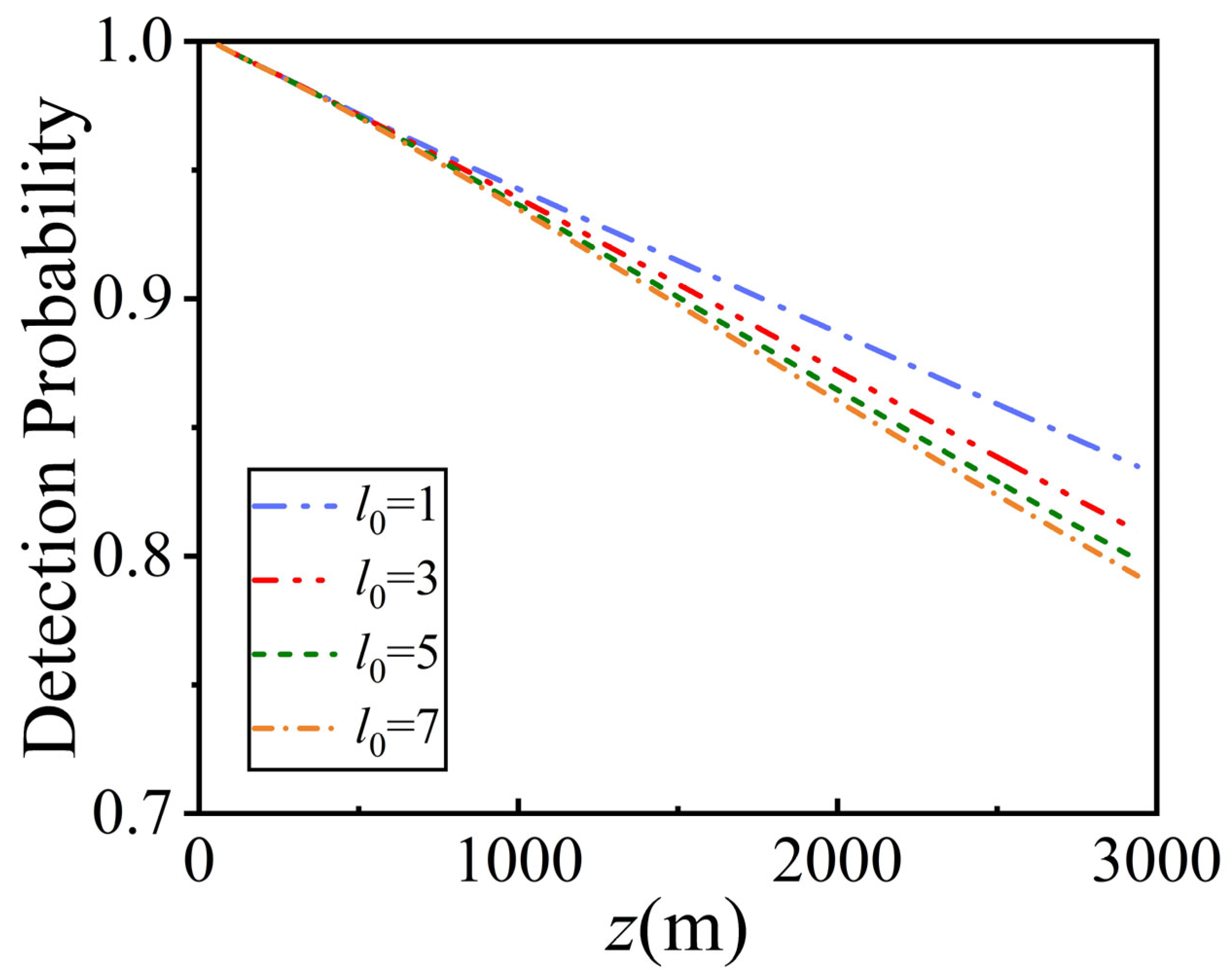
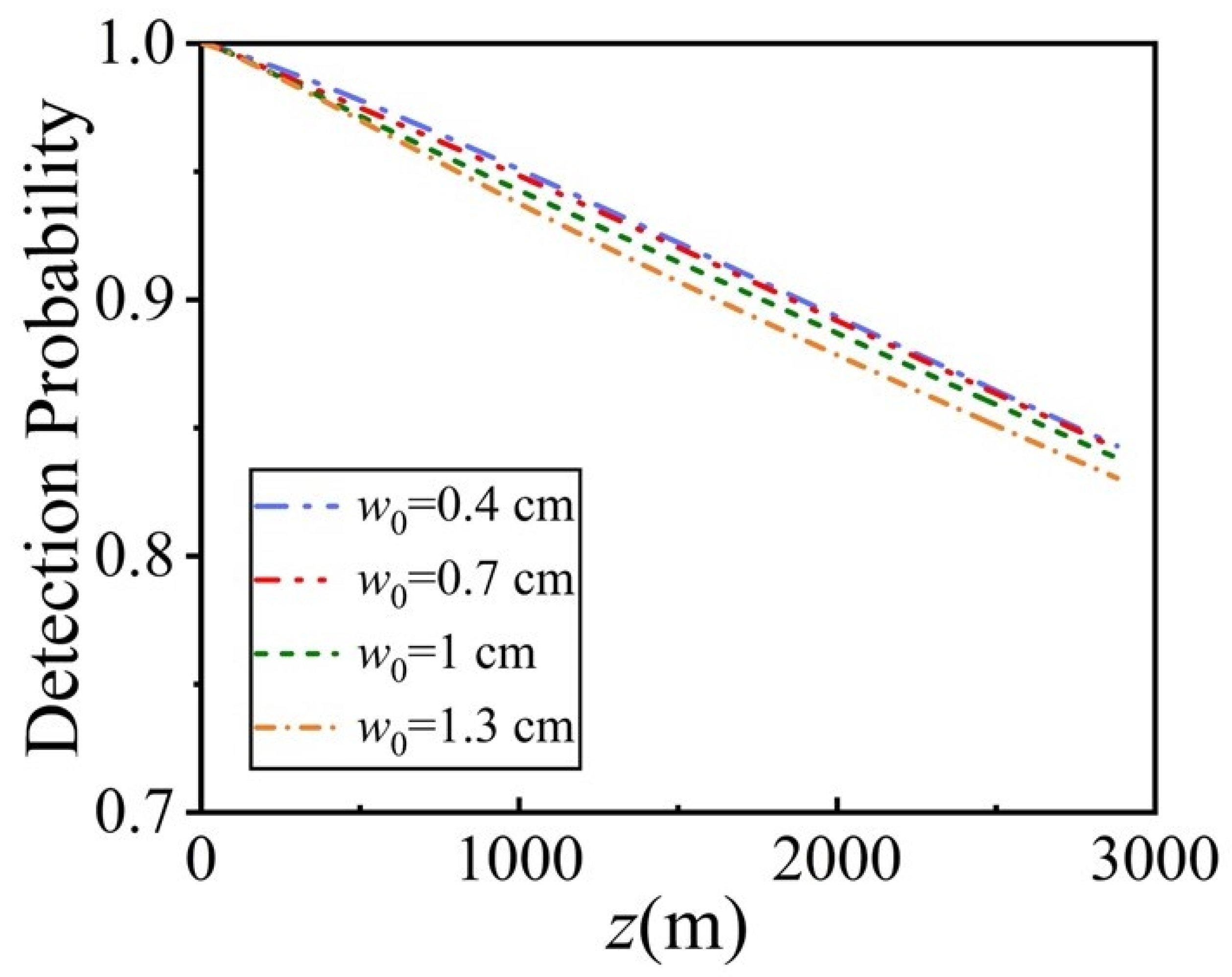
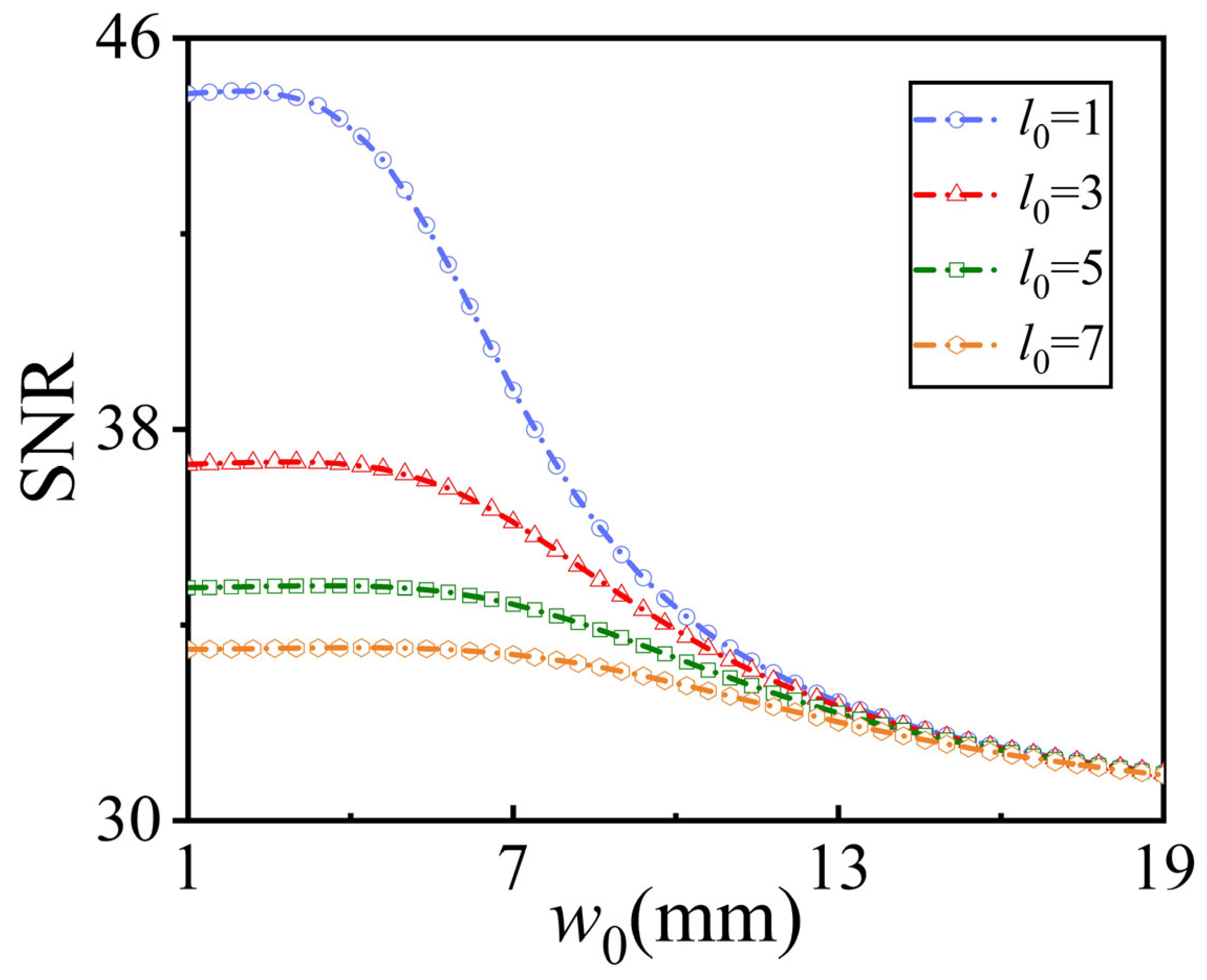
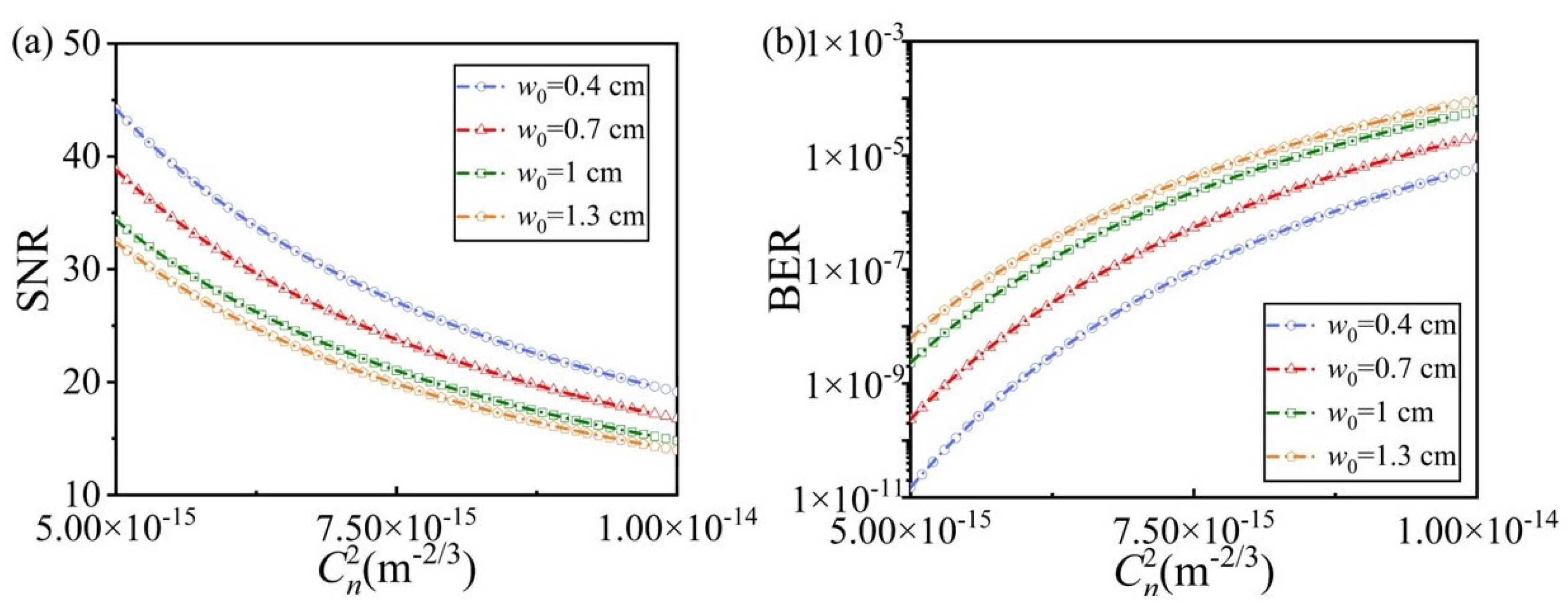
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Yang, J.; Fazal, I.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.G.; Liu, N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Wang, H.; Zhan, Z.; Hu, F.; Meng, Y.; Liu, Z.; Fu, X.; Liu, Q. Intelligent optoelectronic processor for orbital angular momentum spectrum measurement. PhotoniX 2023, 4, 9. [Google Scholar] [CrossRef]
- Paterson, C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl. Opt. 2008, 47, 2414–2429. [Google Scholar] [CrossRef] [PubMed]
- Tyler, G.A.; Boyd, R.W. Influence of atmospheric turbulence on the propagation of quantum states of light carrying orbital angular momentum. Opt. Lett. 2009, 34, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, B.; Lavery, M.P.J.; Malik, M.; O’Sullivan, M.N.; Mirhosseini, M.; Robertson, D.J.; Padgett, M.; Boyd, R.W. Influence of atmospheric turbulence on states of light carrying orbital angular momentum. Opt. Lett. 2012, 37, 3735–3737. [Google Scholar] [CrossRef]
- Acevedo, C.; Eshaghi, M.; Dogariu, A. Propagation of asymmetric optical vortex beams through turbulence and evolution of their OAM spectra. J. Opt. Soc. Am. A 2023, 40, 2135. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Mao, S.; Yu, Y.; Gu, H.; Deng, D.; Song, Y.; Pang, F.; Zhuang, L.; Yang, S.; et al. Synthesizing the crosstalk between OAM modes of vortex beam by simultaneously propagation a probe vortex beam in free space. Opt. Laser Technol. 2023, 165, 109622. [Google Scholar] [CrossRef]
- Ju, P.; Fan, W.; Gao, W.; Li, Z.; Gao, Q.; Jiang, X.; Zhang, T. Atmospheric turbulence effects on the performance of orbital angular momentum multiplexed free-space optical links using coherent beam combining. Photonics 2023, 10, 634. [Google Scholar] [CrossRef]
- Chen, M.; Yu, L.; Zhang, Y. Signal/noise ratio of orbital angular momentum modes for a partially coherent modified Bessel-correlated beam in a biological tissue. J. Opt. Soc. Am. A 2017, 34, 2046–2051. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, Y.; Tan, L.; Yu, S.; Du, W. Influence of beam wander on bit-error rate in a ground-to-satellite laser uplink communication system. Opt. Lett. 2008, 33, 2611–2613. [Google Scholar] [CrossRef]
- Mahdieh, M.H.; Pournoury, M. Atmospheric turbulence and numerical evaluation of bit error rate (BER) in free-space communication. Opt. Laser Technol. 2010, 42, 55–60. [Google Scholar] [CrossRef]
- Qiao, N.; Zhang, B.; Pan, P.; Dan, Y. Scintillation index and bit error rate of hollow Gaussian beams in atmospheric turbulence. J. Mod. Opt. 2011, 58, 939–944. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Zhang, X.; He, Y.; Zhou, X.; Ye, H.; Li, Y.; Xu, S.; Chen, S.; Fan, D. Deep learning based atmospheric turbulence compensation for orbital angular momentum beam distortion and communication. Opt. Express 2019, 27, 16671–16688. [Google Scholar] [CrossRef]
- Cheng, M.; Dong, K.; Shi, C.; Mohammed, A.H.T.; Guo, L.; Yi, X.; Wang, P.; Li, J. Enhancing Performance of Air–Ground OAM Communication System Utilizing Vector Vortex Beams in the Atmosphere. Photonics 2023, 10, 41. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, X.; Wang, F.; Chen, Y.; Cai, Y. Research progress on manipulating spatial coherence structure of light beam and its applications. Prog. Quant. Electron. 2023, 91–92, 100486. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; McDuffie, S.; Najjar, S.M.A.M.; Rafsanjani, S.M.H.; Korotkova, O. Mitigation of atmospheric turbulence with random light carrying OAM. Opt. Commun. 2019, 446, 178–185. [Google Scholar] [CrossRef]
- Akbucak, V.; Aymelek, G.; Yolcu, B.; Kayam, O.; Ünal, O.; Gökçe, M.C.; Baykal, Y. Effect of partial coherence on signal-to-noise ratio performance of free space optical communication system in weak turbulence. Opt. Commun. 2022, 518, 128395. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric optical communication with a Gaussian Schell beam. J. Opt. Soc. Am. A 2003, 20, 856–866. [Google Scholar] [CrossRef]
- Pan, P.; Zhang, B.; Qiao, N.; Dan, Y. Characteristics of scintillations and bit error rate of partially coherent rectangular array beams in turbulence. Opt. Commun. 2011, 284, 1019–1025. [Google Scholar] [CrossRef]
- Mays, J.; Gbur, G. Angular momentum of vector-twisted-vortex Gaussian Schell-model beams. J. Opt. Soc. Am. A. 2023, 40, 1417. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, D.; Zhou, Z. The propagation of radially polarized partially coherent beam through an optical system in turbulent atmosphere. Appl. Phys. B 2010, 101, 361. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, L.; Zhang, Y. Spiral spectrum of Airy–Schell beams through non-Kolmogorov turbulence. Chin. Opt. Lett. 2016, 14, 042101. [Google Scholar]
- Wu, K.; Huai, Y.; Zhao, T.; Jin, Y. Propagation of partially coherent four-petal elliptic Gaussian vortex beams in atmospheric turbulence. Opt. Express 2018, 26, 30061–30075. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y. Scintillation index and bit error rate of partially coherent twisted Gaussian beams in turbulent atmosphere. Opt. Quantum Electron. 2023, 55, 519. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Nonuniformly correlated light beams in uniformly correlated media. Opt. Lett. 2012, 37, 3240–3242. [Google Scholar] [CrossRef]
- Mei, Z.; Tong, Z.; Korotkova, O. Electromagnetic non-uniformly correlated beams in turbulent atmosphere. Opt. Express 2012, 20, 26458–26463. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Electromagnetic nonuniformly correlated beams. J. Opt. Soc. Am. A 2012, 29, 2154–2158. [Google Scholar] [CrossRef]
- Hyde, M.; Bose-Pillai, S.; Wood, R. Synthesis of non-uniformly correlated partially coherent sources using a deformable mirror. Appl. Phys. Lett. 2017, 111, 101106. [Google Scholar] [CrossRef]
- Lin, R.; Chen, M.; Liu, Y.; Zhang, H.; Gbur, G.; Cai, Y.; Yu, J. Measuring refractive indices of a uniaxial crystal by structured light with non-uniform correlation. Opt. Lett. 2021, 46, 2268–2271. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Xu, Y.; Lin, S.; Zhu, X.; Gbur, G.; Cai, Y. Longitudinal optical trapping and manipulating rayleigh particles by spatial nonuniform coherence engineering. Phys. Rev. A 2022, 106, 033511. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of nonuniformly correlated beams in atmospheric turbulence. Opt. Lett. 2013, 38, 1395–1397. [Google Scholar] [CrossRef]
- Yang, X.; Fu, W. Propagation of radially polarized beams with a Hermite non-uniformly correlated array in free space and turbulent atmosphere. Opt. Express 2023, 31, 14403. [Google Scholar] [CrossRef] [PubMed]
- Dao, W.; Liang, C.; Wang, F.; Cai, Y.; Hoenders, B.J. Effects of Anisotropic Turbulence on Propagation Characteristics of Partially Coherent Beams with Spatially Varying Coherence. Appl. Sci. 2018, 8, 2025. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, Z.; Yuan, X. Research on performance of convex partially coherent flat-topped beams in vertical atmospheric turbulent paths. Opt. Commun. 2021, 482, 126577. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Z.; Wang, Y.; Liu, L.; Zhu, X.; Guo, B.; Yu, J. Second-Order Statistics of Partially Coherent Beams with Laguerre Non-Uniform Coherence Properties under Turbulence. Photonics 2023, 10, 837. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y.; Lin, S.; Chang, H.; Zhu, X.; Cai, Y.; Yu, J. Enhancing fiber-coupling efficiency of beam-to-fiber links in turbulence by spatial non-uniform coherence engineering. Opt. Express 2023, 31, 25680–25690. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, Z.; Zhang, H.; Gao, Y.; Cai, Y.; Yuan, Y. Performance of Orbital Angular Momentum Communication for a Non-Uniformly Correlated High-Order Bessel–Gaussian Beam in a Turbulent Atmosphere. Photonics 2024, 11, 131. https://doi.org/10.3390/photonics11020131
Cong Z, Zhang H, Gao Y, Cai Y, Yuan Y. Performance of Orbital Angular Momentum Communication for a Non-Uniformly Correlated High-Order Bessel–Gaussian Beam in a Turbulent Atmosphere. Photonics. 2024; 11(2):131. https://doi.org/10.3390/photonics11020131
Chicago/Turabian StyleCong, Zihan, Hui Zhang, Yaru Gao, Yangjian Cai, and Yangsheng Yuan. 2024. "Performance of Orbital Angular Momentum Communication for a Non-Uniformly Correlated High-Order Bessel–Gaussian Beam in a Turbulent Atmosphere" Photonics 11, no. 2: 131. https://doi.org/10.3390/photonics11020131
APA StyleCong, Z., Zhang, H., Gao, Y., Cai, Y., & Yuan, Y. (2024). Performance of Orbital Angular Momentum Communication for a Non-Uniformly Correlated High-Order Bessel–Gaussian Beam in a Turbulent Atmosphere. Photonics, 11(2), 131. https://doi.org/10.3390/photonics11020131





