Performance Analysis of Chirped Graded Photonic Crystal Resonator for Biosensing Applications
Abstract
1. Introduction
2. Theoretical Analysis and Methods
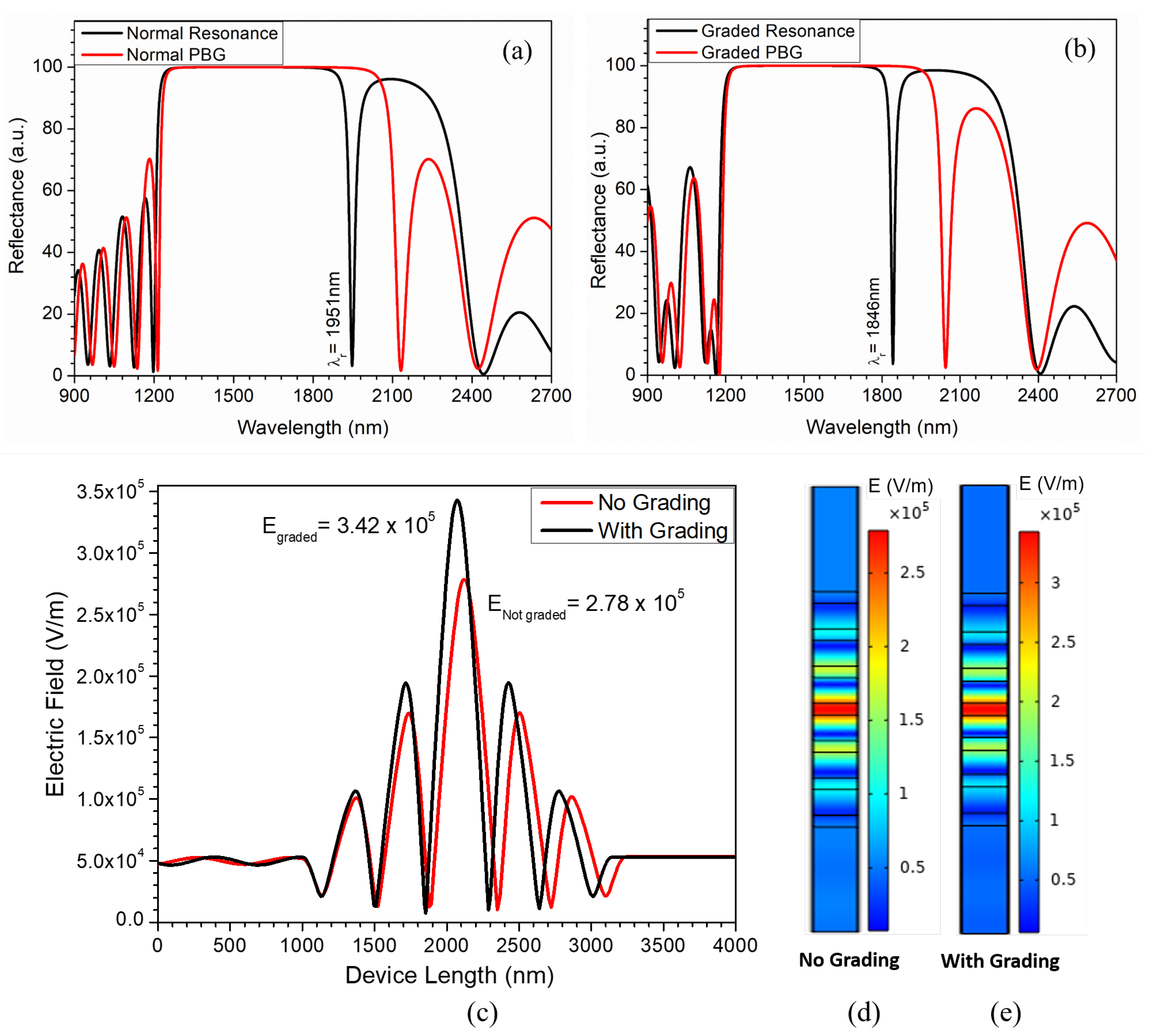
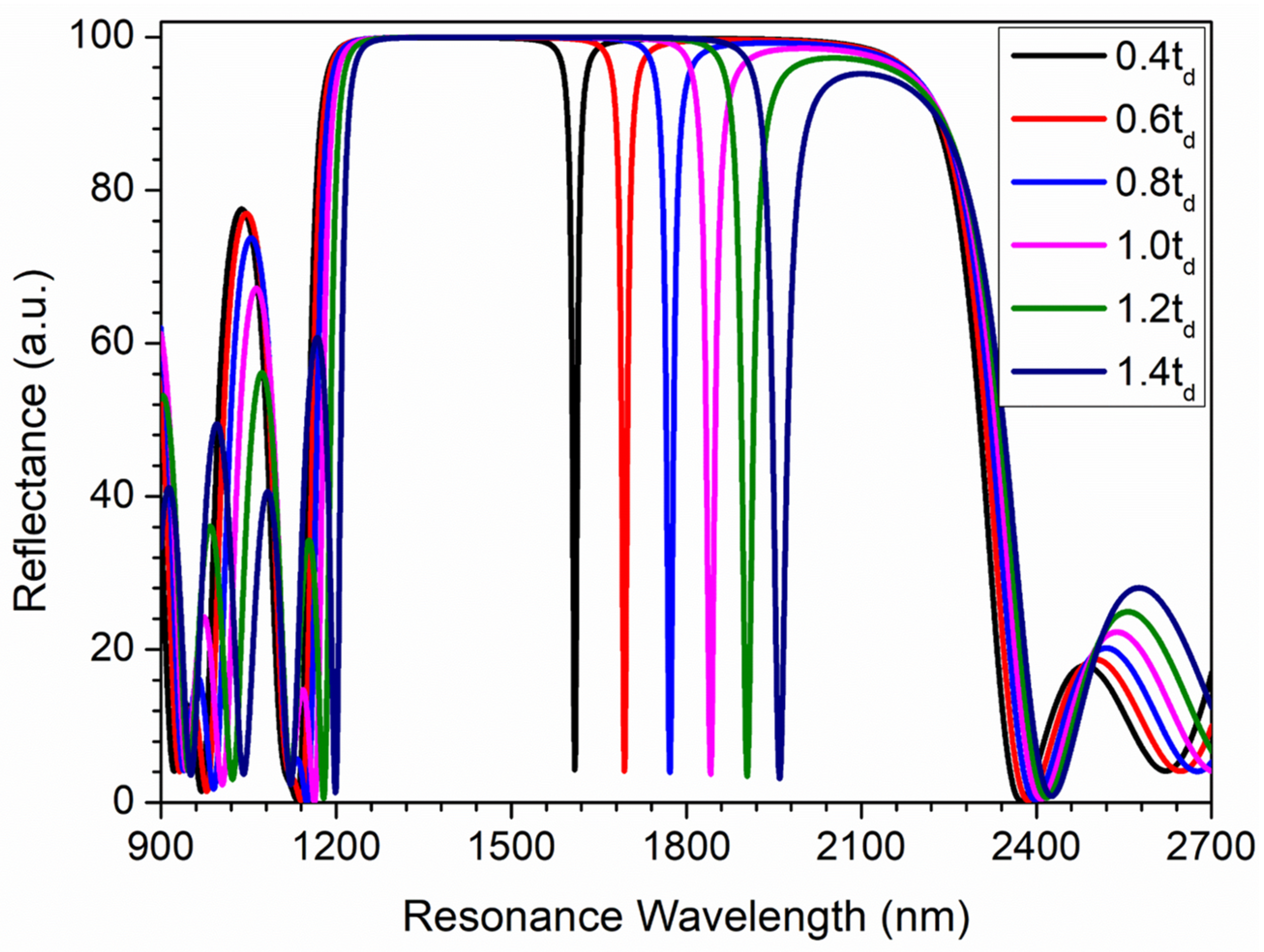
3. Results and Discussion
Sensing Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A dielectric omnidirectional reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Winn, J.N.; Fink, Y.; Fan, S.; Joannopoulos, J.D. Omnidirectional reflection from a one-dimensional photonic crystal. Opt. Lett. 1998, 23, 1573–1575. [Google Scholar] [CrossRef] [PubMed]
- Goyal, A.K.; Divyanshu, D.; Massoud, Y. Excitation of optical tamm state for photonic spin hall enhancement. Sci. Rep. 2024, 14, 175. [Google Scholar] [CrossRef] [PubMed]
- Ratra, K.; Singh, M.; Goyal, A.K. Design and Analysis of Omni-directional Solar Spectrum Reflector using One-dimensional Photonic Crystal. J. Nanophotonics 2020, 14, 026005. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Porous photonic crystal structure for sensing applications. J. Nanophotonics 2018, 12, 040501. [Google Scholar] [CrossRef]
- Wu, F.; Chen, M.; Xiao, S. Wide-angle polarization selectivity based on anomalous defect mode in photonic crystal containing hyperbolic metamaterials. Opt. Lett. 2022, 47, 2153–2156. [Google Scholar] [CrossRef]
- She, Y.; Liu, D.; Li, J.; Yao, M.; Zheng, Y.; Wu, F. Tunable wide-angle high-efficiency polarization selectivity based on a one-dimensional photonic crystal containing elliptical metamaterials. Phys. Lett. A 2024, 494, 129299. [Google Scholar] [CrossRef]
- Goyal, A.K.; Divyanshu, D.; Massoud, Y. Nanophotonic resonator assisted photonic spin Hall enhancement for sensing application. Sci. Rep. 2023, 13, 9292. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M. Optofluidic Microsystems for Chemical and Biological Analysis. Nat. Photonics 2011, 5, 591–597. [Google Scholar] [CrossRef]
- Vollmer, F.; Arnold, S. Whispering-Gallery-Mode Biosensing: Label-Free Detection Down to Single Molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef]
- Jokar, M.H.; Naraghi, A.; Seifouri, M.; Olyaee, S. Photonic crystal bio-sensor for highly sensitive label-free detection of cancer cells. Opt. Quantum Electron. 2023, 55, 660. [Google Scholar] [CrossRef]
- Fatemeh, B.; Samaneh, H. Label-Free cancer cell biosensor based on photonic crystal ring resonator. Results Phys. 2023, 46, 2211–3797. [Google Scholar]
- Gangwar, R.K.; Pathak, A.K.; Kumar, S. Recent Progress in Photonic Crystal Devices and Their Applications: A Review. Photonics 2023, 10, 1199. [Google Scholar] [CrossRef]
- Kurt, H.; Citrin, D.S. Graded index photonic crystals. Opt. Express 2023, 15, 1240–1253. [Google Scholar] [CrossRef] [PubMed]
- Das, D.; Saini, J.; Goyal, A.K.; Massoud, Y. Exponentially index modulated nanophotonic resonator for high-performance sensing applications. Sci. Rep. 2023, 13, 1431. [Google Scholar]
- Dash, D.; Saini, J. Linearly Graded Photonic Crystal with Improved Sensitivity for Sensing Application. In Proceedings of the 2022 8th International Conference on Signal Processing and Communication (ICSC), Noida, India, 1–3 December 2022; pp. 144–146. [Google Scholar]
- Centeno, E.; Cassagne, D. Graded photonic crystals. Opt. Lett 2005, 30, 2278–2280. [Google Scholar] [CrossRef]
- Savotchenko, S.E. Temperature-controlled waveguide properties of the linearly graded-index film in the photorefractive crystal. Appl. Phys. B 2023, 129, 7. [Google Scholar] [CrossRef]
- Rauh, H.; Yampolskaya, G.I.; Yampolskii, S.V. Optical transmittance of photonic structures with logarithmically similar dielectric constituents. J. Opt. 2012, 14, 015101. [Google Scholar] [CrossRef]
- Singh, B.K.; Bambole, V.; Rastogi, V.; Pandey, P.C. Multi-channel photonic bandgap engineering in hyperbolic graded index materials embedded one-dimensional photonic crystals. Opt. Laser Technol. 2020, 129, 106293. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dash, D.; Saini, J.; Massoud, Y. Theoretical analysis of graded-index topological resonator for improved sensing performance. Opt. Express 2024, 32, 4102–4110. [Google Scholar] [CrossRef]
- Savotchenko, S.E. Features of the surface wave propagation along the interface between the hyperbolic graded-index layer and nonlinear medium with a step change in the dielectric constant. Phys. Lett. A 2024, 524, 129822. [Google Scholar] [CrossRef]
- Dash, D.; Saini, J.; Goyal, A.K.; Massoud, Y. Graded Index Nanophotonic Resonator with Improved Sensing Performance. In Proceedings of the Frontiers in Optics + Laser Science (FiOLS-2022) Conference, Rochester, NY, USA, 16–20 October 2022. [Google Scholar]
- Mouldi, A.; Kanzari, M. Broad multilayer antireflection coating by apodized and chirped photonic crystal. Opt. Commun. 2011, 284, 4124–4128. [Google Scholar] [CrossRef]
- Tehranchi, A.; Kashyap, R. Novel step-chirped quasi-phase matched gratings for broadband frequency doublers with high-efficiency flat response in nonlinear optical waveguides. In Proceedings of the 19th General Assembly, Chicago, IL, USA, 7–16 August 2008; pp. 47–51. [Google Scholar]
- Wang, H. A theoretical study of the chirped and apodized photonic crystals. In Proceedings of the Progress in Electromagnetics Research Symposium (PIERS), Hangzhou, China, 22–26 August 2005; pp. 571–574. [Google Scholar]
- Goyal, A.K.; Kumar, A. (Eds.) Recent Advances and Trends in Photonic Crystal Technology; IntechOpen: London, UK, 2024. [Google Scholar] [CrossRef]
- Heidari, F.; Sharifi, A. Design and simulation of a resonant nanoring-based two-dimensional photonic crystal biosensor for cancer cell detection. Results Opt. 2024, 16, 100701. [Google Scholar] [CrossRef]
- Wiederseiner, S.; Andreini, N.; Epely-Chauvin, G.; Ancey, C. Refractive-index and density matching in concentrated particle suspensions: A review. Exp. Fluids 2011, 50, 1183–1206. [Google Scholar] [CrossRef]
- Singh, B.K.; Bijalwan, A.; Pandey, P.C.; Rastogi, V. Multi-channel photonic bandgap consequences in one-dimensional linear, exponential, and hyperbolic graded-index photonic crystals. J. Opt. Soc. Am. B 2020, 37, 523. [Google Scholar] [CrossRef]
- Dhinaa, A.N.; Palanisamy, P.K. Z-Scan Technique for Measurement of Total Cholesterol and Triglycerides in Blood. J. Innov. Opt. Health Sci. 2009, 2, 295–301. [Google Scholar] [CrossRef]
- Bijalwan, A.; Singh, B.K.; Rastogi, V. Analysis of one-dimensional photonic crystal based sensor for detection of blood plasma and cancer cells. Optik 2021, 226, 165994. [Google Scholar] [CrossRef]
- Krishnamoorthi, B.; Caroline, B.E.; Michael, M.; Thirumaran, S. A novel rhombic shaped photonic crystal bio-sensor for identifying disorders in the blood samples. Opt. Quant. Electron. 2023, 55, 312. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Performance optimization of photonic crystal resonator based sensor. Opt. Quantum Electron. 2016, 48, 431. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Superconductor—Semiconductor one-dimensional photonic crystal using a cancer cell as a defect layer. Optik 2020, 224, 165465. [Google Scholar] [CrossRef]
- Ragavendran, L.T.; Priya, A.; Nayak, C. Numerical study of temperature and pressure effect on one dimensional random photonic crystal used as biosensors in the detection of breast cancer cells. Phys. Scr. 2023, 98, 025503. [Google Scholar]
- Yashaswini, P.; Gayathri, H.; Srikanth, P. Performance analysis of photonic crystal based biosensor for the detection of bio-molecules in urine and blood. Mater. Today Proc. 2023, 80, 2247–2254. [Google Scholar] [CrossRef]
- Chowdhury, U.; Mandi, P.; Mukherjee, R. Dual Self-Referenced Refractive Index Sensor Utilizing Tamm Plasmons in Photonic Quasicrystal for Multistage Malaria Parasite Detection. Plasmonics 2024, 1–13. [Google Scholar] [CrossRef]


| Cholesterol Concentration | Refractive Index (RI) |
|---|---|
| 200 mg/dL | 2.49 |
| 220 mg/dL | 2.62 |
| 240 mg/dL | 2.80 |
| 260 mg/dL | 3.06 |
| 280 mg/dL | 3.23 |
| 300 mg/dL | 3.47 |
| Defect Layer Thickness | Resonance Wavelength (nm) | |||||
|---|---|---|---|---|---|---|
| 200 mg/dL | 220 mg/dL | 240 mg/dL | 260 mg/dL | 280 mg/dL | 300 mg/dL | |
| 1842 | 1874 | 1916 | 1972 | 2005 | 2048 | |
| 1297 | 1319 | 1346 | 1401 | 1436 | 1496 | |
| 1537 | 1580 | 1645 | 1738 | 1792 | 1873 | |
| Incidence Angle | Cholesterol Concentration (mg/dL) | Resonance Wavelength (nm) | FWHM (nm) | Sensitivity (nm/RIU) | FOM () |
|---|---|---|---|---|---|
| 0 degrees | 200 | 1537 | 4.0 | - | - |
| 220 | 1580 | 4.5 | 331 | 74 | |
| 240 | 1645 | 5.0 | 348 | 70 | |
| 280 | 1792 | 7.5 | 353 | 59 | |
| 260 | 1738 | 6.0 | 345 | 46 | |
| 300 | 1873 | 11.0 | 343 | 31 | |
| 20 degrees | 200 | 1494 | 3.0 | - | - |
| 220 | 1540 | 3.5 | 354 | 101 | |
| 240 | 1604 | 3.8 | 355 | 93 | |
| 260 | 1700 | 5.0 | 361 | 72 | |
| 280 | 1760 | 6.0 | 360 | 60 | |
| 300 | 1843 | 9.0 | 356 | 40 | |
| 40 degrees | 200 | 1373 | 1.8 | - | - |
| 220 | 1426 | 1.0 | 408 | 408 | |
| 240 | 1502 | 1.5 | 416 | 277 | |
| 260 | 1609 | 2.2 | 414 | 188 | |
| 280 | 1676 | 1.8 | 409 | 227 | |
| 300 | 1766 | 3.0 | 401 | 134 |
| Reference | Average Sensitivity (nm/RIU) | FOM () | Quality Factor | Year |
|---|---|---|---|---|
| Detection of blood plasma and cancer cells [33] | 71.25 | - | 0.02 × | 2021 |
| Blood component [34] | 166 | 392 | 3.7 × | 2023 |
| Malaria parasite detection [39] | 383–425 | - | 0.055 × | 2024 |
| Cancer cell detection [29] | 214.28 | 172.3 | 3.0 × | 2024 |
| Proposed work | 410 | 2.47 × | 0.91 × | 2024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saini, J.; Kumar, A.; Goyal, A.K. Performance Analysis of Chirped Graded Photonic Crystal Resonator for Biosensing Applications. Photonics 2024, 11, 1173. https://doi.org/10.3390/photonics11121173
Saini J, Kumar A, Goyal AK. Performance Analysis of Chirped Graded Photonic Crystal Resonator for Biosensing Applications. Photonics. 2024; 11(12):1173. https://doi.org/10.3390/photonics11121173
Chicago/Turabian StyleSaini, Jasmine, Ajay Kumar, and Amit Kumar Goyal. 2024. "Performance Analysis of Chirped Graded Photonic Crystal Resonator for Biosensing Applications" Photonics 11, no. 12: 1173. https://doi.org/10.3390/photonics11121173
APA StyleSaini, J., Kumar, A., & Goyal, A. K. (2024). Performance Analysis of Chirped Graded Photonic Crystal Resonator for Biosensing Applications. Photonics, 11(12), 1173. https://doi.org/10.3390/photonics11121173







