Outage Probability Analysis and Altitude Optimization of a UAV-Enabled Triple-Hop Mixed RF-FSO-Based Wireless Communication System

Abstract

In this paper, we present the evaluation of network parameters for the unmanned aerial vehicle (UAV)-enabled triple-hop mixed RF/FSO-based wireless communication system, where one relay is a fixed relay and the second relay is a UAV which acts as decode-and-forward relay for communication from the base station (B) to the multiple mobile users $\left(M_i\right), i\in \{1,2\cdots N\}$. The first hop from B to fixed relay (R1) is the radio frequency (RF) link modeled using $\alpha -\kappa -\mu$ fading distribution, the second hop from the relay R1 to the UAV relay (R2) is a free space optics (FSO) link modeled using Gamma-Gamma fading, and the third hop from R2 to the $M_i$ is, again, an RF link modeled using the Rayleigh fading model. The direct communication between the B and the $M_i$ is not feasible due to the very large distance. We derive the closed form analytical expression for the outage probability of the proposed system and find the effect of the base system parameters on the performance of the system. We also analyze the outage probability of the system at high SNR values to get further insights of the system performance. In addition, altitude optimization of UAV is carried out to know the optimal elevation angle in correspondence with UAV’s optimal altitude in order to maximize performance of the system.

1. Introduction

The amalgamation of unmanned aerial vehicles (UAV) in wireless communication has the ability to increase connectivity, enhance network coverage, and upgrade numerous industries and public services. As technology keeps on advancing, we can expect more inventive applications and solutions involving UAVs in the field of wireless communication [1]. An UAV is an autonomous or remotely piloted aircraft without a human onboard. They are provided with sensors, cameras, and communication systems, offering diverse applications, including surveillance, aerial photography, precision agriculture, environmental monitoring, disaster response, and military reconnaissance. UAVs propose cost-effective, flexible solutions, restructuring industries and enhancing data collection capabilities [2].

Radio Frequency (RF) link modeling is a crucial aspect of communication system design, particularly for systems involving wireless transmission such as those used in UAVs, satellite communication, or terrestrial wireless networks. The RF link model helps predict and optimize the performance of the communication link between a transmitter and a receiver. The RF-based communication system provides a reliable, high-bandwidth, and real-time communication link between UAVs and base stations, making it a perfect choice for a wide range of UAV applications [3]. The RF link can be modeled using various fading models like Rician, $\alpha -\kappa -\mu$, $\alpha -\eta -\mu$, nakagami-m, Rayleigh, etc. FSO communication, also known as optical wireless communication, is a technology that utilizes modulated optical signals to transmit data through free space, typically air or vacuum [4]. FSO systems offer high data rates, low latency, and secure communication, making them suitable for various applications, such as high-speed point-to-point communication links, last-mile connectivity, and tactical military communications. In [5], the authors proposed a model for the geometric and misalignment losses for orientation and positioning of UAV; additionally, outage probability and ergodic capacity were derived for high SNR values. The researchers in [6] used the Malaga distribution to study the effect of turbulence, taking into consideration the atmospheric attenuation, angle of arrival (AoA) fluctuation, and pointing error impairments. Also, the expressions for the average bit-error-rate (BER) and ergodic capacity was calculated. Moreover, an asymptotic analysis of BER was also performed using the heterodyne detection technique. In [7], the authors discussed the outage performance of a UAV-based wireless communication system under the hovering fluctuations of UAV. The outage probability and ergodic capacity was calculated under various relaying protocols; asymptotic outage probability was also derived to gain insight in the system performance.

The multi-hop UAV-based wireless networks offers several advantages like enhanced communication, extended battery life, and enables efficient cooperation among UAVs. These advantages make them valuable for various applications, from precision agriculture to surveillance and photography. This emphasizes that direct communication from the base station (B) to multiple mobile users is impractical due to factors like large distances, obstacles, or line-of-sight (LoS) limitations, which are common in challenging or remote environments. The researchers in [8,9,10,11,12] discussed multi-hop relaying wireless networks that not only facilitate the coverage of more users and the support of long-distance communications, but will also be able to handle overloaded networks. The multi-hop relay approach also reduces the overall power requirement for each hop, potentially enhancing energy efficiency, which is advantageous for sustainable and low-power network designs. The hybrid UAV-network-based wireless communication is a concept that combines different communication technologies to enhance the performance and reliability of UAV networks that are employed to establish high-transfer-rate data communication between devices using minimal energy consumption [13]. In some research, a new hybrid network architecture was proposed, where a UAV serving as an aerial base station flies cyclically along the edge of the cell and helps mobile terminals to offload traffic. The minimum throughput among all mobile terminals is maximized by the joint optimization of the UAV trajectory and bandwidth allocation. In other works [14], the combination of FSO (Free Space Optics) and RF, termed as hybrid FSO-RF, has emerged as an effective solution for meeting the growing need for high data rates. These hybrid UAV networks can provide high throughput, reliability, and effective communication coverage due to their high agility, mobility, and robustness of line-of-sight (LoS) channel, as discussed by authors in [15,16,17,18,19,20], along with a performance analysis of a UAV-based wireless network.

The triple-hop architecture enables coverage of a broader geographical area, making it suitable for scenarios where users are widely dispersed. Dividing the transmission into three segments reduces the required transmission power and improves signal stability by introducing decoding and forwarding at each relay, minimizing cumulative losses. A triple-hop hybrid visible light communication (VLC)/FSO method was discussed by the authors in [21], where the VLC link was modeled using the Lambertian emission model and the FSO link was modeled using Gamma-Gamma fading statistics under the influence of atmospheric turbulence, pointing error, and field of view of the receiver. Closed form expression of outage probability, average symbol error rate (ASER), and asymptotic outage probability is investigated at a high signal-to-noise ratio (SNR) regime to study in depth the system parameters. A recent study [22] highlighted that incorporating UAV-assisted multi-hop relays can enhance system performance under various conditions, such as heavy fading and pointing errors in RF and FSO channels, respectively. Additionally, triple-hop structures enable flexibility in UAV deployment, facilitating coverage optimization by adjusting UAV altitudes and positions according to communication needs. This approach is especially beneficial for scenarios requiring high data throughput and reliability, as UAVs can dynamically overcome obstacles and atmospheric disturbances that typically impair FSO links. Moreover, such configurations align well with 6G requirements for ultra-reliable and low-latency communications.

Contributions

• We propose the triple-hop mixed RF-FSO-based system, where one relay is fixed and the second one is the UAV decode-and-forward relay. The expressions for the Probability Density Function (PDF) and Cumulative Distribution Function (CDF) is presented.
• We derive closed-form expressions of end to end outage probability for the proposed system model with multiple mobile users. We evaluate the expressions for Asymptotic Outage Probability, so as to gain deep insight of the system parameters. We also calculate the Coding gain and Diversity order of all the three cases to study the behavior of the system.
• We also optimized the UAV elevation angle and the UAV altitude for the optimum performance of the system with respect to asymptotic outage probability of the proposed system.

The rest of the paper is structured as follows. In Section 2, the system and channel modeling is presented. Section 3 analyzes the performance of the system in terms of outage probability and asymptotic outage probability. Section 4 discuss about the altitude optimization of UAV. The numerical analysis of the hybrid RF-FSO direct link and UAV-assisted hybrid RF-FSO communication system is analyzed by system simulation in Section 5. Finally, conclusions are given in Section 6.

2. System and Channel Modeling

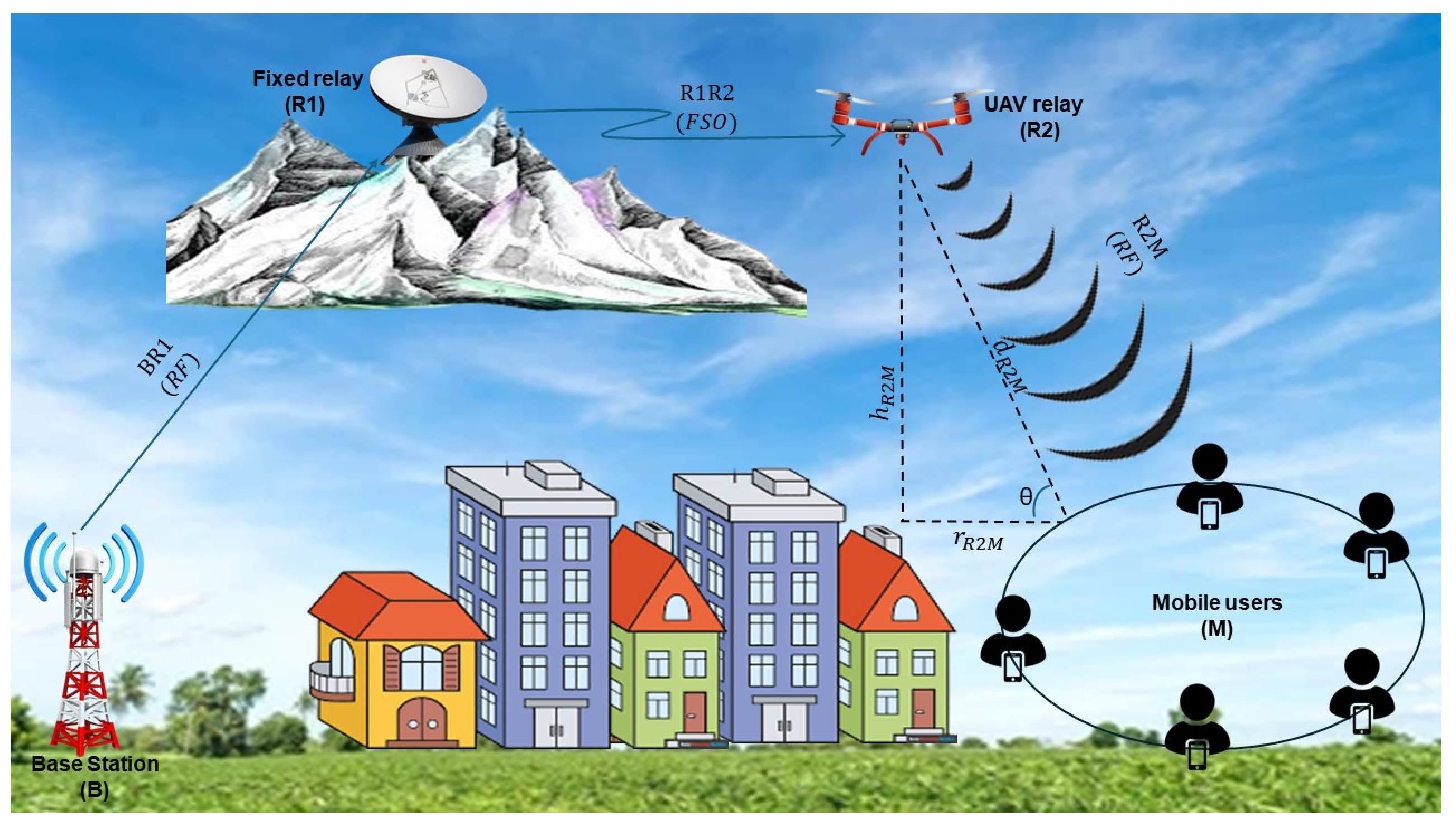
In Figure 1, we consider a triple-hop UAV-based RF-FSO system model with a decode-and-forward (DF) relay scheme, where multiple mobile users are out of the coverage area of the base station and one fixed relay and the other UAV relay is used for the transmission from the base station (B) to the multiple mobile users $\left(M_i\right)$, $i\in \{1,2\cdots N\}$. In the first hop, base station (B) transmits information to the first fixed relay (R1) via an RF link. In the second hop, the relay R1 encodes the RF signal to an optical signal and forwards it to the second UAV relay (R2) via an FSO link. In the third hop, the received optical signal is again decoded and converted to an RF signal, which is forwarded to $M_i$ via an RF link. The first hop, second hop, and third hop are modeled using $\alpha -\kappa -\mu$, FSO, and the Rayleigh fading model, respectively. The distance from R2 to $M_i$ is denoted by $d_{R2M_i}$ and the height of R2 is assumed as $h_{R2M_i}$. Also, it is assumed that R2 is hovering at an altitude $h_{R2M_i}$ under the impact of various impairments that occurred due to multipath fading. Again, it is presumed that R2 has a geographical circular coverage area with radius denoted by $r_{R2M_i}$, and $d_{R2M_i}$ is known as the Euclidean distance. $M_i$ are supposed to be located on the boundary of the circular region. Also, R2 can move vertically so as to cover the maximum coverage area by adjusting its altitude.

Figure 1. Triple-hop UAV-enabled RF/FSO system.

2.1. B to R1 Link

The B to R1 consists of the RF signal with large scale path loss and small scale fading. This link is modeled using $\alpha -\kappa -\mu$ fading statistics, which is a generalized fading model and can be used to express the small scale fading variations along with the LoS component [23]. The signal received at R1 can be given in [24] as:

$$Y_{R1}=\sqrt{P_{BR1}}\sqrt{a_{BR1}}{C}_{BR1}{x}_B+n_{R1}$$

(1)

where $P_{BR1}$ is the B to R1 transmit power, $C_{BR1}$ is the complex channel coefficient of B to R1 link, $x_B$ is the transmitted symbol, $a_{BR1}$ is the path loss attenuation factor, and $n_{R1}$ is the Additive White Gaussian Noise (AWGN) with zero mean and variance as ${\sigma }^2$. The SNR from B to R1 link, ${\gamma }_{BR1}$, is given as:

$${\gamma }_{BR1}={\displaystyle \frac{P_{BR1}{C}_{BR1}^2}{{\sigma }^2{d}_{BR1}^{\beta }}}$$

(2)

where $d_{BR1}$ is the distance between the base station and the relay R1 and $\beta$ is known as the path loss coefficient.

The PDF of the instantaneous SNR of the signal received at R1 from B is given in [25] as:

$$\begin{array}{cc}\hfill f_{{\gamma }_{BR1}}\left(\gamma \right)& =\left[{\displaystyle \frac{\alpha \mu {(1+\kappa )}^{\frac{1+\mu }{2}}{\kappa }^{\frac{1-\mu }{2}}}{e^{\mu \kappa }}}\right]\left[{\left({\displaystyle \frac{\gamma }{\overline{\gamma }}}\right)}^{{\displaystyle \frac{\alpha (1+\mu )}{2}}-1}\right]\hfill \\ \hfill & \times e^{-\left[\mu (1+\kappa ){\left({\displaystyle \frac{\gamma }{\overline{\gamma }}}\right)}^{\alpha }\right]}\times I_{\mu -1}\left(2\mu \sqrt{\kappa (1+\kappa )}{\left({\displaystyle \frac{\gamma }{\overline{\gamma }}}\right)}^{\tilde{\alpha }}\right)\hfill \end{array}$$

(3)

where $\tilde{\alpha }={\displaystyle \frac{\alpha }{2}}$ and $\alpha$ is the parameter of nonlinearity. The nonlinearity parameter often indicates the severity or degree of signal distortion that may occur in wireless channels due to various factors, such as equipment imperfections or environmental influences. This parameter could lead to increased multipath fading or affect the power distribution across the signal paths, thereby impacting the performance across each relay hop. Higher nonlinearity might increase fading severity, causing greater fluctuations in the received signal strength and potentially increasing the likelihood of outages, especially in the first RF hop. Conversely, a lower nonlinearity parameter might suggest a more stable RF link with fewer fluctuations, leading to lower outage probability. A higher nonlinearity parameter could necessitate different UAV positioning to maintain stable communication links.

$\kappa$ is known as the Rician factor [26], described as the ratio of the total power of the dominant wave component and the total power of the scattered wave component, $\mu$ is the number of multi-path clusters, $\overline{\gamma }$ is known as average SNR, $\Gamma (·)$ is known as the Gamma function, and $I_v$ denotes the Bessel’s function of order v.

The expression for the CDF of instantaneous SNR of the signal received at R1 in ([27], Equation (3.381.8)) is given as:

$$F_{{\gamma }_{BR1}}\left(\gamma \right)=\sum _{x=0}^{\infty }{\displaystyle \frac{{\mu }^x{\kappa }^x{e}^{-\kappa \mu }}{x!\Gamma (\mu +x)}}{\rm Y}\left(\mu +x,{\displaystyle \frac{\mu (1+\kappa )}{{\overline{\gamma }}^{\tilde{\alpha }}}}{\gamma }^{\tilde{\alpha }}\right)$$

(4)

$$F_{{\gamma }_{BR1}}\left(\gamma \right)=1-Q_{\mu }{\left(\sqrt{2\mu \kappa },({\displaystyle \frac{\gamma }{\overline{\gamma }}}\right)}^{\tilde{\alpha }}\sqrt{2\mu (1+\kappa )})$$

(5)

where $Q_{\mu }$ denotes the Marcum-Q function and ${\rm Y}$ represents the lower incomplete gamma function.

2.2. R1 to R2 Link

The RF data received at R1 are converted and encoded to an optical signal and is then transmitted to R2 through FSO link. The FSO link is modeled using Gamma-Gamma fading distribution. This fading model is a statistical channel model used to describe the effects of atmospheric turbulence of the transmitted signal [28]. The signal received at UR2 is given as:

$$Y_{R2}=\sqrt{P_{R1R2}}\sqrt{a_{R1R2}}{C}_{R1R2}{x}_{R1}+n_{R2}$$

(6)

where $P_{R1R2}$ is the power of converted and encoded optical signal $x_{R1}$ transmitted from fixed relay R1, $a_{R1R2}$ is the path loss attenuation factor, and $n_{R2}$ is the AWGN with zero mean and variance as $N_0$. $C_{R1R2}$ is the optical channel coefficient of R1 to R2 link depending on fading parameters like AoA fluctuations, atmospheric turbulence, and pointing errors. The AoA is a crucial parameter in FSO link modeling as it affects the link performance and reliability. It can be influenced by misalignment between the transmitter and the receiver. The AoA fluctuations can be reduced by increasing the FOV of the receiver [29]. The SNR of the R1 to R2 link, ${\gamma }_{R1R2}$, is given in [24] as:

$${\gamma }_{R1R2}={\displaystyle \frac{P_{R1R2}{C}_{R1R2}^2}{N_0{d}_{R1R2}^{\beta }}}$$

(7)

where $d_{R1R2}$ is the distance between the fixed relay R1 and UAV relay R2.

The PDF of the instantaneous SNR of the signal received at R2 is given in [30] as:

$$\begin{array}{c}\hfill f_{{\gamma }_{R1R2}}\left(\gamma \right)=exp\left(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}}\right)+\left[1-exp\left(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}}\right)\right]\\ \hfill \times \left[{\displaystyle \frac{{\zeta }^2}{2\gamma \Gamma \left({\alpha }_{at}\right)\Gamma \left({\beta }_{at}\right)}}{G}_{1,3}^{3,0}\left({\displaystyle \frac{{\alpha }_{at}{\beta }_{at}}{A_0{h}_t}}\sqrt{{\displaystyle \frac{\gamma }{{\overline{\gamma }}_{UR1,UR2}}}}{|}_{{\zeta }^2,{\alpha }_{at},{\beta }_{at}}^{1+{\zeta }^2}\right)\right]\end{array}$$

(8)

where ${\theta }_f$ is the field of view (FOV) of the receiver of the FSO link, ${\overline{\gamma }}_{R1R2}$ is the average SNR of the signal received from R1 to R2, ${\sigma }_{\theta }^2$ is the variance of transmitter and receiver misalignment, and $\zeta ={\displaystyle \frac{w_{eq}}{2{\sigma }_s}}$, where $w_{eq}$ is the equivalent beam width at R2 receiver and ${\sigma }_s$ is the standard deviation of misalignment displacement at R2, ${\alpha }_{at}$ and ${\beta }_{at}$ are the atmospheric turbulence parameters linked to atmospheric conditions commonly known as scintillation parameters, $\Gamma (·)$ denotes the standard gamma function, $A_0={\left[erf\left(V\right)\right]}^2$, where $erf(·)$ is the error function, $v={\displaystyle \frac{\sqrt{\pi }{R}_a}{\sqrt{2}{w}_n}}$, where $R_a$ is the radius of aperture of the receiver and $w_n$ is the normalized beam waist by $R_a$, and $h_t$ is the atmospheric turbulence defined in [31].

The CDF of instantaneous SNR, ${\gamma }_{R1R2}$, is given as:

$$\begin{array}{cc}\hfill & F_{{\gamma }_{R1R2}}\left(\gamma \right)=exp(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}})+\left[1-exp\left(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}}\right)\right]\hfill \\ & \times \left[{\displaystyle \frac{{\zeta }^2}{\Gamma \left({\alpha }_{at}\right)\Gamma \left({\beta }_{at}\right)}}{G}_{2,4}^{3,1}\left({\displaystyle \frac{{\alpha }_{at}{\beta }_{at}}{A_0{h}_t}}\sqrt{{\displaystyle \frac{\gamma }{{\overline{\gamma }}_{UR1,UR2}}}}{|}_{{\zeta }^2,{\alpha }_{at},{\beta }_{at},0}^{1,1+{\zeta }^2}\right)\right]\hfill \end{array}$$

(9)

2.3. R2 to $M_i$ Link

The transmission in this section is from UAV relay R2 to the multiple mobile users $\left(M_i\right)$, $i\in \{1,2\cdots N\}$. As it is non line-of-sight (NLOS), this link is modeled using the Rayleigh fading model. The signal obtained at $i^{th}$ mobile user is given as:

$$y_i={\displaystyle \frac{1}{\sqrt{L_{R2M_i}}}}\sqrt{P_{R2M_i}}{C}_i^2{x}_i+n_i,i\in \{1,2\cdots N\}$$

(10)

where $P_{R2M_i}$ is the UAV relay R2 transmit power, $C_i$ is the channel coefficient of $i^{th}$ user which is modeled by Rayleigh distribution, $L_{R2M_i}$ is the path loss of the Rayleigh link and can be expressed as $L_{R2M_i}=\mathcal{A}{d}_{R2M_i}^{\beta }$, where $\beta$ is the path loss exponent and $\mathcal{A}$ is the constant which depends on the frequency of signal and transmission environment, $x_i$ is the signal transmitted from UAV relay R2 to ith mobile user, and $n_i\approx \mathcal{N}(0,N_{0i})$ is the AWGN noise with 0 mean and variance as $N_{0i}$. The distance between the UAV relay R2 and selected mobile user is denoted by $d_{R2M_i}$ and which can be calculated from Figure 1 as $d_{R2M_i}=\sqrt{h_{R2M_i}^2+r_{R2M_i}^2}$, where $h_{R2M_i}$ is the height of UAV from the ground and $r_{R2M_i}$ is the horizontal distance from UAV relay R2 and selected mobile user. The SNR of the signal received at $M_i$ from R2, ${\gamma }_{R2M_i}$, is given as:

$${\gamma }_{R2M_i}={\displaystyle \frac{P_{R2M_i}{\left|C_i\right|}^2}{N_{0i}{d}_{R2M_i}^{\beta }{L}_{R2M_i}}}$$

(11)

where $d_{R2M_i}$ is the distance from UAV relay R2 to the $i^{th}$ user. The average SNR of the links between the R2 and selected $i_{th}$ mobile user is ${\overline{\gamma }}_{R2M_i}={\displaystyle \frac{P_{R2M_i}{d}_{R2M_i}^{-\beta }}{N_{0i}}}$, $i\in \{1,2\cdots N\}$. The mobile user is chosen with maximum SNR (${\gamma }_{max}$) from other multiple mobile users, applying the opportunistic scheduling scheme [32] given by:

$${\gamma }_{max}=\underset{i\in \{1,2\cdots N\}}{max}\left\{{\gamma }_{R2M_i}\right\}$$

(12)

where it is supposed that messages are transmitted periodically by UAV in order to calculate the SNR of the signal received at the destination. When there is a need to choose the mobile user, its instantaneous SNR is calculated and is communicated to the UAV. Then, the UAV will pick the mobile user with the maximum SNR.

The CDF of the instantaneous SNR of the signal received from UR2 to the selected MU is given in [33] as:

$$F_{{\gamma }_{max}}\left(\gamma \right)={\left(1-e^{{\displaystyle \frac{-\gamma }{{\overline{\gamma }}_m}}}\right)}^N$$

(13)

$$F_{{\gamma }_{max}}\left(\gamma \right)=\sum _{k=0}^N\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k}}\right){(-1)}^k{e}^{-{\displaystyle \frac{\gamma k}{{\overline{\gamma }}_m}}}$$

(14)

where ${\overline{\gamma }}_m$ is the average SNR of the signal received at UAV from $i^{th}$ user.

3. Performance Analysis

In this section, we discuss the outage probability and asymptotic outage probability at higher SNR values for the proposed triple-hop wireless communication system.

3.1. Outage Probability

Outage probability is a key performance metric in wireless communication systems. It represents the probability that the instantaneous signal-to-noise ratio (SNR) falls below a certain threshold, causing a loss of communication or “outage”. Outage probability is often used to evaluate the reliability and performance of communication links under various conditions. The SNR of the signal received at the destination is written as:

$${\gamma }_{BM}=min({\gamma }_{BR1},{\gamma }_{R1R2},{\gamma }_{max})$$

(15)

where ${\gamma }_{BR1}$ is the SNR from the B to R1 link, ${\gamma }_{R1R2}$ is the SNR from the R1 to R2 link, and ${\gamma }_{max}$ is the maximum SNR from the R2 to M link.

The CDF for end to end SNR is given by:

$$\begin{array}{cc}\hfill F_{{\gamma }_{BM}}\left(\gamma \right)& =Pr({\gamma }_{BM}\le \gamma )\hfill \\ & =Pr(min({\gamma }_{BR1},{\gamma }_{R1R2},{\gamma }_{max})\le \gamma )\hfill \\ \hfill & =1-[1-F_{{\gamma }_{BR1}}\left(\gamma \right)][1-F_{{\gamma }_{R1R2}}\left(\gamma \right)][1-F_{{\gamma }_{max}}\left(\gamma \right)]\hfill \end{array}$$

(16)

where $F_{{\gamma }_{BR1}}\left(\gamma \right)$ is the CDF of SNR of the signal received from the first hop, $F_{{\gamma }_{R1R2}}\left(\gamma \right)$ is the CDF of SNR of signal received from the second hop, and $F_{{\gamma }_{max}}\left(\gamma \right)$ is the CDF of SNR of signal received from the third hop.

The outage probability $P_{out}^{{\gamma }_{BM}}$ of any hybrid system is given by:

$$P_{out}^{{\gamma }_{BM}}=F_{{\gamma }_{BM}}\left({\gamma }_{th}\right)=Pr({\gamma }_{BM}\le {\gamma }_{th})$$

(17)

where ${\gamma }_{BM}$ is the end-to-end SNR, $P(·)$ is the probability notation, and ${\gamma }_{th}$ describes the SNR threshold. Therefore, to obtain the outage probability, substituting the values of $F_{{\gamma }_{BR1}}\left(\gamma \right)$, $F_{{\gamma }_{R1R2}}\left(\gamma \right)$, and $F_{{\gamma }_{max}}\left(\gamma \right)$ from (5), (9), and (14), respectively, and substituting $\gamma$ by ${\gamma }_{th}$, closed form expression for outage probability obtained is given as:

$$\begin{array}{cc}\hfill P_{out}^{{\gamma }_{BM}}& =1-\left\{1-\left[1-Q_{\mu }\left(\sqrt{2\mu \kappa },{\left({\displaystyle \frac{{\gamma }_{th}}{\overline{\gamma }}}\right)}^{\tilde{\alpha }}\sqrt{2\mu (1+\kappa )}\right)\right]\right\}\hfill \\ & \times \{1-exp(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}})-\left[1-exp\left(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}}\right)\right]\hfill \\ & \times \left[{\displaystyle \frac{{\zeta }^2}{\Gamma \left({\alpha }_{at}\right)\Gamma \left({\beta }_{at}\right)}}{G}_{2,4}^{3,1}\left({\displaystyle \frac{{\alpha }_{at}{\beta }_{at}}{A_0{h}_t}}\sqrt{{\displaystyle \frac{{\gamma }_{th}}{{\overline{\gamma }}_{UR1,UR2}}}}{|}_{{\zeta }^2,{\alpha }_{at},{\beta }_{at},0}^{1,1+{\zeta }^2}\right)\right]\}\hfill \\ & \times \left\{1-\sum _{k=0}^N\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k}}\right){(-1)}^k{e}^{-{\displaystyle \frac{{\gamma }_{th}}{{\overline{\gamma }}_m}}k}\right\}\hfill \end{array}$$

(18)

After some mathematical manipulations and rearrangement, the outage probability $P_{out}^{{\gamma }_{BM}}$ is obtained as:

$$\begin{array}{cc}\hfill P_{out}^{{\gamma }_{BM}}=1& -[\left\{1-\sum _{k=0}^N\left({\displaystyle \genfrac{}{}{0pt}{}{N}{k}}\right){(-1)}^k{e}^{-{\displaystyle \frac{{\gamma }_{th}}{{\overline{\gamma }}_m}}k}\right\}\hfill \\ & \times \left\{Q_{\mu }{\left(\sqrt{2\mu \kappa },({\displaystyle \frac{{\gamma }_{th}}{\overline{\gamma }}}\right)}^{\tilde{\alpha }}\sqrt{2\mu (1+\kappa )}\right)\}\hfill \\ & \times \{1-exp(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}})-\left[1-exp\left(-{\displaystyle \frac{{\theta }_f^2}{2{\sigma }_{\theta }^2}}\right)\right]\hfill \\ \hfill & \times \left[{\displaystyle \frac{{\zeta }^2}{\Gamma \left({\alpha }_{at}\right)\Gamma \left({\beta }_{at}\right)}}{G}_{2,4}^{3,1}\left({\displaystyle \frac{{\alpha }_{at}{\beta }_{at}}{A_0{h}_t}}\sqrt{{\displaystyle \frac{{\gamma }_{th}}{{\overline{\gamma }}_{UR1,UR2}}}}{|}_{{\zeta }^2,{\alpha }_{at},{\beta }_{at},0}^{1,1+{\zeta }^2}\right)\right]\left\}\right]\hfill \end{array}$$

(19)

3.2. Asymptotic Outage Probability

The outage probability obtained of the defined system is very complex, and therefore, its parameters cannot be measured. The asymptotic outage probability is used to describe the behavior of the outage probability as the SNR becomes very large. It provides insights into the system’s performance at high SNR values. Analyzing the asymptotic outage probability provides a high-level view of a communication system’s performance in favorable conditions. We can write outage probability in terms of coding gain and diversity order as $P_{out,\infty }^{{\gamma }_{BM}}\simeq {\left(\mathcal{G}\overline{\gamma }\right)}^{-\mathcal{D}}$, where $\mathcal{G}$ is the system’s coding gain and $\mathcal{D}$ is the diversity order of system [34]"

$$\begin{array}{cc}\hfill P_{out,\infty }^{{\gamma }_{BM}}& =F_{{\gamma }_{BM}}^{\infty }\left({\gamma }_{th}\right)\hfill \\ & =F_{{\gamma }_{BR1}}^{\infty }\left({\gamma }_{th}\right)+F_{{\gamma }_{R1R2}}^{\infty }\left({\gamma }_{th}\right)+F_{{\gamma }_{max}}^{\infty }\left({\gamma }_{th}\right)\hfill \end{array}$$

(20)

where $F_{{\gamma }_{BR1}}^{\infty }\left({\gamma }_{th}\right)$ is CDF of signal received from the first hop at high SNR values, $F_{{\gamma }_{R1R2}}^{\infty }\left({\gamma }_{th}\right)$ is CDF of signal received from the second hop at high SNR values, and $F_{{\gamma }_{max}}^{\infty }\left({\gamma }_{th}\right)$ is the CDF of signal received from the third hop at high SNR values.

3.2.1. $B\to R1$ Link (First Hop)

The CDF of the signal received from the B to R1 link at high values of SNR is obtained by considering Equation (4) and using the properties of gamma function $\gamma (s,x)\simeq {\displaystyle \frac{x^s}{s}}$ as $x\to 0$:

$$\begin{array}{cc}\hfill F_{{\gamma }_{BR1}}^{\infty }\left({\gamma }_{th}\right)& ={\displaystyle \frac{{\mu }^0{\kappa }^0{e}^{-\kappa \mu }}{0!\Gamma (\mu +0)}}{\displaystyle \frac{{\left[\mu (1+\kappa ){\left(\frac{{\gamma }_{th}}{\overline{\gamma }}\right)}^{\tilde{\alpha }}\right]}^{\mu }}{\mu }}\hfill \\ \\ \hfill & =\left({\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}}\right){\overline{\gamma }}^{-\tilde{\alpha }\mu }\hfill \end{array}$$

(21)

3.2.2. $(R1\to R2)$ Link (Second Hop)

The CDF of the signal received from the R1 to R2 link from Equation (9) can be calculated at high SNR using identity [34,35], Equation (6.2.2)] as:

$$\begin{array}{cc}\hfill F_{{\gamma }_{R1R2}}^{\infty }\left({\gamma }_{th}\right)& =X\sum _{n=1}^6{\displaystyle \frac{{\prod }_{m=1}^6\Gamma (y_m-y_n)\Gamma \left(y_n\right)}{{\prod }_{m=2}^3\Gamma (x_m-y_n)\Gamma (1+y_n)}}{Y}^{{\displaystyle \frac{y_n}{2}}}{\left({\displaystyle \frac{{\gamma }_{th}}{\overline{\gamma }}}\right)}^{{\displaystyle \frac{y_n}{2}}}\hfill \\ \\ \hfill & ={\left({\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}}\overline{\gamma }\right)}^{{\displaystyle \frac{-y_n}{2}}}\hfill \end{array}$$

(22)

where $x_m$ = $x_p\left(m\right)$, for $m=$ 1 to 3, $x_1$ = 1, $y_m$ = $=y_q\left(m\right)$, $m=$ 1 to 6, $y_7$ = 0, and $y_n=min\{{\zeta }^2,{\alpha }_{at},{\beta }_{at}\}$, constant Z is equal to $X{\sum }_{n=1}^6{\displaystyle \frac{{\prod }_{m=1}^6\Gamma (y_m-y_n)\Gamma \left(y_n\right)}{{\prod }_{m=2}^3\Gamma (x_m-y_n)\Gamma (1+y_n)}}{Y}^{{\displaystyle \frac{y_n}{2}}}$, $X=\left[1-exp\left({\displaystyle \frac{-{\theta }_f^2}{2{\sigma }_{\theta }}}\right)\times {\displaystyle \frac{2({\alpha }_{at}+{\beta }_{at}-2)}{2\pi \Gamma \left({\alpha }_{at}\right)\Gamma \left({\beta }_{at}\right)}}\right]$ and $Y={\left({\displaystyle \frac{{\left({\alpha }_{at}{\beta }_{at}\right)}^2}{16}}\right)}^{{\displaystyle \frac{y_n}{2}}}$.

3.2.3. $(R2\to M_i)$ Link (Third Hop)

The CDF of signal received from R2 to $M_i$ links given in (13) can be calculated asymptotically by using taylor series for exponential functions and ignoring higher order terms, $F_{{\gamma }_{max}}^{\infty }\left({\gamma }_{th}\right)$ can be written as:

$$F_{{\gamma }_{max}}^{\infty }\left({\gamma }_{th}\right)=1-{\left(1-{\displaystyle \frac{{\gamma }_{th}}{{\overline{\gamma }}_m}}\right)}^N={\left({\overline{\gamma }}_m{\gamma }_{th}^{-1}\right)}^{-N}$$

(23)

After substituting the values of $F_{{\gamma }_{BR1}}^{\infty }\left({\gamma }_{th}\right)$, $F_{{\gamma }_{R1R2}}^{\infty }\left({\gamma }_{th}\right)$. and $F_{{\gamma }_{max}}^{\infty }\left({\gamma }_{th}\right)$ from (21), (22) and (23), respectively, in (20), the asymptotic outage probability is obtained as:

$$\begin{array}{c}\hfill P_{out,\infty }^{{\gamma }_{BM}}=\left({\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}}\right){\overline{\gamma }}^{-\tilde{\alpha }\mu }\\ \hfill +{\left({\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}}\overline{\gamma }\right)}^{{\displaystyle \frac{-y_n}{2}}}+{\left({\overline{\gamma }}_m{\gamma }_{th}^{-1}\right)}^{-N}\end{array}$$

(24)

Therefore, Coding gain ($\mathcal{G}$) and Diversity order ($\mathcal{D}$) can be calculated from (24), representing asymptotic outage probability. It is noted clearly that the system performance is under influence of the worst link parameters among other links. Then, diversity gain of the designed system is $min(\tilde{\alpha }\mu ,{\displaystyle \frac{y_n}{2}},N)$. Based on this, we will consider the three cases to examine the outage performance of the system.

• Case 1: When only one link is dominating out of the three links, then the coding gain and diversity order can be expressed from (24) as:

  $$\begin{array}{c}\hfill G=\left\{\begin{array}{cc}{\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}},\hfill & D=\tilde{\alpha }\mu \hfill \\ {\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}},\hfill & D={\displaystyle \frac{y_n}{2}}\hfill \\ {\gamma }_{th}^{-1},\hfill & D=N\hfill \end{array}\right.\end{array}$$

  (25)
• Case 2: When two links are dominating out of three links, then the coding gain and diversity order can be expressed as:

  $$\begin{array}{c}\hfill G=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}}+{\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}}\right),\hfill & D=\tilde{\alpha }\mu ={\displaystyle \frac{y_n}{2}}\hfill \\ {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}}+{\gamma }_{th}^{-1}\right),\hfill & D={\displaystyle \frac{y_n}{2}}=N\hfill \\ {\displaystyle \frac{1}{2}}\left({\gamma }_{th}^{-1}+{\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}}\right),\hfill & D=N=\tilde{\alpha }\mu \hfill \end{array}\right.\end{array}$$

  (26)
• Case 3: When all the three links are dominating, then the coding gain and diversity order can be expressed as:

  $$\begin{array}{c}\hfill G=\left\{\begin{array}{c}{\displaystyle \frac{1}{3}}({\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa )}^{\mu }{{\gamma }_{th}}^{\widetilde{\alpha \mu }}}{\Gamma \left(\mu \right)e^{\kappa \mu }}}\hfill \\ +{\displaystyle \frac{Z^{\frac{-2}{y_n}}}{{\gamma }_{th}}}+{\gamma }_{th}^{-1}),\hfill & D=\tilde{\alpha }\mu ={\displaystyle \frac{y_n}{2}}=N\hfill \end{array}\right.\end{array}$$

  (27)

3.3. Path Loss Exponent

The line of sight probability and path loss exponent are related [36] as:

$$\beta \left(\theta \right)=x_{1}P\left(\theta \right)+y_1,$$

(28)

where $P\left(\theta \right)$ is the function of elevation angle and can be written as $P\left(\theta \right)={\displaystyle \frac{1}{1+x_2{e}^{-y_2\theta }}}$ and $x_1,y_1,x_2,y_2$ are constants depending upon environmental and transmitted frequency and $\theta$ is the elevation angle of UAV in radians. The Rician factor can also be expressed as a function of elevation angle of UAV. Using Rice factor $k,\kappa \left(\theta \right)$ can be related as:

$$k,\kappa \left(\theta \right)=x_3{e}^{y_3\theta }$$

(29)

where $x_3$ and $y_3$ are constants relying upon transmission frequency and environmental characteristics.

4. Altitude Optimization of UAV

The UAV’s altitude can notably affect the end-to-end performance of the proposed triple-hop mixed RF/FSO system, and thereby, its signal quality. Despite the fact that high altitude enhances the coverage, it also increases the path loss, thereby causing less LoS probability. Due to this, there is a trade-off between the coverage area and the quality of the link. In this section, optimizing the altitude of UAVs involves finding the ideal flight altitude that maximizes the efficiency and performance of the UAV in a given application. To get the optimum altitude of UAV and its optimal value of elevation angle for the horizontal distance from UAV relay R2 and $M_i$, there is a need to minimize the $P_{out,\infty }^{{\gamma }_{BM}}$ with respect to the elevation angle $\theta$. Hence, after some mathematical simplifications and manipulations, the asymptotic outage probability of the proposed system as derived (24) can be rewritten in terms of power, distance, and elevation angle as:

$$\begin{array}{cc}\hfill P_{out,\infty }^{{\gamma }_{BM}}=& {\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa \left({\theta }_1\right))}^{\mu }{\left({\gamma }_{th}{\sigma }^2{d}_{BR1}^{\beta \left({\theta }_1\right)}\right)}^{\tilde{\alpha }\mu }}{\Gamma \left(\mu \right)e^{\kappa \left({\theta }_1\right)\mu }{P_{BR1}}^{\tilde{\alpha }\mu }}}\hfill \\ & +\left({\displaystyle \frac{Z{\left({\gamma }_{th}{N}_0{d}_{R1R2}\right)}^{\frac{y_n}{2}}}{P_{R1R2}^{\frac{y_n}{2}}}}\right)\hfill \\ & +\prod _{i=1}^N\left({\displaystyle \frac{N_{0i}{d_{R2M_i}}^{\beta \left({\theta }_i\right)}{\gamma }_{th}}{P_{R2M_i}}}\right)\hfill \end{array}$$

(30)

where ${\theta }_1$ is the UAV look angle at BS and $d_{BR1}$ is distance from the B to the fixed relay R1. Here, ${\theta }_i$ is the look angle of UAV relay R2 at $i_{th}$ mobile user and $d_{R2M_i}$ is the distance between the UAV and the $i_{th}$ mobile user located at boundary of the geographical area. Now, to perform altitude optimization of UAV relay R2, the asymptotic outage probability is composed as a function of UAV altitude $h_{R2M_i}$ and horizontal distance $r_{R2M_i}$. For the given values of $r_{R2M_i}$, the optimal altitude $h_{R2M_i}$ must obey the condition given by:

$${\widehat{h}}_{R2M_i}=arg\underset{h\in [0,\infty )}{min}{P}_{out,\infty }^{{\gamma }_{BM}}(h_{R2M_i},r_{R2M_i})$$

(31)

To get the optimal elevation angle of UAV and the corresponding optimal altitude of UAV, we minimize the asymptotic outage probability of the triple-hop mixed RF-FSO system by taking the derivative of (30) with respect to ${\theta }_i$ as shown by:

$${\displaystyle \frac{\partial }{\partial {\theta }_i}}{P}_{out,\infty }^{{\gamma }_{BM}}(h_{R2M_i},r_{R2M_i})=0$$

(32)

Now, substituting the value of $P_{out,\infty }^{{\gamma }_{BM}}(h_{R2M_i},r_{R2M_i})$ from (30) in (32) gives:

$${\displaystyle \frac{\partial }{\partial {\theta }_i}}\left[{\zeta }^1+\prod _{i=1}^N\left({\displaystyle \frac{N_{0i}{d_{R2M_i}}^{\beta \left({\theta }_i\right)}{\gamma }_{th}}{P_{R2M_i}}}\right)\right]=0$$

(33)

where ${\zeta }^1={\displaystyle \frac{{\left(\mu \right)}^{\mu -1}{(1+\kappa \left({\theta }_1\right))}^{\mu }{\left({\gamma }_{th}{\sigma }^2{d}_{BR1}^{\beta \left({\theta }_1\right)}\right)}^{\tilde{\alpha }\mu }}{\Gamma \left(\mu \right)e^{\kappa \left({\theta }_1\right)\mu }{P_{BR1}}^{\tilde{\alpha }\mu }}}+\left({\displaystyle \frac{Z{\left({\gamma }_{th}{N}_0{d}_{R1R2}\right)}^{\frac{y_n}{2}}}{P_{R1R2}^{\frac{y_n}{2}}}}\right)$ and is independent of ${\theta }_i$. Now, by taking either single user or multiple users, the radius of coverage area $r_{R2M_i}$ will remain the same as the multiple users that reside on the boundary of geographical area of radius $r_{R2M_i}$. Further substituting the value of $\beta \left({\theta }_i\right)$ from (28) in (33) yields:

$${\displaystyle \frac{\partial }{\partial {\theta }_i}}\left({\displaystyle \frac{N_{0i}{d_{R2M}}^{\left(\frac{x_1}{1+x_2{e}^{-y_2{\theta }_i}}+y_1\right)}{\gamma }_{th}}{P_{R2M}}}\right)=0$$

(34)

or

$$\left({\displaystyle \frac{N_{0i}{\gamma }_{th}}{P_{R2M}}}\right){\displaystyle \frac{\partial }{\partial {\theta }_i}}\left[{d_{R2M}}^{\stackrel{\mathrm{S}}{\left(\overbrace{{\displaystyle \frac{x_1}{1+x_2{e}^{-y_2{\theta }_i}}}+y_1}\right)}}\right]=0$$

(35)

To solve the partial derivative, let $f\left(S\right)={\left(d_{R2M_i}\right)}^S$. Further applying the chain rule and exponential rule gives:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial {\theta }_i}}\left({\left(d_{R2M}\right)}^S\right)={\left(d_{R2M}\right)}^{S}ln\left(d_{R2M}\right){\displaystyle \frac{\partial }{\partial {\theta }_i}}\left(S\right)\end{array}$$

(36)

Assuming $R={\displaystyle \frac{\partial }{\partial {\theta }_i}}\left(S\right)$ and further simplification by substituting value of S yields:

$$R={\displaystyle \frac{\partial }{\partial {\theta }_i}}\left[{\displaystyle \frac{x_1}{1+x_2{e}^{-y_2{\theta }_i}}}\right]+{\displaystyle \frac{\partial }{\partial {\theta }_i}}\left[y_1\right]={\displaystyle \frac{\partial }{\partial {\theta }_i}}\left[{\displaystyle \frac{x_1}{1+x_2{e}^{-y_2{\theta }_i}}}\right]$$

(37)

After solving the above equation, we get:

$$R={\displaystyle \frac{x_1{x}_2{y}_2{e}^{-y_2{\theta }_i}}{(1+x_2{e}^{-y_2{\theta }_i}{)}^2}}$$

(38)

On substituting the value of R from (38) in (36), we get:

$${\displaystyle \frac{\partial }{\partial {\theta }_i}}\left({\left(d_{R2M}\right)}^S\right)={\displaystyle \frac{x_2{y}_2{\left(d_{R2M}\right)}^S{x}_1{e}^{y_2{\theta }_i}ln\left(d_{R2M}\right)}{{(x_2+e^{y_2{\theta }_i})}^2}}$$

(39)

Therefore, we achieved an optimal solution for the elevation angle $\theta$ by substituting the value of partial derivative from (39) in (35). Hence, for the given values of $r_{R2M}$, we get the optimum altitude ${\widehat{h}}_{R2M}$ given by:

$${\widehat{h}}_{R2M}=r_{R2M}tan\left(\widehat{\theta }\right)$$

(40)

where $\theta$ is obtained by (35).

5. Numerical Results

In this section, the numerical expressions of the outage probability and asymptotic outage are plotted and simulated. The UAV altitude of the proposed system is optimized and verified numerically. The effect of various parameters, such as the number of users, SNR threshold value, $\alpha ,\kappa ,\mu$, $\zeta$ parameter, turbulence level, etc., are validated. The Monte Carlo simulation is used to verify the analytical results. The FSO link is modeled using Gamma-Gamma fading distribution taking into account the AoA fluctuations, atmospheric turbulence, path loss, and pointing errors. The simulation parameters used are depicted in Table 1.

Table 1. Table depicting the simulation parameters.

Simulation Parameters
Parameters	Values
SNR Threshold	1.8–7 dB
$\alpha$	4
$\kappa$	1.5–4.5
$\mu$	1–3
N	1–3
$\zeta$	2

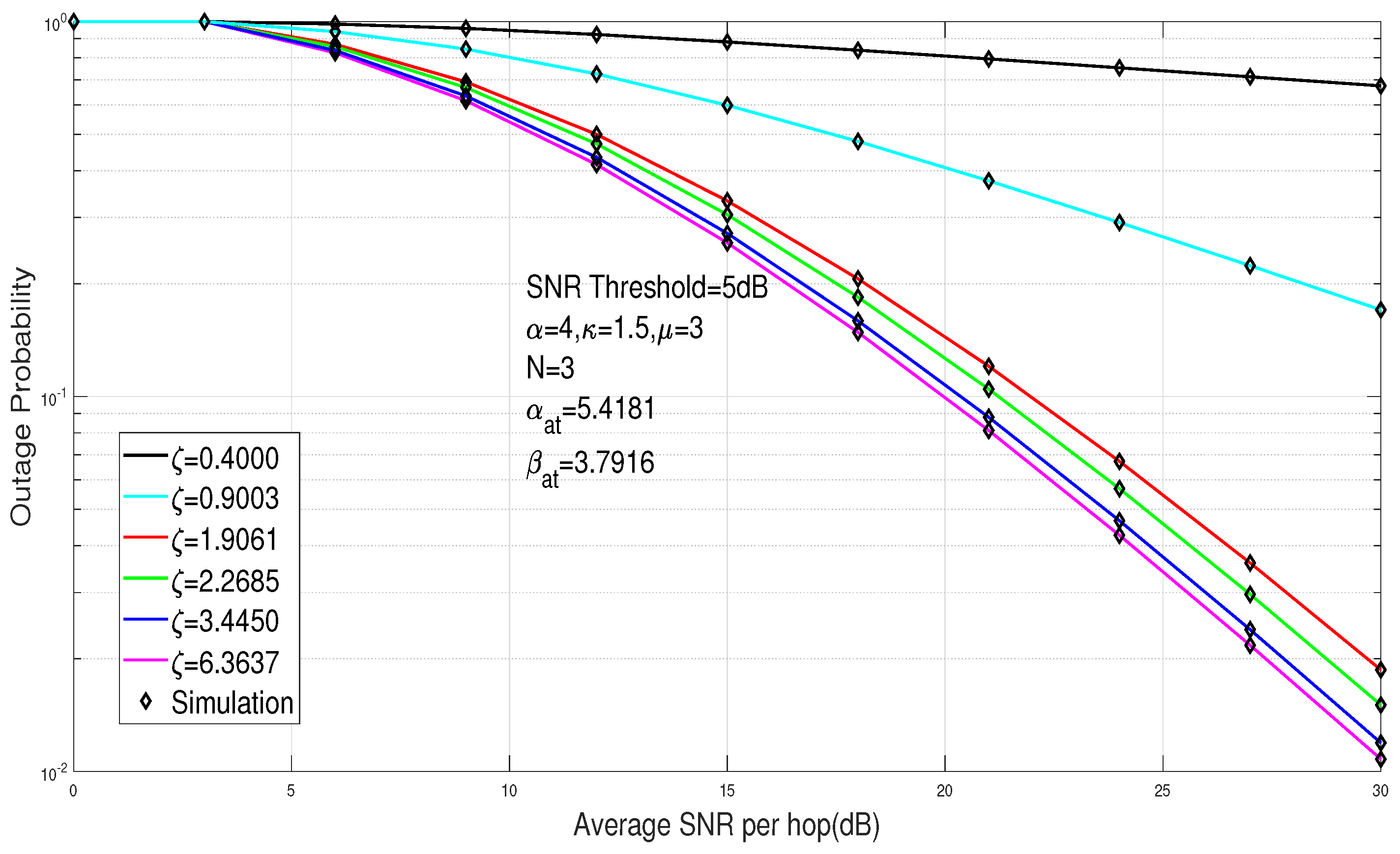
The impact of variation in pointing error of the FSO link against outage probability is demonstrated in Figure 2. The turbulence parameters ${\alpha }_{at}$ and ${\beta }_{at}$ are assumed to be 5.4181 and 3.7916, respectively, assuming moderate turbulence conditions. The predefined SNR threshold is set at 5 dB and $\alpha =4$, $\kappa =1.5$, $\mu =3$, and $N=3$. It can be seen from the plot that for low value of pointing errors (or higher values of $\zeta$), the outage probability of system decreases thereby enhancing the system performance.

Figure 2. Outage probability vs. average SNR per hop (dB) with variation of pointing errors in the FSO link.

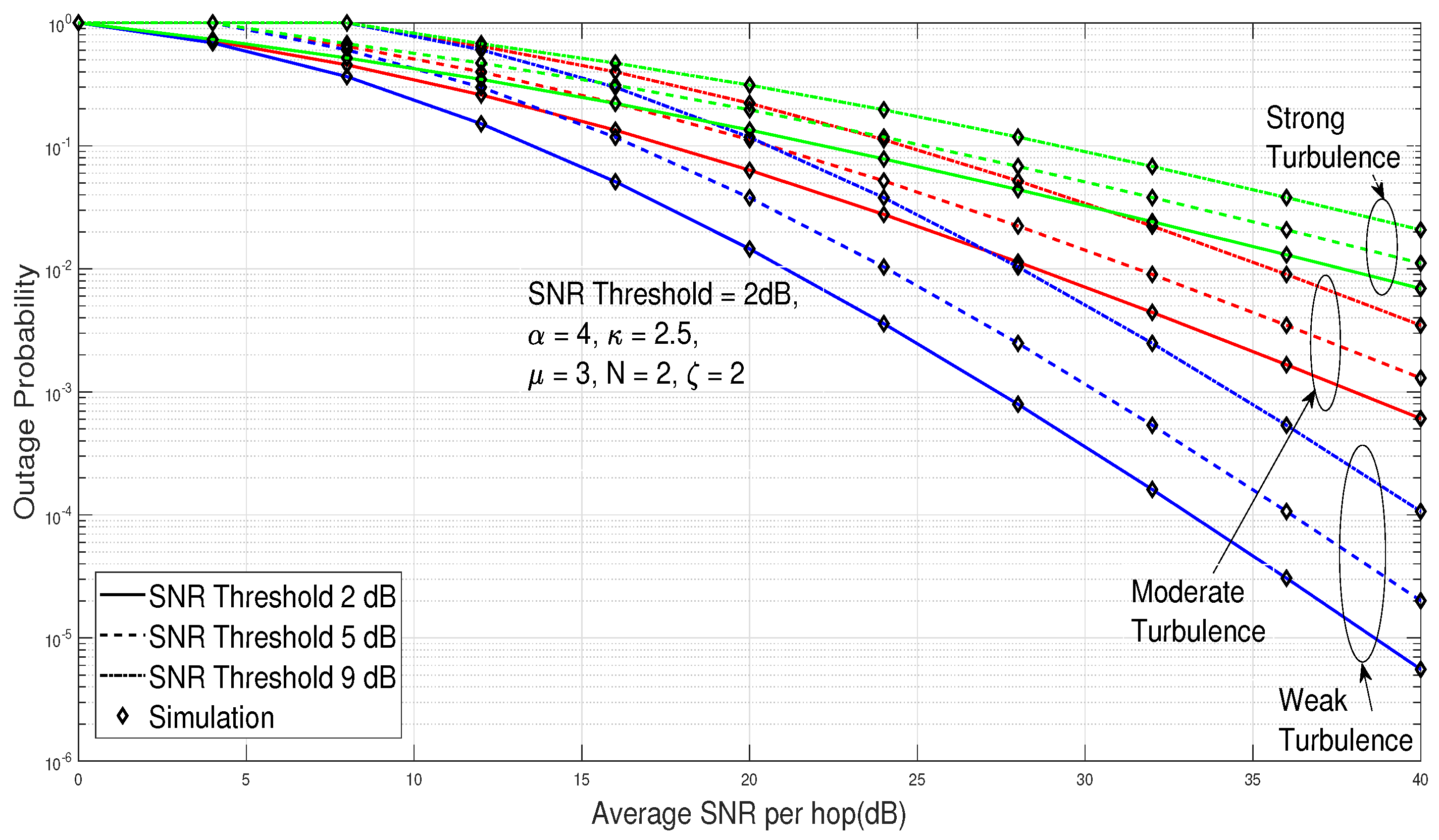
The outage performance of the proposed triple-hop RF/FSO system is depicted in Figure 3 with respect to the average SNR per hop for different SNR threshold values under various turbulence levels. The SNR threshold is assumed to be 2 dB and other parameters are assumed as $\alpha =4$, $\kappa =2.5$, $\mu =3$, $\zeta =2$, and $N=2$. It can be seen from the graph that as we increase the SNR threshold value, the outage probability is decreased and the performance of the system is increased. Also, it can be observed from the plot that as the turbulence level is decreased, the outage probability is also decreased, thereby improving the overall system performance.

Figure 3. Outage probability vs. average SNR per hop (dB) with variation of the SNR threshold at different turbulence levels.

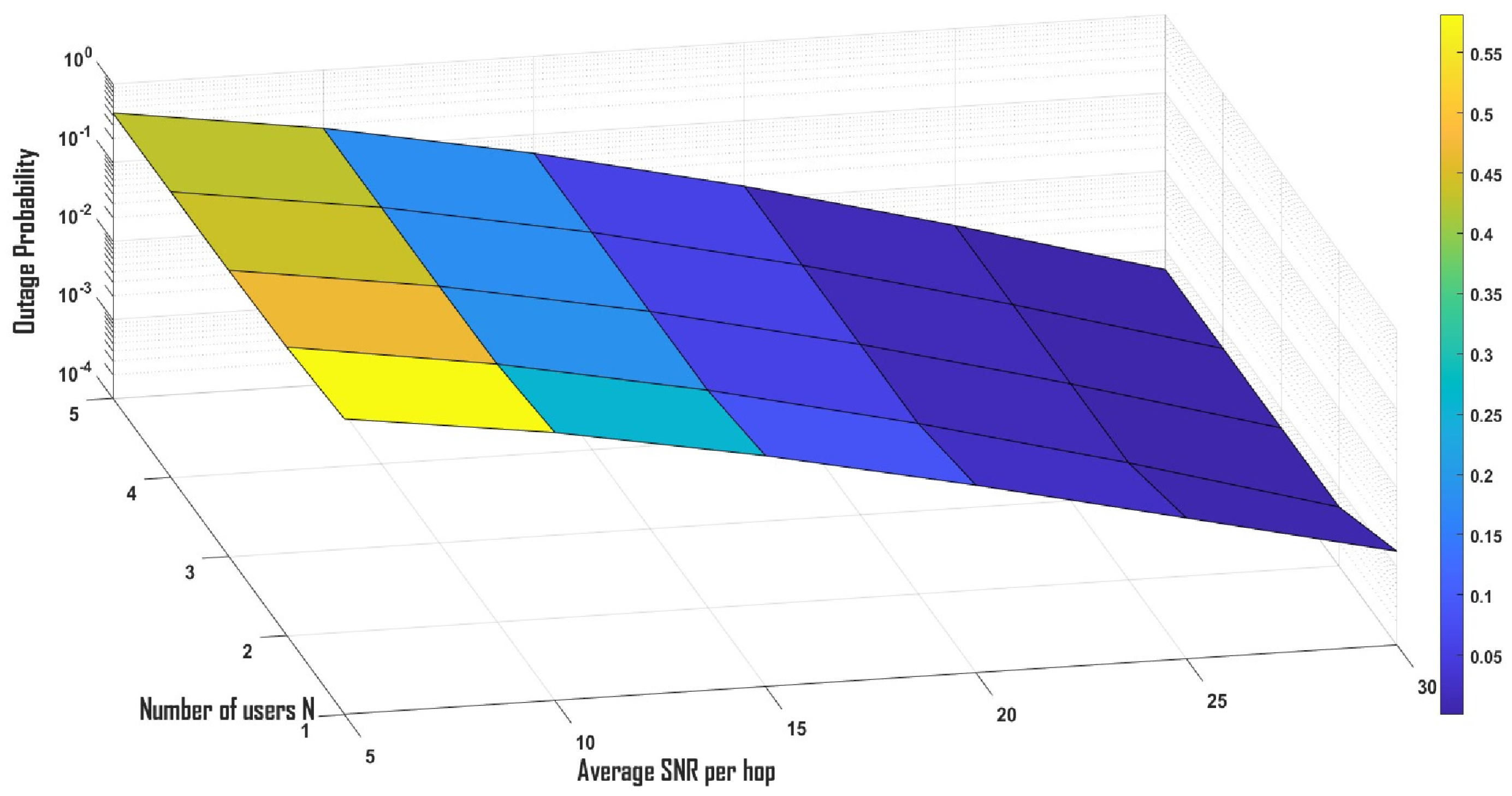
Figure 4 shows the plot of the exact and asymptotic outage probability against average SNR value with ranging number of users. It can be noticed from the graph that exact and asymptotic outage probabilities are matching exactly at the higher SNR values, which validates the numerical analysis. It is observed that as the number of users increases, outage performance is improved. For example, for N = 1, 2, and 3, the outage probability is 0.1466, 0.0215, and 0.0031, respectively. Additionally, to demonstrate the combined effect of both average SNR per hop and number of users N, we have plotted a 3D graph of outage probability against the average SNR per hop and number of users in Figure 5.

Figure 4. Exact and asymptotic outage probability vs. average SNR per hop (dB) with the variation of the number of users.

Figure 5. Outage probability vs. average SNR per hop (dB) and number of users N.

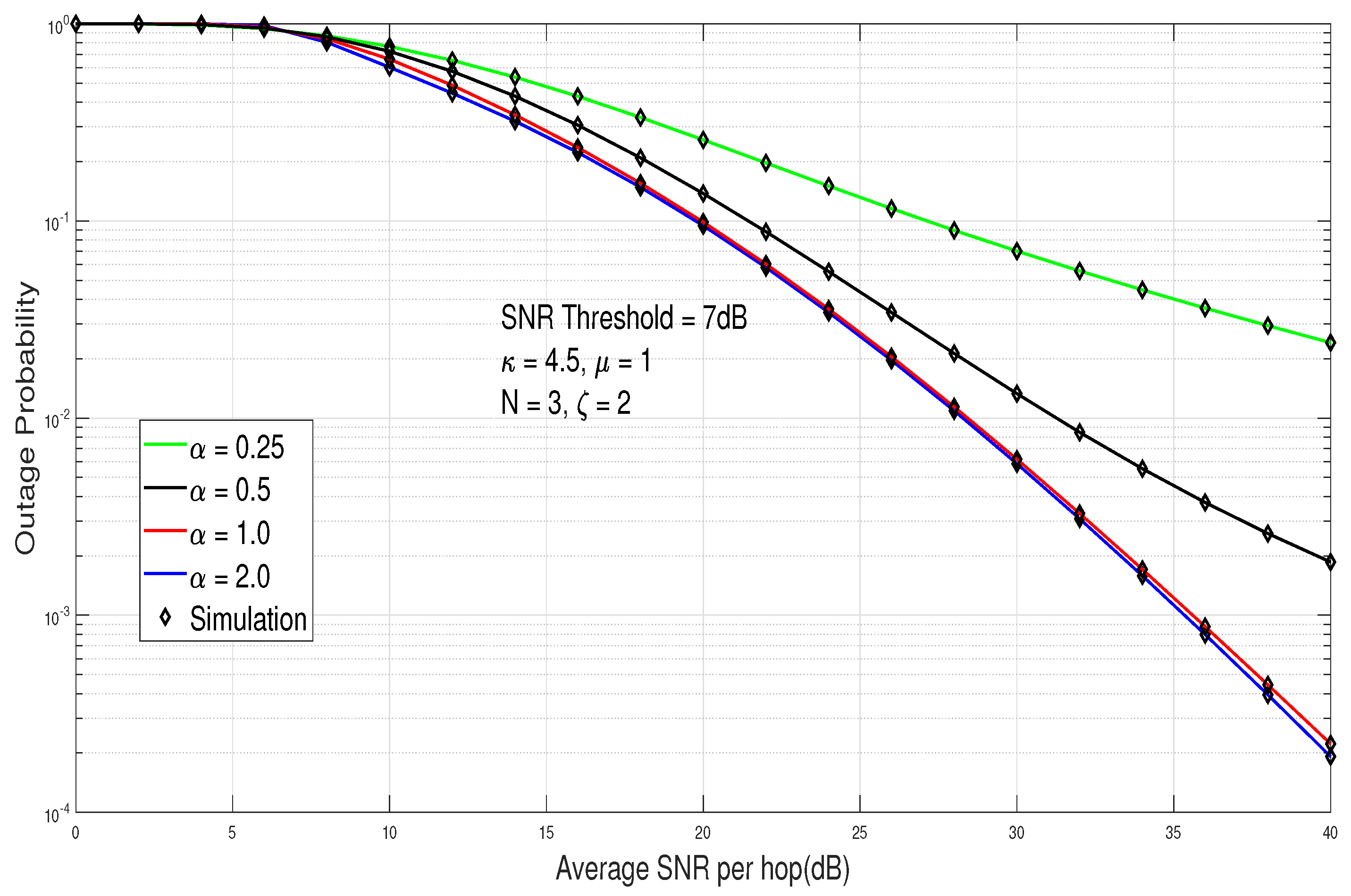
The graph in Figure 6 is simulated for different values of the nonlinearity parameter and alpha against the outage probability as a function of the average SNR. The threshold value is assumed to be 7 dB. It can be clearly seen from the figure that as we increase $\alpha$, outage probability is decreased and the quality of system improves.

Figure 6. Outage probability vs. average SNR per hop (dB) with variation in parameter $\alpha$.

The effect of outage probability with respect to altitude of UAV is demonstrated in Figure 7. The graph is simulated by assuming an SNR threshold of 1.8 dB. The impact of the horizontal distance between the UAV relay R2 and the selected mobile user is seen on the outage performance of the system. It can be noticed from the curve that, as we increase the UAV altitude, the outage probability decreases at first and after a certain optimum value of the UAV altitude, the outage probability starts increasing. Hence, initially, the outage probability of the RF/FSO system is minimized. However, if we further increase the UAV altitude, the outage probability increases abruptly, thereby lowering the system performance. Hence, at a higher altitude, there is an increase in path loss and atmospheric losses, due to which the overall performance of system deteriorates. Therefore, we can conclude that optimal altitude is need to be obtained so as to reduce the overall outage probability of the system and to improve system performance.

Figure 7. Outage probability vs. UAV height (km) for different values of $r_{R2M}$.

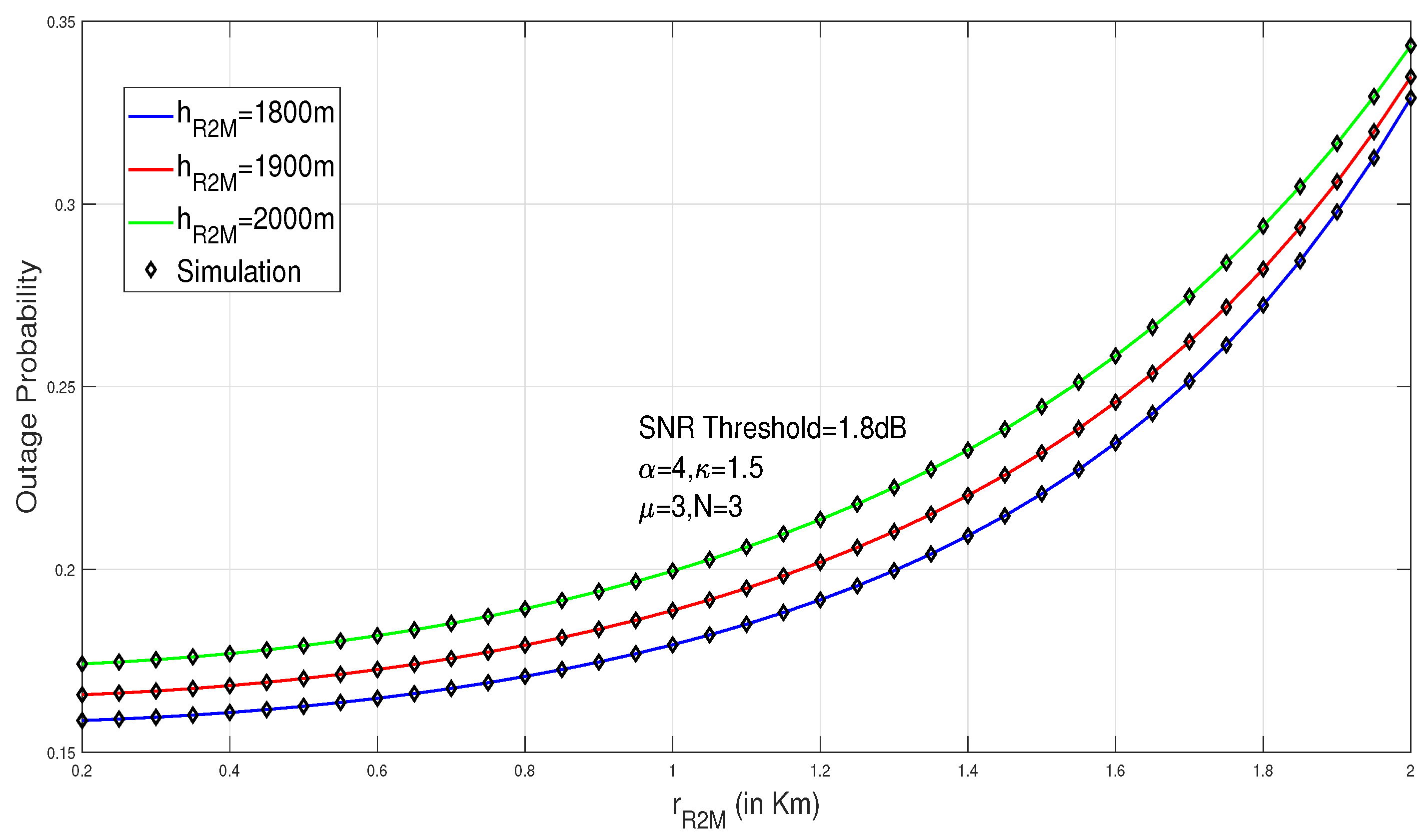
The curves in Figure 8 shows the impact of the radius, $r_{R2M}$, on the outage probability for various UAV relay R2 altitudes. It can be concluded from the plot that, as the horizontal distance between UAV relay and selected mobile user is increased, outage probability also increases. Thus, system performance is decreased at larger value of radius. For example, for $r_{R2M}=1.65$ kms and $h_{R2M}$ = 1800 m, 1900 m, and 2000 m, the outage probability is 0.242689, 0.253698, and 0.266277, respectively, and for $r_{R2M}=1.9$ kms and $h_{R2M}$ = 1800 m, 1900 m, and 2000 m, the outage probability is 0.297845, 0.306088, and 0.316598, respectively. Hence, it is clearly stated that an increase in the coverage area increases the outage probability and lowers the system performance, which results in the trade off between the performance of the system and the coverage area.

Figure 8. Outage probability vs. UAV coverage area for different values of $h_{R2M}$.

Table 2 shows the optimum elevation angle of the UAV with respect to the optimum altitude of the UAV for different values of the horizontal distance between the selected mobile user and the UAV relay. It is depicted from the table that as we increase $r_{UR2,M}$, the UAV elevation angle, $\theta$, also increases, which makes it less vulnerable to the link length. Also, we can say that FSO link parameters and RF link parameters ($\alpha ,\kappa ,\mu$) of the first hop does not depend on the optimum altitude of the UAV.

Table 2. The optimum UAV elevation angle with respect to the optimum height of the UAV for various horizontal distances.

S.No.	${\mathit{r}}_{\mathit{R}2\mathit{M}}$ (in Meters)	${\mathit{h}}_{\mathit{R}2\mathit{M}}$ (in Meters)	$\mathit{\theta }$ (in Degree)
1.	1500	1135	37.11
2.	1600	1220	37.33
3.	1700	1313	37.68
4.	1800	1491	39.64
5.	1900	1589	39.91
6.	2000	1676	39.96
7.	2100	1808	40.73
8.	2200	1904	40.87
9.	2300	1997	40.97
10.	2400	2093	41.10

6. Conclusions

In this paper, the outage probability of a UAV-enabled triple-hop mixed RF/FSO-based wireless communication system is analyzed. The communication is from source to fixed relay R1 in the form of RF signals, which is then decoded and forwarded to the UAV acting as a DF relay R2 in the form of an optical signal. The UAV relay R2 again decodes and forwards the RF signal to the destination. There is no direct communication from source to destination due to human-made and natural obstacles which block the direct transmission path. The system characterization is performed by carrying out the expression of the CDF of end-to-end SNR so as to get the closed form expressions of the outage probability. The asymptotic outage probability is calculated in order to study in depth the system parameters. Also, optimization of altitude is performed by minimizing the asymptotic outage probability of the proposed system in terms of the elevation angle so as to obtain the optimal height for better performance and more reliability of the system. Our numerical results validate the accuracy of the derived expressions under the effect of various parameters, like the number of users, UAV altitude, turbulence level, SNR threshold, etc. Also, the optimal height analysis can help in the designing of a UAV-enabled wireless communication system.