A Sensitive Frequency Band Study for Distributed Acoustical Sensing Monitoring Based on the Coupled Simulation of Gas–Liquid Two-Phase Flow and Acoustic Processes
Abstract
1. Introduction
2. Methods
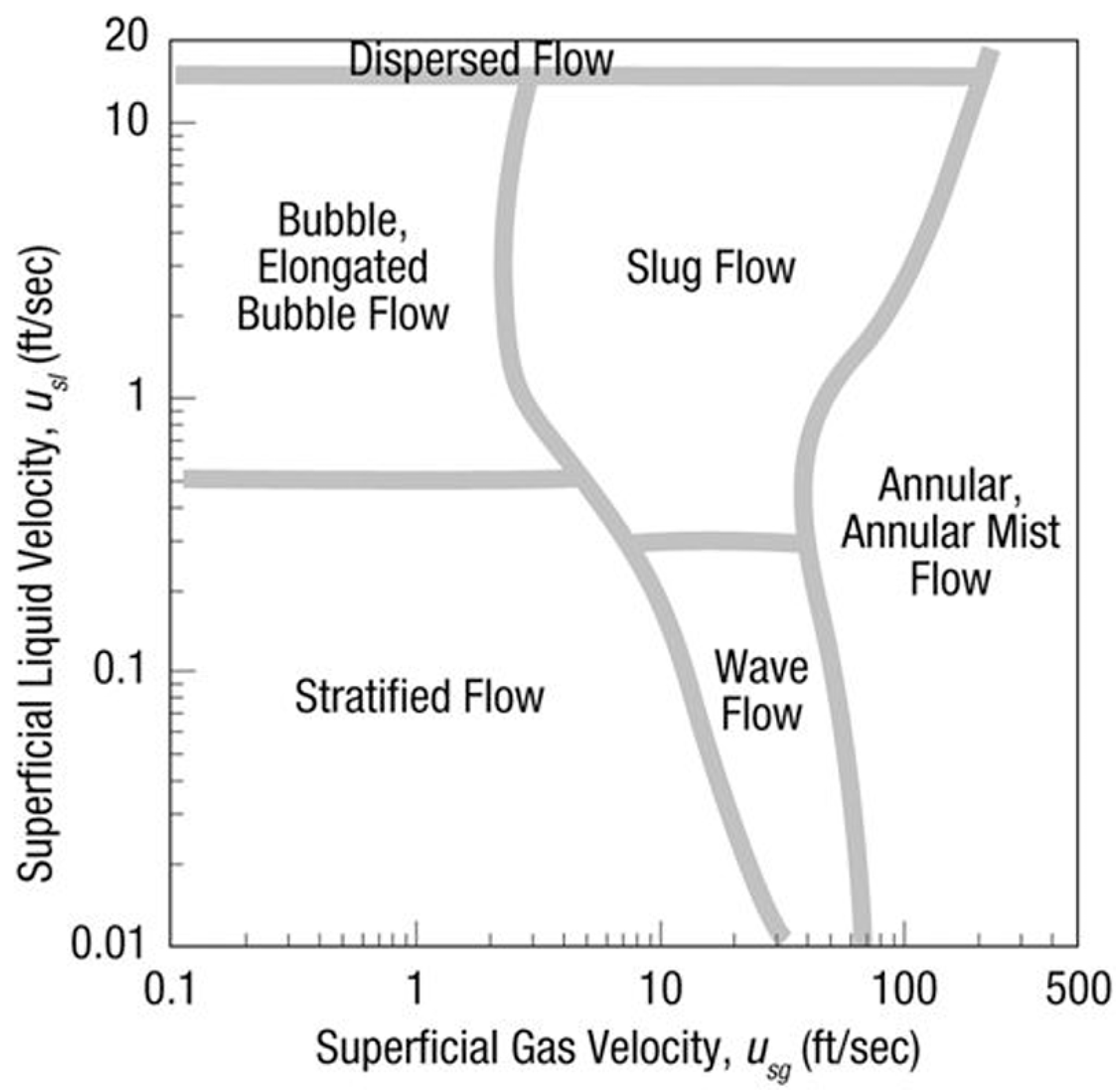
2.1. Gas–Water Separation Flow Model in Horizontal Wellbores
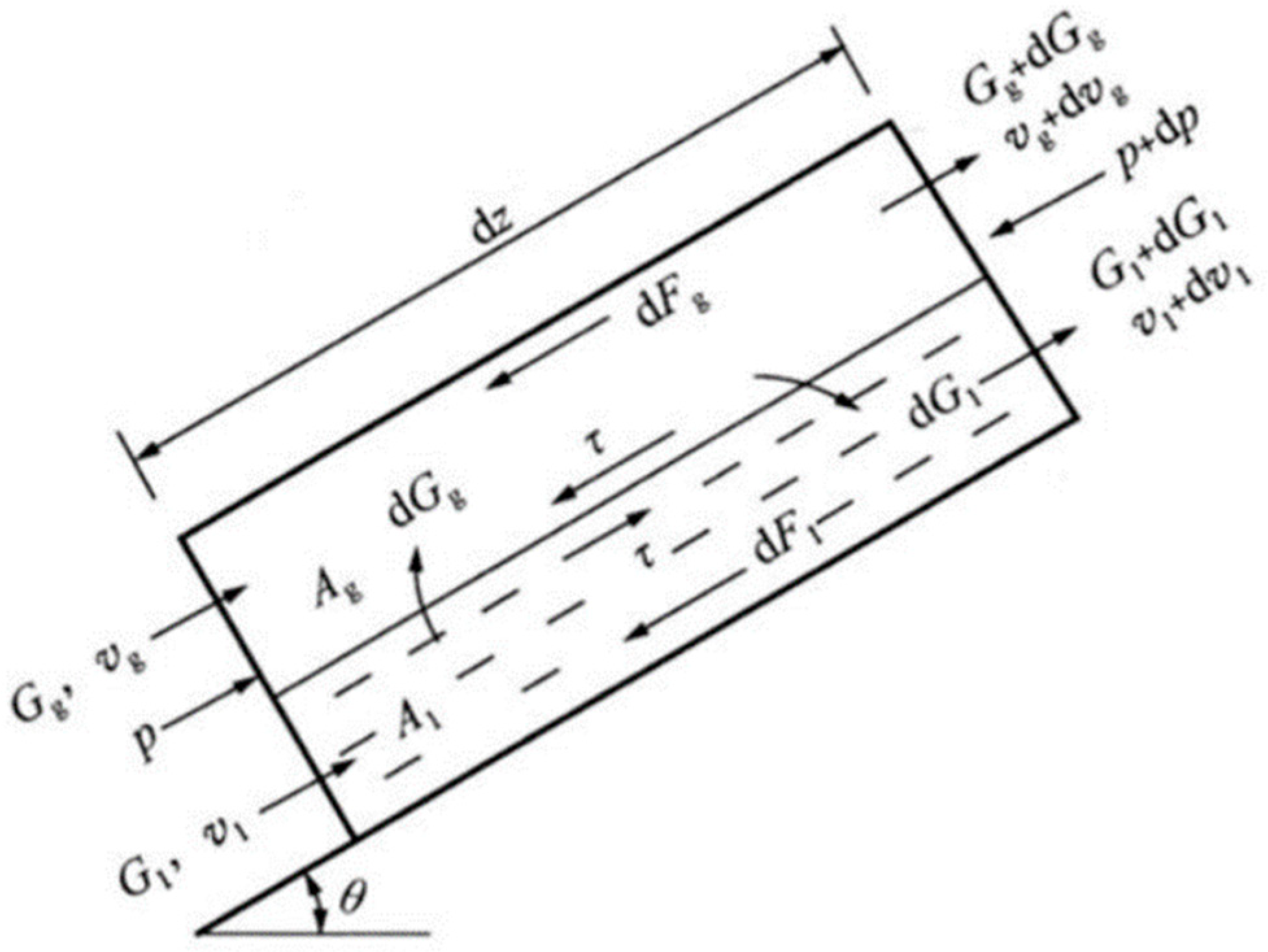
2.1.1. Mass Balance Equation
2.1.2. Momentum Balance Equation
2.1.3. Energy Balance Equation
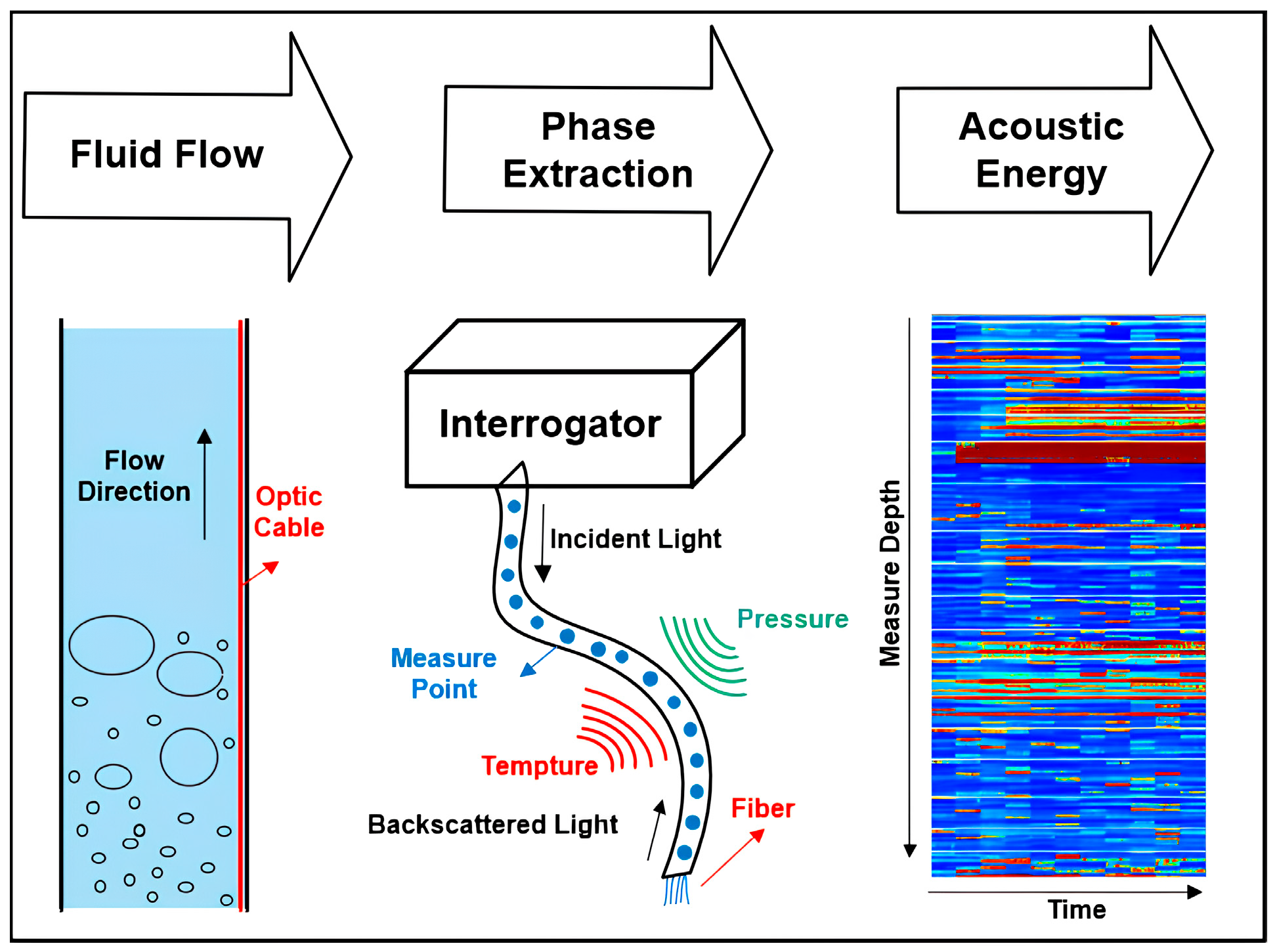
2.2. Gas–Water Two-Phase Acoustic Model in Horizontal Wellbores
2.3. Numerical Model
2.3.1. Model Parameters
2.3.2. Basic Simulation Results
3. Results
3.1. Velocity Field of Gas–Water Two-Phase Flow
3.2. Pressure Field of Gas–Water Two-Phase Flow
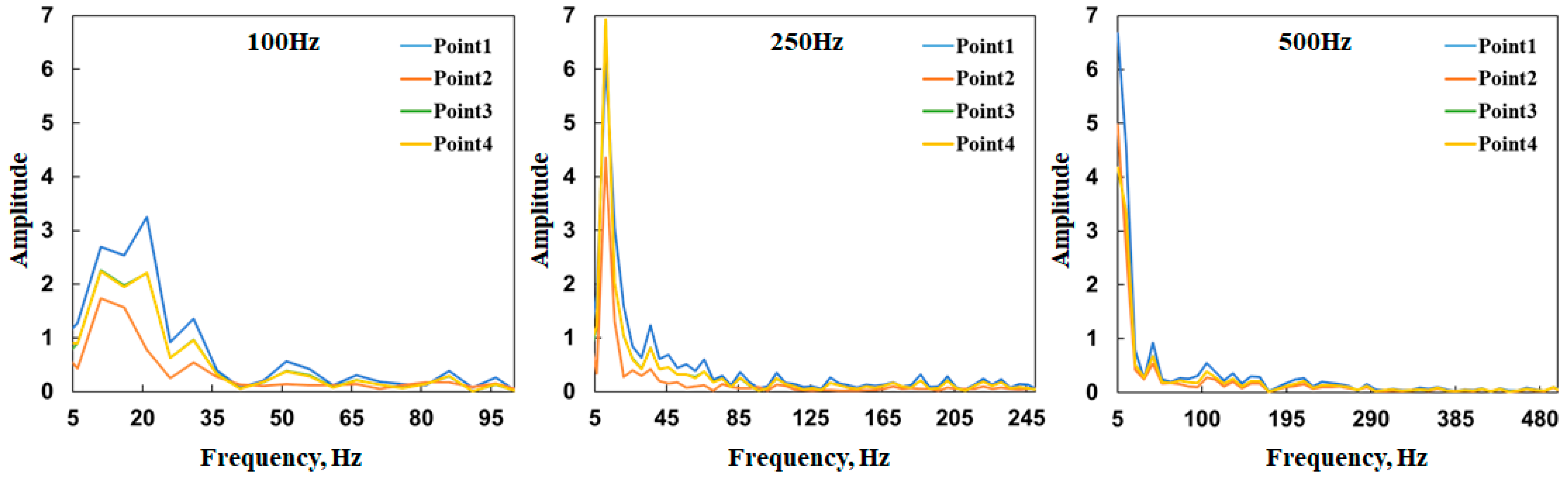
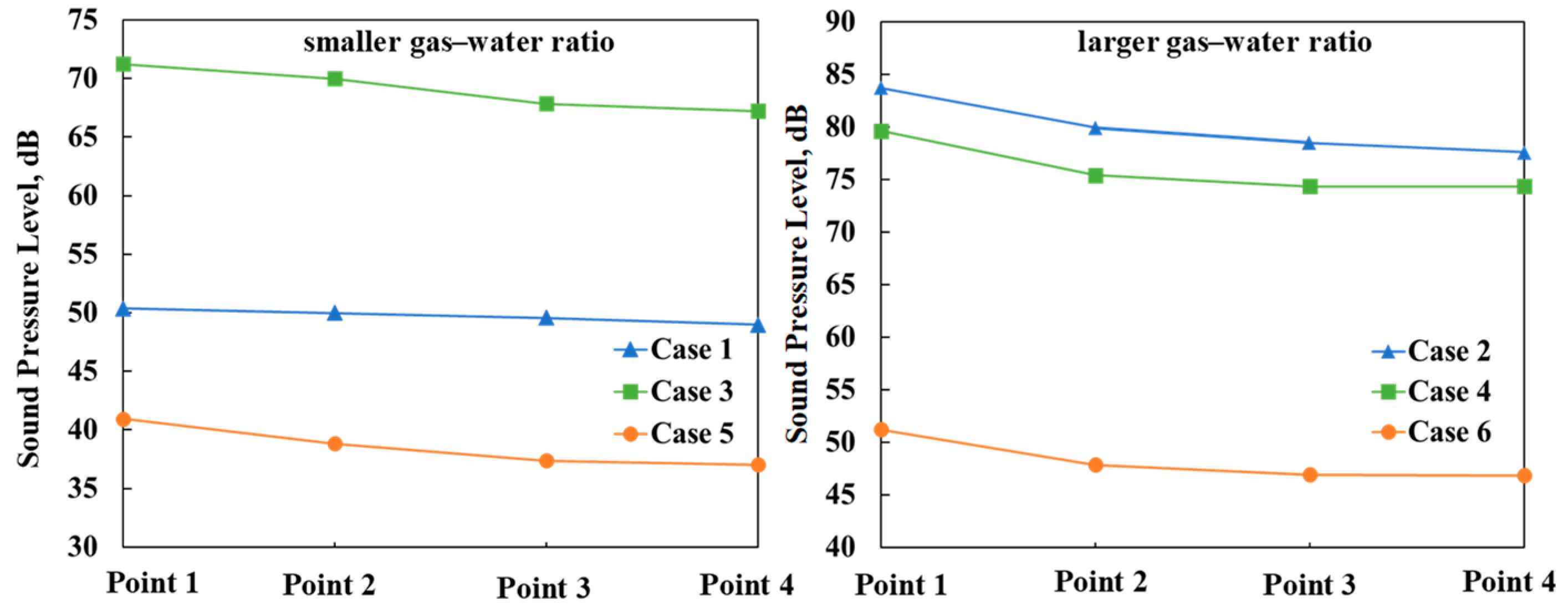
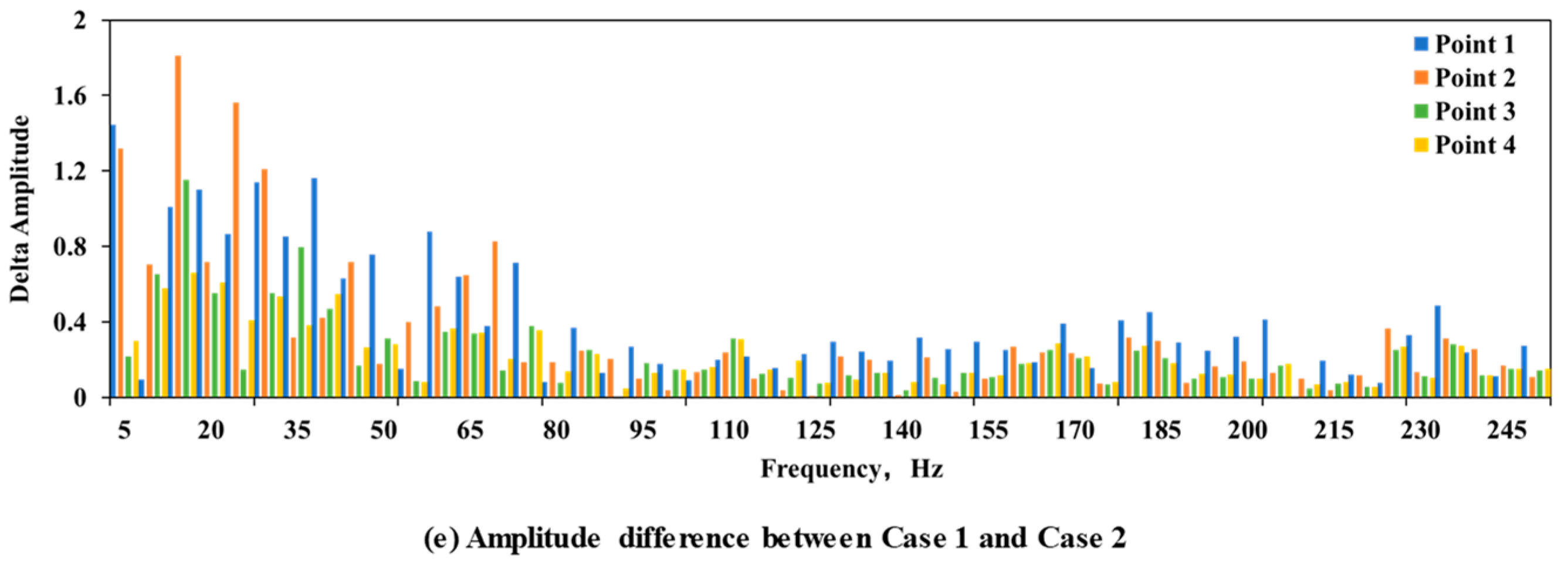
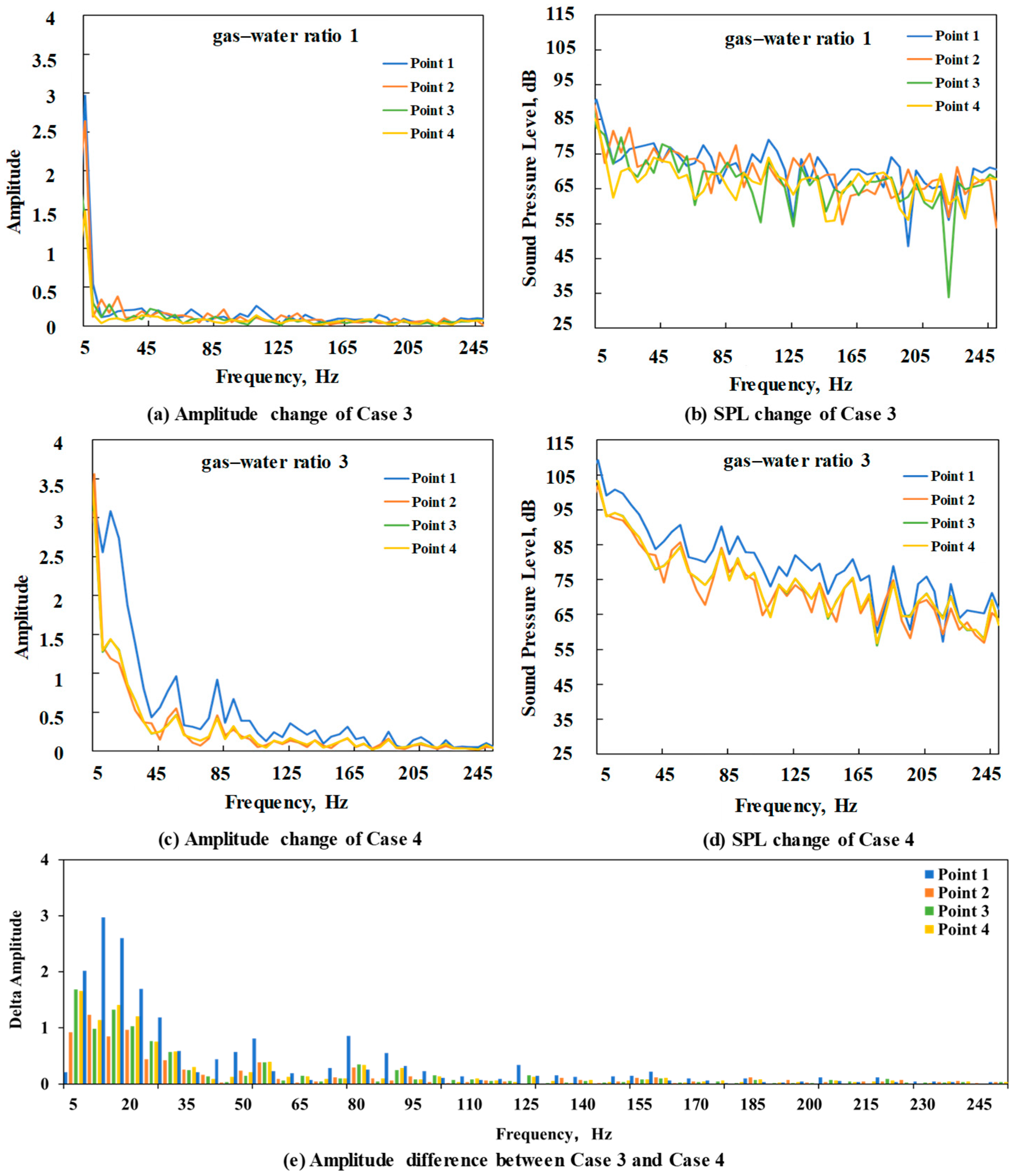
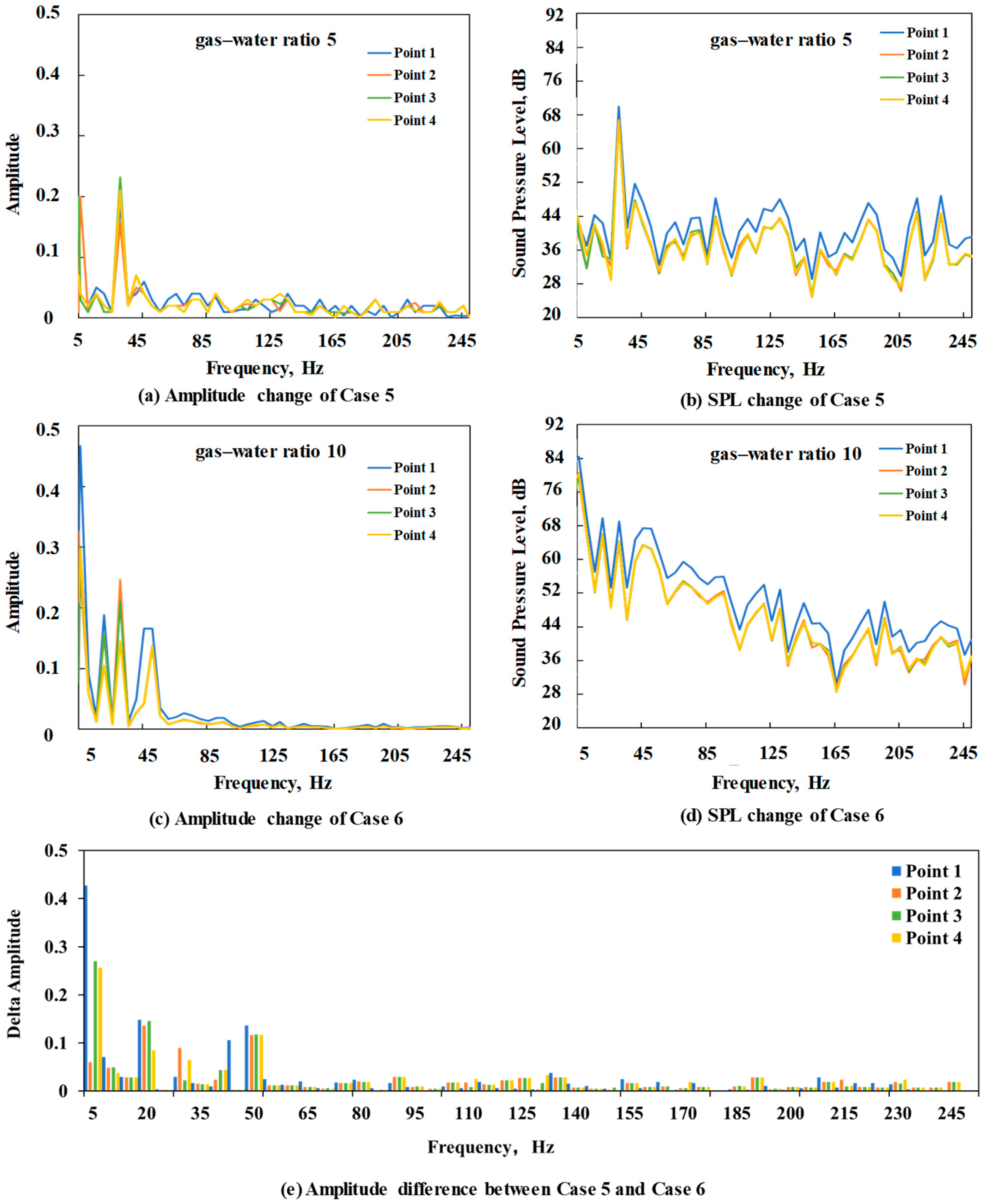
3.3. Sound Field of Gas–Water Two-Phase Flow
4. Validation
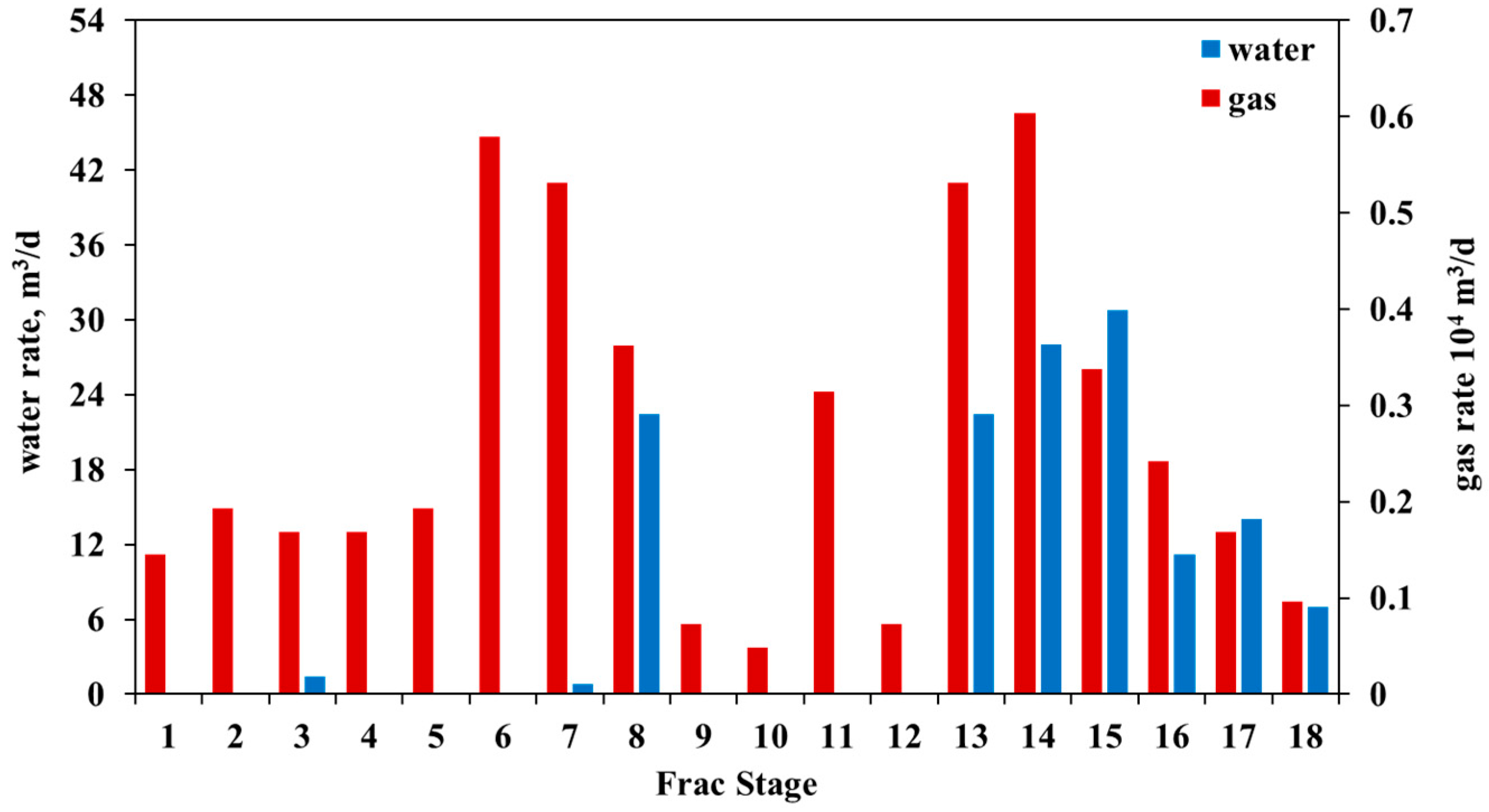
4.1. Basic Information of the Production Well
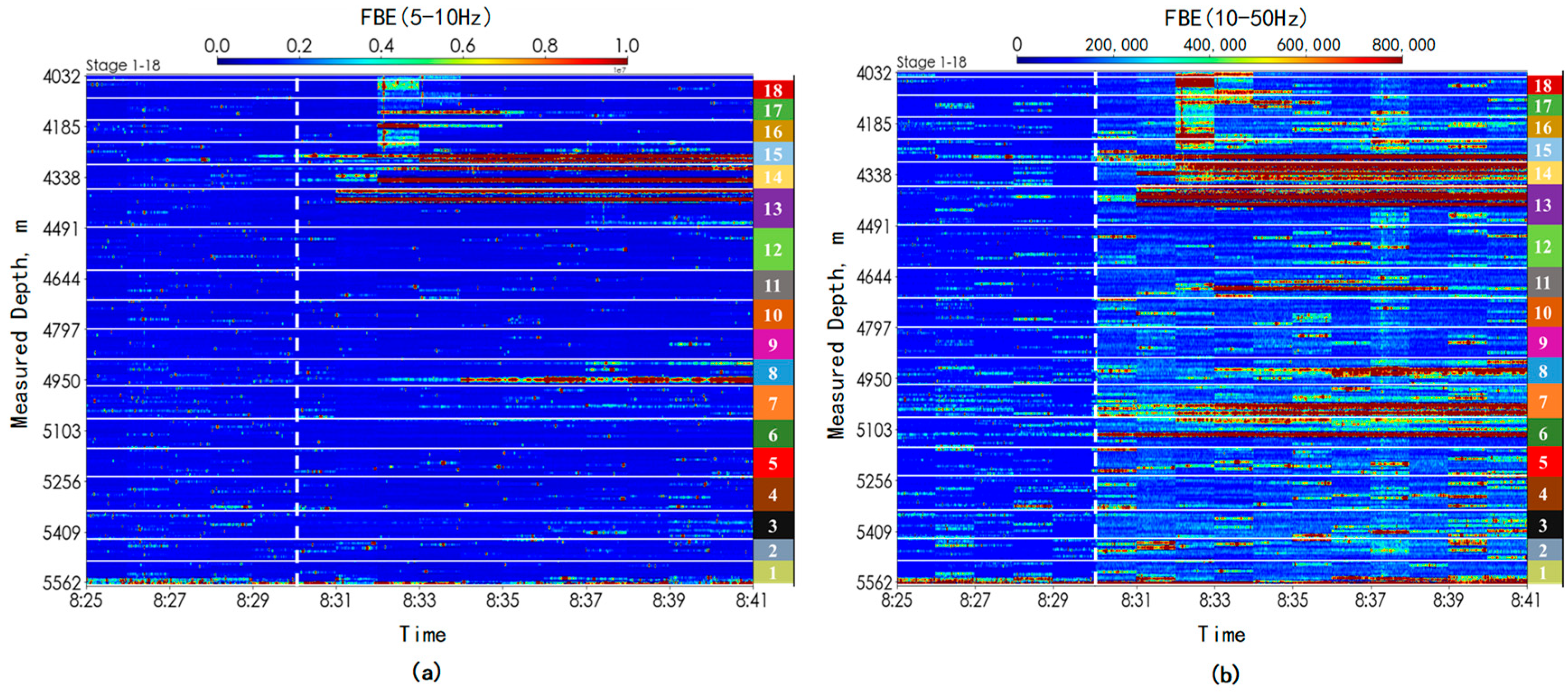
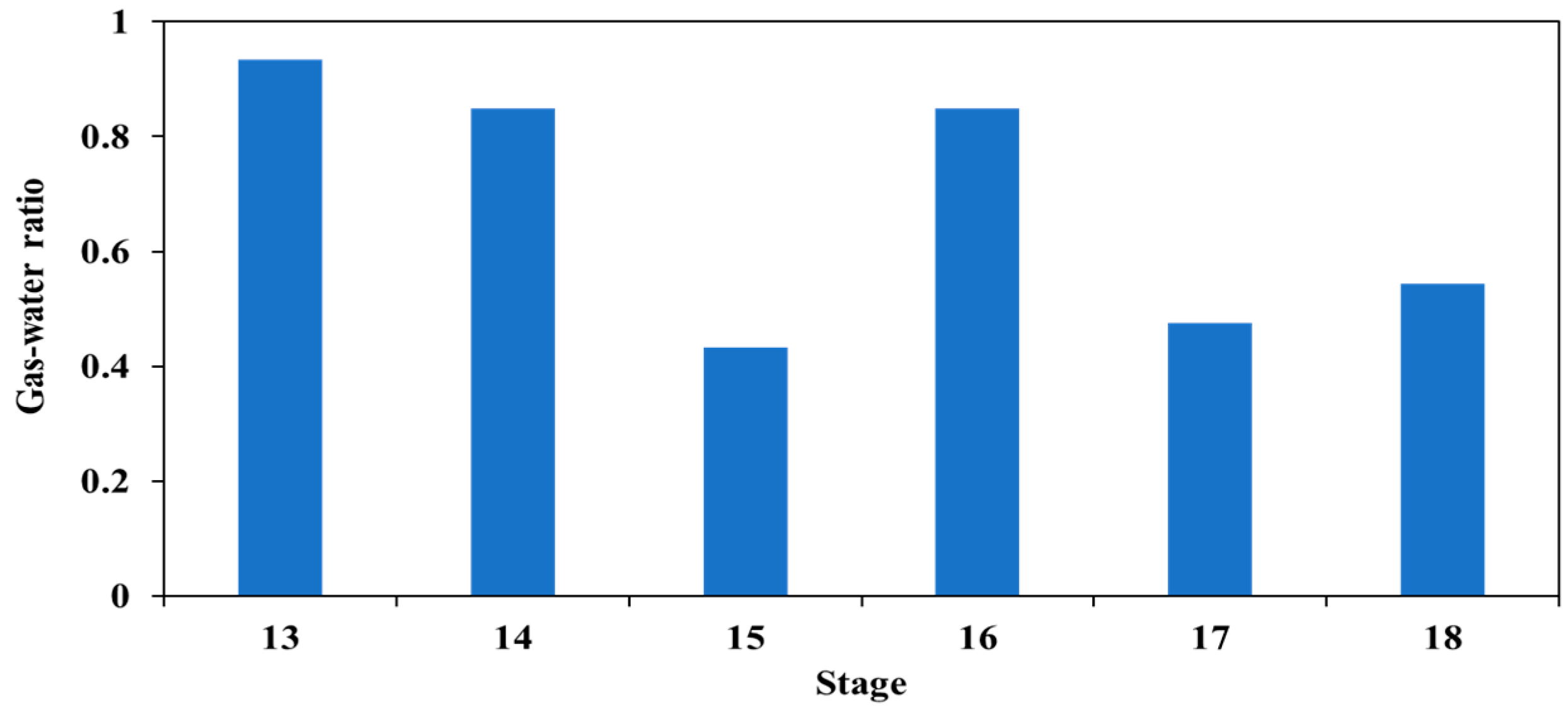
4.2. Production Profile Based on DAS Frequency Band Energy
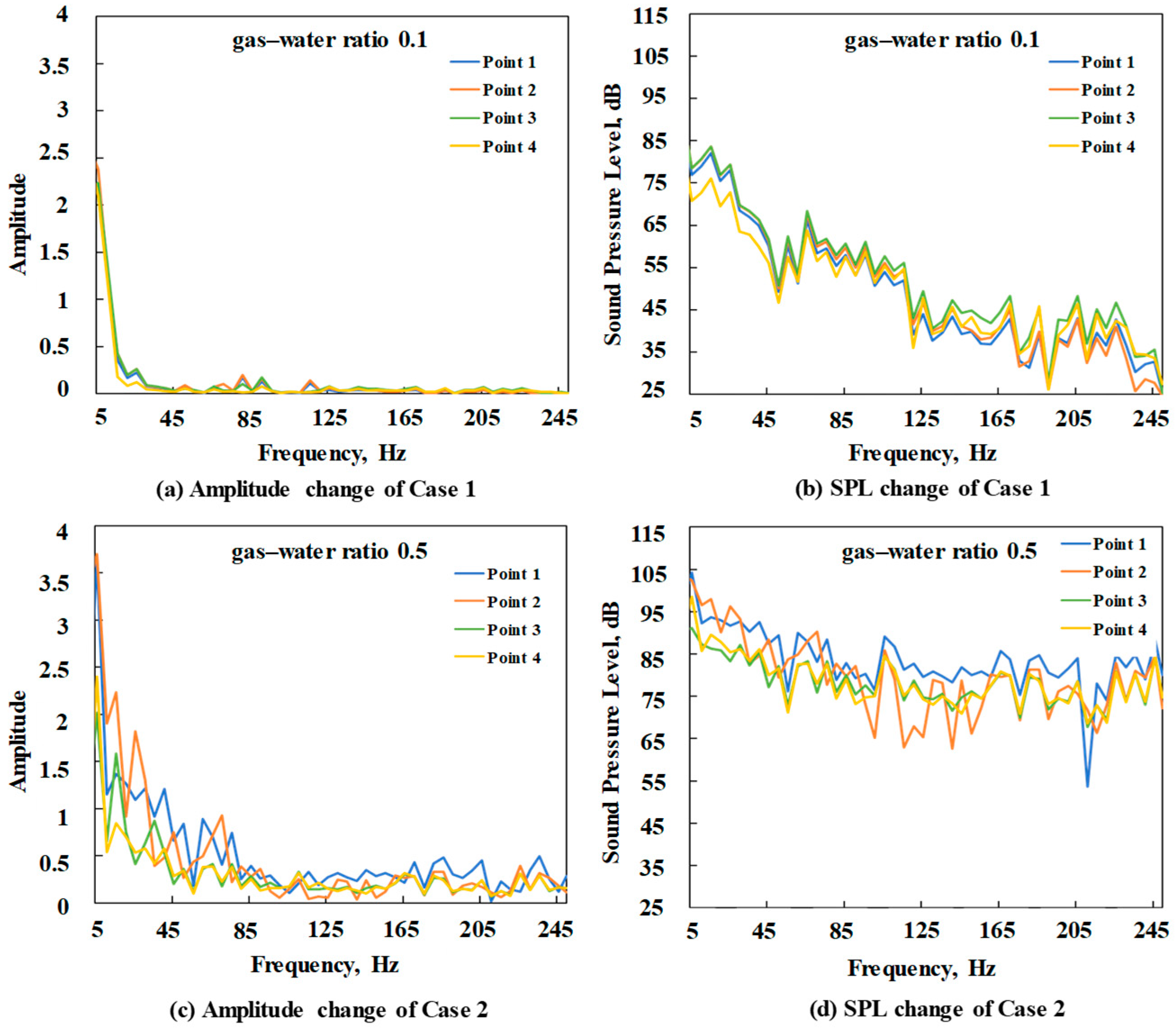
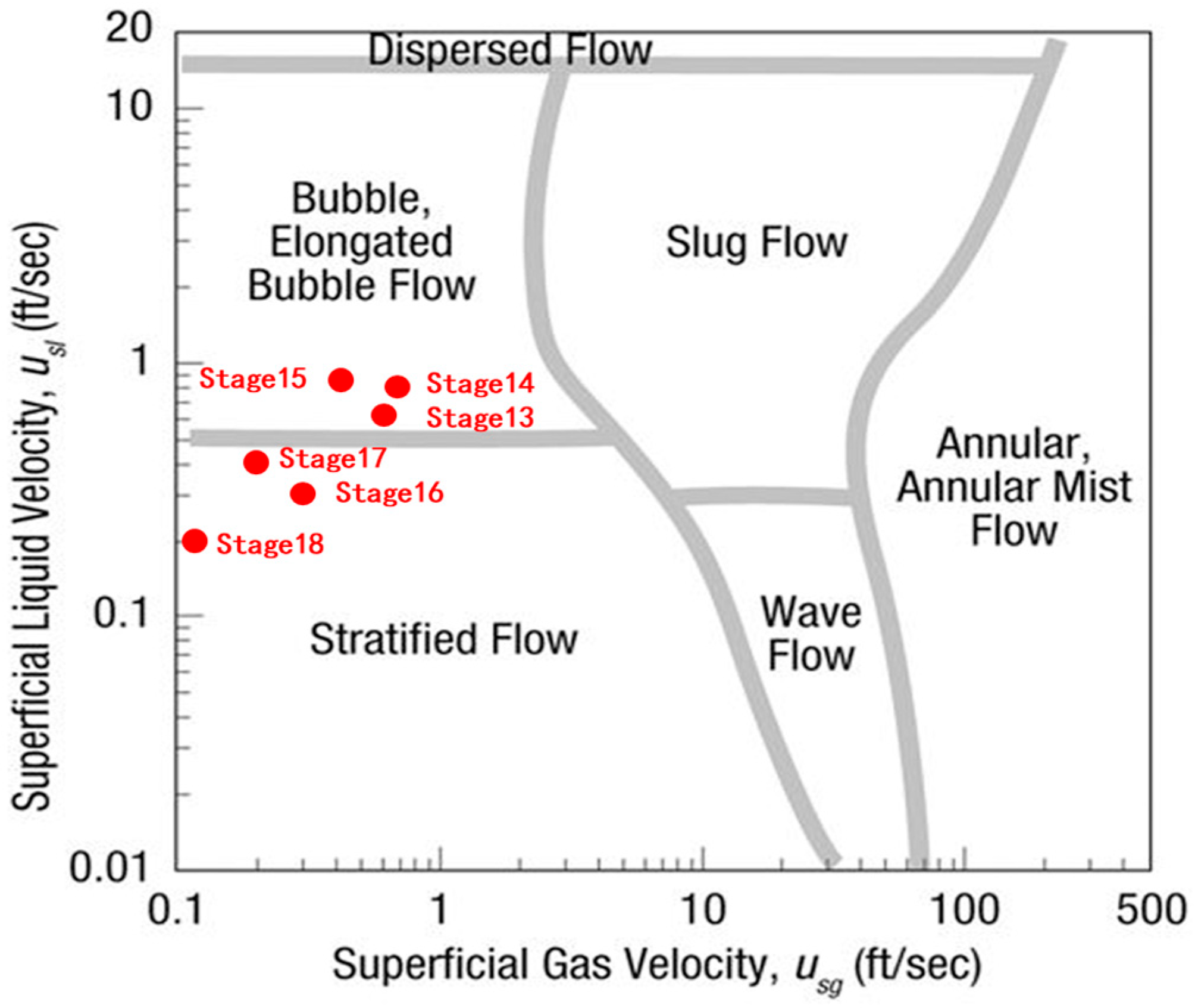
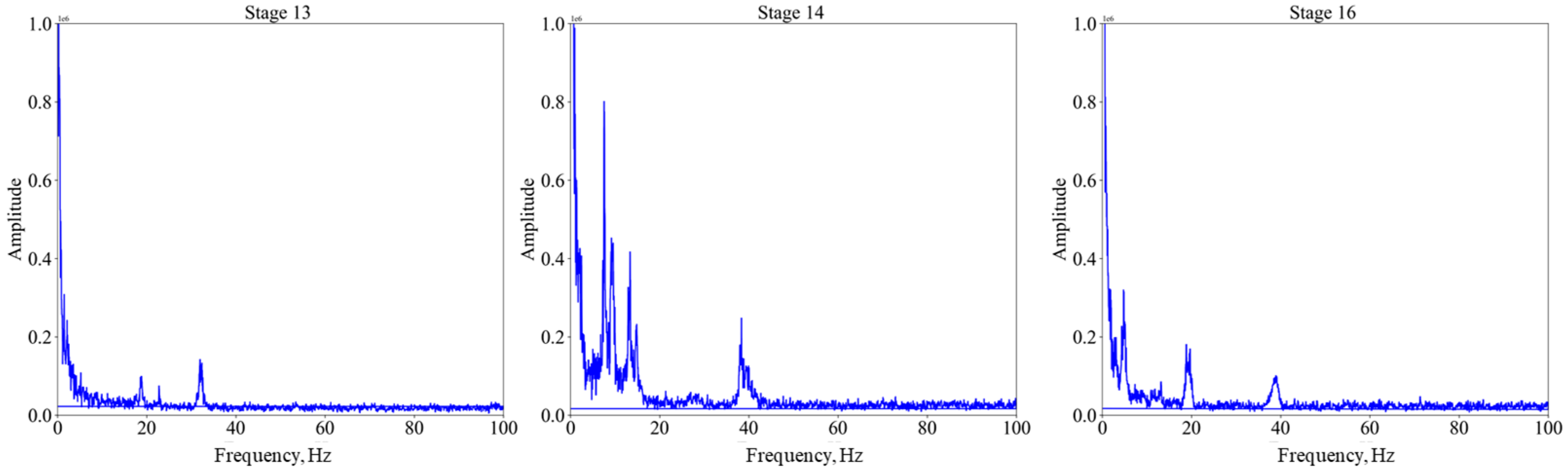
4.3. DAS Amplitude Response Frequency Band Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, K.; Siddhamshetty, P.; Ahn, Y.; El-Halwagi, M.M.; Sang-Il Kwon, J. Evaluating the spatiotemporal variability of water recovery ratios of shale gas wells and their effects on shale gas development. J. Clean. Prod. 2020, 276, 123171. [Google Scholar] [CrossRef]
- Guo, M.; Lu, X.; Nielsen, C.P.; McElroy, M.B.; Shi, W.; Chen, Y.; Xu, Y. Prospects for shale gas production in China: Implications for water demand. Renew. Sustain. Energy Rev. 2016, 66, 742–750. [Google Scholar] [CrossRef]
- Mi, L. Inversion method of discrete fracture network of shale gas based on gas production profile. Acta Pet. Sin. 2021, 42, 481–491. [Google Scholar]
- Wei, P.; Dejia, D.; Jun, M.; Tongyi, Z.; Ying, H.; Shuang, A. Production Logging of Shale Gas Well in China. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24–26 August 2016. [Google Scholar]
- Basov, A.; Bukov, O.; Shevchuk, T.; Lazutkin, D.; Saprykina, K.; Kiselev, V.; Novikov, I.; Drobot, A. Confirmed Effectiveness of Tracers’ Production Logging in Comparison with Conventional Production Logging. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Bali, Indonesia, 29–31 October 2019. [Google Scholar]
- Zhang, J.; Lan, W.; Deng, C.; Wei, F.; Luo, X. Thermal Optimization of High-Temperature Downhole Electronic Devices. IEEE Trans.Compon. Packag. Manuf. Technol. 2021, 11, 1816–1823. [Google Scholar] [CrossRef]
- Haustveit, K.; Haffener, J.; Young, S.; Dwyer, J.; Glaze, G.; Green, B.; Ketter, C.; Williams, T.; Brinkley, K.; Elliott, B. Cementing: The Good, the Bad, and the Isolated—Techniques to Measure Cement Quality and its Impact on Well Performance. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 6–8 February 2024. [Google Scholar]
- Mahue, V.; Jimenez, E.; Dawson, P.; Trujillo, K.; Hull, R. Repeat DAS and DTS Production Logs on a Permanent Fiber Optic Cable for Evaluating Production Changes and Interference with Offset Wells. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 20–22 June 2022. [Google Scholar]
- Ugueto, G.; Wu, K.; Jin, G.; Zhang, Z.; Haffener, J.; Mojtaba, S.; Ratcliff, D.; Bohn, R.; Chavarria, A.; Wu, Y.; et al. A Catalogue of Fiber Optics Strain-Rate Fracture Driven Interactions. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 31 January–2 February 2023. [Google Scholar]
- Cherubini, A.; Richard, S.; Jestin, C.; Calbris, G.; Lanticq, V. Real-Time Downhole Monitoring Using DAS and DTS: A New Technology for Leak Detection and Well Integrity. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 1–3 March 2023. [Google Scholar]
- Sui, W.; Wen, C.; Sun, W.; Li, J.; Guo, H.; Yang, Y.; Song, J. Joint application of distributed optical fiber sensing technologies for hydraulic fracturing monitoring. Nat. Gas Ind. 2023, 43, 87–103. [Google Scholar]
- Wang, Y.; Wu, Z.; Wang, F. Research Progress of Applying Distributed Fiber Optic Measurement Technology in Hydraulic Fracturing and Production Monitoring. Energies 2022, 15, 7519. [Google Scholar] [CrossRef]
- Martinez, R.; Hill, A.D.; Zhu, D. Diagnosis of Fracture Flow Conditions with Acoustic Sensing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Budiansky, B.; Drucker, D.C.; Kino, G.S.; Rice, J.R. Pressure sensitivity of a clad optical fiber. Appl. Opt. 1979, 18, 4085–4088. [Google Scholar] [CrossRef] [PubMed]
- Jayaram, V.; Hull, R.; Wagner, J.; Zhang, S. Hydraulic Fracturing Stimulation Monitoring with Distributed Fiber Optic Sensing and Microseismic in the Permian Wolfcamp Shale Play. In Proceedings of the 7th Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Pakhotina, J.; Zhu, D.; Hill, A.D. Evaluating Perforation Erosion and its Effect on Limited Entry by Distributed Acoustic Sensor DAS Monitoring. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 26–29 October 2020. [Google Scholar]
- Li, X.; Zhang, J.; Grubert, M.; Laing, C.; Chavarria, A.; Cole, S.; Oukaci, Y. Distributed Acoustic and Temperature Sensing Applications for Hydraulic Fracture Diagnostics. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar]
- In’t panhuis, P.; den Boer, H.; van der Horst, J.; Paleja, R.; Randell, D.; Joinson, D.; McIvor, P.; Green, K.; Bartlett, R. Flow Monitoring and Production Profiling Using DAS. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Bukhamsin, A.; Horne, R. Using Distributed Acoustic Sensors to Optimize Production in Intelligent Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- van der Horst, J.; Den Boer, H.; In’t Panhuis, P.; Wyker, B.; Kusters, R.; Mustafina, D.; Groen, L.; Bulushi, N.; Mjeni, R.; Awan, K.F.; et al. Fibre Optic Sensing For Improved Wellbore Production Surveillance. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 19 January 2014. [Google Scholar]
- Moradi, P.; Seabrook, B.; Adair, N.; Garza, R. Resolving Multiphase Fractions in Horizontal Wells Using Speed of Sound Measured with Distributed Acoustic Sensors and a PVT Database. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 17–19 June 2024. [Google Scholar]
- Mandhane, J.M.; Gregory, G.A.; Aziz, K. A flow pattern map for gas—Liquid flow in horizontal pipes. Int. J. Multiph. Flow 1974, 1, 537–553. [Google Scholar] [CrossRef]
- Economides, M.J. Petroleum Production Systems; Prentice Hall: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chen, J.; Chen, T. Petroleum Gas-Liquid Two-Phase Pipe Flow, 2nd ed.; Energy Science; Petroleum Industry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proceedings of the Royal Society of London. Ser. A. Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Williams, B.J.E.F.; Hawkingst, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Jianrong, W.; Spek, A.v.d.; Georgi, D.T.; Chace, D.M. Characterizing Sound Generated by Multiphase Flow. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Sakaida, S.; Pakhotina, I.; Zhu, D.; Hill, A.D. Estimation of Fracture Properties by Combining DAS and DTS Measurements. In Proceedings of the SPE International Hydraulic Fracturing Technology Conference & Exhibition, Muscat, Oman, 11–13 January 2022. [Google Scholar]




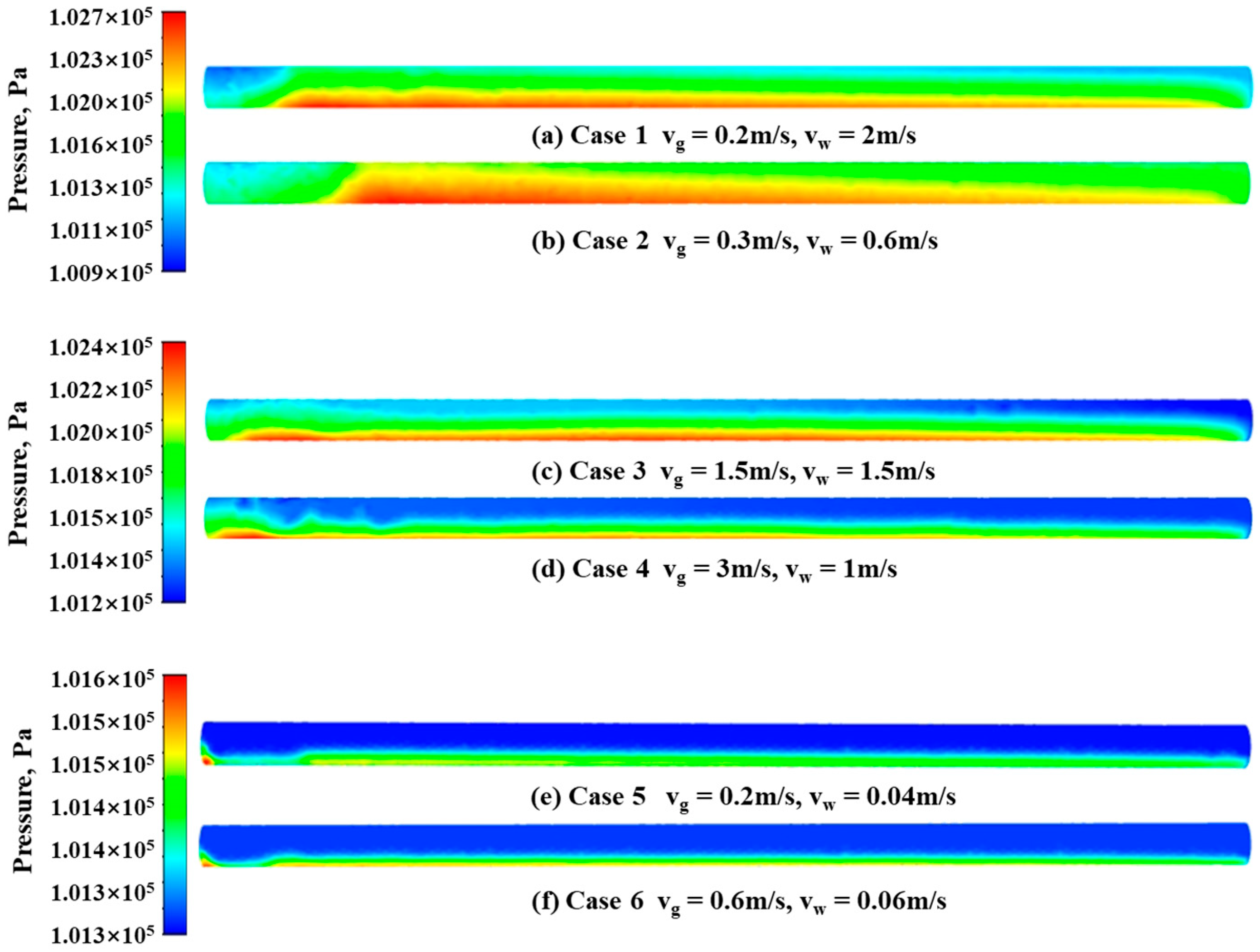



| Case Number | Gas Velocity (m/s) | Water Velocity (m/s) | Gas–Water Ratio | Gas Surface Flow Rate (104 m3/d) | Water Surface Flow Rate (m3/d) |
|---|---|---|---|---|---|
| 1 | 0.2 | 2 | 0.1 | 2.9 | 864 |
| 2 | 0.3 | 0.6 | 0.5 | 4.3 | 260 |
| 3 | 1.5 | 1.5 | 1 | 21.6 | 650 |
| 4 | 3 | 1 | 3 | 43.2 | 430 |
| 5 | 0.2 | 0.04 | 5 | 2.9 | 18 |
| 6 | 0.6 | 0.06 | 10 | 8.6 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wu, Y.; Yang, Y.; Li, M.; Sheng, L.; Guo, H.; Jiao, J.; Li, Z.; Sui, W. A Sensitive Frequency Band Study for Distributed Acoustical Sensing Monitoring Based on the Coupled Simulation of Gas–Liquid Two-Phase Flow and Acoustic Processes. Photonics 2024, 11, 1049. https://doi.org/10.3390/photonics11111049
Li Z, Wu Y, Yang Y, Li M, Sheng L, Guo H, Jiao J, Li Z, Sui W. A Sensitive Frequency Band Study for Distributed Acoustical Sensing Monitoring Based on the Coupled Simulation of Gas–Liquid Two-Phase Flow and Acoustic Processes. Photonics. 2024; 11(11):1049. https://doi.org/10.3390/photonics11111049
Chicago/Turabian StyleLi, Zhong, Yi Wu, Yanming Yang, Mengbo Li, Leixiang Sheng, Huan Guo, Jingang Jiao, Zhenbo Li, and Weibo Sui. 2024. "A Sensitive Frequency Band Study for Distributed Acoustical Sensing Monitoring Based on the Coupled Simulation of Gas–Liquid Two-Phase Flow and Acoustic Processes" Photonics 11, no. 11: 1049. https://doi.org/10.3390/photonics11111049
APA StyleLi, Z., Wu, Y., Yang, Y., Li, M., Sheng, L., Guo, H., Jiao, J., Li, Z., & Sui, W. (2024). A Sensitive Frequency Band Study for Distributed Acoustical Sensing Monitoring Based on the Coupled Simulation of Gas–Liquid Two-Phase Flow and Acoustic Processes. Photonics, 11(11), 1049. https://doi.org/10.3390/photonics11111049




