A Triple-Tunable Dual-Band Metamaterial Absorber Based on Dirac Semimetal and InSb
Abstract
1. Introduction
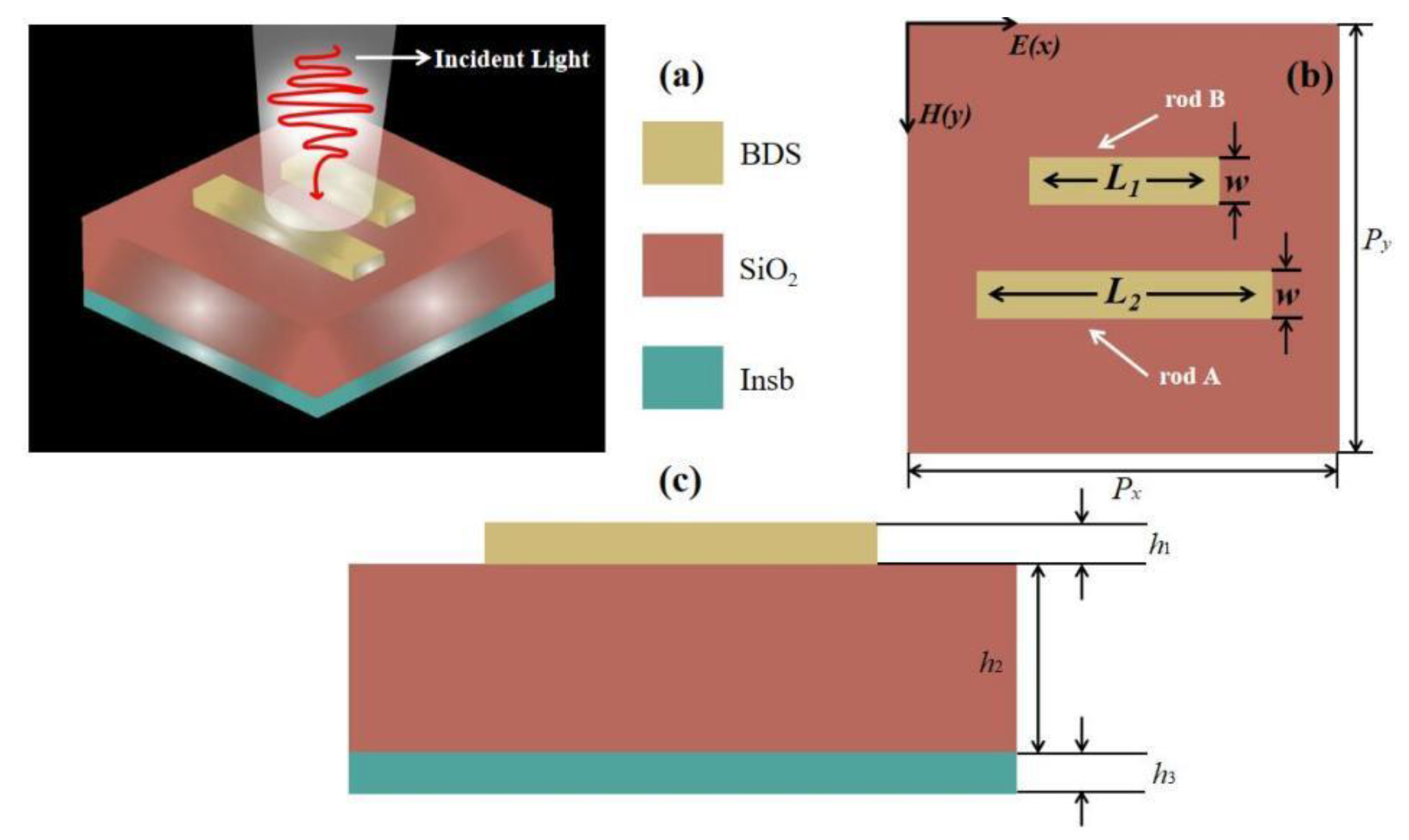
2. Materials and Methods
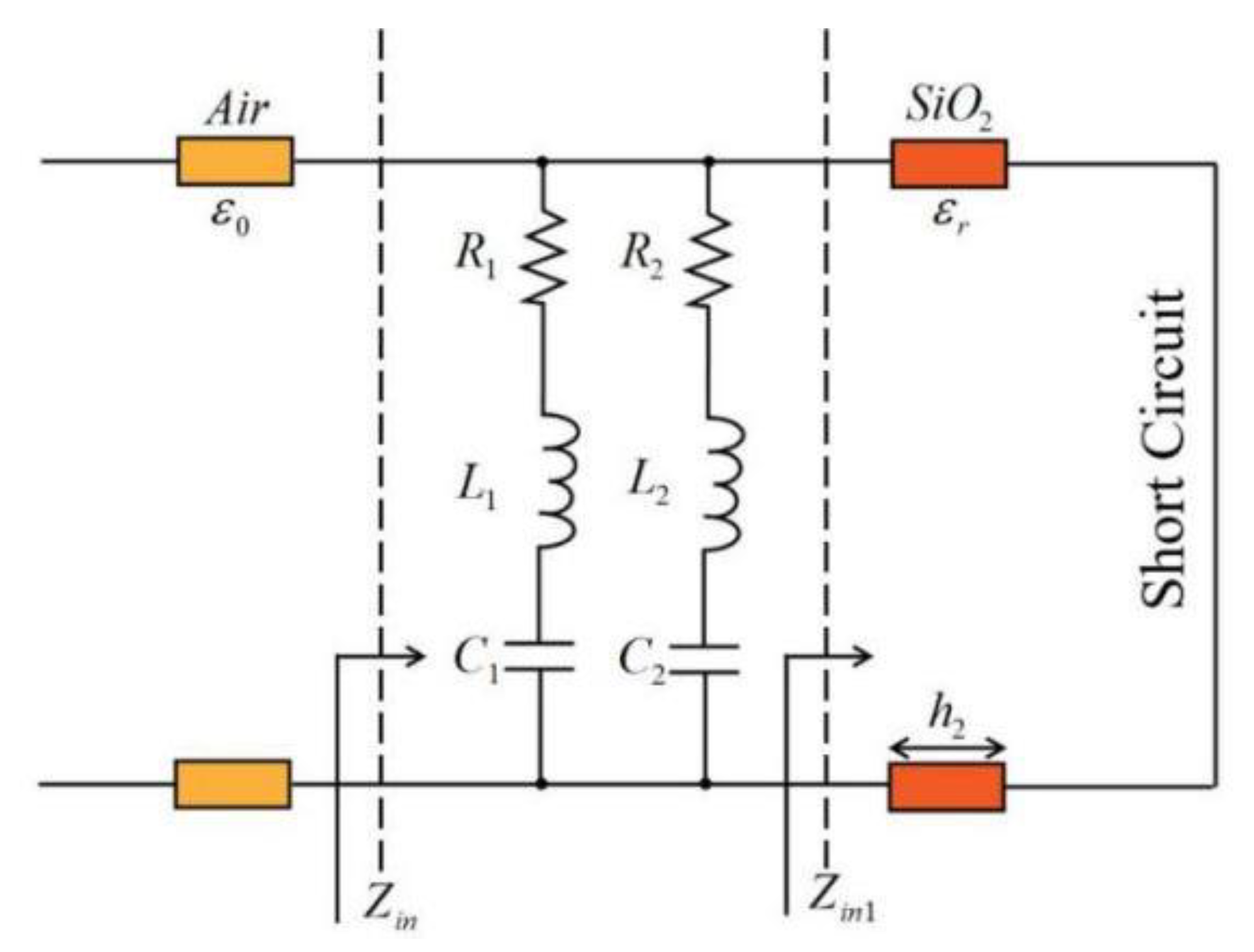
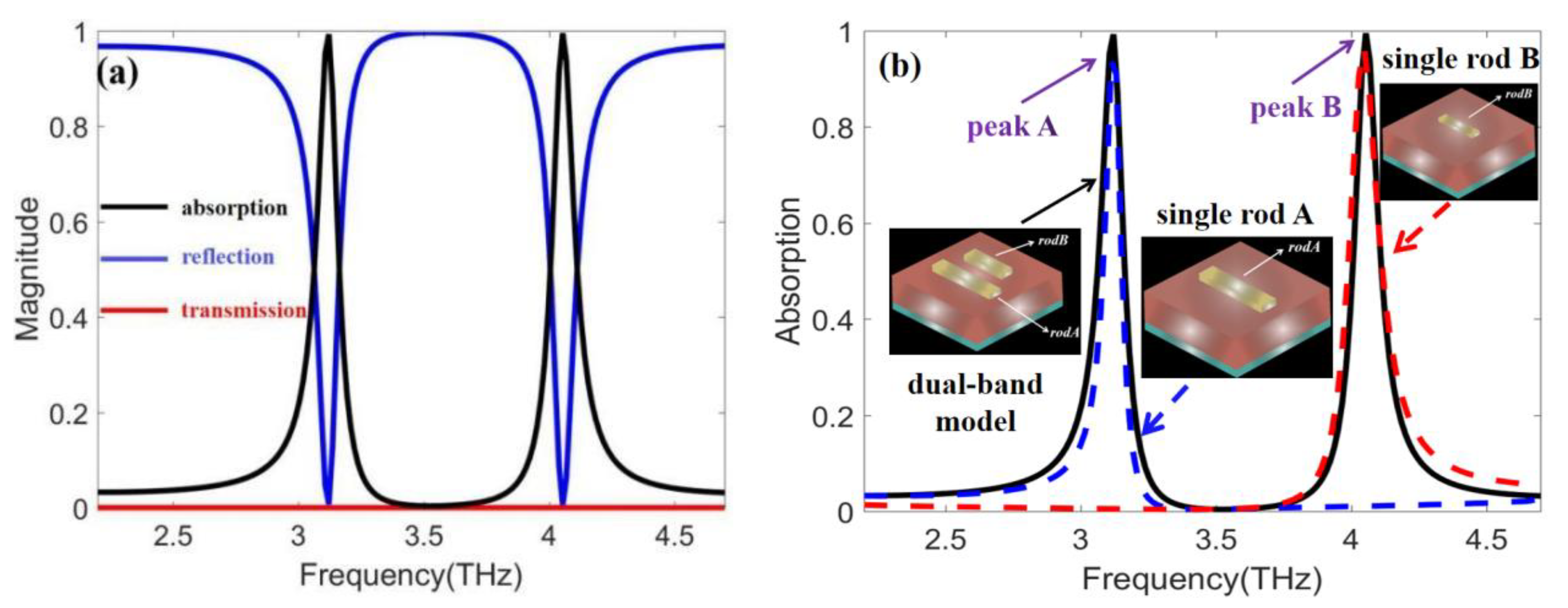
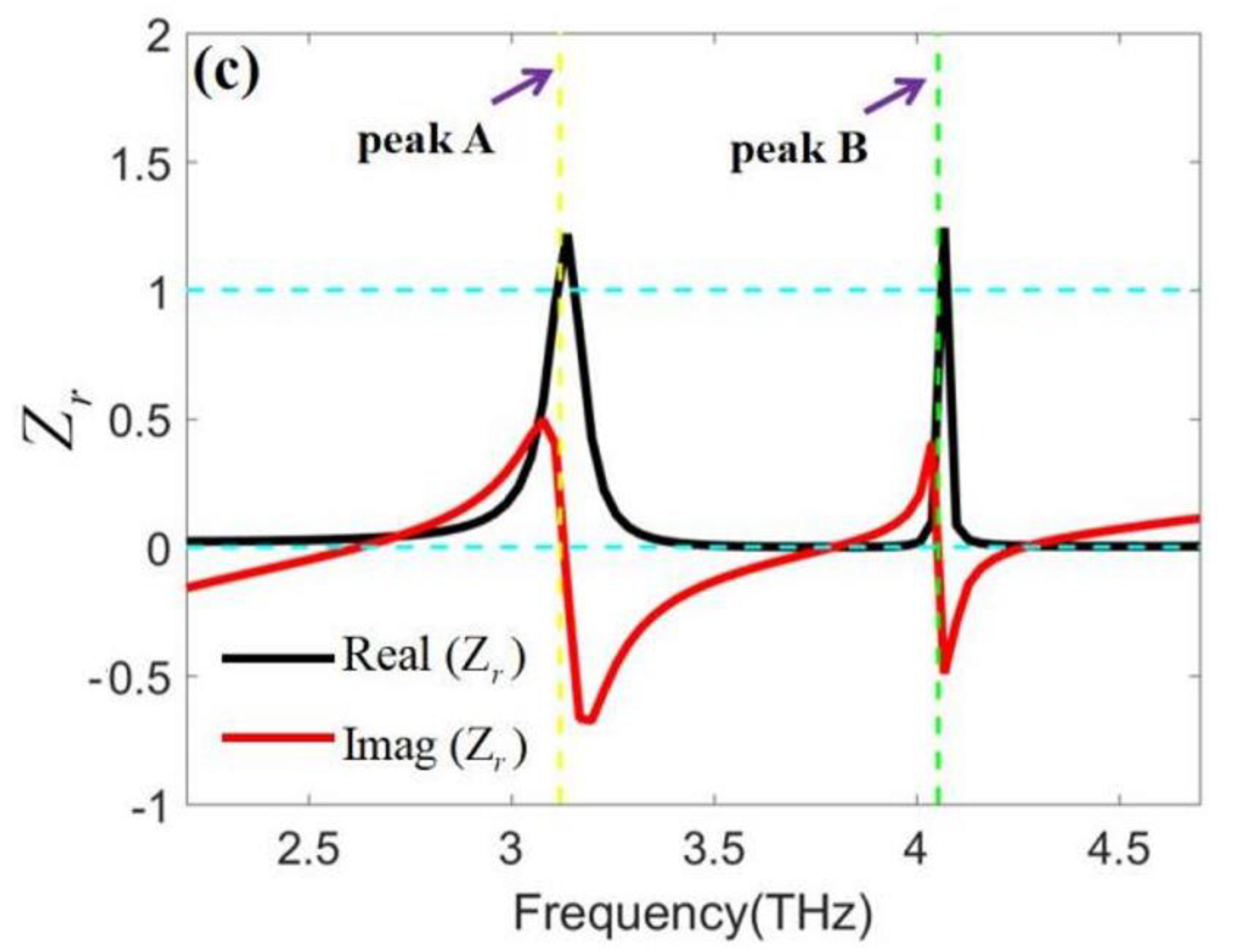
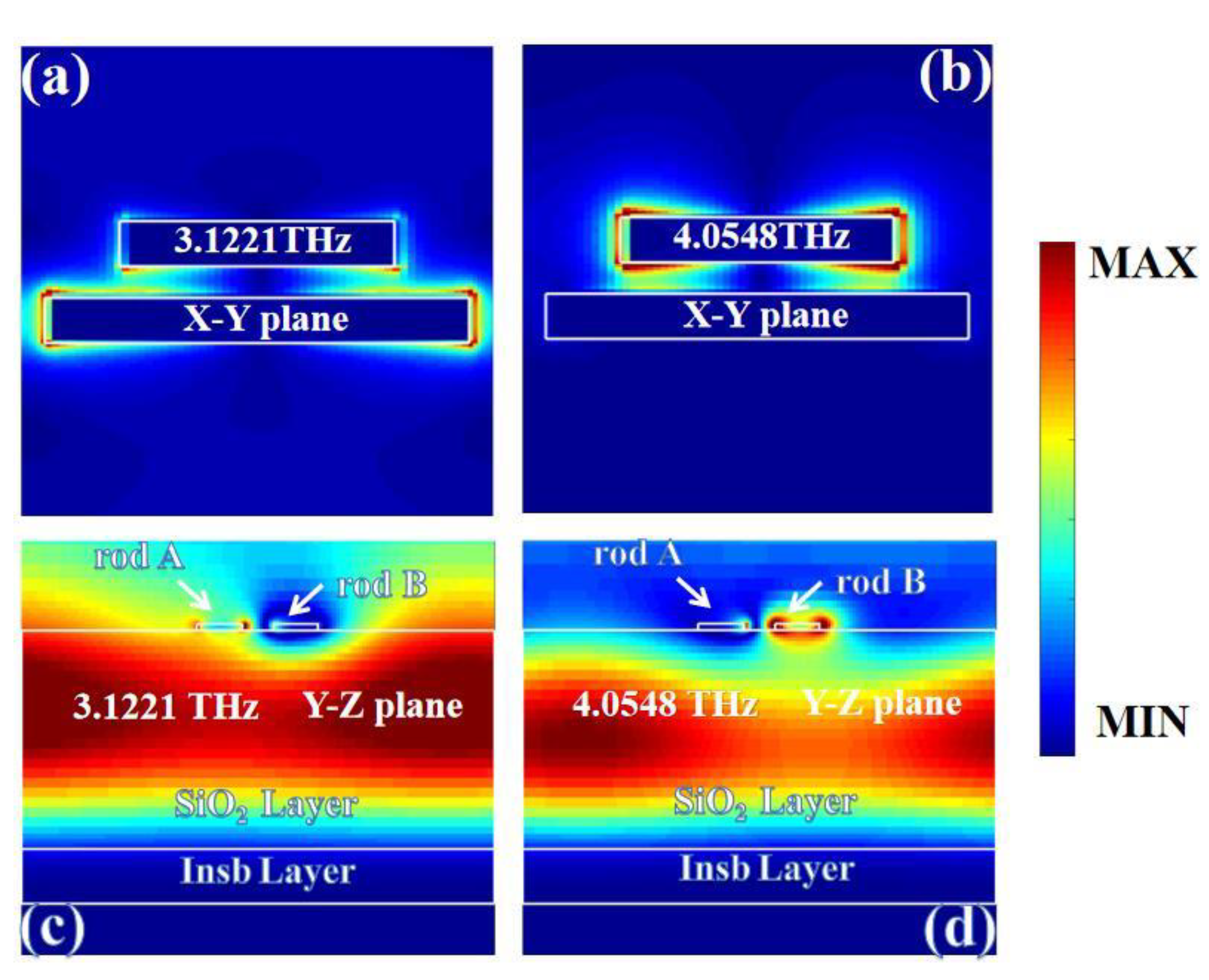
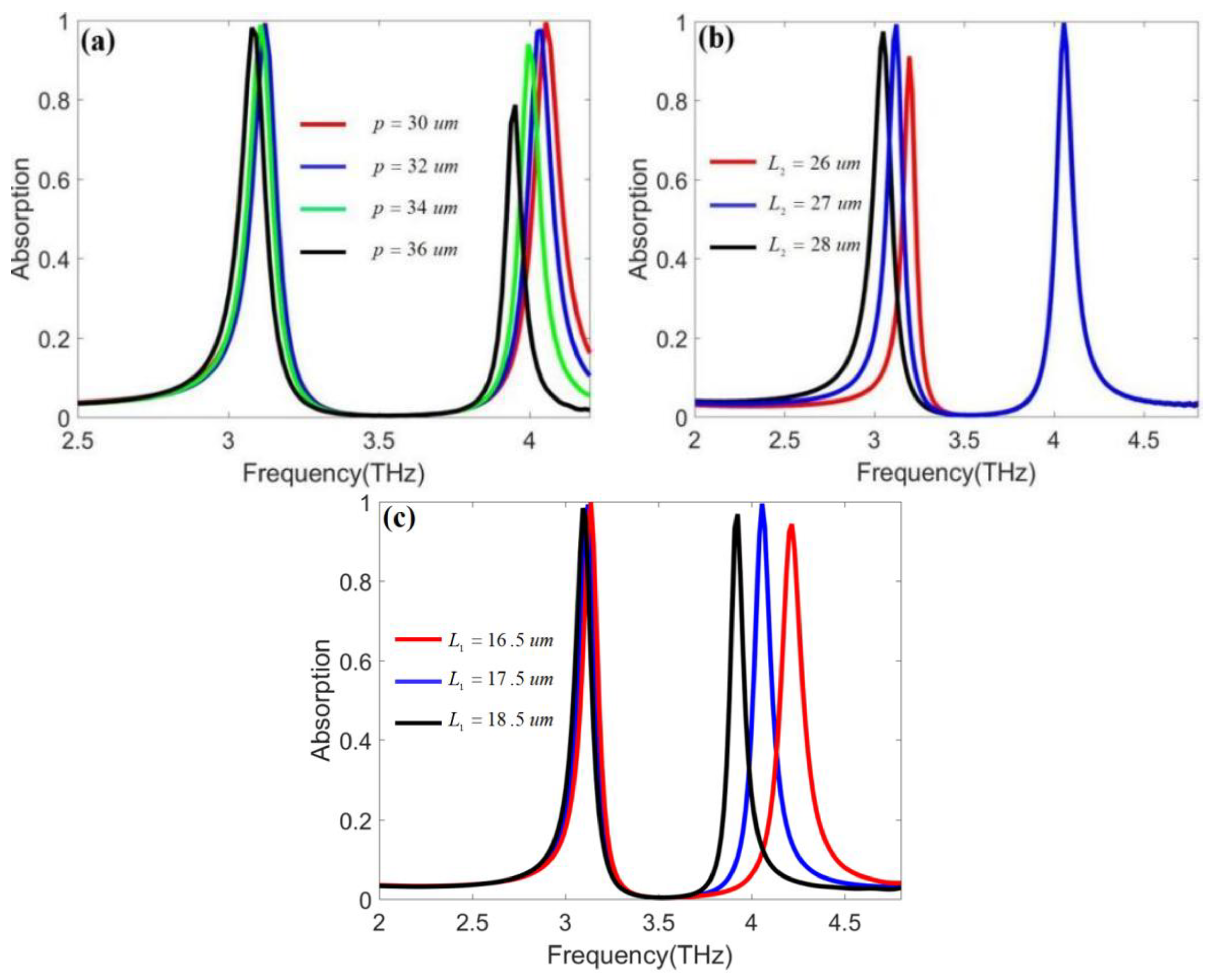
3. Results and Discussion
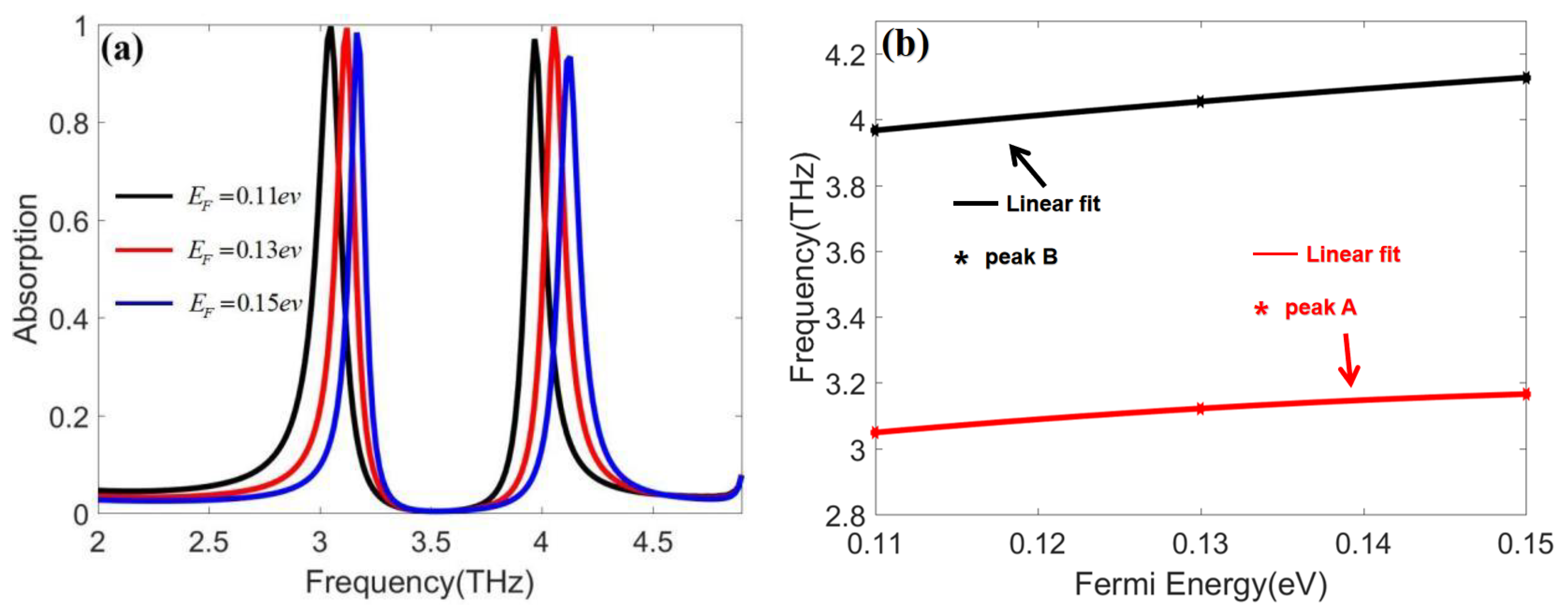
4. Electrically Tunable Characteristics of Dual-Band Absorber
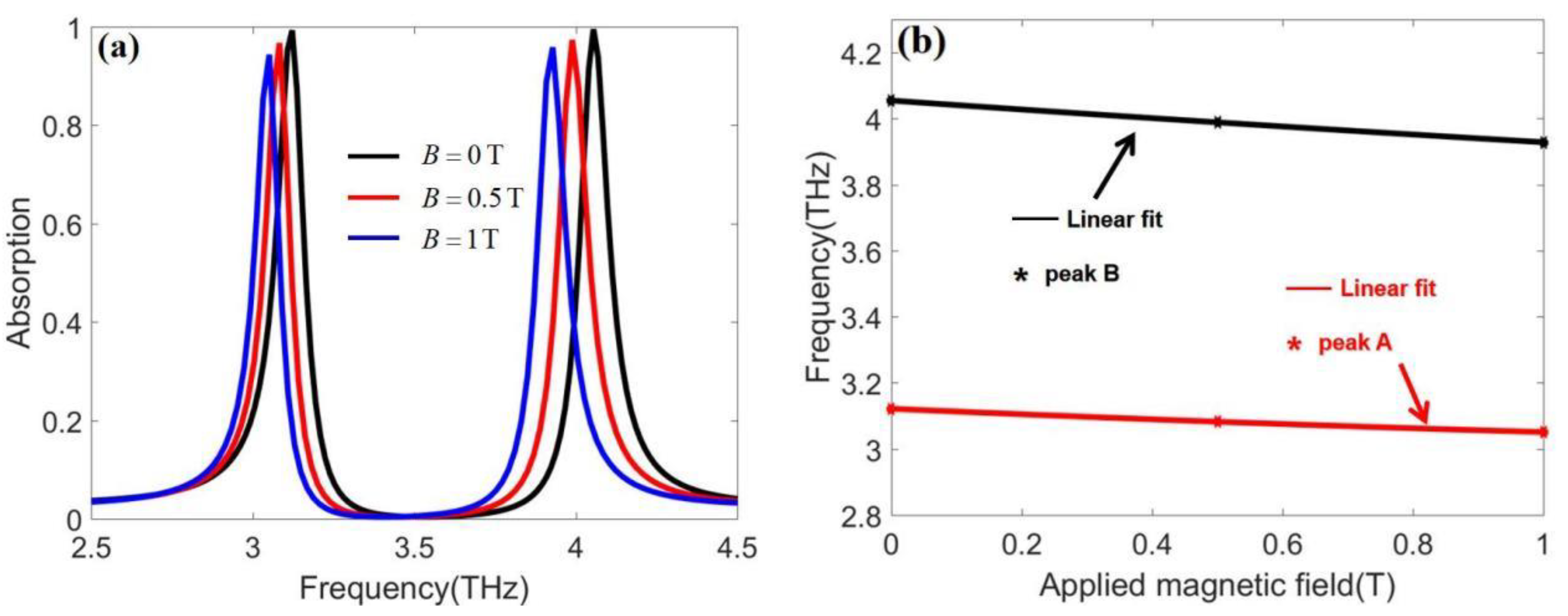
5. Thermally and Magnetically Tunable Characteristics of Dual-Band Absorber
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Withayachumnankul, W.; Abbott, D. Metamaterials in the terahertz regime. IEEE Photonics J. 2009, 1, 99. [Google Scholar] [CrossRef]
- Chen, H.-T.; Padilla, W.J.; Cich, M.J.; Azad, A.K.; Averitt, R.D.; Taylor, A.J. A metamaterial solid-state terahertz phase modulator. Nat. Photonics 2009, 3, 148. [Google Scholar] [CrossRef]
- Fan, K.; Zhao, X.; Zhang, J. Optically tunable terahertz metamaterials on highly flexible substrates. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 702. [Google Scholar] [CrossRef]
- Kojima, S.; Mori, T. Terahertz time-domain spectroscopy of Raman inactive phonon-polariton in strontium titanate. Ferroelectrics 2016, 499, 100. [Google Scholar] [CrossRef]
- Xu, W.; Xie, L.; Ying, Y. Mechanisms and applications of terahertz metamaterial sensing: A review. Nanoscale 2017, 9, 13864. [Google Scholar] [CrossRef]
- Sheta, E.M.; Choudhury, P.K. Graphene-strontium titanate-based metamaterial for optical sensing. Proc. SPIE 2021, 11802, 147. [Google Scholar]
- Diem, M.; Koschny, T.; Soukoulis, C.M. Wide-angle perfect absorber/thermal emitter in the terahertz regime. Phys. Rev. B 2009, 79, 033101. [Google Scholar] [CrossRef]
- Cheng, D.; He, X.; Huang, X.; Zhang, B.; Liu, G.; Shu, G.; Fang, C.; Wang, J.; Luo, Y. Terahertz biosensing metamaterial absorber for virus detection based on spoof surface plasmon polaritons. Int. J. RF Microw. Comput. Aided Eng. 2018, 28, e21448. [Google Scholar] [CrossRef]
- Sekhi, S.Z.; Shokooh-Saremi, M.; Mirsalehi, M.M. Ultra-broadband wide-angle and polarization-insensitive metamaterial perfect absorber for solar energy harvesting. J. Nanophotonics 2020, 14, 046014. [Google Scholar] [CrossRef]
- Wang, H.; Sivan, V.P.; Mitchell, A. Highly efficient selective metamaterial absorber for high-temperature solar thermal energy harvesting. Sol. Energy Mater. Sol. Cells 2015, 137, 235. [Google Scholar] [CrossRef]
- Zhang, Y.; Lv, J.; Que, L. A double-band tunable perfect terahertz metamaterial absorber based on Dirac semimetals. Results Phys. 2019, 15, 102773. [Google Scholar] [CrossRef]
- Meng, W.; Que, L.; Lv, J. A triple-band terahertz metamaterial absorber based on buck Dirac semimetals. Results Phys. 2019, 14, 102461. [Google Scholar] [CrossRef]
- Liu, G.D.; Zhai, X.; Meng, H.Y. Dirac semimetals based tunable narrowband absorber at terahertz frequencies. Opt. Express 2018, 26, 11471–11480. [Google Scholar] [CrossRef] [PubMed]
- Fang, P.; Shi, X.; Liu, C. Single-and dual-band convertible terahertz absorber based on bulk Dirac semimetal. Opt. Commun. 2020, 462, 125333. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Zhou, F. Dynamically tunable electro-optic switch and multimode filter based on twisted bilayer graphene strips. J. Opt. 2021, 23, 025104. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, S.; Yu, P. Dynamically tunable plasmonically induced transparency in periodically patterned graphene nanostrips. Appl. Phys. Lett. 2013, 103, 203112. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Y.; Zhang, X. Dynamically adjustable plasmon-induced transparency and switching application based on bilayer graphene metamaterials. J. Phys. D Appl. Phys. 2020, 54, 054002. [Google Scholar] [CrossRef]
- Lherbier, A.; Biel, B.; Niquet, Y.M. Transport length scales in disordered graphene-based materials: Strong localization regimes and dimensionality effects. Phys. Rev. Lett. 2008, 100, 036803. [Google Scholar] [CrossRef]
- Liang, J.R.; Wu, M.J.; Hu, M. Fabrication of VO2 thin film by rapid thermal annealing in oxygen atmosphere and its metal—Insulator phase transition properties. Chin. Phys. B 2014, 23, 076801. [Google Scholar] [CrossRef]
- Liu, Y.N.; Weng, X.L.; Zhang, P. Ultra-broadband infrared metamaterial absorber for passive radiative cooling. Chin. Phys. Lett. 2021, 38, 034201. [Google Scholar] [CrossRef]
- Nouman, M.T.; Hwang, J.H.; Faiyaz, M. Vanadium dioxide based frequency tunable metasurface filters for realizing reconfigurable terahertz optical phase and polarization control. Opt. Express 2018, 26, 12922. [Google Scholar] [CrossRef] [PubMed]
- Wahlstrand, J.K.; Heilweil, E.J. Contactless THz-based bulk semiconductor mobility measurements using two-photon excitation. Opt. Express 2018, 26, 29848. [Google Scholar] [CrossRef] [PubMed]
- Kowerdziej, R.; Jaroszewicz, L. Tunable dual-band liquid crystal based near-infrared perfect metamaterial absorber with high-loss metal. Liq. Cryst. 2019, 46, 1568. [Google Scholar] [CrossRef]
- Baranzadeh, F.; Nozhat, N. High Performance Plasmonic Nano-Biosensor Based on Tunable Ultra-Narrowband Perfect Absorber Utilizing Liquid Crystal. Plasmonics 2021, 16, 253. [Google Scholar] [CrossRef]
- Mistry, D.; Traugutt, N.A.; Sanborn, B. Soft elasticity optimises dissipation in 3D-printed liquid crystal elastomers. Nature 2021, 12, 6677. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Lakhtakia, A.; Jain, P.K. Tricontrollable pixelated metasurface for absorbing terahertz radiation. Appl. Opt. 2019, 58, 9614. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Pakniyat, S.; Xiang, Y. Temperature-dependent transverse-field magneto-plasmons properties in InSb. Opt. Mater. 2021, 112, 110831. [Google Scholar] [CrossRef]
- Li, H.; Huang, W.; Zhang, W. Thermally controlled electromagnetically induced transparency in hybrid metal-InSb metamaterials at THz frequencies. J. Phys. Conf. Ser. 2020, 1592, 012024. [Google Scholar] [CrossRef]
- Kang, W.; Gao, Q.; Dai, L. Dual-controlled tunable terahertz coherent perfect absorption using Dirac semimetal and vanadium dioxide. Results Phys. 2020, 19, 103866. [Google Scholar] [CrossRef]
- Jing, H.; Wei, Y.; Duan, J. Thermally and magnetically controlled dual-band terahertz metamaterial absorber based on InSb. Opt. Mater. 2022, 129, 112311. [Google Scholar] [CrossRef]
- Hu, B.J.; Huang, M.; Yang, L. Terahertz dual-tunable absorber based on hybrid gold-graphene-strontium titanate-vanadium dioxide configuration. Opt. Mater. Express 2023, 13, 2775. [Google Scholar] [CrossRef]
- Kotov, O.V.; Lozovik, Y.E. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 235417. [Google Scholar] [CrossRef]
- Zhou, J.; Chang, H.R.; Xiao, D. Plasmon mode as a detection of the chiral anomaly in Weyl semimetals. Phys. Rev. B 2015, 91, 035114. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, S.C. Dielectric function, Friedel oscillation and plasmons in Weyl semimetals. Int. J. Mod. Phys. B 2013, 27, 1350177. [Google Scholar] [CrossRef]
- Ziaee, B.M.; Forooraghi, K.; Atlasbaf, Z. Method of lines for analysis of plane wave scattering by periodic arrays of magnetically-biased graphene strips. Sci. Rep. 2021, 11, 7588. [Google Scholar]
- Han, J.; Lakhtakia, A.; Qiu, C.W. Terahertz metamaterials with semiconductor split-ring resonators for magnetostatic tunability. Opt. Express 2008, 16, 14390. [Google Scholar] [CrossRef]
- Huang, J.; Li, J.; Yang, Y. Active controllable dual broadband terahertz absorber based on hybrid metamaterials with vanadium dioxide. Opt. Express 2020, 28, 7018. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.J.; Huang, M.; Li, P. Dynamically dual-tunable dual-band to four-band metamaterial absorbers based on bulk Dirac semimetal and vanadium dioxide. J. Opt. Soc. Am. A 2022, 39, 383. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.M.; Yang, X.X. Polarization-insensitive electromagnetically induced transparency and its sensing performance based on spoof localized surface plasmons in vanadium dioxide-based terahertz metasurfaces. Phys. Chem. Chem. Phys. 2023, 25, 21047. [Google Scholar] [CrossRef]
- Ge, Z.K.; Sang, T.; Luo, C. Configurable dual-topological-interface-states induced reflection in hybrid multilayers consisting of a Ge2Sb2Te5 film. Opt. Express 2024, 32, 16351. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, R.; Lian, Z. Dynamically tunable band stop filter enabled by the metal-graphene metamaterials. Sci. Rep. 2018, 8, 2828. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.; Roh, J.W. Electrically tunable two-dimensional metasurfaces at near-infrared wavelengths. Opt. Express 2017, 25, 25071. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.; Ren, P.; Jia, Y. Active control and large group delay in graphene-based terahertz metamaterials. J. Phys. Chem. C 2019, 123, 18560. [Google Scholar] [CrossRef]
- Xiao, B.; Tong, S.; Fyfe, A. Tunable electromagnetically induced transparency based on graphene metamaterials. Opt. Express 2020, 28, 4048. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Huang, M.; Cai, C.; Yang, L. A Triple-Tunable Dual-Band Metamaterial Absorber Based on Dirac Semimetal and InSb. Photonics 2024, 11, 1039. https://doi.org/10.3390/photonics11111039
Hu B, Huang M, Cai C, Yang L. A Triple-Tunable Dual-Band Metamaterial Absorber Based on Dirac Semimetal and InSb. Photonics. 2024; 11(11):1039. https://doi.org/10.3390/photonics11111039
Chicago/Turabian StyleHu, Baojing, Ming Huang, Changjin Cai, and Li Yang. 2024. "A Triple-Tunable Dual-Band Metamaterial Absorber Based on Dirac Semimetal and InSb" Photonics 11, no. 11: 1039. https://doi.org/10.3390/photonics11111039
APA StyleHu, B., Huang, M., Cai, C., & Yang, L. (2024). A Triple-Tunable Dual-Band Metamaterial Absorber Based on Dirac Semimetal and InSb. Photonics, 11(11), 1039. https://doi.org/10.3390/photonics11111039




