Abstract
In this paper, we analyze the confidentiality of a hybrid radio frequency (RF)/free-space optical (FSO) system with regard to physical layer security (PLS). In this system, signals are transmitted between the source and destination using RF and FSO links, with the destination employing the maximal-ratio combining (MRC) scheme. A non-cooperative target (NCT) is assumed to have eavesdropping capabilities for RF and FSO signals in both collusion and non-collusion strategies. The Nakagami-m distribution models fading RF links, while FSO links are characterized by the Málaga () distribution. Exact closed-form expressions for the system’s secrecy outage probability (SOP) and effective secrecy throughput (EST) are derived based on the generalized Meijer G-function with two variables. Asymptotic expressions for the SOP are also obtained under high-signal-to-noise-ratio (SNR) regimes. These conclusions are validated through Monte Carlo simulations. The superiority of the hybrid RF/FSO system in improving the communication security of a single link is confirmed in its comparison with conventional means of RF communication.
1. Introduction
Unmanned aerial vehicle (UAV)-assisted communication, such as that of cooperative relays and aerial base stations [1,2], provides insights for terrestrial networks to achieve flexible, reliable, and cost-effective communication. Nevertheless, the line-of-sight (LOS) communication and open broadcasting properties of conventional radio frequency (RF) links expose them to potential eavesdropping from malicious nodes. Therefore, establishing secure communication for UAVs has become an urgent issue [3]. RF/free-space optical (FSO) cooperative communication has been extensively studied to enhance communication reliability, owing to the complementary features of two means, in terms of communication rate, interference immunity, and spectrum resources, for example. These can also improve communication security based on the physical layer security (PLS) dimension of information theory [4,5]. This technique can be used to safeguard information confidentiality by utilizing the inherent properties of the wireless channel, independent of users’ computing capabilities, and ensure that UAVs are as lightweight as is required.
The earliest research on PLS techniques originated in information theory published by Shannon, followed by the redefinition of the eavesdropping model by Wyner et al. [6]. Much research has been conducted on the PLS performance of mixed FSO/RF communication systems [7,8,9,10,11,12,13,14]. Some investigated the PLS performance of the system when only one signal-eavesdropping technique (either RF or FSO link eavesdropping) was present at the relay or the destination. In [7], the authors studied the secrecy outage probability (SOP) of a downlink space-air-ground integrated network with a high-altitude-platform station as a relay. The FSO link is used between the satellite and the platform, and FSO eavesdropping is considered. The hybrid FSO/RF system with a hard-switching scheme is used between the platform and the ground. Ref. [8] investigated the mixed RF/FSO system combined with non-orthogonal multiple access (NOMA) techniques, considered the effect of imperfect channel state information (CSI), and compared the confidentiality performance under decode-and-forward and amplify-and-forward protocols. Ref. [9] analyzed the SOP for the mixed RF/FSO system under FSO signal eavesdropping and for the mixed FSO/RF system under RF signal eavesdropping. The simulations show that photo-aperture size, fading parameters, and average eavesdropping signal-to-noise ratio (SNR) are crucial influences on the performance. Ref. [10] analyzed the SOP and effective secrecy throughput (EST) of a mixed multiple-input multiple-output (MIMO) RF/FSO system in the presence of a multi-antenna RF eavesdropper. The CSI of the RF and FSO links were considered outdated and imprecise, respectively. The authors proposed four transmit antenna selection schemes to improve confidentiality performance. Others [11,12,13] considered the secrecy performance of a mixed FSO/RF communication system in the presence of both FSO and RF signal eavesdropping. Refs. [12,13] have been conducted on the mixed FSO/RF simultaneous wireless information and power transfer (SWIPT) system. Ref. [12] investigated the effect of SWIPT parameters and power amplifier efficiency on the secrecy performance by considering a relay equipped with a non-ideal power amplifier. Ref. [13] analyzed its communication reliability (outage probability and average bit error rate) and security (SOP and strictly positive secrecy capacity (SPSC)) performance. A description of related work can be seen in Table 1. However, the information obtained from the respective means was not combined, as the two eavesdropping techniques work independently [14]. Naturally, malicious users expect to make full use of the information obtained from each means of eavesdropping, allowing them to intercept legitimate data. Therefore, obtaining information via both means of eavesdropping aligns more with their needs. Further, the mixed RF/FSO system improves communication security overall, meaning it is more suitable for the multi-hop communication model.

Table 1.
Related work on FSO/RF systems.
In contrast, the hybrid RF/FSO system significantly enhanced communication security for a single link. However, only a few studies on this topic included an analysis of hybrid FSO/RF system PLS performance. The authors of [15,16,17] investigated the security performance of hybrid FSO/RF systems under different combinations of diversity schemes, including a selection combining (SC) and the maximal-ratio combining (MRC) scheme. Specifically, ref. [15] investigated the hybrid RF/FSO system under the influence of a non-cooperative target (NCT), which can interfere with legitimate RF signals while performing eavesdropping behaviors on them, and the authors analyzed the communication performance under the proposed scenario. Ref. [16] proposed to add a power amplifier in the hybrid RF/FSO system to enhance the transmission efficiency and analyzed the average secrecy capacity (ASC) and SOP performance. Contrary to [15,16], which combined RF and FSO signals based on the SC scheme, ref. [17] investigated the hybrid RF/FSO system based on the MRC scheme and studied the security of the system in the presence of RF or FSO signal eavesdropping, respectively. However, this research examined the impact of the two eavesdropping techniques on the system separately, i.e., the two eavesdropping means were not considered simultaneously. Studies on the PLS performance of the hybrid FSO/RF system in the presence of both FSO and RF eavesdropping have yet to be reported. Based on this motivation, we carried out the research presented in this paper. The main contributions of this paper are as follows:
- This paper investigates the confidentiality performance of the hybrid RF/FSO system based on the MRC scheme. Considering the impact of eavesdropping strategies, we assume that the NCT can eavesdrop on RF and FSO signals using collusion or non-collusion eavesdropping strategies. Unlike the existing studies, different eavesdropping strategies require a combination of RF and FSO eavesdropping first, superimposed on the MRC scheme at the legitimate receiver, which makes the derivation of closed-form expressions difficult. However, this can contribute to further studying the hybrid RF/FSO system for enhancing single-link communication performance.
- A closed-form expression for the SOP of the proposed model is derived and is characterized by a generalized Meijer G-function with two variables. In this case, the FSO links consider the effects of atmospheric turbulence, path loss, pointing error, and angle-of-arrival (AoA) fluctuations, among which AoA fluctuations have been neglected in some studies. This paper also investigates the effect of the relevant parameters (channel fading, atmospheric turbulence, pointing error, and AoA fluctuations) on performance.
- Monte Carlo simulations verify the exact results, and asymptotic expressions for the SOP are derived under high-SNR regimes. Furthermore, the EST in both eavesdropping strategies of an NCT is simulated, indicating that an appropriate target secrecy rate contributes to achieving a balance in the system between reliability and secrecy.
The rest of this paper is organized as follows. Section 2 presents the system model and the statistical properties of the channels. In Section 3, closed-form expressions for the SOP and EST are derived for the hybrid RF/FSO system under different eavesdropping strategies. An asymptotic expression for SOP under high-SNR conditions is derived in Section 4. Section 5 offers simulation results and an analysis, while Section 6 concludes this paper.
2. System and Channel Models
Figure 1 illustrates the scenario of hybrid RF/FSO wireless communication in the presence of eavesdroppers, where privacy data are transmitted between high-altitude-platform stations () and the UAV () through RF and FSO links. The receiver employs an MRC scheme to combine the data for enhanced communication. An NCT attempts to eavesdrop using two unauthorized nodes configured with RF antennas () and photodetectors (). On the one hand, due to the wide propagation range of RF signals, the NCT can effectively eavesdrop using the ground RF antenna; on the other hand, due to channel scattering, atmospheric turbulence, pointing deflection, and beam divergence, there is also the possibility of eavesdropping from the FSO link [18]. However, it is necessary to be close to the legitimate FSO signal receivers, and therefore, eavesdropping can be carried out by using a UAV. Thus, the NCT can obtain both RF and FSO eavesdropping signals, and different combining methods correspond to different eavesdropping strategies. The NCT can choose between two strategies, either eavesdropping over the link with the largest SNR (non-collusion) or combining the RF and FSO eavesdropping signals (collusion). The Nakagami-m distribution models the RF links ( and ). In addition, the FSO links ( and ) are assumed to follow the Málaga distribution, considering path loss, pointing errors, and AoA fluctuations.
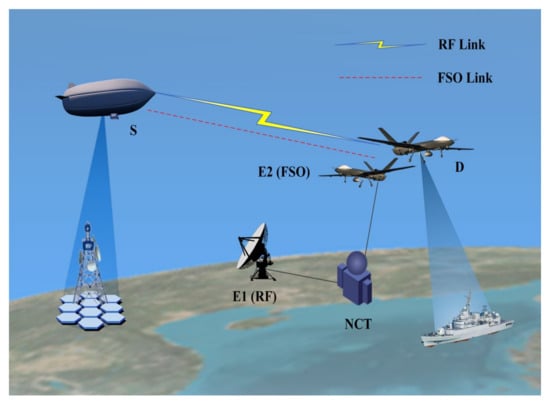
Figure 1.
High altitude platform-UAV communication scenario in the presence of the NCT.
The probability density function (PDF) and the cumulative distribution function (CDF) of the instantaneous SNR for the RF links can be expressed as follows [15]:
where reflects the fading severity and is the average SNR. The subscript is used to distinguish between legitimate and eavesdropping channels. is the gamma function. The PDF and the CDF of the instantaneous SNR for the FSO links are stated as follows [19]:
where is the average SNR. , , , , , , and . , , and . The meaning of each FSO link parameter of the equation can be ascertained by referring to [11]. indicates the effect of AoA fluctuations, denotes the threshold of the field of view, and is the variance of the angle between the incident light and the normal to the receiver aperture. denotes the Meijer G-function, and is the delta function. Using [20], equations (07.34.03.0955.01) and (07.32.02.0001.01), an alternative expression for the PDF and CDF of the instantaneous SNR can be obtained as follows:
where , , , , , , , , and . Furthermore, the convergence of equation [5] has been demonstrated in [21].
3. Secrecy Performance Analysis
In this section, we derive the PDF and CDF of the instantaneous SNR of the received and eavesdropping signals in both collusion and non-collusion strategies. Then, we obtain exact closed-form expressions for the SOP and EST.
3.1. Preliminary
3.1.1. Legitimate Receiver
The instantaneous SNR of the hybrid RF/FSO communication system, based on an MRC scheme, can be expressed as . Since the FSO and RF links are mutually independent, can be stated as follows [17]:
By substituting Equations (1) and (5) into Equation (7), applying [20], equations (07.34.03.0228.01) and (07.34.21.0084.01), a closed-form expression for can be obtained as follows:
where and . Further, its PDF can be obtained as follows:
3.1.2. Collusion Eavesdropping Strategy
In this strategy, the NCT considers using the MRC scheme to combine the information eavesdropped by the RF antennas and the photodetector. Since this is consistent with the method of the legitimate node, the PDF of the instantaneous SNR is that of Equation (8).
3.1.3. Non-Collusion Eavesdropping Strategy
In this case, the NCT employs the SC scheme, where the eavesdropping signal of the link with the highest SNR is chosen. The attainable instantaneous SNR can be represented as . Therefore, the PDF of can be expressed as
3.2. Collusion Eavesdropping Analysis
3.2.1. Secrecy Outage Probability (Collusion)
SOP is a fundamental benchmark of secrecy, indicating the privacy level of a communication system. It is defined as the probability that the instantaneous secrecy capability is lower than the target secrecy rate , with its lower bound derived as follows:
where . If the upper limit of integration approaches infinity, truncating the value of for infinite series will not be feasible, based on the practical implication that and converge to 1 and 0, respectively. A finite value can serve as the upper limit while ensuring that the deviation of the outcome does not surpass 10−4. Substituting Equations (8) and (9) into Equation (11) yields a closed-form expression as in Equation (12).
where . Refer to Appendix A for the derivation.
3.2.2. Effective Secrecy Throughput (Collusion)
EST is another metric for assessing the secrecy performance of a system, and it is crucial for ensuring both reliability and secrecy. It is defined as the multiplication of the target secrecy rate with the probability of the simultaneous guarantee of reliability and secrecy constraints. The EST can be mathematically represented as follows:
3.3. Non-Collusion Eavesdropping Analysis
3.3.1. Secrecy Outage Probability (Non-Collusion)
Substituting Equations (9) and (10) into Equation (11), using the generalized Meijer G-function containing two variables, [20], equation (07.34.21.0084.01) and [22], equation (8.350.1), the closed-form expression for is shown as Equation (14). is the incomplete gamma function, and .
3.3.2. Effective Secrecy Throughput (Non-Collusion)
In the case of non-collusion eavesdropping, the EST is calculated as follows:
4. Asymptotic Secrecy Outage Probability
The closed-form expression of SOP permits us to evaluate the security performance of the system. Due to the complexity of the expression, it is difficult to analyze the impact of RF link-related parameters on the overall system performance. Therefore, this section describes the asymptotic behavior of the above closed-form expressions at high-SNR regimes. In this region (i.e., ), the asymptotic SOP is generally expressed as , where and are the secrecy coding gain and secrecy diversity order. In the case of , Equations (1) and (2) can be approximated as follows:
By substituting Equations (3) and (16) into Equation (7) and solving with [20], equation (07.34.21.0084.01), the PDF and CDF of the instantaneous SNR of the received signal in the high-SNR regimes can be obtained as
By substituting Equations (8) and (19) into Equation (11), the asymptotic SOP expression for the system in the collusion strategy can be derived as Equation (20). Substituting the non-collusion strategy-related equations, the asymptotic SOP expression can be obtained, as shown in Equation (21). The equations used in the derivation process are [20], equations (07.34.21.0081.01), (07.34.21.0084.01), and (07.34.21.0088.01) and [22], equation (8.310.1), as well as the generalized Meijer G-function, which contains two variables. As seen by comparison, the secrecy diversity gain is obtained as in both eavesdropping strategies.
5. Numerical Results
In this section, the exact and asymptotic results are simulated to analyze the security performance of the system. On the one hand, the SOP of the system under different eavesdropping strategies is compared with that of the traditional RF means of communication; on the other hand, we investigate in the SOP the effects of target secrecy rate, the average SNR of eavesdropping links, fading severity, turbulence intensity, AoA fluctuation variance, and pointing errors. As for the simulation parameter settings, by default, the target security rate in the simulation is 1.1 nats/sec/Hz, and the RF links are set to and . The FSO links are set to strong turbulence (, ), with the pointing error coefficient , and the AoA fluctuation coefficient , . In addition, the average SNRs of the legitimate and eavesdropping FSO links are 15 dB and 5 dB. The truncation threshold is set to 28 dB.
Monte Carlo simulation refers to a probabilistic channel simulation method used in the field of communications. It is characterized by the stochastic nature of the channel state, which cannot be described by a deterministic mathematical model. One common application is to simulate the signal transmission process in wireless communication systems. First, the parameters of the channel model, such as path loss and signal fading, need to be determined. Then, Monte Carlo methods are used to generate a series of random numbers to simulate the state of a random channel. These random numbers are based on the known statistical distributions. By iteratively generating the channel states and applying them to the signal transmission process, the transmission results under different channel states can be obtained. Thus, the Monte Carlo simulation can confirm the correctness of the equation from an experimental point of view.
Figure 2 illustrates the secrecy outage probability versus the average SNR of the legitimate RF link under different eavesdropping strategies and schemes. It should be noted that the hybrid RF/FSO system under the collusion eavesdropping strategy offers an SNR gain value of more than 3 dB and 5 dB for and , respectively, to achieve an SOP value of 10−1, compared to the RF-only link. This strongly proves the superiority of hybrid RF/FSO systems in enhancing the communication security of a single link. In addition, the system under the collusion eavesdropping strategy can combine RF and FSO eavesdropping signals. Hence, the SOP under the collusion eavesdropping strategy is significantly inferior to that of the non-collusion strategy. In terms of the NCT, when , the collusion eavesdropping strategy achieves an average gain of 15% in the SOP compared to the non-collusion eavesdropping strategy. As the average eavesdropping SNR increases, the non-collusion eavesdropping strategy already achieves a better eavesdropping effect, but the collusion eavesdropping strategy can still produce an average gain effect of 13%.
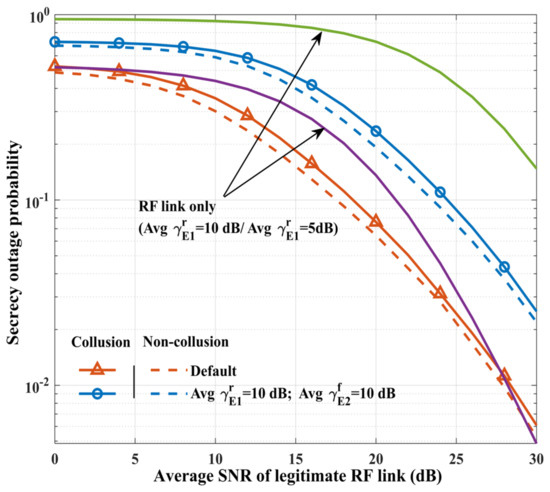
Figure 2.
Secrecy outage probability versus average SNR of legitimate RF link under different eavesdropping strategies and schemes.
Figure 3 illustrates the system’s SOP with respect to each link-related parameter. Each exact result is verified by simulations using Monte Carlo methods, illustrating the correctness of the derived expressions. Moreover, the asymptotic results are similar to the closed-form results in the high-SNR region. The reduction in the target secrecy rate will directly result in a decrease in the outage threshold, corresponding to the instantaneous secrecy capacity, so the system’s SOP is decreased. The changes in the AoA fluctuation variance and pointing error can have an impact on the performance of legitimate or eavesdropping FSO links, causing variations in the system’s SOP.
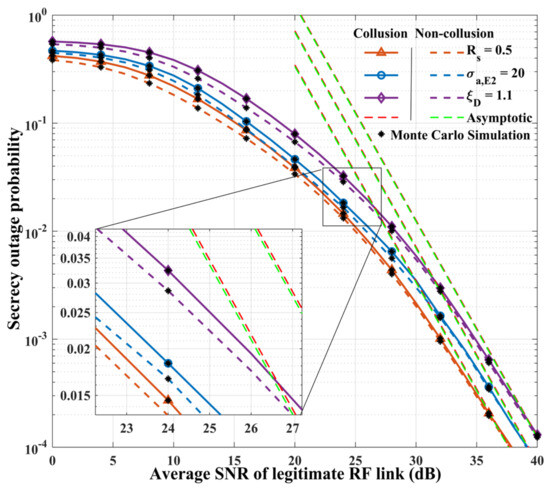
Figure 3.
Secrecy outage probability versus average SNR of legitimate RF link for different parameters.
As can be seen in Figure 4, the severity of the fading of the RF link has a negligible effect on the SOP of the system, which improves slightly when the fading of the eavesdropping RF link increases. However, when the values of and are larger (indicating weaker turbulence intensity), the security performance of the system improves significantly. The reduction in turbulence intensity improves the performance of both the legitimate and eavesdropping FSO links. However, this contributes overall to a reduction in the system’s SOP, which can further illustrate the advantages of FSO links over RF links in terms of communication security. However, the weakening of the turbulence intensity makes the AoA fluctuation effect of the FSO link obvious. However, the weakening of the turbulence intensity makes the AoA fluctuation effect of the FSO link obvious, and the SOP of the system is constrained by the FSO link, which gradually tends to be constant with the rise in the average SNR of the legitimate RF link.
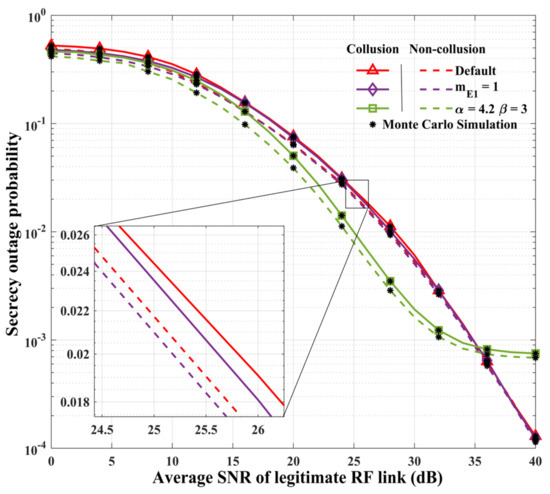
Figure 4.
Secrecy outage probability versus average SNR of legitimate RF link for different channel conditions.
Figure 5 demonstrates the variation in SOP and EST concerning the target secrecy rate for two cases. The two curves under the same eavesdropping strategy are compared for their different average eavesdropping SNRs (case 1, , ; case 2, , ). This figure shows that the SOP increases as the target secrecy rate increases, while the EST increases to a specific value before decreasing. This is because the rate increase comes at the expense of the system’s security. Therefore, setting an appropriate target secrecy rate can achieve a balance between communication rate and communication security. The maximum values of each curve obtained from the simulation are (2.1, 1.303), (2.1, 1.221), (1.8, 0.766), and (1.5, 0.655), respectively. For different average eavesdropping SNRs, the collusion eavesdropping strategy produces a 6.3% and 14.5% deterioration in the EST of the system compared to the non-collusion eavesdropping strategy. Thus, the collusion strategy significantly affects the EST of the system.
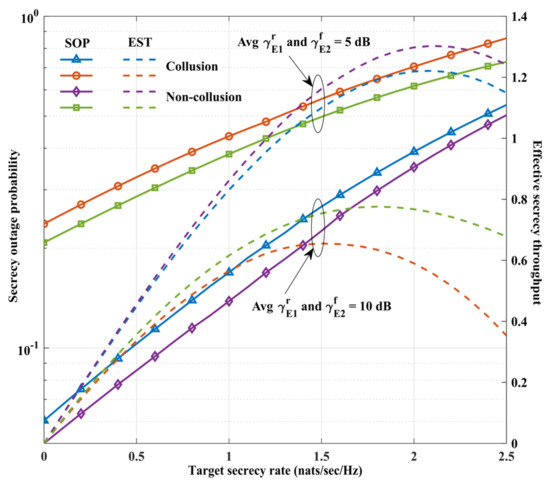
Figure 5.
Secrecy outage probability and effective secrecy throughput against target secrecy rate.
6. Conclusions
This paper investigates the security performance of a hybrid RF/FSO system under different eavesdropping strategies. Specifically, the SOP and EST of the system under collusion and non-collusion strategies are derived, respectively, under the condition that the system employs the MRC scheme. Based on the perspective of legitimate users, the hybrid RF/FSO system has obvious advantages in enhancing the communication security of a single link compared with traditional means of RF communication. Analyzed from the perspective of an NCT, we have shown that making full use of the information obtained from various eavesdropping techniques can improve the signal interception capability, which can contribute to the eavesdropping of private data.
Author Contributions
Formal analysis, S.Z.; data curation, X.L.; writing—original draft preparation, X.S.; writing—review and editing, X.W. and Q.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Basic Research Pan in the Shaanxi Province of China, grant No. 2023-JC-QN-0084.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The Appendix A describes the derivation of the expression . Taking the term containing two Meijer G-functions as an example, the Meijer G-function can be expanded by [22], equation (9.301), as shown in Equation (A1), and Equation (A2) can be obtained by solving the outer integral. The generalized Meijer G-function containing two variables is a special case of the Multivariable Fox H-function [23]. It is defined as shown in Equation (A3), and the specific simulation implementation can be found in [24]. In addition, for terms containing the Meijer G-function and the exponential function, the exponential function can be converted to the Meijer G-function using [20], equation (07.34.03.0228.01). Further, the product term of two exponential functions can be solved using [22], equation (8.310.1).
References
- Sharma, J.; Mehra, P.S. Secure Communication in IOT-Based UAV Networks: A Systematic Survey. Internet Things 2023, 23, 100883. [Google Scholar] [CrossRef]
- Qu, L.; Xu, G.; Zeng, Z.; Zhang, N.; Zhang, Q. UAV-Assisted RF/FSO Relay System for Space-Air-Ground Integrated Network: A Performance Analysis. IEEE Trans. Wirel. Commun. 2022, 21, 6211–6225. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Bankey, V.; Upadhyay, P.K. Physical layer security of multiuser multi relay hybrid satellite-terrestrial relay networks. IEEE Trans. Veh. Technol. 2019, 68, 2488–2501. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Bankey, V.; Sharma, S.; R, S. Physical Layer Security of HAPS-Based Space-Air-Ground-Integrated Network with Hybrid FSO/RF Communication. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4680–4688. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, J. Secrecy performance analysis for a NOMA based FSO-RF system with imperfect CSI. J. Opt. Commun. Netw. 2022, 14, 500–510. [Google Scholar] [CrossRef]
- Erdogan, E.; Altunbas, I.; Kurt, G.K.; Yanikomeroglu, H. The Secrecy Comparison of RF and FSO Eavesdropping Attacks in Mixed RF-FSO Relay Networks. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Lei, H.; Luo, H.; Park, K.-H.; Ansari, I.S.; Lei, W.; Pan, G.; Alouini, M.-S. On Secure Mixed RF-FSO Systems with TAS and Imperfect CSI. IEEE Trans. Commun. 2020, 68, 4461–4475. [Google Scholar] [CrossRef]
- Pattanayak, D.R.; Dwivedi, V.K.; Karwal, V.; Ansari, I.S.; Lei, H.; Alouini, M.-S. On the Physical Layer Security of a Decode and Forward Based Mixed FSO/RF Co-Operative System. IEEE Wirel. Commun. Lett. 2020, 9, 1031–1035. [Google Scholar] [CrossRef]
- Singh, R.; Rawat, M.; Jaiswal, A. On the Physical Layer Security of Mixed FSO-RF SWIPT System with Non-Ideal Power Amplifier. IEEE Photonics J. 2021, 13, 1–17. [Google Scholar] [CrossRef]
- Singh, R.; Rawat, M.; Jaiswal, A. On the Performance of Mixed FSO/RF SWIPT Systems with Secrecy Analysis. IEEE Syst. J. 2022, 16, 339–350. [Google Scholar] [CrossRef]
- Pattanayak, D.R.; Dwivedi, V.K.; Karwal, V. On the Physical Layer Security of Hybrid RF-FSO System in Presence of Multiple Eavesdroppers and Receiver Diversity. Opt. Commun. 2020, 477, 126334. [Google Scholar] [CrossRef]
- Liang, H.; Li, Y.; Miao, M.; Gao, C.; Li, X. Analysis of Selection Combining Hybrid FSO/RF Systems Considering Physical Layer Security and Interference. Opt. Commun. 2021, 497, 127146. [Google Scholar] [CrossRef]
- Ai, Y.; Mathur, A.; Lei, H.; Cheffena, M.; Ansari, I.S. Secrecy Enhancement of RF Backhaul System with Parallel FSO Communication Link. Opt. Commun. 2020, 475, 126193. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, M.; Li, G.; Kong, D. Systematic Performance Analysis of Hybrid FSO/RF System over Generalized Fading Channels with Pointing Errors. Photonics 2022, 9, 873. [Google Scholar] [CrossRef]
- Obeed, M.; Salhab, A.M.; Alouini, M.S.; Zummo, S.A. Survey on physical layer security in optical wireless communication systems. In Proceedings of the 2018 Seventh International Conference on Communications and Networking (ComNet), Hammamet, Tunisia, 1–4 November 2018; pp. 1–5. [Google Scholar]
- Shen, B.; Chen, J.; Xu, G.; Chen, Q.; Wang, J. Performance Analysis of a Drone-Assisted FSO Communication System over Málaga Turbulence under AoA Fluctuations. Drones 2023, 7, 374. [Google Scholar] [CrossRef]
- Wolfram, I. Mathematica Edition; Version 8.0; Wolfram Res. Inc.: Champaign, IL, USA, 2010. [Google Scholar]
- Sharma, S.; Madhukumar, A.; R, S. MIMO Hybrid FSO/RF System Over Generalized Fading Channels. IEEE Trans. Veh. Technol. 2021, 70, 11565–11581. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic: San Diego, CA, USA, 2007. [Google Scholar]
- Sharma, B.L.; Abiodun, R.F.A. Generating function for generalized function of two variables. Proc. Am. Math. Soc. 1974, 46, 69. [Google Scholar] [CrossRef]
- Peppas, K.P. A New Formula for the Average Bit Error Probability of Dual-Hop Amplify-and-Forward Relaying Systems over Generalized Shadowed Fading Channels. IEEE Wirel. Commun. Lett. 2012, 1, 85–88. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).