An Efficient Method for Wavefront Aberration Correction Based on the RUN Optimizer
Abstract
:1. Introduction
2. Principles of the AO Control Method Based on the RUN Optimizer
3. Analysis of Simulations and Results
3.1. The Wavefront Sensorless AO System
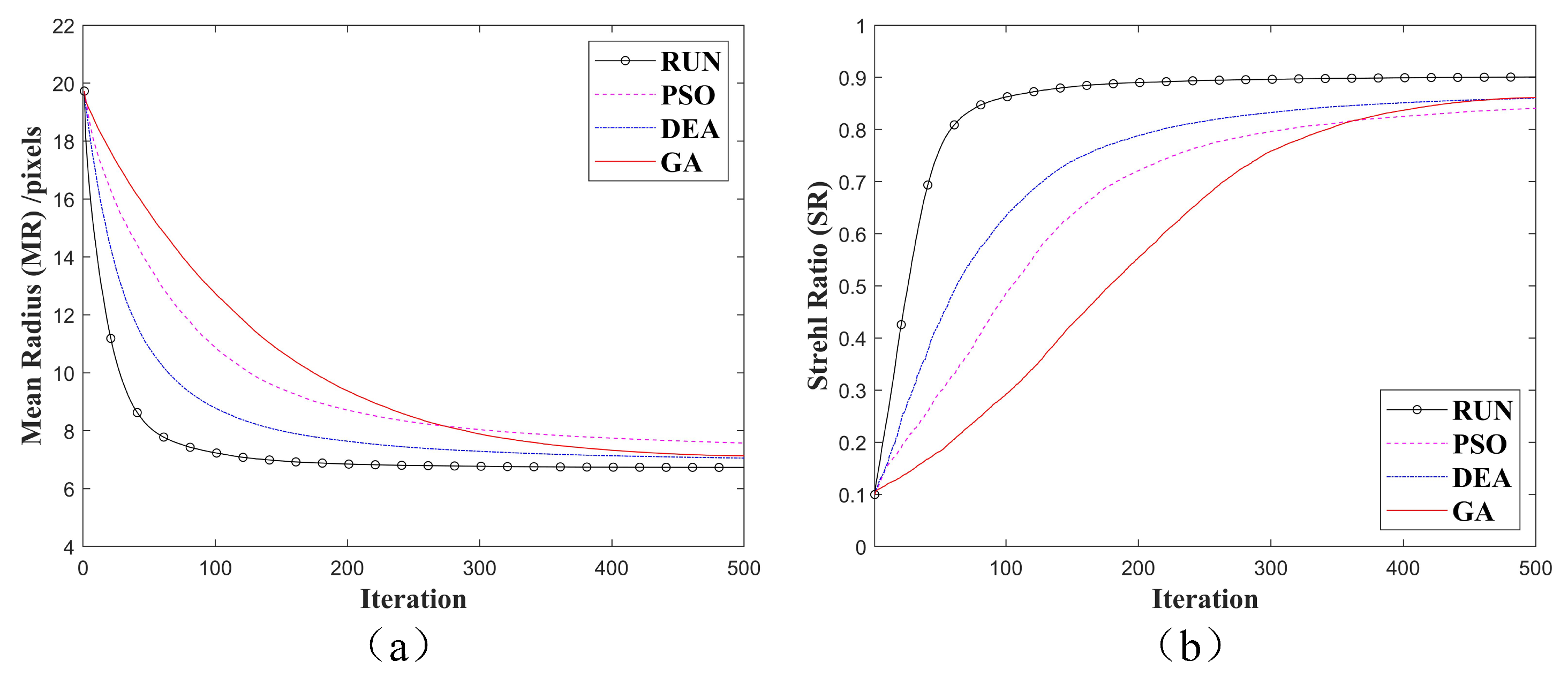
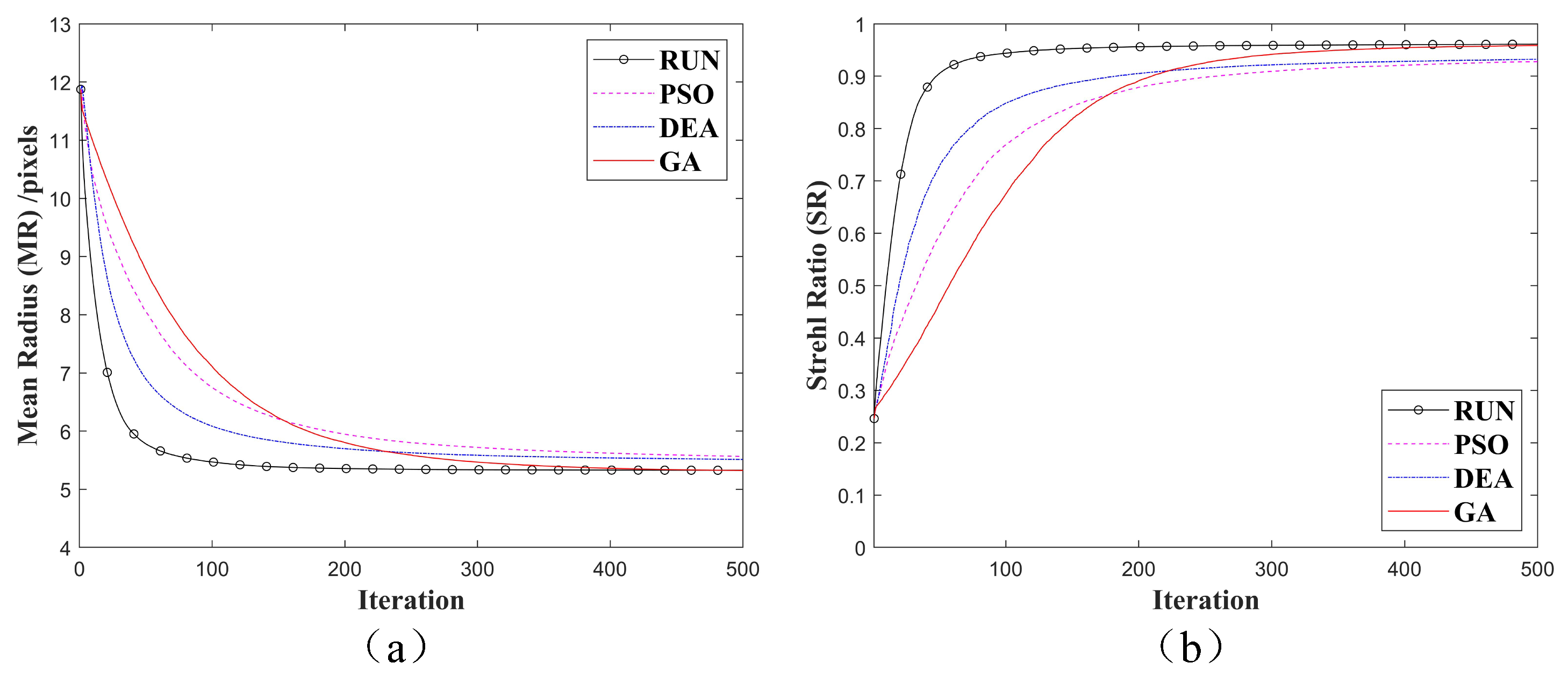
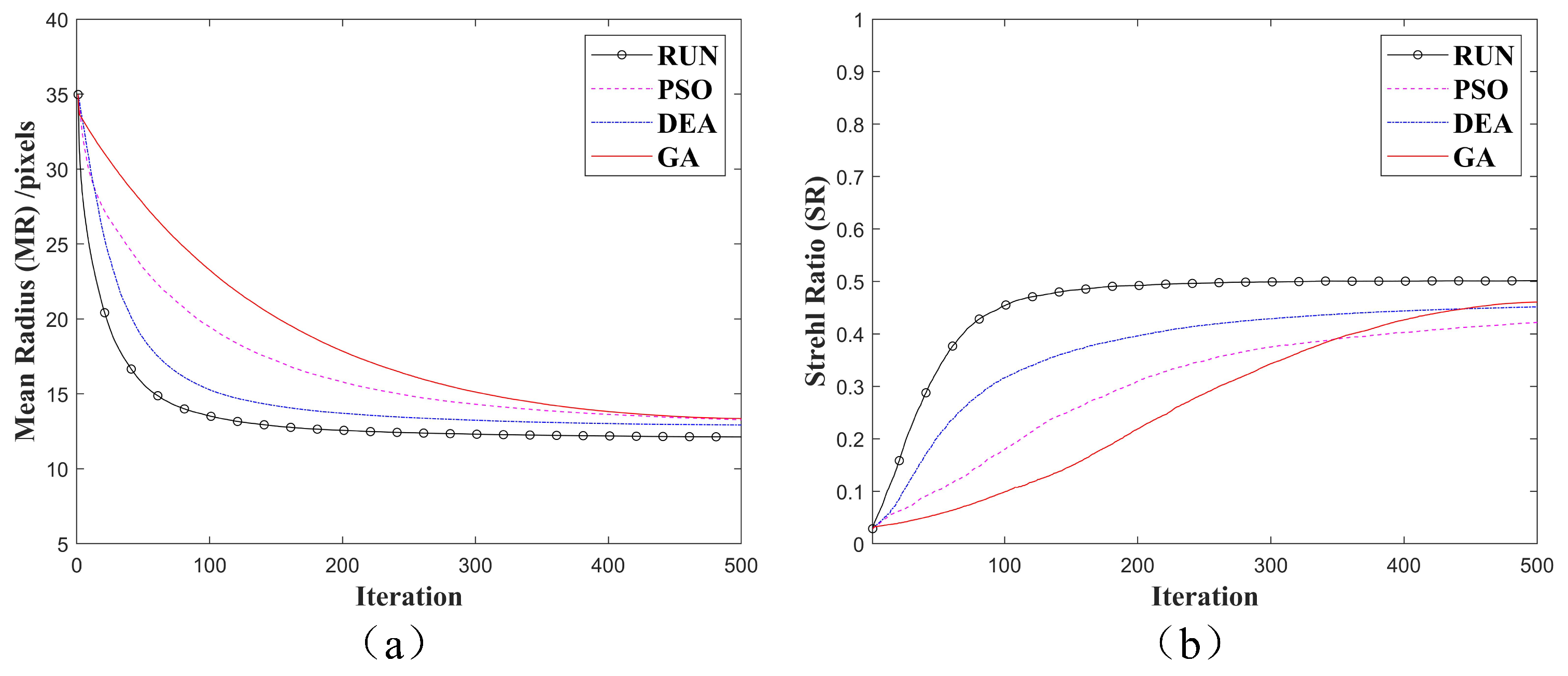
3.2. Simulated Results and Analysis
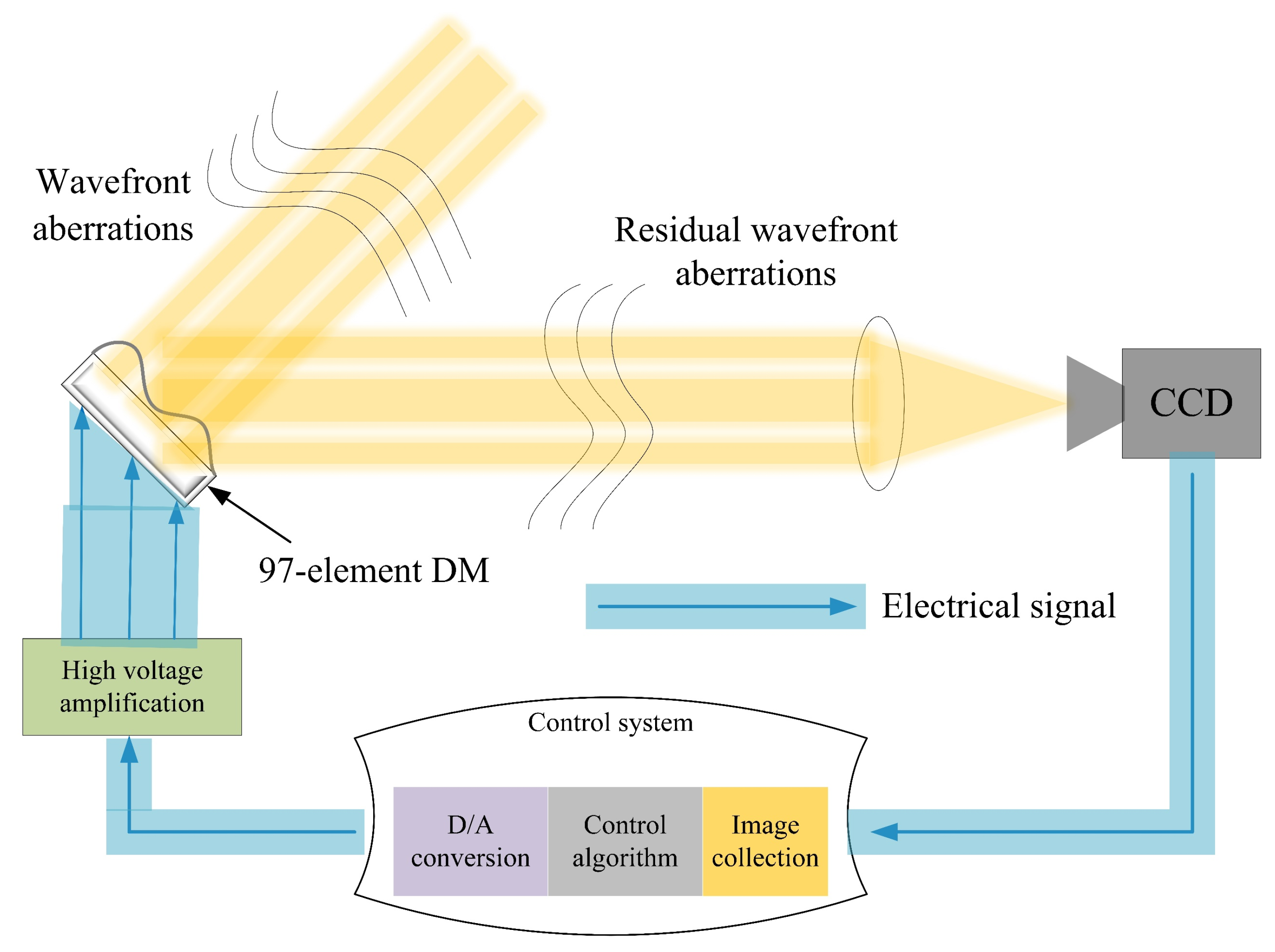
4. Physical Experiments and Results for Large Aberrations
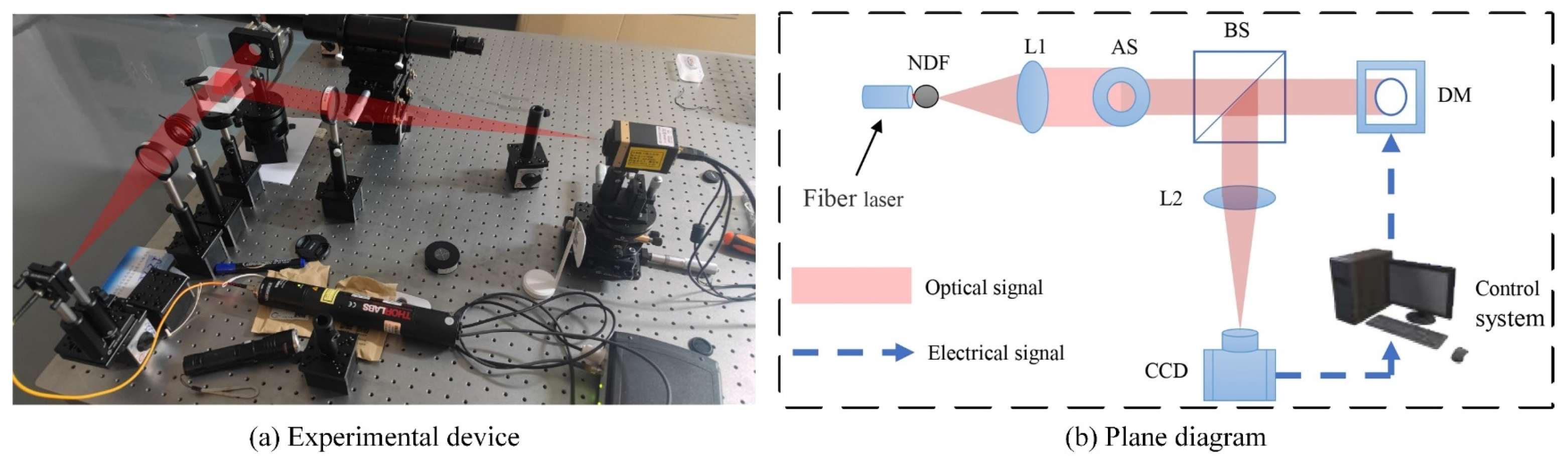
4.1. The Experimental System
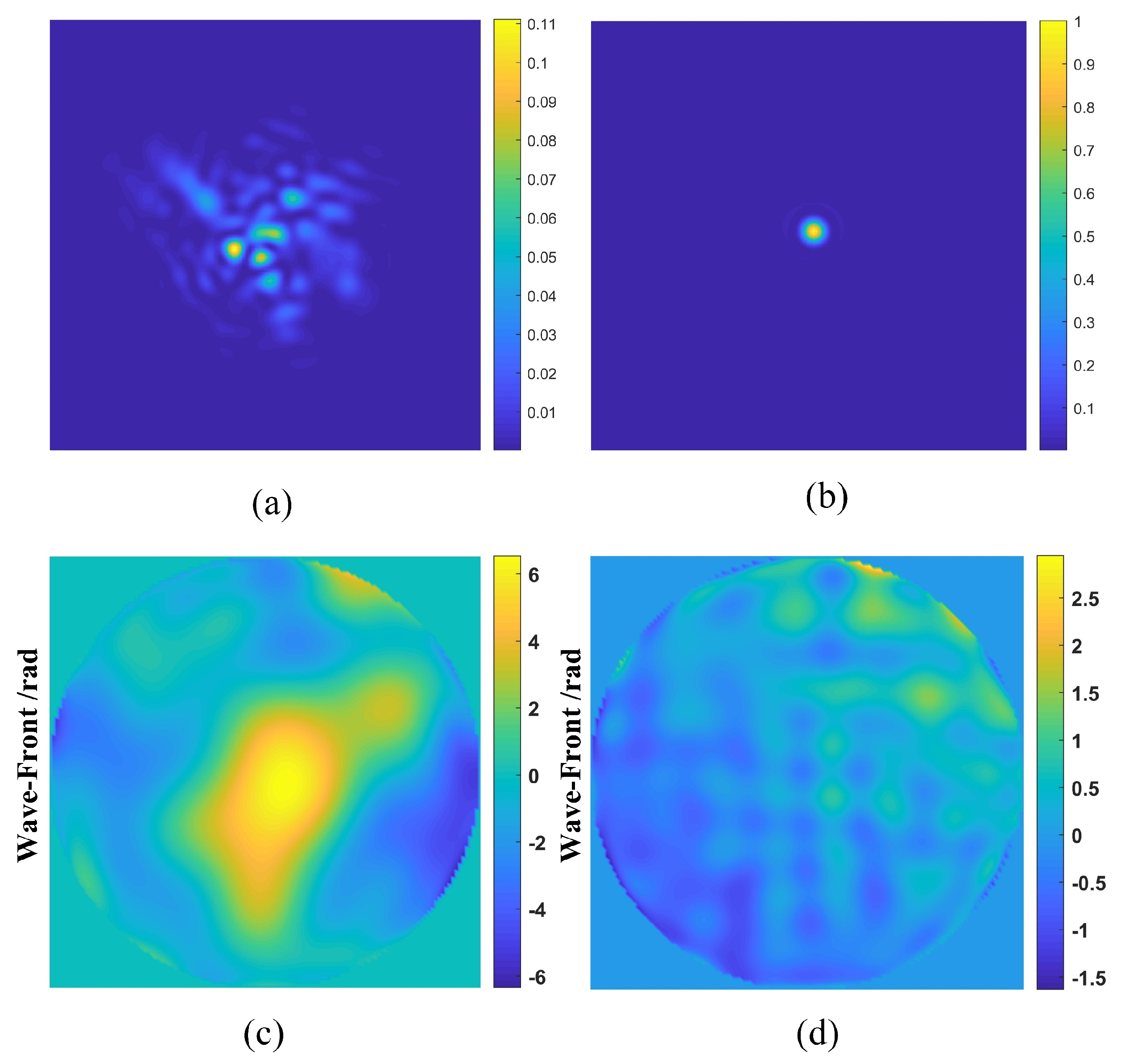
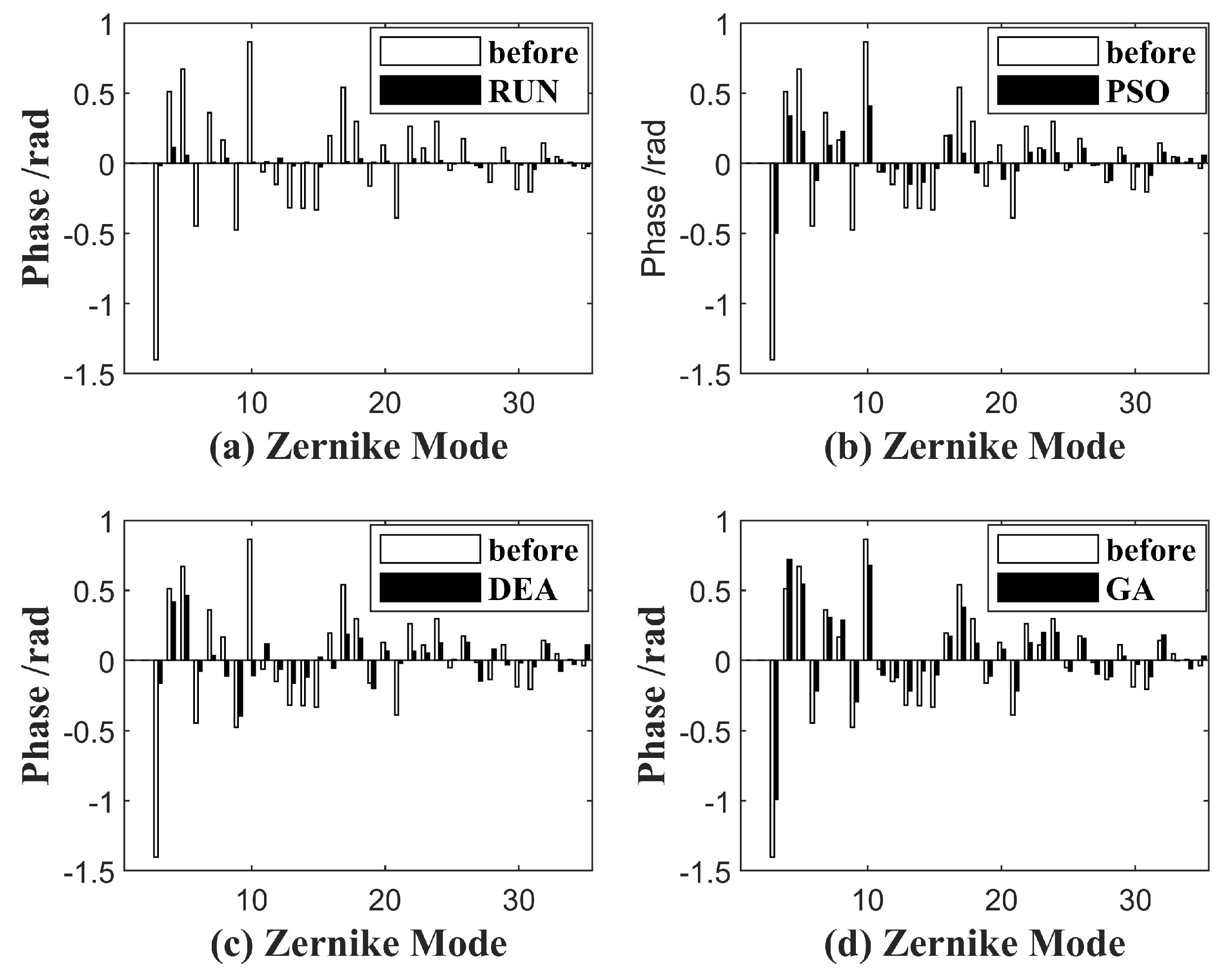
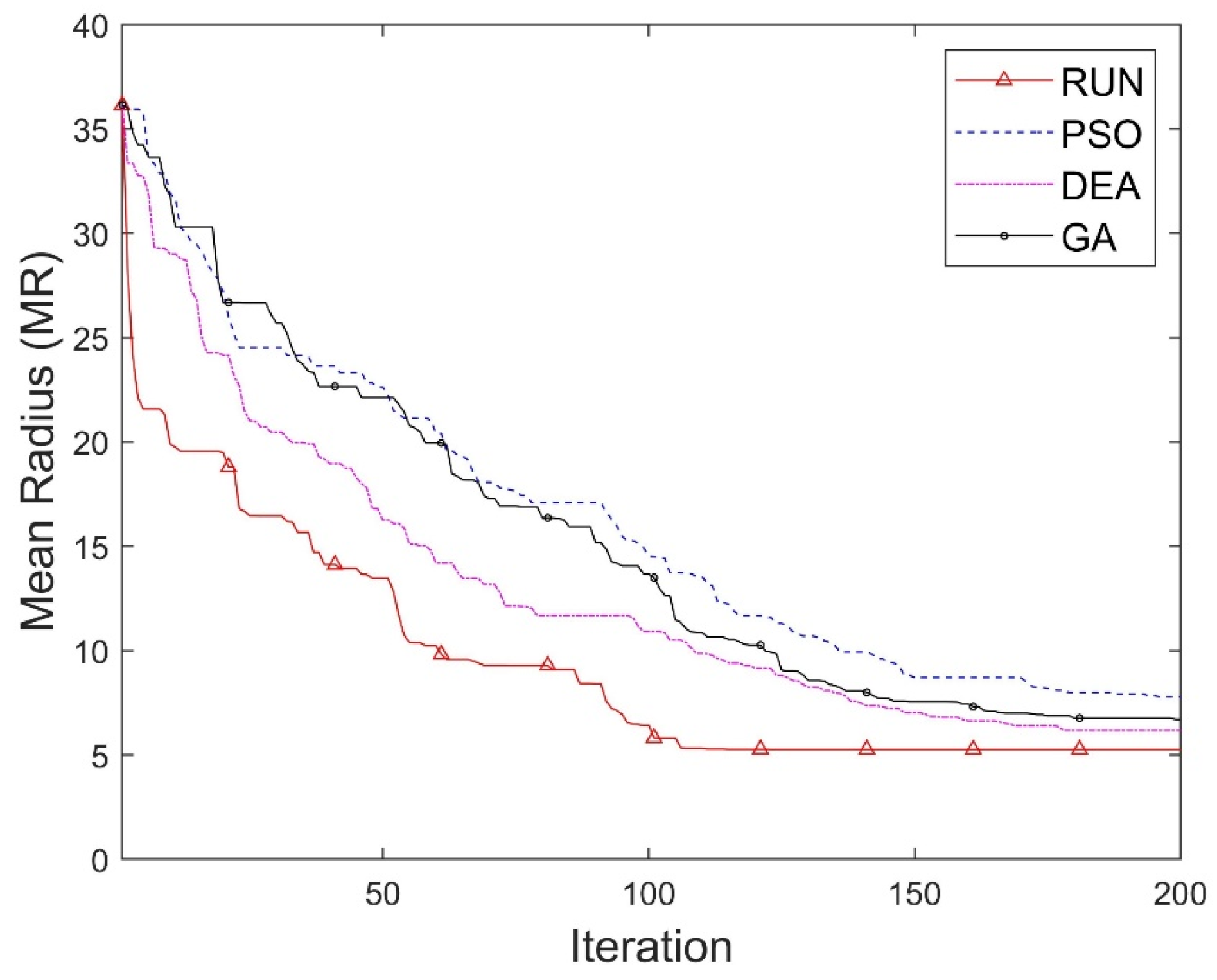
4.2. The Experimental Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tyson, R.K. Principles of Adaptive Optics, 3rd ed.; CRC Press Inc.: New York, NY, USA, 2010. [Google Scholar]
- Muller, R.A.; Buffington, A. Real-time correction of atmospherically degraded telescope images through image sharpening. J. Opt. Soc. Am. A 1974, 64, 1200–1210. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Carhart, G.W.; Cohen, M.; Cauwenberghs, G. Adaptive optics based on analog parallel stochastic optimization: Analysis and experimental demonstration. J. Opt. Soc. Am. A 2000, 17, 1440–1453. [Google Scholar] [CrossRef] [PubMed]
- Pasupathi, T.; Selvi, A.V.J. Real time experimental investigation of adaptive optics compensation technique for free space optical communication. Photonic Netw. Commun. 2022, 44, 102–115. [Google Scholar]
- Stotts, L.B.; Andrews, L.C. Adaptive optics model characterizing turbulence mitigation for free space optical communications link budgets. Opt. Express 2021, 29, 20307–20321. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Dong, B. Fast dynamic correction algorithm for model-based wavefront sensorless adaptive optics in extended objects imaging. Opt. Express 2021, 29, 27951–27960. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Xu, Q.; Wu, Y.; Yang, H.; Yang, H.; Zhou, Y. Extended Object Imaging Correction for Model-Based Wave front Sensorless Adaptive Optics System Under Noise. Chin. J. Lasers 2019, 46, 258–264. [Google Scholar]
- Poland, S.P.; Wright, A.J.; Girkin, J.M. Evaluation of fitness parameters used in an iterative approach to aberration correction in optical sectioning microscopy. Appl. Opt. 2008, 47, 731–736. [Google Scholar] [CrossRef]
- Yang, W.; Springer, M.; Strohaber, J.; Kolomenski, A.; Schuessler, H.; Kattawar, G.; Sokolov, A. Spectral phase retrieval from interferometric autocorrelation by a combination of graduated optimization and genetic algorithms. Opt. Express 2010, 18, 15028–15038. [Google Scholar] [CrossRef]
- Han, L.; Dai, Y.; Qiu, Y. Compensation for aberrant wavefront in UOWC based on adaptive optics technique employing genetic algorithm. Optik 2023, 281, 170832. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y. Particle Swarm Optimization for Control of Adaptive Optics System. AISS Adv. Inf. Sci. Serv. Sci. 2012, 4, 390–396. [Google Scholar]
- Tehrani, K.F.; Zhang, Y.; Shen, P.; Kner, P. Adaptive optics stochastic optical reconstruction microscopy (AO-STORM) by particle swarm optimization. Biomed. Opt. Express 2017, 8, 5087–5097. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Sui, X.; Zhou, S.; Chen, Q.; Gu, G.; Bai, H.; Li, W. A novel method of global optimisation for wavefront shaping based on the differential evolution algorithm. Opt. Commun. 2021, 481, 126541. [Google Scholar] [CrossRef]
- Chen, B.; Yang, H.; Li, X.; Jiang, W. Adaptive optics correction experiment based on stochastic parallel gradient descent algorithm. In Proceedings of the Fourth International Symposium on Precision Mechanical Measurements, Anhui, China, 25–29 August 2008; SPIE: Bellingham, WA, USA, 2008; Volume 7130, pp. 910–915. [Google Scholar]
- Xu, L.; Wang, J.; Yang, L.; Zhang, H. Design and Performance Analysis of NadamSPGD Algorithm for Sensor-Less Adaptive Optics in Coherent FSOC Systems. Photonics 2022, 9, 77. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, L.; Guo, Y.; Cao, J.; Liu, W.; Yang, L. Application of AdamSPGD algorithm to sensor-less adaptive optics in coherent free-space optical communication system. Opt. Express 2022, 30, 7477–7490. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Luo, Y.; Yang, H.; Su, H.; Liu, J. CoolMomentum-SPGD Algorithm for Wavefront Sensor-Less Adaptive Optics Systems. Photonics 2023, 10, 102. [Google Scholar] [CrossRef]
- Linhai, H.; Rao, C. Wavefront sensorless adaptive optics: A general model-based approach. Opt. Express 2011, 19, 371–379. [Google Scholar] [CrossRef]
- Lianghua, W.; Yang, P.; Shuai, W.; Wenjing, L.; Shanqiu, C.; Xu, B. A high speed model-based approach for wavefront sensorless adaptive optics systems. Opt. Laser Technol. 2018, 99, 124–132. [Google Scholar] [CrossRef]
- Ren, H.; Dong, B. Improved model-based wavefront sensorless adaptive optics for extended objects using N+ 2 images. Opt. Express 2020, 28, 14414–14427. [Google Scholar] [CrossRef]
- Liu, M.; Dong, B. Efficient wavefront sensorless adaptive optics based on large dynamic crosstalk-free holographic modal wavefront sensing. Opt. Express 2022, 30, 9088–9102. [Google Scholar] [CrossRef]
- Hu, K.; Xu, Z.; Yang, W.; Xu, B. Build the structure of wfsless ao system through deep reinforcement learning. IEEE Photonics Technol. Lett. 2018, 30, 2033–2036. [Google Scholar] [CrossRef]
- Landman, R.; Haffert, S.Y.; Radhakrishnan, V.M.; Keller, C.U. Self-optimizing adaptive optics control with reinforcement learning. In Proceedings of the Adaptive Optics Systems VII, Online, 14–18 December 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11448, pp. 842–856. [Google Scholar]
- Nousiainen, J.; Rajani, C.; Kasper, M.; Helin, T. Adaptive optics control using model-based reinforcement learning. Opt. Express 2021, 29, 15327–15344. [Google Scholar] [CrossRef] [PubMed]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Kutta, W. Beitrag zur näherungsweisen Integration totaler Differentialgleichungen. Z. Math. Phys. 1901, 46, 435–453. [Google Scholar]
- Runge, C. Über die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef]
- Gafar, M.; Ginidi, A.; El-Sehiemy, R.; Sarhan, S. Improved SNS algorithm with high exploitative strategy for dynamic combined heat and power dispatch in co-generation systems. Energy Rep. 2022, 8, 8857–8873. [Google Scholar] [CrossRef]
- Chen, H.; Ahmadianfar, I.; Liang, G.; Bakhsizadeh, H.; Azad, B.; Chu, X. A successful candidate strategy with Runge-Kutta optimization for multi-hydropower reservoir optimization. Expert Syst. Appl. 2022, 209, 118383. [Google Scholar] [CrossRef]
- Roddier, N.A. Atmospheric wavefront simulation using Zernike polynomials. Opt. Eng. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]
- Hardy, J.W. Adaptive optics for astronomical telescopes. Phys. Today 1998, 53, 69. [Google Scholar] [CrossRef]
- Jiang, W.; Ling, N.; Rao, X.; Shi, F. Fitting capability of deformable mirror. In Proceedings of the Active and Adaptive Optical Systems, San Diego, CA, USA, 21-21 July 1991; SPIE: Bellingham, WA, USA, 1991; Volume 1542, pp. 130–137. [Google Scholar]
- Piatrou, P.; Roggemann, M. Beaconless stochastic parallel gradient descent laser beam control: Numerical experiments. Appl. Opt. 2007, 46, 6831–6842. [Google Scholar] [CrossRef]




| RUN | PSO | DEA | GA | |
|---|---|---|---|---|
| The number of iterations | 34 | 150 | 80 | 202 |
| Time consumption (scaled) | 1 | |||
| Final convergence value of the MR |
| RUN | PSO | DEA | GA | |
|---|---|---|---|---|
| The number of iterations | 25 | 106 | 59 | 123 |
| Time consumption (scaled) | 1 | |||
| Final convergence value of the MR |
| RUN | PSO | DEA | GA | |
|---|---|---|---|---|
| The number of iterations | 40 | 164 | 72 | 234 |
| Time consumption (scaled) | 1 | |||
| Final convergence value of the MR |
| RUN | PSO | DEA | GA | |
|---|---|---|---|---|
| Number of iterations | 54 | 124 | 98 | 105 |
| Time consumption (scaled) | 1 | |||
| Final convergence value of the MR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zang, X.; Chen, P.; Hu, X.; Miao, Y.; Yan, Z.; Zhang, Z. An Efficient Method for Wavefront Aberration Correction Based on the RUN Optimizer. Photonics 2024, 11, 29. https://doi.org/10.3390/photonics11010029
Yang H, Zang X, Chen P, Hu X, Miao Y, Yan Z, Zhang Z. An Efficient Method for Wavefront Aberration Correction Based on the RUN Optimizer. Photonics. 2024; 11(1):29. https://doi.org/10.3390/photonics11010029
Chicago/Turabian StyleYang, Huizhen, Xiangdong Zang, Peng Chen, Xingliu Hu, Yongqiang Miao, Zhaojun Yan, and Zhiguang Zhang. 2024. "An Efficient Method for Wavefront Aberration Correction Based on the RUN Optimizer" Photonics 11, no. 1: 29. https://doi.org/10.3390/photonics11010029
APA StyleYang, H., Zang, X., Chen, P., Hu, X., Miao, Y., Yan, Z., & Zhang, Z. (2024). An Efficient Method for Wavefront Aberration Correction Based on the RUN Optimizer. Photonics, 11(1), 29. https://doi.org/10.3390/photonics11010029





