Multiplane Holographic Imaging Using the Spatial Light Modulator

Abstract

The optimization of imaging accuracy and speed is a crucial issue in the development of computer-generated holograms (CGH) for three-dimensional (3D) displays. This paper proposes an optimized iterative algorithm based on the angular spectrum method (ASM) to achieve high-quality holographic imaging across multiple planes. To effectively utilize spatial resources for multi-image reconstruction and mitigate the speckle noise caused by the overlapping of target images, constraint factors are introduced between different layers within the same region. The seeking rule of the constraint factor is also analyzed. By utilizing both constraint factors and variable factors, the presented method is able to calculate phase holograms for target figure imaging at four different planes. Simulation and experimental results demonstrate that the proposed method effectively improves the overall quality of the different planes, thus holding great potential for wide-ranging applications in the field of holography.

1. Introduction

Holographic display is a type of 3D display technology that has been extensively researched and developed [1,2,3,4,5]. This display technology utilizes wavefront information to reconstruct a 3D field [6]. In recent years, spatial light modulators (SLMs) have gained popularity as programmable devices for dynamic optical modulation. By recording the wavefront of a beam, holograms can store the amplitude and phase information of an object, thus accurately reproducing the intensity and depth of a 3D target [7,8,9,10]. Notably, CGHs have emerged as a promising approach for simulating and controlling optical processes in the context of electronic holography [11,12,13]. However, improper methods for generating phase holograms can result in the presence of severe speckle or ghosting artifacts during optical reconstructions. Therefore, enhancing the quality of phase hologram generation is of utmost importance in the development of holographic display technology.

Nowadays, the advancements in computer technology and digital encoders have made it possible to achieve the interference recording process in traditional holography through numerical calculations in a computer [14]. The rapid generation of high-precision computer-generated holograms (CGHs) is a crucial task in the development of holographic 3D displays. The recent developments in metal surfaces present opportunities for high-resolution spatial light modulators (SLMs) under subwavelength pixel sizes. The point-based method is one of the most developed methods used for generating CGHs of 3D scenes [15,16]. However, the calculation of holograms in this method is time-consuming, and sampling of the scene requires careful considerations. An improved generation method utilizes 2D planes to construct 3D objects instead of point clouds and is commonly referred to as the layer-based method, which is based on the fast Fourier transform (FFT) [17,18,19]. This method divides the three-dimensional object into multiple planes based on its depth. To expedite the computation, a prevalent strategy is to utilize layer-based algorithms based on Fresnel diffraction [20,21,22]. However, the Paraxial approximation involved in the technology based on Fresnel diffraction may cause a decline in the quality of optical reconstruction. Therefore, there is a need to further improve the efficiency and accuracy of CGH generation methods for holographic 3D displays.

To overcome the limitations of the paraxial approximation, Yan Zhao et al. proposed a layer-based CGH algorithm based on the angular spectrum [23]. This algorithm divides 3D complex scenes into multiple layers based on depth information and employs the ASM to simulate the optical propagation process from these parallel layers to the hologram, preserving accurate depth information without relying on the paraxial approximation. To improve the quality of reconstructed phase holograms, an iterative approach can be incorporated into the ASM [24,25,26]. This iterative process searches for and optimizes the phase profile of the hologram based on a specific target image, progressively refining the phase hologram to approximate the true phase information of the target image [27]. Nevertheless, when reconstructing multiple images or 3D objects in the axial direction, especially when they are occluded or overlapping, the reconstructed images may suffer from strong axial cross-talk noise. As the number of 3D objects increases, the speckle noise becomes more pronounced. Existing iterative methods do not adequately address this issue [28,29,30].

This article proposes an efficient calculation method for generating high-quality holograms based on ASM. This method optimizes the initial phase and re-expresses the complex amplitude using constraint factors and intelligent algorithms during the iteration process. The feasibility and effectiveness of this method were verified by numerical simulation and experimental imaging results. This method can improve the imaging accuracy of each plane when the target image is occluded, and solve the problem of low accuracy of the far layer image, which proves the application potential of this method in iterative reconstruction algorithms and 3D displays that require images of different depths in the same x–y plane.

2. Materials and Methods

The object function can be generated through the diffraction propagation of the hologram function. However, the determination of the hologram function requires compliance with three crucial constraints: consistency in the reconstruction strength of the hologram and the target object, a distribution of limited bandwidth, and a homogeneous strength distribution. It is important to note that the object phase only has a floating variable between the hologram plane and the object plane, represented by φ. Thus, the solution to the phase hologram can be transformed into the calculation of the phase that satisfies the constraint conditions φ.

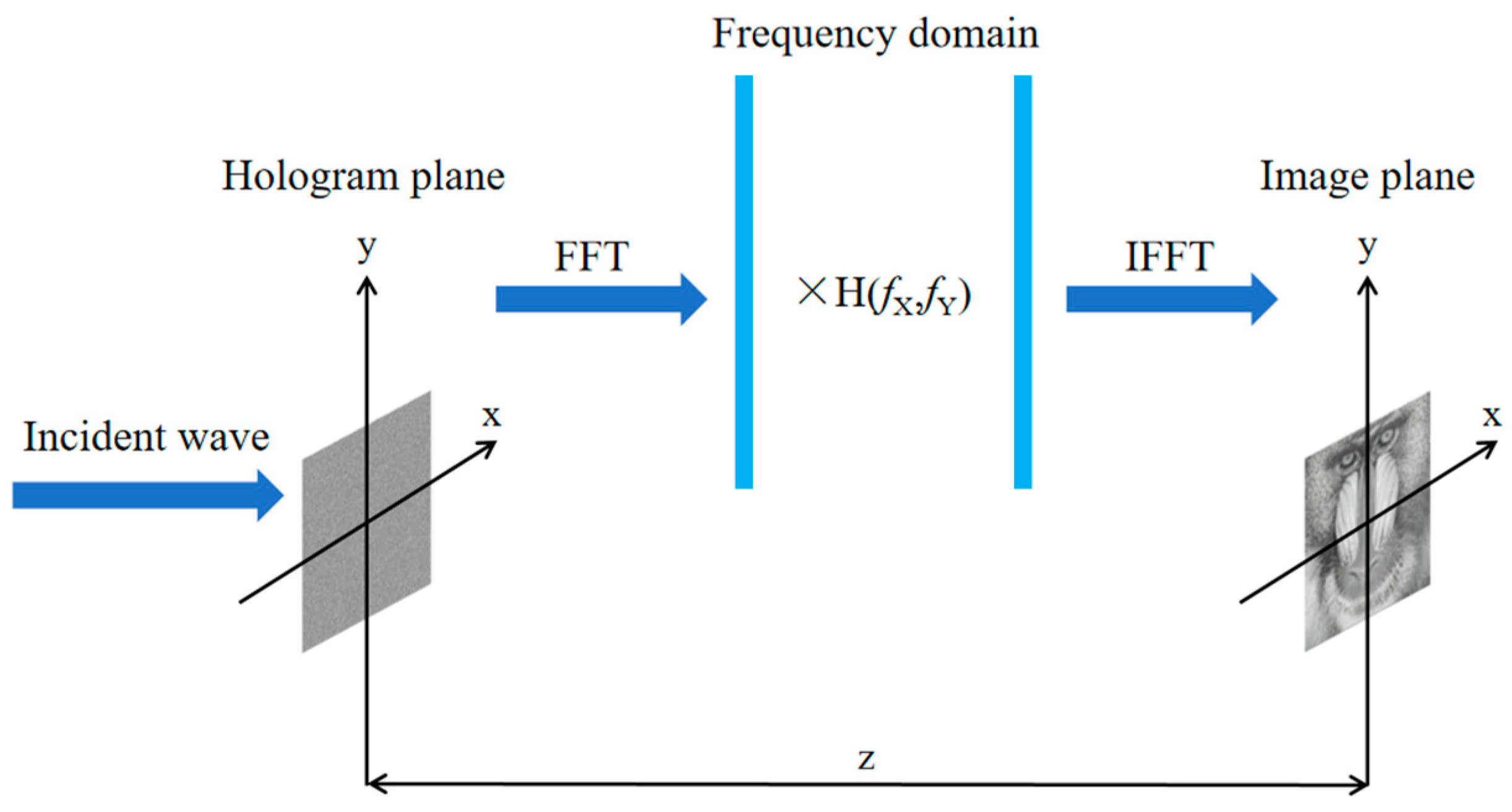
The angular spectrum theory is a frequency domain framework that utilizes the Fourier transform and inverse Fourier transform to compute the field distribution in a parallel plane at a distance (z) from the incidence plane, as shown in Figure 1. Unlike the point-by-point method, the angular spectrum layer-oriented method reduces computational complexity, and using Fourier transform instead of Fresnel diffraction can significantly improve the calculation speed. In Figure 1, FFT is the Fourier transform and IFFT is the inverse Fourier transform, and H(f_X, f_Y) is the angular spectrum transfer function.

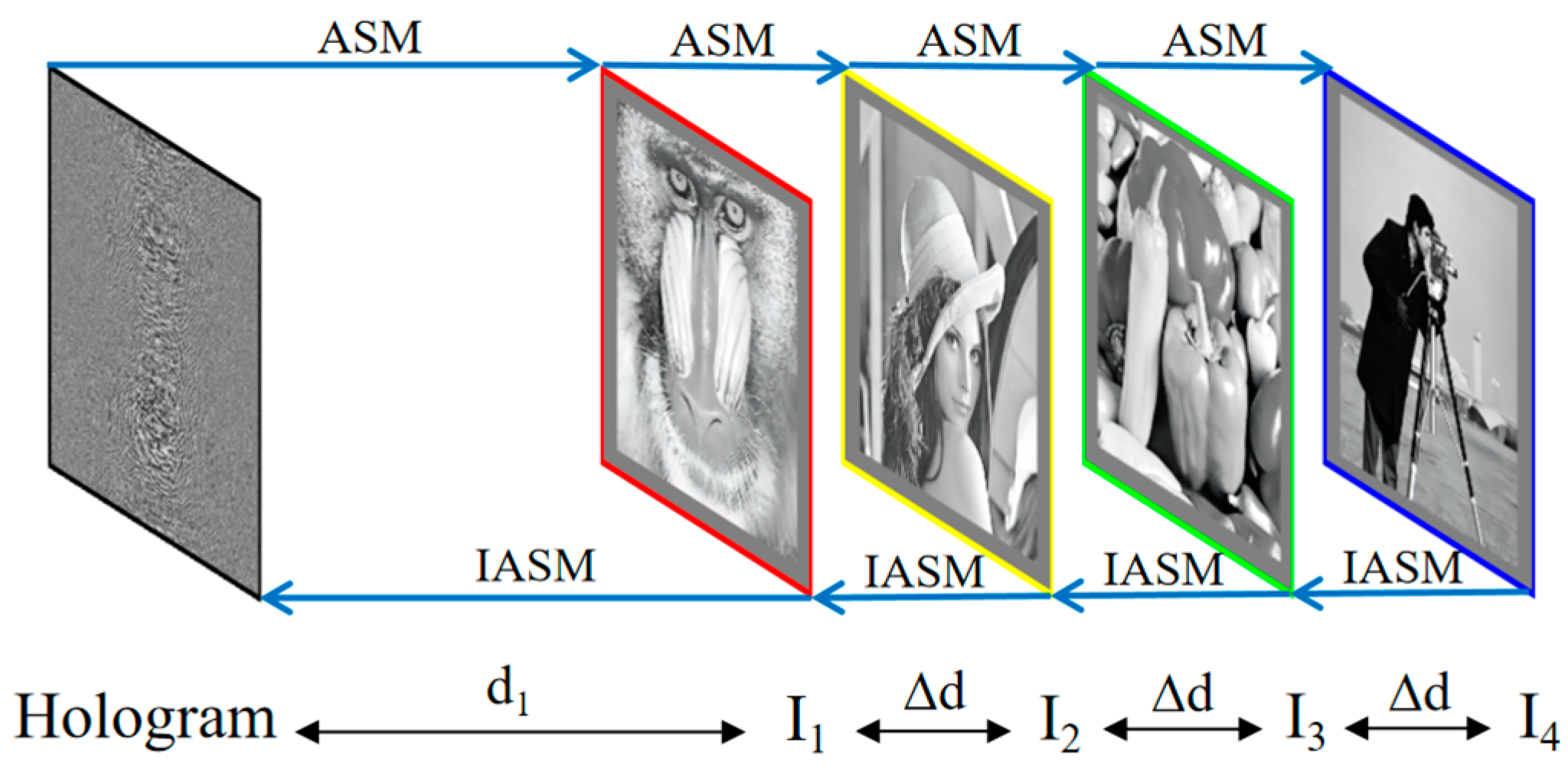
The sequential optimization method, which combines the ASM, is capable of calculating holograms with multiple planes comprising different distances. However, due to the in-depth order of hologram propagation, the accuracy of reconstructing an object layer situated farther away can be negatively impacted by the reconstruction error of an object layer closer to the hologram, leading to a decrease in the overall reconstructed image quality. As a result, the sequential optimization method exhibits superior reconstruction accuracy for the object layer closest to the hologram plane, while the accuracy of far layer planar reconstruction is relatively low. The algorithmic flowchart is presented in Figure 2, where IASM denotes the inverse angular spectrum method, and z represents the plane spacing.

When in the z = 0 plane, the complex amplitude U(x, y, 0) can be expressed as

$$U\left(x,y,0\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}A\left(f_X,f_Y,0\right)}}\exp \left[j2\pi \left(f_{X}x+f_{Y}y\right)\right]d{f}_{X}d{f}_Y$$

(1)

where f_X and f_Y are the spatial frequencies, A(f_X, f_Y, 0) is the spatial spectrum of the light wave, and the spatial spectrum of the plane can be obtained by the inverse Fourier transform of the complex amplitude U(x, y, 0)

$$A\left(f_X,f_Y,0\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}U\left(x,y,0\right)\exp \left[-j2\pi \left(f_{X}x+f_{Y}y\right)\right]dxdy}}$$

(2)

because the light wave will not change the shape of the wavefront in the process of propagation, but will produce a phase shift related to the propagation distance in the spatial spectrum, which is the transfer function in the light wave propagation phenomenon.

$$H\left(f_X,f_Y\right)=\{\begin{array}{l}\exp \left[jkz\sqrt{1-{\left(\lambda f_X\right)}^2-{\left(\lambda f_Y\right)}^2}\right],\sqrt{{\left(f_X\right)}^2+{\left(f_Y\right)}^2}<\frac{1}{\lambda }\\ 0,\mathrm{others}\end{array}$$

(3)

where k = 2π/λ is the wave number, and z is the transmission distance.

Therefore, when the light wave propagates to another plane with a distance of z, the spatial spectrum can be expressed as

$$A\left(f_X,f_Y,z\right)=A\left(f_X,f_Y,0\right)\cdot H\left(f_X,f_Y\right)$$

(4)

The resolution of the hologram is M × N and the calculation resolution of the diffraction field is Lu × Lv. The discrete form of the transfer function can be expressed as

$$H\left(f_X,f_Y\right)=\exp \left[jkz\sqrt{1-{\left(\lambda mx\right)}^2-{\left(\lambda ny\right)}^2}\right]$$

(5)

where x = 1/L_u, y = 1/L_v, m = −M/2, −M/2 + 1, …, M/2 − 1, n = −N/2, −N/2 + 1, …, N/2 − 1.

From Equation (5), the maximal value of f_X and f_Y can be expressed as

$$f_{X\max }=\frac{M}{2\lambda f},f_{Y\max }=\frac{N}{2\lambda f}$$

(6)

where f is the focal length of the Fourier lens.

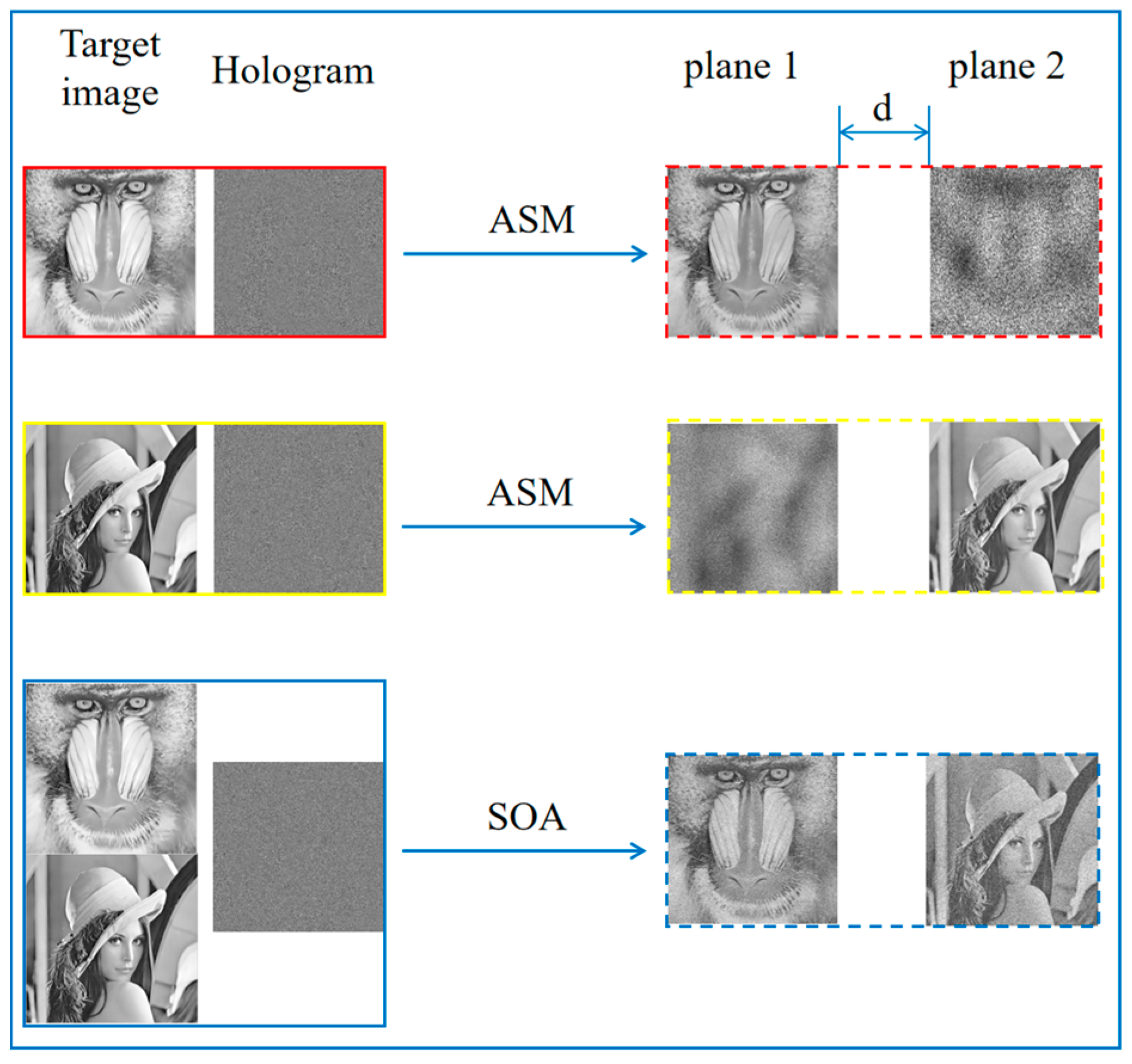
Figure 3 illustrates the relationship between the ASM and the sequential optimization algorithm (SOA). While a hologram generated by the ASM can produce a clear image at a specified distance, it may exhibit speckle noise at other distances. Therefore, each reconstruction plane generated by the sequential optimization algorithm can be affected by speckle noise from other planes, which highlights the need to minimize this impact. Selecting the most appropriate constraint factor for different reconstruction layers can significantly improve their reconstruction accuracy.

The ASM typically employs a random phase distribution as the initial phase, which cannot eliminate speckle noise in the final output. For improving the efficiency of the ASM, a band-limited initial phase form is introduced to reduce speckle noise, and it is represented as

$$\phi =c_1\cdot x^2+c_2\cdot y^2$$

(7)

where c₁ and c₂ are the phase parameters, x and y are pixel coordinates of the image plane. The parameters c₁ and c₂ impact the bandwidth of the band-limited initial phase. Therefore, selecting appropriate values for c₁ and c₂ is essential to ensure that the spectral width is as close as possible to the size of the hologram. Furthermore, its local spatial frequency can be expressed as

$$f_{\phi u}=\frac{1}{2\pi }\frac{\partial \phi }{\partial u}=\frac{c_{1}x}{\pi \mathsf{\Delta }u}$$

(8)

where Δu is the sampling interval in the image plane.

The maximal value of f_u and f_v can expressed as

$$f_{u\max }=\frac{a}{2\lambda f},f_{v\max }=\frac{b}{2\lambda f}$$

(9)

The highest spatial frequency in the reconstructed complex amplitude field along the u-direction is limited by the size of the hologram. From the perspective of light propagation from the edges of the hologram plane, the maximum spatial frequency is determined by the maximum angle θ of the incident light in the image plane. Due to the fact that light rays emitted from the hologram plane with an angle greater than θ with respect to the normal of the hologram plane cannot be effectively focused by the lens onto the image plane, the maximum spatial frequency is determined by the maximum incident angle. Under the paraxial approximation, the maximum incident angle θ is calculated as follows

$$\theta \approx \frac{a}{2f}$$

(10)

where a and b are the size of the SLM, λ is the wavelength, and f is the focal length of the Fourier lens. Therefore, the maximum spatial frequency of the quadratic phase can be expressed as

$$\mathsf{\Delta }u=\frac{1}{2f_{u\max }}=\frac{\lambda f}{M}$$

(11)

Reconstructed intensity distributions would have a larger bandwidth than reconstructed complex amplitude fields. Thus, the spatial frequency range of reconstructed intensity in u direction can be described as follows

$$f_{\phi u}\le 2f_{\phi u\max }=\frac{x}{\lambda f}$$

(12)

To ensure that the target image information can be extended across the entire hologram plane, it is necessary for the maximum spatial frequency of the band-limited initial phase to match that of the CGH. Therefore,

$$c_1=\frac{\pi }{M},c_2=\frac{\pi }{N}$$

(13)

In the sequential optimization method, the quality of the reconstructed image tends to decrease as the object layer gets farther from the holographic plane. This is primarily due to the reconstruction error of the object layer closest to the hologram, which becomes more pronounced as the number of planes increases. To mitigate this impact, a constraint factor is introduced to the reconstruction complex amplitude to constrain it using the current complex amplitude. During each iteration cycle, the new complex amplitude of each plane is replaced with a combination of the target amplitude, current amplitude, and current phase. This is mathematically expressed as

$$U_i\left(u,v\right)=a_i\left(u,v\right)\cdot \left(1-C\right)\cdot \exp \left(j{\phi }_i\left(u,v\right)\right)+C\cdot U_{io}\left(u,v\right)$$

(14)

where U_i(u, v) is the new complex amplitude of the ith plane, a_i(u, v) is the target amplitude of the ith plane, C is the constraint factor, U_io(u, v) is the complex amplitude after the propagation of the previous plane angular spectrum, and φ_i(u, v) is the phase of the previous plane after angular spectrum propagation.

The constraint factor C is used to regulate the influence of the amplitude of other planes on the overall strength distribution. By setting C to 0, the method is reverted back to the standard ASM. However, by selecting different values for C, the impact of distance-induced lower precision on the far plane can be effectively mitigated. This is achieved by constraining the amplitude distribution of each plane to the amplitude distribution of the previous plane, using the current complex amplitude as a reference. The algorithmic flowchart for this process is presented in Figure 4.

The selection of the constraint factor C is important to ensure imaging accuracy. In previous multi-plane imaging algorithms, the constraint factor in iterative algorithms was usually a fixed value, and its magnitude could be determined through multiple simulations. In order to further improve the reconstruction quality and the low accuracy of the far layer plane, different constraint factors are selected for each plane, as shown in Equation (15).

$$U_i\left(u,v\right)=a_i\left(u,v\right)\cdot \left(1-C_k\right)\cdot \exp \left(j{\phi }_i\left(u,v\right)\right)+C_k\cdot U_{io}\left(u,v\right)$$

(15)

where C_k is the constraint factor for each ASM and IASM plane.

Intelligent algorithms, such as the genetic algorithm, can be used as powerful tools to solve the problem of optimizing the selection of constraint factors in the sequential optimization algorithm. In this study, we employed a genetic algorithm to iteratively optimize the selection of constraint factors. Specifically, the constraint factors in the ASM and IASM are treated as unknown variables, while the plane spacing is held constant. Through numerous iterations, the optimal constraint factor and distance value with the highest correlation coefficient can be identified. By utilizing this approach, we significantly reduce the iteration time required to generate holograms through intelligent algorithms.

The structural similarity Index measure (SSIM) is a common method to evaluate the quality of the reconstructed image [31], and it is expressed as

$$\mathrm{SSIM}=\frac{\left(2{\mu }_t{\mu }_r+c_1\right)\cdot \left(2{\sigma }_{t,r}+c_2\right)}{\left({\mu }_t{}^2+{\mu }_r{}^2+c_1\right)\cdot \left({\sigma }_t{}^2+{\sigma }_r{}^2+c_2\right)}$$

(16)

where µ_t and µr are the mean values of the target and reconstructed images, respectively. σ_t and σ_r are the standard deviations of the target and reconstructed images, respectively. σ_t,r is the covariance between the target image and the reconstructed image, c₁ and c₂ are positive constants used to avoid the null denominator. The higher the SSIM, the stronger the correlation between the target image and the reconstructed image will be.

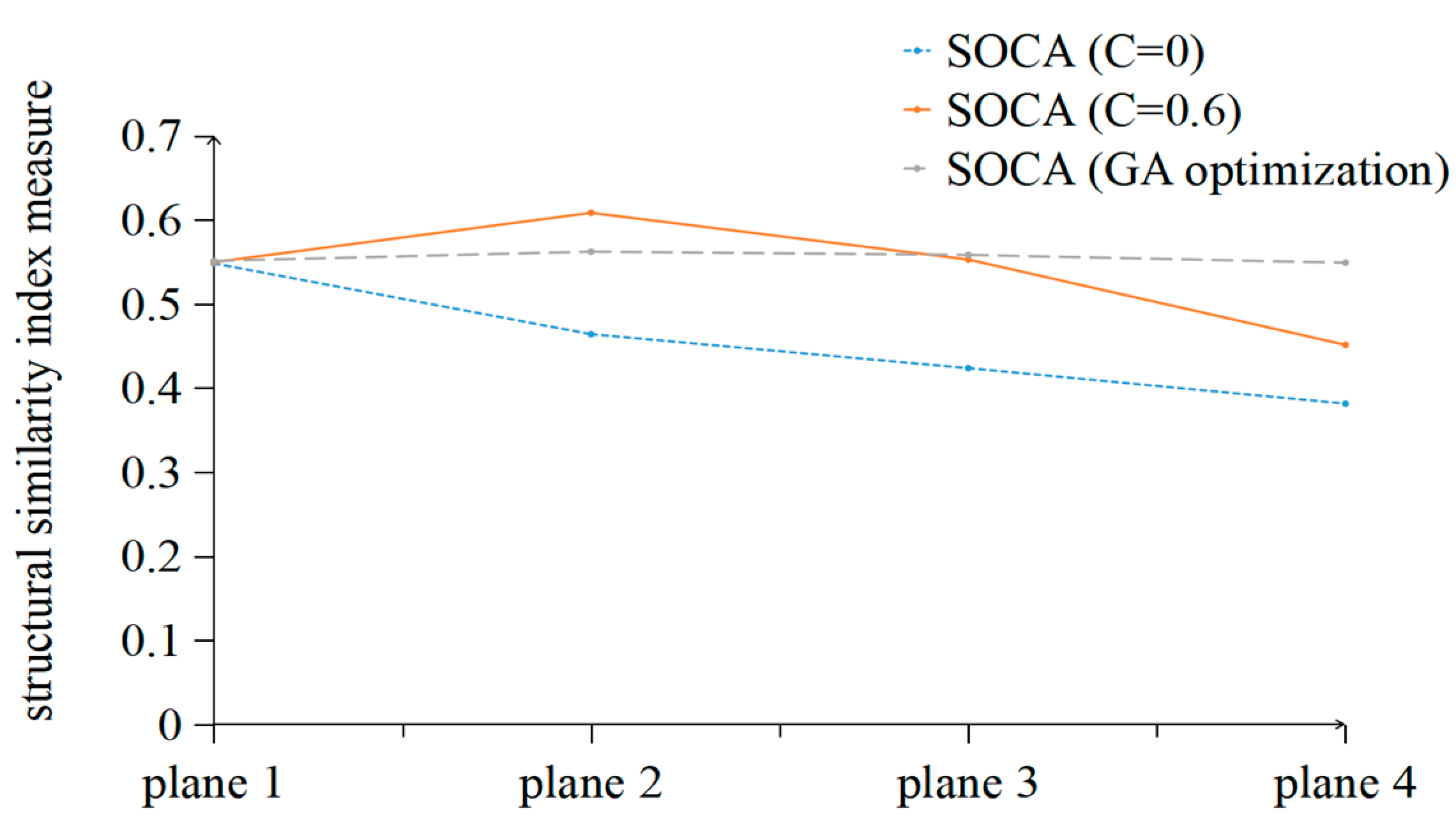
To solve the problem of low accuracy in the far layer plane, we need to find the minimum value P_i of SSIM for all planes, as shown in Equation (14). A genetic algorithm is used to optimize all constraint factors to find the maximum value of P_i. The MATLAB Genetic Algorithm Toolbox is utilized to efficiently compute appropriate values for the constraint factors. The algorithm outlined in this study defines the fitness function as the process of calculating the SSIM value, with the variables set as C1 to C7 representing the seven constraint factors within the range of 0 to 1. The remaining parameters are set to the default values of the genetic algorithm parameters. As a result, the constraint factor values (C1–C7) corresponding to the maximum SSIM value are determined. It should be noted that similar experimental results can be obtained by employing other intelligent algorithms. At this time, the reconstruction accuracy distribution of all planes is relatively uniform, significantly improving the problem of low accuracy in the far layer plane.

$$P_i=\min \left(SSI{M}_i\right)$$

(17)

The amplitude distribution of the diffracted light wave field on a plane parallel to the z = 0 plane and at a distance of z can be obtained by performing an inverse Fourier transform of the complex amplitude space spectrum of the z-plane. By utilizing the angular spectrum algorithm without paraxial approximation, the quality of optical reconstructions can be significantly improved compared to conventional paraxial approximation methods. However, in simulations, the circular discrete FFT-based convolution can introduce errors in the diffraction field and the optical reconstruction due to an inadequate sampling interval selection. To address this issue, the sampling interval of the reconstruction field can be reduced. This will correctly describe speckles and artefacts in the reconstruction field in the simulation by generating a hologram using the zero-padding technique. The quality of the reconstructed image can be reduced due to the clipping operation. To avoid numerical circular convolution and zero-padding, we employ the intermediate ASM to reduce the computation time by utilizing an optical Fourier transform instead of a numerical FFT, which enables obtaining the complete hologram in the optical domain. The specific procedure involves extracting the phase component from the complex amplitude obtained from the first FFT and loading it onto the SLM. A Fourier lens is utilized in place of numerical IFFT computation to generate the hologram.

3. Results

3.1. Simulation Results with Constraint Factor C

To validate the feasibility of the proposed methodology, both numerical simulations and optical experiments were performed. The simulation part was implemented using MATLAB, where the SLM had a pixel spacing of ∆x and ∆y = 8.0 μm. The incident light had a wavelength of 632.8 nm, and the input image resolution was 1000 × 1000 pixels. The iterative process was repeated for 10 iterations. The initial phase coefficients c₁ and c₂ were set to 0.00314 to ensure bandwidth limitation.

Figure 5 and Figure 6 depict the simulation diagrams of SSIM under different constraint factors, where the same constraint factor is selected for each plane. The first-floor plane is located at a distance of 0.4 m from the SLM, and the distance between the planes is 0.1 m. Adding a constraint factor can decrease the imaging accuracy of the first-layer plane, but can improve the imaging accuracy of other planes. When the constraint factor is set to 0, this corresponds to the traditional sequential optimization method. As the constraint factor is increased from 0 to 0.6, the SSIM of all three planes, except the first plane, is improved. However, when the constraint factor exceeds 0.6, the SSIM of all planes decreases. Through extensive simulation analysis, it has been found that using the complex amplitude of the current plane to constrain the reconstruction amplitude can enhance the reconstruction quality of other planes, except the first plane. However, the accuracy of the distal plane is still low, which is due to the uniform selection of constraint factors for each reconstruction layer. To improve the accuracy of the reconstructed image on the distant plane, it is necessary to set different constraint factors. Therefore, more suitable optimization methods are required to enhance image accuracy in distant reconstruction layers.

3.2. Simulation Results with Variable Factors C

The results shown in Figure 5 and Figure 6 demonstrate that the use of constraint factors can improve imaging quality. However, the issue of poor imaging quality in the far plane remains unresolved. To address this, we attempted to select different constraint factors for each plane. To quickly identify suitable constraint factors, we utilized intelligent algorithms such as genetic algorithms to optimize the constraint factors. After several iterations, the simulation results are presented in Figure 7 and Figure 8. It can be observed that the addition of constraint factors to the reconstruction complex amplitude and the use of intelligent algorithms to optimize it can improve the reconstruction quality of each plane, and ensure that each plane has the same reconstruction quality. Specifically, C1 represents the constraint factor for the angular spectrum propagation between the first and second planes, and so on, following this pattern for subsequent planes.

3.3. Experimental Results

The schematic diagram of the experimental setup is shown in Figure 9. The laser beam from a picosecond laser amplifier (beam diameter: D = 2.5 mm, wavelength: λ = 632 nm, pulse duration: t_p = 10 ps, and repetition rate: f_r = 100 kHz) passed through a polarization splitting prism, an attenuator, two mirrors, and a half-wave plate, and was then reflected by the SLM (Hamamatsu X13138-02, Shizuoka, Japan) with a 10° angle of incidence. Two positive lenses (focal length: f₁ = 300 mm, f₂ = 150 mm) formed a 4f imaging system. A CCD camera was used to observe the diffraction patterns. The distance (d) from the first plane to the imaging plane is 0.4 m, and the spacing between planes is 0.1 m.

In the experiment, holograms were loaded onto the SLM, and the resulting images captured by the CCD camera are presented in Figure 10. We calculated the SSIM by comparing it with the single plane imaging experimental image generated by the ASM. Although there may be discrepancies between the experimental and simulation results due to factors such as the experimental optical path, laser beam error, and human error, these results still confirm the validity of the proposed theory. The experimental results presented in Figure 10 show that the sequential optimization with constraint factors has better reconstruction quality. Moreover, the optimized constraint factor ensures that the complex amplitude constraint has the most suitable effect, resulting in well-reconstructed images in the far layer. Additionally, the introduction of the band-limited quadratic phase can effectively reduce speckle noise. The experimental results demonstrate that the proposed method can effectively improve the overall quality of the four different planes.

4. Conclusions and Discussion

This paper presents a novel approach for multi-plane holographic imaging which can overcome the limitations of traditional methods. The proposed method can significantly improve imaging quality and reduce speckle noise by applying the constraint factors and a band-limited quadratic phase function. Moreover, using an intelligent genetic algorithm can obtain better results by optimizing the constraint factors. Four-plane holographic imaging simulations and experiments were carried out, and the results show that the proposed method can effectively improve the overall quality of the different planes, and it is expected to be widely used in the field of holography.

The proposed optimized iterative algorithm based on the ASM holds great potential for practical applications in multi-plane holographic imaging. This method is significant in achieving high-quality holographic imaging and has broad application prospects in fields such as 3D display technology, virtual reality, and augmented reality. By improving reconstruction quality and reducing speckle noise, this algorithm provides an effective solution for holographic imaging that is more realistic and closer to the real visual experience. Moreover, this method can be applied to various fields such as medical imaging, industrial testing, and optical information processing, providing support for high-precision imaging and data analysis. Further research and optimization of this algorithm are expected to lead to more efficient and accurate holographic imaging technology, bringing innovation and progress to practical applications.

Future research efforts can be focused on addressing the limitations of the proposed method and further improving and optimizing the layered CGH algorithm based on angular spectrum propagation. More efficient iterative methods can be explored to enhance reconstruction quality and reduce speckle noise. Furthermore, the combination of other 3D reconstruction techniques and image processing methods can be investigated to further improve the reconstruction and imaging performance of 3D objects. In practical applications, the design and optimization of imaging systems can be considered to achieve higher-quality 3D display effects. This includes the selection of appropriate light sources, the design of optical elements, and the optimization of hologram loading and display techniques. Overall, there is a significant potential for future research to enhance the performance and practical applicability of the proposed method.