Robust Topological Edge States in C6 Photonic Crystals
Abstract
:1. Introduction
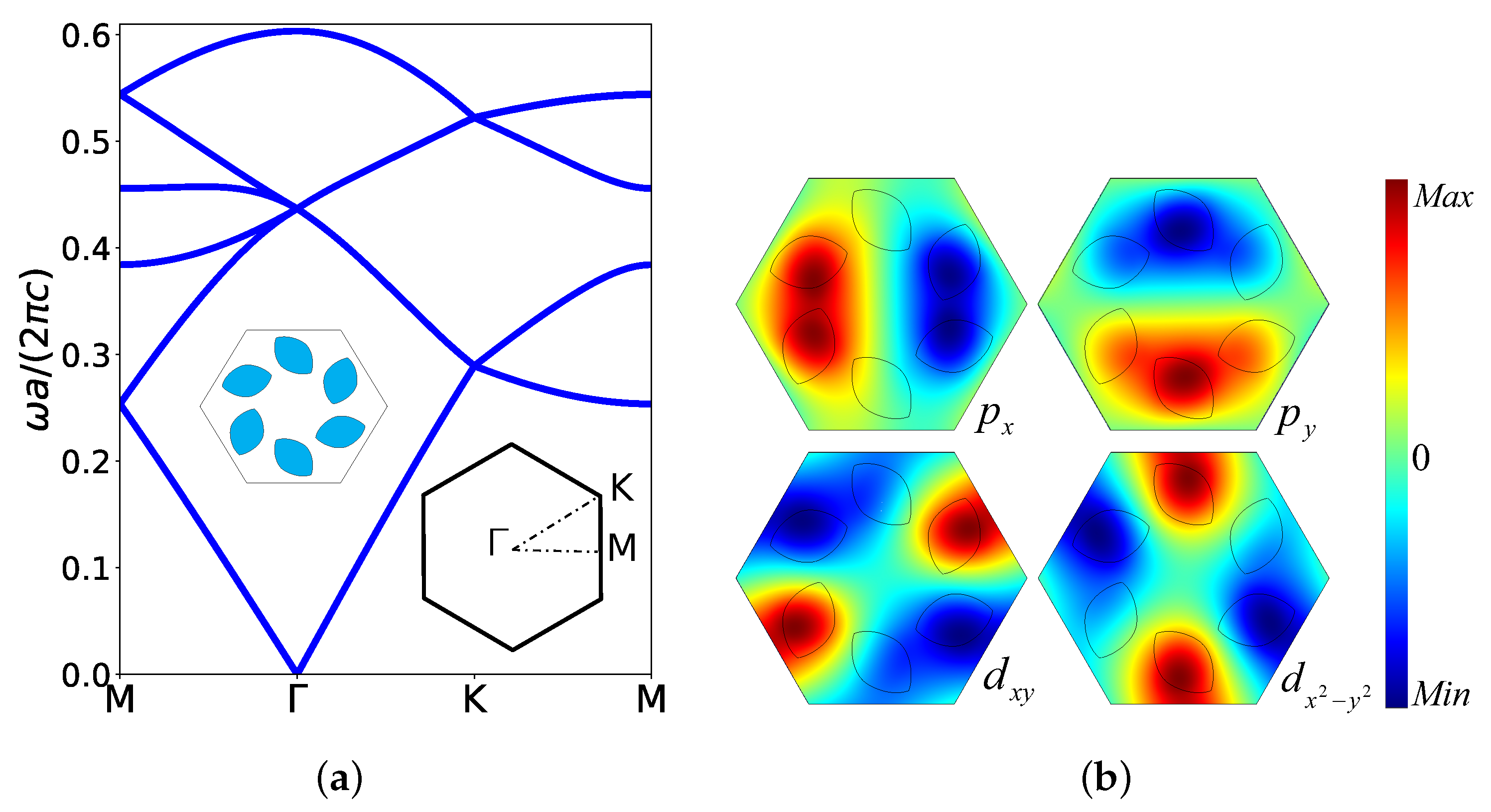
2. The Photonic System
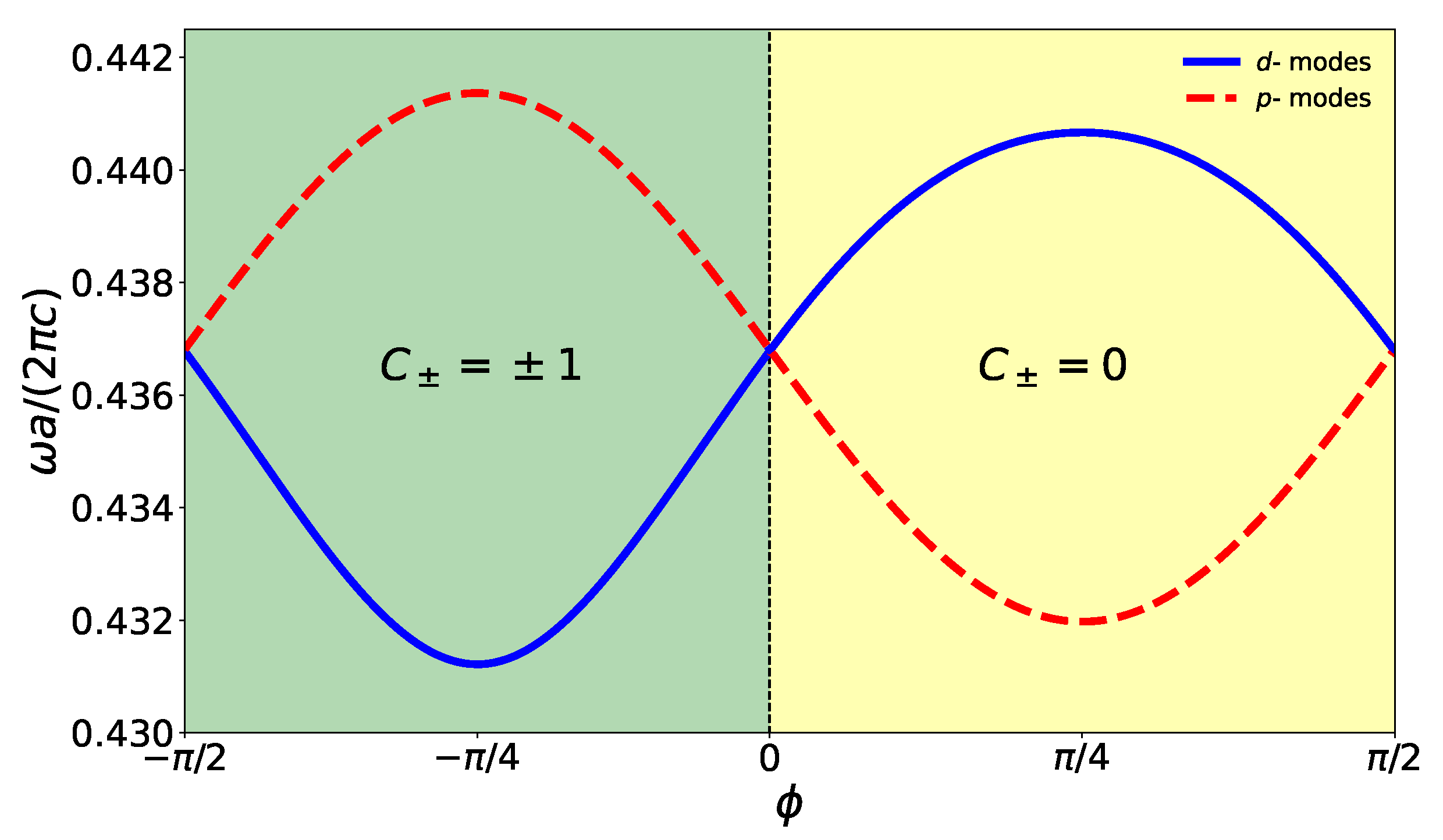
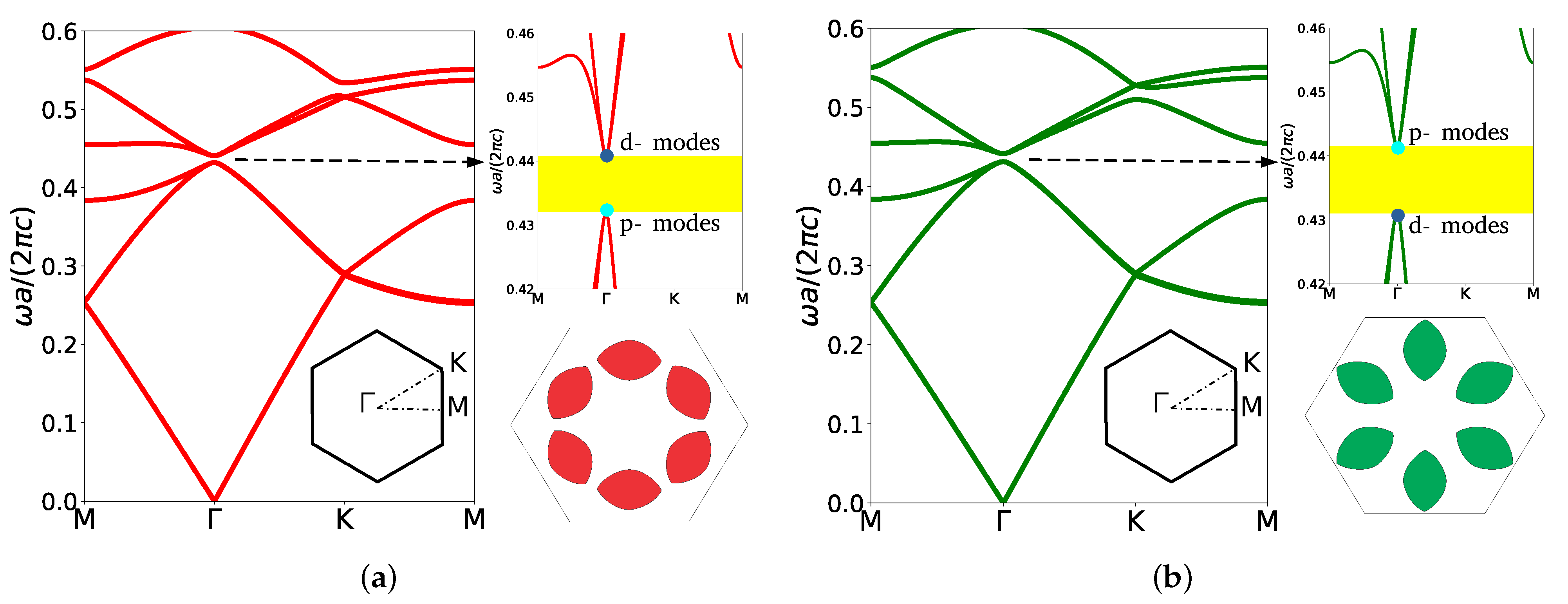
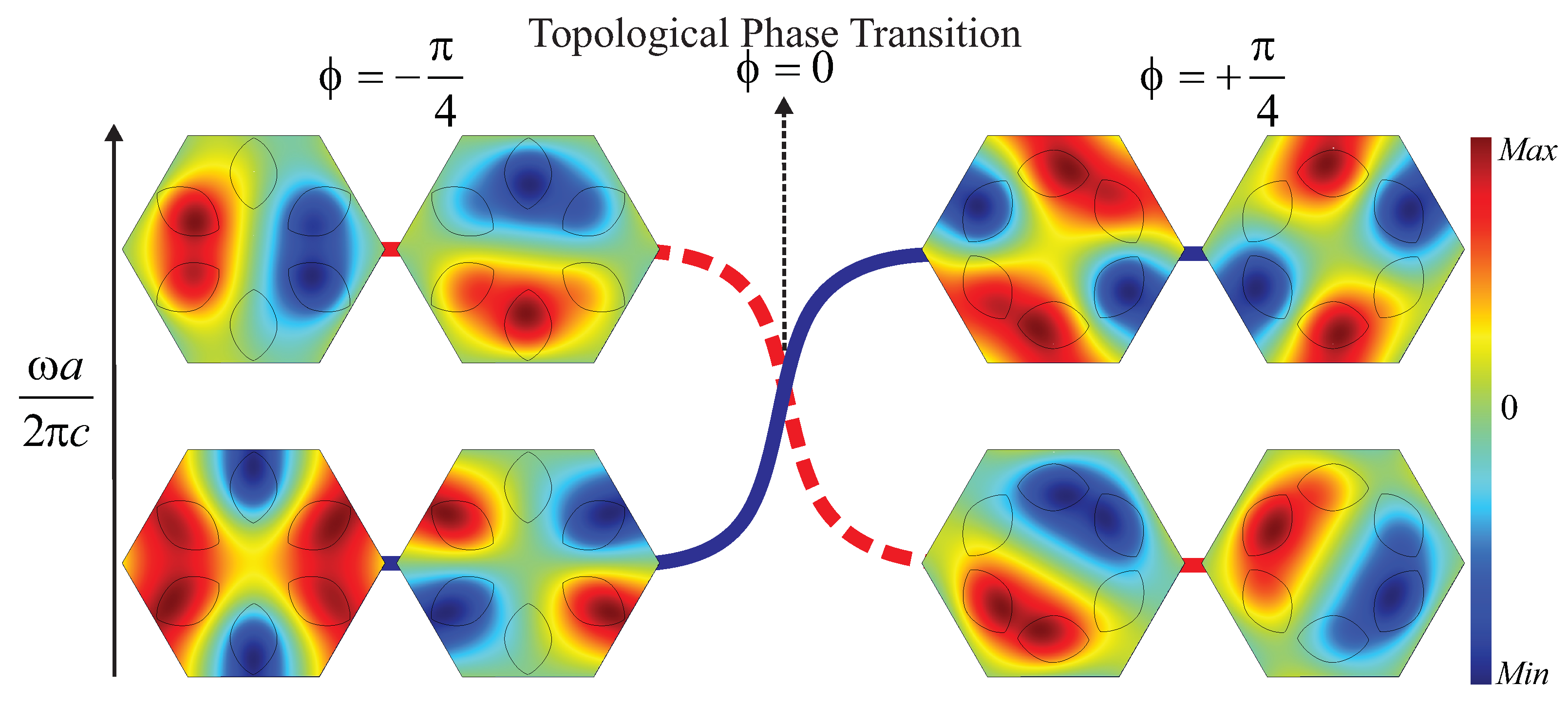
3. Topological Phase Transition
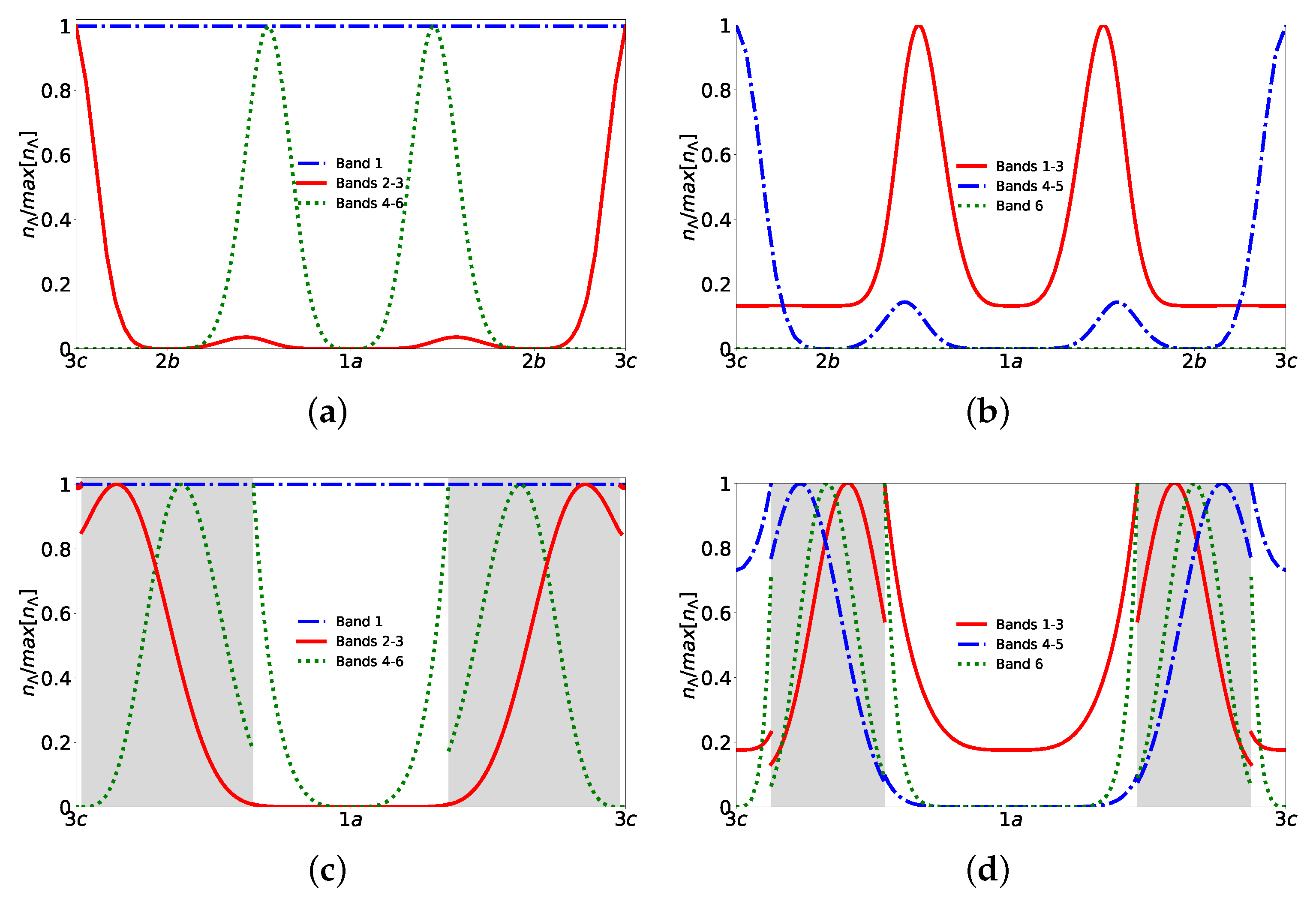
4. Edge States
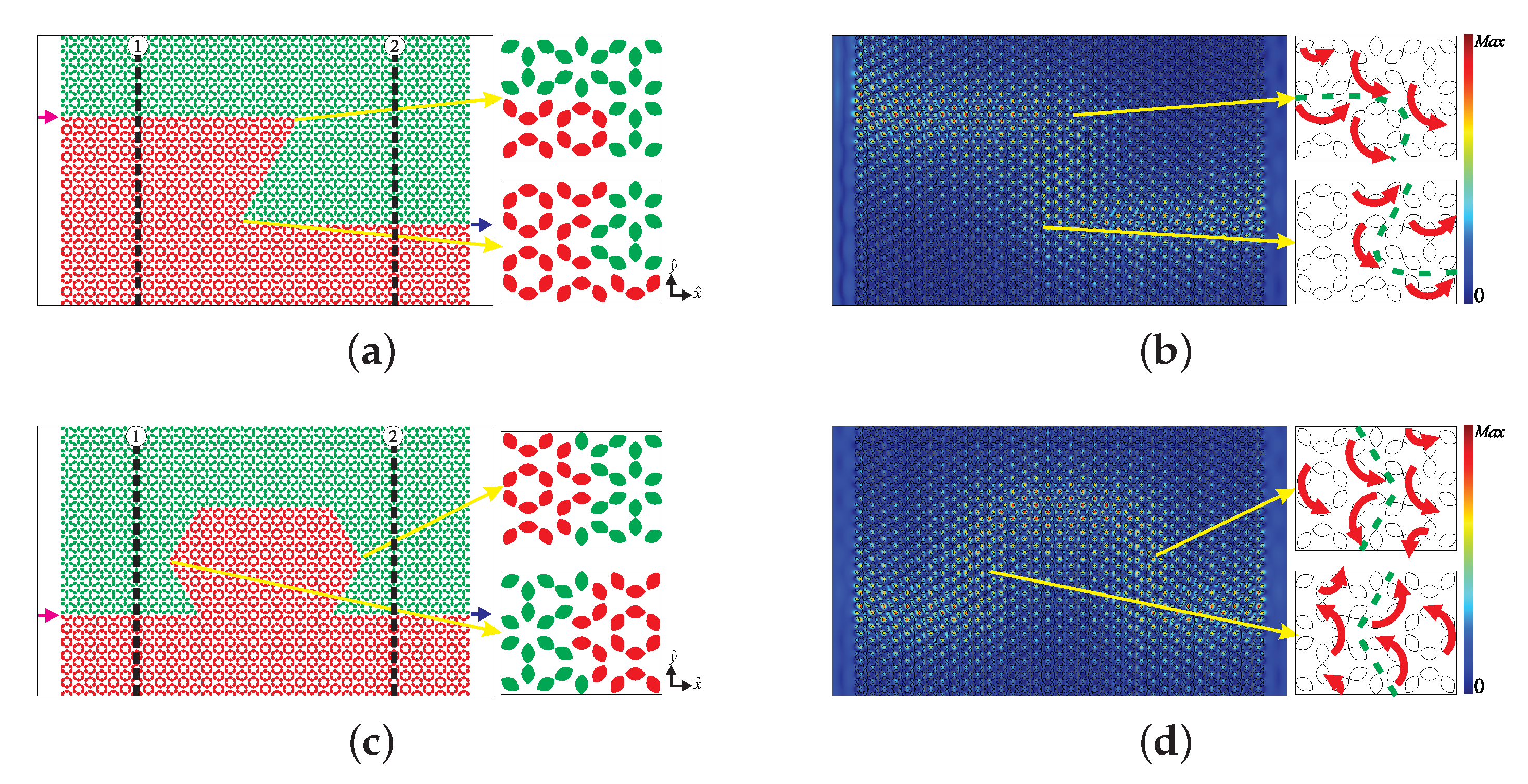
5. Robustness of the Edge States
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 978-0-691-12456-8. [Google Scholar]
- Yang, Z.; Lustig, E.; Lumer, Y.; Segev, M. Photonic Floquet topological insulators in a fractal lattice. Light Sci. Appl. 2020, 9, 128. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.-Y.; Wang, H.-F.; Zhu, X.-Y.; Lu, M.-H.; Wang, Z.D.; Chen, Y.-F. Photonics meets topology. Opt. Express 2018, 26, 24531. [Google Scholar] [CrossRef] [PubMed]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef]
- Liu, F.; Deng, H.-Y.; Wakabayashi, K. Topological photonic crystals with zero Berry curvature. Phys. Rev. B 2018, 97, 035442. [Google Scholar] [CrossRef]
- Dong, J.-W.; Chen, X.-D.; Zhu, H.; Wang, Y.; Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 2017, 16, 298. [Google Scholar] [CrossRef]
- Xie, B.-Y.; Wang, H.-F.; Wang, H.-X.; Zhu, X.-Y.; Jiang, J.-H.; Lu, M.-H.; Chen, Y.-F. Second-order photonic topological insulator with corner states. Phys. Rev. B 2018, 98, 205147. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Yuan, H.; Zhong, J.; Lu, C. Universal numerical calculation method for the Berry curvature and Chern numbers of typical topological photonic crystals. Front. Optoelectron. 2020, 13, 73. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Zhang, X. Tunable topological valley transport in two-dimensional photonic crystals. New J. Phys. 2019, 21, 093020. [Google Scholar] [CrossRef]
- Wu, S.; Jiang, B.; Liu, Y.; Jiang, J.-H. All-dielectric photonic crystal with unconventional higher-order topology. Photon. Res. 2021, 9, 668. [Google Scholar] [CrossRef]
- Wong, S.; Saba, M.; Hess, O.; Oh, S.S. Gapless unidirectional photonic transport using all-dielectric kagome lattices. Phys. Rev. Res. 2020, 2, 012011(R). [Google Scholar] [CrossRef]
- Mittal, S.; Orre, V.V.; Leykam, D.; Chong, Y.D.; Hafezi, M. Photonic Anomalous Quantum Hall Effect. Phys. Rev. Lett. 2019, 123, 043201. [Google Scholar] [CrossRef] [PubMed]
- Jahani, D.; Ghatar, A.; Abaspour, L.; Jahani, T. Photonic Hall effect. J. Appl. Phys. 2018, 124, 043104. [Google Scholar] [CrossRef]
- Xie, B.; Su, G.; Wang, H.-F.; Liu, F.; Hu, L.; Yu, S.-Y.; Zhan, P.; Lu, M.-H.; Wang, Z.; Chen, Y.-F. Higher-order quantum spin Hall effect in a photonic crystal. Nat. Commun. 2020, 11, 3768. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.-D.; Deng, W.-M.; Shi, F.-L.; Zhao, F.-L.; Chen, M.; Dong, J.-W. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys. Rev. Lett. 2019, 122, 233902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, Y.; Lin, Z.-K.; Qin, P.; Chen, Q.; Gao, F.; Li, E.; Jiang, J.-H.; Zhang, B.; Chen, H. Higher-Order Topological States in Surface-Wave Photonic Crystals. Adv. Sci. 2020, 7, 1902724. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, X.; Gong, Q. Reconfigurable topological states in valley photonic crystals. Phys. Rev. Mater. 2018, 2, 122201(R). [Google Scholar] [CrossRef]
- Chen, M.L.N.; Jiang, L.J.; Lan, Z.; Sha, W.E.I. Coexistence of pseudospin- and valley-Hall-like edge states in a photonic crystal with C3v symmetry. Phys. Rev. Res. 2020, 2, 043148. [Google Scholar] [CrossRef]
- Kim, M.; Kim, Y.; Rho, J. Spin-valley locked topological edge states in a staggered chiral photonic crystal. New J. Phys. 2020, 22, 113022. [Google Scholar] [CrossRef]
- Bleu, O.; Solnyshkov, D.D.; Malpuech, G. Quantum valley Hall effect and perfect valley filter based on photonic analogs of transitional metal dichalcogenides. Phys. Rev. B 2017, 95, 235431. [Google Scholar] [CrossRef]
- Wang, X.-X.; Guo, Z.; Song, J.; Jiang, H.; Chen, H.; Hu, X. Unique Huygens-Fresnel electromagnetic transportation of chiral Dirac wavelet in topological photonic crystal. Nat. Commun. 2023, 17, 3040. [Google Scholar] [CrossRef]
- Ruan, B.; Gao, E.; Li, M.; Chang, X.; Zhang, Z.; Li, H. Tunable Fano resonance and optical switching in the one-dimensional topological photonic crystal with graphene. J. Appl. Phys. 2023, 133, 213101. [Google Scholar] [CrossRef]
- Sharifi, M.; Rezaei, B.; Pashaei Adl, H.; Zakerhamidi, M.S. Tunable Fano resonance in coupled topological one-dimensional photonic crystal heterostructure and defective photonic crystal. J. Appl. Phys. 2023, 133, 083102. [Google Scholar] [CrossRef]
- Xi, X.; Yan, B.; Yang, L.; Meng, Y.; Zhu, Z.-X.; Chen, J.-M.; Wang, Z.; Zhou, P.; Shum, P.P.; Yang, Y.; et al. Topological antichiral surface states in a magnetic Weyl photonic crystal. Nat. Commun. 2023, 14, 1991. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lan, Z.; Zhu, J.; Su, Z. Creating anisotropic topological phases within inversely designed photonic crystals. Opt. Laser Technol. 2023, 158, 108865. [Google Scholar] [CrossRef]
- Ota, Y.; Katsumi, R.; Watanabe, K.; Iwamoto, S.; Arakawa, Y. Topological photonic crystal nanocavity laser. Commun. Phys. 2018, 1, 86. [Google Scholar] [CrossRef]
- Tang, G.-J.; He, X.-T.; Shi, F.-L.; Liu, J.-W.; Chen, X.-D.; Dong, J.-W. Topological photonic crystals: Physics, designs, and applications. Laser Photon. Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Hauff, N.V.; Le Jeannic, H.; Lodahl, P.; Hughes, S.; Rotenberg, N. Chiral quantum optics in broken-symmetry and topological photonic crystal waveguides. Phys. Rev. Res. 2022, 4, 023082. [Google Scholar] [CrossRef]
- Jin, M.-C.; Gao, Y.-F.; Huang, G.-Y.; He, Y.-H.; Sun, J.-P.; Song, H. Manipulation of coupling between waveguide and ring resonator in topological photonic crystals. Phys. E 2022, 136, 115013. [Google Scholar] [CrossRef]
- Nussbaum, E.; Sauer, E.; Hughes, S. Inverse design of broadband and lossless topological photonic crystal waveguide modes. Opt. Lett. 2021, 46, 1732. [Google Scholar] [CrossRef]
- Tang, G.; Huang, Y.; Chen, J.; Li, Z.-Y.; Liang, W. A Topological Multichannel Add-Drop Filter Based on Gyromagnetic Photonic Crystals. Nanomaterials 2023, 13, 1711. [Google Scholar] [CrossRef]
- Tang, G.; Huang, Y.; Chen, J.; Li, Z.-Y.; Liang, W. Controllable one-way add-drop filter based on magneto-optical photonic crystal with ring resonator and microcavities. Opt. Express 2022, 30, 28762. [Google Scholar] [CrossRef] [PubMed]
- Shafagh, S.G.; Kaatuzian, H.; Danaie, M. Ahighly sensitive tunable filter using hybrid 1-D photonic crystal and plasmonic MIM waveguide. J. Opt. 2021, 228, 166174. [Google Scholar] [CrossRef]
- Wang, X.-X.; Hu, X. Reconfigurable topological waveguide based on honeycomb lattice of dielectric cuboids. Nanophotonics 2020, 9, 3451. [Google Scholar] [CrossRef]
- Wu, L.-H.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Dai, H.; Liu, T.; Jiao, J.; Xia, B.; Yu, D. Double Dirac cone in two-dimensional phononic crystals beyond circular cells. J. Appl. Phys. 2017, 121, 135105. [Google Scholar] [CrossRef]
- Hajivandi, J.; Pakarzadeh, H.; Kurt, H. Intensity tuning of the edge states in the imperfect topological waveguides based on the photonic crystals with the C3 point group symmetry. Opt. Quantum Electron. 2021, 53, 102. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photon. 2017, 11, 763. [Google Scholar] [CrossRef]
- Sauer, E.; Vasco, J.P.; Hughes, S. Theory of intrinsic propagation losses in topological edge states of planar photonic crystals. Phys. Rev. Res. 2020, 2, 043109. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photon. 2014, 8, 821. [Google Scholar] [CrossRef]
- Arregui, G.; Gomis-Bresco, J.; Sotomayor-Torres, C.M.; Garcia, P.D. Quantifying the robustness of topological slow light. Phys. Rev. Lett. 2021, 126, 027403. [Google Scholar] [CrossRef]
- Huang, H.; Huo, S.; Chen, J. Reconfigurable topological phases in two-dimensional dielectric photonic crystals. Crystals 2019, 9, 221. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter, 1st ed.; Springer: Berlin, Germany, 2007; ISBN 978-3-540-32897-1. [Google Scholar]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.-X.; Jiang, J.-H.; Hu, X.; Hang, Z.H. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef] [PubMed]
- Mead, C.A. Molecular Kramers degeneracy and non-Abelian adiabatic phase factors. Phys. Rev. Lett. 1987, 59, 161. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.-C.; He, C.; Liu, X.-P.; Zou, Y.; Lu, M.-H.; Hu, X.; Chen, Y.-F. Photonic topological states in a two-dimensional gyrotropic photonic crystal. Crystals 2019, 9, 137. [Google Scholar] [CrossRef]
- Fu, L. Topological Crystalline Insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef]
- Lu, L.; Fang, C.; Fu, L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Symmetry-protected topological photonic crystal in three dimensions. Nat. Phys. 2016, 12, 337. [Google Scholar] [CrossRef]
- COMSOL Multiphysics v.6.0. COMSOL AB, Stockholm, Sweden. Available online: www.comsol.com/products/multiphysics/ (accessed on 6 June 2023).
- Yuan, L.; Lin, Q.; Xiao, M.; Fan, S. Synthetic dimension in photonics. Optica 2018, 5, 1396. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, Z. Highly confined topological edge states from two simple triangular lattices with reversed materials. Opt. Commun. 2021, 479, 126451. [Google Scholar] [CrossRef]
- Deng, W.-M.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. Transverse angular momentum in topological photonic crystals. J. Opt. 2018, 20, 014006. [Google Scholar] [CrossRef]
- Smirnova, D.; Leykam, D.; Chong, Y.; Kivshar, Y. Nonlinear topological photonics. Appl. Phys. Rev. 2020, 7, 021306. [Google Scholar] [CrossRef]
- Peng, Y.; Yan, B.; Xie, J.; Liu, E.; Li, H.; Ge, R.; Gao, F.; Liu, J. Variation of Topological Edge States of 2D Honeycomb Lattice Photonic Crystals. Phys. Status Solidi RRL 2020, 14, 2000202. [Google Scholar] [CrossRef]
- Li, Z.; Chan, H.-C.; Xiang, Y. Fragile topology based helical edge states in two-dimensional moon-shaped photonic crystals. Phys. Rev. B 2020, 102, 245149. [Google Scholar] [CrossRef]
- Alexandradinata, A.; Fang, C.; Gilbert, M.J.; Bernevig, B.A. Spin-Orbit-Free Topological Insulators without Time-Reversal Symmetry. Phys. Rev. Lett. 2014, 113, 116403. [Google Scholar] [CrossRef] [PubMed]
- de Paz, M.B.; Herrera, M.A.J.; Arroyo Huidobro, P.; Alaeian, H.; Vergniory, M.G.; Bradlyn, B.; Giedke, G.; García-Etxarri, A.; Bercioux, D. Energy density as a probe of band representations in photonic crystals. J. Phys. Condens. Matter 2022, 34, 314002. [Google Scholar] [CrossRef] [PubMed]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45. [Google Scholar] [CrossRef]
- Albert, J.P.; Jouanin, C.; Cassagne, D.; Monge, D. Photonic crystal modelling using a tight-binding Wannier function method. Opt. Quantum Electron. 2002, 34, 251. [Google Scholar] [CrossRef]
- Parappurath, N.; Alpeggiani, F.; Kuipers, L.; Verhagen, E. Direct observation of topological edge states in silicon photonic crystals: Spin, dispersion, and chiral routing. Sci. Adv. 2020, 6, eaaw4137. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Bulk-edge correspondence for topological photonic continua. Phys. Rev. B. 2016, 94, 205105. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Fang, Y. Embedded topological edge states from reversed two-dimensional photonic crystals. Phys. E 2021, 127, 114517. [Google Scholar] [CrossRef]
- Yang, Y.; Yamagami, Y.; Yu, X.; Pitchappa, P.; Webber, J.; Zhang, B.; Fujita, M.; Nagatsuma, T.; Singh, R. Terahertz topological photonics for on-chip communication. Nat. Photon. 2020, 14, 446. [Google Scholar] [CrossRef]
- Ni, X.; Purtseladze, D.; Smirnova, D.A.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Spin-and valley-polarized one-way Klein tunneling in photonic topological insulators. Sci. Adv. 2018, 4, eaap8802. [Google Scholar] [CrossRef] [PubMed]
- Arora, S.; Bauer, T.; Barczyk, R.; Verhagen, E.; Kuipers, L. Direct quantification of topological protection in symmetry-protected photonic edge states at telecom wavelengths. Light Sci. Appl. 2021, 10, 9. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Huo, S.; Chen, J. Subwavelength elastic topological negative refraction in ternary locally resonant phononic crystals. Int. J. Mech. Sci. 2021, 198, 106391. [Google Scholar] [CrossRef]
- Chen, X.-D.; Shi, F.-L.; Liu, H.; Lu, J.-C.; Deng, W.-M.; Dai, J.-Y.; Cheng, Q.; Dong, J.-W. Tunable Electromagnetic Flow Control in Valley Photonic Crystal Waveguides. Phys. Rev. Appl. 2018, 10, 044002. [Google Scholar] [CrossRef]
- Chen, X.-D.; Zhao, F.-L.; Chen, M.; Dong, J.-W. Valley-contrasting physics in all-dielectric photonic crystals: Orbital angular momentum and topological propagation. Phys. Rev. B 2017, 96, 020202(R). [Google Scholar] [CrossRef]
- He, X.-T.; Liang, E.-T.; Yuan, J.-J.; Qiu, H.-Y.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef]
- Borges-Silva, D. Robust Interface States in Topological Photonic Crystals Composed of Hexagonal Rods. Braz. J. Phys. 2022, 52, 108. [Google Scholar] [CrossRef]
- Borges-Silva, D.; Costa, C.H.; Bezerra, C.G. Topological phase transition and robust pseudospin interface states induced by angular perturbation in 2D topological photonic crystals. Sci. Rep. 2023, 13, 850. [Google Scholar] [CrossRef]
- Borges-Silva, D.; Costa, C.H.; Bezerra, C.G. Pseudospin topological behavior and topological edge states in a two-dimensional photonic crystal composed of Si rods in a triangular lattice. Phys. Rev. B 2023, 107, 075406. [Google Scholar] [CrossRef]
- Borges-Silva, D.; Bezerra, C.G.; Costa, C.H. Topological Phase Transition in C6 Photonic Crystals. In Proceedings of the 6th International Conference on Optics, Photonics and Lasers (OPAL’ 2023), Funchal (Madeira Island), Portugal, 17–19 May 2023; pp. 127–129. [Google Scholar]
- Shalaev, M.I.; Walasik, W.; Tsukernik, A.; Xu, Y.; Litchinitser, N.M. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nat. Nanotechnol. 2019, 14, 31. [Google Scholar] [CrossRef] [PubMed]
- Yoshimi, H.; Yamaguchi, T.; Katsumi, R.; Ota, Y.; Arakawa, Y.; Iwamoto, S. Experimental demonstration of topological slow light waveguides in valley photonic crystals. Opt. Express 2021, 29, 13441. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Qian, X.; Shi, L.; Shen, X.; Wang, Y.; Hang, Z.H. Observation and control of pseudospin switching in a finite-width topological photonic crystal. Opt. Express 2022, 30, 5731. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, H.X.; Liang, L.; Zhu, W.; Fan, L.; Lin, Z.K.; Li, F.; Zhang, X.; Luan, P.G.; Poo, Y.; et al. Hybrid topological photonic crystals. Nat. Commun. 2023, 14, 4457. [Google Scholar] [CrossRef]
- Gong, Y.; Wong, S.; Bennett, A.J.; Huffaker, D.L.; Oh, S.S. Topological insulator laser using valley-Hall photonic crystals. ACS Photon. 2020, 7, 2089. [Google Scholar] [CrossRef]
- Mittal, S.; DeGottardi, W.; Hafezi, M. Topological photonic systems. Opt. Photon. News 2018, 29, 36. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borges-Silva, D.; Costa, C.H.O.; Bezerra, C.G. Robust Topological Edge States in C6 Photonic Crystals. Photonics 2023, 10, 961. https://doi.org/10.3390/photonics10090961
Borges-Silva D, Costa CHO, Bezerra CG. Robust Topological Edge States in C6 Photonic Crystals. Photonics. 2023; 10(9):961. https://doi.org/10.3390/photonics10090961
Chicago/Turabian StyleBorges-Silva, Daniel, Carlos Humberto Oliveira Costa, and Claudionor Gomes Bezerra. 2023. "Robust Topological Edge States in C6 Photonic Crystals" Photonics 10, no. 9: 961. https://doi.org/10.3390/photonics10090961
APA StyleBorges-Silva, D., Costa, C. H. O., & Bezerra, C. G. (2023). Robust Topological Edge States in C6 Photonic Crystals. Photonics, 10(9), 961. https://doi.org/10.3390/photonics10090961






