Mirror Vibration Tolerance Studies in X-ray Free-Electron Laser Oscillator
Abstract
:1. Introduction
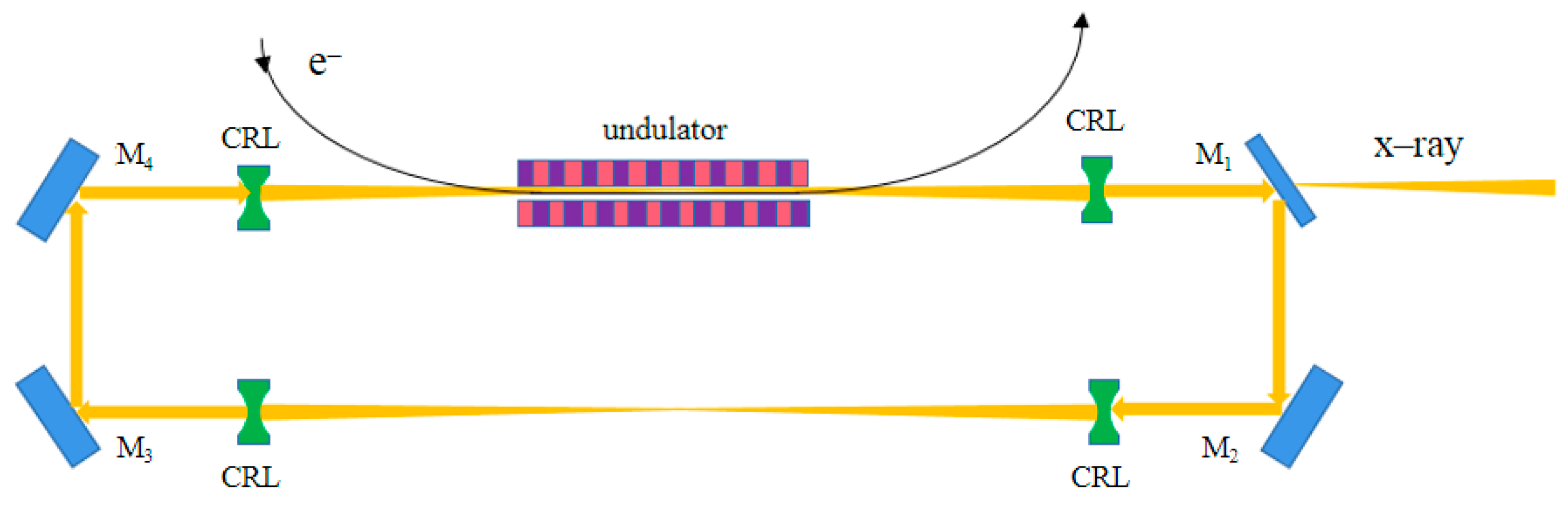
2. The Cavity Design and Parameters
3. Simulation of Mirror Vibration
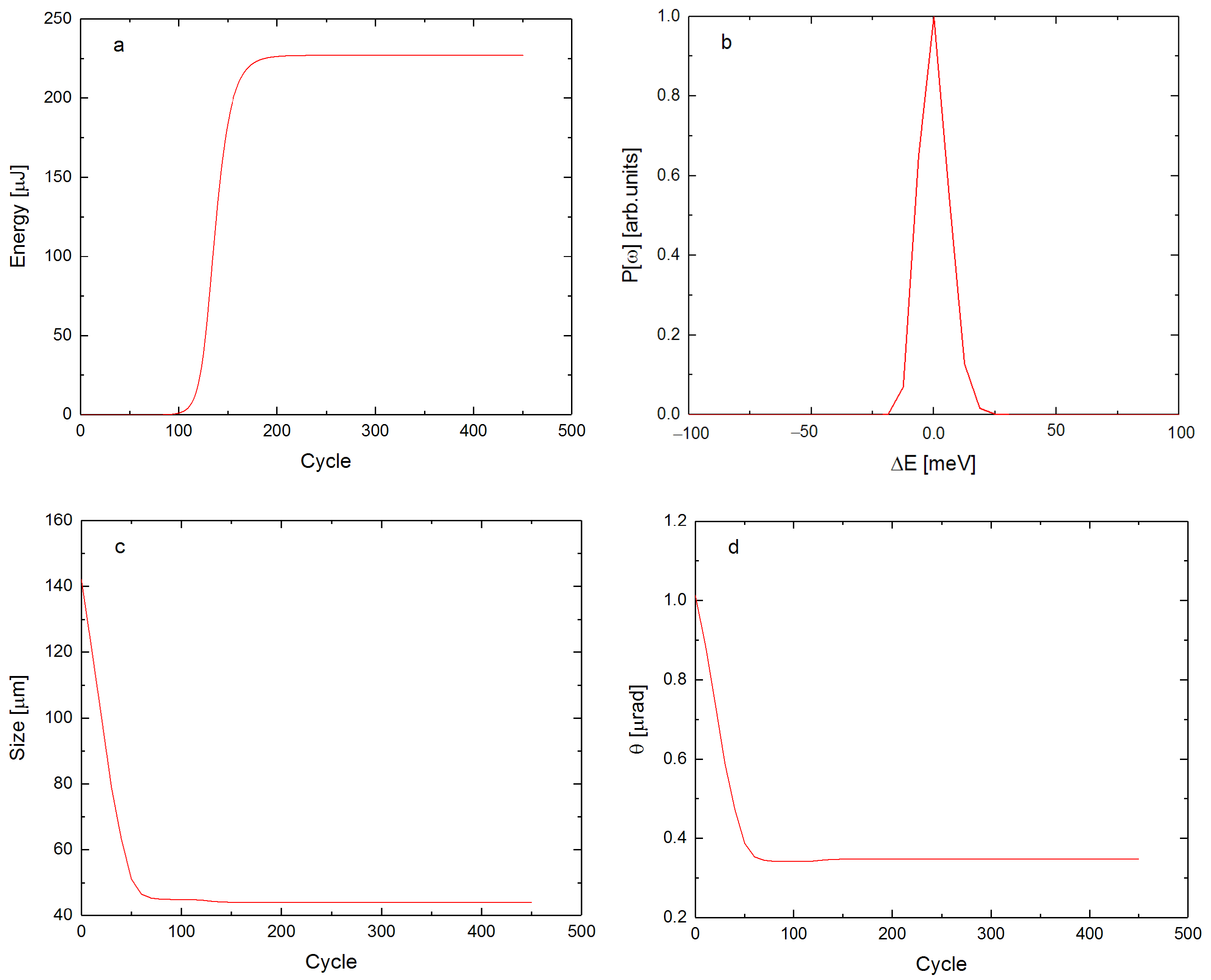
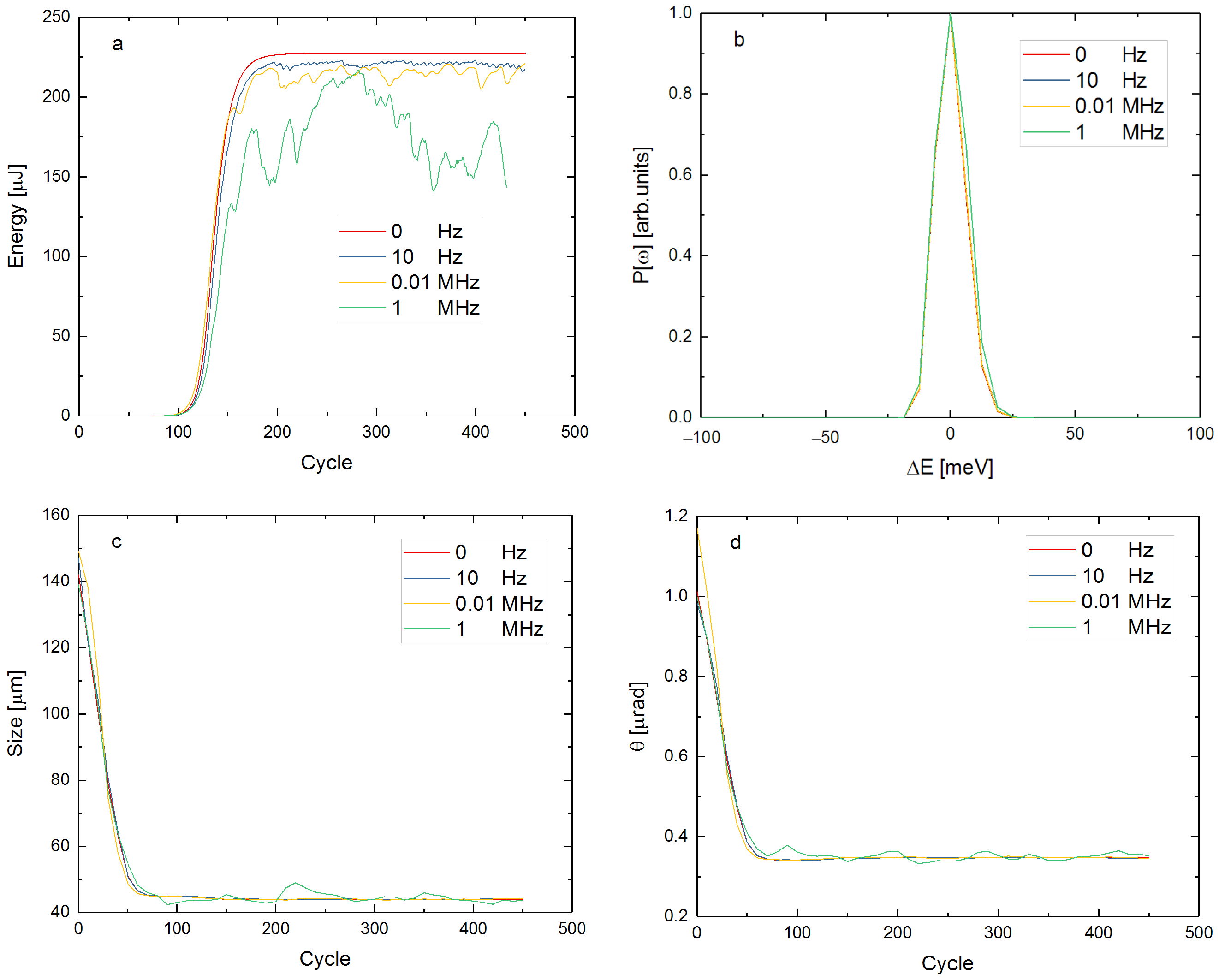
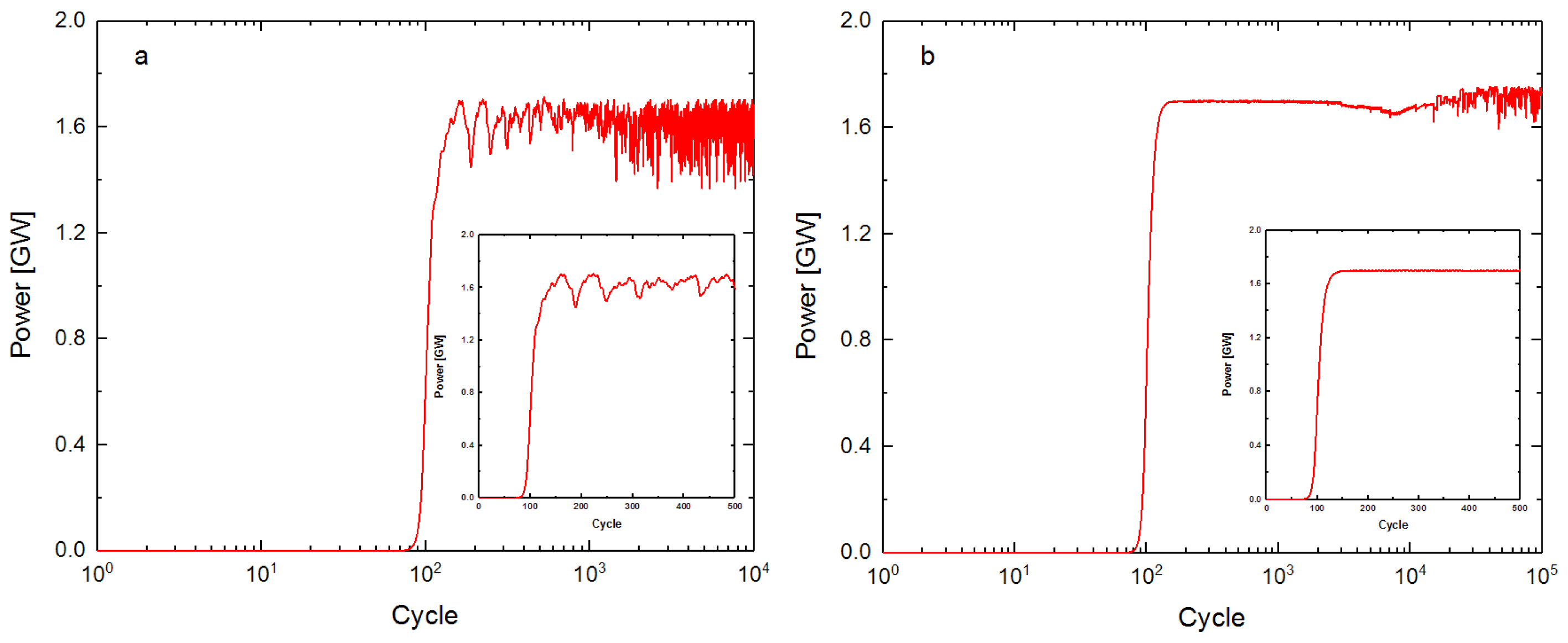
3.1. Perfect Alignment Cavity
3.2. Single Frequency Vibration
3.3. Multi-Frequency Vibrations
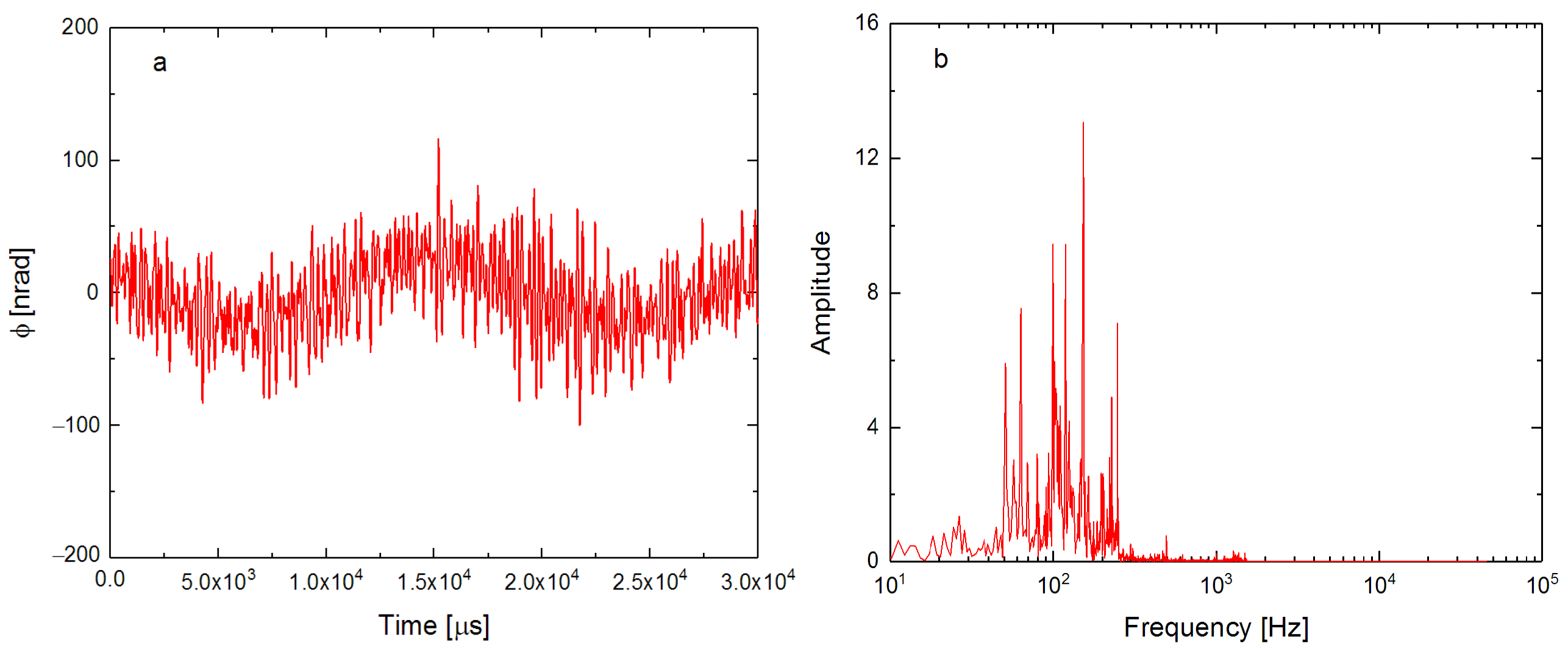
3.4. Realistic Vibration
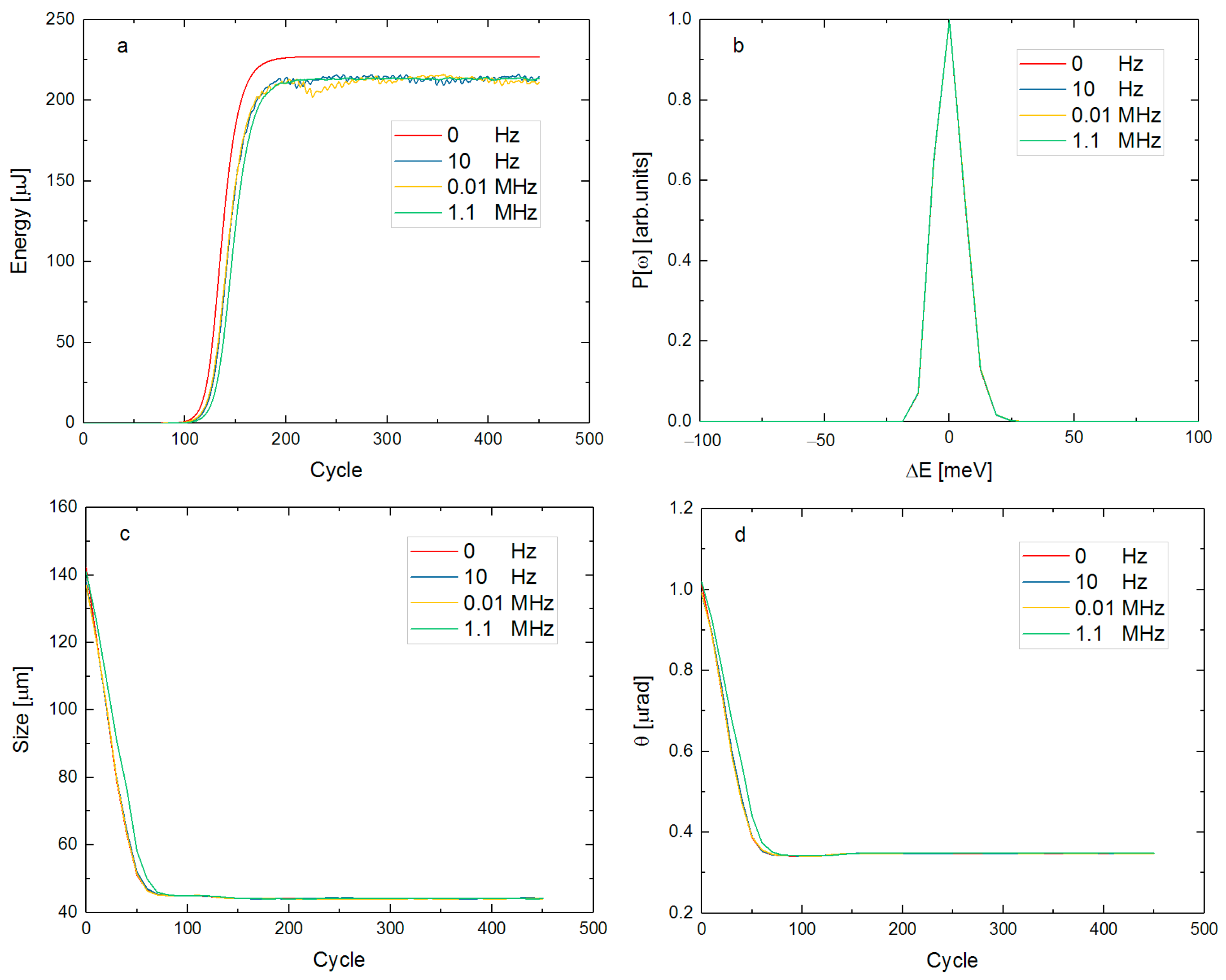
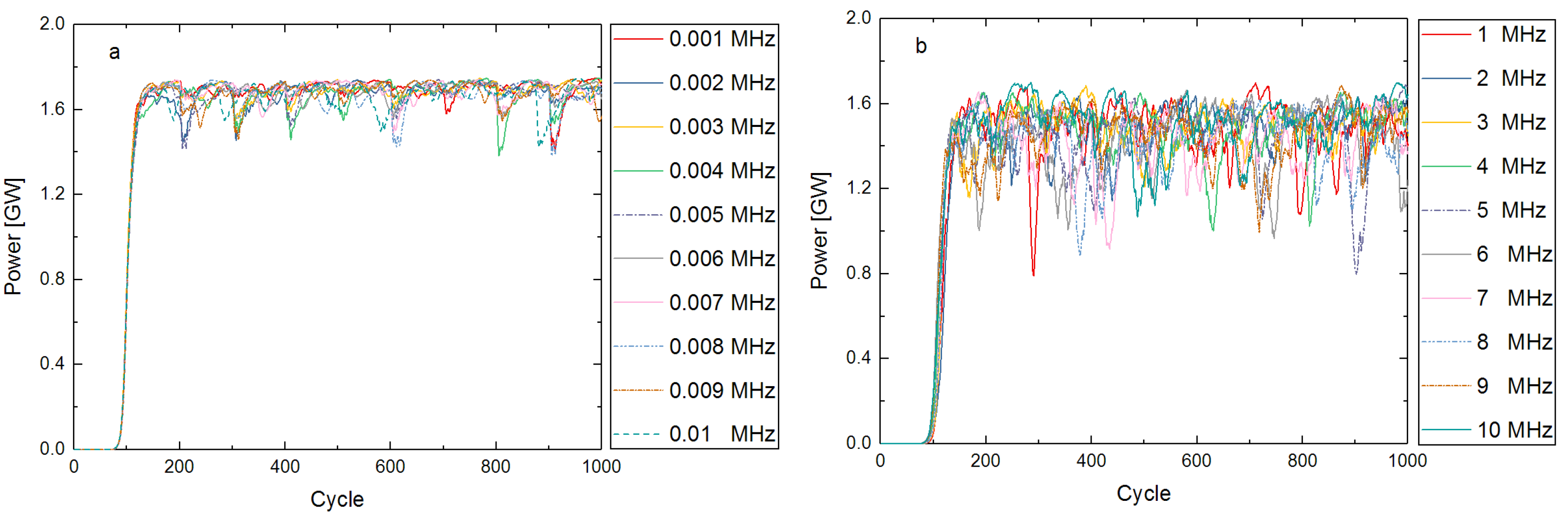
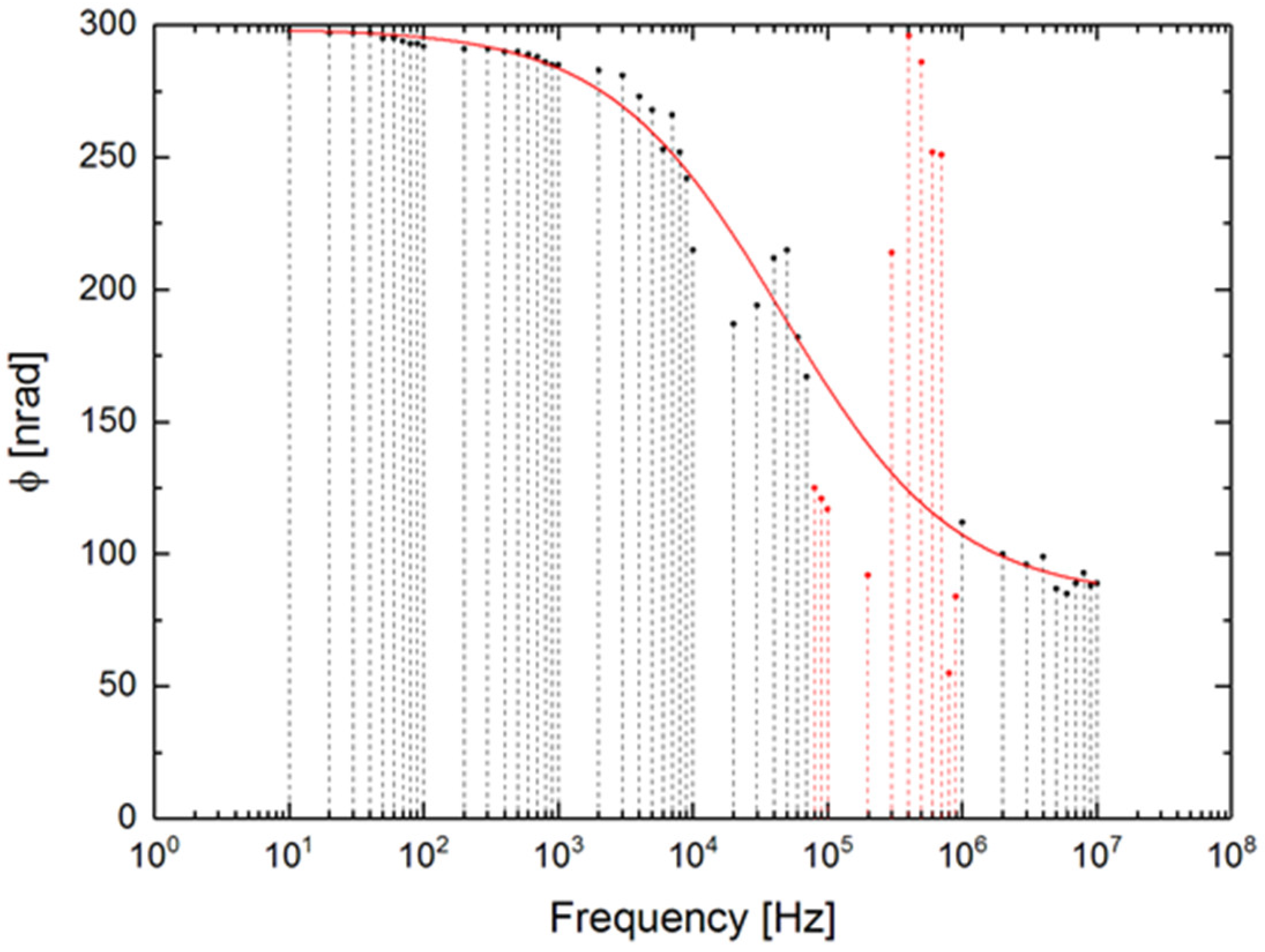
4. The Effect of Different Vibration Frequencies
4.1. Relationship between Frequency and Output Power
4.2. Tolerance of Vibration Amplitude
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bostedt, C.; Boutet, S.; Fritz, D.M.; Huang, Z.; Lee, H.J.; Lemke, H.T.; Robert, A.; Schlotter, W.F.; Turner, J.J.; Williams, G.J. Linac coherent light source: The first five years. Rev. Mod. Phys. 2016, 88, 015007. [Google Scholar] [CrossRef]
- Huang, N.; Deng, H.; Liu, B.; Wang, D.; Zhao, Z. Features and futures of X-ray free-electron lasers. Innovation 2021, 2, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Deng, H.-X. Review of fully coherent free-electron lasers. Nucl. Sci. Tech. 2018, 29, 160. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Review of X-ray free-electron laser theory. Phys. Rev. Spec. Top.-Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Kondratenko, A.; Saldin, E. Generating of coherent radiation by a relativistic electron beam in an ondulator. Part. Accel. 1980, 10, 207–216. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.; Saldin, E. On the possibility of using a free electron laser for polarization of electrons in storage rings. Nucl. Instrum. Methods Phys. Res. 1982, 193, 415–421. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Kim, K.-J.; Shvyd’ko, Y.; Reiche, S. A proposal for an X-ray free-electron laser oscillator with an energy-recovery linac. Phys. Rev. Lett. 2008, 100, 244802. [Google Scholar] [CrossRef]
- Huang, Z.; Ruth, R.D. Fully coherent X-ray pulses from a regenerative-amplifier free-electron laser. Phys. Rev. Lett. 2006, 96, 144801. [Google Scholar] [CrossRef]
- Dai, J.; Deng, H.; Dai, Z. Proposal for an X-ray free electron laser oscillator with intermediate energy electron beam. Phys. Rev. Lett. 2012, 108, 034802. [Google Scholar] [CrossRef]
- Rauer, P.; Decking, W.; Lipka, D.; Thoden, D.; Wohlenberg, T.; Bahns, I.; Brueggmann, U.; Casalbuoni, S.; Di Felice, M.; Dommach, M. Cavity based X-ray free electron laser demonstrator at the European X-ray Free Electron Laser facility. Phys. Rev. Accel. Beams 2023, 26, 020701. [Google Scholar] [CrossRef]
- Lindberg, R.; Kim, K.-J.; Shvyd’ko, Y.; Fawley, W. Performance of the X-ray free-electron laser oscillator with crystal cavity. Phys. Rev. Spec. Top.-Accel. Beams 2011, 14, 010701. [Google Scholar] [CrossRef]
- Li, K.; Deng, H. Gain-guided X-ray free-electron laser oscillator. Appl. Phys. Lett. 2018, 113, 061106. [Google Scholar] [CrossRef]
- Huang, N.; Deng, H. Generating X-rays with orbital angular momentum in a free-electron laser oscillator. Optica 2021, 8, 1020–1023. [Google Scholar] [CrossRef]
- Shvyd’ko, Y.V.; Stoupin, S.; Cunsolo, A.; Said, A.H.; Huang, X. High-reflectivity high-resolution X-ray crystal optics with diamonds. Nat. Phys. 2010, 6, 196–199. [Google Scholar] [CrossRef]
- Shvyd’Ko, Y.; Lindberg, R. Spatiotemporal response of crystals in X-ray Bragg diffraction. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 100702. [Google Scholar] [CrossRef]
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Kolodziej, T.; Stoupin, S.; Grizolli, W.; Krzywinski, J.; Shi, X.; Kim, K.-J.; Qian, J.; Assoufid, L.; Shvyd’ko, Y. Efficiency and coherence preservation studies of Be refractive lenses for XFELO application. J. Synchrotron Radiat. 2018, 25, 354–360. [Google Scholar] [CrossRef]
- Batterman, B.W.; Cole, H. Dynamical diffraction of X-rays by perfect crystals. Rev. Mod. Phys. 1964, 36, 681. [Google Scholar] [CrossRef]
- Huang, N.; Deng, H. Thermal loading on crystals in an X-ray free-electron laser oscillator. Phys. Rev. Accel. Beams 2020, 23, 090704. [Google Scholar] [CrossRef]
- Tiwari, G.; Lindberg, R.R. Misalignment effects on the performance and stability of X-ray free electron laser oscillator. Phys. Rev. Accel. Beams 2022, 25, 090702. [Google Scholar] [CrossRef]
- Qi, P.; Shvyd’ko, Y. Signatures of misalignment in X-ray cavities of cavity-based X-ray free-electron lasers. Phys. Rev. Accel. Beams 2022, 25, 050701. [Google Scholar] [CrossRef]
- Kim, K.-J.; Huang, Z.; Lindberg, R. Synchrotron Radiation and Free-Electron Lasers; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Huang, N.-S.; Liu, Z.-P.; Deng, B.-J.; Zhu, Z.-H.; Li, S.-H.; Liu, T.; Qi, Z.; Yan, J.-W.; Zhang, W.; Xiang, S.-W. The MING proposal at shine: Megahertz cavity enhanced X-ray generation. Nucl. Sci. Tech. 2023, 34, 6. [Google Scholar] [CrossRef]
- Yang, H.; Yan, J.; Deng, H. High-repetition-rate seeded free-electron laser enhanced by self-modulation. Adv. Photonics Nexus 2023, 2, 036004. [Google Scholar] [CrossRef]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- van der Slot, P.J.; Freund, H.; Miner, W., Jr.; Benson, S.; Shinn, M.; Boller, K.-J. Time-dependent, three-dimensional simulation of free-electron-laser oscillators. Phys. Rev. Lett. 2009, 102, 244802. [Google Scholar] [CrossRef]
- Huang, N.-S.; Li, K.; Deng, H.-X. BRIGHT: The three-dimensional X-ray crystal Bragg diffraction code. Nucl. Sci. Tech. 2019, 30, 39. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Electron energy (GeV) | 8 |
| Relative energy spread (%) | 0.01 |
| Repetition rate (MHz) | 1 |
| Peak current (A) | 600 |
| Normalized emittance (mm mrad) | 0.4 |
| Undulator period length (mm) | 26 |
| Light wavelength (nm) | 0.096 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Huang, N.; Zhou, J.; Deng, H. Mirror Vibration Tolerance Studies in X-ray Free-Electron Laser Oscillator. Photonics 2023, 10, 1058. https://doi.org/10.3390/photonics10091058
Li S, Huang N, Zhou J, Deng H. Mirror Vibration Tolerance Studies in X-ray Free-Electron Laser Oscillator. Photonics. 2023; 10(9):1058. https://doi.org/10.3390/photonics10091058
Chicago/Turabian StyleLi, Shaohua, Nanshun Huang, Jianyang Zhou, and Haixiao Deng. 2023. "Mirror Vibration Tolerance Studies in X-ray Free-Electron Laser Oscillator" Photonics 10, no. 9: 1058. https://doi.org/10.3390/photonics10091058
APA StyleLi, S., Huang, N., Zhou, J., & Deng, H. (2023). Mirror Vibration Tolerance Studies in X-ray Free-Electron Laser Oscillator. Photonics, 10(9), 1058. https://doi.org/10.3390/photonics10091058




