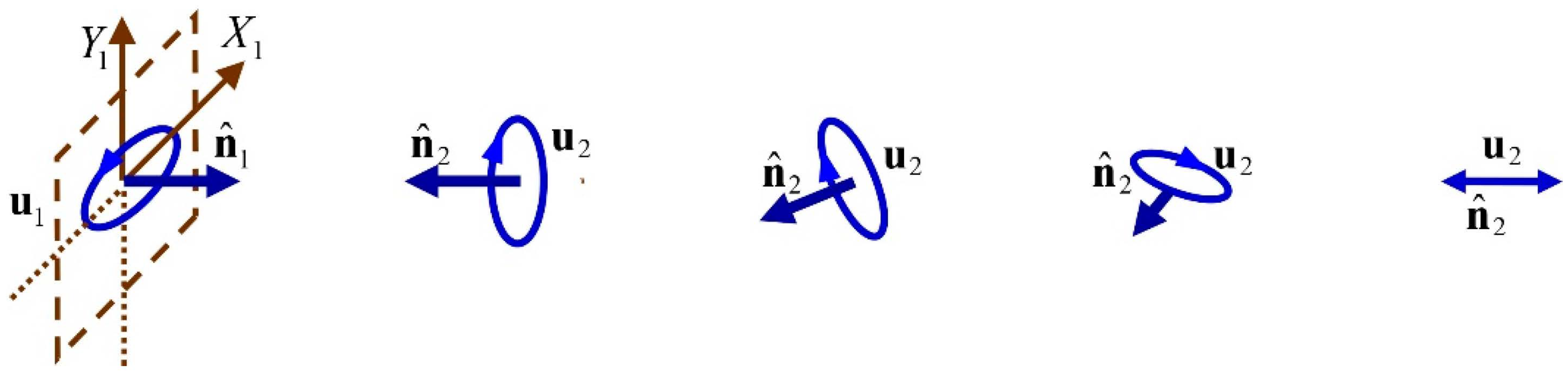Discriminating States of Polarization

Abstract

Equiprobable incoherent mixtures of two totally polarized states of light whose associated three-dimensional Jones vectors are mutually orthogonal are called discriminating states and constitute a peculiar type of state that plays a key role in the characteristic decomposition of a generic state into a totally polarized state, a totally unpolarized state, and a discriminating state. In general, discriminating states are three-dimensional, in the sense that the strengths of the three components of the electric field are nonzero for any Cartesian reference frame considered. In the limiting case that the electric field evolves in a fixed plane, the discriminating state is said to be regular and corresponds to a two-dimensional unpolarized state. The special features of discriminating states cover, e.g., their possible synthesis from infinite pairs of mutually orthogonal states as well as their transverse spin. The nature and properties of discriminating states are comprehensively analyzed based on their associated intrinsic Stokes parameters, which leads to meaningful interpretations in terms of the associated polarization ellipsoids and spin vectors.

1. Introduction

The general, three-dimensional (3D) nature of polarization states of random stationary light should be considered for important physical situations like near fields [1,2,3], tightly focused beams [4,5,6,7,8], or evanescent waves [9]. Thus, the conventional two-dimensional (2D) representation, which is applicable for plane waves or paraxial beams, constitutes a particular case of the general 3D states. Polarization states for which the evolution of the electric field is not constrained to a fixed plane do not admit a two-dimensional formulation and are called genuine 3D states whose properties have recently been extensively studied [10,11,12,13,14,15].

Polarization of a random electromagnetic field refers to the evolution of the end point of the electric field at a given point in space, and its complete characterization would require the knowledge of all n-order moments of the field variables, represented by their associated respective analytic signals. Nevertheless, polarization is commonly represented by the second-order moments, which are arranged as the components of the corresponding polarization matrix. Such a second-order representation is complete for random stationary Gaussian fields and constitutes a sufficient approach for most practical situations.

Thus, the second-order representation of a polarization state is determined by its associated polarization matrix, denoted by R, which in virtue of the so-called characteristic decomposition, can be expressed as a convex sum of three specific characteristic components. These correspond to a fully polarized state (or pure state), a fully unpolarized state, and a discriminating state, which in its turn refers to an incoherent superposition of two pure states whose Jones vectors are mutually orthogonal.

Beyond the key role played by discriminating states in the interpretation of the characteristic decomposition of general polarization states, they exhibit a very peculiar structure. In addition, they can be experimentally generated in different ways and correspond to interesting physical scenarios: for instance, certain types of evanescent waves [9]. Also, since the mathematical formalism dealt with in this work coincides with that applied to quantum qutrit states [16], the results obtained can directly be applied to the corresponding discriminating qutrit states.

The present work is focused on the description, analysis, and physical interpretation of discriminating states and is organized as follows. The necessary concepts and notations are presented in Section 2; Section 3 is devoted to the specific study of discriminating polarization states; and Section 4 summarizes the characteristic properties of these kinds of polarization states.

2. Mathematical Representations and Physical Descriptors of Three-Dimensional Polarization States

The polarization matrix, which contains all the second-order measurable information about the state of polarization (including intensity) of an electromagnetic wave, is defined as the following 3×3 Hermitian matrix:

$$R=⟨\epsilon \left(t\right)\otimes {\epsilon }^{†}\left(t\right)⟩=\left(\begin{array}{ccc}⟨{\epsilon }_1\left(t\right) {\epsilon }_1^{*}\left(t\right)⟩& ⟨{\epsilon }_1\left(t\right) {\epsilon }_2^{*}\left(t\right)⟩& ⟨{\epsilon }_1\left(t\right) {\epsilon }_3^{*}\left(t\right)⟩\\ ⟨{\epsilon }_2\left(t\right) {\epsilon }_1^{*}\left(t\right)⟩& ⟨{\epsilon }_2\left(t\right) {\epsilon }_2^{*}\left(t\right)⟩& ⟨{\epsilon }_2\left(t\right) {\epsilon }_3^{*}\left(t\right)⟩\\ ⟨{\epsilon }_3\left(t\right) {\epsilon }_1^{*}\left(t\right)⟩& ⟨{\epsilon }_3\left(t\right) {\epsilon }_2^{*}\left(t\right)⟩& ⟨{\epsilon }_3\left(t\right) {\epsilon }_3^{*}\left(t\right)⟩\end{array}\right),$$

(1)

whose elements are the second-order moments of the zero-mean analytic signals ${\epsilon }_i(t)$ $(i=1,2,3)$ (complex random processes) associated with the three (real) Cartesian components of the electric field vector at point r in space. Superscript $†$ denotes the conjugate transpose, ⊗ stands for the Kronecker Product, and the brackets ⟨…⟩ indicate time averaging (in the case of stationary and ergodic fields, the brackets can also be interpreted as ensemble averaging over the ensemble of sample realizations). Note that the convention $R=⟨\epsilon (t)\otimes {\epsilon }^{†}(t)⟩$, which is common in polarization optics, is used instead of the convention $R=⟨{\epsilon }^{*}(t)\otimes {\epsilon }^{\mathrm{T}}(t)⟩$ frequently used in optical coherence theory. Thus, R is characterized by nine quantities, which are measurable through the corresponding 3D Stokes parameters [1,17,18,19,20,21,22,23,24,25,26].

Let us consider the unitary similarity transformation that diagonalizes R,

$$R=U\mathrm{diag}\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)U^{†}, \left[{\lambda }_1\ge {\lambda }_2\ge {\lambda }_3\right],$$

(2)

where U is a unitary matrix, and $({\lambda }_1,{\lambda }_2,{\lambda }_3)$ are the real eigenvalues of R, which are necessarily non-negative because of the fact that R has the mathematical structure of a covariance matrix (of three zero-mean functions ${\epsilon }_i (t)$). Without loss of generality, the eigenvalues have been taken in decreasing order $({\lambda }_1\ge {\lambda }_2\ge {\lambda }_3)$. Note that $\mathrm{tr}R={\lambda }_1+{\lambda }_2+{\lambda }_3$ represents the intensity I of the state. For certain purposes, it is useful to define the polarization density matrix $\widehat{R}=R/I$ as the intensity-normalized version of the polarization matrix, whose eigenvalues are denoted as ${\hat{\lambda }}_i={\lambda }_i/I$ $(i=1,2,3)$ with ${\widehat{\lambda }}_1+{\widehat{\lambda }}_2+{\widehat{\lambda }}_3=1$. The above diagonalization of R leads directly to the so-called spectral decomposition

$$\begin{array}{c}R={\widehat{\lambda }}_{1}I {\widehat{R}}_{p1}+{\widehat{\lambda }}_{2}I {\widehat{R}}_{p2}+{\widehat{\lambda }}_{3}I {\widehat{R}}_{p3} ,\\ \left[ {\widehat{R}}_{p1}=U\mathrm{diag}\left(1,0,0\right)U^{†}, {\widehat{R}}_{p2}=U\mathrm{diag}\left(0,1,0\right)U^{†}, {\widehat{R}}_{p3}=U\mathrm{diag}\left(0,0,1\right)U^{†}\right],\end{array}$$

(3)

which shows that R can be interpreted as the incoherent superposition of three pure states whose associated analytic signal vectors are mutually orthogonal.

The spectral decomposition can be rearranged to build the corresponding characteristic decomposition [27]

$$\begin{array}{c}R=P_1 I {\widehat{R}}_p+\left(P_2-P_1\right)I {\widehat{R}}_m+\left(1-P_2\right)I {\widehat{R}}_{u-3D},\\ {\widehat{R}}_p=U\mathrm{diag}\left(1,0,0\right)U^{†}, {\widehat{R}}_m=\frac{1}{2}U\mathrm{diag}\left(1,1,0\right)U^{†}, {\widehat{R}}_{u-3D}=\frac{1}{3}I ,\end{array}$$

(4)

where ${\widehat{R}}_p$ represents a pure state (denoted by ${\widehat{R}}_{p1}$ in Equation (3)), ${\widehat{R}}_{u-3D}$ is a fully unpolarized state, and the middle component ${\widehat{R}}_m$ is called the discriminating state associated with R, while the coefficients of the convex sum are regulated by the indices of polarimetric purity (IPPs) defined from the eigenvalues of $\widehat{R}$ in the following manner [28].

$$P_1 ={\widehat{\lambda }}_1-{\widehat{\lambda }}_2, P_2 ={\widehat{\lambda }}_1+{\widehat{\lambda }}_2-2{\widehat{\lambda }}_3$$

(5)

Note that the convention ${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3$ should be preserved for a proper definition of the above IPPs, and consequently, $0\le P_1\le P_2 \le 1$. The structure of the characteristic decomposition shows that discriminating states, whose polarization and polarization density matrices will be hereafter denoted as $R_m$ and ${\widehat{R}}_m$, respectively, are characterized by $P_1 =0$ and $P_2 =1$. Moreover, pure states are characterized by $P_1=P_2=1$, while fully unpolarized states correspond to $P_1=P_2=0$.

It has also been shown that the IPPs determine the structure of polarimetric randomness of R, while they are insensitive to the type of polarization states associated with the spectral components. The overall polarimetric randomness of a state R is given by the associated degree of polarimetric purity (or degree of polarization) [1,28].

$$P_{3D}=\sqrt{ \frac{3P_1^2+P_2^2}{4}}=\sqrt{ \frac{1}{2}\left(3\mathrm{tr}{\widehat{R}}^2 -1\right)}=\sqrt{ \frac{1}{2}\left(3 {\displaystyle \sum _{i=1}^3{\widehat{\lambda }}_i^2}-1\right)} ,$$

(6)

whose limiting values are $P_{3D} =0$ for fully unpolarized states and $P_{3D} =1$ for fully polarized states.

Other interesting complementary descriptors can be defined through the intrinsic representation of R, which is obtained as follows by means of the diagonalization of the real part $\mathrm{Re}R$ of R. Given R, let us consider the orthogonal (hence, real) matrix Q that allows us to perform the orthogonal similarity transformation [29].

$$\mathrm{Re}R=Q \mathrm{diag}\left(a_1,a_2,a_3\right) Q^{\mathrm{T}} , \left[a_1\ge a_2\ge a_3\right],$$

(7)

where the superscript T indicates the transpose matrix, and the non-negative diagonal elements $(a_1,a_2,a_3)$ (taken in decreasing order) are called the principal intensities of R. When the same orthogonal similarity transformation is applied to the entire R (not only to its real part), it is transformed to the intrinsic polarization matrix $R_O=Q^{\mathrm{T}}RQ$, which represents the same state as R, but refers with respect to the new intrinsic reference frame $X_O{Y}_O{Z}_O$ instead of the generic original one $X Y Z$. Since the real and imaginary parts of R transform independently in this orthogonal transformation, the diagonal elements of $R_O$ coincide with those of R, and therefore, $R_O$ can be expressed as [29,30]

$$\begin{array}{c}{R}_O\equiv \left(\begin{array}{ccc}{a}_1& -i{n}_{O3}/2& i{n}_{O2}/2\\ i{n}_{O3}/2& a_2& -i{n}_{O1}/2\\ -i{n}_{O2}/2& i{n}_{O1}/2& a_3\end{array}\right)=I\left(\begin{array}{ccc}{\widehat{a}}_1& -i{\widehat{n}}_{O3}/2& i{\widehat{n}}_{O2}/2\\ i{\widehat{n}}_{O3}/2& {\widehat{a}}_2& -i{\widehat{n}}_{O1}/2\\ -i{\widehat{n}}_{O2}/2& i{\widehat{n}}_{O1}/2& {\widehat{a}}_3\end{array}\right),\\ \left[a_1\ge a_2\ge a_3, I=a_1+a_2+a_3, {\widehat{a}}_i=a_i/I, {\widehat{n}}_{Oi}=n_{Oi}/I \left(i=1,2,3\right)\right],\end{array}$$

(8)

where the off-diagonal elements are determined by the spin vector $n\equiv {(n_1,n_2,n_3)}^{\mathrm{T}}$ [29,30]. Thus, the complete information contained in the polarization matrix of any polarization state can be parametrized in terms of the following nine parameters: the three principal intensities $(a_1,a_2,a_3)$, the three components $(n_{O1},n_{O2},n_{O3})$ of the spin vector along the respective intrinsic axes $X_O{Y}_O{Z}_O$, and the three angles determining the rotation associated with Q [30,31]. Consequently, leaving aside the spatial orientation of the polarization state, the intrinsic polarization properties are determined by the polarization object constituted by the polarization ellipsoid defined by $(a_1,a_2,a_3)$ and the spin vector.

Moreover, the principal intensities determine three physically significant quantities, namely, the intensity $I=a_1+a_2+a_3$, the degree of linear polarization $P_l={\widehat{a}}_1-{\widehat{a}}_2$, and the degree of directionality $P_d=1-3{\widehat{a}}_3$ (where ${\widehat{a}}_i=a_i/I$ are called the principal variances). Other additional descriptors are the degree of circular polarization $P_c=\left|n\right|/I$, given by the intensity normalized absolute value of the spin vector, and the degree of elliptical purity $P_e=\sqrt{P_l^2+P_c^2}$ [32]. The set $P_l,P_c,P_d$ constitutes the so-called components of purity (CPs) of the polarization state [33].

Contrary to what happens with the IPPs, the CPs hold qualitative information on the type of polarization exhibited by the state R considered. The contributions of the CPs as sources of the overall purity of R are evidenced by the relation [33]

$$P_{3D}=\sqrt{\frac{3\left(P_l^2+P_c^2\right)+P_d^2}{4}} ,$$

(9)

which establishes a link between the IPPs and the CPs via Equation (6). In other words, the degree of polarimetric purity can be determined either through descriptors of polarimetric purity/randomness (IPPs) or through descriptors of the polarization nature (CPs).

The nine 3D Stokes parameters associated with a state R are obtained from the coefficients of the expansion of R in the basis composed of the eight Gell-Mann matrices together with the 3×3 identity matrix [1,19,20,21]. When the state R is transformed to $R_O$ through a rotation from the original Cartesian reference axes $X Y Z$ to the intrinsic axes $X_O{Y}_O{Z}_O$, it adopts the intrinsic form [25,30]

$$R_O=\frac{1}{2}I\left(\begin{array}{ccc}2/3+P_l+P_d/3& -i {\widehat{n}}_{O3}& i {\widehat{n}}_{O2}\\ i {\widehat{n}}_{O3}& 2/3-P_l+P_d/3& -i {\widehat{n}}_{O1}\\ -i {\widehat{n}}_{O2}& i {\widehat{n}}_{O1}& 2/3\left(1-P_d\right)\end{array}\right),$$

(10)

so that, in this intrinsic representation, three Stokes parameters become strictly zero while while the six nonzero intrinsic Stokes parameters are precisely the simple and meaningful quantities $I, P_l, P_d/\sqrt{3}, {\widehat{n}}_{O1}, {\widehat{n}}_{O2}, {\widehat{n}}_{O3}$ [25].

The effective dimensions that take place in the representation of discriminating states are characterized by the polarimetric dimension, defined as [34]

$$D_I\equiv 3-\sqrt{ 3P_l^2+P_d^2} ,$$

(11)

with $1\le D_I\le 3$. The lower limiting value $D_I=1$ is exclusive of linearly polarized states ($P_l=P_d=1$, 1D light), values in the interval $1<D_I\le 2$ correspond to states whose electric field fluctuates in a fixed plane and are not linearly polarized ($P_l<1$, $P_d=1$, 2D light ) and values in the interval $2<D_I\le 3$ are achieved uniquely by genuine 3D states $(P_d<1)$.

Throughout the next sections, all the above structures and properties of general polarization states will be particularized to the case of discriminating states, including their specific interpretations.

3. Structure and Peculiarities of Discriminating States of Polarization

The general form of the polarization density matrix of a discriminating state is [27]

$${\widehat{R}}_m=\frac{1}{2}U\mathrm{diag}\left(1,1,0\right)U^{†}=\frac{1}{2}\left(u_1\otimes u_1^{†}+u_2\otimes u_2^{†}\right),$$

(12)

where U is a unitary matrix, and the unit vectors $u_1$, $u_2$ coincide with the two first columns of U. Since U is unitary, its column vectors $u_1,u_2,u_3$ are mutually orthogonal. From Equation (4), we see that a polarization state is a discriminating state if and only if its IPPs have the specific values $P_1(R_m)=0$ and $P_2(R_m)=1$. Consequently, the degree of polarimetric purity of a discriminating state is always $P_{3D}(R_m)=1/2$.

As for the intrinsic representation $R_{mO}$ of $R_m$, let us first recall that, through straightforward algebraic calculations, it has been shown that the associated intrinsic reference frame $X_O{Y}_O{Z}_O$ coincides with $Z_3(-Y_3)X_3$, $X_3{Y}_3{Z}_3$ being the intrinsic reference frame of the eigenvector $u_3$ associated with the zero eigenvalue of $R_m$ [35]. Thus, when $u_3$ is represented with respect to $X_O{Y}_O{Z}_O$, it takes the form $u_{3O}=e^{i{\gamma }_3}{(0,i\sin \chi ,\cos \chi )}^{\mathrm{T}}$ (${\gamma }_3$ being an arbitrary phase), which corresponds to a pure state whose polarization plane coincides with $Y_O{Z}_O$ and whose ellipticity angle is χ. Consequently, $R_{mO}$ has the general form [35]

$$R_{mO}=\frac{1}{2}I\left(\begin{array}{ccc}1& 0& 0\\ 0& {\cos }^2\chi & -i\cos \chi \sin \chi \\ 0& i\cos \chi \sin \chi & {\sin }^2\chi \end{array}\right), \left[-\pi /4\le \chi \le \pi /4\right],$$

(13)

and the eigenvalues of $\mathrm{Re}{\widehat{R}}_m$ (in decreasing order) are

$${\widehat{a}}_1=\frac{1}{2}, {\widehat{a}}_2=\frac{{\cos }^2\chi }{2}, {\widehat{a}}_3=\frac{{\sin }^2\chi }{2}$$

(14)

.

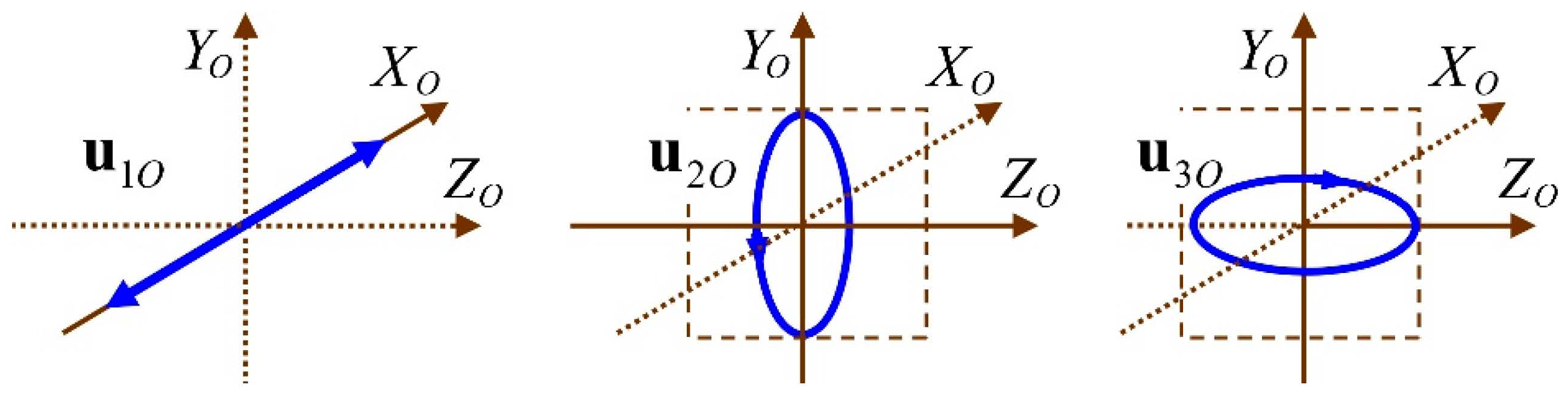
Regarding the remaining intrinsic eigenvectors $u_{1O},u_{2O}$ of $R_m$, the double degeneracy of their common eigenvalue $1/2$ implies that they can take infinite possible forms (notwithstanding that they form the required orthonormal set $u_{1O},u_{2O},u_{3O}$). The simplest choice corresponds to the canonical pair of eigenvectors constituted by $u_{1O}=e^{i{\gamma }_1}{(1,0,0)}^{\mathrm{T}}$ and $u_{2O}=e^{i{\gamma }_2}{(0,-i\cos \chi ,\sin \chi )}^{\mathrm{T}}$ (${\gamma }_1$ and ${\gamma }_2$ being arbitrary phases) which represent, respectively, a linear polarization state whose electric field is oriented along the $X_O$ axis and a pure elliptically polarized state whole polarization plane coincides with that of $u_{3O}$ (see Figure 1).

Figure 1. The canonical set of intrinsic eigenstates of a discriminating state. $u_{1O}$ and $u_{2O}$ correspond to the double degenerate nonzero eigenvalue of the intrinsic polarization matrix ${\widehat{R}}_{mO}$, while $u_{3O}$ corresponds to the single zero eigenvalue of ${\widehat{R}}_{mO}$.

Some possible configurations of arbitrary pairs of orthonormal 3D Jones vectors $(u_1,u_2)$ with associated spin vectors $({\widehat{n}}_1,{\widehat{n}}_2)$ are represented in Figure 2. Equiprobable incoherent mixtures of the polarization matrices of each pair lead always to discriminating states whose spin vector is given by $({\widehat{n}}_1+{\widehat{n}}_2)/2$. It should be noted that, in general, the intrinsic reference frames of the components are different from that of the composed discriminating state.

Figure 2. Representation of a family of pairs of mutually orthogonal eigenstates $(u_1,u_2)$ determining the eigenvector spectrum (with associated equal nonzero eigenvalues) of a discriminating state, with respective spin vectors ${\widehat{n}}_1$ and ${\widehat{n}}_2$. $u_1$ is taken with a fixed ellipticity and determines its own intrinsic reference frame $X_1 Y_1 Z_1$, while different pure states $u_2$, orthogonal to $u_1$, are represented for decreasing absolute values of ${\widehat{n}}_2$. All eigenstates are realized in a common point in space but have been separated for the sake of clarity. For a regular discriminating state, ${\widehat{n}}_2=-{\widehat{n}}_1$, while the polarization planes of $u_1$ and $u_2$ coincide, leading to a 2D-unpolarized state. For nonregular discriminating states, the polarization planes as well as the ellipticities of both eigenstates are different, and $\left|{\widehat{n}}_2\right|$ decreases as the angle subtended by the polarization planes of $u_1$ and $u_2$ increases. Given $u_1$, the maximal degree of nonregularity is achieved when $u_2$ becomes a linearly polarized state $(\left|{\widehat{n}}_2\right|=0)$.

The spin vector of $R_m$, when referred to with respect to the intrinsic reference frame, takes the form $n_O=I {(\cos \chi \sin \chi ,0,0)}^{\mathrm{T}}$, thus lying necessarily along axis $X_O$, showing the intrinsic transverse character of the spin vector of discriminating states. The absolute value of the intensity-normalized spin vector determines the degree of circular polarization $P_c=\left|\cos \chi \sin \chi \right|$.

The nature of discriminating states is evidenced when $R_{mO}$ is decomposed as

$$\begin{array}{l}{R}_{mO}=\frac{1}{2}I {\widehat{R}}_{l-x}+\frac{1}{2}I {\widehat{R}}_{e-x},\\ {\widehat{R}}_{l-x}\equiv u_{1O}\otimes u_{1O}^{†}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\\ {\widehat{R}}_{e-x}\equiv u_{2O}\otimes u_{2O}^{†}=\left(\begin{array}{ccc}0& 0& 0\\ 0& {\cos }^2\chi & -i\cos \chi \sin \chi \\ 0& i\cos \chi \sin \chi & {\sin }^2\chi \end{array}\right),\end{array}$$

(15)

that is, a discriminating state can always be interpreted as an equiprobable incoherent composition of an elliptically polarized pure state and linearly polarized state whose electric field fluctuates along the direction orthogonal to the polarization plane of the elliptically polarized component. Consequently, the information held by a discriminating state is completely characterized by its intensity and four angular parameters: namely, the three angles determining the spatial orientation of the state with respect to its intrinsic reference frame and the ellipticity angle χ.

The extremal values of the achievable range $0\le \left|\chi \right|\le \pi /4$ determine specific limiting physical configurations. The equality $\left|\chi \right|=0$ is entirely equivalent to any of the following statements: $R_m$ lacks spin, $R_m$ is a real matrix, $R_m$ corresponds to a 2D-unpolarized state, i.e., ${\widehat{R}}_{m0}=(1/2) \mathrm{diag} (1,1,0)$, the unitary matrix U is a real-valued matrix, i.e., U is an orthogonal matrix, and $R_m$ is an equiprobable incoherent mixture of two mutually orthogonal polarization states whose polarization planes coincide (including a pair of mutually orthogonal linearly polarized states, for instance). The equality $\left|\chi \right|=\pi /4$ corresponds to an equiprobable mixture of a linearly polarized state and a circularly polarized state with mutually orthogonal polarization planes. A proper measure of the distance of $R_m$ to a 2D-unpolarized state is given by the so-called degree of nonregularity [35]

$$P_N(R_m)=P_N(R_{mO})=2{\sin }^2\chi , \left[-\pi /4\le \chi \le \pi /4\right],$$

(16)

so that $0\le P_N\le 1$, with $P_N=1$ when $\left|\chi \right|=\pi /4$ (perfect nonregular state) and $P_N=0$ when $\left|\chi \right|=0$ (2D-unpolarized state).

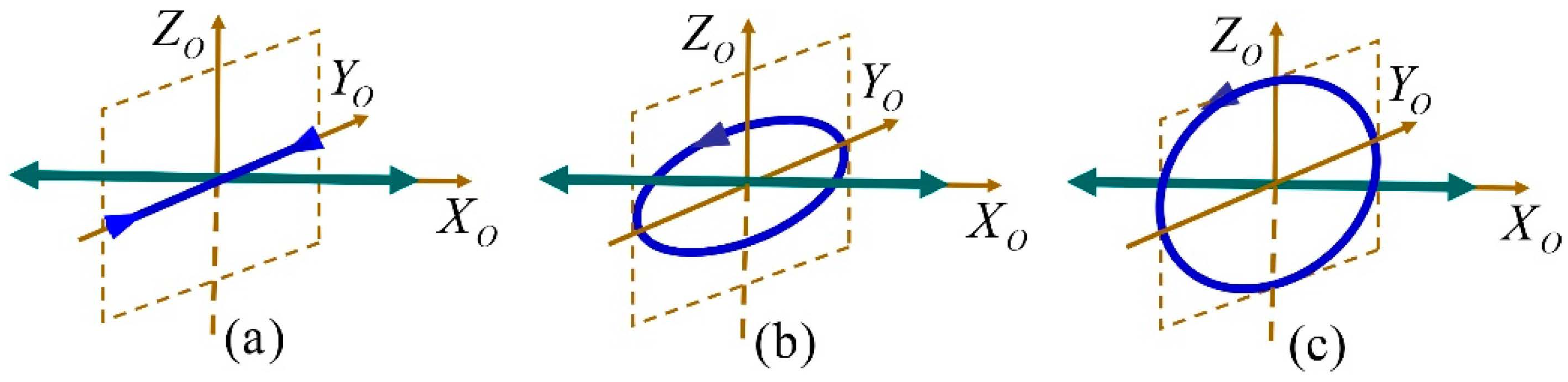
The possible configurations of the canonical eigenstates of a discriminating state are represented in Figure 3. Typical configurations of the polarization object of a discriminating state are shown in Figure 4.

Figure 3. A nonregular discriminating state $R_m$ can always be interpreted as an equiprobable mixture of an elliptically polarized state and a linearly polarized state. $X_O{Y}_O{Z}_O$ represent the intrinsic reference frame associated with $R_m$. (a) When the ellipticity of the component $u_{2O}$ is zero, then $R_m$ corresponds to a 2D-unpolarized state whose electric field fluctuates in the plane $X_O{Y}_O$, this corresponds uniquely to regular discriminating states, $P_N=0$. (b) When the ellipticity of the component $u_{2O}$ is nonzero, its polarization ellipse lies in the plane $Y_O{Z}_O$ orthogonal to the axis $X_O$ along which the electric field of the linearly polarized component fluctuates, $0<P_N\le 1$. (c) Maximal nonregularity, $P_N=1$, is achieved when $u_{2O}$ is a circularly polarized state, regardless of its handedness.

Figure 4. Polarization object of a discriminating state $R_m$$(P_1=0, P_2=1)$ is composed of its polarization ellipsoid and its spin vector. (a) The polarization ellipsoid of a discriminating state with zero spin, $P_c=0$ degenerates in a circle and corresponds uniquely to a 2D-unpolarized state, which constitutes a limiting situation characterizing regularity. (b) Nonregular discriminating states exhibit polarization ellipsoids whose three semiaxes are nonzero. As the third principal variance ${{\displaystyle \widehat{a}}}_3$, increases, the absolute value ${\displaystyle P_c}$ of the intensity normalized spin vector increases. (c) Maximal values for $P_c$ and ${\widehat{a}}_3$ correspond to perfect nonregular states, with $P_c=1/2$ and ${\widehat{a}}_3={\widehat{a}}_2=1/4$. Adapted with permission from Ref. [31] © 2021 by the authors.

From the analyses performed above, the properties of discriminating states of polarization can be summarized as follows.

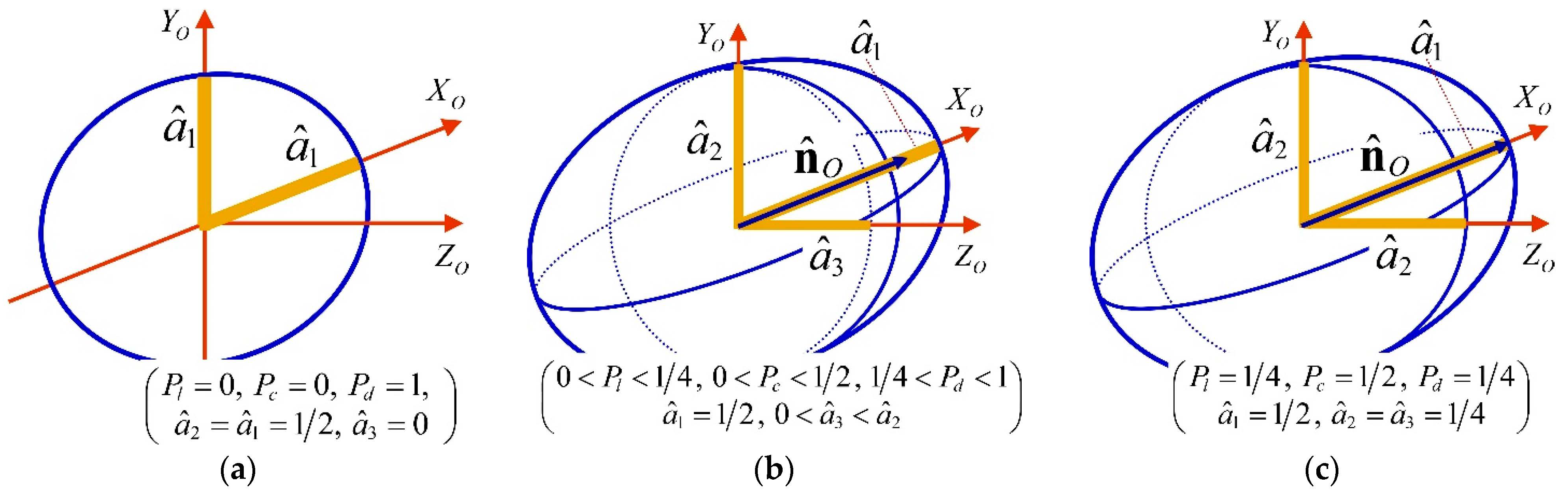
While the IPPs of a discriminating state take fixed values $(P_1=0, P_2=1)$, the achievable values of the CPs depend on the value of $\chi$ (i.e., on the value of $P_N$, see Figure 5)

$$\begin{array}{l}{P}_l=\frac{1}{2}{\sin }^2\chi =\frac{1}{4}{P}_N \Rightarrow \{\begin{array}{l}0\le P_l\le 1/4\hfill \\ P_l=0\iff \chi =0 (\mathrm{regular})\hfill \\ P_l=1/4\iff \chi =\pm \pi /4 (\mathrm{perfect} \mathrm{nonregular})\hfill \end{array}\\ P_d=1-\frac{3}{2}{\sin }^2\chi =1-\frac{3}{4}{P}_N \Rightarrow \{\begin{array}{l}1/4\le P_d\le 1\hfill \\ P_d=1\iff \chi =0 (\mathrm{regular})\hfill \\ P_d=1/4\iff \chi =\pm \pi /4 (\mathrm{perfect} \mathrm{nonregular})\hfill \end{array}\\ P_c=\left|\sin \chi \cos \chi \right|=\frac{1}{2}\sqrt{P_N\left(2-P_N\right)} \Rightarrow \{\begin{array}{l}0\le P_c\le 1/2\hfill \\ P_c=0\iff \chi =0 (\mathrm{regular})\hfill \\ P_c=1/2\iff \chi =\pm \pi /4 (\mathrm{perfect} \mathrm{nonregular})\hfill \end{array}\end{array}$$

(17)

Consequently, the degree of elliptical purity is given by

$$\begin{array}{l}{P}_e=\frac{\left|\sin \chi \right|}{2}\sqrt{1+3{\cos }^2\chi }=\frac{1}{4}\sqrt{P_N\left(8-3P_N\right)}\\ \Rightarrow \{\begin{array}{l}0\le P_e\le \sqrt{5}/4\hfill \\ P_e=0\iff \chi =0 (\mathrm{regular})\hfill \\ P_e=\sqrt{5}/4\iff \chi =\pm \pi /4 (\mathrm{perfect} \mathrm{nonregular})\hfill \end{array}\end{array}$$

(18)

Regarding the polarimetric dimension of discriminating states, it can be expressed as

$$\begin{array}{l}{D}_I=3-\sqrt{1-3{\sin }^2\chi {\cos }^2\chi }=3-\sqrt{1-\left(3/4\right)P_N\left(2-P_N\right) }\\ \Rightarrow \{\begin{array}{l}2\le D_I\le 5/2\hfill \\ D_I=2\iff \chi =0 (\mathrm{regular})\hfill \\ D_I=5/2\iff \chi =\pm \pi /4 (\mathrm{perfect} \mathrm{nonregular})\hfill \end{array}\end{array}$$

(19)

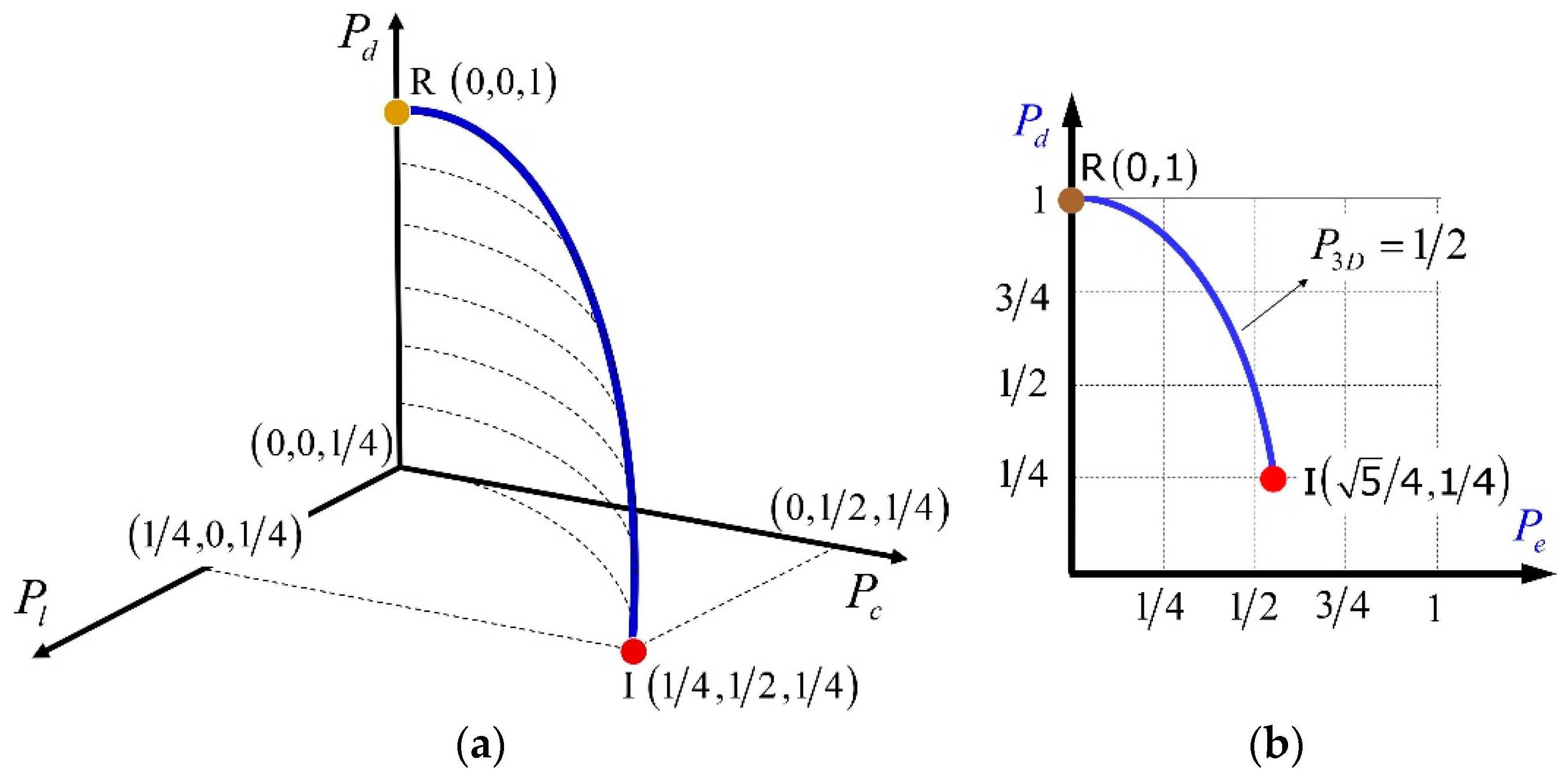
The feasible region for the CPs of a discriminating state is represented in Figure 6, and it is determined by the curve RI lying in the surface of an elliptical cylinder whose basis has semiaxes 1/4 along the positive branch of axis $P_l$, and 1/2 along the positive branch of axis $P_c$.

Figure 5. Achievable values of the components of purity $(P_l, P_c, P_d)$ of a discriminating state as functions of the degree of nonregularity $P_N$. $P_N=0$ corresponds to 2D-unpolarized states, for which $P_l=P_c=0$ and $P_d=1$. As $P_N$ increases up to $P_N=1$ (perfect nonregular states), $P_d$ decreases down to $1/4$, while $P_l$ and $P_c$ increase up to $1/4$ and $1/2$, respectively.

Figure 6. (a) Feasible region for the components of purity of a discriminating state $R_m$, given by a curve on the surface of an elliptical cylinder of semiaxes (1/4,1/2). Point R $(0,0,1)$ represents uniquely regular discriminating states (i.e., 2D-unpolarized states). Point I $(1/4,1/2,1/4)$ represents solely perfect nonregular states. The lower the value of $P_d$, the higher the degree of nonregularity. (b) Purity figure of a discriminating state, where the elliptical branch between points R and I determines the achievable pairs of values $(P_e,P_d)$.

The properties and characteristic values of the main polarization descriptors for discriminating states, including the limiting cases of regular and perfect nonregular states, are summarized in Table 1. Since the eigenvalues of any polarization matrix ${\widehat{R}}_m$ are $(1/2,1/2,0)$, both the indices of polarimetric purity and the degree of polarimetric purity have the fixed values $P_1=0$, $P_2=1$, $P_{3D}=1/2$. Furthermore, except for regular discriminating states, which lack spin, the spin vector lies along the intrinsic axis $X_O$.

Table 1. Characteristic properties of discriminating states.

	Regular	Nonregular	Perfect Nonregular
Degree of nonregularity	$P_N=0$	$0<P_N<1$	$P_N=1$
Components of purity	$P_l=0, P_c=0, P_d=1$	$0<P_l<1/4, 0<P_c<1/2, 1/4<P_d<1$	$P_l=1/4, P_c=1/2, P_d=1/4$
Ellipticity angle of the canonical component $u_{2O}$	$\chi =0$ (linear polarization)	$\left|\chi \right|<\pi /4$ (elliptical polarization)	$\left|\chi \right|=\pi /4$ (circular polarization)
Principal variances	${\widehat{a}}_1=1/2, {\widehat{a}}_2=1/2, {\widehat{a}}_3=0$	${\widehat{a}}_1=1/2, 1/4<{\widehat{a}}_2<1/2, 0< {\widehat{a}}_3<1/4$	${\widehat{a}}_1=1/2, {\widehat{a}}_2= {\widehat{a}}_3=1/4$
Polarization object	Figure 4a	Figure 4b	Figure 4c
Polarization matrix	$\frac{I}{2}\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)$	$\begin{array}{c}\frac{I}{2}Q\left(\begin{array}{ccc}1& 0& 0\\ 0& c_{\chi }^2& -i s_{\chi }{c}_{\chi }\\ 0& i s_{\chi }{c}_{\chi }& s_{\chi }^2\end{array}\right)Q^{\mathrm{T}}\\ \left[Q^{\mathrm{T}}=Q^{-1}, \left|\chi \right|<\pi /4\right]\end{array}$	$\begin{array}{c}\frac{I}{4}Q\left(\begin{array}{ccc}2& 0& 0\\ 0& 1& -i\\ 0& i& 1\end{array}\right)Q^{\mathrm{T}}\\ \left[Q^{\mathrm{T}}=Q^{-1}\right]\end{array}$

4. Summary

As a summary, we analyzed the properties of the discriminating polarization states which are essential in the characteristic decomposition of the 3×3 polarization matrix. Such states are equally-weighted superpositions of two polarization states represented by the eigenvectors of the two largest eigenvalues. In general, a discriminating state is a genuine 3D state, but in a special case, it becomes a 2D-unpolarized state. We evaluated the indices and components of purity, polarimetric and elliptical purity, polarimetric dimension, as well as nonregularity properties of the discriminating states. The results are important for understanding the structure of genuine 3D polarization states which are encountered in high-NA focal fields and optical near fields including the evanescent waves and plasmon surface waves.