Link Resource-Aware RMSA Algorithm for Advance Reservation Requests in Semi-Filterless Optical Networks

Abstract

This paper investigates the routing, modulation, and spectrum assignment (RMSA) problem for advance reservation (AR) requests in semi-filterless optical networks (semi-FONs). A link resource-aware (LRA) algorithm consisting of three parts is proposed. First, in the request scheduling phase, a request sorting strategy based on the flexible window size of the starting time is proposed. This strategy schedules AR requests based on the size of a flexible window with respect to the starting time. Next, in the routing phase, a link resource-aware strategy is proposed. This strategy evenly distributes the requests across the network resources, thereby avoiding request blocking due to excessive resource occupation on a single or few links. In the spectrum assignment phase, a frequency–time block-based metric is employed to measure the availability of each frequency–time block for AR requests. This metric is a sum of two factors: the distance to the block and spectrum boundaries, and the time interval between the request start time and the earliest start time. Our simulation results demonstrate that the proposed LRA algorithm has a lower blocking probability compared to the benchmark algorithms.

1. Introduction

With the development of the digital era, the emergence of large-scale online games, video calls, and short online videos has led to rapid growth in traffic. Operators need to meet the increasing demand for user traffic while controlling costs. As a low-cost networking solution, filterless optical networks (FONs) have gained the favor of operators.

The concept of filterless optical networks (FONs) was first proposed by Christine Tremblay et al. [1]. With the support of coherent transmission and electrical compensation techniques [2,3], FONs utilize optical splitters/combines at network nodes to interconnect optical fiber links, replacing reconfigurable optical add–drop multiplexers (ROADMs) based on optical switches (WSS) at the nodes. The use of economical optical splitters/combiners significantly reduces network costs. However, the absence of optical switches at the nodes causes the optical signal at the input ports to be broadcast to all output ports. As a result, even if the signal reaches its destination, it continues to propagate further [4], leading to a significant waste of spectrum. Due to the broadcasting and selection architecture of FONs, a fiber network needs to establish one or multiple fiber trees [5]; each fiber link must be assigned to exactly one tree, and there should be no closed loops in the tree structure. As all fiber trees are optically isolated from each other [6], signals cannot propagate from one tree to another, which restricts continuous signal broadcasting and prevents laser loops. This leads to an additional drawback, as routing and spectrum assignment are constrained by the established fiber trees. Modifying the fiber interconnections within nodes, i.e., dynamically changing the configuration of fiber trees, is impractical [7].

To address these drawbacks of FONs, the concept of semi-filterless optical networks (semi-FONs) was proposed by J. Chen et al. in 2011 [8]. The method of discarding local signals at certain nodes by inserting passive color components (such as fiber Bragg gratings, red/blue filters, etc.) in an filterless optical network is called a semi-filterless optical network. In the same year, they proposed a heuristic algorithm to solve the placement and wavelength assignment problem for filters [9]. In 2018, O. Ayoub et al. considered the solutions of filterless and semi-filterless architectures in the Metro-HAUL network architecture [10]. They developed a heuristic method to form fiber trees in the network and then solved the routing and spectrum assignment (RSA) problem using an integer linear programming (ILP) approach. The results showed that semi-FONs outperform FONs in terms of spectrum utilization.

This paper investigates the routing, modulation, and spectrum assignment (RMSA) problem for advance reservation (AR) requests in semi-filterless optical networks. First, due to the broadcasting nature of semi-filterless networks, requests may propagate on unnecessary links, resulting in wasted links. The existence of wasted links occupies more spectrum resources, and because spectrum resources in the network are limited, the broadcasting nature of semi-filterless networks reduces the available spectrum resources. As a result, incoming requests may be rejected due to insufficient spectrum resources, leading to an increased blocking probability. Second, the dynamic establishment and teardown of advance reservation requests results in a large number of two-dimensional fragments. The generation of these fragments reduces the availability of resources and increases the blocking probability of requests. Furthermore, advance reservation requests have the characteristics of resource reservation and time flexibility, making the fragmentation problem even more complex. To address these issues, in this paper we propose the link resource-aware (LRA) algorithm, with the following main contributions:

• Request Sorting Strategy: considering the characteristics of advance reservation (AR) requests, which involve resource reservation and time flexibility, it is important to schedule these requests in a reasonable manner in order to avoid subsequent requests being rejected due to a lack of suitable time resources. Therefore, during the request scheduling phase, a request sorting strategy based on the size of a flexible window of the starting time is proposed. Requests arriving in the network at the same time are sorted in ascending order based on the size of this flexible window of the starting time.
• Link Resource-Aware Strategy: considering the broadcasting nature of semi-filterless optical networks, signals occupy more resources as they propagate. Resources in the network are limited, and increased resource occupation leads to reduced availability of resources. To avoid requests being rejected due to excessive resource occupation on a single or few links, a path resource awareness factor is introduced during the routing phase. First, K-shortest path algorithms are used to find K paths and wasted links for each request. Then, the K paths are sorted in ascending order based on the path awareness factor.
• The Frequency–Time Block Metric: the dynamic establishment and teardown of advance reservation (AR) requests generates a large number of two-dimensional fragments, and reducing fragmentation means concentrating idle frequency–time slots. During the spectrum assignment phase, a frequency–time block metric is introduced, which is the sum of two factors: the distance between the block and the spectrum boundary, and the interval between the request start time and the earliest start time.

The effectiveness of the proposed algorithm was validated through performance evaluations on the German-Net and Henan-Net networks. The results demonstrate that the blocking probability of the proposed algorithm is lower than that of the compared algorithms.

The rest of the paper is organized as follows. Section 2 provides an overview of related works. Section 3 introduces the network model. Section 4 provides a detailed description of the link resource-aware (LRA) algorithm. Section 5 presents the simulation results that demonstrate the performance of the algorithm. Finally, Section 6 concludes the paper.

2. Related Work

In recent years, extensive research has been conducted on advance reservation (AR) requests, leading to various research achievements. In this section, we provide a brief overview of the RMSA algorithm for AR requests.

In 2015, Chen et al. proposed a time spectrum consecutiveness-based scheduling algorithm for AR requests [11]. They introduced the concept of time spectrum consecutiveness (TSC) to describe the spectrum fragmentations along the frequency axis and time axis. Based on TSC, they proposed three time-aware routing and spectrum assignment (RSA) algorithms.

In 2016, Afsharlar et al. conducted a study on delayed spectrum allocation methods for advance reservations [12,13]. This approach, called delayed spectrum allocation (DSA), promises network resources to each demand upon request for scheduling, then delays the selection and allocation of those specific resources until immediately before transmission begins.

In 2017, Wang et al. studied the reprovisioning problem for AR applications in elastic optical networks (EONs) [14]. They introduced a reprovisioning-enabled control framework based on SDN and a reprovisioning optimization (RPO) algorithm with three reprovisioning policies.

In 2019, Li et al. studied the RMSA problem for AR requests in EON [15]. They designed an algorithm called Min-RDDR that uses a weighted sum of four factors: the resources consumed by the block ($R_c$), distance between the block and the frequency boundary ($D_f$), distance between the block and the earliest starting time of AR request ($D_t$), and resources degraded by the block ($R_d$).

In 2021, Liu et al. proposed the MRC-2D-FA algorithm [16]. This algorithm consists of two parts. First, a minimum resource consumption routing strategy(MRC) was proposed during the routing phase. Second, in the spectrum allocation phase, a two-dimensional fragmentation-aware spectrum assignment strategy (2D-FA) was proposed. In the same year, Mahala et al. considered the problem of routing and spectrum assignment in EONs for advanced reservation traffic and proposed a suitable technique for this problem [17]. They proposed a strategy called spectrum allocation using prediction and reservation (SAPR). This approach enhances the number of connections served by predicting the traffic demand, and reserves spectrum resources based on the precomputed connection request capacity.

In 2022, Ujjwal et al. presented a method called outright fit advanced resource reservation (OFARR) [18]. This method is divided into two stages. The proposed resource reservation strategy uses an outright fit resource allocation strategy to reserve the spectral resource for a connection request within the absolute best service window while leaving adequate spectral resources for subsequent requests. If a connection request does not receive resources in the first stage, the proposed optimal rescheduling technique then is applied to serve the request.

In 2023, Zhao et al. proposed a fragmentation-aware routing, modulation, and spectrum assignment (RMSA) algorithm for AR requests [19]. A delayed resource allocation is developed for AR requests, followed by a resource allocation sorting strategy based on the relative flexibility of requests. This strategy makes full use of the time characteristics of AR requests to determine their allocation order. Additionally, to address the impact on adjacent resources, a 2D path resource model was introduced to evaluate the impact of 2D fragmentation from the perspective of resource matching degree and resource connectivity. In the same year, Zhao et al. investigated the virtual network mapping problem for static advance reservation in elastic optical networks [20]. The problem involved a set of predefined virtual network requests needing to be scheduled within specified time windows. They proposed an integer linear programming formulation and a heuristic method. In the same year, Wang et al. studied the dynamic RMSA problem in semi-filterless optical networks [21]. They proposed the Minimum Resource Consumption and Fragmentation (Min-RCF) algorithm, consisting of a routing algorithm that sorts routes based on resource consumption and a spectrum assignment algorithm that minimizes fragmentation. Xie et al. proposed a minimum link and boundary distance spectrum assignment algorithm based on adaptive modulation schemes in semi-filterless optical networks [22]. Their algorithm selects the path with the least occupied links during the routing process for spectrum assignment and combines it with a variable adaptive scheme between optical fibers. During the spectrum assignment process, the spectrum resources are divided into two regions, with locations closer to the spectrum boundary selected for spectrum assignment.

In addition, there are studies on immediate and advance reservation requests. Wang et al. considered the RMSA problem for immediate and advance reservation requests in elastic optical networks [23]. They designed a two-dimensional resource model to maintain the status information of resources in both the frequency and time domains and developed a two phase RMSA algorithm. Lu et al. investigated the provision of hybrid immediate reservation (IR) and AR services in elastic optical networks [24]. They proposed an IR+AR scheme that significantly reduces IR service failures as well as RSA reconfigurations in IR service provisioning. Sugihara et al. proposed a dynamic routing and spectrum assignment approach that supports both IR and AR requests [25]. This method includes three parts. First, it divides the priority area based on the frequency slots required by the requests. Second, each priority area is divided into two sub-areas, one dedicated to IR requests and the other shared by IR and AR requests. Third and finally, IR requests can select a routing path among all the routes with minimum hops, while AR requests can only choose a specific route with the minimum number of hops. Zhu et al. proposed a multi-path fragmentation-aware RMSA algorithm for IR and AR in elastic optical networks [26,27]. In their algorithm, a metric called spectrum-time-cut was defined to measure the occurrence of fragmentation when using spectral blocks. In the same year, they proposed a multi-dimensional resource assignment algorithm for IR and AR requests in SDM-EON [28]. Sugihara et al. studied the dynamic resource assignment for IR and AR in SDM-EON [29]. They introduced priority areas to reduce spectrum fragmentation by ordering spectrum resources in the frequency domain and divided the priority into IR-dedicated and shareable sub-areas, allowing the boundary between the two sub-areas to be dynamically controlled in order to manage the blocking probability.

The aforementioned studies on AR requests were all conducted on EON and SDM-EON; there is currently no research on AR request routing, modulation, and spectrum allocation (RMSA) in semi-FONs. Therefore, in this paper we investigate the RMSA problem for advance reservation (AR) requests in semi-filterless optical networks. A link resource-aware (LRA) algorithm is proposed, and simulation experiments are conducted on the German-Net and Henan-Net network topologies. Our results demonstrate that the proposed LRA algorithm exhibits superior performance.

3. Network Model

The network model of a semi-filterless optical network can be represented as a directed graph $G\left(V,E\right)$, where V is the set of nodes and E is the set of links. An advance reservation (AR) request with an unspecified start time and duration can be represented as $R\left(s,d,C,D,t_a,t_{es},W\right)$, where s is the source node of the request, d is the destination node, C is the capacity requirement, D is the duration of the request, $t_a$ is the arrival time, $t_{es}$ is the earliest start time, and W is the size of flexible window of the starting time. The number of frequency slots required for each AR request can be calculated as follows:

$$S_k=⌈\frac{C}{C_{slot}·m_k}⌉+S_p$$

(1)

where $C_{slot}$ is the bandwidth of one frequency slot, $C_{slot}$ = 12.5 Ghz, $m_k$ is the level of the modulation format, $\lceil ·\rceil$ is rounded upward, $S_p$ is the number of protected bandwidth frequency slots, and $S_p=1$.

To describe the resource occupancy of a semi-filterless optical network clearly, the resources on a link are modeled as a two-dimensional link resource model. Each small grid on the link resource model is defined as a frequency–time slot. Each frequency–time slot can be in either an occupied or free state. Assuming that the resources of link l are divided into F frequency slots and T time slots, the state of each frequency–time slot can be represented as $U_{f,t}^l$.

$$U_{f,t}^l=\left\{{}_{1, free}^{0, occupied}\right.$$

(2)

Here, $U_{f,t}^l$ represents the state of the frequency–time slot represented by the $f_{th}$ frequency slot and the $t_{th}$ time slot on link l. When $U_{f,t}^l=0$, it indicates that the frequency–time slot is occupied, while when $U_{f,t}^l=1$ it indicates that the frequency–time slot is free. Consequently, the state matrix of the link resource model can be obtained as follows:

$$U_{F,T}^l={\left[U_{f,t}^l\right]}_{F\times T}$$

(3)

where $U_{F,T}^l$ represents the state matrix of the resource model for link l, $F\times T$ indicating that the matrix has F rows for frequency slots and T columns for time slots. Figure 1 depicts a two-dimensional resource model for a link. As shown in the figure, the horizontal axis represents the time and the vertical axis represents the frequency. The spectrum resources on the link are divided into F frequency slots and the time resources into T time slots.

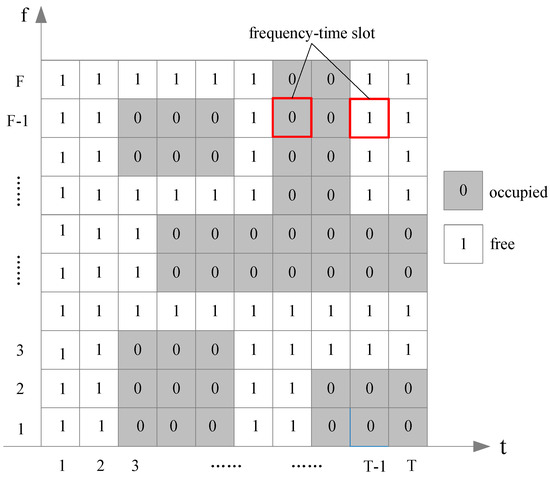
Figure 1. Example of a two-dimensional link resource model.

In a semi-filterless optical network, the allocated resources for a request must be contiguous across all links, meaning that the frequency–time slots used by a request must be the same on all links included in the routing path and in the waste links generated by broadcasting. Assuming that the routing path for the request is P, which consists of L links and $L^{\prime }$ waste links, the state matrix of the path resource model for path P is as follows:

$$U_{F,T}^P={\left[U_{f,t}^P\right]}_{F\times T}$$

(4)

where $U_{F,T}^P$ is the state matrix of the resource model for path P, and expression for $U_{f,t}^P$ is as provided below.

$$U_{f,t}^P=\left\{{}_{1, {\displaystyle \prod _{l\in L_{sum}}}{U}_{f,t}^P=1}^{0, {\displaystyle \prod _{l\in L_{sum}}}{U}_{f,t}^P=0}\right.,L_{sum}=L\cup L^{\prime }$$

(5)

4. Link Resource-Aware (LRA) Algorithm

In this section, we provide a detailed introduction to the link resource-aware RMSA algorithm. The algorithm consists of three subalgorithms: a request sorting strategy, link resource-aware strategy, and frequency–time block metric. During the request scheduling phase, the request sorting strategy is employed. For requests arriving at the same time, requests with a smaller flexible window for the starting time receive priority in scheduling. During the routing phase, the link resource-aware strategy is utilized. This strategy ensures that requests evenly occupy the network resources, avoiding blockages caused by excessive resource occupation on a single link or few links. In the spectrum assignment phase, a metric based on frequency–time blocks is applied to evaluate their quality. It primarily considers the distance between blocks and spectrum boundaries and the time interval between the request start time and the earliest start time.

4.1. Request Sorting Strategy

Advance reservation requests have the characteristics of resource reservation and time flexibility. For requests arriving at the same time $t_a$, the size of flexible window of the starting time W for advance reservations varies. The larger the flexible window of the starting time W for a request, the greater the range of possible start times for the advance reservation. Therefore, advance reservation requests with larger W have a higher possibility of resource assignment. Therefore, during the request scheduling phase any requests arriving in the network at the same time are sorted in ascending order based on the size of the flexible window of the starting time W for advance reservations. The advance reservations are then scheduled according to the sorting results.

4.2. Link Resource-Aware Strategy

In semi-FONs, the broadcast nature of non-filtering nodes results in signal propagation beyond the expected nodes. Therefore, in addition to propagating along the routing path, the signal may propagate on other links. The propagation of requests on more links implies the occupation of more spectrum resources. As the spectrum resources in the network are limited, the broadcast characteristics of the semi-filterless network reduce the available spectrum resources in the network. Requests may be rejected due to insufficient spectrum resources on a single or few links along the path.

To address this issue and reduce the blocking probability of requests in the network, we employ a link resource-aware strategy. We define a link resource-aware factor, denoted as e. Assuming that there are F frequency slots and T time slots on each link and letting U represent the number of occupied frequency–time slots on the link, the expression for the link resource-aware factor e is provided by Equation (6). The link resource-aware factor e can be used to measure the occupancy of link resources.

$$e=\frac{U}{F\ast T}$$

(6)

Assuming that the routing path of request R consists of m links and n wasted links, the request R needs to propagate through $m+n$ links. In both the routing path and the wasted links, if there is even one link without available resources for the request it will result in the request being blocking. Therefore, it is only necessary to determine the maximum link resource-aware factor among the $m+n$ links. Thus, the expression for the path resource-aware factor E can be represented as

$$E=max\left\{e_1,e_2,\cdots e_m,e_1^{\prime },e_2^{\prime },\cdots e_n^{\prime }\right\},$$

(7)

where $e_m$ represents the link resource-aware factor of the $m_{th}$ link on the routing path and $e_n^{\prime }$ represents the link resource-aware factor of the $n_{th}$ wasted link.

As we aim to evenly occupy the network resources with requests and avoid blocking due to excessive resource occupation on a single or few links, during the routing phase we employ the K-shortest path algorithm to find the K shortest paths for each AR request. These K shortest paths are then sorted in ascending order based on the path resource-aware factor E.

We provide an example to illustrate this. Figure 2 shows a network topology diagram with six nodes and nine links. The white nodes represent non-filtering nodes and the yellow nodes represent filtering nodes. The long dashed lines represent fiber tree 1 (Tree1), and the short dashed lines represent fiber tree 2 (Tree2). Each link has a total resource capacity of 10. Figure 2a displays the resource occupancy in the network. Assuming that request $R_1$ is from node 6 to node 3 (6→3), the K-shortest path algorithm finds three routing paths for it. According to the path distance, they are Path1 (6→3), Path2 (6→5→3), and Path3 (6→1→2→3). Due to the broadcast nature of non-filtering nodes, the signal propagates throughout the fiber tree. As shown in Figure 2c, Path2 has two wasted links, namely, link (5,4) and link (4,3). Using Equations (6) and (7), we can calculate the link resource-aware factor for Path1 as $e\left(6,3\right)=\frac{7}{10}$ and the path resource-aware factor as $E\left(Path1\right)=max\left\{e(6,3)\right\}=\frac{7}{10}$. The link resource-aware factor for Path2 is $e\left(6,5\right)=e\left(5,3\right)=e\left(5,4\right)=e\left(4,3\right)=\frac{5}{10}$ and the path resource-aware factor is $E\left(Path2\right)=max\left\{e(6,5),e\left(5,3\right),e\left(5,4\right),e\left(4,3\right)\right\}=\frac{5}{10}$. The link resource-aware factor for Path3 is $e\left(6,1\right)=e\left(1,2\right)=\frac{3}{10},e\left(2,3\right)=\frac{4}{10}$ and the path resource-aware factor is $E\left(Path3\right)=max\left\{e(6,1),e\left(1,2\right),e\left(2,3\right)\right\}=\frac{4}{10}$. Sorting the paths in ascending order based on the path resource-aware factor E, the correct order is Path1 (6→1→2→3), Path2 (6→5→3), Path3 (6→3).

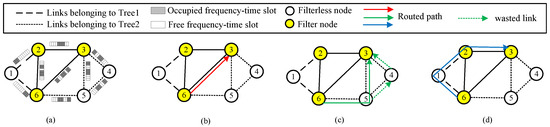
Figure 2. (a) The state of resources in the network. (b) The red path represents Path1. (c) The green path represents Path2 and its wasted links. (d) The blue path represents Path3.

4.3. The Metric of the Frequency–Time Block

During the spectrum assignment phase, there may be multiple available frequency–time blocks for a path to use. Selecting the appropriate frequency–time block for the current request is beneficial in leaving more available resources for subsequent requests. Therefore, we introduce a metric to measure the situation of each available frequency–time block for the AR request. This metric is the sum of two factors, namely, the distance between the block and frequency boundaries and the interval between the start time of the AR request and the earliest start time.

(1) The distance to the spectrum boundary. Spectrum resources have two frequency boundaries. Assume a link has F frequency slots, where $B_s$ is the frequency starting index of the frequency–time block and $B_e$ is the frequency ending index of the frequency–time block. The minimum distance between the frequency–time block and the boundaries is

$$D_f=min\left\{D_{down},D_{up}\right\}$$

(8)

where $D_{down}$ = $B_s-1$, $D_{up}$ = $F-B_e$.

(2) The distance to the earliest start time. The distance between the frequency–time block and the earliest start time can be calculated using the following formula:

$$D_t=t_{start}-t_{es}+1$$

(9)

where $t_{start}$ is the start time of the frequency–time block and $t_{es}$ is the earliest start time of the request.

Spectrum resources have two frequency boundaries. If the frequency–time block is closer to the spectrum boundary it can free up the middle area of the spectrum resources, which is advantageous for allocating spectrum resources to subsequent requests. Additionally, although the start time of the AR request is relatively flexible, subsequent requests will continue to enter the network as time progresses. In order to avoid occupying the time resources of subsequent requests, it is better to allocate resources to the request as early as possible, i.e., when the frequency–time block is closer to the earliest start time $t_{es}$ of the request. Based on these two metrics, we hope to find a frequency–time block that is closer to both the spectrum boundary and the earliest start time of the request. Therefore, we want the value of the metric M for the block to be as small as possible.

$$M=D_f+D_t$$

(10)

In Figure 3, we provide an example of spectrum assignment. Suppose that request $R_1$ has three available frequency–time blocks along a path: $B_1$, $B_2$, and $B_3$. According to Equations (8) and (9), block $B_1$ is closer to the upper spectrum boundary, with $D_f^1=D_{up}=2$ and $D_t^1=3$. Block $B_2$ is closer to the lower spectrum boundary, with $D_f^2=D_{down}=1$ and $D_t^2=5$. Block $B_3$ is equidistant from both the upper and lower spectrum boundaries, with $D_f^3=D_{up}=D_{down}=6$ and $D_t^3=2$. According to Equation (10), we obtain the following metrics for the blocks: $M\left(B_1\right)=2+3=5$, $M\left(B_2\right)=1+5=6$, $M\left(B_3\right)=6+2=8$. Thus, block $B_1$ is the optimal choice among the three available blocks.

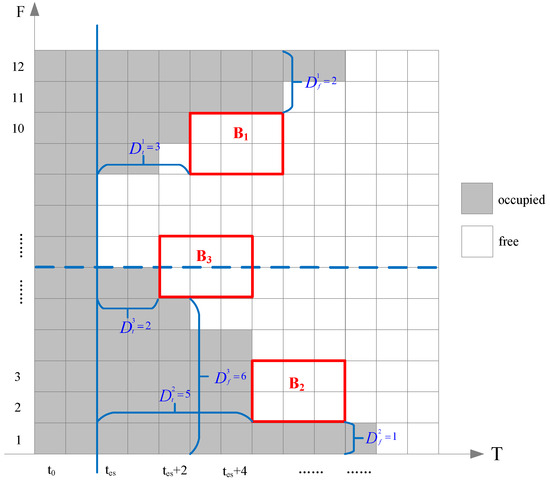
Figure 3. An example showing the investigated factors. (In the graph, $B_1$, $B_2$, and $B_3$ represent frequency–time blocks, $D_f$ is the minimum distance between the frequency–time block and the spectrum boundary, and $D_t$ is the distance between the frequency–time block and the earliest start time).

4.4. Procedure of the Proposed Algorithm

Algorithm 1 describes the detailed process of the LRA algorithm. The input of the algorithm is the physical topology $G\left(V,E,T\right)$ and the set of requests R that arrive at time $t_a$. Here, V represents the set of nodes, E represents the set of fiber links, and T represents the set of fiber trees. The output of the algorithm is the selected path $P_k$ for the request and the frequency–time block $B^{*}$.

The first line of the algorithm is used for initialization. The second line involves sorting the requests using a request sorting strategy during the request scheduling phase. Lines 3–20 find the propagation path and frequency–time block for each request. Lines 4–7 sort the K shortest paths based on the path-aware factor E. Lines 8–19 involve a loop for the K paths. Line 10 calculates the number of frequency slots required for the request on path $P_k$. Line 11 retrieves the frequency–time slot status of the links to find available frequency–time blocks. Line 13 calculates the metric value for the frequency–time block, and lines 14–17 determine the quality of the frequency–time block based on the metric value. Finally, the optimal frequency–time block is selected. Figure 4 shows the flowchart of Algorithm 1.

Algorithm 1: LRA algorithm

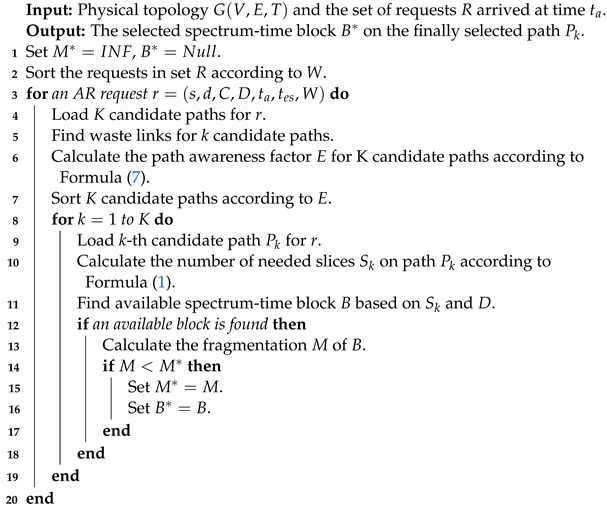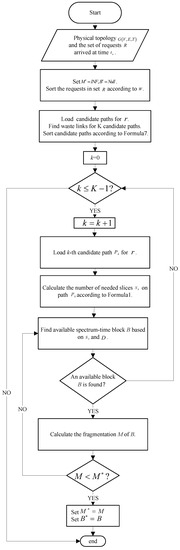
Figure 4. The flowchart of Algorithm 1.

4.5. Complexity Analysis

We denote the number of nodes in the network as $\left|V\right|$, the total number of links as $\left|E\right|$, the number of fiber trees as $\left|T\right|$, the number of frequency slots per link as $\left|F\right|$, the maximum number of path links as $\left|L\right|$, and the maximum number of waste links as $\left|L^{\prime }\right|$, moreover, W is the size of flexible window of the starting time of the request, C is the capacity requirement, and D is the duration of the request.

The LRA algorithm consists of two parts, namely, routing and spectrum assignment. In the routing phase, the first step of Algorithm 1 is to find K shortest paths with a time complexity of $O\left(\left|K\right|·\left|E\right|+\left|V\right|log\left|V\right|\right)$. The fifth line of Algorithm 1 finds the waste links for the K paths, with a time complexity of no more than $O\left(\left|K\right|·\left|L\right|·\left|T\right|\right)$. In the spectrum assignment phase, the frequency–time slot status of a link is checked $O(\left|F\right|·(\left|W\right|+\left|D\right|))$ times. A path checks at most $O(\left(\left|L\right|+\left|L^{\prime }\right|\right)·\left|F\right|·(\left|W\right|+\left|D\right|))$ times. There are K paths, and these K paths need to be looped $\left|K\right|$ times, with a time complexity of no more than $O\left(\left|K\right|·\left|F\right|·\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|)\right)$. Finally, the time complexity of the LRA algorithm is no more than $O\left(\left|K\right|·\left(\left|E\right|+\left|L\right|·\left|T\right|+\left|F\right|·\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|)\right)+\left|V\right|log\left|V\right|\right)$.

In comparison, the time complexity of the RDDR algorithm in the routing phase is $O\left(\left|K\right|·\left(\left|E\right|+\left|L\right|·\left|T\right|\right)+\left|V\right|log\left|V\right|\right)$, while the time complexity in the spectrum assignment phase is $O\left(\left|K\right|·\left|F\right|·\left(\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|)+\left|W\right|·\left|C\right|·\left|D\right|\right)\right)$. The overall time complexity is $O\left(\left|K\right|·\left(\left|E\right|+\left|L\right|·\left|T\right|+\left|F\right|·\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|)\right)+\left|V\right|log\left|V\right|\right)$. In addition, the time complexity of the RFFA algorithm in the routing phase is $O\left(\left|V\right|log\left|V\right|+\left|L\right|·\left|T\right|\right)$, while the time complexity in the spectrum allocation phase is $O\left(\left|F\right|·\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|+\right.$$\left.\left|C\right|)\right)$. The overall time complexity is $O\left(\left|L\right|·\left|T\right|+\left|V\right|log\left|V\right|+\left|F\right|·\left(\left|L\right|+\left|L^{\prime }\right|\right)·(\left|W\right|+\left|D\right|\right.$$\left.+\left|C\right|)\right)$. Therefore, compared to the baseline algorithm, the proposed LRA algorithm has a lower time complexity.

5. Performance Simulations

In this section, the performance of the proposed algorithm is evaluated through simulations. The LRA algorithm proposed in this paper is compared with the Min-RDDR algorithm [15] and the RFFA algorithm [19]. The Min-RDDR algorithm proposed by Li et al. is a weighted sum of four factors: the resources consumed by the block ($R_c$), distance between the block and the frequency boundary ($D_f$), distance between the block and the earliest starting time of AR request ($D_t$), and resources degraded by the block ($R_d$). The RFFA algorithm proposed by Zhao et al. consists of two parts. In the request scheduling phase, an AR request sorting strategy is used to improve resource utilization by prioritizing requests with higher relative flexibility. In the resource provisioning phase, fragmentation is suppressed by increasing connectivity to adjacent occupied resources and reducing the impact on the integrity of free resources. Simulations were conducted on German-Net and Henan-Net to validate the effectiveness of our proposed algorithm. Blocking probability graphs and spectrum utilization graphs are provided to demonstrate the performance.

5.1. Simulation Settings

Figure 5a shows the German network (German-Net) with 17 nodes and 25 links, while Figure 5b depicts the Henan network (Henan-Net) in China with 18 nodes and 25 links. In these figures, the yellow nodes represent filterable nodes and the white nodes represent non-filterable nodes. Links of the same color belong to the same tree (excluding the black links), and the numbers on the links indicate their lengths in kilometers (km).

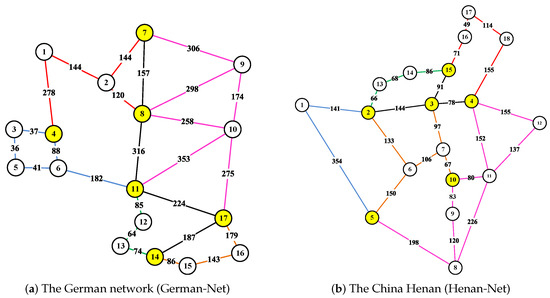
Figure 5. Test networks of (a) 17-node 25-link German-Net and (b) 18-node 25-link Henan-Net.

In the simulation, all links were bidirectional and the spectrum resources in each direction were divided into 320 frequency slots, with each slot having a bandwidth of 12.5 GHz. Additionally, the spectrum resources were divided into time slots of 10 min in size. The arrival intervals of requests followed a Poisson distribution with a parameter of $1/\lambda$, and the duration of requests followed a negative exponential distribution with a time slots parameter of ten. The traffic was uniformly distributed randomly among all nodes. The earliest start time was randomly selected from [1, 30] time slots, while the flexible window size for the start time was chosen from [1, 20] time slots. The selected modulation formats in the simulation were 8-QAM, 16-QAM, and 32-QAM, with respective bit rates per symbol of 3, 4, and 5. The maximum reach distances for the modulation formats were 2500 km, 1250 km, and 625 km, respectively. The required traffic for the requests was simplified as the number of frequency slots (FSs), which were randomly generated between 2 and 18 with an average of 10, equivalent to a traffic demand range of 25–225 Gbps. The traffic load of the network was $u·\lambda ·10$ erlangs, with the parameter u fixed at 10. It was possible to change the traffic load in the network by varying the value of $\lambda$.

5.2. Simulation Results

We conducted tests under different traffic loads using ten sets of 100,000 requests to compare the blocking probability and spectrum utilization of the RCF algorithm with the Min-RDDR algorithm and the RFFA algorithm. To ensure fairness, the comparison algorithms were based on K-shortest path routing, with k = 3. We do not analyze the value of k in this paper. The simulation results had a 95% confidence interval and an error margin within 5%.

The blocking probability (BBP) and spectrum utilization (SU) are important metrics for evaluating algorithm performance [30], and their formulas are shown below:

$$BP=\frac{{BR}_{block}}{{BR}_{total}}$$

(11)

$$SU=\frac{\mu \left({BR}_{total}-{BR}_{block}\right)}{N_{FS}·N_{link}·clock}$$

(12)

where ${BR}_{block}$ represents the set of blocked request bandwidth, ${BR}_{total}$ represents the total bandwidth of requests, $N_{FS}$ represents the total number of frequency slots per link, $N_{link}$ is the total number of links in the network, clock is the simulation time, and $\mu$ is the parameter of the exponential distribution.

Figure 6 shows the blocking probability graphs of the proposed LRA algorithm compared to the Min-RDDR algorithm and the RFFA algorithm in the German network and the Henan network under different traffic loads. From the graph, it can be observed that as the traffic load increases, the blocking probability of requests gradually increases as well. This is because the number of requests entering the network per unit time increases with the increase in traffic load. As the network resources are limited, more requests may have to be rejected due to insufficient resources when requests arrive more densely in the unit time. Furthermore, it is evident that the blocking probability of the LRA algorithm is always lower than that of the Min-RDDR and RFFA algorithms. This is because the proposed LRA algorithm considers three aspects to reduce the blocking probability. It introduces a request sorting strategy in the request scheduling phase, a link-aware factor sorting strategy in the routing phase, and a frequency-time block metric strategy in the spectrum allocation phase.

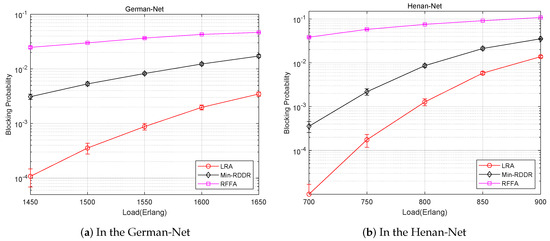
Figure 6. Comparison of blocking probability in (a) German-Net and (b) Henan-Net.

Figure 7 shows the spectrum utilization graphs of the proposed LRA algorithm compared with the Min-RDDR algorithm and the RFFA algorithm on the German network and the Henan network under different traffic loads. As can be seen from the graph, the spectrum utilization gradually increases with the increase in traffic load. This is because as the traffic load increases, the density of requests in the network increases as well, leading to an increase in the occupancy of spectrum resources that gradually increases the spectrum utilization. Additionally, the spectrum utilization of the LRA algorithm consistently remains at a higher level compared to the Min-RDDR algorithm and the RFFA algorithm. This is because the LRA algorithm has the lowest blocking rate under the same traffic load, which means that it can serve more requests and offer improved spectrum utilization.

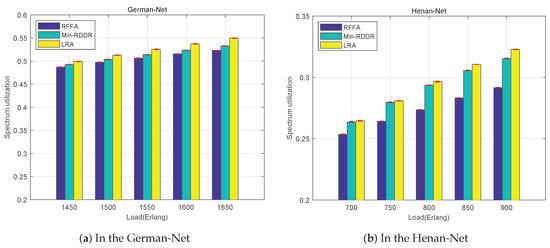
Figure 7. Comparison of spectrum utilization in (a) German-Net and (b) Henan-Net.

We conducted simulations on German-Net, which consists of 17 nodes and 25 links, and Henan-Net, which consists of 18 nodes and 25 links. The network scenarios were fixed. The simulations were performed on a 64-bit computer with six cores, 3 GHz, and 8 GB RAM using Python 3.9 as the simulation tool. The blocking probability and spectrum utilization of the LRA algorithm may be affected by various factors, including network scenarios, experimental tools, the number of experiments, the number of requests, and the value of K.

6. Conclusions

In this paper, we investigated the routing, modulation, and spectrum allocation (RMSA) problem for advance reservation (AR) requests in semi-filterless optical networks (semi-FONs). Due to the broadcast nature of semi-FONs, requests propagate over unnecessary links, occupying more spectrum resources and increasing the blocking probability. Additionally, the dynamic establishment and teardown of AR requests result in a large number of two-dimensional fragments. To address these issues, in this paper we propose a Link Resource Awareness (LRA) algorithm. This algorithm consists of three main strategies: a request sorting strategy in the request scheduling phase, a link resource awareness strategy in the routing phase, and a frequency–time block metric strategy in the spectrum allocation phase. Simulation results demonstrate that the proposed LRA algorithm achieves lower blocking probability compared to the benchmark algorithms.

In this paper, the LRA algorithm has certain limitations in its application scenarios. This is because the LRA algorithm is designed for semi-filterless optical networks with fixed network scenarios. Therefore, when facing different network scenarios the algorithm may exhibit different performance results. Looking towards future research directions, we hope to further investigate the RMSA problem for AR requests in semi-FONs to adapt to the changing network scenarios.

7. Discussion

This paper has investigate the routing, modulation, and spectrum assignment (RMSA) problem for advance reservation (AR) requests in semi-filterless optical networks (semi-FONs). A link resource-aware (LRA) algorithm is proposed, consisting of three parts. First, in the request scheduling phase, a request sorting strategy based on the size of flexible window of the starting time schedules AR requests based on the size of the flexible window of the starting time. Additionally, a link resource-aware strategy is proposed in the routing phase. This strategy evenly distributes the requests across the network resources, avoiding request blocking due to excessive resource occupation on a single link or few links. In the spectrum assignment phase, a metric of frequency–time blocks is employed to measure the availability of each frequency–time block for AR requests. This metric is a sum of two factors, namely, the distance to the block and spectrum boundaries and the time interval between the request start time and the earliest start time.

We conducted simulations on German-Net and Henan-Net to validate the effectiveness of the LRA algorithm. Compared to the Min-RDDR and RFFA benchmark algorithms, the proposed LRA algorithm offered consistently superior performance in terms of blocking probability and spectrum utilization. However, the LRA algorithm has certain limitations in specific application scenarios, and its performance may vary in different network scenarios. Looking towards future research directions, we hope to further investigate the RMSA problem for AR requests in semi-FONs to adapt to the changing network scenarios.