Abstract
Laser beams converging at significant focusing angles have diverse applications, including quartz-enhanced photoacoustic spectroscopy, high spatial resolution imaging, and profilometry. Due to the limited applicability of the paraxial approximation, which is valid solely for smooth focusing scenarios, numerical modeling becomes necessary to achieve optimal parameter optimization for imaging diagnostic systems that utilize converged laser beams. We introduce a novel methodology for the modeling of laser beams sharply focused on the turbid tissue-like scattering medium by employing the unidirectional Helmholtz equation approximation. The suggested modeling approach takes into account the intricate structure of biological tissues, showcasing its ability to effectively simulate a wide variety of random multi-layered media resembling tissue. By applying this methodology to the Gaussian-shaped laser beam with a parabolic wavefront, the prediction reveals the presence of two hotspots near the focus area. The close-to-maximal intensity hotspot area has a longitudinal size of about 3–5 μm and a transversal size of about 1–2 μm. These values are suitable for estimating spatial resolution in tissue imaging when employing sharply focused laser beams. The simulation also predicts a close-to-maximal intensity hotspot area with approximately 1 μm transversal and longitudinal sizes located just behind the focus distance for Bessel-shaped laser beams with a parabolic wavefront. The results of the simulation suggest that optical imaging methods utilizing laser beams with a wavefront produced by an axicon lens would exhibit a limited spatial resolution. The wavelength employed in the modeling studies to evaluate the sizes of the focus spot is selected within a range typical for optical coherence tomography, offering insights into the limitation of spatial resolution. The key advantage of the unidirectional Helmholtz equation approximation approach over the paraxial approximation lies in its capability to simulate the propagation of a laser beam with a non-parabolic wavefront.
1. Introduction
High numerical aperture (NA) optical objective lenses are widely used in high-spatial-resolution optical imaging [1,2] and 3D microfabrication [3]. Spatial resolution is crucial for the optical imaging of tissue microstructure and depends on the lens’s NA and the depth of field (DoF). DoF is defined as the disparity between the maximum and minimum distances of the ‘in-focus’ 2D area within the scene and the lens and is linked to NA as follows:
where is the medium refractive index, and is the wavelength of light.
The application of sharply focused laser beams is widespread in quartz-enhanced photoacoustic spectroscopy (QEPAS), directed precisely between the two prongs of a quartz tuning fork [4]. The distance between prongs for a standard quartz tuning fork is 300 μm, which complicates focusing, especially for the terahertz spectral range.
Typically, laser beams exhibit a Gaussian amplitude profile, while the phase front varies during their propagation. The sharply focused laser beam possesses the potential to improve spatial resolution, wherein the shape and parameters of the wavefront play critical roles and can be effectively corrected using lenses with the appropriate geometry. The conventional lenses typically exhibit spherical or cylindrical curvature forms, whereas the axicon lenses feature a conical-shaped focusing surface. When employing an axicon lens, a Gaussian profile beam is transformed into a converging beam with a transverse profile that comprises a sharp central core surrounded by several rings with varying brightness [5,6]. The most intense part of the central core keeps the shape and size during propagation, forming a non-diffractive zone. Such beams are referred to as the Bessel beams [7]. The electrical field for the axially symmetric Bessel beam is defined as follows:
where is the complex amplitude parameter, are the cylindrical coordinates, are longitudinal and transversal coordinates of the wave vector, and the function is the first kind and th-order Bessel function. The factor provides the beam orbital angular momentum projection on the z-axis proportional to that gives a singularity of beam phase and ‘disappearing’ of beam amplitude [8]. While the ideal case is only approximately realized in practical situations, it, nonetheless, confirms the distinctive properties of Bessel beams. A comparison of focusing of the Gaussian and Bessel beams is schematically presented in Figure 1.
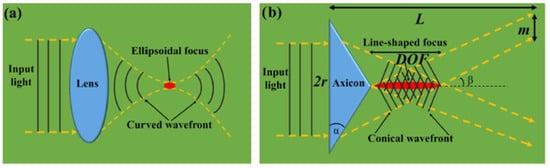
Figure 1.
Focusing on the Gaussian (a) and Bessel (b) beams. Here, is the beam radius, DOF is the depth of focus, and is the optical intensity ring thickness [8].
The axicon lens facilitates achieving a balance between diffraction and focusing [9,10,11], whereas sharply focusing beams with the long focus spot can be used not only for the visualization of optically transparent samples but also for the creation of effective fiber-optics devices [12], as well as in multifocal optical coherence tomography (OCT) [13], submicrometer surface structuring [14], photo-polymerization [15], and other material processing [8,16,17], particle trapping [18], and laser tweezer implementation [19]. Additionally, the focusing of laser beams can be accomplished by utilizing solid immersion lenses [20]. The axicons with a small opening angle [10] and negative axicons [21] play a significant role in scanning near-field optical microscopes. Wide-field light-sheet microscopy with axicon-lens controlled two-photon Bessel beam illumination was suggested [22]. Ultra-broadband axicon transducer was used in optoacoustic endoscopy [23]. The microaxicon lenses allow laser beam super-sharp focusing into a hotspot with transverse and longitudinal diameters less than the beam wavelength [24,25].
A fractal fracxicon generates a transverse phase of the laser beam, being a fractional power function of spatial coordinates [26]. When this power parameter exceeds two, the fractal fracxicon provides faster and sharper focusing compared to a conventional lens. Notably, scattering has been found to enhance the sharpness of the focused laser beam. It has been demonstrated that scattering behind a lens can reduce the focus spot size by ten times compared to the diffraction limit of the same lens [27].
Skin is a heterogeneous optically turbid medium producing absorption, scattering, reflection, and other phenomena in relation to propagating light waves. The main absorbing tissue chromatophores in the visible range are water, melanin in the epidermis, and hemoglobin in the dermis [1]. A lipid-containing membrane formed by keratinocytes (lamellar bodies in the epidermis) also affects absorbance at 650 nm [28]. The scattering in the epidermis is mainly due to keratins and melanosomes, which occupy 18–30% and 1–5% of the tissue volume, respectively [1]. Melanosomes are approximately ten times larger than keratins and have a higher refractive index, contributing significantly to scattering [29]. The shape of scattering inclusions within the skin is also a crucial factor to consider. For example, dead keratins cells (located in the Stratum corneum) are flat, and melanosomes can be round or fragmented depending on their position within the skin [30]. Despite the variations in the shapes of cells found in biological tissues, they are often represented and modeled as spheres with specific diameters in a range of 0.1–20 μm [31,32,33]. It has been demonstrated that the ratio of Rayleigh scattering to Mie scattering at the wavelength of 633–650 nm is, respectively, 10% to 90% [33]. Due to the irregular positions of cells, tissues are frequently regarded as quasi-random media. The beam profile is an important factor in its transformation process in biological tissues. In highly scattered Stratum corneum layer and epidermal layers, the beam intensity exhibits fluctuations of over 50% in transmission and 30% in reflection modes. In weakly scattering the reticular dermal and adipose layers this effect is not larger than 15% [34].
Considering the equivalence of temporal and spatial photodetector averaging in light interference fields, the influence of laser beam geometry on tissue interferometry imaging properties was examined [35]. The experimental findings revealed that interferometers employing a tightly focused probing beam can be deemed a suitable alternative to low-coherence interferometry and can be effectively utilized in OCT. The investigation of speckle pattern statistical and correlation properties, performed by scanning different skin tissues using a sharply focused probing laser beam with a Gaussian shape, demonstrated the suitability of this approach in tissue studies for both medical diagnostics and cosmetology applications [36].
Typically, analogous phenomena in biological tissues are simulated using a statistical Monte Carlo (MC) method-based approach [37,38,39]. This approach in a variant of the FDTD algorithm utilized in [24] simulates the sharp focusing of a radially polarized laser beam with axially symmetric micro-optic elements, but it is not suitable for non-symmetrical cases in random inhomogeneous media.
The geometrical optics-based approach, which involves analytical corrections of the phase and amplitude of the incident field, results in propagation with vector and non-paraxial properties [40]. However, its applicability is restricted to the calculation of light wave transformations by optical elements and transparent homogeneous medium. This method is based on the simulation of the propagation of photon packets representing a randomly selected partial component of the wavefront of the incident laser beam. Thus, the conclusions regarding the propagation of the entire laser beam are drawn by accumulating the outcomes of such numerical experiments and conducting statistical analysis. The fundamental concept of the approach is to leverage randomness to tackle problems that could be deterministic in principle, utilized commonly in various physical and mathematical problems due to its high utility. The use of the MC approach for modeling light wave propagation within biological tissues enables the imitation of the complexity of the randomly structured composition of biological tissues while also considering the partial coherence of the probing laser beam [41,42,43,44,45,46,47,48]. Various limitations of this approach become apparent when the super-sharp focusing occurs, notably with the numerical aperture close to or less than one [40,48,49].
The development of high-resolution optical imaging tools based on sharply focused laser beams and study phenomena in a focus area needs the creation of adequate mathematical models for the simulation of sharply focused laser beam propagation in biological tissue. These models should provide a simulation of tissue optical properties and an adequate description of the laser beam propagation process.
Maxwell’s equations, being the general foundation of light wave propagation tasks, are rarely used in concrete situations because of difficulties of analytical or numerical analysis. A numerical analysis of wave equations, derived from Maxwell’s equations, has high computational costs (see, for example, [50,51,52,53]). When the focal length is much larger than the wavelength, the Debye and the Richards–Wolf approximations can be used for the simulation of a laser beam focusing [54,55]. In the Debye approach, the focal field is evaluated via the interference of plane waves propagating at various angles. The Richards–Wolf model also uses the Debye diffraction integral of the optical field distribution near the focus. The numerical analysis of this diffraction integral is complicated and time consuming. A radiative transfer equation considering photon diffusion kinetics in the medium is an alternative method of optical beam propagation modeling [1]. Typically, diffusion approximation is used for its solution, it is valid when the medium absorption is much smaller than scattering, and medium optical properties vary smoothly [56]. Consequently, this approximation accuracy decreases dramatically near the medium boundaries and in a highly inhomogeneous medium. This method also does not allow interference or diffraction simulation. Various approximations are used to reduce the order of the wave equation or transform its type. A vector diffraction theory allows for solving a tightly focused optical beam propagation problem [57]. A so-called ‘rainbow beam’ approach, based on the spatial separation of the spectral components of laser light into a collection of off-axis beams, was proposed [58,59]. It allows parallel processing and recombining of these components at the focal point of an achromatic objective lens. The Helmholtz equation derived from the wave equation has Kirchhoff’s integral solution, describing spherical waves [54,60,61,62]. This integral calculation needs essential computational resources; it can be partially solved using a spectral-domain presentation [58]. The Helmholtz equation can be simplified using a paraxial approximation, leading to the Leontovitch–Fock equation [63]. The latter is valid for small focusing angles relative to the optical axis (less than 14°) [64,65]. Another way is to use unidirectional Helmholtz equation (UHE) approximation valid for large focusing angles [66]. In this approach, the simplification of laser beam propagation analysis is achieved by neglecting the backward light wave. We used this approach to simulate OCT imaging of the fat cell tissue layer [67]. The OCT model used a large focus distance, the developed tissue model considers the fat cell as a three-layer quasi-regular spheroid. The UHE is widely used for the simulation of laser beams in a quasi-collinear regime, for example, electromagnetic wave propagation in the atmosphere [68].
It should be pointed out that in a simple case of a homogeneous medium and axially symmetric optical beams, the Helmholtz equation is a product of two Kummer functions. It opens a way to achieve an exact analytical presentation of forward and backward propagated laser beams for the non-paraxial geometry [69] and to validate the numerical scheme using the analytical solution in the limit case of a homogeneous medium. The latter condition allows for developing sophisticated analytical approaches in the Helmholtz equation solution [70]. Indeed, analytical methods are scarcely applicable to inhomogeneous media, necessitating the use of numerical methods instead.
Previous studies did not take into account non-paraxial effects, which are crucial for sharply focused laser beams. The objective of current report is to compare the UHE and paraxial approximations in the simulation of a laser beam sharp focused on the skin, represented as a multilayered quasi-random inhomogeneous scattering medium.
2. The Propagation Problem Mathematical Model
2.1. Skin Model
Skin optical properties are described by the absorption coefficient , the scattering coefficient , the total attenuation coefficient , the refractive index , and the phase scattering function , where g defines scattering angle. Here, absorption coefficient determines the energy losses of optical radiation, and almost all of these losses are converted into tissue heating. The scattering coefficient defines changing the optical wave propagation direction that also causes this wave energy losses. The function is in fact the scattering indicatrix, which describes angular distribution of the scattered wave. The refractive index gradient defines medium reflection and refraction. The scattering phase function can be approximated using the Henyey–Greenstein function with different mean cosines of scattering angles corresponding to a different layer according to the forward Mie scattering [71]. Usually, the skin’s surface is considered to be perfectly smooth. The simplest skin model is a homogeneous plane single layer that is very inaccurate. Due to differences in scattering and absorption in the epidermis and dermis, a two-layer model is more acceptable [1]. A plane-stratified multilayered model is an extension of the latter [72,73]. The thickness of skin layers depends on gender, pigmentation, blood content, and body site and varies in range of 100–150 μm for epidermis and 0.35–1.65 mm for dermis [74,75,76,77]. The epidermis and reticular dermis have the following optical parameters for the wavelengths 633 nm and 337 nm, respectively: 3.2 (34.3) cm−1, 107 (165) cm−1, and 0.79 (0.72); 2.7 (23) cm−1, 187 (227) cm−1, and 0.82 (0.72) [71].
In this present study, a skin model in the form of a plane multi-layered quasi-random medium is employed. The refractive index of each layer is represented as the sum of regular and random components as follows:
The probability of appearing a definite value of random component has a Gaussian distribution with a correlation function, which is represented as follows:
where is the correlation radius, is the roughness parameter describing the sharpness of the refractive index fluctuations, is characteristic of the refractive index fluctuation dispersion, and is the wave vector. A set of these parameters determines the type of biological tissue [51]. Medium microscopic parameters , , and are defined as follows:
where , , and , defined according to Henyey–Greenstein formula [78], are the macroscopic modeling parameters mentioned above, as shown in Table 1 for the wavelength of 1 μm.

Table 1.
The used skin model parameters [79].
We see that the highly scattered skin layers (Stratum corneum and epidermis) have total thickness of about 100 μm.
2.2. An Optical Beam Propagation Model
The light wave of the laser beam is denoted as follows:
where is the carrier frequency, and is the complex amplitude of the electric field strength, which fulfills the Helmholtz equation as follows:
where is the wavenumber in vacuum, is the speed of light, and is the medium’s complex permittivity. It is convenient to split the latter into constant and spatially varied parts as follows:
Let a z-axis be oriented along the direction of the beam propagation. Then, Equation (6) can be presented in the following form:
where is the radius-vector in a plane transverse to the z-axis, the transverse Laplacian is: . Further, we consider the forward-propagating laser beam. This UHE approximation imposes restrictions on the function described below. The numerical solution of this equation can be implemented using wavelet transform
The numerical solution of Equation (8) is conducted using an approach based on splitting into physical factors, which considers a physical effect as a virtual spatial layer (screen) with specific characteristics [67,80]. According to this approach, we use two virtual screens. The first one simulates diffraction, absorption, and phase incursion phenomena associated with . The second one simulates absorption and phase incursion associated with . The block diagram of the corresponding parallel numerical algorithm implementation is shown in Figure 2. In our approach, the transformation of a small part of the wavefront of the laser beam via the medium layer is calculated on an individual CPU. Then, transformed functions are merged into the function. Here, are the CPU enumerators. The calculations are conducted for a realization of skin model as a random multi-layer medium. The parameters of the skin model implementation are calculated using data from Table 1 and Equations (3)–(5).
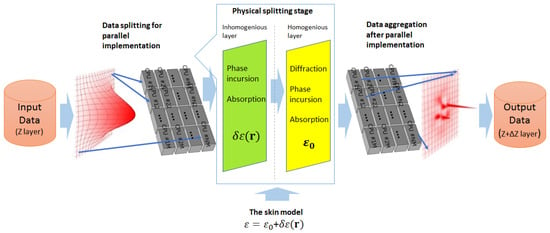
Figure 2.
The block diagram of the used numerical algorithm of propagation task simulation approach, which is based on physical factors splitting.
The following equation describes the step of passing a homogeneous screen as follows:
A Fourier transform of function is expressed as follows:
where is the wave vector associated with . Then, (9) takes the following form:
The solution of (9) for a forward-propagating optical wave is expressed as follows:
The additional condition provides the forward-propagating wave selection.
The following equation describes the step of passing the inhomogeneous screen:
Its solution is expressed as follows:
where is a numerical greed step along the optical wave propagation direction.
2.3. Shape of Laser Beam
The following laser beam initial shapes are used in the modeling studies.
- (i).
- Laser beam with the Gaussian shape of intensity profile and parabolic wave front:
- (ii).
- Laser beam with the Gaussian shape of intensity profile and the wave front produced by axicon lens:
- (iii).
- Laser beam with the Bessel shape of intensity profile and the parabolic wave front:
- (iv). Laser beam with the Bessel shape of intensity profile the wave front produced by axicon lens:
The laser beam parameters used in the simulation include the following: the wavelength was 1 μm, the beam radius 40 μm, and selected focus distances were 50 and 400 μm. The initial shape of the beams’ intensity profiles for the model beams, defined by (16a)–(16d), and wave fronts are shown in Figure 3.
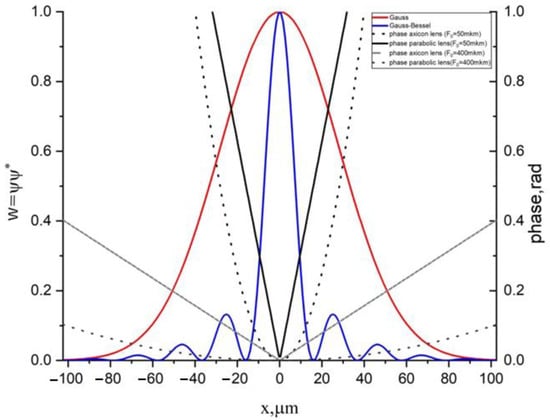
Figure 3.
The initial shapes and the wavefront profiles for the laser beams (12a)–(12c): blue and red lines correspond to amplitudes, whereas black and gray lines correspond to the phase.
Modeling results of these laser beams’ propagation are presented in a term of
describing normalized intensity profile of the laser beam; .
3. Results
3.1. Ultra-Sharp Focusing of Laser Beams in Homogeneous Layer
The solution of (13) in a regular homogeneous layer (with refraction index n = 1) can be presented in the following form:
As an example of admitting an analytical solution, we consider the simplest case of an axially symmetric Gaussian-shape beam with an initial form:
where is the complex parameter determining the beam transverse size and focusing distance. Also, let us take into account the restriction of the spatial area corresponding to the forward propagated light wave: . An expression for the function normalized on its maximum initial value can be written in the following form:
The results of a simulation of the axially symmetric Gaussian-shape beam sharp focusing using the paraxial approximation and Equation (16) are presented in Figure 4. The paraxial approximation does not describe thin details of the beam distortion behind the focus area caught via UHE approximation. The main drawback of the paraxial approximation approach is the ‘super-optimistic’ prediction of a hot spot in the focus area. The UHE approximation predicts the hotspot transversal size of about 4–5 μm at a half-maximum intensity-level map. The hot spot predicted by the paraxial approximation is larger. As shown in Figure 4a, the optical energy flux exhibits a non-symmetrical, bullet-like shape in the longitudinal direction, which represents a significant distinction from the paraxial approximation.
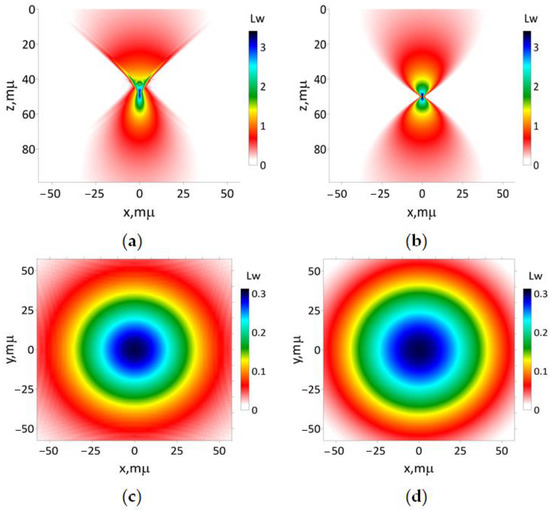
Figure 4.
The results of simulation of modeling beam (16a) focused on a regular homogeneous one-layer medium 50 μm and the medium refractive index 1: (a) according to Equation (18); (b) utilizing paraxial approximation. The transverse intensity distribution (17), respectively, for (c) 0 and (d) 100 μm.
3.2. A simulation of Laser Beams Sharply Focused on the Skin
For the modeling of laser beams sharply focused on the skin, the model used in this study is constructed based on a plane-layered quasi-random medium, and its specific parameters are calculated using Formulas (3)–(5) and parameters presented in Table 1. The random part of the refraction index was defined using function:
where is the Fourier transform. was calculated using the phenomenological model [81]:
An example of the spatial distribution of refractive index within the skin according to the quasi-random model is presented in Figure 5.
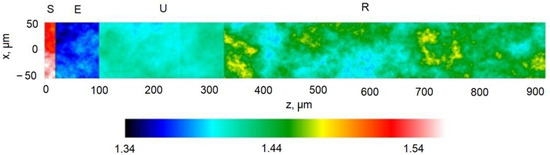
Figure 5.
Spatial distribution of refractive index within the skin. Other modeling optical parameters are presented in Table 1. Here, S denotes Stratum corneum, E is epidermis, U is upper derma, and R is reticular dermis.
The results of modeling of the laser beam (16a) focused on the turbid tissue-like scattering medium are presented in Figure 6.
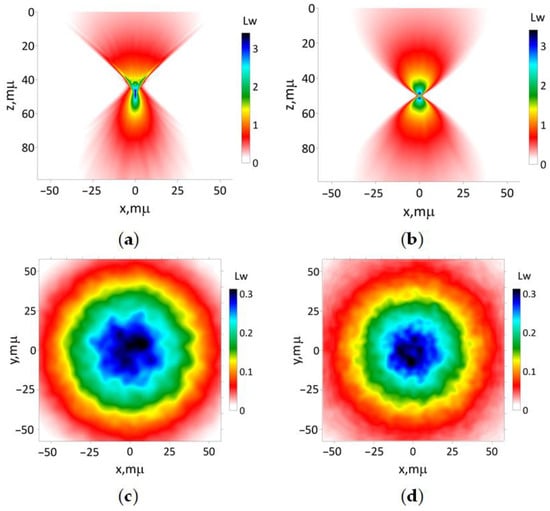
Figure 6.
The results of simulation of modeling beam (16a) focused on the tissue-like medium with 50 μm: (a) according to Equations (13) and (15); (b) utilizing the paraxial approximation. The transverse intensity distribution (17) for (c) z 0 and (d) 100 μm, respectively.
Clearly, the results show that the paraxial approximation is unable to adequately describe the wide cone of light beyond the focus area. Additionally, this approach predicts two hotspots near the focus area, which is not observed in the UHE approximation. The latter demonstrates that the close-to-maximal intensity hotspot area has a longitudinal size of about 3–5 μm and a transversal size of about 1–2 μm. These values can be used for spatial resolution estimations for tissue imaging using sharp-focused laser beams. According to Figure 6a, the optical energy flux near the focus area maintains a non-symmetrical, bullet-like shape in the longitudinal direction (see comments to Figure 4). Interestingly, the hot-spot size predicted by the paraxial approximation is smaller in comparison to the results obtained with the UHE approximation. This observation contradicts the findings for a homogeneous medium. Consequently, the UHE approximation demonstrates a greater accuracy in capturing the influence of small-scale medium inhomogeneities in comparison to the paraxial approximation.
The outcomes of simulating the propagation of the modeling laser beam, characterized by its initial shape described according to (16b), with focusing distance 50 μm, are presented in Figure 7. The interference of secondary beams causes a star-like transversal spatial structure with a very large longitudinal size, appearing in both simulation methods. It means a poor spatial resolution of any optical imaging method using the laser beam with the Gaussian shape of intensity and wavefront produced by an axicon lens.
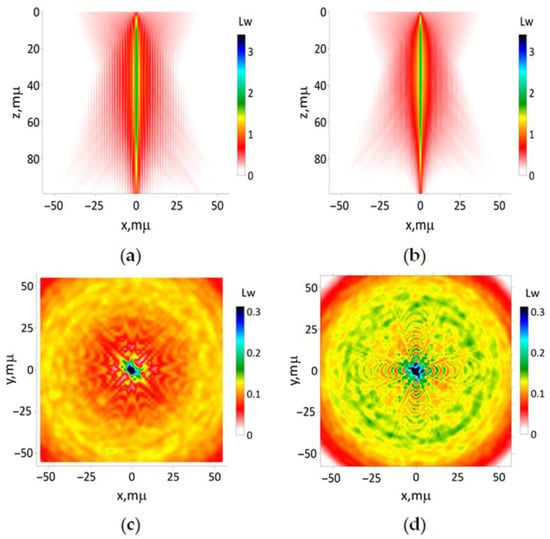
Figure 7.
The results of simulation of the beam (16b) with the focusing distance 50 μm: (a) according to Equations (13) and (15); (b) utilizing paraxial approximation. The transverse intensity distribution (17) for (c) z 0 and (d) 100 μm, respectively.
The results of the simulation of the modeling beam defined by (16c) with the focusing length 50 μm are presented in Figure 8. The application of both approaches yields visually identical results. The Helmholtz unidirectional equation approximation predicts less transversal beam size compared to the paraxial approximation. Also, the former approach predicts the close-to-maximal intensity hotspot area with near 1 μm transversal and longitudinal sizes behind focus distance. The main distinction lies in the non-symmetrical spatial distribution of the light side lobes depicted in Figure 8a, whereas Figure 8b showcases the opposite pattern.
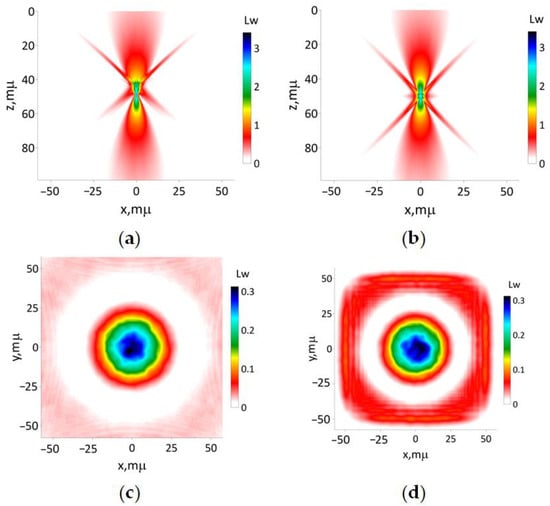
Figure 8.
The results of simulation of modeling beam (16c) with the focusing distance 50 μm: (a) according to Equations (13) and (15); (b) utilizing the paraxial approximation. The transverse intensity distribution (17) for (c) z 0 and (d) 100 μm, respectively.
The results of the simulation of the modeling beam defined by (16d) with the focusing length 50 μm are presented in Figure 9. The interference of secondary beams leads to the emergence of a cruciform transversal spatial structure, which is observed in both simulation methods. Consequently, any optical imaging method utilizing a Bessel-shaped laser beam with a wavefront generated by an axicon lens is expected to suffer from poor spatial resolution, mainly due to the presence of numerous side lobes. On the contrary, the hotspot predicted from the paraxial approximation is smaller compared to the results obtained from the UHE approximation. This confirms the capability of the latter to more accurately capture the influence of small-scale medium inhomogeneities in comparison to the paraxial approximation.
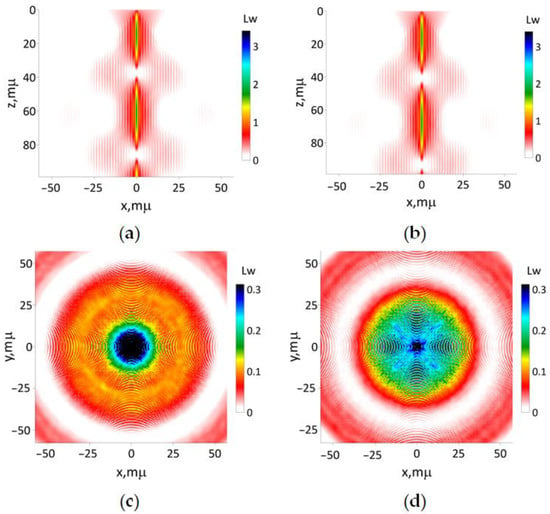
Figure 9.
The results of simulation of modeling beam (16d) with focusing distance 50 μm: (a) according to Equations (13) and (15); (b) utilizing the paraxial approximation. The transverse intensity distribution (17) for (c) z 0 and (d) 100 μm, respectively.
To validate the difference in the prediction of beam shape transformation for a moderate focusing case, we simulated the propagation of the laser beam with the initial shape described by (16b) for the focusing distance of 400 μm (Figure 10). For this specific focusing distance, both approaches exhibit no significant disparity in the transformation of the beam shape. The results of the simulation suggest that any optical imaging method utilizing a Gaussian-shaped laser beam with a wavefront produced by an axicon lens yields poor spatial resolution.
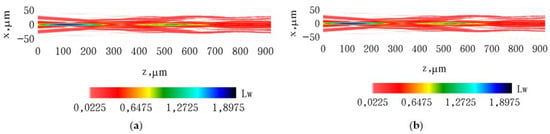
Figure 10.
The results of propagation simulation of the model beam with the initial shape described by (16b) with focusing distance 400 μm in the tissue-like modeling medium: (a) results of simulation according to (13) and (15); (b) results of simulation using the paraxial approximation.
4. Discussion
To sum up, the novelty of this current study lies in the examination of ‘non-paraxial’ effects within the turbid tissue-like medium, which is modeled as a randomly inhomogeneous multi-layered scattering medium. According to the results of numerical simulation for a homogeneous tissue-like scattering medium, the paraxial approximation does not describe in fine detail the beam distortion behind and after the focus area caught by the UHE approximation (see Figure 4). In spite of a shallow topical propagation, the randomness of the used skin model causes an irregularity of the optical beam intensity transversal 2D distribution. For the Gaussian shape beam with a parabolic wave front, the paraxial approximation does not allow describing the wide cone of light after the focus area (see Figure 6). Also, two hotspots near the focus area were predicted using this approach which is not the case for the UHE approximation. The latter demonstrates that the close-to-maximal intensity hotspot area has a longitudinal size of about 3–5 μm and a transversal size of about 1–2 μm. These values can be used for spatial resolution estimations for tissue imaging using sharp-focused optical beams with wavelengths of about 1 μm, which was used in the presented simulation results. Estimations for another wavelength can be achieved using the suggested numerical UHE implementation. The UHE approximation predicts less transversal beam size compared to the paraxial approximation when the Bessel shape optical beams with the parabolic wave front are used (see Figure 8). Also, the former approach predicts the close-to-maximal intensity hotspot area with nearly 1 μm transversal and longitudinal sizes behind the focus distance.
A poor spatial resolution of any optical imaging method using the Gaussian shape laser beams with the wave front produced by an axicon lens was predicted (Figure 7). The same can be concluded for the Bessel-shaped laser beams with the wave front produced by an axicon lens (see Figure 9). For laser beams with the wavefront produced by an axicon lens, a star-like transversal spatial structure appears. Also, the focusing process is accompanied by the appearance of side lobes amplitude-modulated as the result of interference of secondary beams. This drawback of Bessel beams when a decrease in the size of the focal spot is accompanied by the growth of side lobes that worsen the image quality is known in the literature [82,83]. Another drawback of Bessel beams is that forming a non-diffractive zone by them has essential energy cost because only a small part of the optical beam energy focuses on the central spot [8]. Therefore, this regime is not very suitable for use in OCT because these side lobes will appear also in low-coherence laser beams, which will distort essentially the results of tissue OCT visualization. It should be pointed out that used in the simulation wavelength is close to the typical one implemented in the most modern OCT devices (the most spread super-luminescent diodes have wavelengths of 0.905 or 0.93 μm). Therefore, the present estimations of the focus spot sizes can be used as the upper limit of possible spatial resolution of similar imaging methods. The real resolution is worse but can be improved using special methods like immersion lenses [20]. Therefore, according to the simulation results, the imaging of cells, and cell nucleus can be achieved using sharply focused optical beams with the parabolic wave front.
For long focus distances, there are no any essential differences between both approaches (see, Figure 10).
The main differences between the UHE approximation predictions regarding laser beam propagation through tissue compared to the parabolic approximation are as follows:
- (1)
- The optical energy flux of the laser beam with an initially parabolic wave front has a nonsymmetrical longitudinal direction bullet-like shape near the focus area;
- (2)
- The hotspot size predicted via the UHE approximation is larger owing to the more accurate catching influence of small-scale medium inhomogeneities compared to the paraxial approximation;
- (3)
- For a laser beam with a wave front produced by an axicon, light side lobs have non-symmetrical spatial distribution when the numerical simulation is conducted using the UHE approximation.
5. Conclusions
In total, the UHE approximation looks very useful for the analysis of various instrumental methods of optical imaging like optical coherence tomography, multiphoton microscopy, confocal microscopy, and Raman confocal spectroscopy when these methods use optical lenses with short focus distance, or any other technical schemes produced sharply focused laser beams.
The potential impact of tissue anisotropy on the propagation of laser beams in the skin is not taken into account in this current study. The presence of birefringence in the tissue contributes to the depolarization of light, introducing additional complexities to the phenomena under investigation [1,73,84,85]. Across the entire tissue, birefringence exhibits a relatively minor influence throughout the skin’s entire thickness. Furthermore, strong scattering in the Stratum corneum and epidermis contributes to the blurring of birefringence effects [86]. These highly scattered skin layers with a total thickness of up to 100–150 μm, serving as a natural protective screen from sun radiation, limit significantly any sharp focusing of laser beams within the skin. Nevertheless, a thorough investigation of the anisotropy properties of tissue layers [87,88,89,90] necessitates a more comprehensive in-depth analysis, attainable via the expansion of the suggested approach to vector optical fields—a promising avenue for future research endeavors.
Finally, in this current study, we focus solely on linear effects in optical radiation-tissue interaction, rendering our results applicable to optical radiation power levels below 20–30 mW [91]. The estimation of the photo-damage threshold is achieved for a homogeneous turbid tissue-like scattering medium. Taking into account the interaction of incident light with individual cells, more sophisticated phenomena become appeared to see, e.g., photonics jets and fractional photo-damage in lung epithelial cancer cells [92], etc. The introduced approach based on the UHE approximation holds significant promise for investigating similar phenomena in future research endeavors.
Author Contributions
Conceptualization, Y.K. and A.B.; methodology, Y.K. and I.M.; software, A.B.; investigation, Y.K. and A.B.; data curation, A.B.; writing—original draft preparation, Y.K.; writing—review and editing, I.M.; visualization, A.B.; supervision, Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research was carried out with the Tomsk State University Development Program (Priority-2030). I.M. acknowledges the support from ATTRACT II META-HiLight project funded by the European Union’s Horizon 2020 research and innovative program under grant agreement No.101004462, the Academy of Finland (grant project 325097), the Universities UK International (UUKi) and the DSTI—UK government Department for Science, Innovation and Technology (grant project: Light4Body). Y.K. and A.B. also acknowledge the support of the state budget financing of the IOA SB RAS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tuchin, V.V. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnostics, 3rd ed.; SPIE Press: Bellingham, WA, USA, 2015; 988p. [Google Scholar]
- Kistenev, Y.V.; Borisov, A.V.; Vrazhnov, D.A. Medical Applications of Laser Molecular Imaging and Machine Learning; SPIE Press: Bellingham, WA, USA, 2021; Volume PM333, 252p. [Google Scholar]
- Zhan, Q. Focusing Through High–Numerical Aperture Objective. Chapter 7. In Three-Dimensional Microfabrication Using Two-photon Polymerization. Micro and Nano Technologies; Baldacchini, T., Ed.; William Andrew Publishing: Norwich, NY, USA, 2016; pp. 168–189. [Google Scholar]
- Votintsev, A.P.; Borisov, A.V.; Makashev, D.R.; Stoyanova, M.Y.; Kistenev, Y.V. Quartz-Enhanced Photoacoustic Spectroscopy in the Terahertz Spectral Range. Photonics 2023, 10, 835. [Google Scholar] [CrossRef]
- Vaicaitis, V.; Paulikas, S. Formation of Bessel beams with continuously variable cone angle. Opt. Quantum Electron. 2003, 35, 1065–1071. [Google Scholar] [CrossRef]
- Sedukhin, G. Efficient generation of annular cylindrical vector beams by refractive axicons with high-transmission thin-film retarders. Opt. Commun. 2021, 499, 127293. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern Types of Axicons: New Functions and Applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kazanskiy, N.L.; Karpeev, S.V.; Butt, M.A. Bessel Beam: Significance and Applications—A Progressive Review. Micromachines 2020, 11, 997. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Chavez-Cerda, S. Generalized parabolic non-diffracting beams of two orders. JOSA A 2018, 35, 1511–1517. [Google Scholar] [CrossRef]
- Durnin, J. Exact solutions for nondiracting beams. I. The scalar theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J., Jr.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef]
- Alferov, S.V.; Khonina, S.N.; Karpeev, S.V. Study of polarization properties of fiber-optics probes with use of a binary phase plate. J. Opt. Soc. Am. A 2014, 31, 802–807. [Google Scholar] [CrossRef]
- Yi, L.; Sun, L.; Ming, X. Simulation of penetration depth of Bessel beams for multifocal optical coherence tomography. Appl. Opt. 2018, 57, 4809–4814. [Google Scholar] [CrossRef] [PubMed]
- Osbild, M.; Gerhorst, E.-A.; Sivankutty, S.; Pallier, G.; Labroille, G. Submicrometer surface structuring with a Bessel beam generated by a reflective axicon. J. Laser Appl. 2021, 33, 042013. [Google Scholar] [CrossRef]
- Arita, Y.; Lee, J.; Kawaguchi, H.; Matsuo, R.; Miyamoto, K.; Dholakia, K.; Omatsu, T. Photopolymerization with high-order Bessel light beams. Opt. Lett. 2020, 45, 4080–4083. [Google Scholar] [CrossRef] [PubMed]
- Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 081102. [Google Scholar] [CrossRef]
- Duocastella, M.; Arnold, C.B. Bessel and annular beams for materials processing. Laser Photonics Rev. 2012, 6, 607–621. [Google Scholar] [CrossRef]
- Skidanov, R.; Khonina, S.N.; Porfirev, A.; Pavelyev, V.; Kachalov, D. Three-dimensional laser trapping on the base of binary radial diffractive optical element. J. Mod. Opt. 2015, 62, 1183–1186. [Google Scholar] [CrossRef]
- Andrade, U.M.S.; Garcia, A.M.; Rocha, M.S. Bessel beam optical tweezers for manipulating superparamagnetic beads. Appl. Opt. 2021, 60, 3422–3429. [Google Scholar] [CrossRef]
- Smolyanskaya, O.A.; Chernomyrdin, N.V.; Konovko, A.A.; Zaitsev, K.I.; Ozheredov, I.A.; Cherkasova, O.P.; Nazarov, M.M.; Guillet, J.-P.; Kozlov, S.A.; Kistenev, Y.V.; et al. Terahertz biophotonics as a tool for studies of dielectric andspectral properties of biological tissues and liquids. Prog. Quantum Electron. 2018, 62, 1–77. [Google Scholar] [CrossRef]
- Schwarz, S.; Roth, G.-L.; Rung, S.; Esen, C.; Hellmann, R. Fabrication and evaluation of negative axicons for ultrashort pulsed laser applications. Opt. Express 2020, 28, 26207–26217. [Google Scholar] [CrossRef]
- Takanezawa, S.; Saitou, T.; Imamura, T. Wide field light-sheet microscopy with lens-axicon controlled two-photon Bessel beam illumination. Nat. Commun. 2021, 12, 2979. [Google Scholar] [CrossRef]
- Ali, Z.; Zakian, C.; Ntziachristos, V. Ultra-broadband axicon transducer for optoacoustic endoscopy. Sci. Rep. 2021, 11, 1654. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Stafeev, S.S. Sharp focusing of light of radial polarization using microlenses. Comput. Opt. 2019, 32, 155–167. [Google Scholar]
- Kotlyar, V.V.; Stafeev, S.S. Modeling the sharp focus of a radially polarized laser mode using a conical and a binary microaxicon. J. Opt. Soc. Am. B 2010, 27, 1991. [Google Scholar] [CrossRef]
- Khonina, S.N.; Volotovskiy, S.G. Fractal cylindrical fracxicon. Opt. Mem. Neural Netw. 2018, 27, 1–9. [Google Scholar] [CrossRef]
- Vellekoop, M.; Lagendijk, A.; Mosk, A.P. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef]
- Dubin, S.B. Determination of lamellar body size, number density, and concentration by differential light scattering from amniotic fluid: Physical significance of A650. Clin. Chem. 1988, 34, 938–943. [Google Scholar] [CrossRef] [PubMed]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Bhandari, A.; Hamre, B.; Frette, O.; Stamnes, K.; Stamnes, J.J. Modeling optical properties of human skin using Mie theory for particles with different size distributions and refractive indices. Opt. Express 2011, 19, 14549–14567. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical assessment of tissue heterogeneity in biomaterial and implants. Proc. SPIE 2000, 3914, 576–580. [Google Scholar]
- Drezek, R.; Dunn, A.; Richards-Kortum, R. Light scattering from cells: Finite-difference, time-domain simulations and goniometric measurements. Appl. Opt. 1999, 38, 3651–3661. [Google Scholar] [CrossRef]
- Saidi, S.; Jacques, S.L.; Tittel, F.K. Mie and Rayleigh modeling of visible-light scattering in neonatal skin. Appl. Opt. 1995, 34, 7410–7418. [Google Scholar] [CrossRef]
- Bezuglyi, M.; Bezuglaya, N.; Kostuk, S. Influence of laser beam profile on light scattering by human skin during photometry by ellipsoidal reflectors. Devices Methods Meas. 2018, 9, 56–65. [Google Scholar] [CrossRef]
- Ryabukho, V.P.; Khomutov, V.L.; Tuchin, V.V.; Lyakin, D.V.; Konstantinov, K.V. Laser interferometer with an object sharply focused beam as a tool for optical tomography. Proc. SPIE Coherence Domain Opt. Methods Biomed. Sci. Clin. Appl. II 1998, 3251, 247. [Google Scholar]
- Zimnyakov, D.A.; Tuchin, V.V.; Utz, S.R.; Mishin, A.A. Human skin image analysis using coherent focused beam scattering. Proc. SPIE 1995, 2329, 115. [Google Scholar]
- Matveyev, A.L.; Matveev, L.A.; Moiseev, A.A.; Sovetsky, A.A.; Gelikonov, G.V.; Zaitsev, V.Y. Semi-analytical full-wave model for simulations of scans in optical coherence tomography with accounting for beam focusing and the motion of scatterers. Laser Phys. Lett. 2019, 16, 085601. [Google Scholar] [CrossRef]
- Kalkman, J. Fourier-domain optical coherence tomography signal analysis and numerical modeling. Int. J. Opt. 2017, 2017, 9586067. [Google Scholar] [CrossRef]
- Jensen, M.; Israelsen, N.M.; Maria, M.; Feuchter, T.; Podoleanu, A.; Bang, O. All-depth dispersion cancellation in spectral domain optical coherence tomography using numerical intensity correlations. Sci. Rep. 2018, 8, 9170. [Google Scholar] [CrossRef]
- Shipilo, D.E.; Nikolaeva, I.A.; Fedorov, V.Y.; Tzortzakis, S.; Couairon, A.; Panov, N.A.; Kosareva, O.G. Tight focusing of electromagnetic fields by large-aperture mirrors. Phy. Rev. 2019, 100, 033316. [Google Scholar] [CrossRef]
- Meglinski, I.V.; Churmakov, D.Y.; Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. The Enhancement of Confocal Images of Tissues at Bulk Optical Immersion. Laser Phys. 2003, 13, 65–69. [Google Scholar]
- Doronin, A.; Meglinski, I. Peer-to-Peer Monte Carlo simulation of photon migration in topical applications of biomedical optics. J. Biomed. Opt. 2012, 17, 090504. [Google Scholar] [CrossRef] [PubMed]
- Meglinski, I.V.; Kuzmin, V.L.; Churmakov, D.Y.; Greenhalgh, D.A. Monte Carlo Simulation of Coherent Effects in Multiple Scattering. Proc. Roy. Soc. A 2005, 461, 43–53. [Google Scholar] [CrossRef]
- Meglinski, I.V.; Tuchin, V.V. The enhancement of confocal probing with optical clearing. In Advances in Biomedical Photonics and Imaging; Luo, Q., Wang, L.V., Tuchin, V.V., Eds.; World Scientific Publishing Company: Singapore, 2008; pp. 33–38. [Google Scholar]
- Hokr, B.H.; Bixler, J.N.; Elpers, G.; Zollars, B.; Thomas, R.J.; Yakovlev, V.V.; Scully, M.O. Modelling focusing Gaussian beams in a turbid medium with Monte Carlo simulations. Opt. Express 2015, 23, 8699–8705. [Google Scholar] [CrossRef] [PubMed]
- Churmakov, D.; Kuzmin, V.L.; Meglinski, I. Application of the vector Monte Carlo method in Polarization Optical Coherence Tomography. Quantum Electron. 2006, 36, 1009–1015. [Google Scholar] [CrossRef]
- Meglinski, I.; Kirillin, M.; Kuzmin, V.L.; Myllyla, R. Simulation of polarization-sensitive optical coherence tomography images by a Monte Carlo method. Opt. Lett. 2008, 33, 1581–1583. [Google Scholar] [CrossRef] [PubMed]
- Kirillin, M.; Meglinski, I.; Sergeeva, E.; Kuzmin, V.L.; Myllyla, R. Simulation of optical coherence tomography images by Monte Carlo modelling based on polarization vector approach. Opt. Express 2010, 18, 21714–21724. [Google Scholar] [CrossRef]
- Kandidov, V.P.; Militsin, V.O.; Bykov, A.V.; Priezzhev, A.V. Application of corpuscular and wave Monte-Carlo methods in optics of dispersive media. Quantum Electron. 2006, 36, 1003–1008. [Google Scholar] [CrossRef]
- Ortega-Quijano, N.; Romanov, O.G.; Fanjul-Vélez, F.; Salas-García, I.; Tolstik, A.L.; Arce-Diego, J.L. Numerical modeling of light propagation in biological tissues: Time-resolved 3D simulations based on light diffusion model and FDTD solution of Maxwell’s equations. Proc. SPIE 2011, 8088, 80881R. [Google Scholar]
- Silva, A.; Correia, A. From optical coherence tomography to Maxwell’s equations. In Proceedings of the IEEE 3rd Portuguese Meeting in Bioengineering (ENBENG), Braga, Portugal, 20–23 February 2013. [Google Scholar]
- Munro, P.R.T. Three-dimensional full wave model of image formation in optical coherence tomography. Opt. Express 2016, 24, 27016–27031. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Zapata-Rodríguez, C.J. Debye representation of dispersive focused waves. J. Opt. Soc. Am. A 2007, 24, 675–686. [Google Scholar] [CrossRef][Green Version]
- Debye, P. Das Verhalten von Lichtwellen in der Nähe eines Brennpunktes oder einer Brennlinie. Ann. Phys. 1909, 335, 755–776. [Google Scholar] [CrossRef]
- Bochove, E.J.; Rao Gudimetla, V.S. Approach to atmospheric laser-propagation theory based on the extended Huygens–Fresnel principle and a self-consistency concept. J. Opt. Soc. Am. A 2017, 34, 140–145. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Focusing property of a double-ring-shaped radially polarized beam. Opt. Lett. 2006, 31, 820–822. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Howe, J.V.; Durst, M.; Zipfel, W.; Xu, C. Simultaneous spatial and temporal focusing of femtosecond pulses. Opt. Express 2005, 13, 2153–2159. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.Q.; Lv, X.; Zhan, C.; Chen, W.R.; Xiong, W.H.; Luo, Q.; Jacques, S.L. Simultaneous compensation for spatial and temporal dispersion of acousto-optical deflectors for two-dimensional scanning with a single prism. Opt. Lett. 2006, 31, 1091–1093. [Google Scholar] [CrossRef]
- Dudorov, V.V.; Filimonov, G.A.; Kolosov, V.V. Research of the narrow-angle beam diffraction. Proc. SPIE 2004, 5396, 191–197. [Google Scholar]
- Lehmann, P.; Xie, W.; Allendorf, B.; Tereschenko, S. Coherence scanning and phase imaging optical interference microscopy at the lateral resolution limit. Opt. Express 2018, 26, 7376–7389. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar]
- Leontovich, M.A.; Fock, V.A. Solution of the Problem of Propagation of Electromagnetic Waves along the Earth’s Surface by Method of Parabolic Equations. Phys.-Uspekhi 1946, 10, 13–23. [Google Scholar]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. 2014, 31, 2038–2045. [Google Scholar] [CrossRef]
- Bulygin, A.D.; Vrazhnov, D.A.; Sim, E.S.; Meglinski, I.V.; Kistenev, Y.V. Imitation of optical coherence tomography images by wave Monte Carlo-based approach implemented with the Leontovich–Fock equation. Opt. Eng. 2020, 59, 061626. [Google Scholar] [CrossRef]
- Buligin, A.D.; Kistenev, Y.V.; Meglinski, I.V.; Danilkin, E.A.; Vrazhnov, D.A. Imitation of ultra-sharp light focusing within turbid tissue-like scattering medium by using time-independent Helmholtz equation and method Monte Carlo. Proc. SPIE 2020, 11582, 115821N. [Google Scholar]
- Yanina, I.Y.; Dyachenko, P.A.; Abdurashitov, A.S.; Shalin, A.S.; Minin, I.V.; Minin, O.V.; Bulygin, A.D.; Vrazhnov, D.A.; Kistenev, Y.V.; Tuchin, V.V. Light distribution in fat cell layers at physiological temperatures. Sci. Rep. 2023, 13, 1073. [Google Scholar] [CrossRef] [PubMed]
- Lytaev, M.S.; Vladyko, A.G. Split-step Padé approximations of the Helmholtz equation for radio coverage prediction over irregular terrain. In Proceedings of the Advances in Wireless and Optical Communications (RTUWO), Riga, Latvia, 15–16 November 2018; pp. 179–184. [Google Scholar]
- Kotlyar, V.V.; Kovalev, A.A. Nonparaxial hypergeometric beams. J. Opt. A Pure Appl. Op. 2009, 11, 045711. [Google Scholar] [CrossRef]
- Hauge, J.C.; Crowdy, D. A new approach to the complex Helmholtz equation with applications to diffusion wave fields, impedance spectroscopy and unsteady Stokes flow. IMA J. Appl. Math. 2021, 86, 1287–1326. [Google Scholar] [CrossRef]
- Tuchin, V.V.; Utz, S.R.; Yaroslavsky, I.V. Tissue optics, light distribution, and spectroscopy. Opt. Eng. 1994, 33, 3178–3188. [Google Scholar] [CrossRef]
- Meglinski, I.; Matcher, S. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions. Physiol. Meas. 2002, 23, 741–753. [Google Scholar] [CrossRef]
- Tuchin, V.V. Tissue Optics and Photonics: Biological Tissue Structures. J. Biomed. Photonics Eng. 2015, 1, 3–21. [Google Scholar] [CrossRef]
- Sandby-Moller, J.; Poulsen, T.; Wulf, H.C. Epidermal thickness at different body sites: Relationship to age, geander, pigmentation, blood content, skin type and smoking habits. Acta Derm. Venereol. 2003, 83, 410–413. [Google Scholar] [CrossRef]
- Tsukahara, K.; Tamatsu, Y.; Sugawara, Y.; Shimada, K. The relationship between wrinkle depth and dermal thickness in the forehead and lateral canthal region. Arch. Dermatol. 2011, 147, 822–828. [Google Scholar] [CrossRef][Green Version]
- Ha, R.Y.; Nojima, K.; Adams, W.P., Jr.; Brown, S.A. Analysis of facial skin thickness: Defining the relative thickness index. Plast. Reconstr. Surg. 2005, 115, 1769–1773. [Google Scholar] [CrossRef]
- Bashkatov, N.; Genina, E.A.; Tuchin, V.V. Optical properties of skin, subcutaneous, and muscle tissues: A review. J. Innov. Opt. Health Sci. 2011, 4, 9–38. [Google Scholar] [CrossRef]
- Tuchin, V.V. Light scattering study of tissues. Phys. Uspekhi 1997, 40, 495–515. [Google Scholar] [CrossRef]
- Meglinskii, I.V.; Bashkatov, A.N.; Genina, E.A.; Churmakov, D.Y.; Tuchin, V.V. Study of the possibility of increasing the probing depth by the method of reflection confocal microscopy upon immersion clearing of near-surface human skin layers. Quantum Electron. 2002, 32, 875–882. [Google Scholar] [CrossRef]
- Bulygin, A.D. Algorithm of the parallel sweep method for numerical solution of the Gross–Pitaevskii equation with highest nonlinearities. Supercomput. Front. Innov. 2018, 5, 115–118. [Google Scholar]
- Glaser, A.K.; Chen, Y.; Liu, J.T.C. Fractal propagation method enables realistic optical microscopy simulations in biological tissues. Optica 2016, 3, 861–869. [Google Scholar] [CrossRef]
- Moshfeghi, M. Sidelobe suppression in annular array and axicon imaging systems. J. Acoust. Soc. Am. 1988, 83, 2202–2209. [Google Scholar] [CrossRef]
- Mikula, G.; Kolodziejczyk, A.; Makowski, M.; Prokopowicz, C.; Sypek, M. Difractive elements for imaging with extended depth of focus. Opt. Eng. 2005, 44, 058001. [Google Scholar] [CrossRef]
- Pierce, M.C.; Strasswimmer, J.; Hyle Park, B.; Cense, B.; de Boer, J.F. Birefringence measurements in human skin using polarization-sensitive optical coherence tomography. J. Biomed. Opt. 2004, 9, 287–291. [Google Scholar] [CrossRef]
- Varghese, B.; Verhagen, R.; Hussain, A.; Boudot, C.; Tai, Q.; Ding, S.; Holz, J.A.; Uzunbajakava, N.E. Quantitative assessment of birefringent skin structures in scattered light confocal imaging using radially polarized light. Sensors 2013, 13, 12527–12535. [Google Scholar] [CrossRef]
- Borovkova, M.; Bykov, A.; Popov, A.; Meglinski, I. Role of scattering and birefringence in phase retardation revealed by locus of Stokes vector on Poincaré sphere. J. Biomed. Opt. 2020, 25, 057001. [Google Scholar] [CrossRef]
- Sieryi, O.; Ushenko, V.; Syvokorovskaya, A.V.; Dubolazov, A.; Vanchulyak, O.; Ushenko, A.; Ushenko, Y.; Gorsky, M.; Tomka, Y.; Bykov, A.; et al. Optical anisotropy composition of benign and malignant prostate tissues revealed by Mueller matrix imaging. Biomed. Opt. Express 2022, 13, 6019–6034. [Google Scholar] [CrossRef] [PubMed]
- Ushenko, V.; Hogan, B.T.; Dubolazov, A.; Piavchenko, G.; Kuznetsov, S.L.; Ushenko, A.G.; Ushenko, Y.O.; Gorsky, M.; Bykov, A.; Meglinski, I. 3D Mueller matrix mapping of layered distributions of depolarisation degree for analysis of prostate adenoma and carcinoma diffuse tissues. Sci. Rep. 2021, 11, 5162. [Google Scholar] [CrossRef] [PubMed]
- Trifonyuk, L.; Sdobnov, A.; Baranowski, W.; Ushenko, V.; Olar, O.; Dubolazov, A.; Pidkamin, L.; Sidor, M.; Vanchuliak, O.; Motrich, A.; et al. Differential Mueller-matrix imaging of partially depolarizing optically anisotropic biological tissues. Laser. Med. Sci. 2020, 35, 877–891. [Google Scholar] [CrossRef]
- Das, N.K.; Chakraborty, S.; Dey, R.; Panigrahi, P.K.; Meglinski, I.; Ghosh, N. Quantitative assessment of submicron scale anisotropy in tissue multifractality by scattering Mueller matrix in the framework of Born approximation. Opt. Commun. 2018, 413, 172–178. [Google Scholar] [CrossRef]
- Kistenev, Y.V.; Nikolaev, V.V.; Kurochkina, O.S.; Borisov, A.V.; Vrazhnov, D.A.; Sandykova, E.A. Application of multiphoton imaging and machine learning to lymphedema tissue analysis. Biomed. Opt. Express 2019, 14, 3353–3368. [Google Scholar] [CrossRef]
- Martines-Arano, H.; Palacios-Barreto, S.; Castillo-Cruz, J.; Meda-Campaña, J.A.; García-Pérez, B.E.; Torres-Torres, C. Fractional photodamage triggered by chaotic attractors in human lung epithelial cancer cells. Int. J. Therm. Sci. 2022, 181, 107734. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).