Ex Vivo Optical Properties Estimation for Reliable Tissue Characterization
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
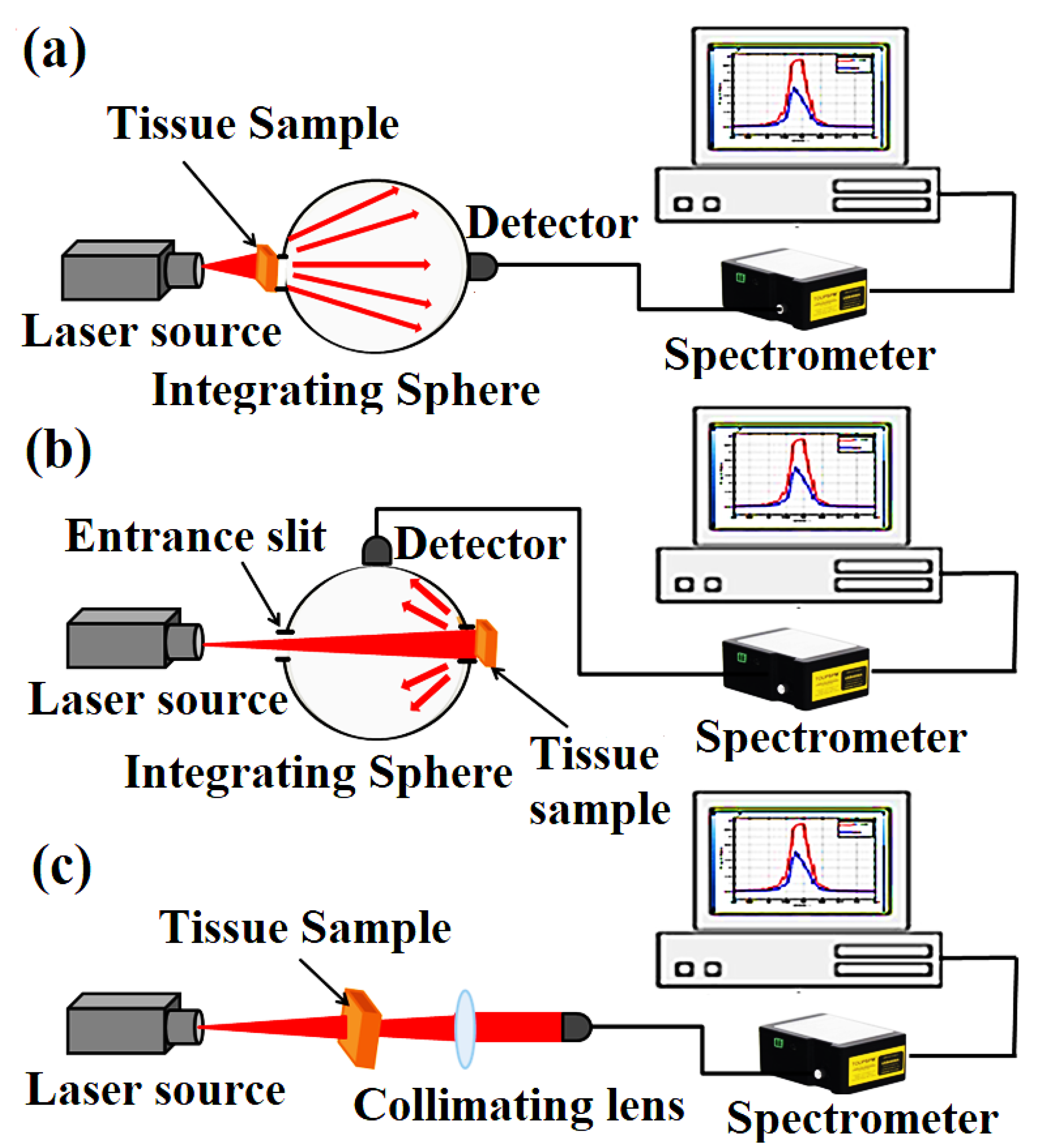
2.2. Tissue Diffuse Reflectance and Transmittance Measurements
2.3. Optical Parameters Estimation
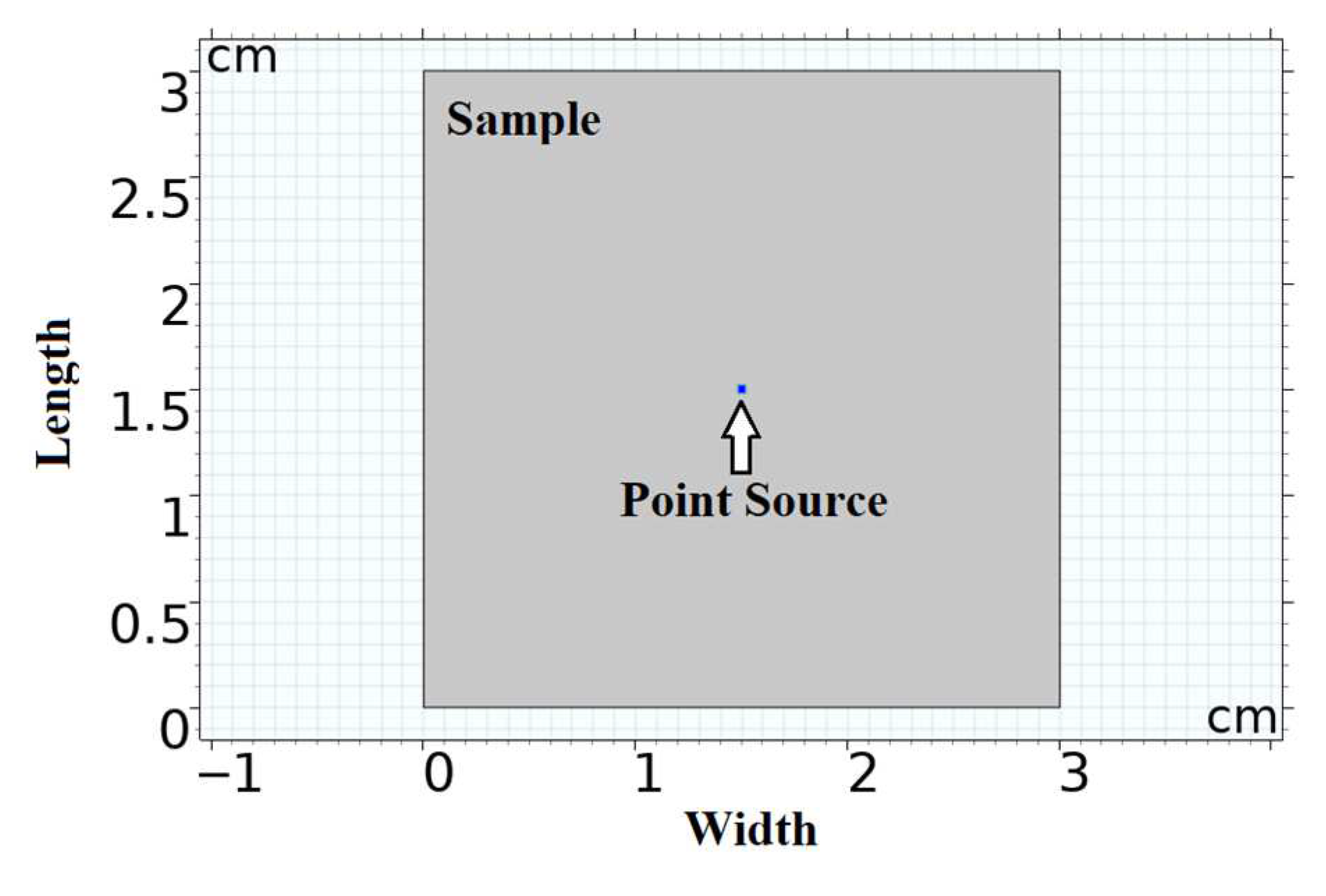
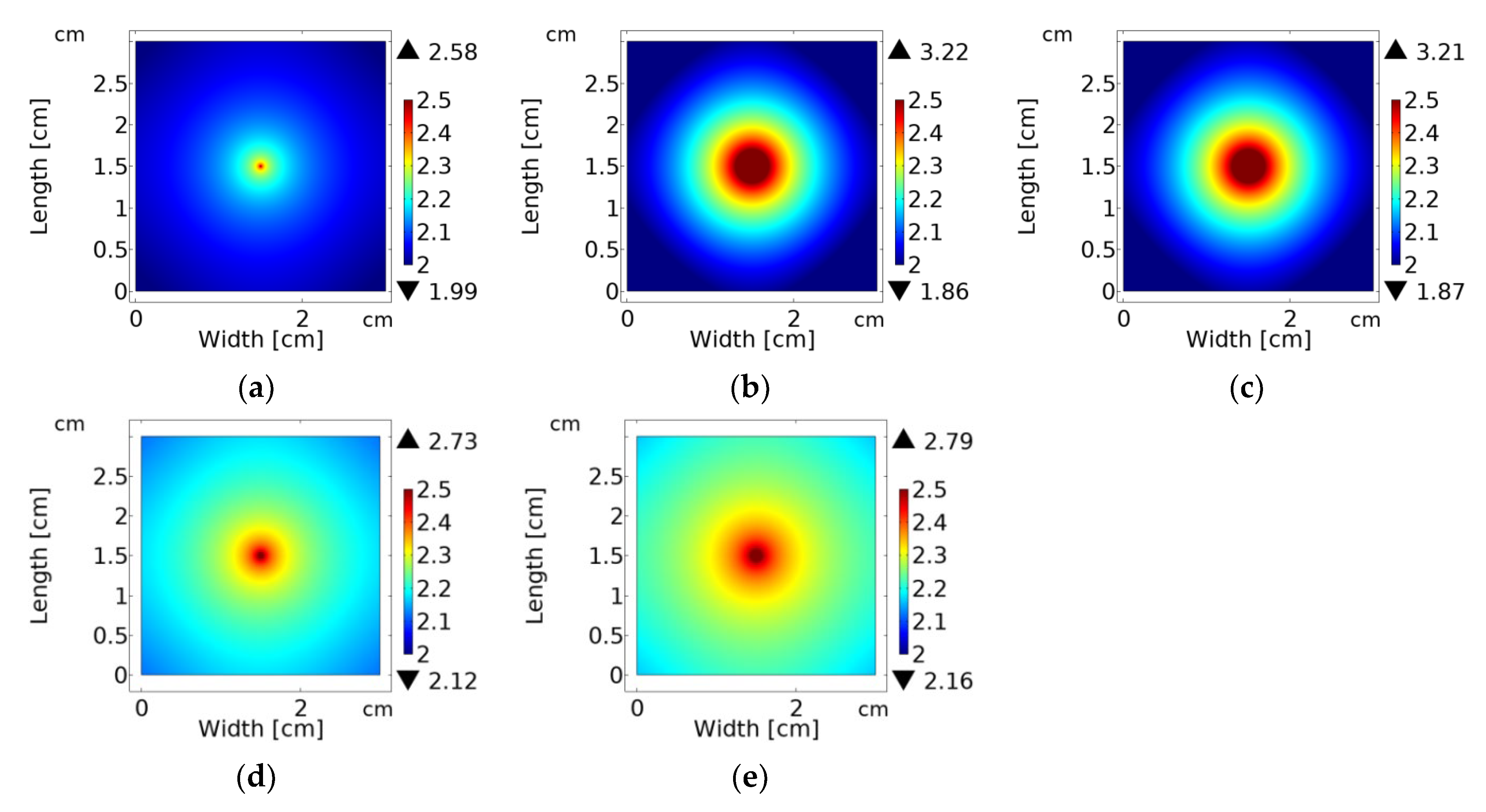
2.4. Simulating the Optical Fluence Rate Distribution
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buch, J.; Hammond, B. Photobiomodulation of the Visual System and Human Health. Int. J. Mol. Sci. 2020, 21, 8020. [Google Scholar] [CrossRef] [PubMed]
- Mester, A. Laser Biostimulation. Photomed. Laser Surg. 2013, 31, 237–239. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Zhang, C.Y.; Gao, J.; Wang, Z. Recent Advances in Photodynamic Therapy for Cancer and Infectious Diseases. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2019, 11, e1560. [Google Scholar] [CrossRef] [PubMed]
- Abdelhalim, I.; Hamdy, O.; Ahmed, A.; Salah, H.; Elnaby, H. Dependence of the Heating Effect on Tissue Absorption Coefficient during Corneal Reshaping Using Different UV Lasers: A Numerical Study. Phys. Eng. Sci. Med. 2021, 44, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Oron, A.; Oron, U. Low-Level Laser Therapy to the Bone Marrow Ameliorates Neurodegenerative Disease Progression in a Mouse Model of Alzheimer’s Disease: A Minireview. Photomed. Laser Surg. 2016, 34, 627–630. [Google Scholar] [CrossRef]
- Shahin, A. Optical Investigation of Bovine Grey and White Matters in Visible and Near-Infrared Ranges. Pol. J. Med. Phys. Eng. 2021, 27, 99–107. [Google Scholar] [CrossRef]
- Tuchin, V.V. Tissue Optics and Photonics: Light-Tissue Interaction. J. Biomed. Photonics Eng. 2015, 1, 98–134. [Google Scholar] [CrossRef]
- Nandy, S.; Mostafa, A.; Kumavor, P.D.; Sanders, M.; Brewer, M.; Zhu, Q. Characterizing Optical Properties and Spatial Heterogeneity of Human Ovarian Tissue Using Spatial Frequency Domain Imaging. J. Biomed. Opt. 2016, 21, 101402. [Google Scholar] [CrossRef]
- Hamdy, O.; Mohammed, H.S. Variations in Tissue Optical Parameters with the Incident Power of an Infrared Laser. PLoS ONE 2022, 17, e0263164. [Google Scholar] [CrossRef]
- Honda, N.; Ishii, K.; Kajimoto, Y.; Kuroiwa, T.; Awazu, K. Determination of Optical Properties of Human Brain Tumor Tissues from 350 to 1000 Nm to Investigate the Cause of False Negatives in Fluorescence-Guided Resection with 5-Aminolevulinic Acid. J. Biomed. Opt. 2018, 23, 075006. [Google Scholar] [CrossRef]
- Hamdy, O.; Youssef, D.; El-Azab, J.; Soluma, N.H. Detection of Breast Diseases Using Numerical Study of Light Propagation. In Proceedings of the 2018 9th Cairo International Biomedical Engineering Conference, CIBEC 2018—Proceedings, Cairo, Egypt, 20–22 December 2018. [Google Scholar]
- Mahdy, S.; Hamdy, O.; Hassan, M.A.; Eldosoky, M.A.A. A Modified Source—Detector Configuration for the Discrimination between Normal and Diseased Human Breast Based on the Continuous—Wave Diffuse Optical Imaging Approach: A Simulation Study. Lasers Med. Sci. 2022, 37, 1855–1864. [Google Scholar] [CrossRef]
- Piguet, D.; Marquet, P.; Gross, J.D.; Tromberg, B.J.; Depeursinge, C. In Vivo Local Determination of Tissue Optical Properties: Applications to Human Brain. Appl. Opt. 1999, 38, 4939–4950. [Google Scholar]
- Pitzschke, A.; Lovisa, B.; Seydoux, O.; Haenggi, M.; Oertel, M.F.; Zellweger, M.; Tardy, Y.; Wagnières, G. Optical Properties of Rabbit Brain in the Red and Near-Infrared: Changes Observed under in Vivo, Postmortem, Frozen, and Formalin-Fixated Conditions. J. Biomed. Opt. 2015, 20, 025006. [Google Scholar] [CrossRef]
- Hamdy, O.; Ismail, T. Study of Optical Power Variations in Multi-Layer Human Skin Model for Monitoring the Light Dose. In Proceedings of the Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 28–30 October 2019; pp. 21–24. [Google Scholar]
- Zhang, H.; Kim, D.M.; Tai, Y.; Zhang, H.; Salo, D.; Kim, D.M.; Komarov, S.; Tai, Y.; Berezin, M.Y. Penetration Depth of Photons in Biological Tissues from Hyperspectral Imaging in Shortwave Infrared in Transmission and Reflection Geometries. J. Biomed. Opt. 2016, 21, 126006. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.; Yodh, A.G. Diffuse Optics for Tissue Monitoring and Tomography. Rep. Prog. Phys. 2010, 73, 076701. [Google Scholar] [CrossRef]
- Cook, P.D.; Bixler, J.N.; Thomas, R.J.; Early, E.A. Prediction of Tissue Optical Properties Using the Monte Carlo Modeling of Photon Transport in Turbid Media and Integrating Spheres. OSA Contin. 2020, 3, 1456–1475. [Google Scholar] [CrossRef]
- Hamdy, O.; Fathy, M.; Al-Saeed, T.A.; El-Azab, J.; Solouma, N.H. Estimation of Optical Parameters and Fluence Rate Distribution in Biological Tissues via a Single Integrating Sphere Optical Setup. Optik 2017, 140, 1004–1009. [Google Scholar] [CrossRef]
- Hamdy, O.; El-Azab, J.; Al-Saeed, T.A.; Hassan, M.F.; Solouma, N.H. A Method for Medical Diagnosis Based on Optical Fluence Rate Distribution at Tissue Surface. Materials 2017, 10, 1104. [Google Scholar] [CrossRef]
- Hamdy, O.; Solouma, N.H. Distant-Detector versus Integrating Sphere Measurements for Estimating Tissue Optical Parameters: A Comparative Experimental Study. Optik 2021, 247, 167981. [Google Scholar] [CrossRef]
- Wang, L.V.; Wu, H. Biomedical Optics: Principles and Imaging; Wiley-Interscience: Hobokon, NJ, USA, 2007; ISBN 9780471743040. [Google Scholar]
- Markolf, N.H. Laser-Tissue Interactions: Fundamentals and Applications; Springer-Verlag: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Farrell, T.J.; Patterson, S.M. A Diffusion Theory Model of Spatially Resolved, Steady-State Diffuse Reflectance for the Noninvasive Determination of Tissue Optical Properties in Vivo. Med. Phys. 1992, 19, 879. [Google Scholar] [CrossRef]
- Hamdy, O.; Alsharafi, S.S.; Hassan, M.F.; Eldib, A.; Solouma, N.H. A Multi-Spot Laser System for Retinal Disorders Treatment: Experimental Study. Opt. Int. J. Light Electron. Opt. 2019, 185, 609–613. [Google Scholar] [CrossRef]
- Abdelhalim, I.; Hamdy, O.; Hassan, A.A.; Elnaby, S.H. Nd:YAG Fourth Harmonic (266-Nm) Generation for Corneal Reshaping Procedure: An Ex-Vivo Experimental Study. PLoS ONE 2021, 16, e0260494. [Google Scholar] [CrossRef] [PubMed]
- Azadgoli, B.; Baker, R.Y. Laser Applications in Surgery. Ann. Transl. Med. 2016, 4, 452. [Google Scholar] [CrossRef] [PubMed]
- Husain, Z.; Alster, T.S. The Role of Lasers and Intense Pulsed Light Technology in Dermatology. Clin. Cosmet. Investig. Dermatol. 2016, 9, 29–40. [Google Scholar] [CrossRef]
- Abdelhalim, I.; Hamdy, O. An Optical Prototype for Simulating the Laser Delivery Method in a Typical LASIK Device. In Proceedings of the Education and Training in Optics & Photonics, Online, 8–10 September 2021; p. F2A.8. [Google Scholar]
- Abdelazeem, R.M.; Agour, M. Optical Inspection of Single Vision Soft Contact Lenses Based on an Active Adaptive Wavefront Sensor. Appl. Opt. 2022, 61, 141–148. [Google Scholar] [CrossRef]
- Hoshi, Y.; Yamada, Y. Overview of Diffuse Optical Tomography and Its Clinical Applications. J. Biomed. Opt. 2016, 21, 091312. [Google Scholar] [CrossRef]
- Kanclerz, P.; Khoramnia, R.; Wang, X. Current Developments in Corneal Topography and Tomography. Diagnostics 2021, 11, 1466. [Google Scholar] [CrossRef]
- Abdelazeem, R.M.; Ahmed, M.M.; Hamdy, O. Monitoring the Optical Diffuse Transmittance of Skin during Thermo-Hydrotherapy via Spatial Frequency Domain Imaging: A Pilot Study. In Proceedings of the Biophotonics Congress: Optics in the Life Sciences, Washington, DC, USA, 12–16 April 2021. [Google Scholar]
- Abdelazeem, R.M.; Hamdy, O. Utilizing the Spatial Frequency Domain Imaging to Investigate Change in Optical Parameters of Skin Exposed to Thermal-Hydrotherapy: Ex-Vivo Study. Int. J. Imaging Syst. Technol. 2022, 32, 1661–1672. [Google Scholar] [CrossRef]
- Tynga, I.M.; Abrahamse, H. Nano-Mediated Photodynamic Therapy for Cancer: Enhancement of Cancer Specificity and Therapeutic Effects Nano-Mediated Photodynamic Therapy for Cancer: Enhancement of Cancer Specificity and Therapeutic Effects. Nanomaterials 2018, 8, 923. [Google Scholar] [CrossRef]
- Mosilhy, E.A.; Alshial, E.E.; Eltaras, M.M.; Rahman, M.M.A.; Helmy, H.I.; Elazoul, A.H.; Hamdy, O.; Mohammed, H.S. Non-Invasive Transcranial Brain Modulation for Neurological Disorders Treatment: A Narrative Review. Life Sci. 2022, 307, 120869. [Google Scholar] [CrossRef]
- Dompe, C.; Moncrieff, L.; Matys, J.; Grzech-Leśniak, K.; Kocherova, I.; Bryja, A.; Bruska, M.; Dominiak, M.; Mozdziak, P.; Skiba, T.H.I.; et al. Photobiomodulation—Underlying Mechanism and Clinical Applications. J. Clin. Med. 2020, 9, 1724. [Google Scholar] [CrossRef]
- Hamdy, O.; Abdel-Salam, Z.; Abdel-Harith, M. Optical Characterization of Biological Tissues Based on Fluorescence, Absorption, and Scattering Properties. Diagnostics 2022, 12, 2846. [Google Scholar] [CrossRef]
- Hamdy, O.; Mohammed, H.S. Investigating the Transmission Profiles of 808 Nm Laser through Different Regions of the Rat’s Head. Lasers Med. Sci. 2021, 36, 803–810. [Google Scholar] [CrossRef]
- Yu, Y.-W.; Huang, P.-D.; Chen, C.-H.; Kuo, C.-H.; Wu, W.-H.; Huang, Y.-H.; Wu, C.-S.; Yang, T.-H.; Sun, C.-C. Total Transmittance Measurement Using an Integrating Sphere Calibrated by a Screen Image Synthesis System. Opt. Contin. 2022, 1, 1451–1455. [Google Scholar] [CrossRef]
- Boas, D.A.; Pitris, C.; Ramanujam, N. Handbook of Biomedical Optics; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Sheet, A.H.; Hamdy, O.; Abdel-Harith, M. Scattering and Absorption Properties Modification of Optically Cleared Skeletal Muscles: An Ex Vivo Study. J. Opt. Soc. Am. A 2023, 40, 1042–1050. [Google Scholar] [CrossRef]
- Hamdy, O.; Tawfik, W. The Effect of Temperature on the Optical and Analytical Properties of PET Polymer Used in Drinking Water Bottles. J. Phys. Conf. Ser. 2020, 1472, 012004. [Google Scholar] [CrossRef]
- Molenaar, R.; ten Bosch, J.J.; Zijp, J.R. Determination of Kubelka–Munk Scattering and Absorption Coefficients by Diffuse Illumination. Appl. Opt. 1999, 38, 2068–2077. [Google Scholar] [CrossRef]
- Masters, B.R. Biomedical Optics: Principles and Imaging. J. Biomed. Opt. 2008, 13, 049902. [Google Scholar] [CrossRef]
- Wang, L.; Jacquesa, S.L.; Zheng, L. MCML-Monte-Carlo Modeling of Light Transport in Multi-Layered Tissues. Comput. Methods Prog. Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Hassan, N.I.; Hassan, Y.M.; Mustafa, T.A.; Hamdy, O. Modeling Optical Fluence and Diffuse Reflectance Distribution in Normal and Cancerous Breast Tissues Exposed to Planar and Gaussian NIR Beam Shapes Using Monte Carlo Simulation. Lasers Med. Sci. 2023, 38, 1–8. [Google Scholar] [CrossRef]
- Beek, J.F.; Blokland, P.; Posthumus, P.; Aalders, M.; Pickering, J.W.; Sterenborg, H.J.C.M.; Van Gemert, M.J.C. In Vitro Double-Integrating-Sphere Optical Properties of Tissues between 630 and 1064 Nm. Phys. Med. Biol. 1997, 42, 2255–2261. [Google Scholar] [CrossRef] [PubMed]
- Firdous, S.; Ikram, M.; Nawaz, M.; Aslam, M. Measurement of Optical Parameters: Absorption Scattering and Auto-Florescence of Skin in Vitro. Int. J. Cancer Res. 2005, 1, 10–15. [Google Scholar]
- Van Beers, R.; Kokawa, M.; Aernouts, B.; Watté, R.; De Smet, S.; Saeys, W. Evolution of the Bulk Optical Properties of Bovine Muscles during Wet Aging. Meat Sci. 2018, 136, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Arslan, H.; Pehlivanöz, B. Effect of Purification, Dehydration, and Coagulation Processes on the Optical Parameters of Biological Tissues. Chin. Opt. Lett. 2021, 19, 011701. [Google Scholar] [CrossRef]
- Soleimanzad, H.; Gurden, H.; Pain, F. Optical Properties of Mice Skull Bone in the 455- to 705-Nm Range. J. Biomed. Opt. 2017, 22, 010503. [Google Scholar] [CrossRef]
- Hamdy, O.; Abdel-Salam, Z.; Abdel-Harith, M. Discrimination between Fresh, Chilled, and Frozen/Thawed Chicken Based on Its Skin’s Spectrochemical and Optical Properties. Anal. Methods 2020, 12, 2093–2101. [Google Scholar] [CrossRef]
- Sheet, A.H.; Hamdy, O.; Abdel-Salam, Z.; Abdel-Harith, M. Combining Laser-Irradiation and Glycerol Immersion of Skeletal Muscles to Improve Their Optical Transparency. Opt. Laser Technol. 2022, 148, 107760. [Google Scholar] [CrossRef]
- Shanshool, A.S.; Lazareva, E.N.; Hamdy, O.; Tuchin, V.V. Optical Properties and Fluence Distribution in Rabbit Head Tissues at Selected Laser Wavelengths. Materials 2022, 15, 5696. [Google Scholar] [CrossRef]
- Fukutomi, D.; Ishii, K.; Awazu, K. Determination of the Scattering Coefficient of Biological Tissue Considering the Wavelength and Absorption Dependence of the Anisotropy Factor. Opt. Rev. 2016, 23, 291–298. [Google Scholar] [CrossRef]
- Tuchin, V.V.; Utz, S.R.; Yaroslavsky, l.V. Tissue Optics, Light Distribution, and Spectroscopy. Opt. Eng. 1994, 33, 3178–3188. [Google Scholar] [CrossRef]
- Martins, I.S.; Silva, H.F.; Lazareva, E.N.; Chernomyrdin, N.V.; Zaytsev, K.I.; Oliveira, L.M.; Tuchin, V.V. Measurement of Tissue Optical Properties in a Wide Spectral Range: A Review. Biomed. Opt. Express 2023, 14, 249–298. [Google Scholar] [CrossRef]
- Priyanka, N.D.; Kumar, A. Effect of Anisotropy and Scattering Coefficient on Light Distribution in a Semi-Infinite Tissue. In Proceedings of the International Conference on Modeling and Simulation of Diffusive Processes and Applications, Varanasi, India, 9–12 October 2012. [Google Scholar]
- Qilesiz, I.F.; Welch, A.J. Light Dosimetry: Effects of Dehydration and Thermal Damage on the Optical Properties of the Human Aorta. Appl. Opt. 1993, 32, 477–487. [Google Scholar] [CrossRef]
- Jaywant, S.; Wilson, B.; Patterson, M.; Lilge, L.; Flott, T.; Woolsey, J.; McCulloch, C. Temperature Dependent Changes in the Optical Absorption and Scattering Spectra of Tissues. SPIE 1993, 1882, 218–229. [Google Scholar] [CrossRef]
- Martines-Arano, H.; Palacios-Barreto, S.; Castillo-Cruz, J.; Meda-Campaña, J.A.; García-Pérez, B.E.; Torres-Torres, C. Fractional Photodamage Triggered by Chaotic Attractors in Human Lung Epithelial Cancer Cells. Int. J. Therm. Sci. 2022, 181, 107734. [Google Scholar] [CrossRef]



| Literature | Tissue | Optical Parameters | ||
|---|---|---|---|---|
| µa, cm−1 | g | |||
| Beek et al. [48] | Rabbit skin | 0.33 ± 0.02 | 31.6 ± 2.2 | 0:898 ± 0:007 |
| Firdous et al. [49] | Chicken breast skin | 2 | 5 | 0.827 |
| Van Beers et al. [50] | Bovine muscle | 0.5 ± 0.05 | 12 ± 3 | 0.91 |
| Pehlivanöz et al. [51] | Chicken liver | 2.5 | 6.5 | -- |
| Soleimanzad et al. [52] | Mice skull | 5 ± 0.2 | 24 ± 1.5 | -- |
| This study | Chicken breast skin | 4.91 ± 0.1 | 3.24 ± 2 | 0.81 ± 0.03 |
| Rabbit skin | 6.04 ± 0.4 | 20.11 ± 2 | 0.85 ± 0.05 | |
| Rabbit skull | 5.91 ± 0.4 | 19.81 ± 1 | 0.90 ± 0.02 | |
| Chicken liver | 1.41 ± 0.2 | 8.18 ± 1 | 0.679 ± 0.05 | |
| Bovine muscle | 0.3 ± 0.11 | 10.02 ± 2 | 0.90 ± 0.01 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solouma, N.; Hamdy, O. Ex Vivo Optical Properties Estimation for Reliable Tissue Characterization. Photonics 2023, 10, 891. https://doi.org/10.3390/photonics10080891
Solouma N, Hamdy O. Ex Vivo Optical Properties Estimation for Reliable Tissue Characterization. Photonics. 2023; 10(8):891. https://doi.org/10.3390/photonics10080891
Chicago/Turabian StyleSolouma, Nahed, and Omnia Hamdy. 2023. "Ex Vivo Optical Properties Estimation for Reliable Tissue Characterization" Photonics 10, no. 8: 891. https://doi.org/10.3390/photonics10080891
APA StyleSolouma, N., & Hamdy, O. (2023). Ex Vivo Optical Properties Estimation for Reliable Tissue Characterization. Photonics, 10(8), 891. https://doi.org/10.3390/photonics10080891





