A Fast Star-Detection Algorithm under Stray-Light Interference
Abstract
1. Introduction
2. Materials and Methods
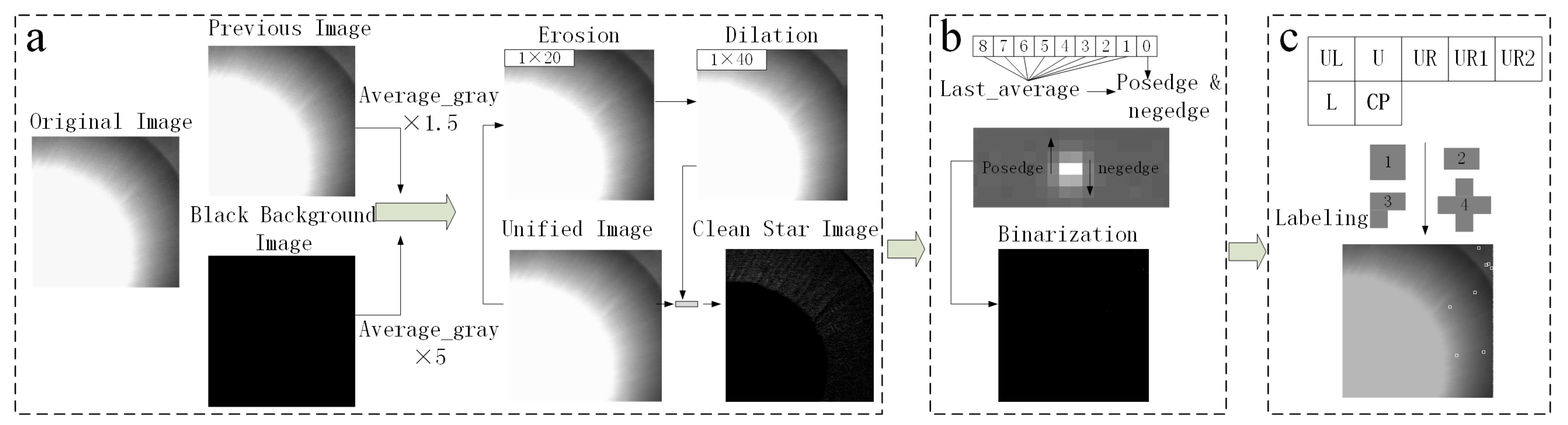
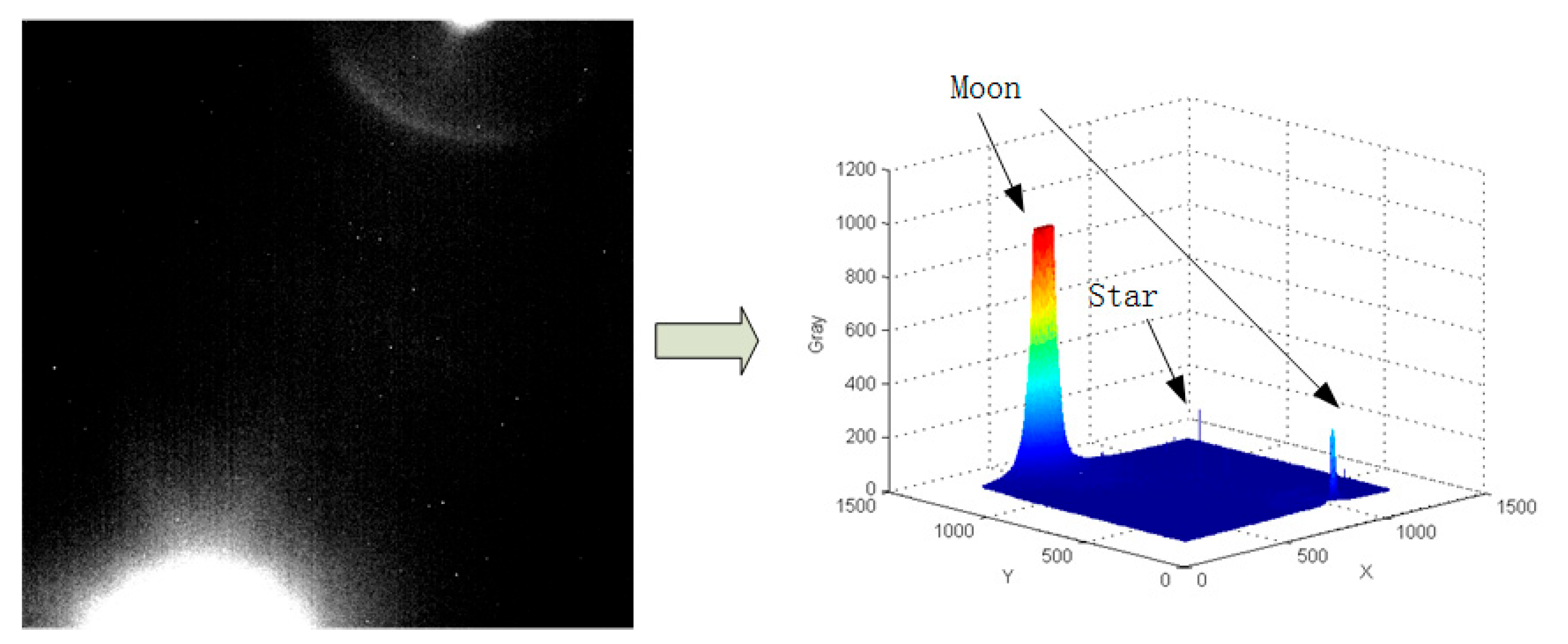
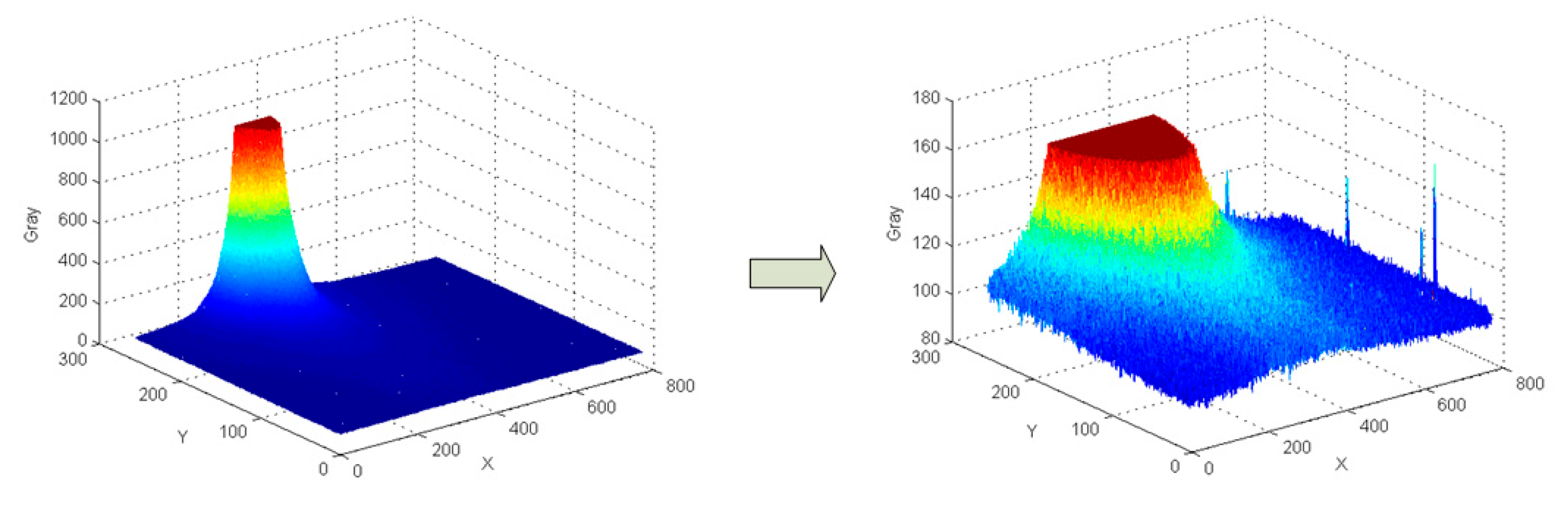
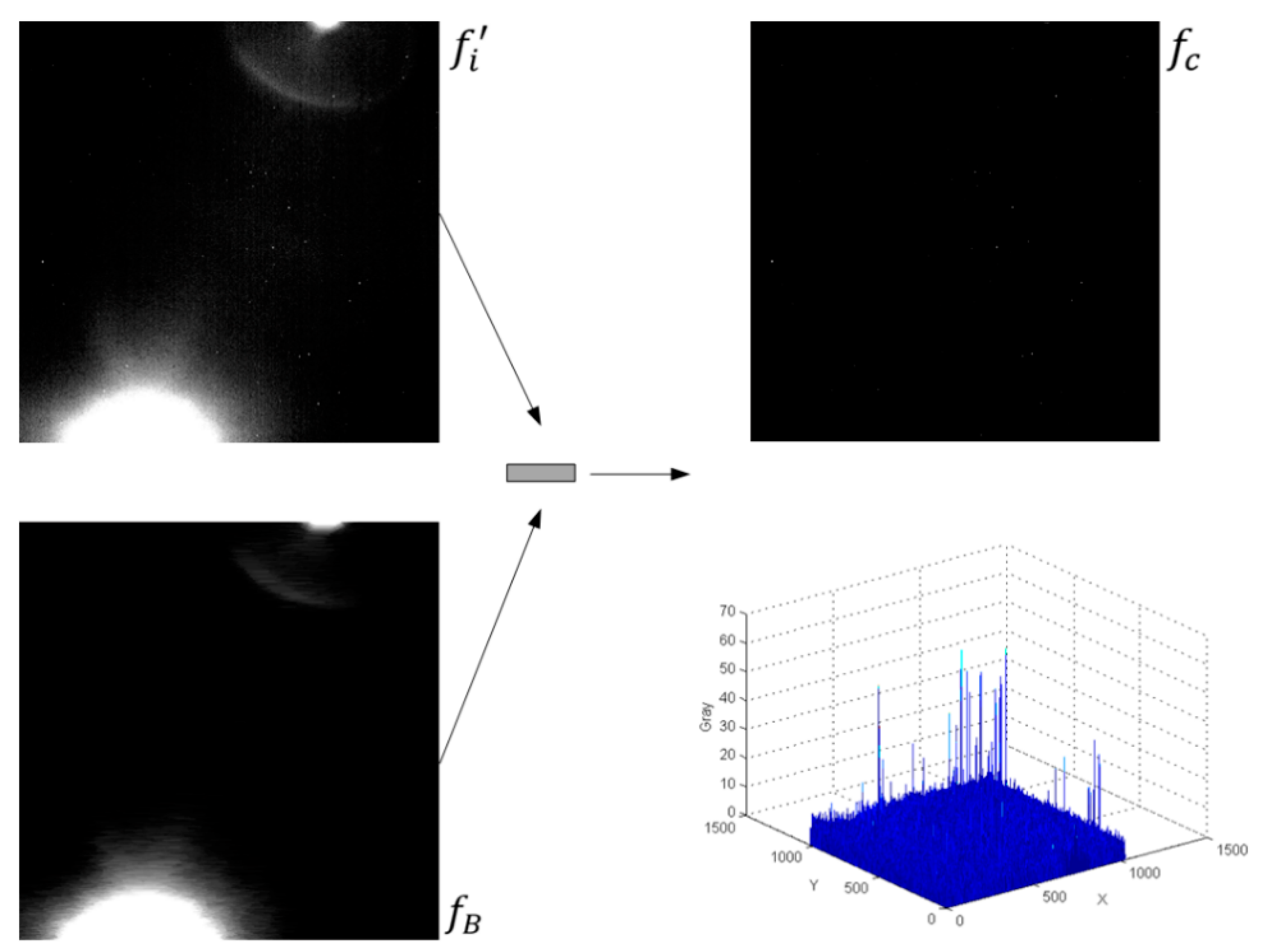
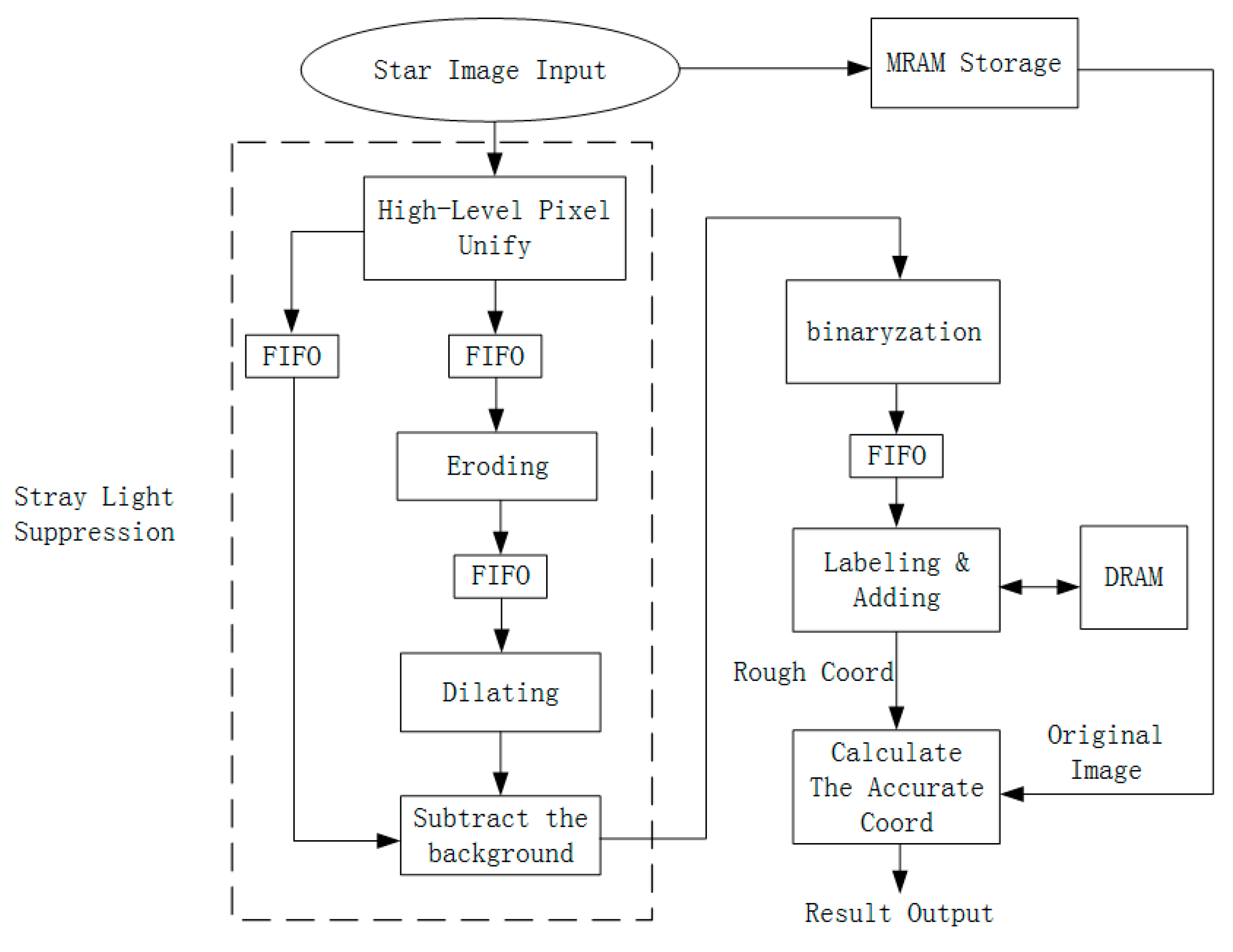
2.1. Stray-Light Suppression
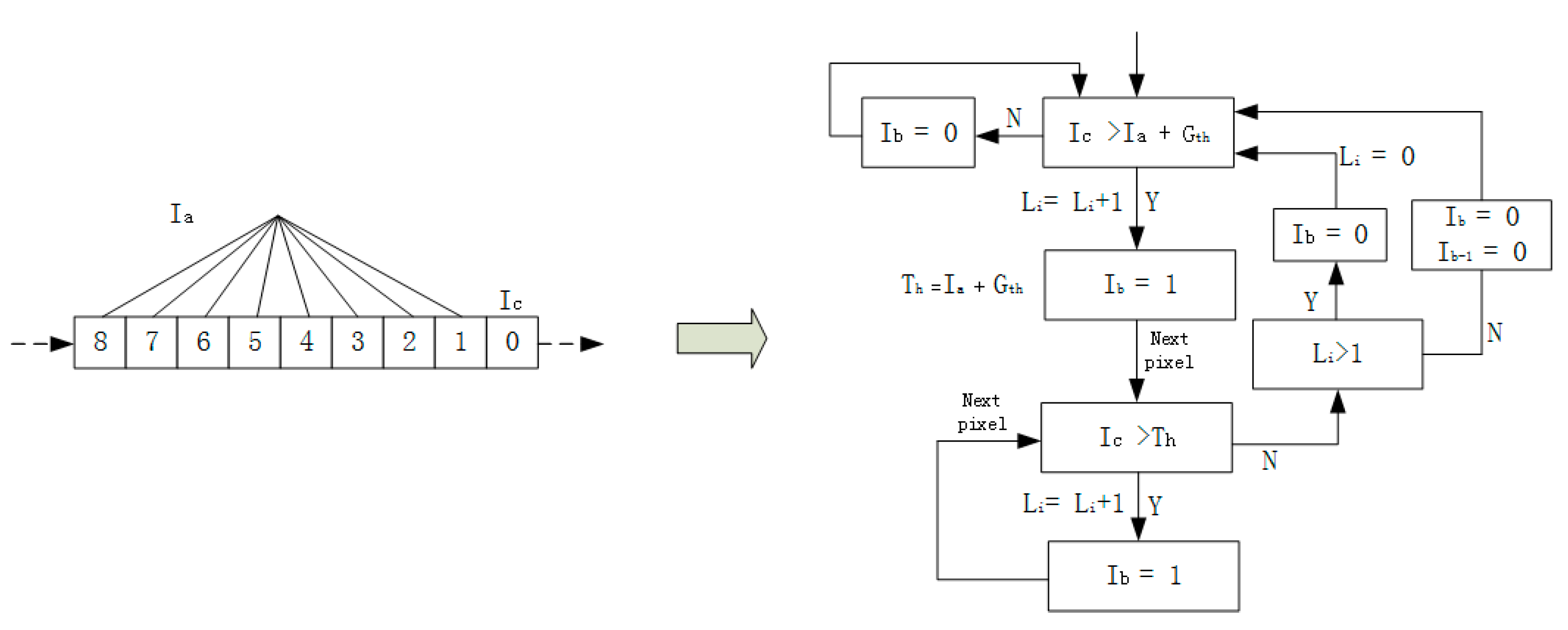
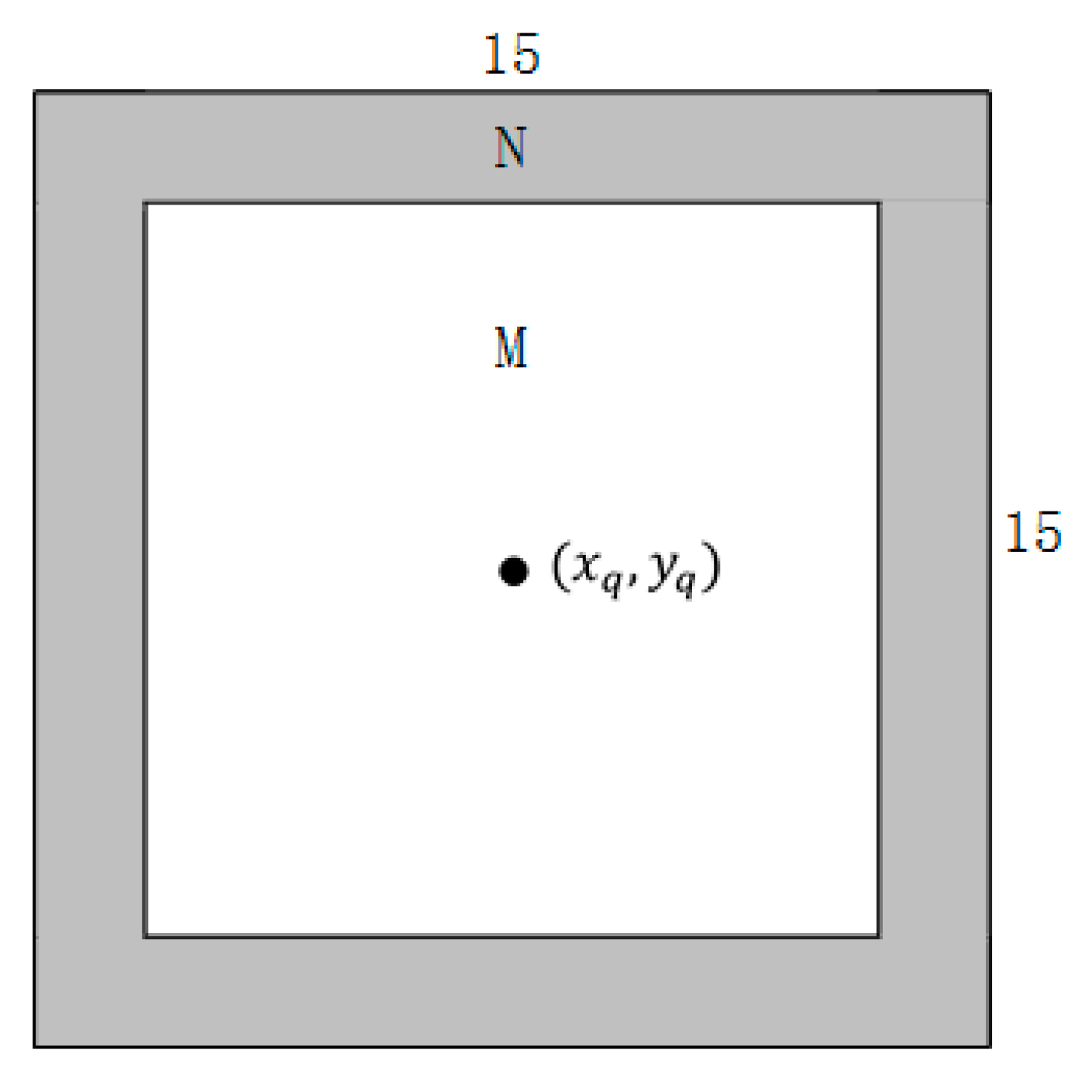
2.2. Binarization
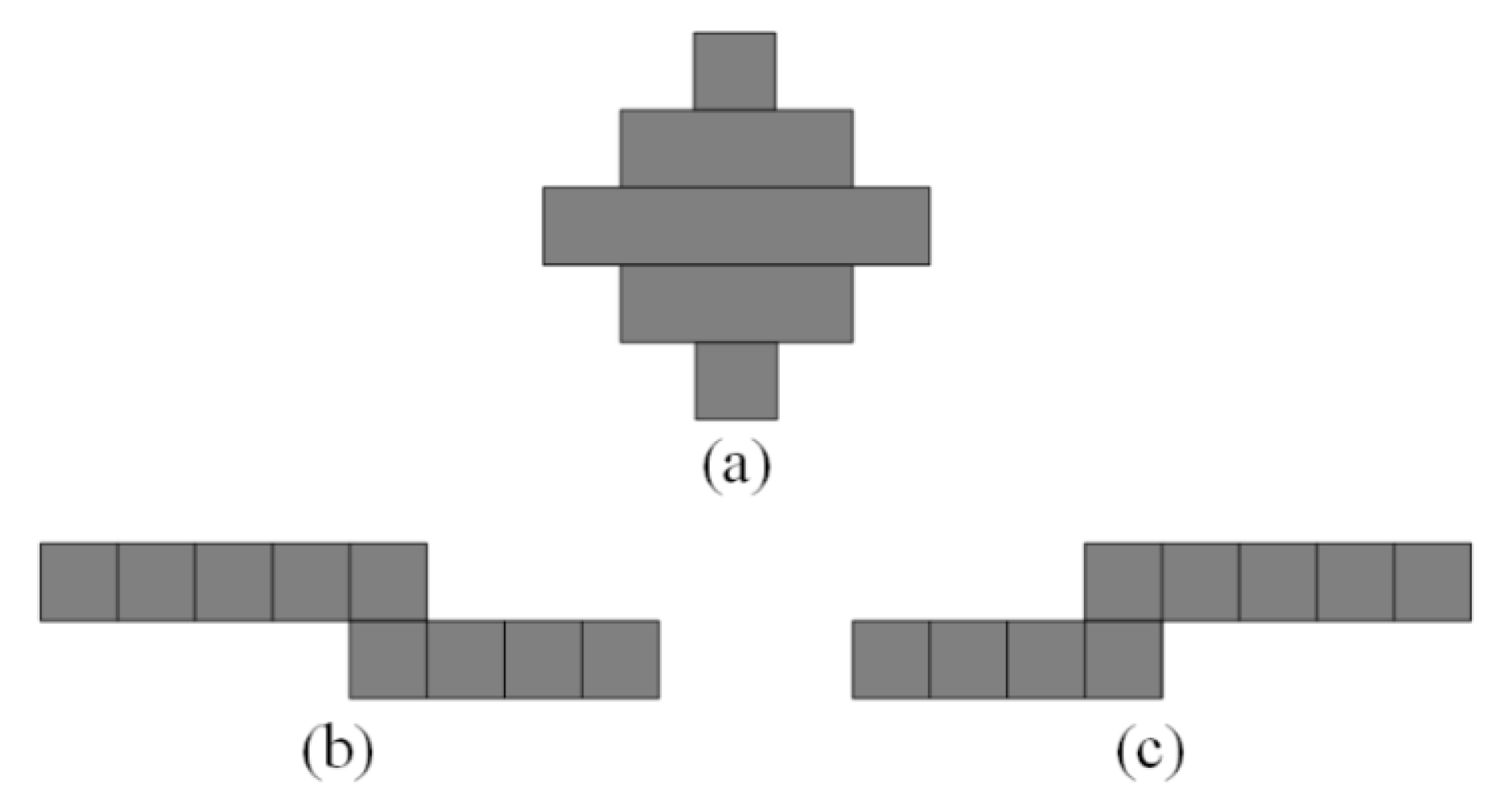
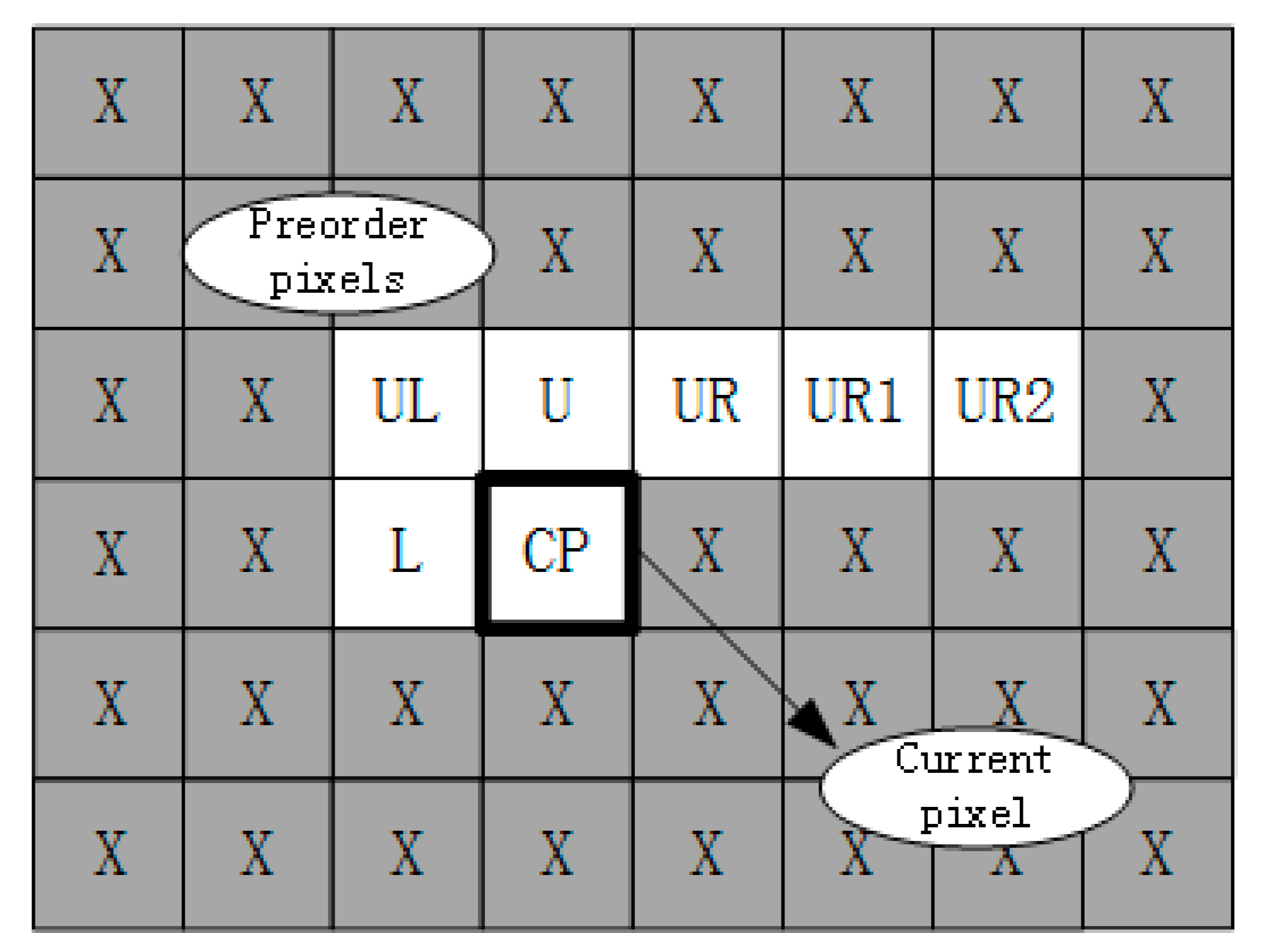
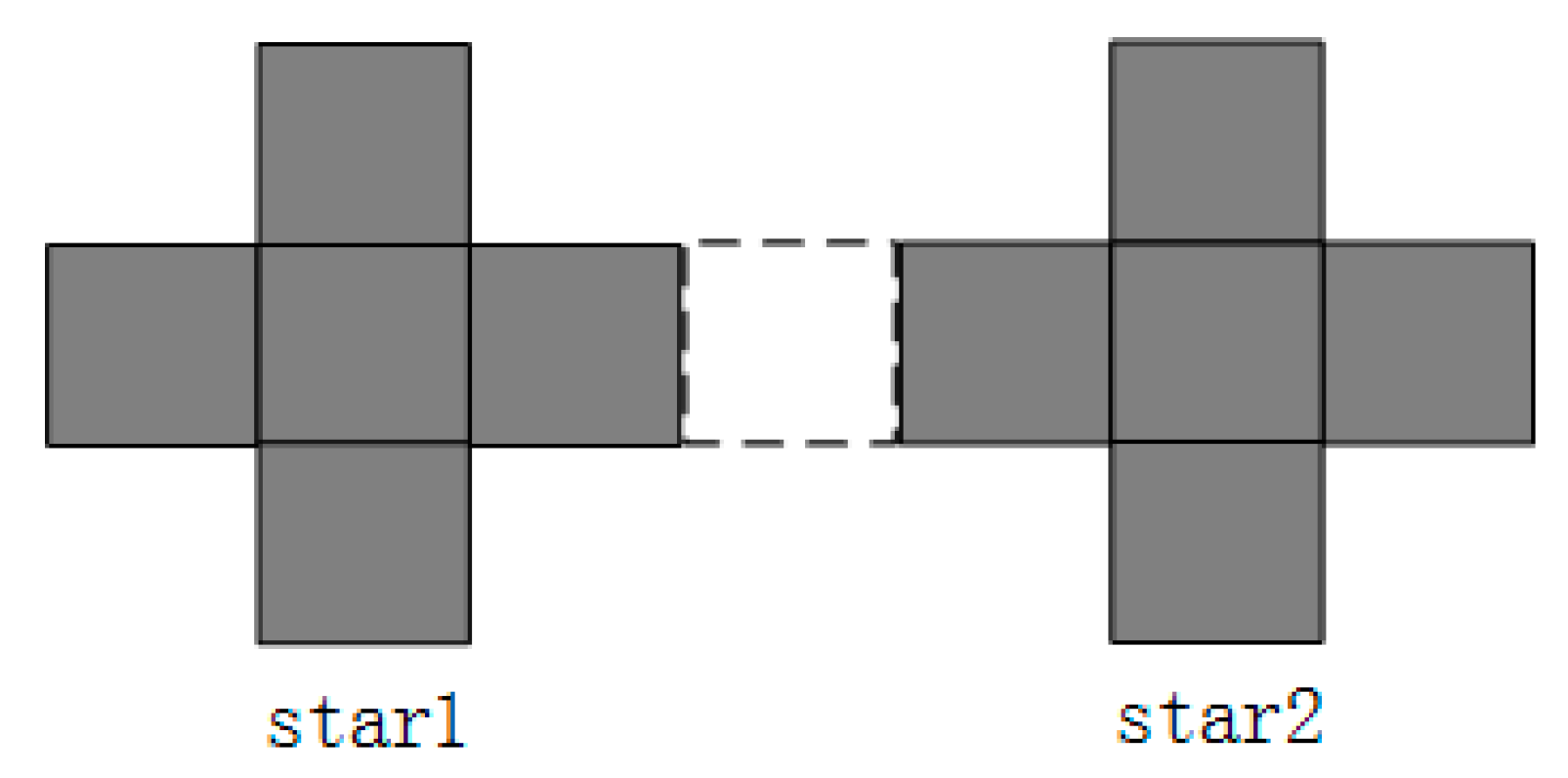
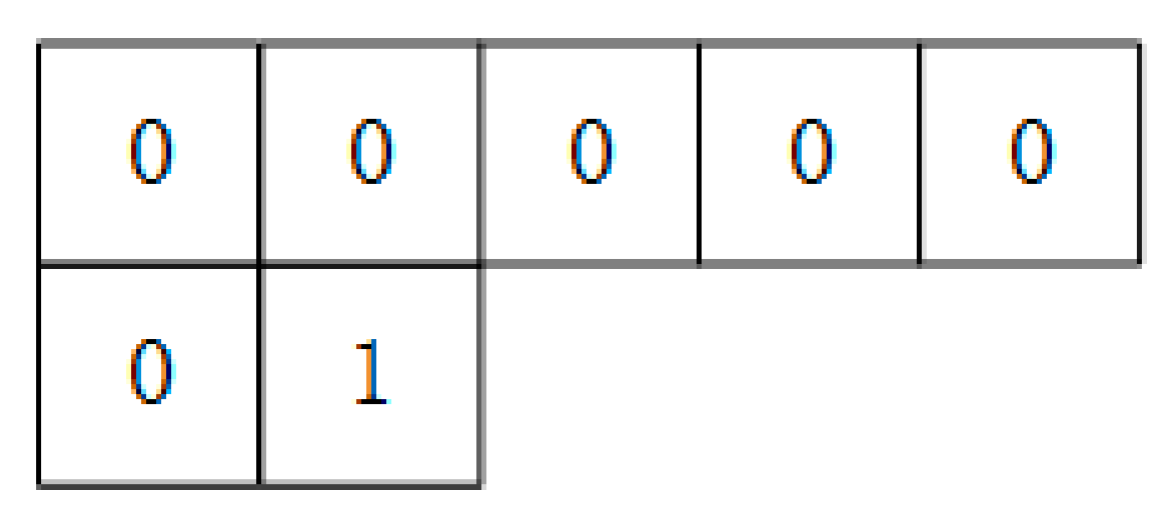
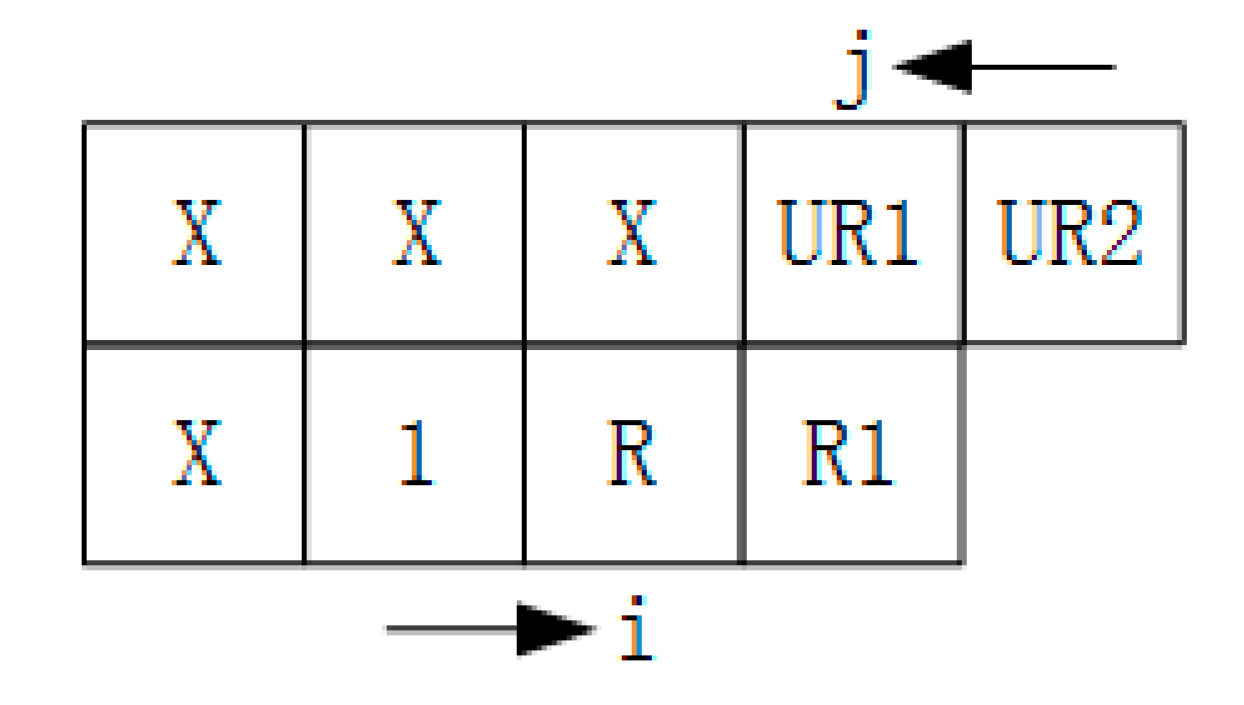
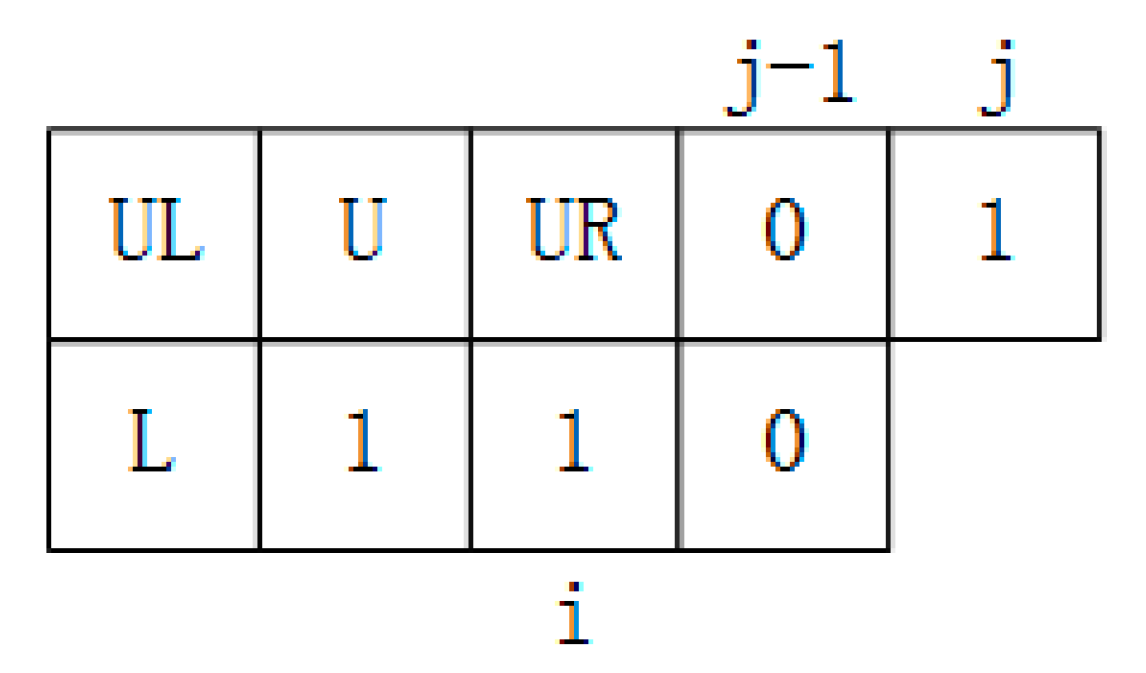
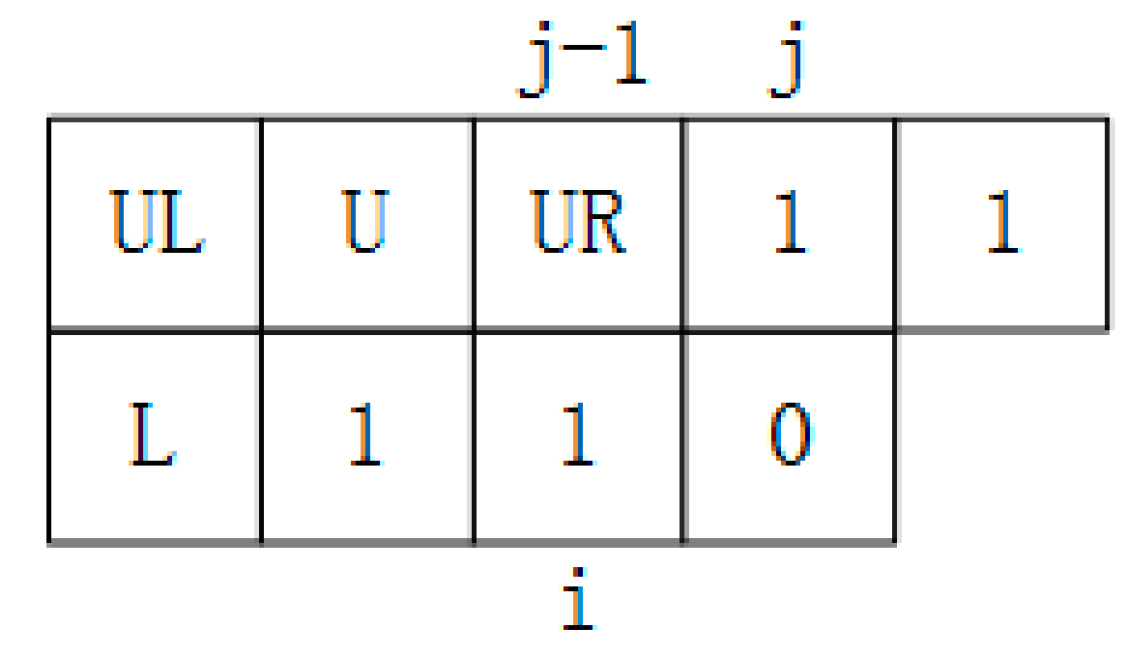
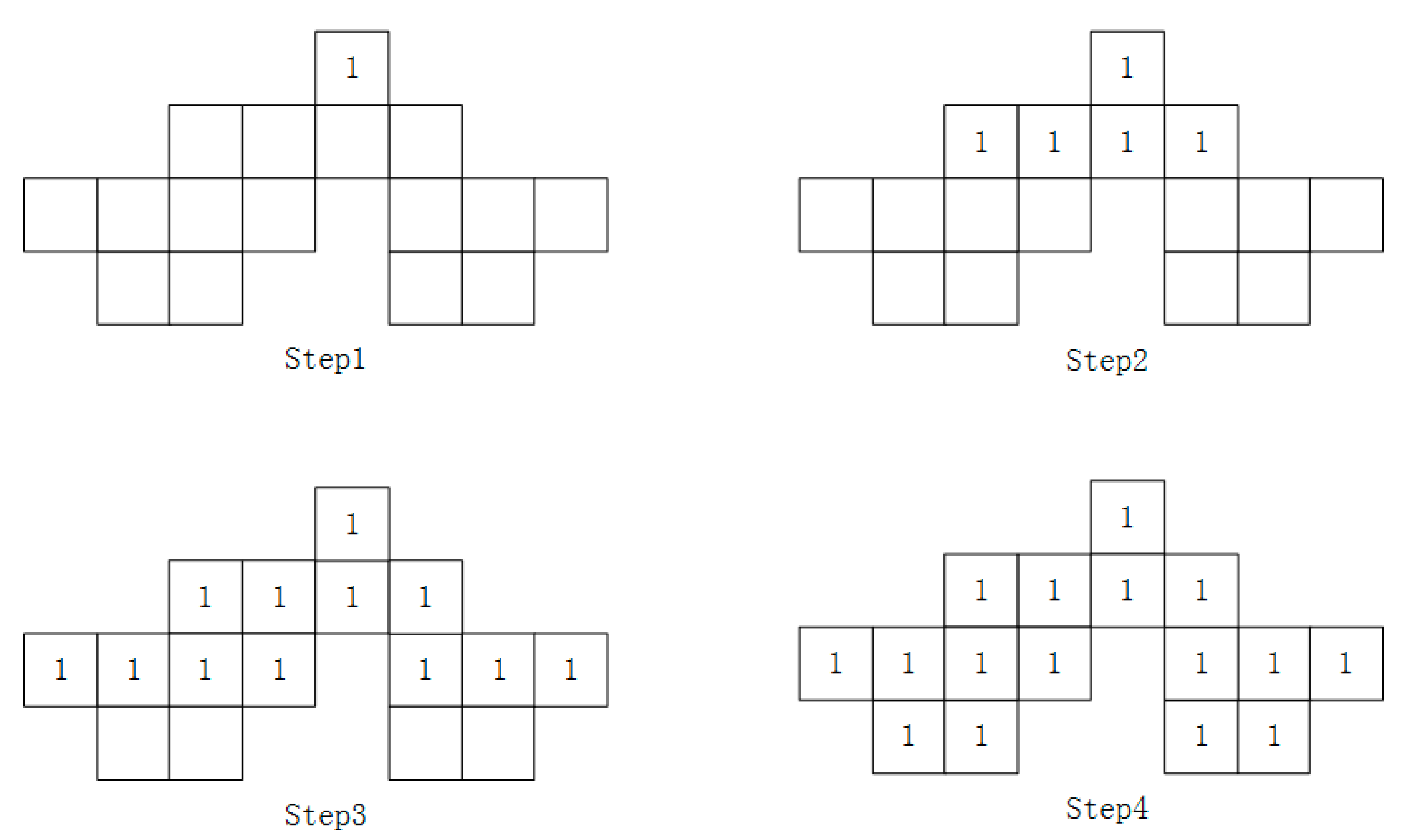
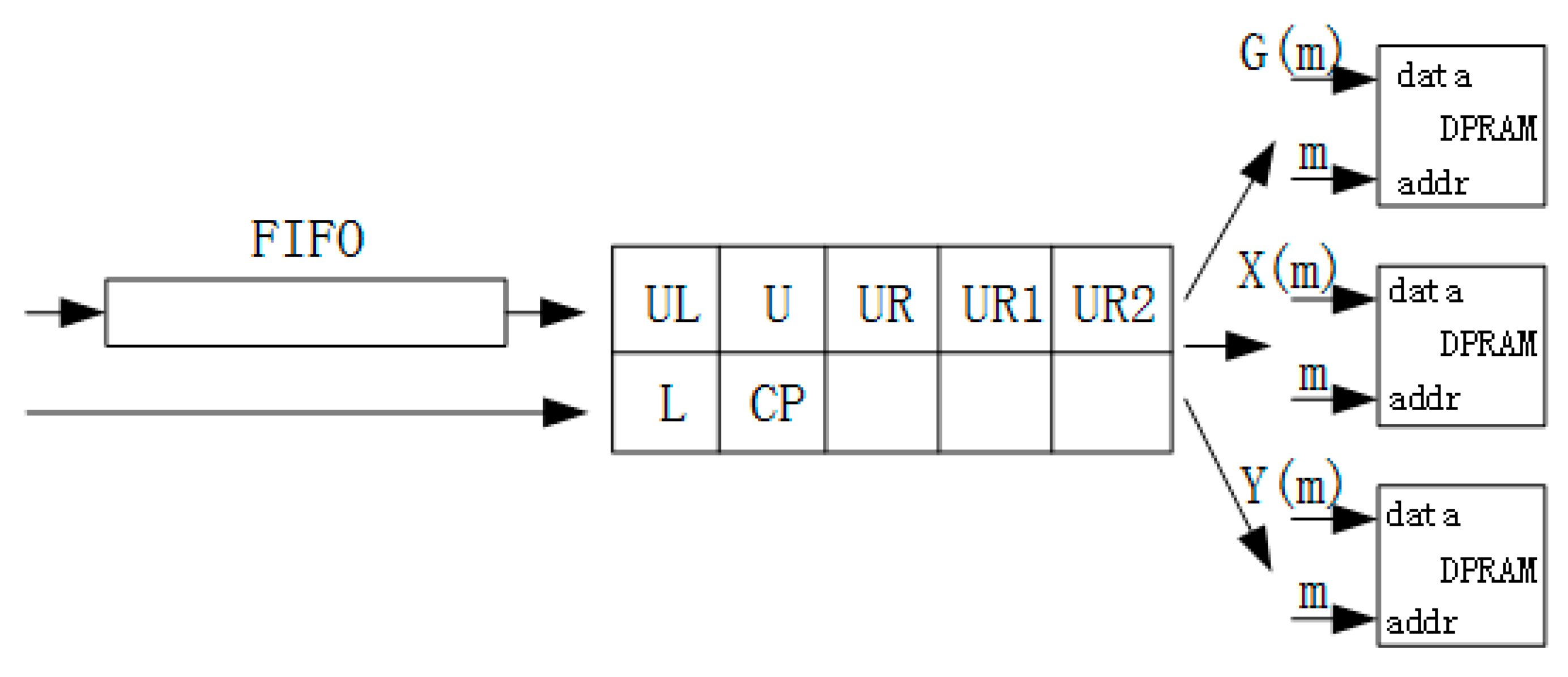
2.3. Labeling
- ➀
- When CP = 1 and there already exists a label number of connected domains for the current pixel (the label numbers of all pixels are 0 initially), then we skip the current pixel and analyze the next pixel.
- ➁
- When CP = 1 and the current label number LN = 0.
2.4. The Hardware Implementation of the Proposed Algorithm
3. Results
3.1. Experimental Conditions
3.2. Experimental Results
3.2.1. The Analysis of Star Detection in Real Image Sequences
3.2.2. The Analysis of Resource Consumption and Delay
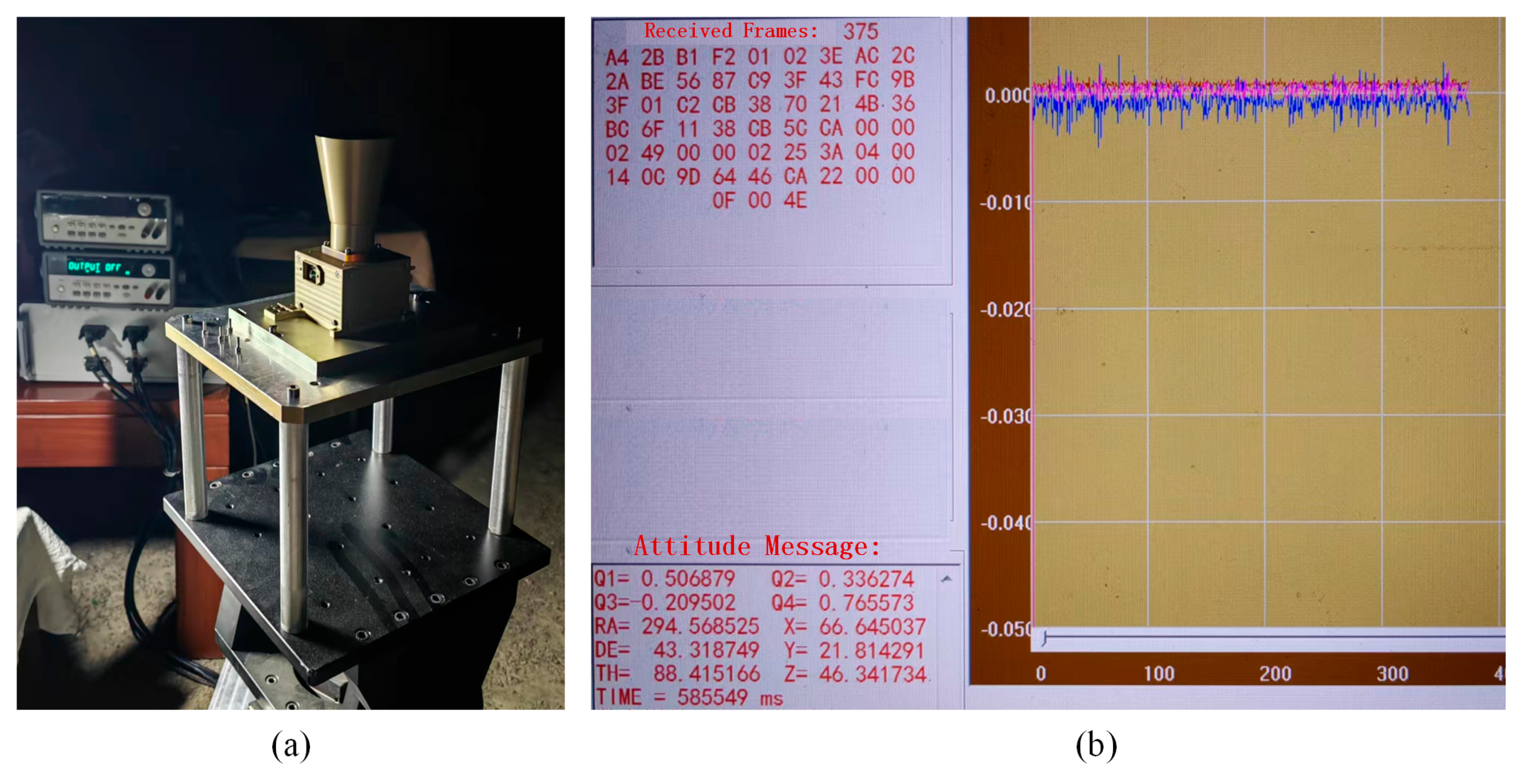
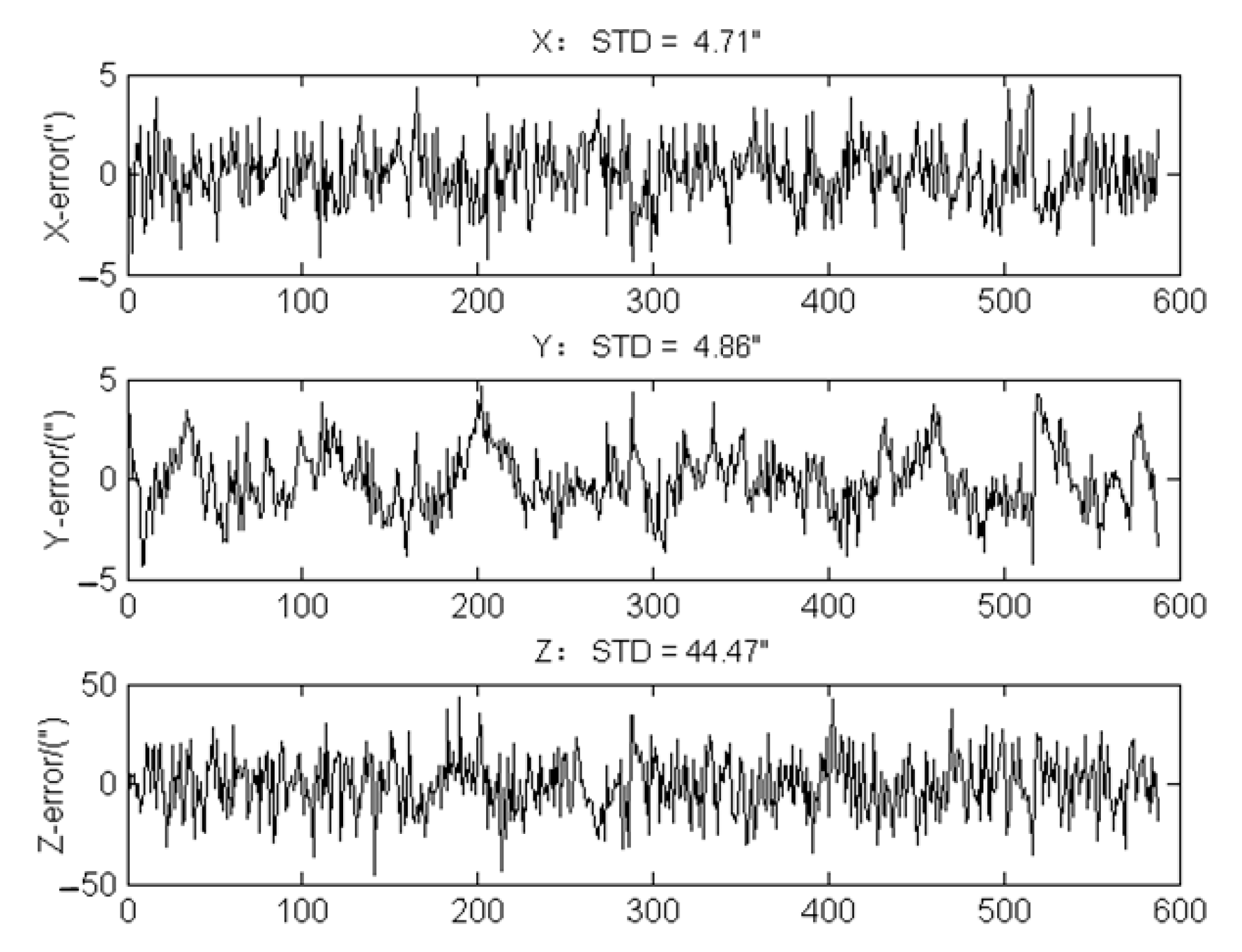
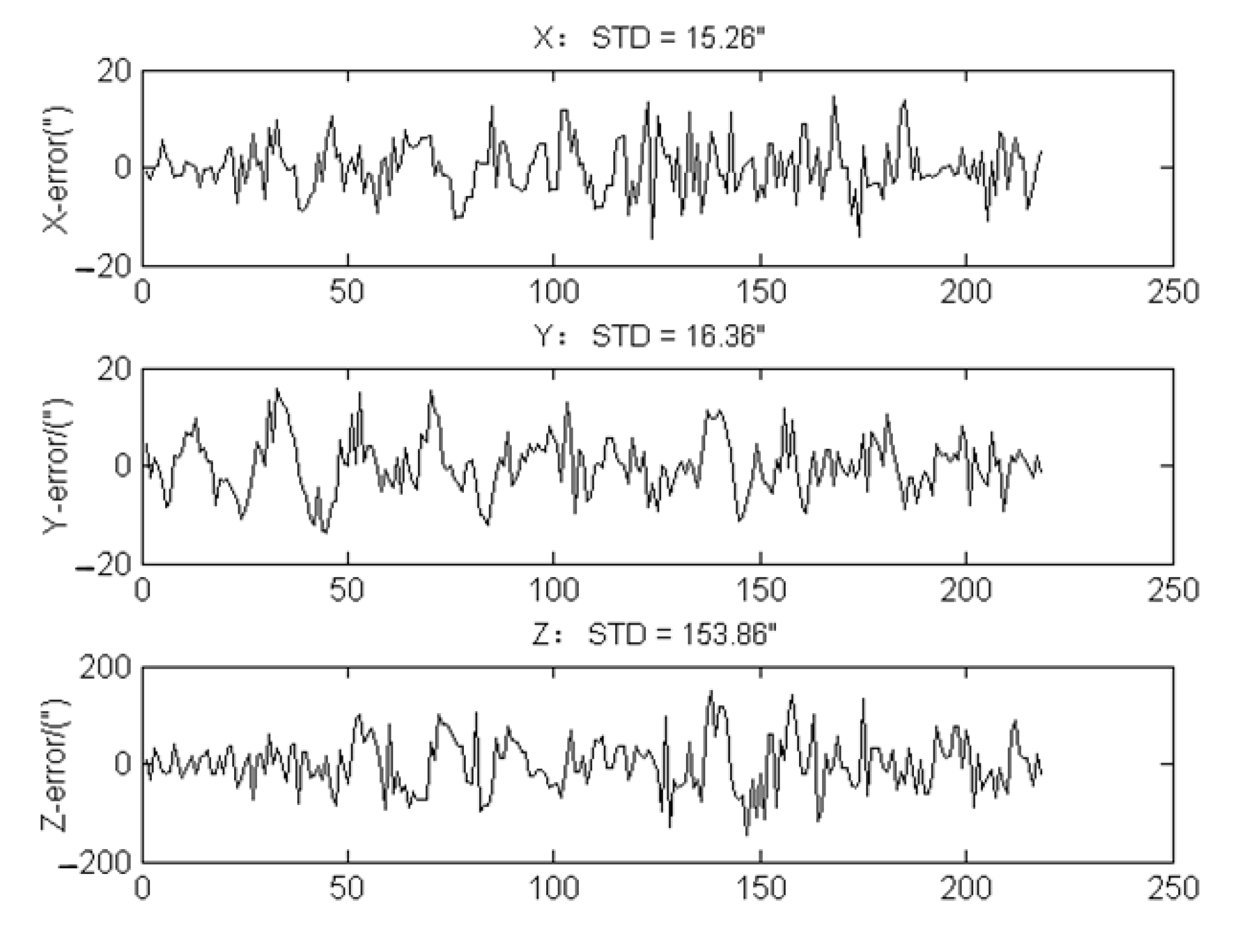
3.2.3. The Field Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liebe, C.C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Clermont, L.; Michel, C.; Stockman, Y. Stray Light Correction Algorithm for High Performance Optical Instruments: The Case of Metop-3MI. Remote Sens. 2022, 14, 1354. [Google Scholar] [CrossRef]
- Roger, J.C.; Santer, R.; Herman, M.; Deuzé, J.L. Polarization of the solar light scattered by the earth-atmosphere system as observed from the U.S. shuttle. Remote Sens. Environ. 1994, 48, 275–290. [Google Scholar] [CrossRef]
- Liu, W.D. Lens-Hood Design of Starlight Semi-Physical Experimental Platform. Laser Optoelectron. Prog. 2012, 49, 162–167. [Google Scholar] [CrossRef]
- Xu, M.Y.; Shi, R.B.; Jin, Y.M.; Wang, W. Miniaturization Design of Star Sensors Optical System Based on Baffle Size and Lens Lagrange Invariant. Acta Opt. Sin. 2016, 36, 0922001. [Google Scholar] [CrossRef]
- Kwang-Yul, K.; Yoan, S. A Distance Boundary with Virtual Nodes for the Weighted Centroid Localization Algorithm. Sensors 2018, 18, 1054. [Google Scholar] [CrossRef]
- Fialho, M.; Mortari, D. Theoretical Limits of Star Sensor Accuracy. Sensors 2019, 19, 5355. [Google Scholar] [CrossRef] [PubMed]
- He, Y.Y.; Wang, H.L.; Feng, L.; You, S.H.; Lu, J.H.; Jiang, W. Centroid extraction algorithm based on grey-gradient for autonomous star sensor. Opt.-Int. J. Light Electron Opt. 2019, 194, 162932. [Google Scholar] [CrossRef]
- Seyed, M.F.; Reza, M.M.; Mahdi, N. Flying small target detection in ir images based on adaptive toggle operator. IET Comput. Vis. 2018, 12, 527–534. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E.; Masters, B.R. Digital Image Processing, Third Edition. J. Biomed. Opt. 2009, 14, 029901. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A spatial filter based framework for target detection in hyperspectral imagery. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Yu, L.W.; Mao, X.N.; Jin, H.; Hu, X.C.; Wu, Y.K. Study on Image Process Method of Star Tracker for Stray Lights Resistance Filtering Based on Background. Aerosp. Shanghai 2016, 33, 26–31. [Google Scholar] [CrossRef]
- Wang, H.T.; Luo, C.Z.; Wang, Y.; Wang, X.Z.; Zhao, S.F. Algorithm for star detection based on self-adaptive background prediction. Opt. Tech. 2009, 35, 412–414. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Lu, R.T.; Yang, X.G.; Li, W.P.; Ji, W.F.; Li, D.L.; Jing, X. Robust infrared small target detection via multidirectional derivative-based weighted contrast measure. IEEE Geosci. Remote Sens. Lett. 2020, 1, 1–5. [Google Scholar] [CrossRef]
- Lu, K.L.; Liu, E.H.; Zhao, R.J.; Zhang, H.; Lin, L.; Tian, H. A Curvature-Based Multidirectional Local Contrast Method for Star Detection of a Star Sensor. Photonics 2022, 9, 13. [Google Scholar] [CrossRef]
- Perri, S.; Spagnolo, F.; Corsonello, P. A Parallel Connected Component Labeling Architecture for Heterogeneous Systems-on-Chip. Electronics 2020, 9, 292. [Google Scholar] [CrossRef]
- Wan, X.W.; Wang, G.Y.; Wei, X.G.; Li, J.; Zhang, G.J. Star Centroiding Based on Fast Gaussian Fitting for Star Sensors. Sensors 2018, 18, 2836. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, W.; Li, H.; Dai, S.; Han, C.; Yang, J. Iterative Decoding of LDPC-Based Product Codes and FPGA-Based Performance Evaluation. Electronics 2020, 9, 122. [Google Scholar] [CrossRef]
- Han, J.L.; Yang, X.B.; Xu, T.T.; Fu, Z.Q.; Chang, L.; Yang, C.L.; Jin, G. An End-to-End Identification Algorithm for Smearing Star Image. Remote Sens. 2021, 13, 4541. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. A novel star identification technique robust to high presence of false objects: The multi-poles algorithm. Adv. Space Res. 2017, 59, 2133–2147. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. Efficient star identification using a neural network. Sensors 2020, 20, 3684. [Google Scholar] [CrossRef] [PubMed]



| Platform | Resource Consumption |
|---|---|
| xc3s700an-4fgg484 | Slice Flip Flops: 50% 4 input LUTs: 65% BRAMS: 20% MULT18×18SIOS: 10% Maximum frequency: 174.642 MHZ |
| A3pe3000L-484FBGA | CORE: 30.87% GLOBAL: 33.33% RAM/FIFO: 48.21% Maximum frequency: 179.856 MHZ |
| M2S090T-1FG484I | LUT: 6.57% DFF: 5.34% RAM64×18: 3.57% RAM1K18: 13.76% Chip Global: 37.50% Maximum frequency: 172.1 MHZ |
| Situation | The Successful Identification Rate |
|---|---|
| Local threshold segmentation algorithm | 53% |
| The proposed algorithm | 98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Li, H.; Lin, L.; Zhao, R.; Liu, E.; Zhao, R. A Fast Star-Detection Algorithm under Stray-Light Interference. Photonics 2023, 10, 889. https://doi.org/10.3390/photonics10080889
Lu K, Li H, Lin L, Zhao R, Liu E, Zhao R. A Fast Star-Detection Algorithm under Stray-Light Interference. Photonics. 2023; 10(8):889. https://doi.org/10.3390/photonics10080889
Chicago/Turabian StyleLu, Kaili, Huakang Li, Ling Lin, Renjie Zhao, Enhai Liu, and Rujin Zhao. 2023. "A Fast Star-Detection Algorithm under Stray-Light Interference" Photonics 10, no. 8: 889. https://doi.org/10.3390/photonics10080889
APA StyleLu, K., Li, H., Lin, L., Zhao, R., Liu, E., & Zhao, R. (2023). A Fast Star-Detection Algorithm under Stray-Light Interference. Photonics, 10(8), 889. https://doi.org/10.3390/photonics10080889




