Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals

Chen, Yixi; Yang, Aowei; Zhou, Yangui; He, Hexiang; Xie, Jianing

doi:10.3390/photonics10070818

Open AccessArticle

Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals

by

Yixi Chen

¹,

Aowei Yang

¹,

Yangui Zhou

^1,2

,

Hexiang He

^1,2,*

and

Jianing Xie

^1,2,*

¹

School of Physics and Optoelectronic Engineering, Foshan University, Foshan 528000, China

²

Guangdong-Hong Kong-Macao Joint Laboratory for Intelligent Micro-Nano Optoelectronic Technology, Foshan University, Foshan 528000, China

^*

Authors to whom correspondence should be addressed.

Photonics 2023, 10(7), 818; https://doi.org/10.3390/photonics10070818

Submission received: 23 May 2023 / Revised: 1 July 2023 / Accepted: 11 July 2023 / Published: 13 July 2023

(This article belongs to the Section Optical Interaction Science)

Download

Browse Figures

Review Reports Versions Notes

Abstract

It is well known that bright vortex solitons are unstable in the

χ^{(2)}

nonlinear media due to the strong azimuthal modulation instability. To solve this problem, a quadratic (

χ^{(2)}

)

LiNb O_{3}

ferroelectric crystal with a special kind of helical-periodically poled structure is proposed. The proposed structure is designed by embedding topological charges into the crystal with a quasi-phase matching technique. Simulation results indicate that vortex solitons containing fundamental-frequency and second-harmonic waves can robustly propagate over a distance. 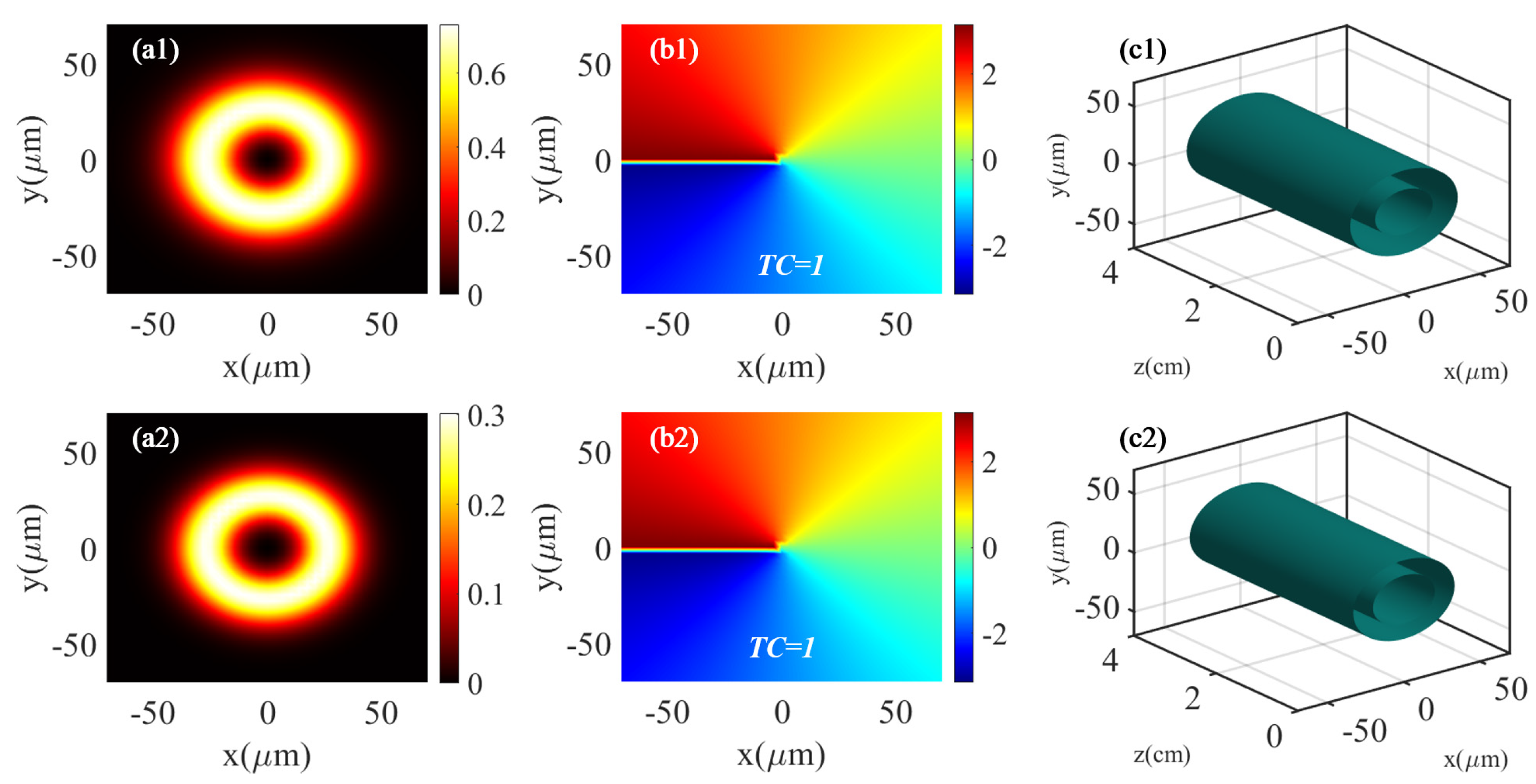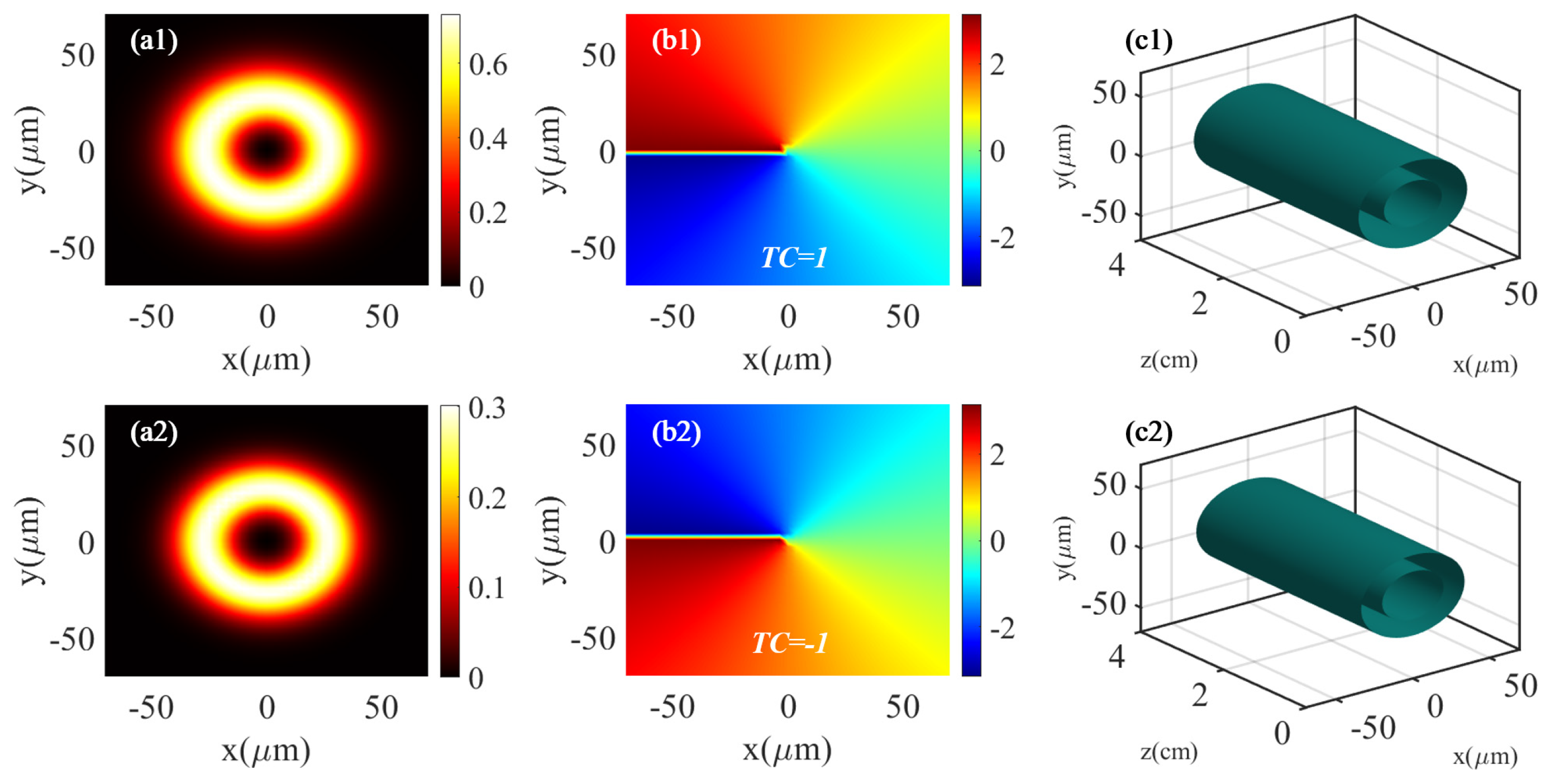Two types of vortex states are obtained: double vortices state and vortex–antivortex state. The dependence of effective area, propagation constants, and maximum light intensity on the control parameters are presented. These results provide a new solution for robust transmission of bright vortex solitons in a

χ^{(2)}

nonlinear media.

Keywords: vortex solitons; quasi-phase matching; quadratic nonlinear effect; helical-periodically poled lithium niobate

Share and Cite

MDPI and ACS Style

Chen, Y.; Yang, A.; Zhou, Y.; He, H.; Xie, J. Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals. Photonics 2023, 10, 818. https://doi.org/10.3390/photonics10070818

AMA Style

Chen Y, Yang A, Zhou Y, He H, Xie J. Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals. Photonics. 2023; 10(7):818. https://doi.org/10.3390/photonics10070818

Chicago/Turabian Style

Chen, Yixi, Aowei Yang, Yangui Zhou, Hexiang He, and Jianing Xie. 2023. "Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals" Photonics 10, no. 7: 818. https://doi.org/10.3390/photonics10070818

APA Style

Chen, Y., Yang, A., Zhou, Y., He, H., & Xie, J. (2023). Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals. Photonics, 10(7), 818. https://doi.org/10.3390/photonics10070818

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Transmission of Vortex Solitons in Three-Dimensional χ⁽²⁾ Helical-Periodically Poled Ferroelectric Crystals

Abstract

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI