Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals
Abstract
1. Introduction
2. Theory and Model
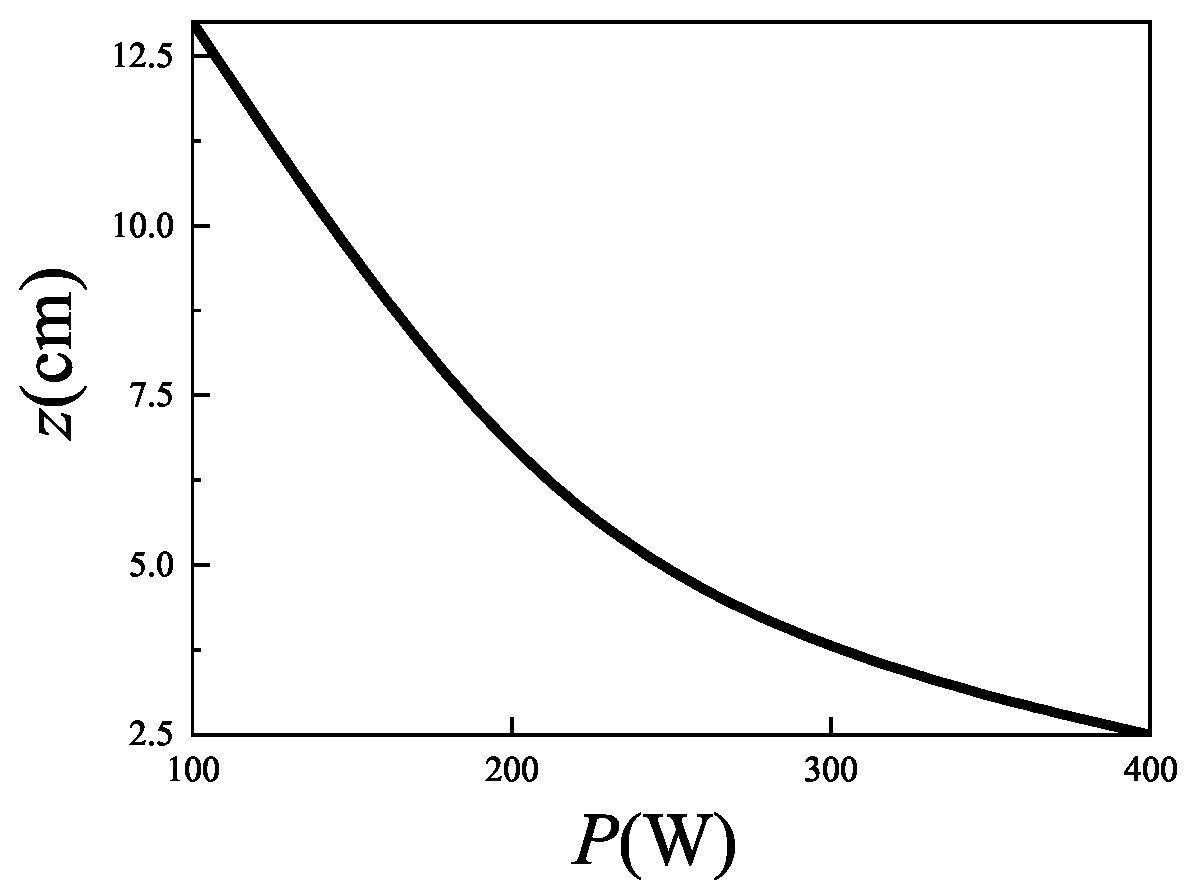
3. Numerical Results
3.1. Double Vortices States
3.2. Vortex–Antivortex States
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QPM | Quasi-Phase Matching |
| FF | Fundamental Frequency |
| SH | Second Harmonic |
| BECs | Bose–Einstein Condensates |
References
- Fedotova, A.; Younesi, M.; Sautter, J.; Vaskin, A.; Löchner, F.J.F.; Steinert, M.; Geiss, R.; Pertsch, T.; Staude, I.; Setzpfandt, F. Second-Harmonic Generation in Resonant Nonlinear Metasurfaces Based on Lithium Niobate. Nano Lett. 2020, 20, 8608–8614. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Ohto, T.; Sun, S.; Rouxel, J.R.; Imoto, S.; Backus, E.H.G.; Mukamel, S.; Bonn, M.; Nagata, Y. Molecular Structure and Modeling of Water-Air and Ice-Air Interfaces Monitored by Sum-Frequency Generation. Chem. Rev. 2020, 120, 3633–3667. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wang, W.; Liu, S.S.; Pan, X.Z.; Du, J.J.; Lou, Y.B.; Yu, S.; Lv, S.C.; Treps, N.; Fabre, C.; et al. Reconfigurable Hexapartite Entanglement by Spatially Multiplexed Four-Wave Mixing Processes. Phys. Rev. Lett. 2020, 124, 090501. [Google Scholar] [CrossRef]
- Stolen, R.H.; Bösch, M.A.; Lin, C. Phase matching in birefringent fibers. Opt. Lett. 1981, 6, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Fiore, A.; Janz, S.; Delobel, L.; Van der Meer, P.; Bravetti, P.; Berger, V.; Rosencher, E.; Nagle, J. Second-harmonic generation at λ = 1.6 μm in AlGaAs/Al2O3 waveguides using birefringence phase matching. Appl. Phys. Lett. 1998, 72, 2942–2944. [Google Scholar] [CrossRef]
- Zhang, B.; Li, L.Q.; Wang, L.; Chen, F. Second harmonic generation in femtosecond laser written lithium niobate waveguides based on birefringent phase matching. Opt. Mater. 2020, 107, 110075. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic: New York, NY, USA, 2008; pp. 69–104. [Google Scholar]
- Armstrong, J.A.; Bloembergen, N.; Ducuing, J.; Pershan, P.S. Interactions between light waves in a nonlinear dielectric. Phys. Rev. 1962, 127, 1918. [Google Scholar] [CrossRef]
- Arie, A.; Voloch, N. Periodic, quasiperiodic and random quadratic nonlinear photonic crystals. Laser Photonics Rev. 2010, 4, 355–373. [Google Scholar] [CrossRef]
- Li, H.; Ma, B. Research development on fabrication and optical properties of nonlinear photonic crystals. Front. Optoelectron. 2020, 13, 35–49. [Google Scholar] [CrossRef]
- Yamada, M.; Nada, N.; Saitoh, M.; Watanabe, K. First-order quasi-phase matched LiNbO3 waveguide periodically poled by applying an external field for efficient blue second-harmonic generation. Appl. Phys. Lett. 1993, 62, 435–436. [Google Scholar] [CrossRef]
- Myers, L.E.; Eckardt, R.C.; Fejer, M.M.; Byer, R.L.; Bosenberg, W.R.; Pierce, J.W. Quasi-phase-matched optical parametric oscillators in bulk periodically poled LiNbO3. J. Opt. Soc. Am. B 1995, 12, 2102–2116. [Google Scholar] [CrossRef]
- Zhu, S.N.; Zhu, Y.Y.; Ming, N.B. Quasi-phase-matched third-harmonic generation in a quasi-periodic optical superlattice. Science 1997, 278, 843–846. [Google Scholar] [CrossRef]
- Arie, A.; Bahabad, A.; Habshoosh, N. Nonlinear interactions in periodic and quasi-periodic nonlinear photonic crystals. In Ferroelectric Crystals for Photonic Applications: Including Nanoscale Fabrication and Characterization Techniques; Springer: Berlin/Heidelberg, Germany, 2009; pp. 259–284. [Google Scholar]
- Wei, D.Z.; Wang, C.W.; Xu, X.Y.; Wang, H.J.; Hu, Y.L.; Chen, P.C.; Li, J.W.; Zhu, Y.Z.; Xin, C.; Hu, X.P.; et al. Efficient nonlinear beam shaping in three-dimensional lithium niobate nonlinear photonic crystals. Nat. Commun. 2019, 10, 4193. [Google Scholar] [CrossRef]
- Chiang, A.C.; Chao, J.H.; Lin, S.T.; Lin, Y.Y. Observation of Neutron-Induced Absorption and Phase-Mismatch for Quasi-Phase-Matched Second Harmonic Generation in Congruent Lithium Niobate. Photonics 2022, 9, 225. [Google Scholar] [CrossRef]
- Sabirov, O.I.; Assanto, G.; Sapaev, U.K. Efficient Third-Harmonic Generation by Inhomogeneous Quasi-Phase-Matching in Quadratic Crystals. Photonics 2022, 10, 76. [Google Scholar] [CrossRef]
- Lai, P.; Chang, C.; Liu, X.; Wei, D. Multiplexing Linear and Nonlinear Bragg Diffractions through Volume Gratings Fabricated by Femtosecond Laser Writing in Lithium Niobate Crystal. Photonics 2023, 10, 562. [Google Scholar] [CrossRef]
- Jia, R.; Liu, M.; Liu, J.M.; Hua, P.R.; Zhang, D.L. A Theoretical Study on Mid-Infrared Difference Frequency Generation Based on Periodically Poled Thin-Film LiNbO3. Photonics 2023, 10, 478. [Google Scholar] [CrossRef]
- Torner, L.; Stegeman, G.I. Soliton evolution in quasi-phase-matched second-harmonic generation. J. Opt. Soc. Am. B 1997, 14, 3127–3133. [Google Scholar] [CrossRef]
- Clausen, C.B.; Bang, O.; Kivshar, Y.S. Spatial solitons and induced Kerr effects in quasi-phase-matched quadratic media. Phys. Rev. Lett. 1997, 78, 4749–4752. [Google Scholar] [CrossRef]
- Desyatnikov, A.S.; Torner, L.; Kivshar, Y.S. Optical Vortices and Vortex Solitons. Prog. Opt. 2005, 47, 291–391. [Google Scholar]
- Malomed, B.A. Vortex solitons: Old results and new perspectives. Phys. D 2019, 399, 108–137. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Vaziri, A.; Pan, J.W.; Jennewein, T.; Weihs, G.; Zeilinger, A. Concentration of higher dimensional entanglement: Qutrits of photon orbital angular momentum. Phys. Rev. Lett. 2003, 91, 227902. [Google Scholar] [CrossRef] [PubMed]
- Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Vaziri, A.; Rehacek, J.; Hradil, Z.; Zeilinger, A. Triggered qutrits for quantum communication protocols. Phys. Rev. Lett. 2004, 92, 167903. [Google Scholar] [CrossRef]
- Etrich, C.; Lederer, F.; Malomed, B.A.; Peschel, T.; Peschel, U. Optical solitons in media with a quadratic nonlinearity. Prog. Opt. 2000, 41, 483–568. [Google Scholar]
- Buryak, A.V.; Trapani, P.D.; Skryabin, D.V.; Trillo, S. Optical solitons due to quadratic nonlinearities: From basic physics to futuristic applications. Phys. Rep. 2002, 370, 63–235. [Google Scholar] [CrossRef]
- Torruellas, W.E.; Wang, Z.; Hagan, D.J.; VanStryland, E.W.; Stegeman, G.I.; Torner, L.; Menyuk, C.R. Observation of Two-Dimensional Spatial Solitary Waves in a Quadratic Medium. Phys. Rev. Lett. 1995, 74, 5036–5039. [Google Scholar] [CrossRef]
- Torruellas, W.E.; Wang, Z.; Torner, L.; Stegeman, G.I. Observation of mutual trapping and dragging of two-dimensional spatial solitary waves in a quadratic medium. Opt. Lett. 1995, 20, 1949–1951. [Google Scholar] [CrossRef]
- Torner, L.; Petrov, D.V. Azimuthal instabilities and self-breaking of beams into sets of solitons in bulk second-harmonic generation. Electron. Lett. 1997, 33, 608–609. [Google Scholar] [CrossRef]
- Firth, W.J.; Skryabin, D.V. Optical solitons carrying orbital angular momentum. Phys. Rev. Lett. 1997, 79, 2450–2453. [Google Scholar] [CrossRef]
- Petrov, D.V.; Torner, L.; Martorell, J.; Vilaseca, R.; Torres, J.P.; Cojocaru, C. Observation of azimuthal modulational instability and formation of patterns of optical solitons in a quadratic nonlinear crystal. Opt. Lett. 1998, 23, 1444–1446. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Crasovan, L.-C.; Towers, I.; Buryak, A.V.; Malomed, B.A.; Torner, L.; Torres, J.P.; Lederer, F. Stable spinning optical solitons in three dimensions. Phys. Rev. Lett. 2002, 88, 073902. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Malomed, B.A.; Lederer, F. Stable vortex solitons in a vectorial cubic-quintic model. J. Opt. B 2004, 6, S341–S350. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Towers, I.; Malomed, B.A.; Lederer, F. Stable two-dimensional spinning solitons in a bimodal cubic-quintic model with four-wave mixing. J. Opt. A 2002, 4, 615–623. [Google Scholar] [CrossRef]
- Towers, I.; Buryak, A.V.; Sammut, R.A.; Malomed, B.A. Stable localized vortex solitons. Phys. Rev. E 2001, 63, 055601. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Malomed, B.A.; Lederer, F. Stable vortex solitons supported by competing quadratic and cubic nonlinearities. Phys. Rev. E 2004, 69, 066614. [Google Scholar] [CrossRef] [PubMed]
- Di Trapani, P.; Chinaglia, W.; Minardi, S.; Piskarskas, A. Observation of quadratic optical vortex solitons. Phys. Rev. Lett 2000, 84, 3843–3846. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Tarruell, L.; Torner, L. Three-dimensional droplets of swirling superfluids. Phys. Rev. A 2018, 98, 013612. [Google Scholar] [CrossRef]
- Li, Y.Y.; Chen, Z.P.; Luo, Z.H.; Huang, C.Q.; Tan, H.S.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Luo, Z.H.; Pang, W.; Liu, B.; Li, Y.Y.; Malomed, B.A. A new form of liquid matter: Quantum droplets. Front. Phys. 2021, 16, 1–21. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett 2016, 117, 100401. [Google Scholar] [CrossRef]
- Lobanov, V.E.; Kalinovich, A.A.; Borovkova, O.V.; Malomed, B.A. Fundamental and vortex dissipative quadratic solitons supported by spatially localized gain. Phys. Rev. A 2022, 105, 013519. [Google Scholar] [CrossRef]
- Zhao, F.Y.; Xu, X.X.; He, H.X.; Zhang, L.; Zhou, Y.G.; Chen, Z.P.; Malomed, B.A.; Li, Y.Y. Vortex solitons in quasi-phase-matched photonic crystals. Phys. Rev. Lett. 2023, 130, 157203. [Google Scholar] [CrossRef]
- Bahabad, A.; Arie, A. Generation of optical vortex beams by nonlinear wave mixing. Opt. Express 2007, 15, 17619–17624. [Google Scholar] [CrossRef]
- Tian, L.H.; Ye, F.W.; Chen, X.F. Optical vortex converter with helical-periodically poled ferroelectric crystal. Opt. Express 2011, 19, 11591–11596. [Google Scholar] [CrossRef]
- Phillips, C.R.; Langrock, C.; Chang, D.; Lin, Y.W.; Gallmann, L.; Fejer, M.M. Apodization of chirped quasi-phasematching devices. J. Opt. Soc. Am. B 2013, 30, 1551–1568. [Google Scholar] [CrossRef]
- Zhao, F.Y.; Lü, J.T.; He, H.X.; Zhou, Y.G.; Fu, S.H.; Li, Y.Y. Geometric phase with full-wedge and half-wedge rotation in nonlinear frequency conversion. Opt. Express 2021, 29, 21820–21832. [Google Scholar] [CrossRef]
- Porat, G.; Arie, A. Efficient, broadband, and robust frequency conversion by fully nonlinear adiabatic three-wave mixing. J. Opt. Soc. Am. B 2013, 30, 1342–1351. [Google Scholar] [CrossRef]
- Chen, Y.X.; Cai, X.Y.; Liu, B.; Jiang, X.D.; Li, Y.Y. Hidden vortices of quantum droplets in quasi-two dimensional space. Acta Phys. Sin. 2022, 71, 200302. [Google Scholar] [CrossRef]
- Yang, J.K.; Lakoba, T.I. Universally-convergent squared-operator iteration methods for solitary waves in general nonlinear wave equations. Stud. Appl. Math 2008, 120, 265–292. [Google Scholar] [CrossRef]
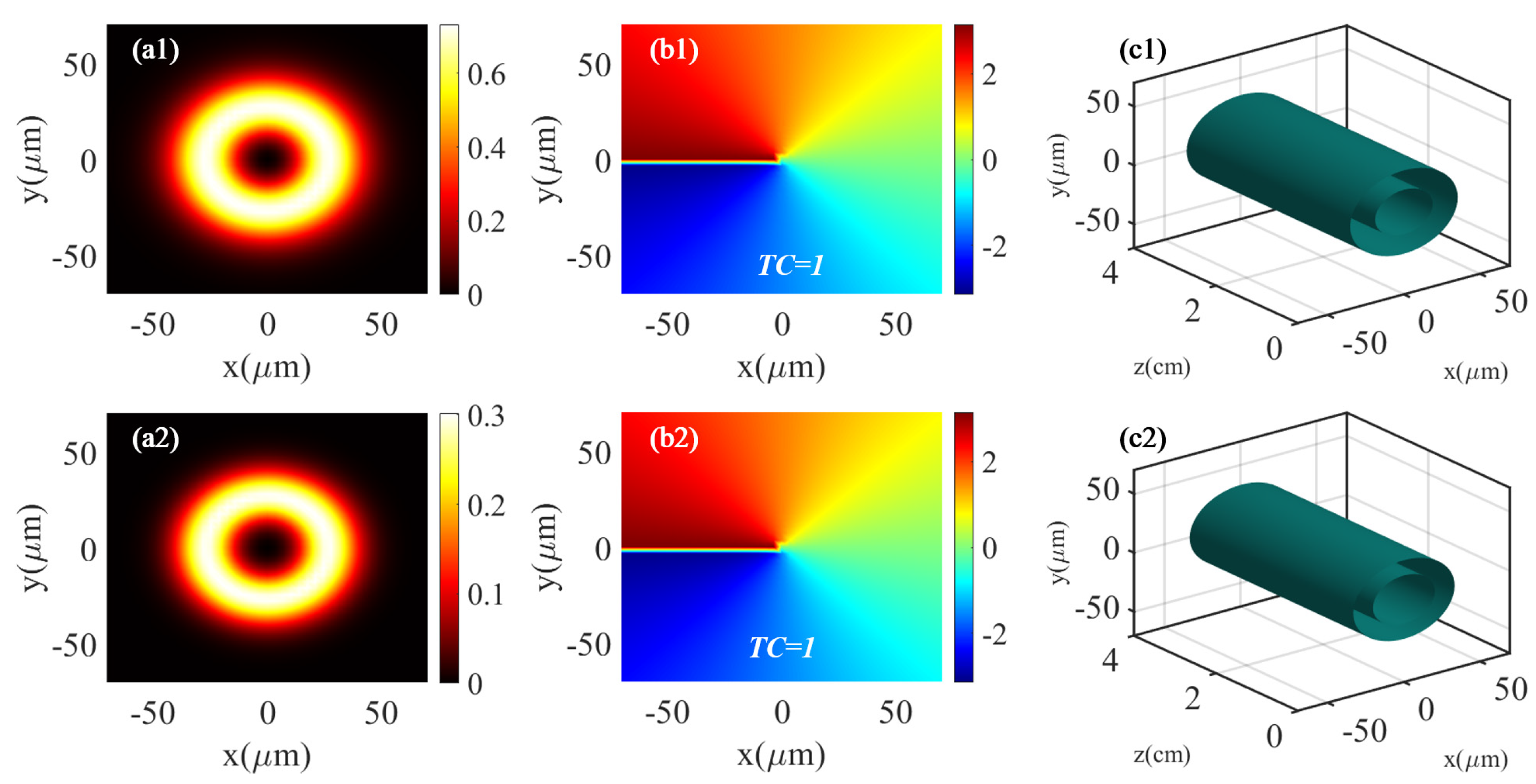


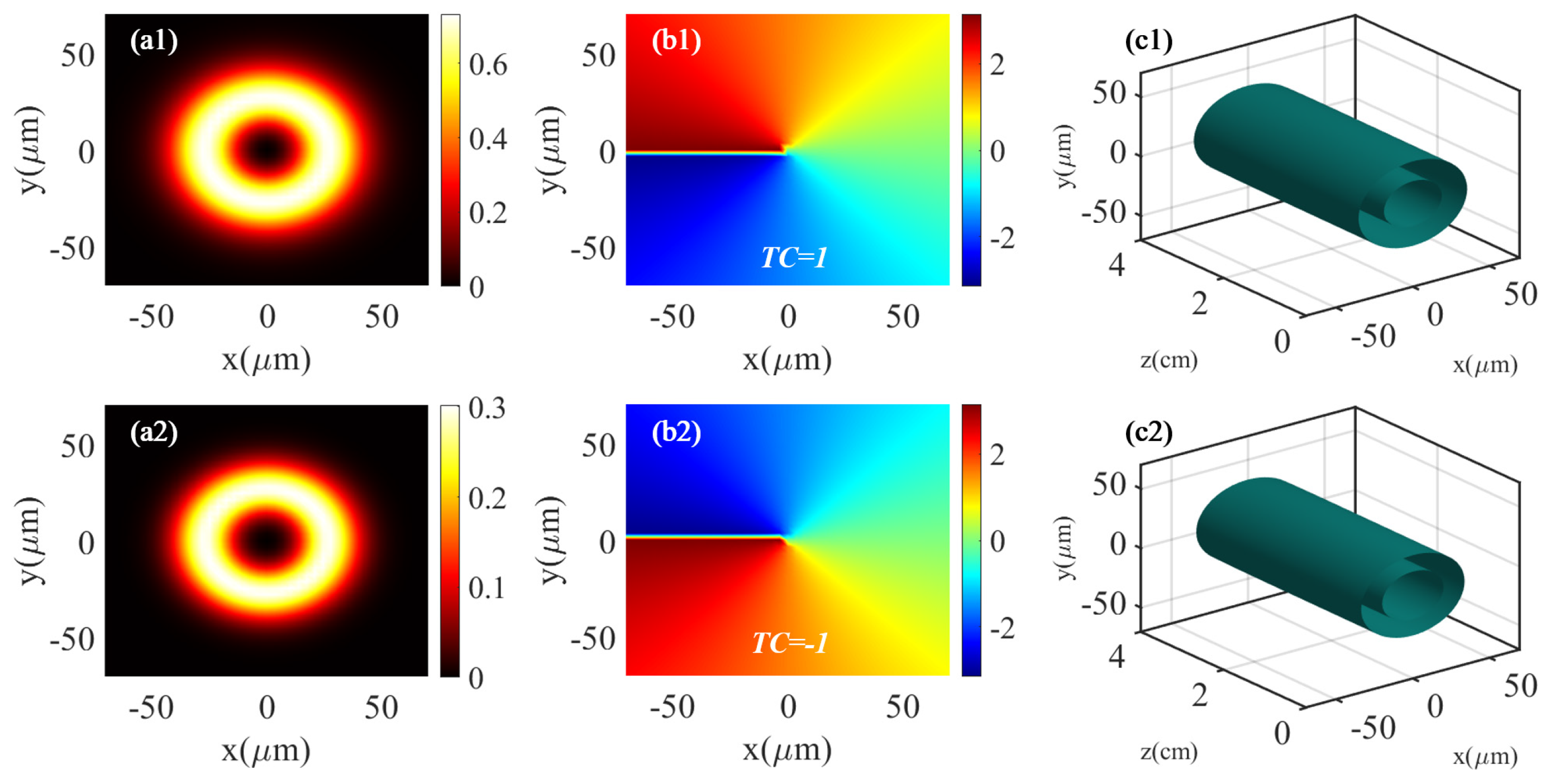

| , | 0.25 cm, 4 |
| , | 14 m |
| , | 5 , 10 |
| 10 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yang, A.; Zhou, Y.; He, H.; Xie, J. Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals. Photonics 2023, 10, 818. https://doi.org/10.3390/photonics10070818
Chen Y, Yang A, Zhou Y, He H, Xie J. Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals. Photonics. 2023; 10(7):818. https://doi.org/10.3390/photonics10070818
Chicago/Turabian StyleChen, Yixi, Aowei Yang, Yangui Zhou, Hexiang He, and Jianing Xie. 2023. "Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals" Photonics 10, no. 7: 818. https://doi.org/10.3390/photonics10070818
APA StyleChen, Y., Yang, A., Zhou, Y., He, H., & Xie, J. (2023). Transmission of Vortex Solitons in Three-Dimensional χ(2) Helical-Periodically Poled Ferroelectric Crystals. Photonics, 10(7), 818. https://doi.org/10.3390/photonics10070818





