Dimensional Analysis of Double-Track Microstructures in a Lithium Niobate Crystal Induced by Ultrashort Laser Pulses
Abstract
1. Introduction
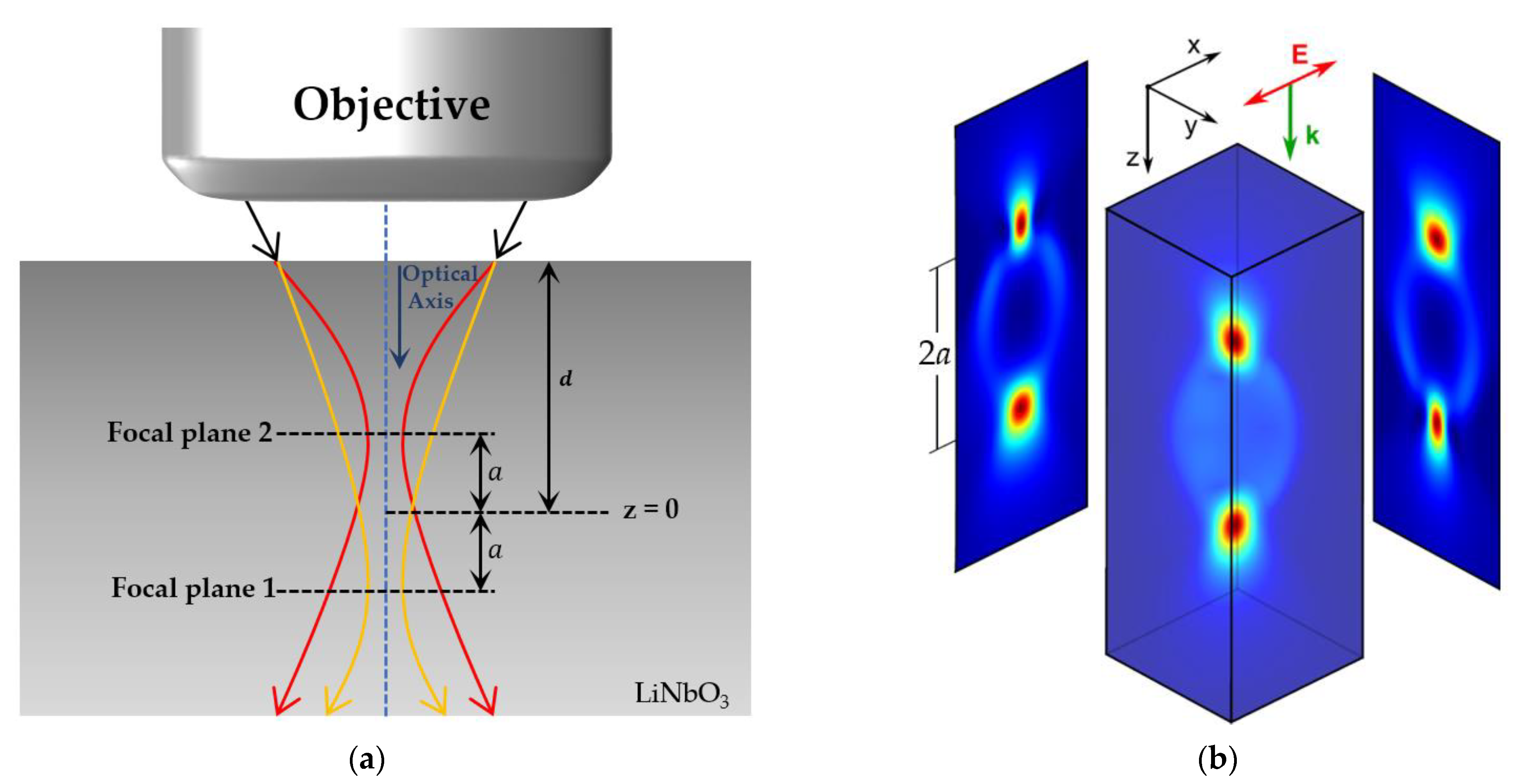
2. Materials and Methods
3. Results and Discussion
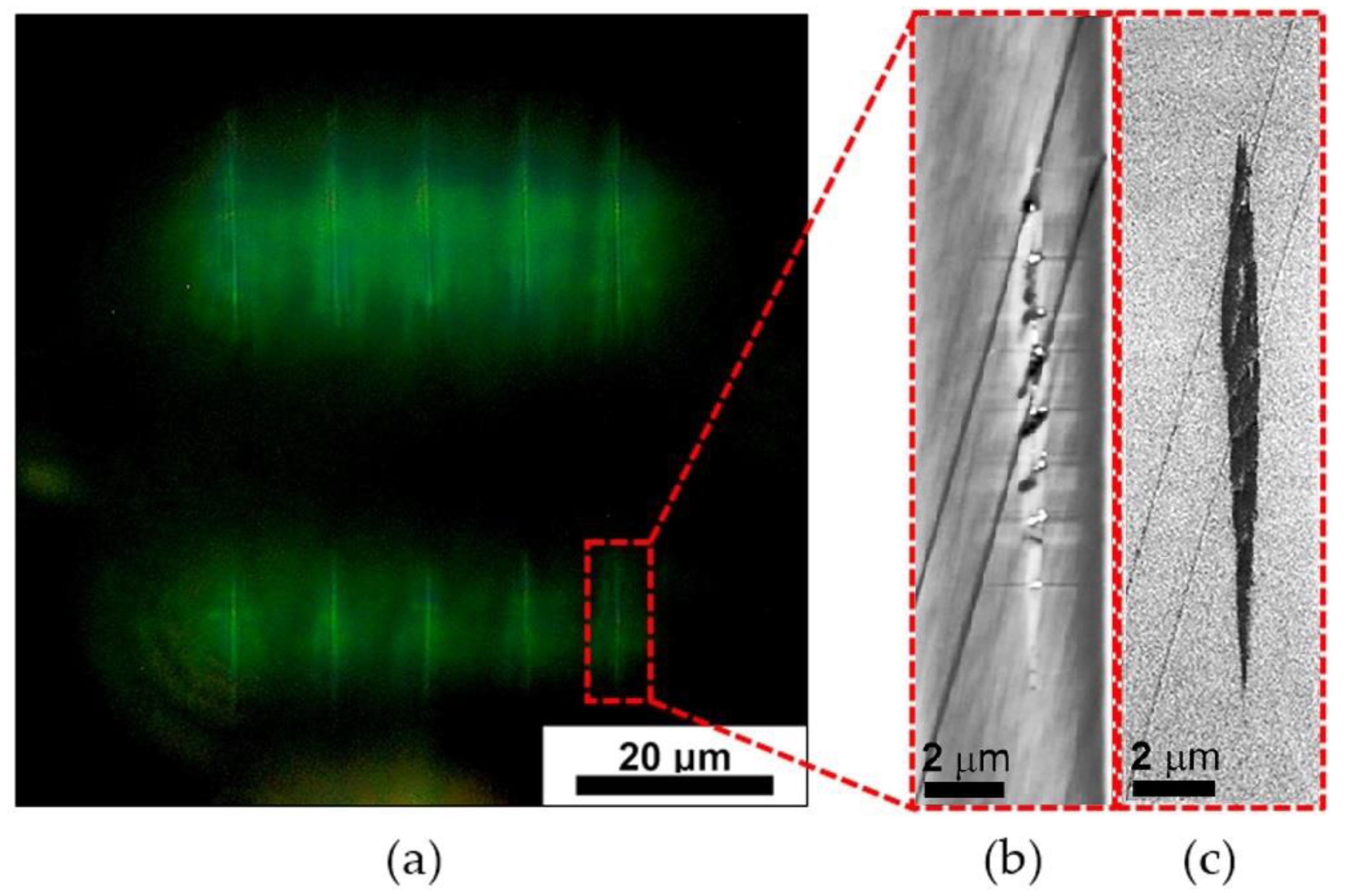
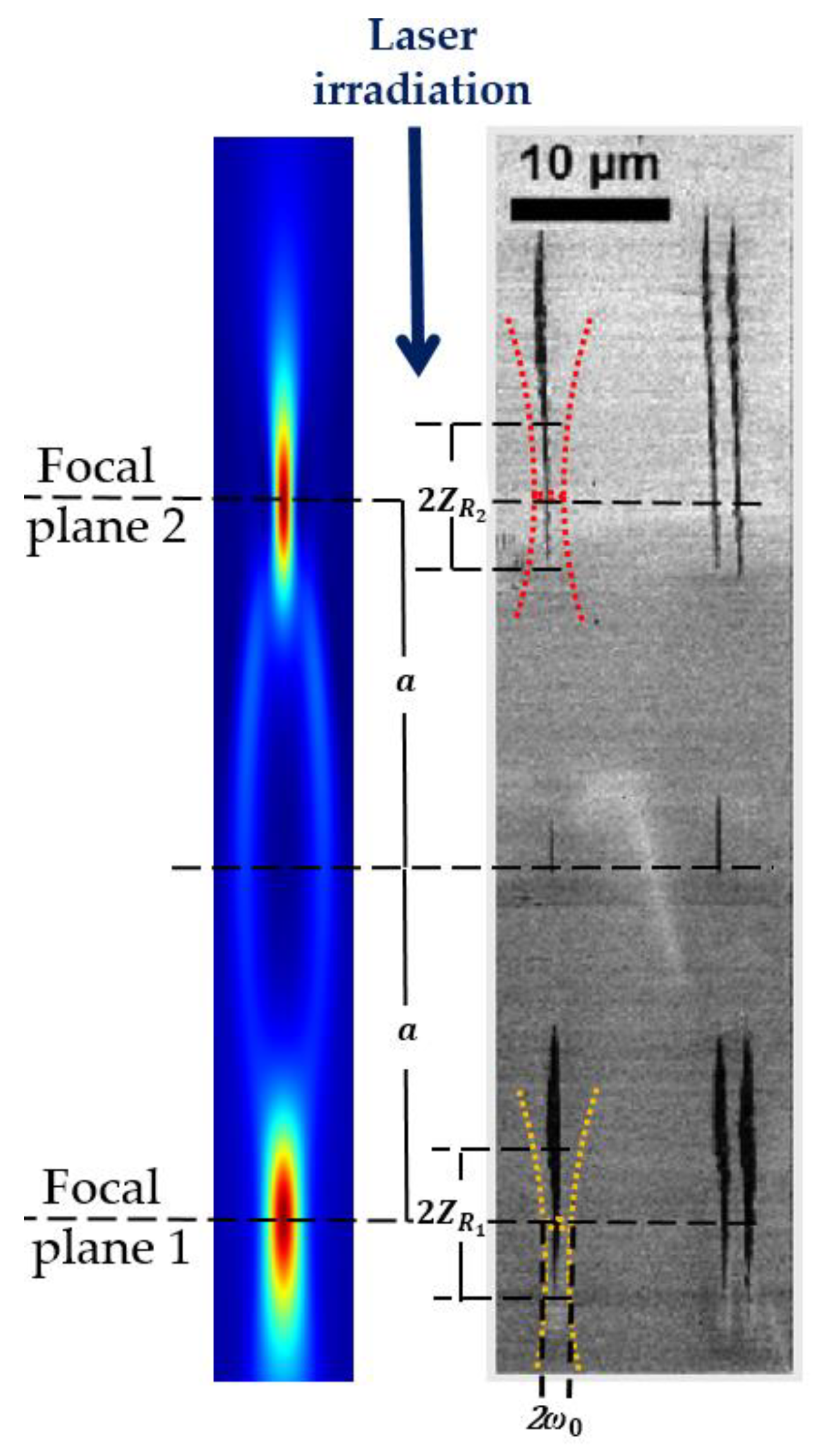
3.1. Formation of Double-Track Structures
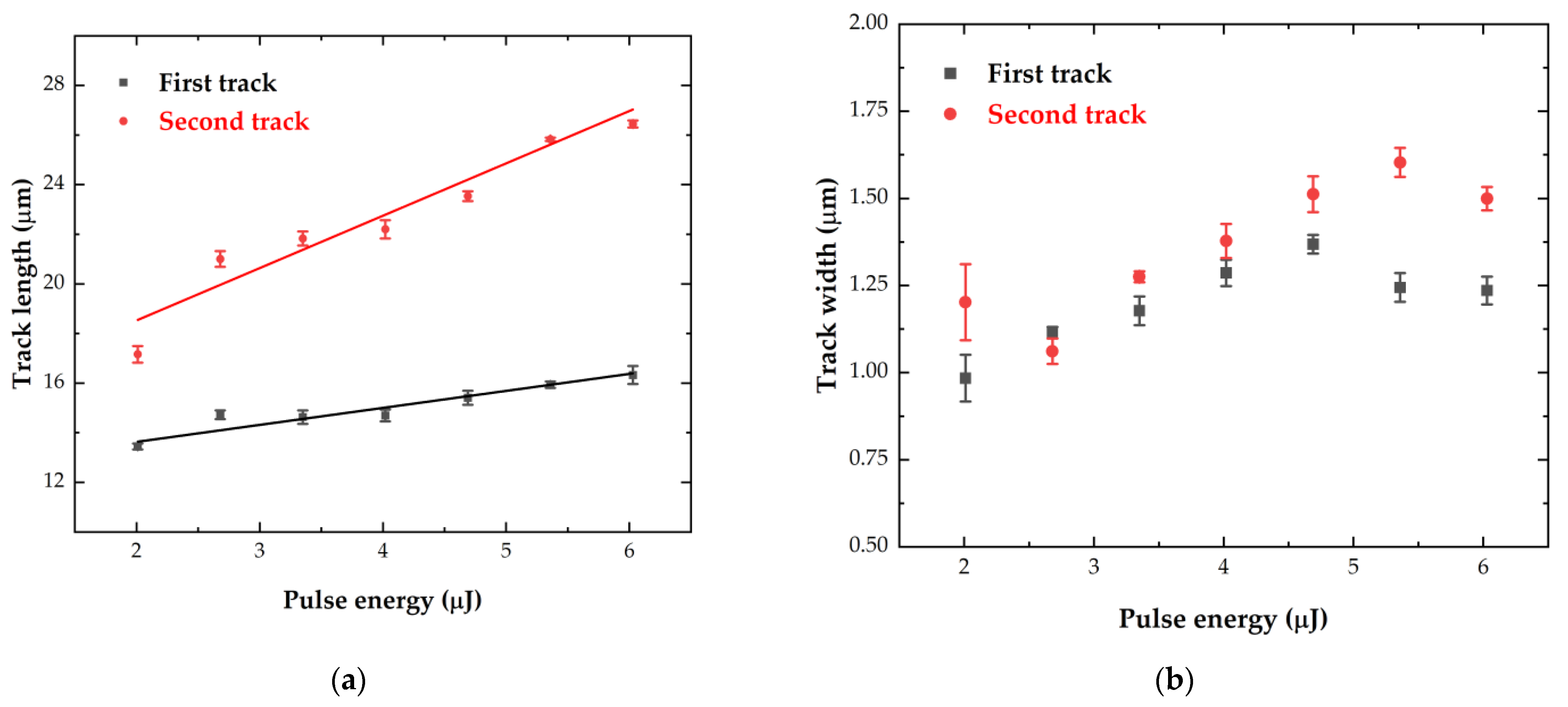
3.2. Dimensional Parameters of Double-Track Structures at Varied Pulse Energies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weis, R.S.; Gaylord, T.K. Lithium Niobate: Summary of Physical Properties and Crystal Structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Piromjitpong, T.; Dubov, M.; Boscolo, S. High-Repetition-Rate Femtosecond-Laser Inscription of Low-Loss Thermally Stable Waveguides in Lithium Niobate. In Frontiers in Optics/Laser Science; Optica Publishing Group: Washington, DC, USA, 2018; p. JTu3A.34. [Google Scholar] [CrossRef]
- Li, L.; Kong, W.; Chen, F. Femtosecond Laser-Inscribed Optical Waveguides in Dielectric Crystals: A Concise Review and Recent Advances. Adv. Photonics 2022, 4, 024002. [Google Scholar] [CrossRef]
- Wang, P.; Qi, J.; Liu, Z.; Liao, Y.; Chu, W.; Cheng, Y. Fabrication of Polarization-Independent Waveguides Deeply Buried in Lithium Niobate Crystal Using Aberration-Corrected Femtosecond Laser Direct Writing. Sci. Rep. 2017, 7, 41211. [Google Scholar] [CrossRef] [PubMed]
- Zisis, G. Laser-Induced Ferroelectric and Photonic Structures in Lithium Niobate Crystals; University of Southampton: Southampton, UK, 2016. [Google Scholar] [CrossRef]
- Horn, W.; Kroesen, S.; Herrmann, J.; Imbrock, J.; Denz, C. Electro-Optical Tunable Waveguide Bragg Gratings in Lithium Niobate Induced by Femtosecond Laser Writing. Opt. Express 2012, 20, 26922–26928. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Xu, Y.; Wang, M.; Qiao, L.; Lin, J.; Fang, W.; Cheng, Y. Monolithic Integration of a Lithium Niobate Microresonator with a Free-Standing Waveguide Using Femtosecond Laser Assisted Ion Beam Writing. Sci. Rep. 2017, 7, 45610. [Google Scholar] [CrossRef]
- Xu, X.; Wang, T.; Chen, P.; Zhou, C.; Ma, J.; Wei, D.; Wang, H.; Niu, B.; Fang, X.; Wu, D. Femtosecond Laser Writing of Lithium Niobate Ferroelectric Nanodomains. Nature 2022, 609, 496–501. [Google Scholar] [CrossRef]
- Colombo, L.; Klemash, M.E.G.; Kiebala, T.M.; Bedair, S.S.; Piazza, G.; Rinaldi, M. VHF and UHF Lithium Niobate MEMS Resonators Exceeding 30 DB of Passive Gain. IEEE Electron. Device Lett. 2021, 42, 1853–1856. [Google Scholar] [CrossRef]
- Kudryashov, S.; Rupasov, A.; Kosobokov, M.; Akhmatkhanov, A.; Krasin, G.; Danilov, P.; Lisjikh, B.; Abramov, A.; Greshnyakov, E.; Kuzmin, E. Hierarchical Multi-Scale Coupled Periodical Photonic and Plasmonic Nanopatterns Inscribed by Femtosecond Laser Pulses in Lithium Niobate. Nanomaterials 2022, 12, 4303. [Google Scholar] [CrossRef]
- Al-Shibaany, Z.Y.A.; Penchev, P.; Hedley, J.; Dimov, S. Laser Micromachining of Lithium Niobate-Based Resonant Sensors towards Medical Devices Applications. Sensors 2020, 20, 2206. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, Y.; Zhu, S.; Xiao, M.; Krolikowski, W. Nonlinear Photonic Crystals: From 2D to 3D. Optica 2021, 8, 372–381. [Google Scholar] [CrossRef]
- Imbrock, J.; Wesemann, L.; Kroesen, S.; Ayoub, M.; Denz, C. Waveguide-Integrated Three-Dimensional Quasi-Phase-Matching Structures. Optica 2020, 7, 28–34. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond Filamentation in Transparent Media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Lancry, M.; Zimmerman, F.; Desmarchelier, R.; Tian, J.; Brisset, F.; Nolte, S.; Poumellec, B. Nanogratings Formation in Multicomponent Silicate Glasses. Appl. Phys. B 2016, 122, 66. [Google Scholar] [CrossRef]
- Fedotov, S.S.; Drevinskas, R.; Lotarev, S.V.; Lipatiev, A.S.; Beresna, M.; Čerkauskaitė, A.; Sigaev, V.N.; Kazansky, P.G. Direct Writing of Birefringent Elements by Ultrafast Laser Nanostructuring in Multicomponent Glass. Appl. Phys. Lett. 2016, 108, 071905. [Google Scholar] [CrossRef]
- Blonskyi, I.; Kadan, V.; Shynkarenko, Y.; Yarusevych, O.; Korenyuk, P.; Puzikov, V.; Grin’, L. Periodic Femtosecond Filamentation in Birefringent Media. Appl. Phys. B 2015, 120, 705–710. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Luo, L.; Guo, H.; Yang, H.; Gong, Q. Multiple Foci and a Long Filament Observed with Focused Femtosecond Pulse Propagation in Fused Silica. Opt. Lett. 2002, 27, 448–450. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zang, H.; Huang, Q.; Liu, C.; Su, Y.; Fu, Y.; Hou, M.; Li, A.; Chen, H.; Chin, S.-L. Polarization-Orthogonal Filament Array Induced by Birefringent Crystals in Air. Opt. Express 2018, 26, 8515–8521. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jiang, H.; Xiao, J.; Gong, Q. The Mechanism of Multi-Focusing of Lasers into Uniaxial Crystals. J. Opt. A Pure Appl. Opt. 2007, 9, 664. [Google Scholar] [CrossRef]
- Karpinski, P.; Shvedov, V.; Krolikowski, W.; Hnatovsky, C. Laser-Writing inside Uniaxially Birefringent Crystals: Fine Morphology of Ultrashort Pulse-Induced Changes in Lithium Niobate. Opt. Express 2016, 24, 7456–7476. [Google Scholar] [CrossRef]
- Zhou, G.; Jesacher, A.; Booth, M.; Wilson, T.; Ródenas, A.; Jaque, D.; Gu, M. Axial Birefringence Induced Focus Splitting in Lithium Niobate. Opt. Express 2009, 17, 17970–17975. [Google Scholar] [CrossRef] [PubMed]
- Kudryashov, S.; Rupasov, A.; Kosobokov, M.; Akhmatkhanov, A.; Krasin, G.; Danilov, P.; Lisjikh, B.; Turygin, A.; Greshnyakov, E.; Kovalev, M. Ferroelectric Nanodomain Engineering in Bulk Lithium Niobate Crystals in Ultrashort-Pulse Laser Nanopatterning Regime. Nanomaterials 2022, 12, 4147. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Lotsberg, J.K.; Stamnes, J.J.; Frette, Ø.; Velauthapillai, D.; Jiang, D.; Zhao, X. Numerical and Experimental Results for Focusing of Three-Dimensional Electromagnetic Waves into Uniaxial Crystals. J. Opt. Soc. Am. A 2009, 26, 691–698. [Google Scholar] [CrossRef] [PubMed]
- Zelmon, D.E.; Small, D.L.; Jundt, D. Infrared corrected Sellmeier coefficients for congruently grown lithium niobate and 5 mol.% magnesium oxide–doped lithium niobate. JOSA B 1997, 14, 3319–3322. [Google Scholar] [CrossRef]
- Bergner, K.; Seyfarth, B.; Lammers, K.A.; Ullsperger, T.; Döring, S.; Heinrich, M.; Nolte, S. Spatio-temporal analysis of glass volume processing using ultrashort laser pulses. Appl. Opt. 2018, 57, 4618–4632. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulina, Y.; Zhu, J.; Gorevoy, A.; Kosobokov, M.; Turygin, A.; Lisjikh, B.; Akhmatkhanov, A.; Shur, V.; Kudryashov, S. Dimensional Analysis of Double-Track Microstructures in a Lithium Niobate Crystal Induced by Ultrashort Laser Pulses. Photonics 2023, 10, 582. https://doi.org/10.3390/photonics10050582
Gulina Y, Zhu J, Gorevoy A, Kosobokov M, Turygin A, Lisjikh B, Akhmatkhanov A, Shur V, Kudryashov S. Dimensional Analysis of Double-Track Microstructures in a Lithium Niobate Crystal Induced by Ultrashort Laser Pulses. Photonics. 2023; 10(5):582. https://doi.org/10.3390/photonics10050582
Chicago/Turabian StyleGulina, Yulia, Jiaqi Zhu, Alexey Gorevoy, Mikhail Kosobokov, Anton Turygin, Boris Lisjikh, Andrey Akhmatkhanov, Vladimir Shur, and Sergey Kudryashov. 2023. "Dimensional Analysis of Double-Track Microstructures in a Lithium Niobate Crystal Induced by Ultrashort Laser Pulses" Photonics 10, no. 5: 582. https://doi.org/10.3390/photonics10050582
APA StyleGulina, Y., Zhu, J., Gorevoy, A., Kosobokov, M., Turygin, A., Lisjikh, B., Akhmatkhanov, A., Shur, V., & Kudryashov, S. (2023). Dimensional Analysis of Double-Track Microstructures in a Lithium Niobate Crystal Induced by Ultrashort Laser Pulses. Photonics, 10(5), 582. https://doi.org/10.3390/photonics10050582





